The coastal or sea-crossing bridges located in seismic regions are experiencing long-term chloride-induced corrosion in their life cycles and have a high risk of suffering from strong earthquakes. Thus, the fragilities of these bridges must be properly evaluated under the multiple hazards of corrosion and earthquake. Conventional fragility assessment requires expensive computational efforts despite extensive applications in previous research. To this end, this paper proposes a life-cycle fragility analysis framework based on the endurance time method to investigate the deterioration impact on the seismic fragility of bridges. An example sea-crossing cable-stayed bridge is utilized as a case study and modeled by OpenSees considering different service years. The life-cycle fragility curves of the example bridge are generated using the artificial endurance time series. Fragility analysis results show that the proposed method is capable of assessing the life-cycle seismic fragility of the bridge with high efficiency. The bearing shows a higher damage probability than the pylon and pier. As the service time increases, the structural deterioration has a marginal impact on the system fragility of the bridge, while the component fragility varies across different components. The structural deterioration results in beneficial effects on the pylon and the bearing at the pylon but exerts adverse effects on the pier and the bearing at the pier.

1 INTRODUCTION

With the increasing construction of transportation infrastructures, a large number of long-span sea-crossing bridges, such as the China East Sea Bridge, the Hangzhou Bay Bridge, the Pingtan Strait Rail-cum-road Bridge, and so forth, have been built in China. Bridges exposed to marine environments are vulnerable to chloride erosion in their service lives, thus leading to structural deterioration and reducing the sustainability of bridges.¹ Generally, chloride diffuses into the concrete and leads to the corrosion of steel rebar, further reducing the load-bearing capacity of the structure.² On the contrary, the sea-crossing bridges located in seismic regions may suffer from earthquakes in their life cycles. Consequently, the pristine seismic design for the bridges may not meet the expected requirements when the bridges deteriorate in a corrosive environment. In addition, the life-cycle contexts of bridges are not considered in current seismic design codes³; thus, the seismic performance of bridges may be overestimated during their lifetime. With the rapid development of bridge construction, the design service life of long-span cable-stayed bridges is prolonged and the life-cycle seismic damage of bridges has received widespread attention. Therefore, the seismic performance of sea-crossing cable-stayed bridges in their lifetime should be properly evaluated to ensure their durability and serviceability.

In the last two decades, a large number of bridge structures exposed to marine environments were observed to experience severe chloride-induced corrosion and performance degradation.¹ As such, extensive research has been performed to investigate the seismic performance and damage of deteriorating bridges.^4-9 For example, Choe et al.⁴ developed a new probabilistic model for the seismic demand of deteriorated reinforced concrete (RC) bridges by considering various uncertainties, and the model was applied to estimate the lifetime seismic fragility of a single-bent bridge. Ghosh et al.⁵ investigated the impact of service life on the seismic fragility of multispan continuous highway bridges exposed to deicing salt environments, and they concluded that the seismic vulnerability of bridges significantly increases throughout their life cycle. In the recent literature, Cui et al.¹⁰ proposed an improved steel bar corrosion model that considers pitting corrosion and a change of the after-cracking corrosion rate, and then the proposed model was used to assess the time-dependent seismic fragility of RC bridges. In addition, based on the fragility analysis method, Vishwanath and Banerjee,¹¹ Mortagi and Ghosh,¹² and Pang et al.¹³ estimated the life-cycle seismic resilience and economic loss of deteriorating bridges. The results demonstrated the importance of seismic fragility assessment in the life-cycle context.

The above-mentioned studies on the time-dependent seismic performance of corroded bridges indicated that the fragility analysis is a common methodology for assessing the safety of bridges under seismic hazards. However, expensive computational efforts are required to obtain the fragility curves of bridges during their lifetime if using conventional methods such as incremental dynamic analysis (IDA) or cloud analysis. To improve the computational efficiency of the structural dynamic analysis, the endurance time method (ETM) is applied to calculate the seismic response of structures by inputting predefined intensifying ground motions.¹⁴ Recently, ETM has been extensively used by contemporary researchers as an efficient technique for structural performance assessment under earthquake events. Guo et al.¹⁵ investigated the seismic behavior of a three-span highway bridge with the inclusion of pounding effects based on ETM and validated the sufficient accuracy compared to the IDA method. Tavazo et al.¹⁶ developed the fragility curves of an RC frame based on ETM and the IDA method, respectively, and found that the ETM-based fragility analysis framework could significantly reduce the computational cost. Additionally, Wei et al.¹⁷ evaluated the fragility of sea-crossing cable-stayed bridges under scour and earthquake hazards. The research results indicated that ETM could reduce the computational effort of fragility analysis with high accuracy. These studies demonstrate that ETM has greater potential for use in the fragility analysis of bridges than the IDA method; thus, the application of ETM for the vulnerability estimation of bridges under multiple-hazard scenarios remains to be further investigated.

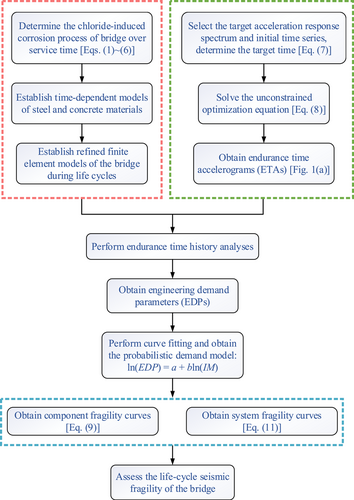
On the basis of the advantages of ETM in the seismic performance assessment of structures, this paper investigated the life-cycle seismic fragility of a sea-crossing cable-stayed bridge under corrosion environments. The chloride-induced corrosion process of RC was introduced at first. The methodology of endurance time analysis was then presented. Based on ETM, the seismic fragility analysis framework of bridges throughout the life cycle was proposed. The time-dependent numerical model of a sea-crossing cable-stayed bridge subjected to chloride corrosion was established. Soil–structure interactions (SSIs) and hydrodynamic effects for piles and pile caps were considered. Then, the time-dependent seismic fragility curves of the bridge were developed according to the ETM-based analysis framework. The impacts of the service time on the seismic fragility of the bridge component and system were comprehensively discussed.

2 ETM-BASED LIFE-CYCLE FRAGILITY ANALYSIS FRAMEWORK CONSIDERING CHLORIDE-INDUCED CORROSION

2.1 Performance degradation of RC members due to chloride-induced corrosion

In the marine environment, chloride-induced corrosion is considered as one of the main causes of performance deterioration of RC bridges. Hence, this paper focuses on corrosion resulting from chloride intrusion. It is widely recognized that the chloride diffusion phase could be modeled by Fick's second law,¹⁸ as shown in the following equation:

()

where C(x, t) is the chloride concentration at depth x from the concrete surface and time t, C_s is the chloride concentration on the concrete surface, D_c is the chloride diffusion coefficient, and erf(•) is the Gaussian error function that can be expressed by

()

It is common to assume that C(x, t) is equal to zero at x ≥ 0 when t = 0, and C(x, t) is equal to a constant value C_s at x = 0 when t > 0. With the chloride ions constantly penetrating into concrete, the passive protective film of steel rebars is destroyed. Then, the corrosion propagation phase is initiated when the chloride concentration on the surface of steel rebars reaches a critical value. Based on the above initial condition and boundary condition, the corrosion initiation time t_i can be calculated as follows:

()

where c is the concrete cover depth and C_cr is the critical chloride concentration.

Once the service time exceeds the corrosion initiation time, the corrosion propagation begins and the time-dependent characteristics of steel rebar can be calculated as follows^{19, 20}:

()

where d_s(t) is the residual diameter of steel rebars at the service time t; d_s0 is the initial diameter of steel rebars; i_corr is the corrosion current density; Q_corr(t) is the percentage of mass loss of steel rebars at time t; f_y(t) is the residual yield strength of steel rebars at time t; and f_y0 is the yield strength of uncorroded steel rebars.

Although some studies indicated that i_corr was time-varying and related to the corrosion pattern and zone,^{8, 10, 21} for simplicity, only the uniform corrosion of steel in the atmospheric zone is taken into account in this paper and the corrosion current density i_corr is assumed to be a constant. The deterioration parameters considered in the chloride-induced corrosion process are listed in Table 1.

Table 1. Deterioration parameters for the chloride-induced corrosion model

Parameter	D_c (mm²/a)	C_s (kg/m³)	C_r (kg/m³)	i_corr (μA/cm²)
Value	63.072	2.95	0.8	3

2.2 Generation of the endurance time acceleration function (ETAF)

ETAF is a generated intensifying ground motion in which the response spectrum at 0 ~ t_Target matches the target spectrum, and it is required that the acceleration response spectrum of ETAF at any time interval 0 ~ t_d should increase linearly with time. According to the literature,¹⁴ the acceleration response spectrum of theoretical ETAF at 0 ~ t_d is defined as follows:

()

where t_Target is the target duration time for scaling ETAF and S_aD(T) is the target spectrum. In this paper, the target duration time is set to 10 s according to the literature,¹⁴ and the design spectrum under E1 earthquakes is selected as the target spectrum referring to the seismic design code.³

To minimize the error between the response spectrum of ETAF and the target spectrum and satisfy Equation (7), an unconstrained optimization problem needs to be solved as follows¹⁴:

()

where ü_g is the target ETAF; S_a(T, t_d) is the acceleration response spectrum of ü_g; and T_max and t_max are the maximum periods considered in the optimization process and the time duration of ETAF, respectively.

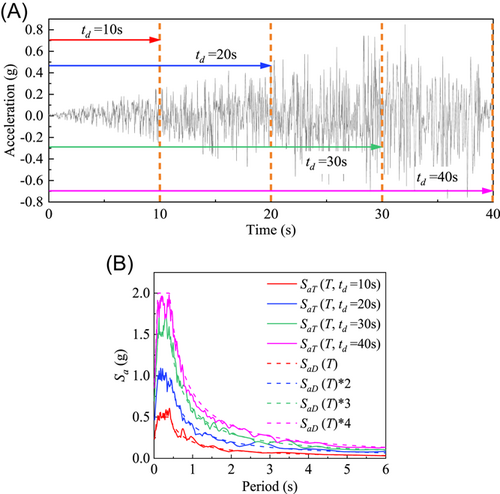
Based on Equations (7) and (8), four ETAFs are generated using the ETAG (Endurance Time Accelerogram Generator) programmed in MATLAB; herein, only the acceleration time series and response spectra of ETAF-1# are shown in Figure 1 for brevity. Figure 1 shows that the amplitude of ETAF-1# increases with the time duration, and the response spectra during different duration times are in good agreement with the corresponding target spectra.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Schematic diagram of endurance time–acceleration function-1#: (A) the time series and (B) acceleration response spectra

2.3 Component- and system-level fragility analysis based on ETM

Seismic fragility of structures describes the probability that the seismic demand exceeds the seismic capacity under a given earthquake intensity measure (IM). Generally, the seismic demand and structural capacity are assumed to follow lognormal distributions so that the fragility can be expressed as²²

()

where Φ(•) is the cumulative distribution function of a standard normal distribution; μ_d and μ_c are the medians of the seismic demand and structural capacity, respectively; and β_d and β_c are the dispersions of the seismic demand and structural capacity, respectively.

For the probabilistic seismic demand model, it can be expressed by the following linear regression equation in the logarithmic scale²³:

()

where a and b are regression parameters in the linear regression analysis.

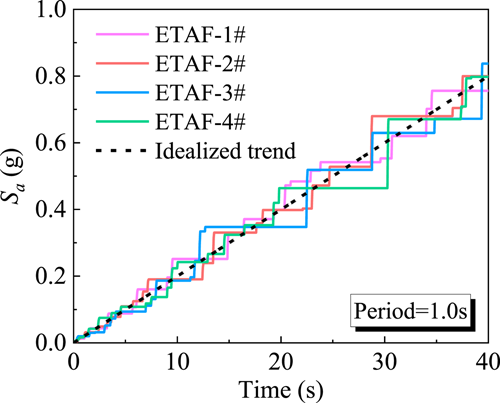
It is noteworthy that the calculation of seismic fragility also depends on IMs. Previous fragility research indicated that both the peak ground acceleration (PGA) and spectral acceleration (S_a) were used as IMs. However, the ETAF is synthesized based on the target response spectrum and the dispersion of the regression model is minor when S_a is used as IM. Also, Hariri-Ardebili et al.²⁴ suggested that S_a was more appropriate than PGA to be used as IM when estimating the seismic fragility of structures through ETM. Therefore, the spectral acceleration of ETAF with a structural period equaling 1.0 s is used as IM in this study. For the conventional fragility analysis (e.g., IDA method), the ground motion is usually scaled up and down to generate n seismic inputs with different intensities and obtain the structural demand through dynamic analyses. Thus, n time–history analyses are required to calculate the parameters of a probabilistic demand model. A larger value of n results in a more accurate probabilistic demand model. However, compared to the conventional method, the ETM-based method only requires one time–history analysis to obtain the demand model since the ETAF has continuously amplified intensities and thus the computational efficiency is improved by n times. Figure 2 shows the change in spectral acceleration (IM) of four generated ETAFs over time and shows good consistency with the idealized trend. By inputting the four ETAFs, the enveloped demand (EDP) of structures over time could be obtained. By combining IM and EDP, the probabilistic demand model can be acquired by the linear regression in Equation (10). According to the suggestions of HAZUS99,²⁵ the value of in Equation (9) can be taken as 0.4 when using S_a as IM. Furthermore, the structural capacity is affected by chloride intrusion; thus, the seismic capacity (μ_c) of structures is considered to change with service time in this study. By combining Equation (9) and (10), the seismic fragility of different bridge components based on ETM can be calculated.

To assess the overall seismic performance of the cable-stayed bridge, the system fragility of bridges should be estimated. Rigorously, the cable-stayed bridge is a hybrid system composed of serial and parallel components. However, the damage of any component may result in the failure of structural integrity. Hence, the cable-stayed bridge is considered as a serial system in this study, and the system fragility of the bridge can be evaluated in accordance with the first-order reliability theory²⁶:

()

where P_fi is the failure probability of the ith component; P_sys is the failure probability of the system; and n is the total number of components. In this study, the bearing, pylon, and pier are considered as the critical components to calculate the system fragility as they are vulnerable to earthquakes. Once the fragility of all components is determined according to Equation (9), the system fragility of the bridge can be computed using Equation (11). The lower bound in Equation (11) demonstrates that all the bridge components are completely related, while the upper bound indicates that the components are completely independent. The flowchart of life-cycle fragility analysis of the bridge based on ETM is shown in Figure 3.

3 NUMERICAL MODELING OF THE EXAMPLE BRIDGE DURING A LIFETIME

3.1 Description of the example cable-stayed bridge

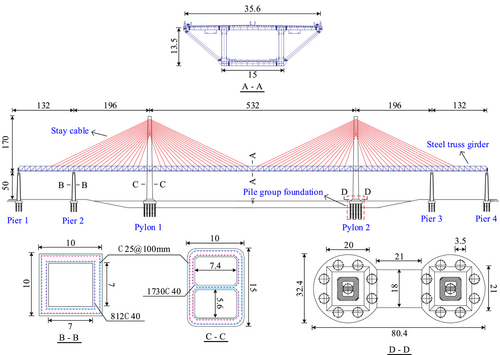
A double-pylon sea-crossing cable-stayed bridge is selected as the example bridge. The elevation view and cross-sections of the bridge are shown in Figure 4. The bridge has a length of 132 + 196 + 532 + 196 + 132 = 1188 m and consists of two RC pylons, four RC piers, a steel truss girder with a uniform cross-section, and double-plane cables with a semifan arrangement. The heights of the pylon and the pier are 220 and 50 m, respectively. The girder has a width of 35.6 m and a height of 13.5 m, respectively. The substructure of pylons is composed of a dumbbell-shaped pile cap with the dimension of 80.4 m × 32.4 m × 10 m and 18 piles with a diameter of 4.5 m and a length of 47 m. The upper 21 m of the pile group foundation is submerged in seawater and the residual part is embedded in the soil, whose effective weight is 30 kN/m³. The compressive strength of concrete for the pylon is 55 MPa, and the compressive strength of concrete for the pier and pile is 45 MPa. The cross-section and steel reinforcement arrangement for the pylon and pier are shown in Figure 4. The yield strengths of longitudinal reinforcements and stirrups are 400 and 335 MPa, respectively. The stay cables with a tensile strength of 1680 MPa are installed between the pylon and the bridge deck. The fixed bearing is installed between Pylon 1 and the girder, and the movable bearing in the longitudinal direction is installed on the piers and Pylon 2.

3.2 Finite element modeling

The finite element model of the example bridge is built using OpenSees software, as shown in Figure 5. The steel truss girder is modeled using elastic beam–column elements as it is expected to remain elastic during earthquakes. Nonlinear beam–column elements are used to capture the inelastic behavior of the pylon, pier, and pile foundations. The concrete model is established using Concrete01 material in OpenSees and the stress–strain relationship of steel bars is modeled using Steel02 material. The zero-length element is used to model the movable bearing in the longitudinal direction. The constitutive laws of concrete, steel bar, and bearing are shown in Figure 5. The initial strain material (InitStrainMaterial) and truss element are used to simulate the steel cables with the initial strain. For the pile group foundation of pylons located in seawater and soil, the SSI effect is simulated using p–y spring models according to the formulae suggested by API,²⁷ and the added mass is calculated using the Morison equation and potential flow theory to consider the hydrodynamic effect.²⁸ The pile cap is generally assumed to be a rigid body under seismic excitations; thus, it is modeled by the lumped mass and connects the piles with rigid links. Because the piers are located on the rocky site, the piles for the piers are neglected and fixed constraints are used to the base of the piers in this study.

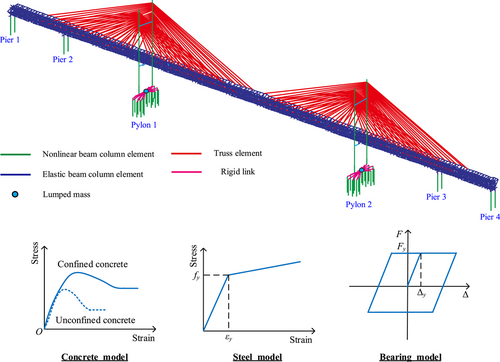
3.3 Time-dependent characteristic of structural deterioration

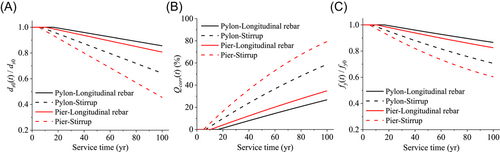
Once the corrosion initiation time t_i is determined, the time-dependent characteristics of steel bars can be obtained by combining Equations (4)–(6). It should be noted that only the corrosion of the pylon and pier is considered in this paper. The corrosion effects on the bearing and cables are not considered as they are maintained annually and replaced almost every 10 years. The truss beams and cables are not discussed in this paper since they usually remain elastic and undamaged during earthquakes.²⁹ Figure 6 shows the time-dependent properties of longitudinal steel rebars and stirrups for the pylon and pier. As shown in Figure 6, the diameter and yield strength of steel rebars remain constant in the first few years as corrosion is not initiated. With the accumulation of chloride ions, the steel surface starts to rust and the net cross-sectional area of the steel rebar decreases over service time, thus resulting in an increase in the corrosion ratio and reduction in the yield strength. Additionally, the steel rebar for the pier shows a faster corrosion rate than that for the pylon because the pier has a smaller cover depth. Similarly, the stirrup corrodes faster than the longitudinal rebar whether for the pylon or for the pier.

With increasing service time, corrosion of stirrups can lead to a reduction in concrete confinement and degradation in structural capacity. Therefore, the deterioration of confined concrete is considered based on Mander's model³⁰ in this paper. Note that, for the unconfined concrete, the deterioration effect is neglected since it has marginal impacts on the seismic performance of bridges.

Different bridge components may suffer various extents of damage under seismic loadings. Hence, the structural capacity, namely, μ_c in Equation (9) can take on various damage limit values to calculate the seismic fragility of components under different damage states. In this paper, the values of μ_c for pylons, piers, and bearings are determined on the basis of the damage indexes suggested by Choi et al.²⁶ The damage indexes for different components are divided into four damage states, that is, slight, moderate, extensive, and complete. Table 2 summarizes the four damage states and the values of damage indexes for the pylon, pier, and bearing.

Table 2. Damage states for different components of the cable-stayed bridge

Component	Damage index	Unit	Damage state
Component	Damage index	Unit	Slight	Moderate	Extensive	Complete
Pylon and Pier	Curvature ductility (μ_ϕ)	-	1 < μ_ϕ < 2	2 < μ_ϕ < 4	4 < μ_ϕ < 7	μ_ϕ > 7
Bearing	Displacement (Δ)	mm	50 < Δ < 100	100 < Δ < 150	150 < Δ < 255	Δ > 255

4 LIFETIME SEISMIC FRAGILITY ASSESSMENT OF THE EXAMPLE BRIDGE

4.1 Component fragility curves of the bridge in a lifetime

The ETM-based fragility analysis framework proposed in Section 2 is used to develop the fragility curves of bridge components at different service years. In this study, the pristine state and five service years equaling 20, 40, 60, 80, and 100 years are considered to investigate the time-dependent seismic fragility of the bridge in a lifetime. Only the fragility of the example bridge along the longitudinal direction is discussed because the bridge is more vulnerable to earthquakes in the longitudinal direction than in the transverse direction.

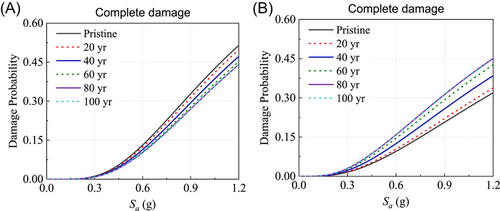
Figure 7 shows the life-cycle fragility of the bearings for the pylon and the pier under complete damage states. For brevity, the fragility curves under other damage states are not shown herein. As shown in Figure 7, for the same service time, the bearing at the pylon is more vulnerable than that at the pier under strong ground motions. For example, at the pristine state (i.e., service time = 0 year) and S_a = 1.0 g, the damage probability of the bearing at the pylon is 39.4%, which is higher than that of the bearing at the pier (24.5%). On the contrary, with increasing service years, the damage probability of the bearing at the pylon decreases, while the damage probability of the bearing at the pier increases. Taking S_a = 0.8 g as an example, the damage probability of the bearing at 100 years for the pylon and the pier changed by around −19% (drop) and 55.2% (rise), respectively, compared to the pristine state. Note that the change is amplified with increasing S_a. It can be seen that the structural deterioration has beneficial and adverse effects on the bearing fragility for the pylon and the pier, respectively. This phenomenon may result from the difference in the corrosion level between the pylon and the pier.

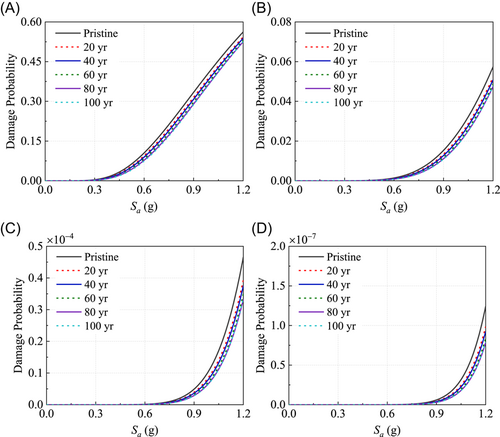
The time-dependent fragility curves for the pylon and the pier under different damage states are shown in Figures 8 and 9, respectively. It can be observed that the pier is more fragile than the pylon under earthquakes because of the higher damage probability. At the pristine state, the maximum probability of slight damage for the pylon is about 56.2%, while that for the pier is about 92%. Figure 8 shows that the pylon tends to show slight or moderate damage in the range of earthquake intensities considered in this study. This is because it has quite low damage probabilities under the extensive and complete damage states. Similarly, Figure 9 shows that the pier hardly suffers complete damage due to the low damage probability (below 0.05%). Moreover, the fragility curves of the pylon in Figure 8 demonstrate that the damage probability decreases marginally before 40 year over the service time, but remains almost unchanged after that. On the contrary, as shown in Figure 9, the fragility of the pier increases over service time. For example, at S_a = 0.6 g, the probability of the pier developing slight and moderate damage increases by around 11.7% and 57.7% in a lifetime (from the pristine state to 100 years), respectively.

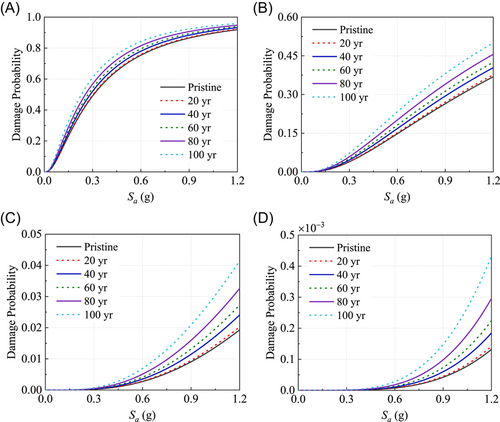
Overall, the impacts of chloride-induced corrosion on the component fragility of the bridge vary with components. For the pylon and the bearing at the pylon, structural deterioration or an increase of service time can reduce the seismic vulnerability with a small amplitude. However, for the pier and the bearing at the pier, the fragility increases under the life-cycle deterioration effect. The main reason is that the concrete cover of the pier is thinner than the concrete cover of the pylon. Consequently, the pier is more vulnerable to corrosion effects than the pylon during a lifetime. The pier shows a higher corrosion level than the pylon at the same service time. Due to the discrepancy in the corrosion level between the pier and the pylon, the structural dynamic properties are changed and the vibration mode shape participation of the overall bridge is redistributed. Under the seismic excitations, more seismic energy is transferred from the pylon to the pier.

4.2 System fragility curves of the bridge in lifetime

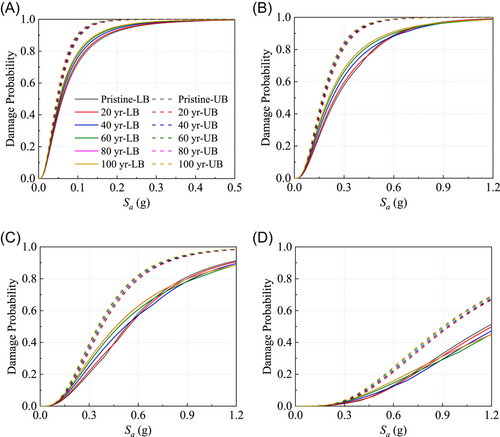
The system fragility curves of the example bridge during a lifetime are plotted in Figure 10. As shown, the damage probability of the bridge system is higher than the damage probability of any component. The actual system fragility of the bridge is between the lower bound (LB) and the upper bound (UB). It can be seen that the upper bounds of system damage probability at different service times are almost identical or show a very slight increase, whereas the lower bounds show some differences depending on the damage states and S_a. For the slight damage state of the bridge system, it is clear that the upper bound increases with the service time in a small range of earthquake intensity. However, the lower bounds under moderate, extensive, and complete damage states vary with the change of S_a. With S_a below 0.4 g, the lower bound shows a similar change to the upper bound, which shows a slight increase over the service time. As S_a increases, the lower bound tends to decrease with the service time. This change is due to the fact that the lower bound is related to the maximum damage probability of components according to Equation (11). Under minor earthquakes, the bearing fragility for the pier dominates the system fragility due to the higher damage probability. Thus, the system fragility increases with the service time, which is consistent with the time-dependent law of the bearing fragility for the pier. With increasing earthquake intensity, the bearing fragility for the pylon may exceed that for the pier and affect the system fragility of the bridge. Therefore, the time-dependent law of system fragility is compatible with the bearing fragility at the pylon. In general, structural deterioration has little effect on the system fragility of the example bridge, while the influence of deterioration on the component fragility cannot be neglected during the life cycle.

5 CONCLUSIONS

This paper presents an efficient fragility analysis framework based on ETM to assess the life-cycle fragility of bridges under chloride-induced corrosion. An example sea-crossing cable-stayed bridge is modeled using OpenSees with the consideration of structural deterioration over time, SSI, and hydrodynamic added mass. The endurance time–history analyses are performed to calculate the component and system fragility of the example bridge. The life-cycle fragility curves of the bridge are developed and the impacts of service time on the component and system fragility of the bridge are discussed. The main conclusions can be drawn as follows:

The proposed ETM-based fragility analysis approach can be used to efficiently compute the fragility of the bridge through only several dynamic analyses. The comparison of fragility for different bridge components indicates that the bearing is more vulnerable than the pylon and the pier under earthquakes due to its higher damage probability. Within the range of considered earthquake intensities in this study, the damages of the pylon and pier area in the almost below moderate and extensive damage states, respectively.

The influence of structural deterioration on the component-level fragility of the bridge varies with the components. As the service time increases, the deterioration effect increases the fragility of the pier while decreasing the fragility of the pylon, which is identical to the time-dependent fragility law of the bearing at the pier and the pylon, respectively. Due to the larger corrosion level, the pier is more vulnerable than the pylon under earthquakes and the structural deterioration tends to transfer the damage from the pylon to the pier.

With increasing service years, chloride-induced corrosion has little impact on the system-level fragility of the bridge. However, the structural deterioration may exert negative effects on the bearing at the pier and the pier. The component fragility of the example bridge during a lifetime may be underestimated without consideration of the deterioration effects.

In summary, the ETM-based fragility analysis framework proposed in this paper is capable of rationally assessing the life-cycle seismic fragility of sea-crossing cable-stayed bridges. In the meantime, the computational efficiency of the fragility analysis is improved as well. The proposed methodology provides an efficient tool for the seismic fragility analysis of bridges during life cycles. In addition, this method can be extended to the seismic performance assessments of other engineering structures exposed to corrosion environments.

ACKNOWLEDGMENTS

The authors would like to acknowledge the financial support of the National Natural Science Foundation of China (Grant No. 51978578) and the Scientific Research Fund (No. ASFL-21-001) of the Key Laboratory of Seismic Engineering Technology in Sichuan.

CONFLICTS OF INTEREST

The authors declare no conflicts of interest.

REFERENCES

1Herrmann AW. ASCE 2013 report card for America's infrastructure[C]//IABSE Symposium report. Int Assoc Bridge Struct Eng. 2013; 99(33): 9-10.
Google Scholar
2Andisheh K, Scott A, Palermo A. Effects of corrosion on stress–strain behavior of confined concrete. J Struct Eng. 2021; 147(7):04021087.
10.1061/(ASCE)ST.1943-541X.0003005
Web of Science® Google Scholar
3 JTG/T. Specifications for Seismic Design of Highway Bridges. Communications Press; 2020 [In Chinese].
Google Scholar
4Choe DE, Gardoni P, Rosowsky D, Haukaas T. Seismic fragility estimates for reinforced concrete bridges subject to corrosion. Struct Saf. 2009; 31(4): 275-283.
10.1016/j.strusafe.2008.10.001
Web of Science® Google Scholar
5Ghosh J, Padgett JE. Aging considerations in the development of time-dependent seismic fragility curves. J Struct Eng. 2010; 136(12): 1497-1511.
10.1061/(ASCE)ST.1943-541X.0000260
Web of Science® Google Scholar
6Simon J, Bracci JM, Gardoni P. Seismic response and fragility of deteriorated reinforced concrete bridges. J Struct Eng. 2010; 136(10): 1273-1281.
10.1061/(ASCE)ST.1943-541X.0000220
Web of Science® Google Scholar
7Alipour A, Shafei B, Shinozuka M. Performance evaluation of deteriorating highway bridges located in high seismic areas. J Bridge Eng. 2011; 16(5): 597-611.
10.1061/(ASCE)BE.1943-5592.0000197
Web of Science® Google Scholar
8Guo Y, Trejo D, Yim S. New model for estimating the time-variant seismic performance of corroding RC bridge columns. J Struct Eng. 2015; 141(6):04014158.
10.1061/(ASCE)ST.1943-541X.0001145
Web of Science® Google Scholar
9Thanapol Y, Akiyama M, Frangopol DM. Updating the seismic reliability of existing RC structures in a marine environment by incorporating the spatial steel corrosion distribution: application to bridge piers. J Bridge Eng. 2016; 21(7):04016031.
10.1061/(ASCE)BE.1943-5592.0000889
Web of Science® Google Scholar
10Cui F, Zhang H, Ghosn M, Xu Y. Seismic fragility analysis of deteriorating RC bridge substructures subject to marine chloride-induced corrosion. Eng Struct. 2018; 155: 61-72.
10.1016/j.engstruct.2017.10.067
Web of Science® Google Scholar
11Vishwanath BS, Banerjee S. Life-cycle resilience of aging bridges under earthquakes. J Bridge Eng. 2019; 24(11):04019106.
10.1061/(ASCE)BE.1943-5592.0001491
Web of Science® Google Scholar
12Mortagi M, Ghosh J. Consideration of climate change effects on the seismic life-cycle cost analysis of deteriorating highway bridges. J Bridge Eng. 2022; 27(2):04021103.
10.1061/(ASCE)BE.1943-5592.0001815
Web of Science® Google Scholar
13Pang Y, Wei K, Yuan W. Life-cycle seismic resilience assessment of highway bridges with fiber-reinforced concrete piers in the corrosive environment. Eng Struct. 2020; 222:111120.
10.1016/j.engstruct.2020.111120
Web of Science® Google Scholar
14Estekanchi HE, Riahi HT, Vafai A. Application of endurance time method in seismic assessment of steel frames. Eng Struct. 2011; 33(9): 2535-2546.
10.1016/j.engstruct.2011.04.025
Web of Science® Google Scholar
15Guo A, Shen Y, Bai J, Li H. Application of the endurance time method to the seismic analysis and evaluation of highway bridges considering pounding effects. Eng Struct. 2017; 131: 220-230.
10.1016/j.engstruct.2016.11.009
Web of Science® Google Scholar
16Tavazo HA, Ranjbaran A. Fragility analysis of 3D reinforced concrete frames based on endurance time method with derived standard deviation. J Earthq Tsunami. 2017; 11(04):1750011.
10.1142/S1793431117500117
Web of Science® Google Scholar
17Wei K, He H, Zhang J, Yang C, Qin S. An endurance time method-based fragility analysis framework for cable-stayed bridge systems under scour and earthquake. Ocean Eng. 2021; 232:109128.
10.1016/j.oceaneng.2021.109128
Web of Science® Google Scholar
18Stewart MG, Rosowsky DV. Structural safety and serviceability of concrete bridges subject to corrosion. J Infrastruct Syst. 1998; 4(4): 146-155.
10.1061/(ASCE)1076-0342(1998)4:4(146)
Google Scholar
19Andrade C, Alonso C, Molina FJ. Cover cracking as a function of bar corrosion: part I—experimental test. Mater Struct. 1993; 26(8): 453-464.
10.1007/BF02472805
CAS Web of Science® Google Scholar
20Du YG, Clark LA, Chan AHC. Residual capacity of corroded reinforcing bars. Mag Concr Res. 2005; 57(3): 135-147.
10.1680/macr.2005.57.3.135
CAS Web of Science® Google Scholar
21Stewart MG, Al-Harthy A. Pitting corrosion and structural reliability of corroding RC structures: experimental data and probabilistic analysis. Reliab Eng Syst Saf. 2008; 93(3): 373-382.
10.1016/j.ress.2006.12.013
Web of Science® Google Scholar
22Nielson BG, DesRoches R. Seismic fragility methodology for highway bridges using a component level approach. Earthq Eng Struct Dyn. 2007; 36(6): 823-839.
10.1002/eqe.655
Web of Science® Google Scholar
23Cornell CA, Jalayer F, Hamburger RO, Foutch DA. Probabilistic basis for 2000 SAC federal emergency management agency steel moment frame guidelines. J Struct Eng. 2002; 128(4): 526-533.
10.1061/(ASCE)0733-9445(2002)128:4(526)
Web of Science® Google Scholar
24Hariri-Ardebili MA, Sattar S, Estekanchi HE. Performance-based seismic assessment of steel frames using endurance time analysis. Eng Struct. 2014; 69: 216-234.
10.1016/j.engstruct.2014.03.019
Web of Science® Google Scholar
25 FEMA. Multi-Hazard Loss Estimation Methodology: Earthquake Model. Department of Homeland Security; 2003: 235-260.
Google Scholar
26Choi E, DesRoches R, Nielson B. Seismic fragility of typical bridges in moderate seismic zones. Eng Struct. 2004; 26(2): 187-199.
10.1016/j.engstruct.2003.09.006
Web of Science® Google Scholar
27 API. Recommended Practice for Planning, Designing, and Constructing Fixed Offshore Platforms-Working Stress Design: Upstream Segment. API Recommended Practice 2A-WSD (RP 2A-WSD): Errata and Supplement 1, December 2002. American Petroleum Institute; 2000.
Google Scholar
28Zhang J, Wei K, Pang Y, Zhang M, Qin S. Numerical investigation into hydrodynamic effects on the seismic response of complex hollow bridge pier submerged in reservoir: case study. J Bridge Eng. 2019; 24(2):05018016.
10.1061/(ASCE)BE.1943-5592.0001340
Web of Science® Google Scholar
29Yi J, Li J. Experimental and numerical study on seismic response of inclined tower legs of cable-stayed bridges during earthquakes. Eng Struct. 2019; 183: 180-194.
10.1016/j.engstruct.2018.12.081
Web of Science® Google Scholar
30Mander JB, Priestley MJN, Park R. Theoretical stress-strain model for confined concrete. J Struct Eng. 1988; 114(8): 1804-1826.
10.1061/(ASCE)0733-9445(1988)114:8(1804)
Web of Science® Google Scholar

Citing Literature

Volume1, Issue1

March 2022

Pages 60-72

This article also appears in:

Resilience of Cities and Infrastructures

Life-cycle seismic fragility of a cable-stayed bridge considering chloride-induced corrosion

Abstract

1 INTRODUCTION

2 ETM-BASED LIFE-CYCLE FRAGILITY ANALYSIS FRAMEWORK CONSIDERING CHLORIDE-INDUCED CORROSION

2.1 Performance degradation of RC members due to chloride-induced corrosion

2.2 Generation of the endurance time acceleration function (ETAF)

2.3 Component- and system-level fragility analysis based on ETM

3 NUMERICAL MODELING OF THE EXAMPLE BRIDGE DURING A LIFETIME

3.1 Description of the example cable-stayed bridge

3.2 Finite element modeling

3.3 Time-dependent characteristic of structural deterioration

4 LIFETIME SEISMIC FRAGILITY ASSESSMENT OF THE EXAMPLE BRIDGE

4.1 Component fragility curves of the bridge in a lifetime

4.2 System fragility curves of the bridge in lifetime

5 CONCLUSIONS

ACKNOWLEDGMENTS

CONFLICTS OF INTEREST

REFERENCES

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Life-cycle seismic fragility of a cable-stayed bridge considering chloride-induced corrosion

Abstract

1 INTRODUCTION

2 ETM-BASED LIFE-CYCLE FRAGILITY ANALYSIS FRAMEWORK CONSIDERING CHLORIDE-INDUCED CORROSION

2.1 Performance degradation of RC members due to chloride-induced corrosion

2.2 Generation of the endurance time acceleration function (ETAF)

2.3 Component- and system-level fragility analysis based on ETM

3 NUMERICAL MODELING OF THE EXAMPLE BRIDGE DURING A LIFETIME

3.1 Description of the example cable-stayed bridge

3.2 Finite element modeling

3.3 Time-dependent characteristic of structural deterioration

4 LIFETIME SEISMIC FRAGILITY ASSESSMENT OF THE EXAMPLE BRIDGE

4.1 Component fragility curves of the bridge in a lifetime

4.2 System fragility curves of the bridge in lifetime

5 CONCLUSIONS

ACKNOWLEDGMENTS

CONFLICTS OF INTEREST

REFERENCES

Citing Literature

Figures

References

Related

Information