RESEARCH ARTICLE

Open Access

Time-dependent seismic resilience of aging repairable structures considering multiple damage states

Corresponding Author

Cao Wang

[email protected]

School of Civil, Mining and Environmental Engineering, Faculty of Engineering and Information Sciences, University of Wollongong, Wollongong, New South Wales, Australia

Correspondence Cao Wang, School of Civil, Mining and Environmental Engineering, Faculty of Engineering and Information Sciences, University of Wollongong, Wollongong, Room 132, Bldg 4, NSW 2522, Australia.

Email: [email protected]

Search for more papers by this author

Bilal M. Ayyub,

Bilal M. Ayyub

Department of Civil and Environmental Engineering, Center for Technology and Systems Management, University of Maryland, College Park, Maryland, USA

Search for more papers by this author

Cao Wang,

Corresponding Author

Cao Wang

[email protected]

School of Civil, Mining and Environmental Engineering, Faculty of Engineering and Information Sciences, University of Wollongong, Wollongong, New South Wales, Australia

Email: [email protected]

Search for more papers by this author

Bilal M. Ayyub,

Bilal M. Ayyub

Department of Civil and Environmental Engineering, Center for Technology and Systems Management, University of Maryland, College Park, Maryland, USA

Search for more papers by this author

First published: 18 April 2022

https://doi.org/10.1002/eer2.5

Citations: 5

Share a link

Email
Wechat
Bluesky

Abstract

Earthquakes are among the natural hazards threatening the serviceafbility, functionality, and safety of engineering structures significantly. Posthazard structures may suffer from different damage states and correspondingly different functionality losses/recovery processes in the aftermath of hazardous events. This paper proposes a measure for structural time-dependent seismic resilience considering multiple damage states. Its specific case (i.e., considering damage–no damage scenario) reduces to the existing resilience measure in the literature. The time-variant fragility curves and the generalized seismic capacities are used to determine the damage states conditional on the peak ground motion (PGA). The proposed measure is applicable for both of the following two cases: (1) the earthquake occurrence rate and the magnitude of PGA conditional on earthquake occurrence are known; (2) the probability distribution of annual maximum PGA is known. In terms of the latter, the annual seismic hazard function can be used to describe the seismic load uncertainty. A numerical example is presented to demonstrate the applicability of the proposed resilience measure. It is shown that the proposed measure can be used to quantitatively guide structural design to meet the target resilience level.

1 INTRODUCTION

Earthquakes are responsible for a significant portion of natural hazard-induced damages to civil structures and infrastructures around the world. According to a report by the Federal Emergency Management Agency (FEMA)¹ in 2017, earthquakes cost the United States approximately $6.1 billion annually in the national building stock. In China, the annual direct economic loss due to earthquakes is about 24.6 billion CNY² for the period of 2009–2019. Apart from the seismic hazards, in-service structures also suffer from performance (e.g., stiffness, strength) deterioration due to environmental attacks such as spalling of reinforced concrete members, and corrosion of steel reinforcement.^3-7 For example, the 2021 Report Card for America's Infrastructure, released by the American Society of Civil Engineers (https://infrastructurereportcard.org/), showed that 42% of all the bridges in the United States are at least 50 years old, and about 7.5% of them are structurally deficient (i.e., in “poor” condition). While the deterioration of structural performance does not necessarily mean an immediate failure, the structure becomes increasingly more susceptible to hazardous events with time. In practice, due to the constraints of available resources, it is not practically and economically implementable to maintain the performances of all in-service structures as good as new. Instead, reliability and resilience assessment is a powerful tool to quantitatively measure the structural ability to fulfill service requirements, based on which planners and decision-makers can optimize the maintenance strategies and allocate limited resources wisely. Structural reliability is defined as the probability of survival (withstanding external load effects),^8-10 while resilience is indicative of structural ability in terms of preparing for and adapting to hazardous events and recovering rapidly from the disruptions.^11-15

Among the early attempts to derive a closed-form solution for time-dependent reliability is the work by Mori and Ellingwood,⁸ which considered the impacts of structural resistance deterioration and the randomness associated with the load process. For a reference period of

, modeling the load occurrence as a stationary Poisson process, the time-dependent reliability,

, is computed by⁸

()

in which

is the occurrence rate of loads,

is the cumulative distribution function (CDF) of load effect conditional on occurrence, and

is the structural resistance at time

. The reliability method in Equation (1) was later adopted in the International Standard Bases for design of structures—Assessment of existing structures.¹⁶ An improved version of Equation (1) was proposed by Li et al.,⁹ where the nonstationarity associated with the load process (in terms of both the occurrence rate and magnitude) can be taken into account. However, in the presence of seismic loads, Equation (1) would be typically sufficient since a stationary Poisson process cannot be rejected statistically for modeling the earthquake occurrence.^{17, 18} One may refer to Wang et al.¹⁹ for a review of assessment methods for structural time-dependent reliability.

The concept of structural resilience can be treated as an extension of structural reliability;²⁰ it considers not only the probability of failure but also the posthazard recovery process. Key components to be included in a quantitative resilience measure are known as four R's^{21, 22}: (1) Robustness, measuring structural ability to withstand hazardous events without suffering from significant functionality loss; (2) Redundancy, represented by whether the structure remains functional in the aftermath of a disruptive event; (3) Resourcefulness, indicating the ability to diagnose and prioritizing problems and initiating solutions based on the available resources; (4) Rapidity, reflecting the rate of restoring functionality. Bruneau et al.²³ proposed an index to measure resilience loss, taking the form of

, in which

is the performance/quality of a structure (varying within

is the occurrence time of a hazardous event, and

is the time of full recovery. A normalized, dimensionless version of this resilience measure was later proposed by Attoh-Okine et al.²⁴ However, the randomness associated with the hazard occurrence time and the probability of functionality loss conditional upon load occurrence were not incorporated in both works.^{23, 24} Ayyub¹³ proposed a measure for structural resilience, taking into account the time-variation (degradation) of the functionality

due to aging effects and using a homogeneous Poisson process to describe the load occurrence process. If a load event occurs at time

, causing structural failure (

) at time

and subsequently a recovery process (

) until time

, the resilience measure is a function of

, as well as the failure profile

and the recovery profile

. The randomness associated with

is represented by its CDF,

, being equal to

, in which

is as in Equation (1). Although the resilience measure by Ayyub¹³ is more advantageous due to its capacity of considering additional aspects of resilience (the failure profile

is a measure of robustness and redundancy, while the recovery profile

measures resourcefulness and rapidity), it takes a relatively complicated form, which could halter its application in engineering practice. Wang and Ayyub²⁰ proposed a measure for structural time-dependent resilience for a time horizon of

, as a generalized form of that by Ayyub,²⁵ which can account for the non-stationarity associated with the load process and performance deterioration. Within

, if the load process is stationary, the structural time-dependent resilience, denoted by

, is as follows²⁰:

()

where

is the resilience measure associated with a single failure-causing event occurring at time

is the mean value of the variable in the brackets, and the remaining variables are the same as those in Equation (1). In Equation (2), if the load occurrence rate is time-variant, denoted by

, one can simply replace the item

with

, accounting for the nonstationarity in frequency associated with general load types. This paper will focus on structural seismic resilience. Note that a postearthquake structure may suffer from different damage states and correspondingly different values of

. However, the resilience measure in Equation (2) has only considered one (ultimate) limit state, and thus cannot account for the multiple posthazard damage states.

This paper presents a measure for time-dependent seismic resilience of aging structures that incorporates different postearthquake damage states. The focus is on the resilience of repairable structures, that is, the structural functionality, if being reduced due to earthquake load, can be restored via some repair measures to the prehazard state or some other state to account for adaptability. It is shown that the proposed measure is a generalized form of Equation (2). A numerical example is presented to demonstrate the applicability of the proposed resilience measure.

2 STRUCTURAL SEISMIC PERFORMANCE

2.1 Seismic fragility curve

Seismic fragility curves are representative of the probability of structural damage conditional on the occurrence of one earthquake event.^26-29 The seismic fragility, by definition, is expressed as follows:

()

in which

denotes the probability of damage,

denotes the probability of the event in the brackets,

is the seismic capacity,

is the demand, and

is the intensity measure (e.g., peak ground acceleration [PGA]). Cornell et al.²⁶ assumed that the capacity

follows a lognormal distribution with a median value of

and a dispersion of

, while the demand

is determined by

, in which

is the annual maximum intensity measure,

and

are two constants to be calibrated through regression analysis. Modeling

, conditional on

, as a lognormal variable with a median value of

and a dispersion of

, it follows that, for an arbitrary

()

and

()

with which

()

The generalized seismic capacity, denoted by

, has been used in several studies,^30-33 which integrates the characteristics of both

and

. The CDF of

is exactly the fragility curve with respect to the intensity measure, and the following relationship holds:

()

Observing Equation (6), it is found that follows a lognormal distribution with a median value of and dispersion of . In Equation (3), the intensity measure of PGA has been widely used in seismic fragility analysis due to its simplicity,^34-37 although some other measures could behave better in some specific cases.^{38, 39} In this paper, the fragility curves with respect to PGA will be considered only, in an attempt that the developed resilience measure can be conveniently adopted by the engineering practice.

If taking into account the impact of structural deterioration, the seismic fragility curve would be time-variant.^{28, 29, 40, 41} For example, in the presence of corrosion-induced degradation, the corrosion propagation is often represented by the metal loss of reinforced bars.^{42, 43} With the reduction of the cross-sectional area of reinforced bars, as well as the deteriorated concrete-reinforcement bond, the structural performance (e.g., bending moment) deterioration can be further calculated, which plays an important role in the estimation of time-variant seismic fragility curves. Other deterioration mechanisms, such as sulfate attack and diffusion-controlled aging,^{8, 44} may also be dominant, depending on the service environment of the structure. In this context, Equation (7) would be rewritten as to reflect its time-variant characteristics, where denotes time. The notation of , representing the evolution of the fragility curve on the temporal scale, will be used in the derivation of the resilience measure in Section 3.

2.2 Resilience associated with a single earthquake event

In the aftermath of an earthquake event, structures suffer from a specific damage state, followed by a recovery process. The resilience measure by Attoh-Okine et al.²⁴ can be used to estimate the structural resilience associated with a single earthquake event (with a known occurrence time). The structural resilience would be dependent on the earthquake-induced functionality loss, as well as the recovery path. Some common damage modes (e.g., brittle, ductile, graceful) and recovery strategies (e.g., expeditiously as good as new, as good as old, and others) were discussed by Ayyub.¹³ The impact of functionality deterioration (a gradual process due to aging effects) on structural resilience should also be taken into account. Wang and Ayyub²⁰ derived a closed-form solution for the mean value of resilience measure associated with a single event occurring at time

(see

in Equation 2), considering a linear functionality deterioration process

, a linear recovery process, and an as-good-as-old repair strategy. Let

be the deterioration rate of structural functionality (i.e.,

), and

the ratio of functionality loss (a time-variant variable). Assume that

follows an exponential distribution, and the recovery rate is uniformly distributed within

. With this, it follows that²⁰:

()

where

()

In Equation (9), is the exponential integral function, defined as . For more general cases (with other distribution types of , recovery strategies, etc.), an explicit form of is not necessarily available; in such a case, one may use a fitting-based approach to approximate the expression for . The resilience associated with a single earthquake event will be incorporated in the estimation of structural time-dependent resilience, as shown in Section 3.

3 PROPOSED RESILIENCE MEASURE CONSIDERING MULTIPLE DAMAGE STATES

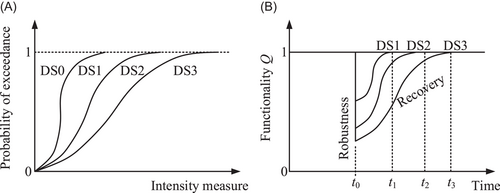
For a posthazard structure, its functionality loss and the subsequent recovery process would be dependent on the specific damage state. In a probabilistic manner, the damage states can be determined through the use of fragility curves. Figure 1A shows an example of three fragility curves and the associated four damage states (DS0 through to DS3, where DS0 refers to “no damage”). The damage state-dependent recovery processes are illustrated in Figure 1B.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Illustration of (A) seismic fragility curves and (B) recovery processes associated with different damage states

For a service period of

, a Poisson process is used to model the occurrence of earthquake events. Let

be the occurrence rate, and

is the number of earthquake events within

. The probability mass function (PMF) of

is,

()

In this paper, totally

damage states (referred to as the 0th, 1st, …,

th) will be considered, with the 0th being “no damage.” For the

th (

) event and the

th (

) damage state, a Bernoulli random variable

is introduced, which equals 1 if the structure suffers from the

th damage state due to the

th earthquake event, and 0 otherwise. Let

be the probability of

, where

is the occurrence time of the

th earthquake event. Clearly, it follows that

. For the totally

fragility curves, the corresponding generalized seismic capacities are denoted by

, respectively at time

. Assume that

has a median value of

and a dispersion of

, with which the probability distribution function (PDF) of

()

For the purpose of further derivation, an additional capacity

is introduced, which has a median value of

so that

. With this, it follows that

()

in which

denotes PGA,

is the CDF of

, and

is the PDF of

for

(see Equation 11). Using the law of total probability,¹⁰ one has

()

in which

is the resilience measure due to the

th earthquake event occurring at time

(the subscript unc means that

is unconditional on any specific damage state), and

is the resilience measure associated with the

th damage state and the

th earthquake event occurring at time

. It is straightforward to see that

Based on the resilience models proposed by Ayyub²⁵ and Wang and Ayyub,²⁰ the resilience measure for a reference period of

, is defined by

()

Assume that each

is statistically independent mutually. Using the law of total expectation,¹⁰ one has

()

Taking into account the PMF of

in Equation (10), Equation (15) becomes,

()

Furthermore, substituting Equation (13) into Equation (16) yields

()

Equation (17) is the proposed measure for structural time-dependent seismic resilience, which takes into account the multiple damage states and the associated resilience measures . Based on Equation (17), the seismic nonresilience, denoted by , is simply equal to .

Note that Equation (17) has been derived based on the information of earthquake occurrence rate and the probability distribution of PGA associated with each earthquake event (see

). Next, an equivalent form of Equation (17) will be derived, considering the case where the CDF of annual maximum PGA is available, denoted by

. To this end, the relationship between

and

is firstly discussed. Using the law of total probability, it follows that:

()

where

is the earthquake occurrence rate, having a unit of “/year.” Using an Extreme Type II distribution to model the annual maximum PGA,^{10, 45} it follows that:

()

where

is scale parameter and

is shape parameter. Thus,

()

Substituting Equation (20) into Equation (12) yields

()

Furthermore, note that

()

Define

()

with which Equation (17) becomes

()

Note that Equation (24), which is an equivalent form of Equation (17), does not involve the items

and

, and thus is applicable when the probability distribution of the maximum annual PGA is known.

Finally, a brief discussion on

in Equation (23) is presented. Note that

()

where

is the annual seismic hazard function. Equation (25) is consistent with the result in Cornell et al.²⁶

4 DISCUSSION ON THE PROPOSED TIME-DEPENDENT RESILIENCE MEASURE

4.1 Properties of the proposed measure

The seismic resilience measure in Equation (17) presents a straightforward link between the resilience and the duration of the reference period of interest,

. If one subdivides this period into two intervals, namely

, it follows that:

()

which clearly demonstrates that the product of resilience measures associated with the subdivided time intervals equals the resilience of the whole reference period. This observation can be naturally extended to the case of more than two subintervals. For the equivalent form in Equation (24), a similar relationship as in Equation (26) also holds, that is,

It is suggested in Equation (17) that, if

is close to 1, the seismic nonresilience is approximately proportional to the occurrence rate of earthquake events. This can be shown by

()

Note that in Equation (17), totally

damage states have been incorporated. For a special case that

(i.e., only two states are considered, no damage and damage), the probability of no damage at time

while its complement,

equals the probability of damage. Since

, and

, it follows that:

()

with which Equation (17) reduces to

()

which is consistent with Equation (2). As a result, it is concluded that the proposed resilience measure in Equation (17) is a generalized form of that in Equation (2).

In Equation (17), if only considering one single damage limit state (out of the

states), the resilience measure would be underestimated. This is can be easily verified since for any

()

As such, one should consider all the possible damage states to reasonably estimate the structural time-dependent resilience.

Consider the following scenario for a posthazard structure: the structure is repairable in the presence of the first

(

) damage states and is nonrepairable otherwise. In such a case,

for

and thus, Equation (17) becomes

()

One example for Equation (31) is that a postearthquake structure is repairable if its damage state is slight or moderate, but nonrepairable for extensive damage and collapse. Specifically, if

, Equation (31) is further simplified as follows:

()

which takes a similar form as the structural time-dependent reliability in Equation (1) (they would become the same if the limit state in Equation (1) is regarding the occurrence of the first damage state).

4.2 Resilience-oriented performance-based structural design

The concept of performance-based design has been widely accepted in structural seismic design in the past decades. It is a design methodology with criteria expressed in terms of achieving a set of explicit, quantifiable performance objectives in the presence of multiple performance and hazard levels.⁴⁶ Such objectives may be defined with respect to any response parameters such as stress, displacement, acceleration, and others. For example, the performance objective could be related to a specific damage state or the failure probability associated with a prescribed demand level. Motivated by the proposed seismic resilience measure in Equation (17) or (24), the performance objective could also be regarding the minimum resilience of a structure within a reference period of interest. That being the case, an adequate design procedure would require the assessment of structural fragility, functionality loss, and recovery process at all the performance levels of interest. It is also an essential step to develop appropriate design criteria regarding the minimum requirement on structural seismic resilience. Mathematically, the design criterion takes a form of

()

in which

is the target resilience level.

5 EXAMPLE

In this section, a numerical example is presented to demonstrate the applicability of the proposed seismic resilience measure. Consider a multispan continuous (MCS) steel girder bridge that was studied by Ghosh and Padgett⁴⁰ (see Figure 2), which is representative of the median dimensions of the steel girder bridges in the Central and Southeastern United States (CSUS). Taking into account the impact of corrosion of anchor bolts, the ultimate lateral strength of fixed bearings along the longitudinal direction can be approximated by a two-stage model as follows,

()

where

is time (in years). In Equation (34), the time of deterioration initiation (8.8 years) corresponds to the corrosion initiation time, determined by the instant where the chloride concentration at the reinforcement surface reaches a critical value causing the dissolution of the protective passive film. For illustration purposes, it is assumed in this example that the functionality deterioration of the bridge is parallel to the deterioration of

as in Equation (34). With this, it follows that:

()

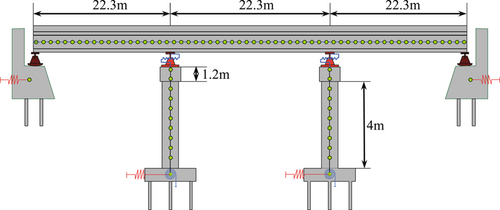
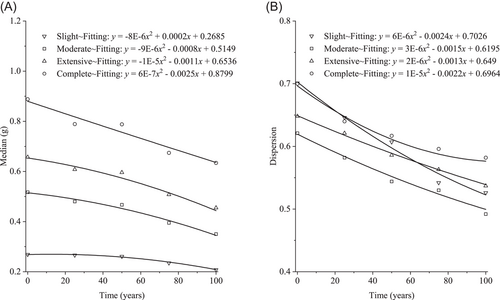
The overall time-variant fragility curve of the bridge is obtained by considering the bridge as a series system consisting of different components. Based on Equation (7), the time-variant median values (in terms of the acceleration of gravity, ) and dispersions are presented in Figure 3, in the presence of totally five damage states (): none, slight, moderate, extensive, and complete. In the aftermath of an earthquake event, the damage state-dependent restriction strategies and recovery rates are shown in Table 1. It is further assumed that the postearthquake functionality loss increases with time as follows: over a reference period of 100 years, (a) slight damage, from 25% (as in Table 1) to 50%; (b) moderate damage, from 50% to 75%; (c) extensive damage, from 75% to 90%. The recovery rate for the damage state of “collapse” is not applicable in Table 1, indicating that the bridge is not repairable after collapse (with which ). For the other damage states (slight, moderate, and extensive), the idle time of the posthazard bridge (i.e., the time between the occurrence of earthquake and the start of the recovery process) is not considered.

Table 1. Functionality loss and recovery speed of the postearthquake bridge

Damage state	Restriction strategy⁴⁷	Functionality loss⁴⁷ (percentage of normal serviceability)	Recovery rate (days)⁴⁸
Damage state	Restriction strategy⁴⁷	Functionality loss⁴⁷ (percentage of normal serviceability)	Lower bound	Upper bound
No damage	Immediate access	0	n.a.	n.a.
Slight damage	Weight restriction	25	0.1	1
Moderate damage	One lane open only	50	1	5
Extensive damage	Emergency access only	75	30	120
Collapse	Closed	100	n.a.	n.a.

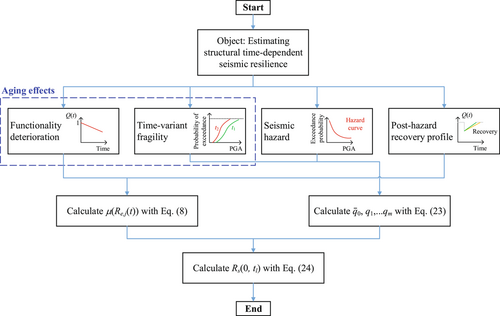
Two representative locations from the CSUS will be chosen for the bridge, namely St. Louis, Missouri, and Memphis, Tennessee. The seismic hazard curves associated with the two locations are available at the United States Geological Survey (USGS; https://earthquake.usgs.gov/hazards/interactive/). The former has a characteristic value of about 0.1g corresponding to a return period of 475 years, while the latter has a characteristic value of 0.2g. Using the edition of Conterminous U.S. 2014 (V4.0.x), the hazard curves (annual exceedance probability) can be approximated by the Extreme Type II distribution.³³ For St. Louis, the shape and scale parameters (see Equation 19) are and , respectively; for Memphis, and . With the above configuration, the bridge's time-dependent seismic resilience will be evaluated using Equation (24) (see Figure 4 for a flowchart of the calculation steps).

First, the time-variant resilience measures associated with a single earthquake event, , are computed by Equation (8) and are presented in Figure 5 for slight, moderate, and extensive damage states. It is seen that for each , the resilience measure decreases with time, due to the increasing posthazard functionality loss. The resilience measure associated with the slight damage state is the greatest, followed by those associated with the moderate and extensive damage states, respectively. With the results in Figure 5, the bridge's time-dependent nonresiliences for reference periods up to 100 years are calculated according to Equation (24) and are shown in Figure 6 (see the legend “”). The structural nonresilience increases with time due to the accumulation of damage potential of the bridge with time. For the two locations, the nonresilience associated with St. Louis is smaller than that of Memphis, because the seismic risk at Memphis is greater, as reflected by the statistics of the annual seismic hazard curves. In Figure 6, the nonresiliences associated with other values of are also presented. The case of corresponds to the structural failure probability as estimated by Equation (1), which serves as an upper bound for structural nonresilience. A greater value of results in a smaller nonresilience, due to the consideration of more repairable damage scenarios of the postearthquake bridge. For instance, at St. Louis, the nonresilience for 100 years is 0.062 with , which is approximately 2.7 times that associated with . Furthermore, the results in Figure 6 can also be used to predict the bridge's service life, given the target resilience level. For example, if the nonresilience threshold is 0.01 for St. Louis, the structural service life is predicted to be 49.5 years. With the same target level, the service life becomes 15.7 years if the bridge is located in Memphis. If the target nonresilience measure is raised to be 0.03 for Memphis, the service life increases to 45.6 years.

During the design phase of the bridge, one may adjust the structural design so that the resilience measure can meet a predefined threshold. Illustratively, an adjustment factor is introduced, with which the median values of the time-variant fragility curves become times the original ones in Figure 3A. The variation of reflects the adjustment process of the design scheme. Given the target resilience goal, the desired structural design would be achieved through a trial-and-error approach. Based on the results in Figure 6, the dependence of structural nonresilience on the value of is shown in Figure 7. Clearly, a greater value of results in a smaller nonresilience due to the enhanced seismic performance of the bridge. For example, at St. Louis, if the median values increase by 40%, the nonresilience for a reference period of 100 years decreases from 0.023 to 0.013. Furthermore, if the nonresilience threshold is 0.01 for a service life of 75 years at St. Louis, the median values are required to increase by at least 35% (i.e., ). Similarly, if the target nonresilience is 0.03 over 75 years for Memphis, one would need to enhance the median values of the fragility curves by 50%, corresponding to , at the minimum. Although it is out of the scope of this paper to discuss how to determine the target resilience level, the results herein demonstrate that the resilience-based design is promising to become a useful tool for use in structural design, in conjunction with the traditional reliability-based design.

6 CONCLUSIONS

In this paper, a new measure for structural time-dependent seismic resilience has been proposed, which takes into account the multiple postearthquake damage states. The following conclusions can be drawn from this paper.

1.
The proposed time-dependent resilience measure is a generalized form of that in the literature, incorporating the multiple posthazard damage states as well as the associated resilience measures conditional on earthquake occurrence. It also reduces structural time-dependent reliability if the structure is nonrepairable once suffering from any damage/failure.
2.
The structural nonresilience would be overestimated if not considering all the postearthquake damage scenarios with which the structure is repairable. For example, for the illustrative bridge located in St. Louis, the seismic nonresilience for a reference period of 100 years is overestimated by about 170% if assuming that the structure is nonrepairable in the presence of any damage state.
3.
The proposed resilience measure can be used to probabilistically predict structural service life and to quantitatively guide the design of structures given a resilience threshold, where a trial-and-error process can be used to ensure that the resilience requirement is met.

ACKNOWLEDGMENT

The authors would like to acknowledge the thoughtful suggestions of three anonymous reviewers, which substantially improved the present paper. Open access publishing facilitated by University of Wollongong, as part of the Wiley - University of Wollongong agreement via the Council of Australian University Librarians.

CONFLICTS OF INTEREST

The authors declare no conflicts of interest.

REFERENCES

1 Federal Emergency Management Agency (FEMA). Hazus® Estimated Annualized Earthquake Losses for the United States, FEMA P-366. tech. rep. Hyattsville, MD; 2017. https://www.fema.gov/sites/default/files/2020-07/fema_earthquakes_hazus-estimated-annualized-earthquake-losses-for-the-united-states_20170401.pdf
Google Scholar
2 Statista. Direct economic loss caused by earthquakes in China from 2009 to 2019. Accessed November 15, 2021. https://www.statista.com/statistics/225128/economic-loss-caused-by-earthquakes-in-china/
Google Scholar
3Stewart MG, Rosowsky DV. Time-dependent reliability of deteriorating reinforced concrete bridge decks. Struct Safety. 1998; 20(1): 91-109.
10.1016/S0167-4730(97)00021-0
Web of Science® Google Scholar
4Dieulle L, Bérenguer C, Grall A, Roussignol M. Sequential condition-based maintenance scheduling for a deteriorating system. Eur J Operat Res. 2003; 150(2): 451-461.
10.1016/S0377-2217(02)00593-3
Web of Science® Google Scholar
5Ma Y, Zhang J, Wang L, Liu Y. Probabilistic prediction with Bayesian updating for strength degradation of RC bridge beams. Struct Safety. 2013; 44: 102-109.
10.1016/j.strusafe.2013.07.006
Web of Science® Google Scholar
6Ayyub BM, Stambaugh KA, McAllister TA, de Souzad GF, Webb D. Structural life expectancy of marine vessels: ultimate strength, corrosion, fatigue, fracture, and systems. ASCE-ASME J Risk Uncertain Eng Syst B Mech Eng. 2015; 1(1):011001.
Google Scholar
7Wang C, Zhang H, Li Q. Reliability assessment of aging structures subjected to gradual and shock deteriorations. Reliab Eng Syst Safety. 2017; 161: 78-86.
10.1016/j.ress.2017.01.014
Web of Science® Google Scholar
8Mori Y, Ellingwood BR. Reliability-based service-life assessment of aging concrete structures. J Struct Eng. 1993; 119(5): 1600-1621.
10.1061/(ASCE)0733-9445(1993)119:5(1600)
Web of Science® Google Scholar
9Li Q, Wang C, Ellingwood BR. Time-dependent reliability of aging structures in the presence of non-stationary loads and degradation. Struct Safety. 2015; 52: 132-141.
10.1016/j.strusafe.2014.10.003
Web of Science® Google Scholar
10Wang C. Structural Reliability and Time-Dependent Reliability. Springer Nature; 2021.
10.1007/978-3-030-62505-4
Google Scholar
11 National Research Council. Disaster resilience: a national imperative. The National Academies Press; 2012.
Google Scholar
12McAllister T. Developing Guidelines and Standards for Disaster Resilience of the Built Environment: A Research Needs Assessment. US Department of Commerce, National Institute of Standards and Technology; 2013.
10.6028/NIST.TN.1795
Google Scholar
13Ayyub BM. Systems resilience for multihazard environments: definition, metrics, and valuation for decision making. Risk Anal. 2014; 34(2): 340-355.
10.1111/risa.12093
PubMed Web of Science® Google Scholar
14Salomon J, Broggi M, Kruse S, Weber S, Beer M. Resilience decision-making for complex systems. ASCE-ASME J Risk Uncertain Eng Syst B Mech Eng. 2020; 6(2):020901.
Web of Science® Google Scholar
15RedaTaha M, Ayyub BM, Soga K, et al. Emerging technologies for resilient infrastructure: conspectus and roadmap. ASCE-ASME J Risk Uncertain Eng Syst A Civil Eng. 2021; 7(2):03121002.
10.1061/AJRUA6.0001134
Web of Science® Google Scholar
16 ISO. Bases for Design of Structures–Assessment of Existing Structures. ISO 13822: 2010(E). 2010.
Google Scholar
17Gardner J, Knopoff L. Is the sequence of earthquakes in Southern California, with aftershocks removed, Poissonian? Bull Seismol Society Am. 1974; 64(5): 1363-1367.
10.1785/BSSA0640051363
Google Scholar
18Beroza GC. How many great earthquakes should we expect? Proc Natl Acad Sci USA. 2012; 109(3): 651-652.
10.1073/pnas.1120744109
CAS PubMed Web of Science® Google Scholar
19Wang C, Beer M, Ayyub BM. Time-dependent reliability of aging structures: overview of assessment methods. ASCE-ASME J Risk Uncertain Eng Syst A Civil Eng. 2021; 7(4):03121003.
10.1061/AJRUA6.0001176
Web of Science® Google Scholar
20Wang C, Ayyub BM. Time-dependent resilience of repairable structures subjected to non-stationary load and deterioration for analysis and design. ASCE-ASME J Risk Uncertain Eng Syst A Civil Eng. 2022. doi:10.1061/AJRUA6.0001246
Google Scholar
21Bruneau M, Reinhorn A. Exploring the concept of seismic resilience for acute care facilities. Earthq Spectra. 2007; 23(1): 41-62.
10.1193/1.2431396
Web of Science® Google Scholar
22Tierney K, Bruneau M. Conceptualizing and measuring resilience: a key to disaster loss reduction. TR News. 2007; 250: 14-17.
Google Scholar
23Bruneau M, Chang SE, Eguchi RT, et al. A framework to quantitatively assess and enhance the seismic resilience of communities. Earthq Spectra. 2003; 19(4): 733-752.
10.1193/1.1623497
Web of Science® Google Scholar
24Attoh-Okine NO, Cooper AT, Mensah SA. Formulation of resilience index of urban infrastructure using belief functions. IEEE Syst J. 2009; 3(2): 147-153.
10.1109/JSYST.2009.2019148
Web of Science® Google Scholar
25Ayyub BM. Practical resilience metrics for planning, design, and decision making. ASCE-ASME J Risk Uncertain Eng Syst A Civil Eng. 2015; 1(3):04015008.
10.1061/AJRUA6.0000826
Web of Science® Google Scholar
26Cornell CA, Jalayer F, Hamburger RO, Foutch DA. Probabilistic basis for 2000 SAC Federal Emergency Management Agency steel moment frame guidelines. J Struct Eng. 2002; 128(4): 526-533.
10.1061/(ASCE)0733-9445(2002)128:4(526)
Web of Science® Google Scholar
27Li Y, Ellingwood BR. Hurricane damage to residential construction in the US: importance of uncertainty modeling in risk assessment. Eng Struct. 2006; 28(7): 1009-1018.
10.1016/j.engstruct.2005.11.005
Web of Science® Google Scholar
28Cui F, Zhang H, Ghosn M, Xu Y. Seismic fragility analysis of deteriorating RC bridge substructures subject to marine chloride-induced corrosion. Eng Struct. 2018; 155: 61-72.
10.1016/j.engstruct.2017.10.067
Web of Science® Google Scholar
29Guo X, Wu Y, Guo Y. Time-dependent seismic fragility analysis of bridge systems under scour hazard and earthquake loads. Eng Struct. 2016; 121: 52-60.
10.1016/j.engstruct.2016.04.038
Web of Science® Google Scholar
30Baker JW. Introducing correlation among fragility functions for multiple components. Proceedings of the 14th World Conference on Earthquake Engineering, October 12–17, 2008, Beijing, China; 2008.
Google Scholar
31Wang C, Zhang H, Ellingwood BR, Guo Y, Mahmoud H, Li Q. Assessing post-hazard damage costs to a community's residential buildings exposed to tropical cyclones. Struct Infrastruct Eng. 2020; 17(4): 443-453.
10.1080/15732479.2020.1845215
Web of Science® Google Scholar
32Wang C, Zhang H. Assessing the seismic resilience of power grid systems considering the component deterioration and correlation. ASCE-ASME J Risk Uncertain Eng Syst A Civil Eng. 2020; 6(2):020903.
10.1115/1.4046394
Web of Science® Google Scholar
33Wang C, Teh LH. Time-dependent seismic reliability of aging structures. ASCE-ASME J Risk Uncertain Eng Syst A Civil Eng. 2022; 8(2):04022010. doi:10.1061/ajrua6.0001224
Google Scholar
34Kennedy R, Ravindra M. Seismic fragilities for nuclear power plant risk studies. Nucl Eng Design. 1984; 79(1): 47-68.
10.1016/0029-5493(84)90188-2
Web of Science® Google Scholar
35Ang AS, Pires J, Villaverde R. A model for the seismic reliability assessment of electric power transmission systems. Reliab Eng Syst Safety. 1996; 51(1): 7-22.
10.1016/0951-8320(95)00101-8
Web of Science® Google Scholar
36Shinozuka M, Feng MQ, Lee J, Naganuma T. Statistical analysis of fragility curves. J Eng Mech. 2000; 126(12): 1224-1231.
10.1061/(ASCE)0733-9399(2000)126:12(1224)
Web of Science® Google Scholar
37Straub D, Der Kiureghian A. Improved seismic fragility modeling from empirical data. Struct Safety. 2008; 30(4): 320-336.
10.1016/j.strusafe.2007.05.004
Web of Science® Google Scholar
38Dimova SL, Hirata K. Simplified seismic fragility analysis of structures with two types of friction devices. Earthq Eng Struct Dynam. 2000; 29(8): 1153-1175.
10.1002/1096-9845(200008)29:8<1153::AID-EQE961>3.0.CO;2-Y
Web of Science® Google Scholar
39Elenas A. Correlation between seismic acceleration parameters and overall structural damage indices of buildings. Soil Dynam Earthq Eng. 2000; 20(1-4): 93-100.
10.1016/S0267-7261(00)00041-5
Web of Science® Google Scholar
40Ghosh J, Padgett JE. Aging considerations in the development of time-dependent seismic fragility curves. J Struct Eng. 2010; 136(12): 1497-1511.
10.1061/(ASCE)ST.1943-541X.0000260
Web of Science® Google Scholar
41Li H, Li L, Zhou G, Xu L. Time-dependent seismic fragility assessment for aging highway bridges subject to non-uniform chloride-induced corrosion. J Earthq Eng. 2020; 1-31. doi:10.1080/13632469.2020.1809561
Web of Science® Google Scholar
42Andrade C, Alonso C. Corrosion rate monitoring in the laboratory and on-site. Construct Build Mater. 1996; 10(5): 315-328.
10.1016/0950-0618(95)00044-5
Web of Science® Google Scholar
43Val DV, Stewart MG, Melchers RE. Effect of reinforcement corrosion on reliability of highway bridges. Eng Struct. 1998; 20(11): 1010-1019.
10.1016/S0141-0296(97)00197-1
Web of Science® Google Scholar
44Wang C, Li Q, Zou A, Zhang L. A realistic resistance deterioration model for time-dependent reliability analysis of aging bridges. J Zhejiang Univ Sci A. 2015; 16(7): 513-524.
10.1631/jzus.A1500018
Web of Science® Google Scholar
45Cornell CA. Engineering seismic risk analysis. Bull Seismol Society Am. 1968; 58(5): 1583-1606.
10.1785/BSSA0580051583
Web of Science® Google Scholar
46Ghobarah A. Performance-based design in earthquake engineering: state of development. Eng Struct. 2001; 23(8): 878-884.
10.1016/S0141-0296(01)00036-0
Web of Science® Google Scholar
47Mackie K, Stojadinović B. Post-earthquake functionality of highway overpass bridges. Earthq Eng Struct Dyn. 2006; 35(1): 77-93.
10.1002/eqe.534
Web of Science® Google Scholar
48Dong Y, Frangopol DM. Risk and resilience assessment of bridges under mainshock and aftershocks incorporating uncertainties. Eng Struct. 2015; 83: 198-208.
10.1016/j.engstruct.2014.10.050
Web of Science® Google Scholar

Citing Literature

Volume1, Issue1

March 2022

Pages 73-87

This article also appears in:

Resilience of Cities and Infrastructures

Time-dependent seismic resilience of aging repairable structures considering multiple damage states

Abstract

1 INTRODUCTION

2 STRUCTURAL SEISMIC PERFORMANCE

2.1 Seismic fragility curve

2.2 Resilience associated with a single earthquake event

3 PROPOSED RESILIENCE MEASURE CONSIDERING MULTIPLE DAMAGE STATES

4 DISCUSSION ON THE PROPOSED TIME-DEPENDENT RESILIENCE MEASURE

4.1 Properties of the proposed measure

4.2 Resilience-oriented performance-based structural design

5 EXAMPLE

6 CONCLUSIONS

ACKNOWLEDGMENT

CONFLICTS OF INTEREST

REFERENCES

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Time-dependent seismic resilience of aging repairable structures considering multiple damage states

Abstract

1 INTRODUCTION

2 STRUCTURAL SEISMIC PERFORMANCE

2.1 Seismic fragility curve

2.2 Resilience associated with a single earthquake event

3 PROPOSED RESILIENCE MEASURE CONSIDERING MULTIPLE DAMAGE STATES

4 DISCUSSION ON THE PROPOSED TIME-DEPENDENT RESILIENCE MEASURE

4.1 Properties of the proposed measure

4.2 Resilience-oriented performance-based structural design

5 EXAMPLE

6 CONCLUSIONS

ACKNOWLEDGMENT

CONFLICTS OF INTEREST

REFERENCES

Citing Literature

Figures

References

Related

Information