Calibration of an evapotranspiration algorithm in a semiarid sagebrush steppe using a 3-ha lysimeter and Landsat normalized difference vegetation index data
Funding information: U.S. Department of Energy Office of Legacy Management; U.S. Environmental Protection Agency
Abstract
In arid and semiarid environments, evapotranspiration (ET) is the primary discharge component in the water balance, with potential ET exceeding precipitation. For this reason, reliable estimates of ET are needed to construct accurate water budgets in these environments. Remote sensing affords the ability to provide fast, accurate, field-scale ET estimates, but these methods have largely been restricted to deep rooted (phreatophytic) plant communities underlain by shallow groundwater. We used 13 years of data from a 3-ha drainage lysimeter in a semiarid sagebrush steppe and Landsat normalized difference vegetation index (NDVI) data to calibrate a generalized least squares model capable of predicting vadose zone ET in a high elevation upland ecosystem. Annual precipitation was the best predictor of annual ET, as they were nearly balanced every year analysed (mean difference = 3 mm). We incorporated reference crop ET and a linear combination of NDVI and precipitation to capably predict ET on a subannual, lag-determined interval of 48 days, with a mean error of only 9.92% across all observations. To our knowledge, this is the first vegetation index-ET algorithm calibrated in a semiarid upland plant community using field-scale lysimetry. Vadose zone ET is particularly important at waste disposal sites in the Desert Southwest, where accurate and spatially explicit ET estimates are needed for monitoring potential mobilization and transport of contaminants past the root zone into local aquifers and for monitoring and modelling effects of recharge on flow and transport of contaminants in underlying aquifers.
1 INTRODUCTION
In arid and semiarid environments, water lost through transpiration and evaporation (collectively termed evapotranspiration [ET]), is the primary discharge component of the water balance, with potential ET exceeding precipitation (Wilcox et al., 2003). In dry regions where plants access shallow groundwater (i.e., phreatophytes), ET often represents the primary outflow component of the water budget. As a result, ET estimates are important for constructing accurate water balances in such areas. Many ground methods have been developed to estimate actual ET (ETa), including lysimetry, Bowen ratio and eddy flux towers, but these methods can be costly and may not be practical over large expanses (e.g., Hill et al., 2017; Waugh et al., 1991). Because of these limitations, remote sensing methods for estimating ETa have become increasingly popular in recent years (e.g., Glenn et al., 2007; Kalma et al., 2008). These methods fall into two general categories: (1) surface energy balance (SEB), which calculate latent heat flux (ETa) as a residual of the SEB equation, and (2) vegetation index (VI) methods, which typically estimate green foliage density by leveraging differences in reflectance between visible and near-infrared (NIR) wavelengths of light (the focus of the current study).
VI methods are possible because chlorophyll, the pigment responsible for green coloration in plants, absorbs most blue and red light, while the surrounding plant tissues reflect in the NIR (Buschmann & Nagel, 1993). Because chlorophyll is the primary pigment responsible for absorbing the light that drives photosynthesis, the rate of photosynthesis is directly related to the amount of chlorophyll present (Tucker & Sellers, 1986). Therefore, VIs (e.g., the normalized difference vegetation index [NDVI]) respond to actively photosynthesizing material, increasing as the quantity of green biomass increases (Burgan & Hartford, 1993). Since photosynthesis requires leaf conductance for uptake of carbon dioxide, water is lost during this process through transpiration.
One unique advantage of VI methods is that VI values tend to be stable over days to weeks, allowing for long-term ETa monitoring via satellite sensors with a lower image acquisition frequency (Nagler et al., 2013). Revisit times of the sensors commonly used to derive VIs range from near daily for the Moderate Resolution Imaging Spectroradiometer (MODIS) onboard the Terra Satellite to 16 days for the Landsat suite of satellites (combined repeat of 8 days). However, lower temporal resolution can be problematic in areas prone to cloud cover, where phenologically significant periods might be missed. Additionally, more frequent observations will typically lead to more accurate ETa predictions but at the cost of coarser spatial resolution (Nagler et al., 2013). For example, MODIS enhanced vegetation index (EVI) and NDVI products are provided at 250-m pixel resolution, while comparable Landsat products are acquired at 30 m.
The coarser resolution of MODIS VI products may preclude their application over small areas (Jarchow et al., 2018), necessitating the application of higher resolution imagery. This requires adequately capturing the phenology of vegetation during the growing season with a temporally limited number of images. Phreatophytic systems underlain by shallow groundwater are unique in that they are not limited by availability of water as are other plant communities in arid, temperate environments but are instead regulated primarily by temperature (Menzel, 2002; Robinson, 1958; Young et al., 1985). As a result, phreatophytic communities exhibit a more predictable and consistent greenup pattern (peaking in mid-growing season), allowing for the prediction of ETa with a temporally limited number of images. For example, Groeneveld et al. (2007) and Jarchow et al. (2020) used only a single mid-summer or peak season Landsat NDVI scene to predict annual ETa of phreatophytic plant communities in the arid southwestern United States.
Whereas the more predictable greenup pattern observed in phreatophytic systems makes these communities easier to characterize with temporally limited satellite datasets, it can be more difficult to assess plant communities that do not have access to shallow groundwater. The latter may refer to shallow rooted upland species but also facultative phreatophytes in areas without shallow groundwater. In these situations, growth is driven primarily by local precipitation (e.g., Liu et al., 2016), making it less predictable and difficult to adequately assess greenness, and by extension ETa, over the entire growing season using a sensor with a lower temporal resolution. This presents a problem over small areas where vadose zone ET must be assessed.
For example, at some hazardous waste sites in the Desert Southwest, plants have been identified as a key tool to help control the spread of contaminants into groundwater by limiting the infiltration of water through the vadose zone (Bresloff et al., 2013; DOE, 2016; Glenn et al., 2016; Jordan et al., 2008; McKeon et al., 2005; McKeon et al., 2006). Low percolation and recharge in these arid environments make them more suitable than humid areas for long-term storage of radioactive and other hazardous waste materials (Reith & Thompson, 1992; Winograd, 1981) because leaching of contaminants into groundwater is minimized (Gee et al., 1994; Glenn et al., 2016). In these areas, ETa estimation is critical to assessing the potential for precipitation to mobilize and transport contaminants from the vadose zone into local aquifers. However, in some of these areas, an aquifer-root connection does not exist, making it difficult to accurately assess ETa using VI methods. Our objective was to develop an ETa algorithm using 19 years of data from a 3-ha lysimeter at a Comprehensive Environmental Response, Compensation, and Liability Act (CERCLA) site in Monticello, Utah, USA that could accurately predict ETa in an upland plant community using lower temporal, higher spatial resolution Landsat NDVI data.
2 METHODS
2.1 Study area
We measured ground ETa using a 3-ha, instrumented drainage lysimeter (Figure 1) embedded in an in-service uranium mill tailings disposal cell managed by the U.S. Department of Energy (DOE) near the town of Monticello in southeastern Utah (https://www.energy.gov/lm/office-legacy-management). The Monticello mill was operated from 1942 to 1960 to produce uranium and vanadium for military purposes. Remedial action at the abandoned mill, completed in 2000, was regulated under CERCLA. The disposal cell has an engineered earthen cover designed to limit release of radon gas into the atmosphere and percolation of water into underlying tailings (Waugh et al., 2009).
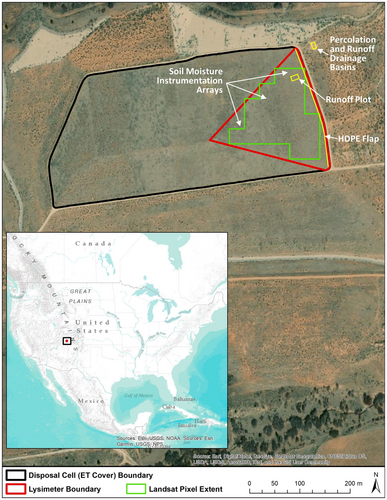
Monticello is semiarid with cold, windy winters and mild summers. The average annual precipitation (PPT) is 390 mm, the average minimum January temperature is −10.5°C, and the average July maximum temperature is 28.9°C. Three seasons occur with respect to soil–water balance: November–March, the season of deep infiltration and moisture accumulation in soils (PPT averages 160 mm); April–June, a moisture-depletion period when plants are most active (PPT averages 60 mm); and July–October, a season of near-surface moisture accumulation and depletion resulting from monsoonal convection storms (PPT averages 170 mm). Annual snowfall averages 160–170 cm. The clay loam to sandy loam soils (Monticello very fine sandy loam) within the footprint of the Monticello disposal cell were formed in Pleistocene loess (USDA, 1945). The potential natural vegetation for this soil consists primarily of western wheatgrass (Pascopyrum smithii), Sandberg bluegrass (Poa secunda), blue grama (Bouteloua gracilis), mountain big sagebrush (Artemisia tridentata subsp. vaseyana), and rubber rabbitbrush (Ericameria nauseosa) and typically has a canopy coverage of 50%–60% based on annual ground surveys.
The Monticello disposal cell cover, sometimes called an ET cover, was designed to limit percolation into underlying tailings and subsequent leaching of contaminants into groundwater. The design mimics the favourable ecology and water balance of the deep aeolian soils occurring in the landscape surrounding the disposal site (Waugh et al., 2006). The ET cover design relies on the water storage capacity of a 163-cm, fine-textured layer of the aeolian soil overlying a 38-cm sand capillary barrier layer to store PPT and on ET to seasonally release stored water back to the atmosphere (Albright et al., 2004; Waugh et al., 2009; Waugh & Richardson, 1997). Capillary barriers composed of coarse-textured sand and gravel placed below a soil ‘sponge’ can enhance water storage capacity and limit unsaturated flow (Stormont & Morris, 1998; Ward & Gee, 1997). Water movement past the capillary barrier can occur when water accumulation at the fine soil/coarse sand interface approaches saturation and soil water tensions decrease sufficiently for water to enter the larger pores of the sand layer. Hydraulic performance can be evaluated as the probability that ET is sufficient to prevent water accumulation in the soil sponge from exceeding the storage capacity in any given year. The sustainability of the ET cover will depend, in part, on the establishment and resilience of a diverse plant community (Waugh, 1997). Long-term changes in the plant community inhabiting a cover will influence soil water movement, ET rates and the water balance of the cover.
2.2 Ground ETa measurements
The 3-ha drainage lysimeter at Monticello (Figure 1) functions as a large-scale water collection system. A high-density polyethylene (HDPE) geomembrane, required by the regulator, made creation of the water collection system possible. The geomembrane, placed below the capillary barrier at a depth of 201 cm, formed the floor of the lysimeter. An HDPE flap welded to the geomembrane (Figure 1) directs percolation to a sump at the lower corner of the 3-ha facet of the cover. We collected surface runoff in a 10 × 20-m subplot formed with treated lumber sidewalls and installed within the 3-ha embedded lysimeter (Figure 1).
Lysimeter instruments monitored flow (percolation and runoff), state variables within the cover profile (soil water content and temperature) and meteorology. We routed percolation and runoff from sumps through pipes into separate drainage basins located downslope of the lysimeter (Figure 1). Basins were equipped with tipping buckets, pressure transducers and flouts. The percolation basin has a 70-ml tipper and a 1-L tipper in series (Hydrological Services TB1L/70) for redundant measurement of low and high flows. The runoff basin has a single 1-L tipper. Flouts drain the basins at the high-water point. The basins are capable of measuring percolation and surface runoff flows with a precision better than 1 mm/year (Waugh et al., 2009). We monitored volumetric soil water content with low-frequency (40 MHz) water content reflectometer (WCR) probes (Model 615; Campbell Scientific, Logan, Utah), and soil water matric potential with co-located heat dissipation sensors (HDS) (Model 229; Campbell Scientific). WCRs and HDSs were installed in vertical arrays to a depth of 2 m in three locations at quarter points along a downslope transect through the lysimeter test section (Figure 1). We determined water storage in the profile by integration of the WCR point water content measurements and compared meteorological parameters at an onsite weather station to meteorological data from nearby National Weather Service stations.
2.3 Vegetation monitoring
Revegetation goals for the Monticello cover included plants that (1) were well-adapted to the engineered soil habitat, (2) were capable of high transpiration rates, (3) limited soil erosion and (4) were structurally and functionally resilient. Diverse mixtures of native and naturalized plants growing on engineered covers are thought to maximize water removal and remain resilient given variable and unpredictable changes in the environment resulting from pathogen and pest outbreaks, disturbances (overgrazing, fire, etc.) and climatic fluctuations (Link, Waugh, & Downs, 1994).
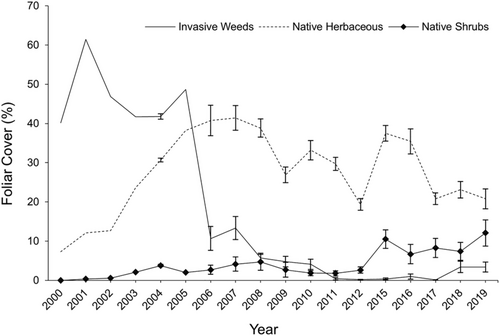
We seeded and planted the Monticello cover in September 2000 with a mixture of grasses, forbs and shrubs (DOE, 2006). Our goal was to mimic the potential natural vegetation as documented on native soil used to construct the ET cover. We measured species composition, percent cover, and shrub density for most years since 2001 and leaf area index (LAI) from 2001 to 2006 and again in 2011. Vegetation sampling methods included ocular point intercept (Floyd & Anderson, 1982) and quadrat methods (Daubenmire, 1959) for plant foliar cover, a point-quarter-distance method for shrub density (Eberhardt, 1967), and a radiometric method for LAI using an LAI-2000 (www.licor.com), all measured in mid-to-late summer. Invasive weeds, primarily Russian thistle (Salsola tragus) followed by cheatgrass (Bromus tectorum), dominated the plant community from 2000 through 2005 (Figure 2). Foliar cover of native herbaceous species increased as weedy species decreased during that period. Between 2005 and 2006, a rather abrupt decrease in weeds resulted in a burgeoning sagebrush steppe community dominated by western wheatgrass and maturing mountain big sagebrush.
2.4 ETo calculations
We calculated monthly Penman–Monteith ETo following the recommendations and methods outlined in Allen et al. (1998) and FAO (2012). The Penman–Monteith equation explicitly incorporates a suite of climatic parameters, but only temperature data were available in our region. Therefore, we calculated Penman–Monteith ETo for temperature-only datasets assuming the average wind speed was light-moderate and the climate was arid–semiarid. We set the elevation to 2,141 m and centred the location on 37.85°N, 109.33°W (closest to the lysimeter). We obtained daily maximum and minimum temperature from 1-km gridded Daymet data over the lysimeter (Thornton et al., 2020).
2.5 Remote sensing data
Year 2012 represents the period between the decommissioning of Landsat 5 and the launch of Landsat 8. Because of the Scan Line Corrector (SLC) failure on Landsat 7 in 2003, images collected after this period contained streaks of missing data, precluding application of this platform in some areas. Initially, we included Landsat 7 imagery in our analysis but were unable to resolve inconsistencies in the spectral response of the VI over time (explained in the discussion); therefore, 2012 (and Landsat 7) was excluded from our study.
To ensure NDVI data were of sufficient quality for ET calibration, we first eliminated all scenes with >10% cloud cover. We then implemented a per-pixel quality assurance screening that retained only high-quality, clear pixels based on the quality assessment band provided by the USGS. To further minimize the impact of adjacent clouds and cloud shadow, we removed a 4-pixel-wide buffer around all potential cloud or shadow pixels. Finally, we eliminated scenes with less than the full complement of 22 pixels corresponding to the lysimeter. Only data that passed this strict filtering process were retained for further analysis, resulting in two to eight images per growing season and a total of 47 scenes for the period of study (Table 1).
| Year | Sensor | Scenes (n) | Mean NDVI* | Mean NDVI | Months (n) | ETa | PPT |
|---|---|---|---|---|---|---|---|
| 2006 | LT05 | 5 | 0.1634 | 0.2161 | 4 | 333.2 | 349.1 |
| 2007 | LT05 | 2 | 0.1026 | 0.1677 | 2 | 360.3 | 350.6 |
| 2008 | LT05 | 4 | 0.1820 | 0.2291 | 3 | 361.0 | 354.2 |
| 2009 | LT05 | 3 | 0.1244 | 0.1895 | 3 | 284.7 | 284.9 |
| 2010 | LT05 | 3 | 0.2293 | 0.2780 | 3 | 407.6 | 431.0 |
| 2011 | LT05 | 5 | 0.1358 | 0.1993 | 4 | 395.8 | 387.8 |
| 2013 | LC08 | 3 | 0.1117 | 0.2123 | 2 | 290.0 | 292.6 |
| 2014 | LC08 | 3 | 0.1665 | 0.2566 | 2 | 379.2 | 380.8 |
| 2015 | LC08 | 2 | 0.2203 | 0.3059 | 1 | 488.2 | 477.4 |
| 2016 | LC08 | 2 | 0.2045 | 0.2895 | 2 | 525.5 | 539.0 |
| 2017 | LC08 | 5 | 0.1265 | 0.2186 | 5 | 339.0 | 364.2 |
| 2018 | LC08 | 8 | 0.0800 | 0.1762 | 4 | 225.3 | 215.7 |
| 2019 | LC08 | 2 | 0.2609 | 0.3325 | 2 | 602.4 | 602.1 |
- Note: NDVI* is scaled NDVI of the lysimeter for each growing season. Months (n) is the number of calendar months for which at least one Landsat image was available following our image filtering process. Actual evapotranspiration (ETa as measured by lysimetry) and precipitation (PPT) are water-year totals in mm.
2.6 NDVI scaling
Because this stretching process relies on saturated values of NDVI, we only used scenes acquired during the growing season. We subsequently calculated mean NDVI* for each growing season (mean annual NDVI*) using the scenes that passed the filtering process described above. We digitized the perimeter of the lysimeter and converted this polygon to a 30-m raster registered to the Landsat grid (n = 22 pixels; Figure 1). Mean NDVI* of the 22 lysimeter pixels was used in all subsequent analyses.
2.7 ET modelling
ET was modelled on both an annual scale and the 48-day period prior to each Landsat acquisition date. Sixteen- and 32-day timesteps were also tested, but, because of the immense volume of the lysimeter, a significant lag was discovered between the onset of rainfall and resultant changes in soil water storage and percolation. This lag sometimes led to negative or near-zero ET values over periods <32 days. The 48-day timestep was chosen because it both resolved this lag over all Landsat acquisition periods and corresponded to the Landsat acquisition repeat period of 16 days. We subsequently added daily ETo, ETa and PPT over each 48-day period. We excluded the Landsat image from 19 June 2010 because of spurious lysimetry data recorded during this period. To ensure the 48-day period did not include a significant portion of the non-growing season, we also excluded scenes acquired before 15 June, resulting in a total of 36 imagery periods. On an annual scale, we added lysimeter ETa and PPT to derive water-year totals (October 1–September 30) for each component.
2.8 Statistical procedures
All statistical modelling was conducted in RStudio (RStudio Team, 2016). Ordinary least squares (OLS) regression was initially used to model the relationship between ETa, ETa normalized by ETo (ETa/ETo), PPT and NDVI* on 48-day and annual timescales. Assumptions of independence and homogeneity were then assessed, and models were selected following methods in Zuur et al. (2009). For the 48-day ETa/ETo models, residual heterogeneity was resolved using generalized least squares (GLS) regression with a fixed variance structure proportional to NDVI*. A linear correlation function was also included in the GLS to resolve significant temporal autocorrelation observed at lag step 1. Multiple variance and correlation structures were compared and ranked by the corrected Akaike information criterion (AICc), and those with the lowest AICc were selected. We also included spatial correlation functions in this process because they can potentially handle missing and irregularly spaced data better than temporal functions (Zuur et al., 2009). The optimal fixed component of the GLS was subsequently determined by dropping all non-significant terms from the full model.
3 RESULTS AND DISCUSSION
3.1 Annual modelling of ETa
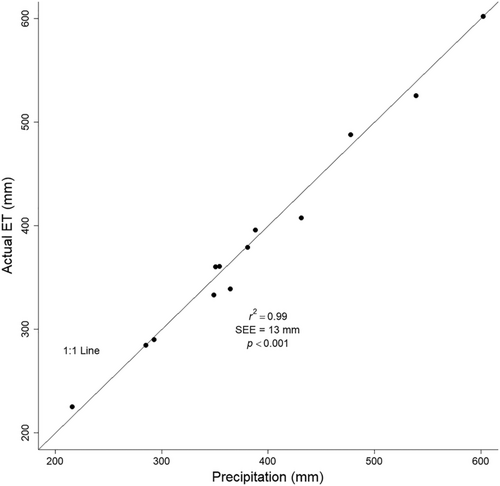
Our lysimetry NDVI* dataset ranged from a mean growing season high of 0.2609 in 2019 to a low of 0.0800 in 2018 (Table 1). Annual ETa ranged from 225.3 mm in 2018 to 602.4 mm in 2019, which was 18 to 53% of ETo, respectively (Table 1). NDVI* was a decent predictor of annual ETa (r2 = 0.75; SEE = 54.6 mm, p < 0.001), but annual PPT best explained ETa over the same period (r2 = 0.99; SEE = 13.1 mm; p < 0.001; Figure 3). This finding is not surprising for an upland semiarid ecosystem, where ET is expected to be balanced with PPT (Glenn et al., 2016; Wilcox et al., 2003). Also as expected, annual PPT was correlated with growing season NDVI* (r = 0.88). To test the assumption that peak seasonal NDVI* (compared to mean NDVI*) would not adequately explain annual ETa of upland vegetation on the lysimeter, we constructed and compared the simple NDVI*–ETa linear models using both forms of NDVI*. Mean NDVI* outperformed peak NDVI* based on AICc.
3.2 Subannual modelling of ETa
On the 48-day scale, NDVI* ranged from a low of 0.0501 on 25 June 2018 to a high of 0.2862 on 28 June 2019 (Table 2). NDVI* was highly correlated with ETa (r = 0.89; SEE = 17.3 mm; p < 0.001; Figure 4), while PPT alone was not (r = 0.39; SEE = 35.1 mm; p = 0.02). Although NDVI* and ETa were correlated, NDVI* alone fails to account for evaporative demand of the local environment, limiting or precluding application of this model to other sites with different evaporative forcing; however, this limitation can be overcome by incorporating ETo, which accounts for variation in evaporative driving force of the atmosphere (Groeneveld et al., 2007; Nagler et al., 2013).
| Acquisition date | Sensor | Mean NDVI* | PPT | ETo | ETa | ETa/ETo | ETModeled | Residual error (mm/48-days) | Residual error (% of ETa) |
|---|---|---|---|---|---|---|---|---|---|
| 6/24/2006 | LT05 | 0.0861 | 8.4 | 270.3 | 28.1 | 0.1040 | 31.8 | 3.7 | 13.17 |
| 7/26/2006 | LT05 | 0.0984 | 66.7 | 281.8 | 51.6 | 0.1831 | 71.0 | 19.4 | 37.60 |
| 8/27/2006 | LT05 | 0.2061 | 66.0 | 258.4 | 82.3 | 0.3185 | 123.4 | 41.1 | 49.94 |
| 9/12/2006 | LT05 | 0.2132 | 116.2 | 227.0 | 100.9 | 0.4445 | 133.0 | 32.1 | 31.81 |
| 9/28/2006 | LT05 | 0.2130 | 105.6 | 194.8 | 97.1 | 0.4985 | 110.2 | 13.1 | 13.49 |
| 6/27/2007 | LT05 | 0.1372 | 13.6 | 263.9 | 59.4 | 0.2251 | 62.0 | 2.6 | 4.38 |
| 8/30/2007 | LT05 | 0.0679 | 40.1 | 258.6 | 40.8 | 0.1578 | 35.8 | −5.0 | −12.25 |
| 6/29/2008 | LT05 | 0.2074 | 42.6 | 251.9 | 126.7 | 0.5030 | 110.0 | −16.7 | −13.18 |
| 7/15/2008 | LT05 | 0.1996 | 16.8 | 280.2 | 117.3 | 0.4186 | 104.3 | −13.0 | −11.08 |
| 7/31/2008 | LT05 | 0.1685 | 10.9 | 290.4 | 90.3 | 0.3110 | 85.9 | −4.4 | −4.87 |
| 7/18/2009 | LT05 | 0.1417 | 38.0 | 262.3 | 63.1 | 0.2406 | 76.0 | 12.9 | 20.44 |
| 8/19/2009 | LT05 | 0.1247 | 52.8 | 278.3 | 49.4 | 0.1775 | 78.3 | 28.9 | 58.50 |
| 7/5/2010 | LT05 | 0.2229 | 11.2 | 262.9 | 114.9 | 0.4370 | 108.0 | −6.9 | −6.01 |
| 8/6/2010 | LT05 | 0.2367 | 83.0 | 272.1 | 149.0 | 0.5476 | 156.0 | 7.0 | 4.70 |
| 6/22/2011 | LT05 | 0.1441 | 35.2 | 231.4 | 96.9 | 0.4188 | 67.0 | −29.9 | −30.86 |
| 7/24/2011 | LT05 | 0.1181 | 39.6 | 275.5 | 54.5 | 0.1978 | 66.9 | 12.4 | 22.75 |
| 8/9/2011 | LT05 | 0.0991 | 67.5 | 274.3 | 69.9 | 0.2548 | 69.9 | 0.0 | 0.00 |
| 6/27/2013 | LC08 | 0.1051 | 3.4 | 262.2 | 24.9 | 0.0950 | 38.9 | 14.0 | 56.22 |
| 7/13/2013 | LC08 | 0.1047 | 5.1 | 282.9 | 20.9 | 0.0739 | 42.6 | 21.7 | 103.83 |
| 8/17/2014 | LC08 | 0.1074 | 92.8 | 263.7 | 70.7 | 0.2681 | 84.3 | 13.6 | 19.24 |
| 9/2/2014 | LC08 | 0.1574 | 91.4 | 238.0 | 72.0 | 0.3025 | 100.5 | 28.5 | 39.58 |
| 9/18/2014 | LC08 | 0.2346 | 122.7 | 212.7 | 114.9 | 0.5402 | 136.7 | 21.8 | 18.97 |
| 6/17/2015 | LC08 | 0.2264 | 130.9 | 207.1 | 152.1 | 0.7344 | 132.7 | −19.4 | −12.75 |
| 6/19/2016 | LC08 | 0.2014 | 30.4 | 239.2 | 124.5 | 0.5205 | 96.0 | −28.5 | −22.89 |
| 7/5/2016 | LC08 | 0.2076 | 17.4 | 267.0 | 124.6 | 0.4667 | 104.2 | −20.4 | −16.37 |
| 6/22/2017 | LC08 | 0.1564 | 34.5 | 249.6 | 101.5 | 0.4067 | 78.4 | −23.1 | −22.76 |
| 7/8/2017 | LC08 | 0.1324 | 4.3 | 289.1 | 89.7 | 0.3103 | 60.0 | −29.7 | −33.11 |
| 8/25/2017 | LC08 | 0.1045 | 77.2 | 253.8 | 84.5 | 0.3329 | 72.2 | −12.3 | −14.56 |
| 9/10/2017 | LC08 | 0.1045 | 50.7 | 241.0 | 58.7 | 0.2436 | 56.6 | −2.1 | −3.58 |
| 6/25/2018 | LC08 | 0.0501 | 0.0 | 269.0 | 5.0 | 0.0186 | 7.0 | 2.0 | 40.00 |
| 8/12/2018 | LC08 | 0.0864 | 68.6 | 291.3 | 55.5 | 0.1905 | 67.1 | 11.6 | 20.90 |
| 8/28/2018 | LC08 | 0.1032 | 66.6 | 268.7 | 68.7 | 0.2557 | 70.4 | 1.7 | 2.47 |
| 9/13/2018 | LC08 | 0.1211 | 41.0 | 246.2 | 60.5 | 0.2457 | 62.0 | 1.5 | 2.48 |
| 9/29/2018 | LC08 | 0.1040 | 36.7 | 216.6 | 54.4 | 0.2512 | 45.0 | −9.4 | −17.28 |
| 6/28/2019 | LC08 | 0.2862 | 64.5 | 229.7 | 146.8 | 0.6391 | 147.8 | 1.0 | 0.68 |
| 8/15/2019 | LC08 | 0.2356 | 42.6 | 276.6 | 116.8 | 0.4223 | 137.2 | 20.4 | 17.47 |
- Note: NDVI* is scaled NDVI of the lysimeter. Actual evapotranspiration (ETa as measured by lysimetry), reference crop ET (ETo), modelled ET, and precipitation (PPT) are 48-day totals (mm) leading up to the corresponding Landsat acquisition date.

| Variable | Coefficient | SE | p value | SEE |
|---|---|---|---|---|
| Full model | 0.1754 | |||
| Intercept | −0.1172 | 0.0430 | 0.01 | |
| NDVI* | 2.5461 | 0.3214 | <0.000 | |
| PPT | 0.0021 | 0.0008 | 0.017 | |
| NDVI*:PPT | −0.0058 | 0.0050 | 0.257 | |
| Final model | 0.1863 | |||
| Intercept | −0.0793 | 0.0319 | 0.018 | |
| NDVI* | 2.1057 | 0.2303 | <0.000 | |
| PPT | 0.0019 | 0.0003 | <0.000 | |
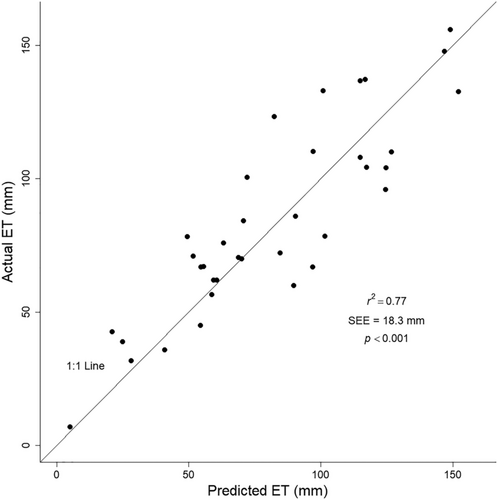
A plot of ETa versus ETa predicted (modelled) by Equation 9 revealed a good, balanced fit, without any strong outliers (Figure 5).
3.3 Error in ET estimates
In order to quantify the error resulting from ETa estimates predicted using Equation 9, we compared the 48-day modelled ETa values to ETa measured by the lysimeter. While individual residual errors (% of ETa) ranged from −33.11% to +103.83%, these errors tended to cancel each other out, with an average of only 9.92% across all observations (Table 2). The highest residual error is likely explained by rainfall that occurred just prior to that 48-day period, resulting in a substantial overprediction of ETa. PMRE in the current study was also reasonably low at 22.23%.
Average error in our ETa model was similar to that reported by Groeneveld et al. (2007), who modelled ETa in phreatophytic vegetation communities using Landsat NDVI. Average error across sites in their study ranged from 2.2% to 12.5%, with individual errors as high as 175.1%. Ramón-Reinozo et al. (2019) used Landsat NDVI and EVI to estimate ETa in a high elevation region of Ecuador and reported a mean percent error of −36.0% and −32.1%, respectively. Error in our study was higher than that reported by Nagler et al. (2013), who calibrated an ETa equation using MODIS EVI. Average error across sites in their study was 5.4%, with a lower range of values compared to our study (2.9%–9.3%). PMRE in our study was comparable to the global MODIS ET product (24.1%–24.6%; Mu et al., 2011). Overall, our VI-ETa model performed as well as, and in some cases better than, similar models described in the literature.
3.4 Assumptions and limitations
Although the average residual error of our ETa model was reasonably low, the algorithm has several key limitations and assumptions that must be considered prior to its application over a particular area. (1) Plants primarily moderate soil water loss, and soil evaporation is limited. One unique feature of our algorithm is that it predicts ET in an upland plant community, as opposed to phreatophytic systems where canopy expression is not limited by availability of water. While phreatophytes predominantly moderate soil water loss, soil evaporation will likely be a larger contributor to ETa in upland environments. Our algorithm likely performed well for the upland species in Monticello because the area is cool and the lysimeter was mostly shaded or covered by plants and mulch, which both reduce soil evaporation (20-year mean bare ground = 13.7%). For this reason, in areas that are warmer and/or more exposed (e.g., large areas of bare soil), evaporation will likely contribute more to ETa, which will not be captured by NDVI*. (2) The climate must be arid to semiarid, emphasizing the point that plants and atmospheric evaporative demand (via ETo) predominantly moderate soil water loss. (3) Because greenup of upland plants will primarily be dependent on local PPT, mean NDVI* of these communities must adequately capture canopy expression over the growing season.
It must be stressed that our model is limited to Landsat 5 TM and Landsat 8 OLI sensors. We initially included Landsat 7 ETM+ in our calibration but found a disproportionate spectral response between NDVI0 and NDVIs that the scaling process did not resolve. It is unclear if the issues we encountered were due to the SLC failure on Landsat 7 (resulting in missing pixels), but the Groeneveld and Baugh (2007) scaling technique may not properly stretch values over a scene if true NDVIs is not captured. Therefore, we do not recommend Landsat 7 data be applied to our ETa model. Another factor that could limit temporal continuity of our model is the lag between rainfall and resultant changes in soil water storage and percolation (i.e., 48-day periodicity). This could be problematic where cloud cover is likely to contaminate Landsat scenes.
The linear relationship between ETa and NDVI* in the current study is consistent for a sagebrush steppe (Prater & DeLucia, 2006); however, as we observed in the current study, low NDVI* values characterize these plant communities (Kremer & Running, 1993; Prater & DeLucia, 2006); therefore, it is unknown how the ETa–NDVI* relationship might change for higher VI values. In other vegetation communities, a similar linear relationship was observed between ETa/ETo and low VI values, while the relationship was distinctly non-linear at higher values (Nagler et al., 2013). For this reason, our model should not be applied to areas where NDVI* values greatly exceed those included in our calibration. Additionally, because we were limited to approximating Penman–Monteith ETo for temperature-only datasets, this likely contributed to additional uncertainty in our model. Ideally, a complete set of meteorological variables measured onsite would be used in the calculation of ETo, but, since these variables are rarely available, our approach broadens its applicability to areas where only temperature is known.
3.5 Management implications
Traditionally, VI-ETa studies, especially in the arid Desert Southwest, have focused on phreatophytic systems and groundwater discharge (e.g., Glenn et al., 2016; Jarchow et al., 2020; Jarchow, Nagler, Glenn, Ramírez-Hernández, & Rodríguez-Burgueño, 2017; Nagler et al., 2016). To our knowledge, this is the first VI-ETa algorithm calibrated in a semiarid upland plant community using field-scale lysimetry. Despite the limitations discussed in the previous section, our algorithm has important management implications, especially for situations where vadose zone water use is of interest. For example, in waste disposal areas such as Uranium Mill Tailings Radiation Control Act sites, accurate and spatially explicit ETa estimates are important for monitoring potential mobilization and transport of contaminants past the root zone into local aquifers and for monitoring and modelling effects of recharge on flow and transport of contaminants in underlying aquifers. Therefore, in such areas dominated by shallow rooted upland species, it is imperative to determine if PPT exceeds ETa, which could mobilize vadose zone contaminants and increase flow and transport of groundwater contaminants. Landscape-scale monitoring of ETa is also important for evaluations of engineered covers overlying waste contained in disposal cells, like at the Monticello site, that rely on ET to limit percolation into underlying waste. Additionally, because plant communities, soil properties and soil covers vary across the landscape, detection of spatial variability in ETa is needed to identify localized areas where recharge may occur (Link, Waugh, Downs, Thiede, et al., 1994).
ACKNOWLEDGEMENTS
We would like to thank the late Dr. Edward Glenn, whose ideas inspired the development and pursuit of this study, and the two anonymous reviewers who helped improve this manuscript. Dr. William Albright and Dr. Craig Benson collaborated on lysimetry. Aaron Tigar and Chris Holmes maintained lysimeter instrumentation. Linda Sheader, Marilyn Kastens, David Holbrook and Danika Marshall monitored vegetation annually. Funding was provided by the U.S. Department of Energy Office of Legacy Management and the U.S. Environmental Protection Agency. Any use of trade, firm or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government.
Open Research
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are available from the corresponding author upon reasonable request.




