Comparison of three machine learning algorithms for classification of B-cell neoplasms using clinical flow cytometry data
Abstract
Multiparameter flow cytometry data is visually inspected by expert personnel as part of standard clinical disease diagnosis practice. This is a demanding and costly process, and recent research has demonstrated that it is possible to utilize artificial intelligence (AI) algorithms to assist in the interpretive process. Here we report our examination of three previously published machine learning methods for classification of flow cytometry data and apply these to a B-cell neoplasm dataset to obtain predicted disease subtypes. Each of the examined methods classifies samples according to specific disease categories using ungated flow cytometry data. We compare and contrast the three algorithms with respect to their architectures, and we report the multiclass classification accuracies and relative required computation times. Despite different architectures, two of the methods, flowCat and EnsembleCNN, had similarly good accuracies with relatively fast computational times. We note a speed advantage for EnsembleCNN, particularly in the case of addition of training data and retraining of the classifier.
1 INTRODUCTION
In pathology, flow cytometry has found broad applications in the diagnosis, classification, and monitoring of various diseases. It is particularly valuable in hematopathology, where it plays a crucial role in the evaluation of blood disorders, such as leukemia and lymphoma. The data generated by flow cytometry is typically presented in the form of two-dimensional scatter plots or histograms of marker properties such as forward scatter, side scatter, and biomarker fluorescence intensity. These plots allow for the visualization and interpretation of heterogenous cellular populations. Flow cytometry “gating” is a crucial step in the data analysis process that helps to identify and isolate specific populations of cells within a sample. It involves the selection of specific regions or subsets within two-dimensional scatter plots to focus the analysis on relevant cell populations and exclude unwanted background noise. The process may be repeated for subsets of cells identified in this manner, resulting in a consecutive series of such gates.
Given this manner of manual classification of flow cytometry data, it stands to reason that a machine learning technique might be designed to automatically carry out this process, and, indeed, there is a history of published research literature in the application of various machine learning approaches to classification of flow cytometry data (Aghaeepour et al., 2013; 2011; Ge & Sealfon, 2012). Note that we use “machine learning” as an umbrella term for learning methods such that it includes both deep learning methods (i.e., deep neural network-based methods) as well as other approaches that do not fall under the term “deep learning” (e.g., random forests, support vector machines). There are many examples of prior applications of machine learning and related computational methods to flow cytometry. One application is the unsupervised clustering of flow cytometry events to identify subpopulations of cells, and many clustering algorithms have been developed (Aghaeepour et al., 2013; Liu et al., 2019; Weber & Robinson, 2016). This approach offers what is expected to be a less biased approach to identifying cell subpopulations since the algorithms can identify subpopulations beyond those that the human operator is looking for via traditional gating, and it is not restricted to two-dimensionally-based polygon gates. In another application, traditional gating can be enhanced by algorithm-assisted gating, which allows detailed, visual interpretation of the algorithm's approach to division of data into subpopulations and is more similar to traditional practice; some of these algorithms include FlowDensity, FlowType, and FlowLearn (Aghaeepour et al., 2012; Lux et al., 2018; Malek et al., 2015). In some applications, the immunophenotypes of various cell populations (e.g., neoplastic cells of chronic lymphocytic leukemia) are well defined and distinct from the background population of cells. In these cases, classification of single cells can be performed which can be particularly useful, for example, in minimal residual disease analysis, wherein the number of neoplastic cells is very small (Salama et al., 2022). In situations in which a diagnosis might be more accurately rendered by considering the context of the cell population as a whole (which classification methods are the focus of examination of this paper); most of these approaches require some sort of dimensionality reduction step to reduce a list of individual cells to an overall population representation. These dimensionality reduction approaches can also aid in visualization of flow cytometry data that can help identify clustering of cells in a way that cannot be easily achieved using the traditional series of two-dimensional plots. Some of these dimensionality reduction approaches include principal component analysis (PCA), t-SNE, UMAP, self-organizing models (SOMs), SPADE, Wanderlust, Citrus, and PhenoGraph (Brinkman, 2020). We note that in addition to clustering, classification, and dimensionality reduction algorithms, much work has also been invested in accompanying quality control and scaling/normalization algorithms, which help to filter out low quality events (e.g., “doublets”, data collected during interruptions in fluid flow, and laser excitation interruptions) and scale data to minimize batch to batch differences. Some available quality control packages include flowAI (Monaco et al., 2016), flowClean (Fletez-Brant et al., 2016), and PeacoQC (Emmaneel et al., 2022), while various scaling and batch normalization packages include gaussNorm (Hahne et al., 2010), fdaNorm (Finak et al., 2014), and CytoNorm (Van Gassen et al., 2020).
While there are numerous advantages of an automated process for classifying flow cytometry data, two major considerations are of great interest to the clinical laboratory: first, it could significantly ease the workload burden on the part of pathology personnel, and, second, it could potentially reveal possibilities for more accurate classification of cases for which a straightforward gating structure may not be immediately apparent to the human eye. We will return to these ideas and others in our Discussion.
Here we present a comparison of three recently published machine learning methods for classification of clinical flow cytometry data. Each of the examined methods classifies samples according to specific disease categories using ungated flow cytometry data. The first classifier employed here is “Flowcat”, published by Zhao et al. (2020). The algorithm has been presented in the context of classification of subtypes of mature B cell neoplasms along with normal cases (we perform our analyses under the same classification problem; see Methods – Section 2). Flow cytometry routinely plays a significant role in the diagnosis of many types of B cell neoplasms (Seegmiller et al., 2019). This approach uses self-organizing maps as a dimensionality reduction tool to preprocess the data before the application of a convolutional neural network (Li et al., 2022) to obtain the classification results.
The second classifier we apply is “EnsembleCNN”, first presented by Simonson et al. (2021) for diagnostic binary classification of presence or absence of classic Hodgkin lymphoma, followed by prediction of need for additional antibody panels in real-time (Simonson et al., 2022). While this approach also utilizes convolutional neural networks, rather than train a single CNN as with Flowcat, EnsembleCNN trains a set of CNNs, one for each possible pairwise marker combination that can be generated from the antibody panels available (see Methods – Section 2). Dimensionality reduction is achieved by generating a series of two-dimensional histograms, one for each possible pairwise marker combination. The output of these CNNs is then aggregated through a random forest classifier to obtain the final predictive labels.
Finally, (Ng & Zuromski, 2021) presented an approach for classification of clinical flow cytometry data that uses uniform manifold approximation and projection (UMAP; McInnes et al., 2018) as a dimensionality reduction approach with a Random Forest (Ho, 1995) to perform the classification task, which we abbreviate as UMAP-RF here and is our third algorithm we review herein. In Ng and Zuromski (2021) UMAP-RF is applied to the detection and classification of B-cell malignancies from peripheral blood derived flow cytometry data with a 10-color B-cell panel. The 12-parameter data (10 fluorescence parameters along with forward scatter and side scatter) was first reduced to two dimensions through UMAP embeddings and then summarized as two-dimensional histograms, which served as input for random forest classification.
Here, we report a comparison of these classifiers and evaluate them in terms of classification accuracy and relevant performance metrics as well as computational efficiency in terms of computing time (Figure 1). We also discuss the relevant explainability potential of each of these classifiers.
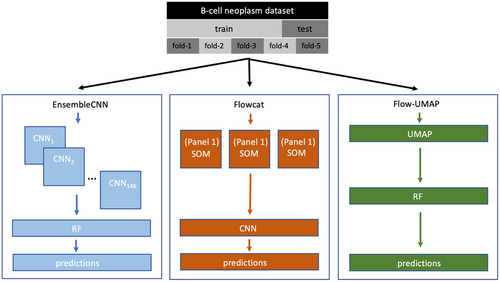
2 METHODS
2.1 Flow cytometry dataset
The clinical flow cytometry dataset analyzed in this work is comprised of 21,152 total cases from the Munich Leukemia Laboratory (MLL) spanning normal controls and eight different B-cell neoplasm subtypes according to the provided diagnosis. Specimens consisted of either peripheral blood or bone marrow aspirate, and the data were collected using Navios instruments (personal communication). The case dates vary from 2016-01-02 to 2018-12-13 and have been made publicly available in association with publication of the Flowcat classifier (Zhao et al., 2020). Thus, our analysis of this dataset with respect to the Flowcat classifier will in large part be an independent reproduction of the results presented in Zhao et al. (2020). Note that we are using the data as it has been curated for the Flowcat project, which involves pre-processing of the data as described by Zhao et al. (2020). This includes linear gain with a factor for SS and FS channels, and exponential scaling for other channels, as well as visual inspection of channel plots to detect machine calibration issues. In the deposited data, apart from the case date, no additional metadata was available that could be used for pre-processing of the cases on our end.
The cases have reported neoplastic cell levels varying from 0% to 97% (mean = 15.82%). Most cases have 3 antibody panels (n = 20,738) while some have only 2 panels (n = 414), with these being comprised of 7 panels in total. Note that institution specific and cytometer specific variables were not available for possible batch-wise adjustments.
Selection of cases that include the top 3 most widely available marker panel subsets provides us with a set of 20,731 cases with the subtype specific counts shown in Table 1 and the selected antibody panels in Table S1. The selected files range from 10,028 to 50,000 cells (mean = 47,781.5). The selected markers are as follows; for panel 1, forward scatter (FS), side scatter (SS), FMC7-FITC, CD10-PE, IgM-ECD, CD79b-PC5.5, CD20-PC7, CD23-APC, CD19-APCA750, CD5-PacBlue, CD45-KrOr. For panel 2: FS, SS, Kappa-FITC, Lambda-PE, CD38-ECD, CD25-PC5.5, CD11c-PC7, CD103-APC, CD19-APCA750, CD22-PacBlue, CD45-KrOr. For panel 3: FS, SS, CD8-FITC, CD4-PE, CD3-ECD, CD56-APC, CD19-APCA750, HLA-DR-PacBlue, CD45-KrOr.
| Type | Count | Description |
|---|---|---|
| Normal | 11,373 | Normal |
| CLL | 4442 | Chronic lymphocytic leukemia |
| MBL | 1614 | Monoclonal B-cell lymphocytosis |
| MZL | 1121 | Marginal zone lymphoma |
| LPL | 731 | Lymphoplasmacytic lymphoma |
| PL | 593 | Prolymphocytic leukemia |
| MCL | 313 | Mantle cell lymphoma |
| FL | 250 | Follicular lymphoma |
| HCL | 225 | Hairy cell leukemia |
We omit hairy cell leukemia variant (HCLv), given the insufficient case counts (n = 69) to allow for training, testing, and validation. We use the remaining data for multi-class classification between 9 labels (normal and 8 B-cell neoplasm subtypes). We will use the subtype abbreviations presented in Table 1 to discuss our results from here on. It is important to note that the sub-type labels presented here are clinic-pathologic diagnoses and not decisions solely derived from analysis of flow data. Zhao et al. (2020) notes that the diagnoses were confirmed by complementary tests where necessary based on histology, cytomorpholoty, fluorescence in situ hybridization and/or molecular genetics.
2.2 Classifiers
2.2.1 Flowcat
Flowcat utilizes convolutional neural networks in conjunction with self-organizing maps (SOMs; Kohonen, 1990, 2013), an approach designed to convert flow cytometry data into lower dimensional representations. In the context of MFC data, SOMs have been utilized in previous research to obtain two dimensional representations, most notably by the FlowSOM method, presented by Quintelier et al. (2021) and Van Gassen et al. (2015). In FlowSOM, the two-dimensional representations are developed predominantly as a visualization tool in addition to obtaining a clustering of cells by cell type. However, in the context of Flowcat, the aim is to obtain a two-dimensional representation of the higher dimensional panel-level cell data to be utilized as input for a convolutional neural network. For example, a case analyzed using three antibody panels (resulting in three LMD, or listmode data, files, which contain all the raw data generated during acquisition and can be converted to the flow cytometry standard, or FCS, format) will be reduced to three m × m weight matrices computed independently of each other, which may then be treated similarly to typical image data.
The convolutional neural network portion of Flowcat can be described as follows: each panel (and resulting SOM weight matrix/dimensionality reduction) is processed through a separate pipeline of convolutional filters, with three levels of filters of gradually decreasing sizes applied, followed by global max pooling. The pooled outputs are then concatenated across the panels to form a single case-level input layer to a neural network comprised of two fully connected hidden layers (of 64 and 32 nodes, respectively), completed by an output layer with a set of nodes corresponding to the expected output classes (i.e., classification subtypes).
2.2.2 EnsembleCNN
EnsembleCNN also employs CNNs to perform classification; however, the overall architecture is significantly different from that of Flowcat. In EnsembleCNN, a separate CNN is trained for each possible pairwise combination of markers, conceptually similar to interpretation of the two-dimensional scatterplots typically observed during human analysis of flow cytometry data (Figure S1). The ensemble of outputs from the CNNs is passed to a random forest classifier for final classification of a given case.
Given that, the data curated is comprised of 3 marker panels of 11, 11, and 9 markers (see Table S1), EnsembleCNN trains CNNs. Each marker combination (represented by a CNN) has 9 output nodes, one for each of the possible classification labels, resulting in a total of 1314 outputs being provided as input to the random forest. The random forest itself is trained to produce a categorical 9-class label output. Note that these panels may share certain markers in common, and this does not affect the procedure.
To prepare the data to be provided as input to these CNNs, the following process is applied: for every pair of markers considered, the cells/events from a single file (i.e., LMD file corresponding to a single case and antibody panel) will form 2D histograms of size b × b where b is the number of bins along a given axis, with histograms being converted to log scale, with each bin value x being transformed as log(x + 1) and standardized to the [0, 1] range. Then the values on these b × b matrices will represent the proportion of cells corresponding to that region of the scatterplot.
The architecture of each CNN is depicted in Figure S1, which involves multiple convolutional filters with 10% dropout between them and max pooling at two levels. The output obtained from the final convolution layer is flattened into a single vector and provided as input to a single densely connected hidden layer of 64 nodes, followed by the output layer with softmax activation, with these last two layers incorporating L2 regularization to mitigate overfitting.
2.2.3 UMAP-RF
In UMAP-RF, a two-dimensional representation of each panel for all cases is obtained through the UMAP algorithm. Given that the training data in most classification scenarios would be hundreds or thousands of cases and thus total many millions of cells, it would be computationally exhaustive in typical laboratory resource settings to use all of the training data to build a UMAP representation. Therefore, a down sampling approach is suggested by Ng and Zuromski (2021) where a smaller subset of cells (ranging between 8.6 million and 21 million in the results presented) is selected across all subtypes to build a two-dimensional UMAP. Following this, both the training and testing data are embedded in two dimensions via this UMAP projection.
The 2D embeddings obtained in this way are then condensed into two-dimensional histograms of 32 × 32 bins. For example, a file containing 50,000 cells and 11 markers would first be projected to the UMAP space to obtain a matrix of 50,000 × 2 dimensions, and the resulting 2D scatterplot would then be further reduced to a 32 × 32 matrix of densities. This process would be performed independently for each panel of markers.
The resulting 2D histograms are then flattened and concatenated across the panels to obtain a single vector for each case. These vectors are then provided as input to train a random forest classifier, which provides the 9-class output labels. The testing cases can then be processed in the same manner and subjected to the random forest classifier to obtain the desired predictive labels.
2.3 Explainability tools
In terms of classifier feature importance, the primary measures we utilize here with respect to EnsembleCNN are Shapley Additive Explanation (SHAP) values. Originally introduced in the context of game theory (Shapley, 1988), it has been adapted as a tool for measuring the marginal contributions of each feature of a machine learning model to the outputs obtained (Lundberg & Lee, 2017). The approach involves computing a null or “background” set of values for each feature and running various subsets of feature combinations by replacement of each feature value for each datapoint tested with the background value. The outputs obtained from the model are then compared with the outputs obtained for the correct feature value, and the difference in outputs are aggregated to estimate the contribution of each feature to the output.
Given the architecture of EnsembleCNN, we can perform explainability operations at the level of the random forest classifier. This allows us to deduce which pairs of features are of high importance for each predicted class. Further, it is possible to apply SHAP based methods to identify from each individual histogram the most impactful bin regions; see Simonson et al. (2021) for an explanation of this approach.
In Zhao et al. (2020), the contribution of various markers to the CNN output is estimated through occlusion analysis, where the output is computed with each marker omitted, and comparison of the differences in the predictions obtained are indicative of the importance of each marker to each subtype. Zhao et al. (2020) also note that saliency maps can be used to map regions of FlowSOM networks to specific diagnoses. By mapping individual flow cytometry events to the FlowSOM nodes, it is possible to plot increased or decreased numbers of cells corresponding to a given region of two-dimensional flow cytometry plots, which can aid in highlighting cells with immunophenotypes that are important for diagnosis.
2.4 Software and programming
For working with Flowcat, the python code base was obtained through the relevant GitHub repository (Zhao, 2020). Due to the large number of dependencies of this codebase, we were unable to work with Flowcat with the more recent python versions, and instead the Flowcat analysis was performed using python 3.6, the version in which it was originally deployed. The classifier is implemented using the keras/tensorflow library (Abadi et al., 2016), and we made minimal modifications to the code—only for the purpose of replacing deprecated functions with their newer counterparts. Flowcat was then run through a high-level script, which calls various Flowcat operations, and the resulting prediction files were then analyzed.
For EnsembleCNN, we adapted the python code made available by the senior author, which was deployed using python 3.9. We did not significantly modify the CNN architecture beyond expanding the output layer from 2 nodes (binary classification) to 9 (multiclass classification), with softmax activation. The code utilizes the keras/tensorflow library, and we made use of the random forest classifier made available through sklearn (Pedregosa et al., 2011).
The analysis of UMAP-RF was also performed using python 3.9. We did not use any existing codebase for this approach besides standard python libraries and the UMAP and random forest functionalities made available through the umap-learn and sklearn libraries. For some of the UMAP generations, we utilized the Google Cloud Platform due to significant memory requirements.
For UMAP-RF, we attempted two versions: one that sampled 10 million events from the training cases (for each panel), and one that sampled 22 million events. The total number of events to be sampled would be divided by 9 to obtain the number of events to be sampled for each group, and then further divided by the number of cases in each group to determine the number of cells to sample from each individual case. These cells were used to build a UMAP, onto which all training and testing data (including all cells from these cases) were projected. This process was repeated for each of the three antibody panels used in the analysis. Following this, all UMAP projected data were converted to 32 × 32 standardized histograms, and the flattened versions of these histograms were concatenated across the three panels; this produced a single vector of length 3072, representing one case for input to the RF. With the 22 million events sampling, we encountered issues with memory requirements on our local GPU server available and resorted to using Google Cloud Platform functionality to build some of the UMAPs. These UMAP objects were then copied over to the standard computing server where the projection of individual cases and the subsequent random forest training and validation was performed.
Note that all classifiers were run on the same server with GPU processing made available through tensorflow compiled to enable GPU functionality where possible. The time command (available on Unix platforms) was used to measure the time taken by each method to perform the overall training and testing pipeline. With the exception of using a Google cloud computing environment for the generation of some large UMAPs, all other analyses were performed on our local GPU server which includes 376 GB RAM, two Intel(R) Xeon(R) Gold 6226R CPUs @ 2.90 GHz, and two NVidia Quadro RTX 6000 GPUs with 24 GB VRAM each.
3 RESULTS
We performed several analyses based on the B cell neoplasm subtype classification problem. First, we performed a classification analysis based on a training and testing split of the data as presented in Zhao et al. (2020). We also performed a 5-fold cross validation with the Flowcat and EnsembleCNN classifiers to compare the predictions obtained for the entire dataset (UMAP-RF was not run by 5-fold cross validation due to greatly increased computation time required).
3.1 EnsembleCNN: Effect of histogram bin size
With EnsembleCNN, we tested the performance of varying the number of bins along a given axis for values 5, 10, 25, 50, 75 and 100 (See Figure S2 for an example of forward scatter versus CD45 for different numbers of bins). We first used the portion of training data reserved for training the random forest classifier to perform training and testing of the random forest with different parameters for each of the number of bins tested. With respect to the weighted averages of class-wise precision and recall, bin numbers in the range of 25 to 75 remained fairly optimal and consistent; however with respect to the macro averages, a bin number of 25 was optimal, and we observed a small decrease in performance for certain classes (and therefore the resulting macro averages) for bin numbers 50 and 75. We also computed accuracies using the test set data for the histogram bin numbers to further investigate the effect of this parameter. Table S4 shows the class specific sensitivities (recall) and precisions obtained for the test set data at different bin numbers. These results are also conveyed in Figure S7 which shows the corresponding averaged precision, recall, and F1-scores (both macro and weighted by class size).
Interestingly, we observed that while classification performance increased with number of bins increasing from 5 to 25, towards the higher end of the range tested there was a decline in performance, especially at 100 bins per axis. This behavior is particularly striking for mantle cell lymphoma (MCL), marginal zone lymphoma (MZL), and prolymphocytic leukemia (PL). For most other classes, the performance remains fairly consistent or fluctuates somewhat as in the case of follicular lymphoma (FL). In the case of hairy cell leukemia (HCL), the recall reaches a maximum bins = 100.
As a result of this comparison of numbers of bins, we selected a bin number of 25 (per axis) as our optimal parameter for comparison of EnsembleCNN results with the other classifiers.
Our tuning of the random forest within the training data suggested 1000 estimators and a maximum cutoff of 100 leaf nodes as optimal.
3.2 Primary classification analysis using held-out test set
The creation of the held-out test set from the overall case set by Zhao et al. (2020) employs a date-specific cutoff (2018-07-01) for selecting the test set (2348 cases). This was done to simulate a laboratory deployment situation in which a classifier may be trained on existing cases and then tested on the incoming cases following the training of the classifier. We applied the same training and testing split to all three classifiers to compare the resulting predictions obtained (see Table 2). For EnsembleCNN, the training set was split again, with 50% randomly selected cases from each class being used for training the CNNs, and the remainder used for training the RF component.
| Group | Train | Test | |
|---|---|---|---|
| CNN | RF | ||
| CLL | 2016 | 2019 | 403 |
| MBL | 776 | 778 | 60 |
| MCL | 136 | 139 | 38 |
| PL | 278 | 277 | 36 |
| LPL | 320 | 322 | 84 |
| MZL | 498 | 499 | 116 |
| FL | 110 | 112 | 24 |
| HCL | 100 | 101 | 24 |
| Normal | 4900 | 4903 | 1563 |
For UMAP-RF, we performed two sets of tests with different levels of sampling to build the UMAPs. In the first instance we sampled approximately 10 million events from each panel. To balance the sampling across the classes, this was equally distributed across the classes: for example, since there are 201 HCL cases in the training set, 10,000,000/(9 × 201) = 5527 events would be sampled from each HCL case in the training set for each panel. In the second instance, we sampled 22 million events from each panel. Figures S5 and S6 show the classification results obtained for these samplings, with the 22 million events sampling providing a significantly better result than the 10 million events sampling even with just 2 panels (the 10 million events sampling was performed for all 3 panels), and we have used this result as the benchmark for comparison with the other classifiers as it is to date the best performance we have obtained with UMAP-RF.
Table 3 shows the classification performances obtained for comparison (with UMAP-RF results being those obtained with a 22 million events sampling from each panel). Both EnsembleCNN and Flowcat yielded better performances than UMAP-RF, and the remaining focus of our comparative analysis will be predominantly on these two classifiers.
| Precision | Recall | F1-score | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Flowcat | EnsembleCNN | UMAP-RF | Flowcat | EnsembleCNN | UMAP-RF | Flowcat | EnsembleCNN | UMAP-RF | |
| CLL | 0.93 | 0.98 | 0.95 | 0.89 | 0.85 | 0.88 | 0.91 | 0.91 | 0.92 |
| FL | 0.51 | 0.75 | 0.62 | 0.83 | 0.75 | 0.75 | 0.63 | 0.75 | 0.68 |
| HCL | 0.92 | 1 | 0.92 | 1 | 0.96 | 0.92 | 0.96 | 0.98 | 0.92 |
| LPL | 0.64 | 0.54 | 0.34 | 0.5 | 0.63 | 0.51 | 0.56 | 0.58 | 0.41 |
| MBL | 0.44 | 0.47 | 0.44 | 0.6 | 0.75 | 0.58 | 0.51 | 0.58 | 0.50 |
| MCL | 0.67 | 0.76 | 0.61 | 0.37 | 0.58 | 0.37 | 0.47 | 0.66 | 0.46 |
| MZL | 0.75 | 0.72 | 0.67 | 0.68 | 0.71 | 0.55 | 0.71 | 0.71 | 0.61 |
| PL | 0.46 | 0.48 | 0.46 | 0.67 | 0.78 | 0.67 | 0.55 | 0.6 | 0.55 |
| Normal | 0.97 | 0.97 | 0.95 | 0.98 | 0.97 | 0.94 | 0.97 | 0.97 | 0.94 |
| Macro average | 0.7 | 0.74 | 0.66 | 0.72 | 0.77 | 0.69 | 0.7 | 0.75 | 0.66 |
| Weighted average | 0.91 | 0.92 | 0.88 | 0.9 | 0.91 | 0.87 | 0.91 | 0.91 | 0.87 |
- Note: Values in bold indicate the best performance value for the given diagnosis.
Comparing Flowcat and EnsembleCNN, normal cases are classified at 98% and 97% (sensitivity/recall), respectively, by both classifiers. The difference here amounts to 16 more normal cases being predicted correctly by Flowcat (see Figures S3–S6). HCL is predicted with perfect accuracy by both classifiers, and CLL is predicted at 89% and 86% sensitivity, respectively. For the remaining groups, there are larger differences in sensitivity by the two classifiers. MBL, MCL, PL, LPL are predicted with higher sensitivity by EnsembleCNN while FL and MZL are predicted with higher sensitivity by Flowcat.
Note that the F1-score is the harmonic mean of precision and recall and is considered a summary statistic of the two (F1 = 2 [precision × recall]/[precision + recall]). Table 3 also shows macro (all classes being weighted equally) and weighted (classes being weighted with respect to their sizes) results. The weighted averages for precision and recall (and hence the F1 score) are comparable between the two classifiers; for precision, Flowcat provides 91%, EnsembleCNN provides 92%, and UMAP-RF provides 88%; for recall they are 90%, 91%, and 87%, respectively; the F1-scores are respectively, 0.91, 0.91 and 0.87. When compared using the macro averaged results, EnsembleCNN performed slightly better. While some of the class specific results differ from those originally presented for Flowcat (Zhao et al., 2020), the F1-scores are on par with the previously reported weighted F1 of 0.92 and an averaged F1 of 0.73.
3.3 Five-fold cross validation
We performed 5-fold cross validations from random splits of the data (original training and testing sets combined) for both Flowcat and EnsembleCNN. The exact same data splits were processed with both classifiers. Figure 2 shows the cross-validation predictions aggregated across the 5-fold in the form of confusion matrix heatmaps. The rows in the heatmaps indicate the true labels and the columns indicate the predicted labels; hence, the diagonal indicates the recall/sensitivity obtained for each class.
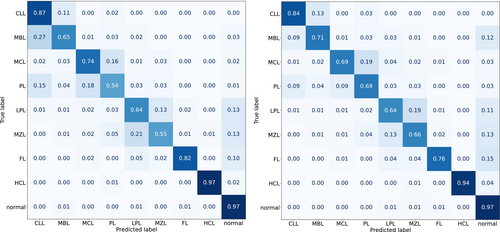
The results obtained are fairly similar to those obtained for the two classifiers in the previous held-out-test-set analysis. Normal samples are classified with 97% recall by both classifiers. For the remaining classes, there are fairly close levels of agreement (i.e., at most 6% difference) with the exceptions of prolymphocytic leukemia (PL), marginal zone lymphoma (MZL), and follicular lymphoma (FL). With PL, Flowcat obtained 54% recall across the 5-fold whereas EnsembleCNN obtained 69%. With MZL, Flowcat obtained 55% recall and EnsembleCNN obtained 66% recall. The reverse performance is true for the remaining case: for FL, EnsembleCNN performed at recall 76% while Flowcat obtained 82% recall.
The full precision, recall, and F1-score results are shown in Table S2. The weighted averaged results for the two classifiers are on par with each other, in the 87%–88% range for both precision and recall; however, the macro averages show some differences: for precision, Flowcat provides 72% while EnsembleCNN provides 66%. For Recall, Flowcat provides 75% for EnsembleCNN it is 69%. Summarizing these results, Flowcat obtains an F1-score of 0.73 while for EnsembleCNN it is 0.67.
3.4 Explainability analysis with EnsembleCNN classifier
For EnsembleCNN, we used the python shap package to perform an analysis of feature importance for the random forest classifier through Shapley Additive Explanations. The summary of the analysis performed with respect to the predicted outputs of the testing data are shown in Figure 3.
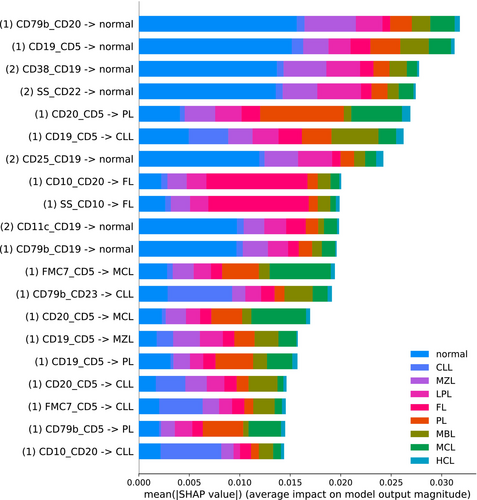
Note again that each of the 146 CNN classifiers have 9 outputs corresponding to probabilities predicting classes. Therefore, each input received by the random forest classifier can be labeled by the pair of markers derived from one of the three panels and the respective class label of the CNN output node, and feature labels derived in this manner are shown in the summary plot. For example, the topmost row has the label “(1) CD79b – CD20 –> normal”, which indicates that this corresponds to the normal class output from the CNN for the CD79 and CD20 marker combination from panel 1. The color scheme indicates that this feature is of high importance for prediction of normal cases, as are the next three features. The fifth row shows that CD20 versus CD5 is most impactful in identifying prolymphocytic leukemia, while the sixth row shows that CD19 versus CD5 is most impactful for identifying chronic lymphocytic leukemia. Additional associations can be determined in a similar manner.
Our SHAP value analysis also suggests that the most important marker pairs are found in panels 1 and 2. This is expected, as panel 3 is predominantly T-cell associated and therefore unlikely to be as relevant for the diagnostic purposes here in comparison to panels 1 and 2.
Explainability analysis was not performed using the Flowcat or UMAP-RF classifiers.
3.5 Resource usage
We also examined the classifiers with respect to their computational time usage to carry out the training and testing analyses referred to above. We analyzed the clock time elapsed as well as CPU/GPU time used by the system. A comparison of results is provided in Table S3 in minutes and seconds. The “real” time indicates the elapsed time as measured by the system clock; the ‘user’ and ‘sys’ times indicate the CPU time spent (by all cores) in user and system code, and the sum of the latter two indicate the total CPU time spent.
With Flowcat, the time for building the reference SOM was about 2 min on average, with the projection of all case data across all panels taking between 15 to 18 h on different iterations of the analysis carried out. The final CNN training was completed between 2 and 3 min in all the analyses performed. For the result provided in Table S3, the total clock time spent was 17.1 h, and the CPU time was 201.2 h.
For EnsembleCNN, the time taken in total (including the building of histograms) was much less. For 50 bins per axis, the time taken for training the 146 CNNs and the subsequent operations with the random forest amounted to about 1.5 h (with the time taken by the RF being negligible in comparison to the CNNs). The total clock time spent was 3.85 h and the CPU time was 3.55 h, with smaller numbers of bins taking even less time.
UMAP-RF had the highest time usage in our comparison, with multiple days being required to compute the projections of all cases. The timing results provided in Table S3 are with respect to the sampling of 10 million events from each panel, and the sampling of 22 million events took much longer for building the UMAP and obtaining the subsequent projections for all cases. For the 10 million events sampling, building the UMAP for a single panel took 1.8 h in clock time and 58.81 h in CPU time. The subsequent case projection (for both training and testing) took 225.76 h (about 9 days) in clock time and 13422.78 in CPU time. Note that these results need to be multiplied by ~3 to obtain the time required to process all 3 panels, unless there are computational resources adequate for performing UMAP analysis of all 3 panels concurrently. The training and testing of the random forest classifier itself only took about 3 min.
With UMAP-RF, we were also met with considerable challenges with respect to memory usage. The training of the UMAP requires a considerable amount of memory. For example, with the sampling of 10 million events, for each panel a matrix of 10,000,000 cells and 11 markers (or 9 markers for panel 3) need to be processed by the UMAP algorithm. With the 22 million events sampling, we could not complete some of the UMAP building on our local GPU server due to insufficient memory and resorted to using the Google Cloud Platform. For this level of sampling, the projection of individual cases with a single UMAP panel took nearly 15 days with the maximum available parallelized resource usage (i.e., ~45 days for all 3 panels and about 20,000 cases).
Overall, EnsembleCNN represented a significant time-advantage in these experiments when compared for overall training time. The times required for applying the EnsembleCNN and Flowcat classifiers to test sets is negligible by comparison. UMAP-RF requires considerably more resources in terms of both memory and time, and the results we have obtained so far do not suggest UMAP-RF as implemented here will be able to outperform the other two algorithms for most scenarios.
4 DISCUSSION
Our main classification results show modest distinctions between EnsembleCNN and Flowcat, both of which considerably outperformed our implementation of UMAP-RF. Macro averaging of precision values across the classes (i.e., average precision irrespective of class size) showed a very slightly higher averaged precision for EnsembleCNN than Flowcat, and the same holds true for recall values. Weighted averaging of precision values and recall values also demonstrated very similar performance.
With regard to misclassifications, we observed that both classifiers are likely to misclassify CLL as MBL, though the reverse (classify MBL as CLL) was predominantly observed for Flowcat. Both classifiers were also somewhat likely to misclassify mantle cell lymphoma and prolymphocytic leukemia as each other and the same pattern can be observed between lymphoplasmacytic lymphoma and marginal zone lymphoma. The misclassifications between CLL and MBL can be expected to a certain degree since MBL may be considered a precursor to CLL (Scarfò et al., 2013). Similarly, the confusion between mantle cell lymphoma and prolymphocytic leukemia for both classifiers is not surprising given the expected immunophenotypic similarities between the two entities, and similarly for marginal zone lymphoma versus lymphoplasmacytic lymphoma. Both classifiers infrequently mis-identify tumor cases from multiple classes as normal.
Given that the subtype level diagnostic labels associated with the cases have been derived through clinical diagnostic processes (including validation through complementary testing), it is to the credit of many of these algorithms that once trained, a substantial proportion of the labels could be derived through analysis of flow data alone. However, some degree of misclassification is expected, and we expect to perform further analysis regarding the misclassifications provided by each classifier in future work.
With regard to EnsembleCNN, the effect of varying the number of histogram bins on classification performance is noteworthy, and we believe this merits further investigation in the future, specifically with respect to the decrease in performance with regard to certain classes with increasing bin number beyond 25. One possibility for this might be that at higher resolution more noise is captured in the histogram whereas at lower resolutions only the more globally relevant levels of variability in cell immunophenotypes are represented. These results also suggest that the same bin size may not be the optimal setting for all classes or pairwise histogram being analyzed here; that is, different bin sizes, or combinations thereof, might yield more accurate classification.
Our analysis of training time usage demonstrated a considerable advantage for EnsembleCNN, by a factor of 2.5×–3.2× versus Flowcat. This could be of considerable importance in a clinical deployment setting where a classifier would be expected to be re-trained with additional incoming cases regularly to improve performance, as well as to ensure that the classifier is being trained to handle any time specific biases being introduced into the data. The time advantage would multiply for retraining since for EnsembleCNN the majority of time is spent in creating and saving two-dimensional histograms, which can be reused by simply concatenating the histograms with new data, while retraining with Flowcat would involve recalculating all FlowSOM embeddings each time.
Given that the UMAP-RF classifier took a considerably longer time than the other two classifiers, with much of that time being used for the projection of cases into UMAP embeddings, and given that it was unable to perform classification tasks as well as the other two, we believe it would not be a suitable competitor for a real-time deployment setting among this set of classifiers. While the 22 million events sampling provided a significantly better performance in comparison to the 10 million events sampling, it came at the cost of requiring considerably more memory to compute the UMAPs, as well as taking a considerable amount of time to compute the subsequent projections of individual cases. Given the time requirement, it became very prohibitive to carry out the 5-fold cross validation experiments that we carried out with the other two classifiers. We do note that the classification accuracy might be considerably improved for the UMAP-RF if variability in day-to-day or instrument-to-instrument signal intensities can be corrected; however, given that the instrument identification was not seen in the raw data files, it was not practical to attempt such a correction. If such corrections can be performed and a method is found to accelerate the UMAP algorithm, the approach's prediction accuracy could be more useful for real-time analysis.
In the course of this work, we carried out some simple explainability analysis by calculating SHAP values for the EnsembleCNN algorithm. The use of a separate CNN for each marker pair in EnsembleCNN allows an easy analysis of important marker pairs to be performed at the level of the random forest classifier. Further analysis of each individual CNN is also possible through a SHAP value analysis to deduce important regions of various marker combination histograms, and ultimately estimated for individual cells, as demonstrated in (Simonson et al., 2021). An alternative approach would be to train a CNN to perform cell-level classification (normal vs. neoplastic, for example), and then subsequently utilize the cell-level predictions to provide a diagnostic prediction. Indeed, we aim to provide an example of such an approach for flow data based diagnostic work in future publications. However, it should also be noted that the approach described here has the advantage of revealing possible hitherto un-used or under-used markers and/or bystander cells to arrive at a specific diagnosis prediction.
We did not conduct an explainability analysis for the Flowcat classifier or UMAP-RF classifier due to the time and resource requirements that it would entail. However, in the original FlowCat publication (Zhao et al., 2020), marker importance analysis was carried out through an occlusion analysis whereby each marker is replaced with zero values and the SOM generation, projection, and classifier training is repeated to compare the results obtained. A similar occlusion approach explainability analysis focused on marker importance could be performed for the UMAP-RF approach. Single cell highlighting in saliency maps could be performed for the FlowCat approach; we also note that further development of the software to employ Shapley Additive Explanations (SHAP) could help to identify predictive features more specific to individual cases.
Per the original article that introduced the data set (Zhao et al. 2020), the data were collected at the Munich Leukemia Laboratory (MLL). In a follow up study, the FlowSOM approach was applied to data from other labs using the previously learned weights and a transfer learning approach wherein additional learning was performed using data from the outside laboratories, which resulted in improved performance at those laboratories (Mallesh et al., 2021). While transfer of learning to other labs has thus been established for the FlowSOM approach, transfer learning for the other approaches has not been established. It is expected that retraining or transfer learning will be required for the other algorithms, similar to that of the FlowSOM algorithm. While it was not specified whether the data are of various specimen types (blood, lymph node, bone marrow, etc.), given that the three tested algorithms make their classification predictions using the ungated sample data, which therefore provides context for any abnormal cells for a given specimen type, it is therefore expected that with enough training data the classifiers might perform well for multiple sample types, though a comparison of algorithms trained on specific specimen types could be very informative, and we predict that with sufficient training data, specimen type specific classifiers would perform better.
This study has focused on the application of these algorithms for the classification of B-cell neoplasms, though it is expected that these and other artificial intelligence algorithms can be applied to many more diagnoses. Some examples include detection of acute myeloid leukemia (Ko et al., 2018), myelodysplastic syndrome (Duetz et al., 2021), chronic myeloid leukemia (Ni et al., 2013), acute lymphoblastic leukemia minimal residual disease detection (Fišer et al., 2012; Reiter et al., 2019), and chronic lymphocytic leukemia minimal residual disease detection (Salama et al., 2022). There are several ways in which such algorithms could be used to enhance the practice of clinical flow cytometry generally. All three of the algorithms could be used to automatically review flow cytometry to flag cases for priority review by a pathologist to help in the quicker diagnosis of patients with aggressive disease. The algorithms could also be used for automated flagging of cases that require additional flow cytometry antibody panels work-up. Simonson et al. previously demonstrated this in reporting a real-time, prospective study of the potential utilization of the EnsembleCNN algorithm to flag cases that would require an additional flow cytometry antibody panel to help discriminate chronic lymphocytic leukemia from mantle cell lymphoma (Simonson et al., 2022).
In that study, the EnsembleCNN algorithm frequently checked the flow cytometry data file server for newly available data, and if the probability score threshold of needing the additional antibody panel was met, an email was immediately sent to one of the authors of the study. The conclusion of the study was that the algorithm performed very well when compared with the actual ordering of the additional antibody panel and could eventually be used to expedite work-up of cases and require less time of technologists and hematopathologists. Alternatively, identification of such cases could be used to batch similar cases for more efficient laboratory workflow when speed of work-up is not the highest priority. It is also noted that, in the current study, it is recognized that several of the diagnoses will not be made based on flow cytometry alone (e.g., marginal zone lymphoma and plasma cell lymphoma); however, the probability scores for those diagnoses could be used to help notify the hematopathologist early regarding the potential need to order relevant immunohistochemical and special stains, which could aid in meeting time cutoffs for placing orders for stains. The predictions made by the algorithms could also be used to create draft or templated reports, which can save hematopathologists time and promote consistency in reporting. These algorithms could also be used for potential quality improvement by flagging cases for additional review for which the diagnoses rendered in draft reports by staff members do not match the diagnoses predicted by the algorithm, potentially helping improve diagnostic accuracy. Finally, with further development and validation, it is conceivable that these algorithms could serve in the place of a second official hematopathology reviewer, decreasing the workload for hematopathologists that often must serve this role for select kinds of cases/diagnoses. In short, the opportunities for using artificial intelligence to assist in and improve flow cytometry are plentiful.
In summary, while accuracy metrics are very similar for Flowcat and EnsembleCNN approaches, computational time required to train the algorithms was less for EnsembleCNN. UMAP-RF, as implemented for this publication, was an order of magnitude slower for training and was less accurate in diagnosis predictions. It is expected that additional feature engineering in combination with explainability analysis could improve the performance of all three algorithms, which will be the subject of future work.
ACKNOWLEDGMENTS
This work was supported by the Department of Pathology and Laboratory Medicine at Weill Cornell Medicine, Cornell University, with the support of National Institutes of Health awards U54CA273956 and R01CA200859. We thank Lauren Zuromski for their assistance with manuscript reviewing and Nanditha Mallesh for assistance with flowCat setup.
CONFLICT OF INTEREST STATEMENT
The authors declare no conflicts of interest.
Open Research
DATA AVAILABILITY STATEMENT
Source code will be made available on GitHub (https://github.com/wikum/flowComparison/) with publication of the manuscript. [Corrections added on May 24, 2024, after first online publication: Data Availability Statement has been updated.]




