A framework for dense triangular matrix kernels on various manycore architectures
Summary
We present a new high-performance framework for dense triangular Basic Linear Algebra Subroutines (BLAS) kernels, ie, triangular matrix-matrix multiplication (TRMM) and triangular solve (TRSM), on various manycore architectures. This is an extension of a previous work on a single GPU by the same authors, presented at the EuroPar'16 conference, in which we demonstrated the effectiveness of recursive formulations in enhancing the performance of these kernels. In this paper, the performance of triangular BLAS kernels on a single GPU is further enhanced by implementing customized in-place CUDA kernels for TRMM and TRSM, which are called at the bottom of the recursion. In addition, a multi-GPU implementation of TRMM and TRSM is proposed and we show an almost linear performance scaling, as the number of GPUs increases. Finally, the algorithmic recursive formulation of these triangular BLAS kernels is in fact oblivious to the targeted hardware architecture. We, therefore, port these recursive kernels to homogeneous x86 hardware architectures by relying on the vendor optimized BLAS implementations. Results reported on various hardware architectures highlight a significant performance improvement against state-of-the-art implementations. These new kernels are freely available in the KAUST BLAS (KBLAS) open-source library at https://github.com/ecrc/kblas.
1 INTRODUCTION
Basic Linear Algebra Subroutines (BLAS) are fundamental dense matrix operation kernels for implementing high-performance computing applications, eg, ranging from dense direct solvers to eigenvalue solvers and singular value decomposition. Although they are extensively optimized by hardware vendors1-3 and often available in open-source libraries,4-6 some BLAS kernels operating on general triangular matrix structures, coming from the symmetry or the upper/lower matrix formats, do not run at the sustained bandwidth (Levels 1 and 2 BLAS)7 or peak performance (Level 3 BLAS). The kernels from the latter BLAS family have often been taken for granted in extracting hardware performance due to their high arithmetic intensity, which usually results in performing matrix-matrix multiplication operations. In fact, it turns out that the dense triangular Level 3 BLAS kernels, ie, the triangular matrix-matrix multiplication (TRMM:B=α A B), and the triangular solve with multiple right-hand sides (TRSM:A X=α B), suffer from performance losses, as demonstrated in a previous work from the authors.8 To remedy these losses, current high-performance implementations3, 9 rely on an out-of-place (OOP) design of these aforementioned kernels, which help exposing more parallelism by weakening the thread synchronizations encountered during the Write After Read (WAR) and Read After Write (RAW) data dependency hazards for TRMM and TRSM kernels, respectively. In particular, we addressed in Charara et al8 4 resulting drawbacks, due to the OOP design as opposed to the in-place (IP) design, in the context of a single GPU platform: (1) extra memory allocation, thus limiting the size of problems achievable in scarce memory resources, especially on GPUs, (2) extra data movement, causing extra data transfer time, (3) inefficient use of caches that need to serve one extra matrix, thus increasing cache misses, and most importantly, (4) violation of the standard legacy BLAS API.
In this paper, we extend the work in Charara et al8—in which we demonstrated the effectiveness of recursive formulations in enhancing the performance of these kernels—and present a new high-performance framework for dense TRMM and TRSM BLAS kernels on various hardware architectures. We further enhance the performance of these triangular BLAS kernels on a single GPU by implementing customized CUDA kernels for TRMM and TRSM, which are called at the bottom of the recursion. In addition, a multi-GPU implementation of TRMM and TRSM is proposed and shows an almost linear performance scaling, as the number of GPUs increases. Last but not the least, the algorithmic recursive formulation of these triangular BLAS kernels is in fact oblivious to the targeted hardware architecture. We propose, therefore, to port these recursive kernel designs to homogeneous ×86 hardware architectures by relying on the underlying vendor or open-source optimized BLAS implementations to further boost the performance of the respective native triangular BLAS kernels. Results reported on various hardware architectures and optimized BLAS implementations highlight a significant performance improvement against state-of-the-art BLAS libraries. These new kernels are freely available in the KAUST BLAS (KBLAS) open-source library at https://github.com/ecrc/kblas.
The remainder of the paper is organized as follows. Section 2 provides a literature review for the kernels of interest. Section 3 recalls the uniform design strategy for recursive high performance TRMM and TRSM BLAS kernels, as detailed in Charara et al,8 and motivates the need for further enhancements. Section 4 describes the implementation of the proposed customized kernels, on single and multiple GPUs, as well as the design portability on Intel x86 hardware against various BLAS libraries. Section 5 presents performance results (in single and double precision arithmetic) and comparisons against existing high-performance BLAS implementations. We conclude in Section 6.
2 RELATED WORK
Various hardware vendors and third-party academic software libraries provide support for highly tuned dense linear algebra (DLA) operations for the scientific community. On x86 architectures, of the most widely used libraries are the Intel MKL1 and OpenBLAS.4 Both libraries provide an in-place (IP) variant of the triangular Level 3 BLAS kernels on CPUs in congruence with legacy BLAS API. However, both libraries exhibit TRMM and TRSM kernels performances much inferior to the sustained peak performance, calculated from the matrix-matrix multiplication (GEMM) kernel, which is a legitimate upper bound for compute-bound BLAS kernels.
On GPU hardware accelerators, the NVIDIA cuBLAS and cuBLAS-XT libraries3 provide support for TRMM and TRSM kernels on single and multiple GPUs, respectively. The cuBLAS library maintains both IP and OOP variants of TRMM, and the IP variant of TRSM, while assuming data resides on the GPU global memory. On the other hand, cuBLAS-XT provides a CPU API, which assumes the matrix resides on the CPU host memory and transparently manages the data movement between CPU and GPU main memories. The cuBLAS-XT library provides an OOP and IP variants of TRMM and TRSM, respectively.
Matrix Algebra on GPU and Multicore Architectures (MAGMA)9, 10 provides an OOP implementation for TRSM supporting single and multiple GPUs. To achieve better performance, MAGMA inverts the diagonal blocks of the triangular input matrix and casts the remaining computations into GEMM calls. Besides the overhead of additional memory allocations, numerical accuracy issues may be encountered during diagonal block inversions.
BLASX is a highly optimized multi-GPU Level 3 BLAS library that has been recently introduced and released.6 It claims significant speedups against cuBLAS-XT, MAGMA, and other multi-GPU numerical libraries with runtime systems. BLASX uses the tile algorithm with a dynamic runtime scheduler to achieve load balance across GPUs and multilevel caching techniques with peer-to-peer GPU communication to minimize data transfer time.
KAUST BLAS (KBLAS) is an open-source library that provides highly optimized implementations for a subset of BLAS routines on NVIDIA GPUs as well as x86 architectures.7, 8, 11-13 In particular, the authors have already demonstrated significant performance gains for IP TRSM and TRMM against cuBLAS IP and MAGMA OOP implementations on a single NVIDIA GPU.8 They use a recursive formulation of TRSM and TRMM that converts most of the computations into GEMM operations, while optimizing the data access pattern.
Finally, converting DLA kernels into GEMM-like operations has been well studied in the literature14-16 due to the fact that GEMM is embarrassingly parallel, maps well to the hierarchical memory of modern CPUs and GPUs, and performs very close to the theoretical peak performance. Recursive formulations of DLA kernels are one way to further enrich them with GEMM calls. Employing a recursive formulation is also not a new technique in DLA.17-22 Recursive DLA algorithms have been employed to minimize data motion across the hierarchical memory layers on x86 architectures.19, 20 It has been also applied in the context of speeding up large bandwidth-limited workloads seen during the panel factorizations of dense matrices.
3 BACKGROUND ON GENERAL RECURSIVE TRMM AND TRSM KERNELS
In this section, we briefly recall the uniform design strategy for recursive high-performance TRMM and TRSM BLAS kernels and motivate the need for further enhancements of these kernels.
3.1 Recursive formulations
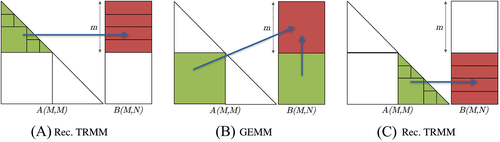
In Charara et al,8 we addressed the performance optimizations of triangular Level 3 BLAS operations (TRMM and TRSM) on single GPU and proposed using a recursive formulation that converts most of the computations to GEMM calls. The recursive TRMM operation RecTRMM: B=αA×B can be expressed recursively as follows. Consider the left/lower/transpose case, and let M and N be the number of rows and columns of B, respectively. We use the following notation for submatrices: Xr1:r2,c1:c2 is the submatrix of X whose rows indices range from r1 until r2 inclusive and whose column indices range from c1 until c2 inclusive (array indices starting with 1). Consider m=M/2, with m preferred to be the largest power of 2 less than M, for smoother further recursive splits.
Then, we proceed with three subsequent steps: (1) operate recursively on B1:m,1:N with RecTRMM:
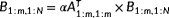, as illustrated in Figure 1A, (2) apply GEMM:
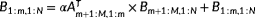, as illustrated in Figure 1B, and (3) operate recursively on Bm+1:M,1:N with RecTRMM:
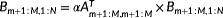, as illustrated in Figure 1C. By the same token, this recursive formulation applies for the TRSM kernel. Other variants of TRMM and TRSM operations (right/upper/transpose, etc) can be expressed in a similar recursive theme. We stop the recursion and resort to calling the native TRMM/TRSM routines at the bottom of recursion at a size where original implementations usually exhibit decent performance, rather than continuing recursion until very small sizes, where kernel launch overheads may dominate (experimentally, 128 is a good choice). It is noteworthy to mention that these recursive formulations do not incur any additional flops relative to the original serial algorithm (O(M2N) for left sided TRMM/TRSM, O(MN2) for right-sided TRMM/TRSM).
3.2 Motivation for further enhancements
As recalled above, the recursive formulation of TRSM and TRMM kernels converts most of the computations into GEMM calls. Figure 2 illustrates how the innermost calls to TRSM or TRMM routines at the leaves of the recursion operate on small triangular blocks located in the diagonal along with a thin and wide portion of the output matrix (ie, a general matrix for TRMM or a matrix containing the right-hand sides for TRSM), where number of columns N may be larger than number of rows M.
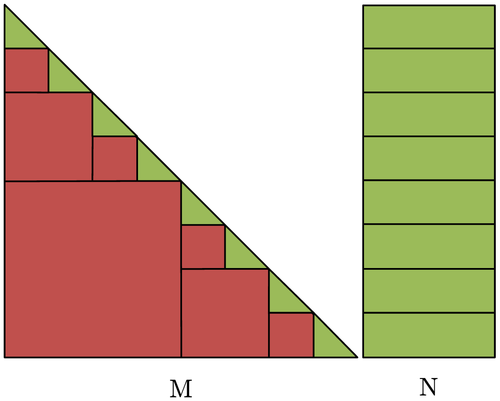
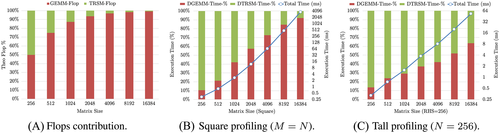
Figure 3 highlights the profiling of native DTRSM and DGEMM calls within the recursive KBLAS DTRSM, in terms of flops and time breakdown. In particular, Figure 3A shows that most of the flops consumed by RecTRSM are carried by GEMM calls involving large matrices, while the flops consumed by native TRSM/TRMM calls diminish with the increase in matrix size. Nevertheless, the time breakdown of RecTRSM, as drawn in Figure 3B,C and for square and tall matrix profiles, respectively, shows that native TRSM kernel calls with thin and wide matrices still consume a large percentage of the overall execution time, especially when operating on small number of right-hand sides (see Figure 3C). This is mostly due to a low hardware occupancy engendered by a limited concurrency. A similar profiling trend for RecTRMM, although less significant, has also been identified. These observations motivate the need for optimizing the native TRMM and TRSM CUDA kernels for small number of rows involving diagonal blocks with thin and wide output matrices, which may potentially improve the overall RecTRSM and RecTRMM performances.
4 IMPLEMENTATION DETAILS
In this section, we describe our design criteria and implementation of our CUDA-based native TRSM and TRMM kernels to better handle short and wide output matrices, which we use in return to enhance the overall RecTRSM and RecTRMM performances on GPUs. We also describe our multi-GPU implementation of these kernels and port the same recursive formulation on Intel ×86 CPU architectures using various BLAS libraries.
4.1 KBLAS CUDA TRSM and TRMM implementations for low RHS
4.1.1 Data dependencies
We briefly recall the TRSM and TRMM operations to properly design a CUDA kernel for each. Assume M and N are the number of rows and columns of matrix B, respectively. In a left/lower/non-transpose TRSM:A×X=αB operation, an entry
can be computed as long as the entries
have already been updated to ensure numerical correctness. In a similar way, in a left/lower/transpose TRMM:B=αATB, an entry
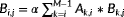can be calculated as long as the entries
have not been updated yet. It is easy to notice that the concurrency in the left side variant of TRSM or TRMM operations is limited by the number of columns of the output matrix (or the number of rows for the right side variant).
4.1.2 Hardware occupancy
In the context of CUDA programming best practices,23 achieving high occupancy, which transforms into high latency hiding, is usually a useful metric for achieving high performance (this metric can be ignored in some cases when the resources of the Streaming Multiprocessor (SM) is otherwise properly utilized). Occupancy is measured as the number of active warps per maximum number of supported concurrent warps in an SM. In the case of TRSM or TRMM with thin and wide output matrix, assigning one CUDA thread to compute all the entries of a single column of the B-matrix would not involve enough threads to properly address high occupancy. It is necessary, thus, to involve multiple threads for the computation of each B-matrix column. Given that computation of each B-column requires reading all the entries of the A-matrix, it is preferable to load blocks of matrix A in shared memory and share it across multiple threads computing multiple B-columns.
4.1.3 Tile algorithmic design
Given the limitation of resources in a SM (register file size, shared memory size, etc), we need to adopt a blocking technique to be able to compute many rows of matrix B in one single thread-block. In this context, the tile algorithm may be a very efficient method to investigate. Note that we refer to tile algorithm as a blocking technique without altering the underlying data layout. The tile algorithm for TRMM and TRSM kernel design offers 2 looking variants, as seen in the literature for general DLA operations. In the case of the TRSM kernel, upon a TRSM update of a B-column block by a diagonal A-block, the right-looking variant partially updates its lower blocks with a GEMM and writes them back to memory, before proceeding to the next TRSM update. Instead, the left-looking variant updates a B-column block by GEMMs from its upper blocks and a TRSM from a diagonal A-block before writing it back to memory. We use the left-looking variant since it trades fewer writes to memory, and therefore, less data movement, for an equivalent extra number of reads (the later are faster than the former especially with GPU texture caching). A similar scenario can be drawn for TRMM.
4.1.4 GPU shuffle instructions
Moreover, a TRSM / TRMM operation of a diagonal A-block on a B-block requires that CUDA threads share values of the same column. In order to avoid extra shared memory allocation and to avoid the latency of shared memory accesses, we cache the B-columns in registers and share their values across the CUDA threads of each warp using the novel shuffle instruction, recently introduced by NVIDIA. A shuffle instruction consumes less cycles and thus less latency than a shared memory access. This fact motivates us to store the B-blocks in registers only. Since the register sharing is possible among threads of a warp only (32 threads), it is favorable to choose the tile size to be congruent with the warp size. Last but not the least, assigning one warp to process one (or multiple) B-columns reduces the possible expensive divergence within one warp due to thread synchronizations.
4.1.5 Pseudocodes
Given the design considerations discussed above, Algorithms 1 and 2 present the corresponding pseudocodes for the TRSM and TRMM CUDA kernels, respectively. For simplicity, we do not show the code for handling matrices whose sizes are not multiple of the assumed tile size (32). Indeed, the side comments detail the 3 paramount low-level optimizations aforementioned: (1) the increase of concurrency for better hardware occupancy, (2) the tile algorithm and left-looking variant for better caching and register reuse, and (3) the use of efficient shuffle instructions to weaken the impact of thread synchronizations. The thread block (TB) and TB-grid used to launch these kernels are governed by the tile size they can process. The kernels depicted in Algorithms 1 and 2 assume that a warp of threads would work on a column of 32 elements (mandated by the shuffle instruction). Therefore, the tile size for matrix A is statically configured to be 32×32. Introducing the constant WPB (warps per block), we configure the TB size as (32,WPB) threads, processing WPB columns of B. Consequently, we launch a one-dimensional grid of size N/WPB to process all the columns of matrix B. WPB is left as a tuning parameter; however, experiments indicate that WPB=8 produces best performance. The pseudocodes are templated for precision generations.
4.2 KBLAS multi-GPU RecTRSM and RecTRMM
The purpose of a multi-GPU API for TRSM and TRMM is to provide a function call that can replace an existing CPU function call with as little code intrusion as possible, as may be required by some GPU-based libraries. As such, the data is assumed to reside on CPU memory. The multi-GPU routine should transparently manage the data transfer from/to GPU main memory, and thus, relieving the developer from this burden, especially since multi-GPU represents a challenging platform for high-performance computing.
of GPU kernels is recursively handled on the CPU code, we can hide the data transfer (from/to CPU to/from GPU memory), while performing computations. For that purpose, dedicated CUDA streams are created to handle data transfer to/from GPU, which are separate from the computation streams. Synchronization between data-transfer streams and computation streams is handled by CUDA events. Data transfer from CPU is invoked at the beginning, based on the recursive splitting depicted in Figure 1, while the sequence of operations is statically predetermined. As soon as portions of matrices A and B needed for the next computation kernel reach GPU's main memory, its corresponding
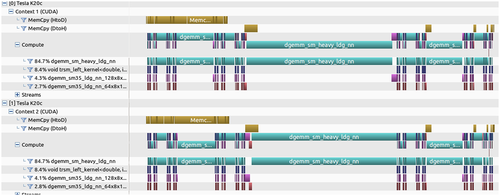
computation kernel is invoked, while other data transfers are still active in the background. Figure 4, captured with nvprof visual profiler from NVIDIA, illustrates the complete overlap of computation and communication on a RecTRSM operation of size M=N=16000 running on 2 K20 GPUs.
Since the concurrency of the left-side variant of TRMM and TRSM operations is limited to the number of columns of matrix B(number of rows for the right-side variant), as discussed in Section 4, and to minimize cross-GPU stream synchronization, we distribute the output matrix B on the multiple devices, while input matrix A is shipped for each device. However, this may limit the problem size that can be computed. To resolve this limitation, we design 2 stages for the algorithm. The first stage computes the operations using the recursive scheme described above as long as the GPU memory can fit the data. A second stage is invoked when the next GEMM data cannot be fitted on the multiple GPUs memory, at which an out-of-core multi-GPU GEMM is invoked for the subsequent GEMM calls. After that, the execution returns to the recursive scheme to process the remaining subsequent portions of the recursion. Highly efficient multi-GPU GEMM implementations can be utilized for this purpose and are available from cuBLAS-XT,3 BLASX,6 and KBLAS.13
In order to compensate for the time of memory allocation (for subsequent GEMM and TRSM or TRMM calls), we pre-allocate a big memory pool that is enough for all data needed on the GPU. The size of data needed on GPU is determined by number of participating GPU devices on which matrix B is distributed, and the lower or upper portions of matrix A. With this scheme in place, the scaling of multi-GPU TRSM/TRMM calls is not affected by any cross-GPU communications and may, therefore, be almost linear.
4.3 On Intel ×86 CPU architectures
We further extend the recursive formulation of Level 3 BLAS triangular operations into Intel ×86 architectures: multi-core CPUs and Xeon Phi. Although only Intel architectures are considered in this section, the recursive formulation is oblivious to the CPU vendors and can be seamlessly ported to any CPU vendors (eg, IBM and AMD). The strategy follows the one we adopted in Charara et al,8 where the TRSM and TRMM operations are recursively split into GEMM and 2 RecTRSM and RecTRMM subsequent operations, respectively, where the subsequent GEMM calls rely on a highly optimized BLAS library implementation of choice. Similarly, the TRSM and TRMM calls at the bottom of recursion use again the native TRSM and TRMM implementations from the corresponding BLAS library. The stopping size of the recursion on ×86 CPU is a tuning parameter that varies across libraries and hardware. This parameter is determined empirically and corresponds to a trade-off between the kernel launch overhead and the single kernel performance.
5 EXPERIMENTAL RESULTS
In this section, we present the performance results of our KBLAS implementation for both TRMM and TRSM kernels on various architectures and compare it against state-of-the-art BLAS libraries. Since all our implementations are equivalent in flop count to the native versions, we report performance results in flops per second, which are obtained by dividing the flop count by the execution time, or in speedups, over a range of input sizes.
5.1 Environment settings
Experiments have been conducted on single and multiple NVIDIA K40 GPUs across all subsequent GPU performance plots (unless noted otherwise).
We use CUDA v7.5 and MAGMA v2.0.2 on GPU platforms. Performance of BLASX library have been extracted from their corresponding plots in Wang et al,6 since their open-source software distribution does not include the testing code of the kernels considered in this paper yet. For the experiments on Intel ×86 architectures, we report experiments on a dual-socket 10-core Intel Ivy Bridge system running at 2.8 GHz and having 128 GB of memory. Experiments on Intel Xeon Phi were conducted on a system with a Knights Corner (KNC) coprocessor having 61 cores and 15.5 GB of memory. For both systems, we rely on Intel compilers v15 and the corresponding Intel MKL along with OpenBLAS v0.2.14, BLIS v0.1.6-56, for optimized BLAS libraries. All CPU and GPU performance reported correspond to an average of 10 and 5 consecutive runs, respectively. Only single (SP) and double precision (DP) arithmetic are studied in this paper, although KAUST BLAS (KBLAS) open-source library (https://github.com/ecrc/kblas) supports all 4 precisions.
5.2 Performance on single GPU
Figure 5 shows the performance gain obtained with the RecTRSM from KBLAS using the new native customized TRSM kernel introduced in this paper, against the RecTRSM from KBLAS using the corresponding cuBLAS kernel instead, as introduced in Charara et al.8 Most of the performance improvements occur in SP and DP arithmetic for a small number of right-hand sides (up to 73% and 40%), as highlighted in Figure 5A,B, respectively. To have a better perspective, we also compare our implementations against corresponding native MAGMA and cuBLAS implementations. Note that MAGMA implementation of TRSM is out-of-place (OOP), requires twice the memory allocation and data transfer, thus limiting the size of problems that can be solved on the GPU's scarce memory. The gain with square matrices for SP and DP RecTRSM, as seen in Figure 5C,D, respectively, is minimal due to the high concurrency already engendered by large matrix sizes.
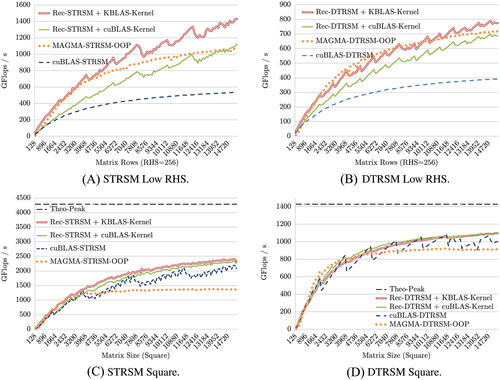
By the same token, the new customized KBLAS TRMM kernel brings another factor of performance gain on top of RecTRMM in DP, but mostly in SP (up to 30%), with small number of right-hand sides, as reported in Figure 6B,A, respectively. The gain is, however, limited for square matrices, as shown in Figure 6C,D, for the same aforementioned reasons.
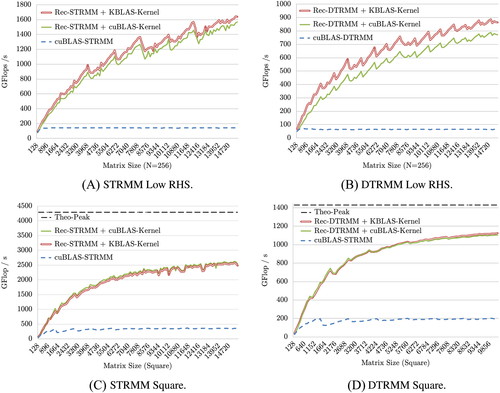
For all subsequent GPU performance graphs, we refer to RecTRSM and RecTRMM as the KBLAS recursive kernel containing the new customized TRSM and TRMM CUDA kernels, respectively.
5.3 Performance on various single GPU hardware generations
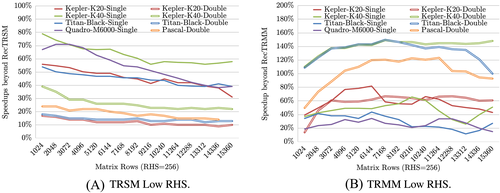
Figure 7 reports the performance gain on various GPU generations (including the most recent Pascal P100 GPU) of KBLAS RecTRMM and RecTRSM kernels, in SP and DP, with a small number of right-hand sides, against previous corresponding kernels from Charara et al.8 The gain in performance ranges from 40% to 70% for STRSM, from 10% to 30% for DTRSM, from 20% to 60% for STRMM, and from 60% to 140% for DTRMM. The main goal of this section is to show the backward and forward compatibilities of our recursive implementations, besides the additional performance improvements.
5.4 Performance on multiple GPUs
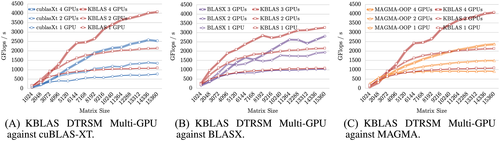
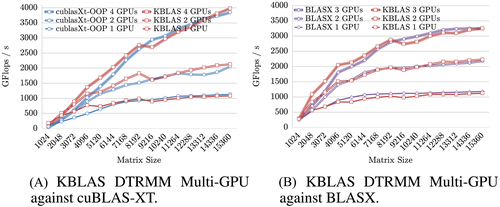
We report next the performance gain of both RecTRSM and RecTRMM multi-GPU implementations from KBLAS against those from cuBLAS-XT,3 MAGMA,9, 10 and BLASX.6 The performance numbers from the latter have been extracted from the paper by Wang et al,6 which only reports performance on three GPUs. The multi-GPU implementation assumes the matrix data is residing on the host-CPU memory, and thus, the reported performance numbers accounts for both data transfer and computations execution times. Figure 8A,B demonstrates significant performance gain with KBLAS DTRSM against that of multi-GPU cuBLAS-XT (up to 2×) and the recent BLASX libraries (up to 30%), respectively. Figure 8C reports a similar performance gain against MAGMA library (up to 76%), which is an OOP implementation and does not account for data transfer from CPU memory. On the other hand, Figure 9A,B shows that KBLAS multi-GPU DTRMM can match the OOP implementation from cuBLAS-XT (which also requires twice the memory allocations and data transfers), as well as the performance of the more sophisticated dynamic runtime system from BLASX.
5.5 Performance comparisons on Intel ×86 architectures
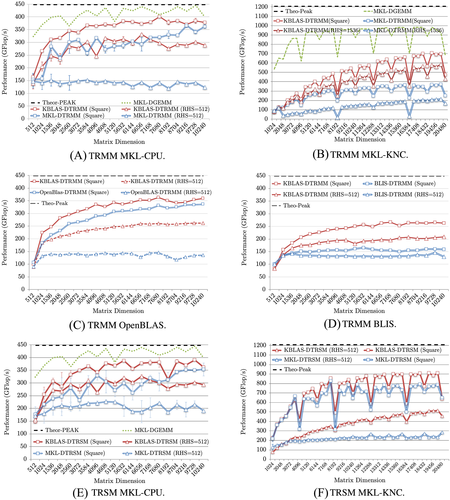
Figure 10 demonstrates the performance gain of RecTRSM and RecTRMM kernels on Intel ×86 architectures, ie, an Ivy Bridge 20-core system and a Knights Corner (KNC), against various BLAS libraries. The tuning parameter for stopping the recursion has been experimentally determined and set from 256 up to 512 on the CPU depending on the matrix size. On the Intel Xeon Phi, the tuning parameter is much higher and has been set from 1000 up to 1500 to be the most effective. In particular, Figure 10A-D highlights the performance speedup of KBLAS RecTRMM against the corresponding native TRMM kernels (square/tall-and-skinny) from MKL-CPU (up to 40%/250%), MKL-KNC (up to 100%/300%), OpenBLAS (up to 20%/100%), and BLIS (up to 70%/55%), respectively. Figure 10E,F, shows the performance speedup of KBLAS RecTRSM against the corresponding native TRSM kernels (square/tall-and-skinny) from MKL-CPU (up to 50%/70%) and MKL-KNC (up to 23%/120%), respectively.
6 CONCLUSION AND FUTURE WORK
We have presented new high-performance in-place TRSM and TRMM BLAS CUDA kernels, for matrices with a small number of RHS on single GPU, that enhance the performance of RecTRSM and RecTRMM by up to 70% and 140%, respectively, while outperforming corresponding cuBLAS kernels by more than 2× and 10×, respectively. We have also highlighted a multi-GPU implementation of these kernels, which outperforms cuBLAS, MAGMA, and BLASX corresponding implementations by up to 100%, 76%, and 30% respectively. We have ported the proposed recursive formulations of these kernels to BLAS libraries running on Intel ×86 architectures including the Knights Corner co-processor, and demonstrated significant speedups (reaching up to 3×) on various vendor and open-source BLAS libraries, especially on tall-and-skinny output matrices (ie, general matrix for TRMM with small number of columns and solution matrix with small number of right hand sides for TRSM). Similar to other BLAS kernels, these triangular kernels are central building blocks for many scientific applications. The single GPU RecTRSM and RecTRMM kernel implementations have already been integrated in NVIDIA cuBLAS v8.0 and the CPU variants are also considered for integration in Cray Scientific Library (LibSci). All precisions and kernel variants are supported in the KAUST BLAS (KBLAS) open-source library available at https://github.com/ecrc/kblas.
For future work, we plan to extend our approach to other triangular BLAS kernels and also investigate the impact of recursive DLA schemes to the recent batched BLAS trend in the scientific community,24 in the context of machine/deep learning applications.25 The triangular matrix shapes and the in-place nature of such operations, combined with the need to a batched execution mode, which consists of processing thousands of small and independent operations in parallel, poses a problem that tends to be memory-bound and may greatly benefit from our recursive formulations and low-level optimizations on various manycore architectures.
ACKNOWLEDGMENTS
We would like to thank NVIDIA for hardware donations in the context of a GPU Research Center and Intel for support in the form of a Parallel Computing Center award to the Extreme Computing Research Center at King Abdullah University of Science and Technology and KAUST IT Research Computing for their hardware support on the GPU-based system.
