Volume 3, Issue 6 e1194

SPECIAL ISSUE PAPER

Full Access

Controlling crop pest with a farming awareness based integrated approach and optimal control

Teklebirhan Abraha,

Teklebirhan Abraha

Department of Mathematics, Adama Science and Technology University, Adama, Ethiopia

Search for more papers by this author

Fahad Al Basir,

Fahad Al Basir

Department of Mathematics, Asansol Girls' College, Asansol, India

Search for more papers by this author

Legesse Lemecha Obsu,

Legesse Lemecha Obsu

Department of Mathematics, Adama Science and Technology University, Adama, Ethiopia

Search for more papers by this author

Delfim F. M. Torres,

Corresponding Author

Delfim F. M. Torres

[email protected]

R&D Unit CIDMA, Department of Mathematics, University of Aveiro, Aveiro, Portugal

Correspondence Delfim F. M. Torres, R&D Unit CIDMA, Department of Mathematics, University of Aveiro, 3810-193 Aveiro, Portugal.

Email: [email protected]

Search for more papers by this author

Teklebirhan Abraha,

Teklebirhan Abraha

Department of Mathematics, Adama Science and Technology University, Adama, Ethiopia

Search for more papers by this author

Fahad Al Basir,

Fahad Al Basir

Department of Mathematics, Asansol Girls' College, Asansol, India

Search for more papers by this author

Legesse Lemecha Obsu,

Legesse Lemecha Obsu

Department of Mathematics, Adama Science and Technology University, Adama, Ethiopia

Search for more papers by this author

Delfim F. M. Torres,

Corresponding Author

Delfim F. M. Torres

[email protected]

R&D Unit CIDMA, Department of Mathematics, University of Aveiro, Aveiro, Portugal

Correspondence Delfim F. M. Torres, R&D Unit CIDMA, Department of Mathematics, University of Aveiro, 3810-193 Aveiro, Portugal.

Email: [email protected]

Search for more papers by this author

First published: 28 September 2021

https://doi.org/10.1002/cmm4.1194

Citations: 6

Funding information: Adama Science and Technology University (ASTU), ASTU/SP-R/027/19; Fundação para a Ciência e a Tecnologia, UIDB/04106/2020

Share a link

Email
Wechat
Bluesky

Abstract

We investigate a mathematical model in crop pest controlling, considering plant biomass, pest, and the effect of farming awareness. The pest population is divided into two compartments: susceptible pests and infected pests. We assume that the growth rate of self-aware people is proportional to the density of susceptible pests existing in the crop arena. Impacts of awareness are modeled through the usual mass action term and a saturated term. It is further assumed that self-aware people will adopt chemical and biological control methods, namely, integrated pest management. Bio-pesticides are costly and require a long-term process, expensive to impose. However, if chemical pesticides are introduced in the farming system along with bio-pesticides, the process will be faster as well as cost-effective. Also, farming knowledge is equally important. In this article, a mathematical model is derived for controlling crop pests through an awareness-based integrated approach. In order to reduce the negative effects of pesticides, we apply optimal control theory.

1 INTRODUCTION

Problems connected with pests have become evident around the world as cultivation began. World's food supply is being wasted due to the cause of pests in agriculture. On the other hand, major side-effects of synthetic pesticides on the environment, human health, and biodiversity are generating widespread concerns. Thus, farmers' awareness of the risk of synthetic pesticides uses is one of the important factors to consider. The use of biological contents to protect crops against pests needs indigenous knowledge to implement such contents in pest management.^{1, 2}

There are several good modeling studies on pest control. For example, Chowdhury et al.^{3, 4} have proposed and analyzed mathematical models for biological pest control using the virus as a controlling agent. In fact, all eco-epidemic models with susceptible prey, infected prey, and predators can be used to discuss the nature of the susceptible pest, infected pest, and their predators.⁵ Zhang et al.⁶ used a delayed stage-structured epidemic model for pest management strategy. Wang and Song⁷ used mathematical models to control a pest population by infected pests. However, they did not use the influence of the predator populations on their works.

Many researchers utilize mathematical models for pest control in order to study different aspects of pest management policies with probable outcomes for improved applications, using system's analysis within the mathematical paradigm. Most of them suggest using chemical pesticides.^{8, 9} However, it is recorded that chemical pesticides have resulted in pest resurgence, acute and chronic health problems, and environmental pollution.¹⁰ Thus, to resolve this type of problem, the concept of IPM is becoming more popular among researchers with increasing application in the field by marginal farmers.

In this article, we formulate a mathematical model, incorporating the farming awareness based integrated approach. The main focus is to compare the basic advantage of favoring the biological and combined strategy to minimize the pest problem and predict new insights on the pest management, in general. In order to reduce the negative effects of pesticides, we apply an optimal control approach. The dynamic of the system, without application of control, is analyzed through stability and bifurcation theory. Then, we formulate a three control parameter optimal control problem and solve it by applying PMP to find out the optimal level of both pesticide and the advertisement cost for cost effectiveness and minimizing the negative effect due to pesticides. Numerical simulations illustrate the analytical results. Finally, we discuss the outcomes with a conclusion.

2 DESCRIPTION AND MODEL FORMULATION

We consider four populations into our mathematical model, namely, plants biomass

X (t)

, susceptible pest

S (t)

, infected pest

I (t)

, and level of awareness

A (t)

. The following assumptions are made to formulate the mathematical model:

Under influence of bio-pesticides, healthy pest population becomes infected. Infected pest can attack the plant but the rate is very lesser than susceptible pest. We assume that infected pest can consume the plant biomass following a Holling type II response, whereas susceptible pest consume following a Holling type I response function.
Due to the finite size of crop field, we assume logistic growth for the density of crop biomass, with net growth rate r and carrying capacity K.
Susceptible attacks the crop, thereby causing considerable crop reduction. If we infect the susceptible pest by pesticides, then the attack by pest can be controlled. Here we assume that aware farmers will adopt biological pesticides for the control of the crop pest, as it has less side effects and is also environment friendly. Biopesticides are used to infect the healthy pest. Infected pest has an additional mortality due to infection.
Let $α$ be the consumption rate of pests. There is a pest infection rate, $λ$ , because of aware human interactions and activity such as use of biopesticides (e.g., NPV), modeled via the usual mass action term $λ A S$ . We denote by d the natural mortality rate of pest and by $δ$ the additional mortality rate of infected pest due to aware people activity.
It is assumed that the level of awareness will increase at a rate $ω$ , proportional to the number of pests per plant noticed in the farming system. There could be fading of interest in this exploitation. We let $η$ be the rate of fading of interest of aware people.
To speed up the pest control process, chemical synthetic pesticides are introduced. It causes additional death to both susceptible and infected pest populations. Following Reference 11, we model the situation by the terms $\frac{γ S A}{1 + A}$ and $\frac{γ I A}{1 + A}$ , respectively.

Based on the above assumptions, we have the following mathematical model:

\{\begin{cases} \frac{d X}{d t} = r X (1 - \frac{X}{K}) - α X S - \frac{ϕ α X I}{a + X}, \\ \frac{d S}{d t} = m_{1} α X S - λ A S - d S - \frac{γ S A}{1 + A}, \\ \frac{d I}{d t} = \frac{m_{2} ϕ α X I}{a + X} + λ A S - (d + δ) I - \frac{γ I A}{1 + A}, \\ \frac{d A}{d t} = ω + σ (S + I) - η A, \end{cases}

()

subject to the initial conditions

X (0) \geq 0, S (0) \geq 0, I (0) \geq 0, A (0) \geq 0 .

()

Here

α

is the attack rate of pests on crop. Infected pests can also attack the crop but with a lower rate,

ϕ α

, with

ϕ < 1

; a is the half saturation constant,

m_{1}

and

m_{2}

are the “conversion efficiency” of susceptible and infected pests, respectively, that is, they measure how efficiently can the pests utilize plant resource. Since pesticide affected pests have lowered efficiency,

m_{1} > m_{2}

, and

γ

denotes the increase of level from global advertisement by radio, TV, and so forth. It is natural to assume that all the parameters of model (1) are positive.

3 POSITIVITY OF SOLUTIONS AND THE INVARIANT REGION

Existence and positivity of the solutions are the main properties that system (1) must satisfy for the model to be well-posed. Such properties are proved in this section. They describe the range in which the solution of the equations is biologically important.

The feasible region is given by

Ω = {(X, S, I, A) \in ℝ_{+}^{4} : X \geq 0, S \geq 0, I \geq 0, A \geq 0} .

To show that the first two equations of the system (1) are positive, we use the following lemma.

Lemma 1.Any solution of the differential equation $\frac{d X}{d t} = X ψ (X, Y)$ is always positive.

Proof.A differential equation of the form $\frac{d X}{d t} = X ψ (X, Y)$ can be written as $\frac{d X}{X} = X ψ (X, Y) d t$ . Integrating, we can write that $\ln X = C_{0} + \int ψ (X, Y) d t$ , that is, we have $X = C_{1} e^{\int ψ (X, Y) d t} > 0$ for $C_{1} > 0$ .

Theorem 1. (Non-negativeness of the solutions)The solutions of system (1) subject to given non-negative initial conditions (2) remain non-negative for all $t > 0$ .

Proof.Let $(X (t), S (t), I (t), A (t))$ be a solution of system (1) with its initial conditions (2). We use Lemma 1 to prove the positivity of the equations in the system. Let us consider $X (t)$ for $t \in [0, T]$ . We obtain, from the first equation of system (1), that

\frac{d X}{d t} = X [r (1 - \frac{X}{K}) - α S - \frac{ϕ α I}{a + X}] \Rightarrow \frac{d X}{X} = [r (1 - \frac{X}{K}) - \frac{α S + ϕ α I}{c + X}] d t .

Hence,

\ln X = D_{0} + \int_{0}^{t} [r (1 - \frac{X}{K}) - α S - \frac{ϕ α I}{a + X}] d u,

so that

X (t) = D_{1} e^{\int_{0}^{t} [r (1 - \frac{X}{K}) - α S - \frac{ϕ α I}{a + X}] d u} > 0 (∵ D_{1} = e^{D_{0}}) .

From the second equation of system (1), we have

\frac{d S}{d t} = S [m_{1} α X - λ A - d - \frac{γ A}{1 + A}] \Rightarrow \frac{d S}{S} = [m_{1} α X - λ A - d - \frac{γ A}{1 + A}] d t .

Hence,

\ln S = K_{0} + \int_{0}^{t} (m_{1} α X - λ A - d - \frac{γ A}{1 + A}) d u,

so that

S (t) = K_{1} e^{\int_{0}^{t} (m_{1} α X - λ A - d - \frac{γ A}{1 + A}) d u} > 0 .

To show that I and A are non-negative, consider the following sub-system of (1):

\begin{align} \frac{d I}{d t} & = \frac{m_{2} ϕ α X I}{a + X} + λ A S - (d + δ) I - \frac{γ I A}{1 + A}, \\ \frac{d A}{d t} & = ω + σ (S + I) - η A . \end{align}

()

To show the positivity of

I (t)

, we do the proof by contradiction. Suppose there exists

t_{0} \in (0, T)

such that

I (t_{0}) = 0

I^{'} (t_{0}) \leq 0

, and

I (t) > 0

for

t \in [0, t_{0})

. Then,

A_{0} > 0

for

t \in [0, t_{0})

. If this is not to be the case, then there exists

t_{1} \in [0, t_{0})

such that

A (t_{1}) = 0

A^{'} (t_{1}) \leq 0

and

A (t) > 0

for

t \in [0, t_{0})

. Integrating the third equation of the system (1) gives

\begin{align} I (t) & = I (0) \exp (\int_{0}^{t} (\frac{m_{2} ϕ α X (τ)}{a + X (τ)} - \frac{γ A (τ)}{1 + A (τ)}) d τ - (d + δ) t) \\ + [\exp (\int_{0}^{t} (\frac{m_{2} ϕ α X (τ)}{a + X (τ)} - \frac{γ A (τ)}{1 + A (τ)}) d τ - (d + δ) t)] \\ \times [\int_{0}^{t} λ A (τ) S (τ) d τ \exp ((d + δ) t - \int_{0}^{t} (\frac{m_{2} ϕ α X (τ)}{a + X (τ)} - \frac{γ A (τ)}{1 + A (τ)}) d τ)] > 0, for t \in [0, t_{1}] . \end{align}

Then,

A^{'} (t_{1}) = γ + σ (S (t_{1}) + I (t_{1})) > 0

. This is a contradiction. Hence,

I (t) > 0

for all

t \in [0, t_{0})

. Finally, from the second equation of subsystem (3), we have

\frac{d A}{d t} = ω + σ (S + I) - η A .

Integration gives

A (t) = A (0) e^{η t} + e^{η t} \int_{0}^{t} (ω + σ (S (τ) + I (τ))) e^{- η t} d t > 0,

that is,

A (t) > 0

for all

t \in (0, T)

Theorem 2. (Boundedness of solutions)Every solution of system (1) that start in $ℝ_{+}^{4}$ is uniformly bounded in the region $𝒱$ defined by

𝒱 = \{(X, S, I, A) \in ℝ_{+}^{4} : 0 < X + S + I \leq \frac{L}{d}, 0 < A \leq \frac{ω d + σ L}{η d}\}, with L = \frac{K {(r + d)}^{2}}{4 r} .

Proof.We choose $m = \max \{m_{1}, m_{2}\} = m_{1}$ , because in our assumptions we assume that $m_{1} > m_{2}$ . Now, at any time t, let $W = X + \frac{1}{m_{1}} S + \frac{1}{m_{1}} I$ . Then the time derivative of W along the solution of system (1) is given by

\begin{align} \frac{d W (t)}{d t} & = r X [1 - \frac{X}{K}] - α X S - \frac{ϕ α X I}{a + X} + α X S - \frac{λ}{m_{1}} A S + \frac{λ}{m_{1}} A S \\ + \frac{m_{2}}{m_{1}} \frac{ϕ α X I}{a + X} - \frac{d}{m_{1}} S - (\frac{d + δ}{m_{1}}) I - (S + I) \frac{γ}{m_{1}} \frac{A}{1 + A} \\ = r X [1 - \frac{X}{K}] - (\frac{m_{1} - m_{2}}{m_{1}}) \frac{ϕ α X I}{a + X} \\ - (\frac{d + δ}{m_{1}}) I - \frac{d}{m_{1}} S - (S + I) \frac{γ}{m_{1}} \frac{A}{1 + A} \\ \leq r X [1 - \frac{X}{K}] - \frac{d}{m_{1}} S - \frac{d}{m_{1}} I \\ = r X (1 - \frac{X}{K}) - \frac{d}{m_{1}} (S + I) - d X + d X \\ = r X (1 - \frac{X}{K}) - (\frac{d}{m_{1}} S + \frac{d}{m_{1}} I + d X) + d X . \end{align}

Then, we have from the above that

\frac{d W}{d t} \leq r X (1 - \frac{X}{K}) - d W + d X,

that is,

\frac{d W}{d t} + d W \leq r X (1 - \frac{X}{K}) + d X = (r + d) X - \frac{r X^{2}}{K} = : Φ (X) .

Now,

Φ (X)

is a concave parabola for which its maximum value is attained at the vertex whose abscissa is

X_{v} = \frac{K (r + d)}{2 r}

. Therefore, it follows

Φ (X) \leq Φ (X_{v}) = \frac{1}{4 r} K {(r + d)}^{2} = Φ^{*} .

Thus, we have a constant

L = \frac{K {(r + d)}^{2}}{4 r}

such that

\frac{d W}{d t} + d W \leq L .

To solve this, we apply the differential inequality

\begin{align} e^{d t} (\frac{d W}{d t} + d W) \leq e^{d t} L & \Rightarrow \frac{d}{d t} (W e^{d t}) \leq e^{d t} L \\ \Rightarrow W e^{d t} \leq \int (L e^{d t}) d t + C \\ \Rightarrow W (X, S, I) \leq e^{- d t} [d L e^{d t}] + C e^{- d t} \\ \Rightarrow W (X (0), S (0), I (0)) \leq \frac{L}{d} + C \\ ∴ W (X, S, I) \leq \frac{L}{d} (1 - e^{- d t}) + W (X (0), S (0), I (0)) e^{- d t} . \end{align}

Hence, we get

0 < W (X, S, I) \leq \frac{L}{d} (1 - e^{- d t}) + W (X (0), S (0), I (0)) e^{- d t}

and, for

t \to \infty

, we have

0 < X + S + I \leq \frac{L}{d} .

From the fourth equation of system (1), we have

\begin{align} \frac{d A}{d t} & = ω + σ (S + I) - η A \\ \leq ω + σ (\frac{L m_{1}}{d}) - η A \\ = \frac{d ω + σ L}{d} - η A \\ \Leftrightarrow \frac{d A}{d t} + η A \leq \frac{d ω + σ L}{d} . \end{align}

Again, applying the method of differential inequality, we have

\begin{align} e^{η t} (\frac{d A}{d t} + η A) \leq e^{η t} (\frac{d ω + σ L}{d}) & \Rightarrow \frac{d}{d t} (A e^{η t}) \leq e^{η t} (\frac{d ω + σ L}{d}) \\ \Rightarrow A e^{η t} \leq \int (\frac{d ω + σ L}{d}) e^{η t} d t + C \\ \Rightarrow A (t) \leq (\frac{d ω + σ L}{η d}) + C e^{- η t} \\ \Rightarrow A (0) \leq \frac{ω d + L σ}{η d} + C . \end{align}

This results in

0 < A \leq \frac{ω d + σ L}{η d} + C e^{- η t} .

Thus, for

t \to \infty

, we obtain that

0 < A \leq \frac{ω d + σ L}{η d} .

Hence, all solutions of (1) originating in

ℝ_{+}^{4}

are confined to the region

𝒱 = \{(X, S, I, A) \in ℝ_{+}^{4} : 0 < X + S + I \leq \frac{L}{d} + ϵ, 0 < A \leq \frac{ω d + σ L}{η d}\}

for any

ϵ > 0

and for

t \to \infty

. Thus, the system (1) is always uniformly bounded.

4 EQUILIBRIA ASSESSMENT

To get the fixed points of our system, we put the right-hand sides of system (1) equal to zero:

\{\begin{cases} r X (1 - \frac{X}{K}) - α X S - \frac{ϕ α X I}{a + X} = 0, \\ m_{1} α X S - λ A S - d S - \frac{γ S A}{1 + A} = 0, \\ \frac{m_{2} ϕ α X I}{a + X} + λ A S - (d + δ) I - \frac{γ I A}{1 + A} = 0, \\ ω + σ (S + I) - η A = 0 . \end{cases}

()

We conclude that system (1) has five possible equilibrium points, denoted by

E_{i}

i = 0, 1, 2, 3

, and

E^{*}

(i)
The axial equilibrium point $E_{0} = (0, 0, 0, \frac{ω}{η})$ , which always exists.
(ii)
The pest free equilibrium point $E_{1} = (K, 0, 0, \frac{ω}{η})$ , which, again, always exists.
(iii)
The boundary equilibrium point $E_{2} = (0, S_{1}, I_{1}, A_{1})$ , where
$S_{1} = \frac{((d + δ + γ) A + d + δ) (η A - ω)}{(A^{2} λ + (d + δ + γ + λ) A + d + δ) σ},$

$I_{1} = \frac{(A η - ω) λ A (1 + A)}{(A^{2} λ + (d + δ + γ + λ) A + d + δ) σ},$
and $A_{1}$ is the positive root of the equation $λ A^{2} + (γ + d + λ) A + d = 0$ . Unfortunately, this quadratic equation has no positive roots and, hence, such an equilibrium does not occur.
(iv)
The healthy pest free equilibrium point $E_{3} = (\overline{X}, 0, Ī, Ā)$ , where $\overline{X}$ , $Ī$ , and $Ā$ are computed as follows. If we set $S = 0$ in system (4), then
$\{\begin{cases} r X [1 - \frac{X}{K}] - \frac{ϕ α X I}{a + X} = 0, \\ \frac{m_{2} ϕ α X I}{a + X} - (d + δ + \frac{γ A}{1 + A}) I = 0, \\ ω + σ I - η A = 0 . \end{cases}$ ()
From the first equation of the nonlinear system (5), we have
$r [1 - \frac{X}{K}] - \frac{ϕ α I}{a + X} = 0 \Rightarrow \frac{ϕ α I}{a + \overline{X}} = \frac{r (K - \overline{X})}{K}$

$\Rightarrow ϕ α I = \frac{r (a + \overline{X}) (K - \overline{X})}{K} \Rightarrow Ī = \frac{r (a + \overline{X}) (K - \overline{X})}{ϕ α K}$
and, from the third equation of system (5), we get
$ω + σ I - η A = 0 \Rightarrow η A = ω + σ I \Rightarrow Ā = \frac{ω + σ Ī}{η} = \frac{r (a + \overline{X}) (K - \overline{X}) σ + ω K α ϕ}{K α η ϕ} .$
Finally, solving for X from the second equation of system (5), we see that $\overline{X}$ is the positive root of equation
$X^{3} + a_{1} X^{2} + a_{2} X + a_{3} = 0,$ ()
where
$\begin{align} a_{1} & = \frac{(α ϕ m_{2} - d - δ - γ) K - a (α ϕ m_{2} - 2 d - 2 δ - 2 γ)}{- α ϕ m_{2} + d + δ + γ}, \\ a_{2} & = \frac{((α ϕ m_{2} - 2 d - 2 δ - 2 γ) K + a (d + δ + γ)) a}{- α ϕ m_{2} + d + δ + γ} - \frac{K ((- α ϕ m_{2} + d + δ + γ) ω + η (- α ϕ m_{2} + d + δ)) ϕ α}{r σ (- α ϕ m_{2} + d + δ + γ)}, \\ a_{3} & = - \frac{K a^{2} r (d + δ + γ) σ + K ϕ a α ((d + δ + γ) ω + η (d + δ))}{r σ (- α ϕ m_{2} + d + δ + γ)} . \end{align}$
The model system (1) may have one or more healthy pest free equilibrium points $E_{3}$ , depending on the positive solutions of Equation (6). The healthy pest free equilibrium point $E_{3}$ exists only if Equation (6) has a positive root $\overline{X}$ and $K - \overline{X} > 0$ .
(v)
Our model system (1) has an equilibrium point in the presence of pest, $X (t) \geq 0$ , $S (t) \geq 0$ , $I (t) \geq 0$ , $A (t) \geq 0$ , called the interior or coexistence or endemic equilibrium point, which is denoted by $E^{*} = (X^{*}, S^{*}, I^{*}, A^{*}) \neq 0$ . Note that $E^{*}$ is the steady state solution where pest persist in the crop biomass population. It is obtained by setting each equation of system (1) equal to zero, that is,
$\frac{d X}{d t} = \frac{d S}{d t} = \frac{d I}{d t} = \frac{d A}{d t} = 0 .$
From the second equation of system (4), we get $(m_{1} α X - λ A - d - \frac{γ A}{1 + A}) S = 0$ , that is, $m_{1} α X - λ A - d - \frac{γ A}{1 + A} = 0$ , from which we obtain
$X^{*} = \frac{λ A^{2} + (d + λ + γ) A + d}{m_{1} α (1 + A)} .$
From the first equation of system (4), we have
$\begin{align} r (1 - \frac{X}{K}) - α S - \frac{ϕ α I}{a + X} = 0 & \Rightarrow α S + \frac{ϕ α I}{a + X} = r (1 - \frac{X}{K}) = \frac{r (K - X)}{K} \\ \Rightarrow α S + \frac{ϕ α I}{a + X} = \frac{r (K - X)}{K} \\ \Rightarrow α (a + X) S + ϕ α I = \frac{r (K - X) (a + X)}{K} \end{align}$ ()
and from the last equation of system (4) we get
$α (a + X) S + ϕ α I = \frac{r (K - X) (a + X)}{K} .$ ()
Solving Equations (7) and (8) simultaneously, one obtains
$\begin{align} S^{*} = \frac{r (a + X) (K - X) σ - K ϕ α (η A - ω)}{K α σ (X + a - ϕ)}, \\ I^{*} = \frac{(a + X) (A K α η - K α ω - K r σ + σ r X)}{K α σ (X + a - ϕ)} . \end{align}$
Therefore, $E^{*} = (X^{*}, S^{*}, I^{*}, A^{*})$ is the coexistence steady state with
$\begin{align} X^{*} & = \frac{λ A^{2} + (d + λ + γ) A + d}{m_{1} α (1 + A)}, \\ S^{*} & = \frac{r (a + X) (K - X) σ - K ϕ α (A η - ω)}{K σ α (X + a - ϕ)}, \\ I^{*} & = \frac{(a + X) (((A η - ω) α - σ r) K + σ r X)}{K σ α (X + a - ϕ)}, \end{align}$
and $A^{*}$ a positive root of equation
$f (A) = A^{6} + a_{1} A^{5} + a_{2} A^{4} + a_{3} A^{3} + a_{4} A^{2} + a_{5} A + a_{6} = 0,$ ()
whose coefficients are given by
$\begin{align} a_{1} & = \frac{3 λ^{2} r σ - r σ (((K - a) m_{1} + m_{2} ϕ) α - 3 d - δ - 3 γ) λ}{λ^{2} r σ} + \frac{m_{1} η (ϕ (m_{1} - m_{2}) α + d + δ + γ) α^{2}}{λ^{2} r σ}, \\ a_{2} & = \frac{3 σ λ^{3} r - 3 σ r (((K - a) m_{1} + m_{2} ϕ) α - 3 d - δ - 2 γ) λ^{2}}{σ λ^{3} r} \\ - \frac{m_{1} K (ϕ (m_{1} - m_{2}) (ω - 3 η) α + ω (d + δ + γ) + (- 3 d - 3 δ - 2 γ) η + σ r (m_{1} a - m_{2} ϕ)) α^{2}}{λ^{2} r σ} \\ + \frac{(- 2 (K - a) (d + δ / 2 + γ) m_{1} - 2 m_{2} ϕ (d + γ)) α + 3 (d + γ) (d + 2 / 3 δ + γ)}{λ^{2}} \\ + \frac{K η ((a (d + δ + γ) m_{1} - m_{2} ϕ (d + γ)) α + (d + γ) (d + δ + γ)) m_{1} α^{2}}{σ λ^{3} r}, \end{align}$

$\begin{align} a_{3} & = - 3 \frac{{m_{1}}^{2} K α^{3} (ϕ (ω - η) λ + 1 / 3 a (ω (d + δ + γ) - 3 η (d + δ + 2 / 3 γ)))}{σ λ^{3} r} \\ + 3 \frac{m_{1} K α^{3} ϕ ((λ + d / 3 + γ / 3) ω - (λ + d + 2 / 3 γ) η) m_{2}}{σ λ^{3} r} \\ + 3 \frac{m_{1} K (σ a r (λ + d / 3 + δ / 3 + γ / 3) m_{1} - (λ + d / 3 + γ / 3) ϕ m_{2} r σ + (ω / 3 - η / 3) γ^{2}) α^{2}}{{σ λ}^{3} r} \\ - 3 \frac{m_{1} K (((2 / 3 ω - 4 / 3 η) d + (2 / 3 ω - η / 3) λ + 1 / 3 δ (ω - 2 η)) γ + (ω / 3 - η) d) α^{2}}{{σ λ}^{3} r} \\ + \frac{- (K - a) (d^{2} + (δ + 2 γ + 6 λ) d + γ (δ + 3 γ + 4 λ)) m_{1} - ϕ (d^{2} + 6 λ d + 3 λ^{2}) m_{2}}{3 λ^{3} r} \\ + \frac{λ^{3} + (9 d + 3 δ + 3 γ) λ^{2} + (3 γ^{2} + (12 d + 4 δ) γ + 9 d^{2} + 6 d δ) λ + {(d + γ)}^{2} (d + δ + γ)}{λ^{3}}, \\ a_{4} & = \frac{((a (ω - η) d + ϕ (ω - η / 3) λ + a γ + δ (ω - η)) m_{1} - (ω - η / 3 + λ + 2 / 3 ω γ) ϕ m_{2}) K α^{3}}{σ λ^{3} r} \\ - 3 \frac{m_{1} K (σ a r (λ + d + δ) m_{1} - (λ + d + 2 / 3 γ) ϕ m_{2} r σ + δ (ω - η) + δ (ω - η / 3) λ) α^{2}}{σ λ^{3} r} \\ - 3 \frac{((K - a) (6 λ + 3 δ + 4 γ) d + (λ^{2} + (3 δ + 2 γ) λ + 2 δ γ + γ^{2}) m_{1} + ϕ (3 d^{2} + (6 λ + 4 γ) d) m_{2}) α}{λ^{3}} \\ - 9 \frac{σ (d^{3} + (3 λ + δ + 2 γ) d^{2} + (λ^{2} + (2 δ + 2 γ) λ + 4 / 3 δ γ + γ^{2}) d + 1 / 3 δ {(λ + γ)}^{2})}{λ^{3}}, \\ a_{5} & = - \frac{K (((λ ϕ + 3 (d + δ + γ / 3) a) ω - a η (d + δ)) m_{1} - m_{2} ((λ + 3 d + γ) ω - d η) ϕ) α^{3} m_{1}}{σ λ^{3} r} \\ - \frac{m_{1} (σ a r (λ + 3 δ + γ) m_{1} - m_{2} r ϕ (λ + 3 d) σ + (δ (3 ω - η) + ω (λ + 2 γ)) d) K α^{2}}{σ λ^{3} r} \\ - 2 \frac{((K - a) (3 / 2 d^{2} + (λ + 3 / 2 δ + γ) d + 1 / 2 δ (λ + γ)) m_{1} + m_{2} ϕ d (λ + 3 / 2 d + γ)) α}{λ^{3}} \\ + 3 \frac{(d^{2} + (λ + δ + γ) d + 2 / 3 δ (λ + γ)) d}{λ^{3}}, \\ a_{6} & = \frac{m_{2} d α (K α^{2} ω m_{1} + K α r σ m_{1} - d r σ) ϕ}{σ λ^{3} r} - \frac{((a d m_{1} + a δ m_{1}) α + d (d + δ)) (K α^{2} ω m_{1} + K α r σ m_{1} - d r σ)}{σ λ^{3} r} . \end{align}$
The coexistence equilibrium point $E^{*}$ exists only if the characteristic equation (9) has a positive root in A with $A > \frac{α ω + r σ}{α η}$ .

5 STABILITY OF THE EQUILIBRIA

The stability analysis is done by linearization of the nonlinear system (1). We write the Jacobian matrix J at the fixed points of the system and compute the characteristic equation. Then, the stability of the equilibrium point is studied depending on the eigenvalues of the corresponding Jacobian, which are functions of the model parameters. The Jacobian matrix for system (1), at a steady state

(X, S, I, A)

, is given by

J (X, S, I, A) = [\begin{array}{cccc} r (1 - \frac{2 X}{K}) - α S - \frac{ϕ α a I}{{(a + X)}^{2}} & - α X & - \frac{ϕ α X}{a + X} & 0 \\ m_{1} α S & m_{1} α X - λ A - d - \frac{γ A}{1 + A} & 0 & - λ S - \frac{γ S}{{(1 + A)}^{2}} \\ \frac{m_{2} ϕ α a I}{{(a + X)}^{2}} & λ A & \frac{m_{2} ϕ α X}{a + X} - d - δ - \frac{γ A}{1 + A} & - λ S - \frac{γ I}{{(1 + A)}^{2}} \\ 0 & σ & σ & - η \end{array}] .

()

Theorem 3. (Stability of the crop-pest free equilibrium)The system is always unstable around the crop-pest free equilibrium point $E_{0}$ .

Proof.The Jacobian matrix (10) at the crop-pest free equilibrium $E_{0}$ is given by

J (0, 0, 0, \frac{ω}{η}) = [\begin{array}{cccc} r & 0 & 0 & 0 \\ 0 & - \frac{λ ω}{η} - d - \frac{γ ω}{η + ω} & 0 & 0 \\ 0 & \frac{λ ω}{η} & - d - δ - \frac{γ ω}{η + ω} & 0 \\ 0 & σ & σ & - η \end{array}],

whose characteristic equation is

|ρ - J (E_{0})| = |\begin{array}{cccc} ρ - r & 0 & 0 & 0 \\ 0 & ρ + (\frac{λ ω}{η} + d + \frac{γ ω}{η + ω}) & 0 & 0 \\ 0 & - \frac{λ ω}{η} & ρ + (d + δ + \frac{γ ω}{η + ω}) & 0 \\ 0 & - σ & - σ & ρ + η \end{array}| = 0,

that is,

(ρ - r) (ρ + \frac{λ ω}{η} + d + \frac{γ ω}{η + ω}) (ρ + d + δ + \frac{γ ω}{η + ω}) (ρ + η) = 0 .

The corresponding eigenvalues are:

ρ_{1} = r > 0, ρ_{2} = - η < 0, ρ_{3} = - (\frac{λ ω}{η} + d + \frac{γ ω}{η + ω}) < 0, ρ_{4} = - (d + δ + \frac{γ ω}{η + ω}) < 0 .

Since one eigenvalue is positive,

ρ_{1} = r > 0

, the axial equilibrium

E_{0}

is always unstable.

Theorem 4. (Stability of the pest free equilibrium)The pest free steady state $E_{1}$ is locally asymptotically stable if the two critical parameters $R_{0}$ and $R_{1}$ ,

\begin{align} R_{0} & : = \frac{m_{1} α K η (η + ω)}{λ ω (η + ω) + η γ ω + d η (η + ω)}, \\ R_{1} & : = \frac{m_{2} ϕ α K (η + ω)}{(a + K) (d + δ) (η + ω) + (a + K) γ ω}, \end{align}

()

satisfy

R_{0} < 1

and

R_{1} < 1

. Otherwise,

E_{1}

is unstable.

Proof.The Jacobian matrix $J (E_{1})$ , at the pest free equilibrium point $E_{1} = (K, 0, 0, \frac{ω}{η})$ , is given by

J (K, 0, 0, \frac{ω}{η}) = [\begin{array}{cccc} - r & - K α & - \frac{ϕ α K}{a + K} & 0 \\ 0 & m_{1} α K - \frac{λ ω}{η} - d - \frac{γ ω}{η + ω} & 0 & 0 \\ 0 & \frac{λ ω}{η} & \frac{m_{2} ϕ α K}{a + K} - d - δ - \frac{γ ω}{η + ω} & 0 \\ 0 & σ & σ & - η \end{array}] .

The characteristic equation in

ρ

E_{1}

| ρ I - J (E_{1}) | = |\begin{array}{cccc} ρ + r & K α & \frac{ϕ α K}{a + K} & 0 \\ 0 & ρ - m_{1} α K + \frac{λ ω}{η} + d + \frac{γ ω}{η + ω} & 0 & 0 \\ 0 & - \frac{λ ω}{η} & ρ - \frac{m_{2} ϕ α K}{a + K} + d + δ + \frac{γ ω}{η + ω} & 0 \\ 0 & - σ & - σ & ρ + η \end{array}| = 0,

which gives

(ρ + r) (ρ - m_{1} α K + \frac{λ ω}{η} + d + \frac{γ ω}{η + ω}) (ρ - \frac{m_{2} ϕ α K}{a + K} + d + δ + \frac{γ ω}{η + ω}) (ρ + η) = 0 .

Thus, the eigenvalues are

λ_{1} = - r

λ_{2} = m_{1} α K - \frac{λ ω}{η} - d - \frac{γ ω}{η + ω}

λ_{3} = \frac{m_{2} ϕ α K}{a + K} - d - δ - \frac{γ ω}{η + ω}

, and

λ_{4} = - η

. We have that

(E_{1})

is locally asymptotically stable if all the four eigenvalues

λ_{1}

λ_{2}

λ_{3}

, and

λ_{4}

are negative. It is clearly seen that

λ_{1} = - r < 0

λ_{4} = - η < 0

, since

r > 0

and

η > 0

. So, for the stability existence of

E_{1}

, we should have

λ_{2} < 0

and

λ_{3} < 0

, that is,

\begin{align} m_{1} α K - \frac{λ ω}{η} - d - \frac{γ ω}{η + ω} < 0 and \frac{m_{2} ϕ α K}{a + K} - d - δ - \frac{γ ω}{η + ω} < 0 \\ \Rightarrow m_{1} α K < \frac{λ ω}{η} + d + \frac{γ ω}{η + ω} and \frac{m_{2} ϕ α K}{a + K} < d + δ + \frac{γ ω}{η + ω} \\ \Rightarrow m_{1} α K < \frac{λ ω (η + ω) + η γ ω + d η (η + ω)}{η (η + ω)} and \frac{m_{2} ϕ α K}{a + K} < \frac{(d + δ) (η + ω) + γ ω}{η + ω} \\ \Rightarrow m_{1} α K η (η + ω) < λ ω (η + ω) + η γ ω + d η (η + ω) and \\ m_{2} ϕ α K (η + ω) < (a + K) (d + δ) (η + ω) + (a + K) γ ω \\ \Rightarrow \frac{m_{1} α K η (η + ω)}{λ ω (η + ω) + η γ ω + d η (η + ω)} < 1 and \frac{m_{2} ϕ α K (η + ω)}{(a + K) (d + δ) (η + ω) + (a + K) γ ω} < 1 \end{align}

or, equivalently,

R_{0} < 1

and

R_{1} < 1

with the critical parameters

R_{0}

and

R_{1}

given by (11).

The conditions for stability of the pest free equilibrium point $E_{1}$ indicate that if the attack rate of the pest population $α$ is low, then the system may stabilize to the pest free steady state.

Theorem 5. (Stability of the healthy pest free equilibrium)The healthy pest free equilibrium $E_{3} = (\overline{X}, 0, Ī, Ā)$ is locally asymptotically stable if, and only if,

(i)
$\overline{X} < \frac{λ Ā^{2} + (λ + d + γ) Ā + d}{m_{1} α (1 + Ā)}$ ,
(ii)
$C_{i} > 0$ , $i = 1, 3$ ,
(iii)
$C_{1} C_{2} - C_{3} > 0$ ,

where

\begin{align} C_{1} & = - F_{11} - F_{33} + η, \\ C_{2} & = (F_{11} - η) F_{33} - F_{11} η + \frac{(γ σ (X^{3} + 3 {\overline{X}}^{2} a + 3 a) + m_{2} ϕ^{2} α^{2} {(1 + Ā)}^{2}) Ī}{({\overline{X}}^{3} + a) {(1 + Ā)}^{2}}, \\ C_{3} & = η F_{11} F_{33} + \frac{Ī \overline{X} a α^{2} η ϕ^{2} m_{2} {(1 + Ā)}^{2} - σ I γ {(a + \overline{X})}^{3} F_{11}}{({\overline{X}}^{3} + a) {(1 + Ā)}^{2}}, \end{align}

()

with

\begin{align} F_{11} & = r (1 - \frac{2 \overline{X}}{K}) - \frac{ϕ α a Ī}{{(a + \overline{X})}^{2}}, \\ F_{22} & = m_{1} α \overline{X} - λ Ā - d - \frac{γ Ā}{1 + Ā}, \\ F_{33} & = \frac{m_{2} ϕ α \overline{X}}{a + \overline{X}} - d - δ - \frac{γ Ā}{1 + Ā} . \end{align}

()

Proof.At the healthy pest free fixed point $E_{3} = (\overline{X}, 0, Ī, Ā)$ , the Jacobian matrix is given by

J (E_{3}) = [\begin{array}{cccc} F_{11} & - α \overline{X} & - \frac{ϕ α \overline{X}}{a + \overline{X}} & 0 \\ 0 & F_{22} & 0 & 0 \\ \frac{m_{2} ϕ α a Ī}{{(a + \overline{X})}^{2}} & λ Ā & F_{33} & - \frac{γ Ī}{{(1 + Ā)}^{2}} \\ 0 & σ & σ & - η \end{array}]

with

F_{i i}

i = 1, 2, 3

as in (13). The characteristic equation in

ρ

is then given by

(ρ - F_{22}) [ρ^{3} + C_{1} ρ^{2} + C_{2} ρ + C_{3}] = 0,

()

where the

C_{i}

i = 1, 2, 3

are defined by (12). The equilibrium

E_{3}

is locally asymptotically stable if and only if all roots of the polynomial (14) have negative real parts. Equation (14) has one root

ρ = F_{22}

and the other three roots are solution of

ρ^{3} + C_{1} ρ^{2} + C_{2} ρ + C_{3} = 0 .

()

To conclude about the stability behavior of

E_{3}

, we analyze the (three) roots of the cubic polynomial (15). The Routh–Hurwitz criteria applied to the third degree polynomial (15) tell us that a necessary and sufficient condition for the local stability of the system is that all eigenvalues must have negative real part, that is,

C_{1} > 0

C_{2} > 0

C_{3} > 0

, and

C_{1} C_{2} - C_{3} > 0

must hold. Hence,

E_{3}

is locally asymptotically stable if, and only if, the following conditions hold:

(i)
$F_{22} = m_{1} α \overline{X} - λ Ā - d - \frac{γ A}{1 + A} < 0 \Rightarrow \overline{X} < \frac{λ Ā^{2} + (λ + d + γ) Ā + d}{m_{1} α (1 + Ā)}$ ;
(ii)
$C_{1} > 0, C_{3} > 0$ ;
(iii)
$C_{1} C_{2} - C_{3} > 0$ .

The proof is complete.

Theorem 6. (Stability of the interior equilibrium point)System (1) at the interior equilibrium point $E^{*} = (X^{*}, S^{*}, I^{*}, A^{*})$ is locally asymptotically stable if, and only if,

\begin{array}{c} y_{4} > 0, \\ y_{1} y_{2} - y_{3} > 0, \\ y_{1} y_{2} y_{3} - {y_{3}}^{2} - {y_{1}}^{2} y_{4} > 0, \end{array}

()

where

\begin{align} y_{1} & = - (F_{11} + F_{22} + F_{33}) + η, \\ y_{2} & = (F_{22} + F_{33} - η) F_{11} + (F_{33} - η) F_{22} - η F_{33} + S^{*} X^{*} α^{2} m_{1} - \frac{γ (I^{*} + S^{*}) σ}{{(1 + A^{*})}^{2} (X^{*} + a)} - \frac{m_{2} ϕ^{2} α^{2} a I^{*} X^{*}}{{(X^{*} + a)}^{3}}, \\ y_{3} & = ((- F_{33} + η) F_{22} + η F_{33} + \frac{γ (I^{*} + S^{*}) σ}{{(1 + A^{*})}^{2}}) F_{11} + (η F_{33} + (- λ S^{*} + \frac{γ I^{*}}{{(1 + A^{*})}^{2}}) σ + \frac{m_{2} ϕ^{2} α^{2} a I^{*} X^{*}}{{(X^{*} + a)}^{3}}) F_{22} \\ + (- S^{*} X^{*} α^{2} m_{1} + σ (λ S^{*} + \frac{γ S^{*}}{{(1 + A^{*})}^{2}})) F_{33} + S α^{2} (η + \frac{A^{*} λ ϕ}{X^{*} + a}) X^{*} m_{1} \\ - A^{*} (λ S^{*} + \frac{γ S^{*}}{{(1 + A^{*})}^{2}}) σ λ - \frac{m_{2} ϕ^{2} α^{2} a I^{*} X^{*} η}{{(X^{*} + a)}^{3}}, \\ y_{4} & = ((λ S^{*} - \frac{γ I^{*}}{{(1 + A^{*})}^{2}}) σ - η F_{33}) F_{22} - σ (λ S^{*} + \frac{γ S^{*}}{{(1 + A^{*})}^{2}}) F_{33} + A^{*} (λ S^{*} + \frac{γ S^{*}}{{(1 + A^{*})}^{2}}) σ λ F_{11} \\ + \frac{α^{2} ϕ^{2} η X^{*} F_{22} m_{2} a I}{{(X^{*} + a)}^{3}} - S^{*} X^{*} α^{2} η m_{1} F_{33} - \frac{(X^{*} + a - ϕ) m_{2} I^{*} σ a α^{2} (λ {(1 + A^{*})}^{2} + γ) ϕ X^{*} S}{{(1 + A^{*})}^{2} {(X^{*} + a)}^{3}} \\ + \frac{((S^{*} (X^{*} + a - ϕ) σ + A^{*} η ϕ) {(1 + A^{*})}^{2} λ - I^{*} γ σ (X^{*} + a - ϕ)) S^{*} X^{*} α^{2} m_{1}}{{(1 + A^{*})}^{2} (X^{*} + a)}, \end{align}

()

with

\begin{align} F_{11} & = r (1 - \frac{2 X^{*}}{K}) - α \overline{S} - \frac{ϕ α a I^{*}}{{(a + X^{*})}^{2}}, \\ F_{22} & = m_{1} α X^{*} - λ A^{*} - d - \frac{γ A^{*}}{1 + A^{*}}, \\ F_{33} & = \frac{m_{2} ϕ α X^{*}}{a + X^{*}} - d - δ - \frac{γ A^{*}}{1 + A^{*}} . \end{align}

()

Proof.The Jacobian matrix at the coexistence equilibrium point $E^{*}$ is given by

J (E^{*}) = [\begin{array}{cccc} F_{11} & - α X^{*} & - \frac{ϕ α X^{*}}{a + X^{*}} & 0 \\ m_{1} α S^{*} & F_{22} & 0 & - λ S^{*} - \frac{γ S^{*}}{{(1 + A^{*})}^{2}} \\ \frac{m_{2} ϕ α a I^{*}}{{(a + X^{*})}^{2}} & λ A^{*} & F_{33} & λ S^{*} - \frac{γ I^{*}}{{(1 + A^{*})}^{2}} \\ 0 & σ & σ & - η \end{array}],

where

F_{i i}

i = 1, 2, 3

, are given by (18). The characteristic equation in

ρ

for the Jacobian matrix

J (E^{*})

is given by

| ρ I - J (E^{*}) | = |\begin{array}{cccc} ρ - F_{11} & α X^{*} & \frac{ϕ α X^{*}}{a + X^{*}} & 0 \\ - m_{1} α S^{*} & ρ - F_{22} & 0 & λ S^{*} + \frac{γ S^{*}}{{(1 + A^{*})}^{2}} \\ - \frac{m_{2} ϕ α a I^{*}}{{(a + X^{*})}^{2}} & - λ A^{*} & ρ - F_{33} & - λ S^{*} + \frac{γ I^{*}}{{(1 + A^{*})}^{2}} \\ 0 & - σ & - σ & ρ + η \end{array}| = 0,

which gives

ρ^{4} + y_{1} ρ^{3} + y_{2} ρ^{2} + y_{3} ρ + y_{4} = 0

()

with

y_{i}

i = 1, \dots, 4

, defined by (17). Then, noting that

y_{1} > 0

, it follows from the Routh–Hurwitz criterion that the interior equilibrium

E^{*}

is locally asymptotically stable if (16) hold and unstable otherwise.

Next, we shall find out conditions for which the system enters into Hopf bifurcation around the interior equilibrium $E^{*}$ . We focus on the pest consumption rate $α$ , which is considered as the most biologically significant parameter.

6 HOPF-BIFURCATION

Let us define the continuously differentiable function

Ψ : (0, \infty) \to ℝ

α

as follows:

Ψ (α) ≔ y_{1} (α) y_{2} (α) y_{3} (α) - {y_{3}}^{2} (α) - y_{4} (α) {y_{1}}^{2} (α),

()

where we look to expressions (17) as functions of

α

. The conditions for occurrence of a Hopf-bifurcation tell us that the spectrum

σ (α)

of the characteristic equation should satisfy the following conditions:

(i)
There exists $α^{*} \in (0, \infty)$ at which a pair of complex eigenvalues $ρ (α^{*}), \overline{ρ} (α^{*}) \in σ (α)$ are such that
$ℜ e ρ (α^{*}) = 0, I m ρ (α^{*}) = ω_{0} > 0$
with transversality condition
${\frac{d ℜ e [ρ (α)]}{d α}|}_{α^{*}} \neq 0;$
(ii)
All other elements of $σ (α)$ have negative real parts.

We obtain the following result.

Theorem 7. (Hopf bifurcation around the interior equilibrium with respect to the pest consumption rate $α$ )Let $Ψ (α)$ be given as in (20) and let $α^{*} \in (0, \infty)$ be such that $Ψ (α^{*}) = 0$ . System (1) enters into a Hopf bifurcation around the coexistence equilibrium $E^{*}$ at $α^{*}$ if and only if $A (α^{*}) C (α^{*}) + B (α^{*}) D (α^{*}) \neq 0$ , where

\begin{align} A (α) & = 4 {β_{1}}^{3} - 12 β_{1} {β_{2}}^{2} + 3 y_{1} ({β_{1}}^{2} - {β_{2}}^{2}) + 2 y_{2} β_{1} + y_{3}, \\ B (α) & = 12 {β_{1}}^{2} β_{2} + 6 y_{1} β_{1} β_{2} - 4 {β_{2}}^{3} + 2 y_{2} β_{2}, \\ C (α) & = ({β_{1}}^{3} - 3 β_{1} {β_{2}}^{2}) y_{1}^{'} + ({β_{1}}^{2} - {β_{2}}^{2}) y_{2}^{'} + β_{1} y_{3}^{'} + y_{4}^{'}, \\ D (α) & = (3 {β_{1}}^{2} β_{2} - {β_{2}}^{3}) y_{1}^{'} + 2 β_{1} β_{2} y_{2}^{'} + β_{2} y_{3}^{'}, \end{align}

()

with

ρ_{1} = β_{1} + i β_{2}

and

ρ_{2} = β_{1} - i β_{2}

the pair of conjugate complex eigenvalues, solutions of the characteristic equation (19), with

ρ_{i} (α)

purely imaginary at

α = α^{*}

i = 1, 2

, and where the other eigenvalues

ρ_{3}

and

ρ_{4}

, solutions of (19), have negative real parts.

Proof.The critical value $α^{*}$ is obtained from the equation $Ψ (α) = 0$ . For $α = α^{*}$ , we have

\begin{align} Ψ (α) = 0 & \Rightarrow y_{1} (α) y_{2} (α) y_{3} (α) - {y_{3}}^{2} (α) - y_{4} (α) y_{1}^{2} (α) = 0 \\ \Rightarrow y_{1} (α) y_{2} (α) y_{3} (α) = {y_{3}}^{2} (α) + y_{4} (α) y_{1}^{2} (α) = 0 \\ \Rightarrow y_{1} y_{2} y_{3} = {y_{3}}^{2} + y_{4} {y_{1}}^{2}, \end{align}

from which we get

y_{2} = \frac{y_{3}}{y_{1}} + \frac{y_{4} y_{1}}{y_{3}} .

Then, the characteristic equation (19) becomes

\begin{align} ρ^{4} + y_{1} ρ^{3} + (\frac{y_{3}}{y_{1}} + \frac{y_{1} y_{4}}{y_{3}}) ρ^{2} + y_{3} ρ + y_{4} = 0 & \Rightarrow ρ^{4} + y_{1} ρ^{3} + \frac{y_{1} y_{4}}{y_{3}} ρ^{2} + \frac{y_{3}}{y_{1}} ρ^{2} + y_{3} ρ + y_{4} = 0 \\ \Rightarrow ρ^{2} (ρ^{2} + y_{1} ρ + \frac{y_{1} y_{4}}{y_{3}}) + \frac{y_{3}}{y_{1}} (ρ^{2} + y_{1} ρ + \frac{y_{1} y_{4}}{y_{3}}) = 0, \end{align}

that is,

(ρ^{2} + \frac{y_{3}}{y_{1}}) (ρ^{2} + y_{1} ρ + \frac{y_{1} y_{4}}{y_{3}}) = 0 .

()

We suppose Equation (22) has four roots

ρ_{i}

i = 1, 2, 3, 4

, with the pair of purely imaginary roots

ρ_{1}

and

ρ_{2}

α = α^{*}

ρ_{1} = \overline{ρ_{2}}

. We get

\begin{align} ρ_{3} + ρ_{4} & = - y_{1}, \\ ω_{0}^{2} + ρ_{3} ρ_{4} & = y_{2}, \\ ω_{0}^{2} (ρ_{3} + ρ_{4}) & = - y_{3}, \\ ω_{0}^{2} ρ_{3} ρ_{4} & = y_{4}, \end{align}

()

where

ω_{0} = I m ρ_{1} (α^{*})

. From these relations, we obtain that

{ω_{0}}^{2} = \frac{y_{3}}{y_{1}}

. Now, if

ρ_{3}

and

ρ_{4}

are complex conjugate, then from the first part of (23), it follows that

2 ℜ e ρ_{3} = - y_{1}

. If they are real roots, then by the first and last parts of (23),

ρ_{3} < 0

and

ρ_{4} < 0

. Further, as

ψ (α^{*})

is a continuous function of all its roots, there exists an open interval

α \in (α^{*} - ϵ, α^{*} + ϵ)

such that

ρ_{1}

and

ρ_{2}

are complex conjugate for

α

. Suppose their general forms in this neighborhood are

\begin{align} ρ_{1} (α) & = β_{1} (α) + i β_{2} (α), \\ ρ_{2} (α) & = β_{1} (α) - i β_{2} (α) . \end{align}

Now, we verify the transversality condition

{\frac{d ℜ e [ρ_{j} (α)]}{d α}|}_{α = α^{*}} \neq 0, j = 1, 2 .

()

Substituting

ρ_{j} (α) = β_{1} (α) \pm i β_{2} (α)

into (19), we get the following equation:

{(β_{1} (α) + i β_{2} (α))}^{4} + y_{1} {(β_{1} (α) + i β_{2} (α))}^{3} + y_{2} {(β_{1} (α) + i β_{2} (α))}^{2} + y_{3} (β_{1} (α) + i β_{2} (α)) + y_{4} = 0 .

Differentiating with respect to

α

, we have

\begin{align} 4 {(β_{1} (α) + i β_{2} (α))}^{3} ({β_{1}}^{'} (α) + i {β_{2}}^{'} (α)) + {y_{1}}^{'} {(β_{1} (α) + i β_{2} (α))}^{3} + 3 y_{1} {(β_{1} (α) + i β_{2} (α))}^{2} ({β_{1}}^{'} (α) + i {β_{2}}^{'} (α)) \\ + {y_{2}}^{'} {(β_{1} (α) + i β_{2} (α))}^{2} + 2 y_{2} (β_{1} (α) + i β_{2} (α)) ({β_{1}}^{'} (α) + i {β_{2}}^{'} (α)) \\ + {y_{3}}^{'} (β_{1} (α) + i β_{2} (α)) + y_{3} ({β_{1}}^{'} (α) + i {β_{2}}^{'} (α)) + {y_{4}}^{'} = 0, \end{align}

that is,

\begin{align} \underset{⏟}{4 i {β_{1}}^{3} {β_{2}}^{'} + 12 i {β_{1}}^{2} β_{2} β_{1}^{'} + 3 i {β_{1}}^{2} β_{2} y_{1}^{'} + 3 i {β_{1}}^{2} β_{2}^{'} y_{1} - 12 i β_{1} {β_{2}}^{2} β_{2}^{'} + 6 i β_{1} β_{2} β_{1}^{'} y_{1}} \\ \underset{⏟}{- 4 i {β_{2}}^{3} β_{1}^{'} - i {β_{2}}^{3} y_{1}^{'} - 3 i {β_{2}}^{2} β_{2}^{'} y_{1} + 2 i β_{1} β_{2} y_{2}^{'} + 2 i β_{1} β_{2}^{'} y_{2} + 2 i β_{2} β_{1}^{'} y_{2}} \\ \overset{⏞}{+ 4 {β_{1}}^{3} β_{1}^{'} + {β_{1}}^{3} y_{1}^{'} - 12 {β_{1}}^{2} β_{2} β_{2}^{'} + 3 {β_{1}}^{2} β_{1}^{'} y_{1} - 12 β_{1} {β_{2}}^{2} β_{1}^{'} - 3 β_{1} {β_{2}}^{2} y_{1}^{'} - 6 β_{1} β_{2} β_{2}^{'} y_{1} + 4 {β_{2}}^{3} β_{2}^{'}} \\ \overset{⏞}{- 3 {β_{2}}^{2} β_{1}^{'} y_{1} + i β_{2} y_{3}^{'} + i β_{2}^{'} y_{3} + {β_{1}}^{2} y_{2}^{'} + 2 β_{1} β_{1}^{'} y_{2} - {β_{2}}^{2} y_{2}^{'} - 2 β_{2} β_{2}^{'} y_{2} + β_{1} y_{3}^{'} + β_{1}^{'} y_{3} + y_{4}^{'}} = 0 . \end{align}

Comparing the real and imaginary parts, we get

\begin{align} (4 {β_{1}}^{3} - 12 β_{1} {β_{2}}^{2} + 3 y_{1} ({β_{1}}^{2} - {β_{2}}^{2}) + 2 β_{1} y_{2} + y_{3}) β_{1}^{'} & + (- 12 {β_{1}}^{2} β_{2} - 6 β_{1} β_{2} y_{1} + 4 {β_{2}}^{3} - 2 β_{2} y_{2}) β_{2}^{'} \\ + ({β_{1}}^{3} - 3 β_{1} {β_{2}}^{2}) y_{1}^{'} + ({β_{1}}^{2} - {β_{2}}^{2}) y_{2}^{'} + β_{1} y_{3}^{'} + y_{4}^{'} = 0 \end{align}

()

and

\begin{align} (12 {β_{1}}^{2} β_{2} + 6 β_{1} β_{2} y_{1} - 4 {β_{2}}^{3} + 2 β_{2} y_{2}) β_{1}^{'} + (4 {β_{1}}^{3} - 12 β_{1} {β_{2}}^{2} + 3 y_{1} ({β_{1}}^{2} - {β_{2}}^{2}) + 2 β_{1} y_{2} + y_{3}) β_{2}^{'} \\ + (3 {β_{1}}^{2} β_{2} - {β_{2}}^{3}) y_{1}^{'} + 2 β_{1} β_{2} y_{2}^{'} + β_{2} y_{3}^{'} = 0 . \end{align}

()

Equivalently, we can write (25) and (26), in a compact form, as

\begin{align} A (α) β_{1}^{'} (α) - B (α) β_{2}^{'} (α) + C (α) & = 0, \\ B (α) β_{1}^{'} (α) + A (α) β_{2}^{'} (α) + D (α) & = 0, \end{align}

()

where

A (α)

B (α)

C (α)

, and

D (α)

are defined by (21). Hence, solving system (27) for

β_{1}^{'} (α^{*})

, we get

{\frac{d ℜ e [ρ_{j} (α)]}{d α}|}_{α = α^{*}} = {β_{1}^{'} (α)|}_{α = α^{*}} = - \frac{A (α^{*}) C (α^{*}) + B (α^{*}) D (α^{*})}{A^{2} (α^{*}) + B^{2} (α^{*})} \neq 0 .

Thus, the transversality conditions hold if and only if

A (α^{*}) C (α^{*}) + B (α^{*}) D (α^{*}) \neq 0

, in which case a Hopf bifurcation occurs at

α = α^{*}

We have restricted ourselves here to study the Hopf bifurcation around the interior equilibrium point with respect to the pest consumption rate $α$ , because it is the most biologically significant parameter. However, by replacing $α$ by other model parameters, such as $λ$ , $γ$ , or $σ$ , one can also study the Hopf bifurcation around the interior equilibrium point with respect to such parameters of the model.

7 THE OPTIMAL CONTROL PROBLEM

In this section, we introduce an optimal control problem that consists to minimize the negative effects of chemical pesticides and to minimize the cost of pest management. We extend the model system (1) by incorporating three time-dependent controls:

u_{1} (t)

u_{2} (t)

, and

u_{3} (t)

, where the first control

u_{1}

is for controlling the use of chemical pesticides, the second control

u_{2}

is for bio-pesticides, and the third control

u_{3}

is for advertisement. The objective is to reduce the price of announcement for farming awareness via radio, TV, telephony, and other social media, while taking into account the price regarding the control measures. Our target is to find optimal functions

{u_{1}}^{*} (t)

{u_{2}}^{*} (t)

, and

{u_{3}}^{*} (t)

using the PMP.¹² In agreement, our system (1) is modified into the induced nonlinear dynamic control system given by

\{\begin{cases} \frac{d X}{d t} = r X (1 - \frac{X}{K}) - α X S - \frac{ϕ α X I}{a + X}, \\ \frac{d S}{d t} = m_{1} α X S - u_{2} λ A S - d S - \frac{u_{1} γ S A}{1 + A}, \\ \frac{d I}{d t} = \frac{m_{2} ϕ α X I}{a + X} + u_{2} λ A S - (d + δ) I - \frac{u_{1} γ I A}{1 + A}, \\ \frac{d A}{d t} = u_{3} ω + σ (S + I) - η A, \end{cases}

()

with given initial conditions

X (0) = X_{0}, S (0) = S_{0}, I (0) = I_{0}, and A (0) = A_{0} .

()

We need to reduce the number of pests and also the price of pest administration by reducing the cost of pesticides and exploiting the stage of awareness. The objective cost functional for the minimization problem is denoted by

J (u_{1}, u_{2}, u_{3})

and defined as follows:

J (u_{1} (\cdot), u_{2} (\cdot), u_{3} (\cdot)) = \int_{0}^{t_{f}} g (t, Φ (t), u (t)) d t = \int_{0}^{t_{f}} [\frac{P_{1} {u_{1}}^{2} (t)}{2} + \frac{P_{2} {u_{2}}^{2} (t)}{2} + \frac{P_{3} {u_{3}}^{2} (t)}{2} + Q S^{2} (t) - R A^{2} (t)] d t,

()

where

Φ (t) = (X (t), S (t), I (t), A (t))

is the solution to the induced control system (28)–(29),

t \in [0, t_{f}]

, for the specific control

u (t) = (u_{1} (t), u_{2} (t), u_{3} (t))

; the amounts

\frac{P_{1}}{2}, \frac{P_{2}}{2}

, and

\frac{P_{3}}{2}

are the positive weight constants on the benefit of the cost; and the terms Q and R are the penalty multipliers. We prefer a quadratic cost functional on the controls, as an approximation for the nonlinear function depending on the assumption that the cost takes a nonlinear form, and also to prevent the bang-bang or singular optimal control cases. The control set is defined on

[t_{0}, t_{f}]

subject to the constraints

0 \leq u_{i} (t) \leq 1

i = 1, 2, 3

, where

t_{0}

and

t_{f}

are the starting and final times of the optimal control problem, respectively. The aim is to find the optimal profile of

u_{1} (t), u_{2} (t)

, and

u_{3} (t)

, denoted by

{u_{i}}^{*} (t)

i = 1, 2, 3

, so that the cost functional J has a minimum value, that is,

J (u_{1}^{*}, u_{2}^{*}, u_{3}^{*}) = \min (J (u_{1}, u_{2}, u_{3}) : (u_{1}, u_{2}, u_{3}) \in 𝒰)

()

subject to (28)–(29), where

𝒰 = \{u = (u_{1}, u_{2}, u_{3}) \in L^{1} | 0 \leq u_{1} (t) \leq 1, 0 \leq u_{2} (t) \leq 1, 0 \leq u_{3} (t) \leq 1, t \in [0, t_{f}]\}

()

is the admissible control set with

L^{1}

the class of Lebesgue measurable functions. The PMP¹³ is used to find the optimal control triplet

u^{*} = (u_{1}^{*}, u_{2}^{*}, u_{3}^{*})

. For that the Hamiltonian function is defined as

ℋ = [\frac{P_{1} u_{1}^{2}}{2} + \frac{P_{2} u_{2}^{2}}{2} \frac{+ P_{3} u_{3}^{2}}{2} + Q S^{2} - R A^{2}] + \sum_{i = 1}^{4} λ_{i} f_{i} (X, S, I, A),

()

where

λ_{i}

i = 1, 2, \dots, 4

, are the adjoint variables and

f_{i}

i = 1, 2, 3, 4

, are the right-hand sides of system (28) at the ith state. Before trying to find the solution of the optimal control problem through the PMP, one first needs to prove that the problem has a solution.

7.1 Existence of solution

The existence of an optimal control triple can be guaranteed by using well-known results.¹² Since all the state variables involved in the model are continuously differentiable, existence of solution is guaranteed under the following conditions:^12-14

(i)
The set of trajectories to system (28)–(29) on the admissible class of controls (32) is non-empty.
(ii)
The set where the controls take values is convex and closed.
(iii)
Each right-hand side of the state system (28) is continuous, is bounded above by a sum of the bounded control and the state, and can be written as a linear function of u with coefficients depending on time and the state variables.
(iv)
The integrand $g (t, Φ, u)$ of the objective functional (30) is convex with respect to the control variables.
(v)
There exist positive numbers $ℓ_{1}, ℓ_{2}, ℓ_{3}, ℓ_{4}$ and a constant $ℓ > 1$ such that
$g (t, Φ, u) \geq - ℓ_{1} + ℓ_{2} | u_{1} |^{ℓ} + ℓ_{3} | u_{2} |^{ℓ} + ℓ_{4} | u_{3} |^{ℓ} .$

We obtain the following existence result.

Theorem 8.Consider the optimal control problem defined by: the objective functional (30) on (32); the control system (28); and nonnegative initial conditions (29). Then there exists an optimal control triple $u^{*} = (u_{1}^{*}, u_{2}^{*}, u_{3}^{*})$ and corresponding state trajectory $Φ^{*} = (X^{*}, S^{*}, I^{*}, A^{*})$ such that $J (u_{1}^{*}, u_{2}^{*}, u_{3}^{*}) = \min_{𝒰} J (u_{1}, u_{2}, u_{3})$ subject to (28)–(29).

Proof.The proof is done verifying each of the five items (i)–(v) stated above.

(i)
Since $𝒰$ is a nonempty set of real valued measurable functions on the finite time interval $0 \leq t \leq t_{f}$ , the system (28) has bounded coefficients and hence any solutions are bounded on $[0, t_{f}]$ (see Theorem 2). It follows that the corresponding solutions for system (28)–(29) exist.¹⁵
(ii)
In our case, the set $Ω$ where the admissible controls take values is $Ω = \{u \in ℝ^{3} : | | u | | \leq 1\}$ , which is clearly a convex and closed set.
(iii)
The right-hand sides of equations of system (28) are continuous. All variables $X, S, I, A$ , and u are bounded on $[0, t_{f}]$ and can be written as a linear function of $u_{1}, u_{2},$ and $u_{3}$ with coefficients depending on time and state variables.
(iv)
The integrand $g (t, Φ, u)$ of (30) is quadratic with respect to the control variables, so it is trivially convex.
(v)
Finally, it remains to show that there exists a constant $ℓ^{*} > 1$ and positive constants $ℓ_{1}, ℓ_{2}, ℓ_{3}$ , and $ℓ_{4}$ such that
$\frac{P_{1} {u_{1}}^{2}}{2} + \frac{P_{2} {u_{2}}^{2}}{2} + \frac{P_{3} {u_{3}}^{2}}{2} + Q S^{2} - R A^{2} \geq - ℓ_{1} + ℓ_{2} | u_{1} |^{ℓ} + ℓ_{3} | u_{2} |^{ℓ} + ℓ_{4} | u_{3} |^{ℓ} .$
In Section 2, we already showed that the state variables are bounded. Let $ℓ_{1} = \sup (Q S^{2} - R A^{2})$ , $ℓ_{2} = P_{1}$ , $ℓ_{3} = P_{2}$ , $ℓ_{4} = P_{3}$ , and $ℓ = 2$ . It follows that
$\frac{P_{1} {u_{1}}^{2}}{2} + \frac{P_{2} {u_{2}}^{2}}{2} + \frac{P_{3} {u_{3}}^{2}}{2} + Q S^{2} - R A^{2} \geq - ℓ_{1} + ℓ_{2} | u_{1} |^{ℓ} + ℓ_{3} | u_{2} |^{ℓ} + ℓ_{4} | u_{3} |^{ℓ} .$

We conclude that there exists an optimal control triple.¹²

7.2 Characterization of the solution

Since we know that there exists an optimal control triple for minimizing the functional

J (u_{1}, u_{2}, u_{3}) = \int_{0}^{t_{f}} [\frac{P_{1} {u_{1}}^{2} (t)}{2} + \frac{P_{2} {u_{2}}^{2} (t)}{2} + \frac{P_{3} {u_{3}}^{2} (t)}{2} + Q S^{2} (t) - R A^{2} (t)] d t

subject to the controlled system (28) and initial conditions (29), we now derive, using the PMP, necessary conditions to characterize and find the optimal control triple.^{12, 13} The necessary conditions include: the minimality condition, the adjoint system, and the transversality conditions, which come from the PMP.¹³ Roughly speaking, the PMP reduces the optimal control problem, a dynamic optimization problem, into a static optimization problem that consists of minimizing point-wise the Hamiltonian function

ℋ

. The Hamiltonian associated to our problem is explicitly given by

\begin{align} ℋ (t, Φ, u, λ) & = \frac{P_{1} {u_{1}}^{2}}{2} + \frac{P_{2} {u_{2}}^{2}}{2} + \frac{P_{3} {u_{3}}^{2}}{2} + Q S^{2} - R A^{2} \\ + λ_{1} (r X (1 - \frac{X}{K}) - α X S - \frac{ϕ α X I}{a + X}) \\ + λ_{2} (m_{1} α X S - u_{2} λ A S - d S - \frac{u_{1} γ S A}{1 + A}) \\ + λ_{3} (\frac{m_{2} ϕ α X I}{a + X} + u_{2} λ A S - (d + δ) I - \frac{u_{1} γ I A}{1 + A}) \\ + λ_{4} (u_{3} ω + σ (S + I) - η A) . \end{align}

The PMP asserts that if the control

u^{*} = (u_{1}^{*}, {u_{2}}^{*}, {u_{3}}^{*})

and the corresponding state

Φ^{*} = (X^{*}, S^{*}, I^{*}, A^{*})

form an optimal couple, then, necessarily, there exists a nontrivial adjoint vector

λ = (λ_{1}, λ_{2}, λ_{3}, λ_{4})

satisfying the following Hamiltonian system:¹⁶

\{\begin{cases} \frac{d Φ}{d t} = \frac{\partial ℋ (t, Φ, u, λ)}{\partial λ}, \\ \frac{d λ}{d t} = - \frac{\partial ℋ (t, Φ, u, λ)}{\partial Φ}, \end{cases}

subject to initial conditions (29) and transversality conditions

λ (t_{f}) = 0

. Moreover, at each point of time t, the optimal controls are characterized by

\{\begin{cases} u_{i}^{*} = 1, & if \frac{\partial ℋ}{\partial u_{i}} < 0, \\ {u_{i}}^{*} = 0, & if \frac{\partial ℋ}{\partial u_{i}} > 0 . \end{cases}

()

Theorem 9.If the controls $({u_{1}}^{*}, {u_{2}}^{*}, {u_{3}}^{*})$ and the corresponding trajectories $(H^{*}, S^{*}, I^{*}, A^{*})$ are optimal, then there exist adjoint variables $λ_{1}$ , $λ_{2}$ , $λ_{3}$ , and $λ_{4}$ satisfying the system of equations

\{\begin{cases} \frac{d λ_{1}}{d t} & = λ_{1} (α S + \frac{ϕ α a I}{{(a + X)}^{2}} - r (1 - \frac{2 X}{K})) - λ_{2} m_{1} α S - λ_{3} \frac{m_{2} ϕ α a I}{{(a + X)}^{2}}, \\ \frac{d λ_{2}}{d t} & = - 2 Q S + λ_{1} α X + λ_{2} (\frac{u_{1} γ A}{1 + A} + u_{2} λ A + d - m_{1} α X) - λ_{3} u_{2} λ A - λ_{4} σ, \\ \frac{d λ_{3}}{d t} & = λ_{1} \frac{ϕ α X}{a + X} + λ_{3} (\frac{u_{1} γ A}{1 + A} + d + δ - \frac{m_{2} ϕ α X}{a + X}) - λ_{4} σ, \\ \frac{d λ_{4}}{d t} & = 2 R A + λ_{2} (\frac{u_{1} γ S}{{(1 + A)}^{2}} + u_{2} λ S) + λ_{3} (\frac{u_{1} γ I}{{(1 + A)}^{2}} - u_{2} λ S) + λ_{4} η, \end{cases}

()

with transversality conditions

λ_{i} (t_{f}) = 0, i = 1, 2, 3, 4 .

()

Furthermore, for

t \in [0, t_{f}]

, the optimal controls

u_{1}^{*}, u_{2}^{*}

and

u_{3}^{*}

are characterized by

\begin{align} {u_{1}}^{*} (t) & = \max \{0, \min \{1, \frac{(λ_{2} (t) S (t) + λ_{3} (t) I (t)) γ A (t)}{P_{1} (1 + A (t))}\}\}, \\ {u_{2}}^{*} (t) & = \max \{0, \min \{1, \frac{(λ_{2} (t) - λ_{3} (t)) λ A (t) S (t)}{P_{2}}\}\}, \\ {u_{3}}^{*} (t) & = \max \{0, \min \{1, - \frac{λ_{4} (t) ω}{P_{3}}\}\} . \end{align}

()

Proof.The result is a direct consequence of the PMP.

In order to confirm the nature of the Pontryagin extremals given by Theorem 9, we check the Hessian matrix of the Hamiltonian

ℋ

. Because the Hessian matrix of

ℋ

with respect to the control variables is given by

\frac{\partial^{2} ℋ}{\partial u^{2}} = [\begin{array}{ccc} \frac{\partial^{2} ℋ}{\partial u_{1}^{2}} & \frac{\partial^{2} ℋ}{\partial u_{1} \partial u_{2}} & \frac{\partial^{2} ℋ}{\partial u_{1} \partial u_{3}} \\ \frac{\partial^{2} ℋ}{\partial u_{2} \partial u_{1}} & \frac{\partial^{2} ℋ}{\partial u_{2}^{2}} & \frac{\partial^{2} ℋ}{\partial u_{2} \partial u_{3}} \\ \frac{\partial^{2} ℋ}{\partial u_{3} \partial u_{1}} & \frac{\partial^{2} ℋ}{\partial u_{3} \partial u_{2}} & \frac{\partial^{2} ℋ}{\partial u_{3}^{2}} \end{array}] = [\begin{array}{ccc} P_{1} & 0 & 0 \\ 0 & P_{2} & 0 \\ 0 & 0 & P_{3} \end{array}],

which is a positive definite matrix as a consequence of the positive weights

P_{1}, P_{2}, P_{3}

, the Hamiltonian

ℋ

is convex with respect to the control variables and, as a result, the Pontryagin extremals will be minimizers and not maximizers.

7.3 The method to solve the optimal control problem

The optimal controls and the corresponding state functions are found by solving a system of dynamics called the optimality system, and consisting of

(i)
the state system (28) together with their initial conditions (29);
(ii)
the adjoint system (35);
(iii)
the terminal conditions (36);
(iv)
and the characterization of the optimal controls (37).

TABLE 1. Parameter values used in our numerical simulations

Parameters	Description	Value	Source
r	Growth rate of crop biomass	0.05 per day	17
K	Maximum density of crop biomass	1 m $^{- 2}$	1
$λ$	Aware people activity rate	0.025 per day	5
d	Natural mortality of pest	0.01 day $^{- 1}$	1
$m_{1}$	Conversion efficacy of susceptible pests	0.8	5
$m_{2}$	Conversion efficiency of infected pest	0.6	5
$δ$	Disease related mortality rate	0.1 per day	1
a	Half saturation constant	0.2	17
$α$	Attack rate of pest	0.025 pest $^{- 1}$ per day	5
$σ$	Local rate of increase of awareness	0.015 per day	Assumed
$γ$	The increase of level from global advertisement	0.025	4
$η$	Fading of memory of aware people	0.015 day $^{- 1}$	17
$ω$	Rate of global awareness (via TV, radio)	0.003 day $^{- 1}$	Assumed

In combination, the method consists to solve the system

\{\begin{cases} \frac{d X}{d t} = r X (1 - \frac{X}{K}) - α X S - \frac{ϕ α X I}{a + X}, \\ \frac{d S}{d t} = m_{1} α X S - u_{2} λ A S - d S - \frac{u_{1} γ S A}{1 + A}, \\ \frac{d I}{d t} = \frac{m_{2} ϕ α X I}{a + X} + u_{2} λ A S - (d + δ) I - \frac{u_{1} γ I A}{1 + A}, \\ \frac{d A}{d t} = u_{3} ω + σ (S + I) - η A, \\ X (0) = X_{0} \geq 0, S (0) = S_{0} \geq 0, I (0) = I_{0} \geq 0, A (0) = A_{0} \geq 0, \\ \frac{d λ_{1}}{d t} = λ_{1} (α S + \frac{ϕ α a I}{{(a + X)}^{2}} - r (1 - \frac{2 X}{K})) - λ_{2} m_{1} α S - λ_{3} \frac{m_{2} ϕ α a I}{{(a + X)}^{2}}, \\ \frac{d λ_{2}}{d t} = - 2 Q S + λ_{1} α X + λ_{2} (\frac{u_{1} γ A}{(1 + A)} + u_{2} λ A + d - m_{1} α X) - λ_{3} u_{2} λ A - λ_{4} σ, \\ \frac{d λ_{3}}{d t} = λ_{1} \frac{ϕ α X}{a + X} + λ_{3} (\frac{u_{1} γ A}{1 + A} + d + δ - \frac{m_{2} ϕ α X}{a + X}) - λ_{4} σ, \\ \frac{d λ_{4}}{d t} = 2 R A + λ_{2} (\frac{u_{1} γ S}{{(1 + A)}^{2}} + u_{2} λ S) + λ_{3} (\frac{u_{1} γ I}{{(1 + A)}^{2}} - u_{2} λ S) + λ_{4} η, \\ λ_{1} (t_{f}) = λ_{2} (t_{f}) = λ_{3} (t_{f}) = λ_{4} (t_{f}) = 0, \end{cases}

()

where

u_{1}

u_{2}

, and

u_{3}

are given as in (37). It is important to note that the adjoint system (35) is also linear in

λ_{i}

for

i = 1, 2, 3, 4

with bounded coefficients. Thus, there exists a positive real number M such that

| λ_{i} | \leq M

t \in [0, t_{f}]

. Hence, for a sufficiently small time

t_{f}

, the solution to the optimality system (38) is unique. The need for a small time interval in order to guarantee uniqueness of solution is due to the opposite time direction/orientations of the optimality system: the state system has initial values while the adjoint system has terminal values. Solving (38) analytically is not possible. Consequently, we use a numerical method to find the approximate optimal solutions

Φ^{*}

and

u^{*}

In Section 8, we solve the optimal control problem numerically and observe the behavior of some solutions as time varies.

8 NUMERICAL SIMULATIONS

Since the analytical solution of system (1) is not practical to analyze, the numerical results play a great role in characterizing the dynamics. Our numerical simulations show how realistic our results are and illustrate well the predicted analytical behavior. We begin by analyzing system (1) without controls, then our control system (28) subject to the optimal controls, as characterized by the PMP. Our numerical simulations are acquired with a set of parameter values as given in Table 1. For our numerical experiments of the uncontrolled system, we take $t_{f} = 600$ days; while for the numerical simulations of the optimal control problem we fix $t_{f} = 60$ days. The values of the weight function are taken as $P_{1} = 0.8$ , $P_{2} = 0.5$ , $P_{3} = 0.5$ , $Q = 10$ , and $R = 10$ , and the initial state variables as $X (0) = 0.2$ , $S (0) = 0.07$ , $I (0) = 0.05$ , $A (0) = 0.5$ . In Figures 1 and 2, the time series solution of model system (1) are sketched with different values of the parameters $α$ and $γ$ . It is observed that our model variables $X (t)$ , $S (t)$ , $I (t)$ , and $A (t)$ become oscillating as the values of the rates (i.e., $α$ and $γ$ ) get larger and finally become stable. Also, the steady state value of both pest population (when they exist) are decreased as $α$ and $γ$ rise. A bifurcation illustration is shown in Figure 3, taking $α$ as the main parameter.

Algorithm 1. Forward–backward sweep method

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Numerical solution of system (1) for different values of the rate $α$ of pest: $α = 0.12$ (blue line), $α = 0.16$ (red line), $α = 0.18$ (black line). Other parameter values as in Table 1

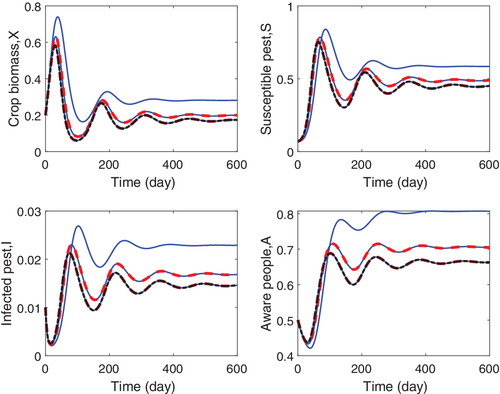
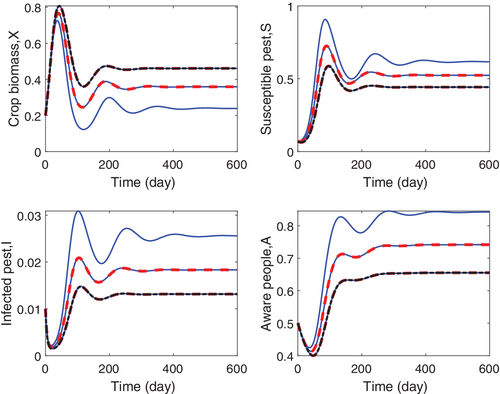
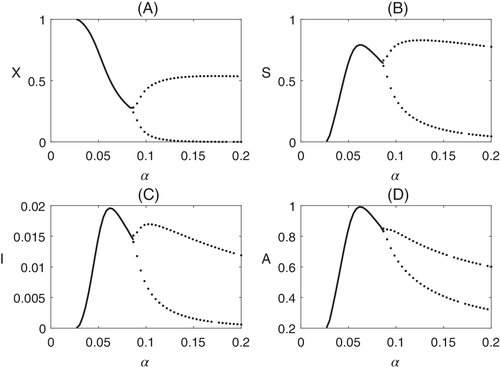
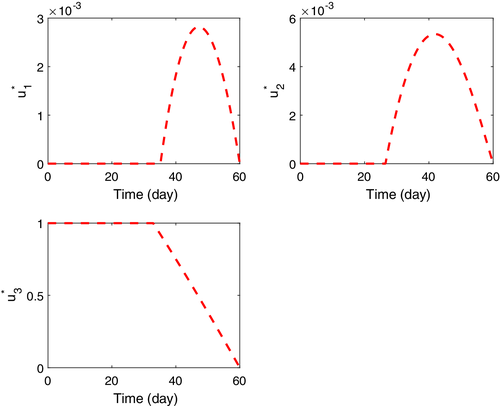
Critical values depend on many parameters, such as the conversion rates $m_{1}$ and $m_{2}$ , the rate of the awareness program $σ$ , the recruitment rate of global awareness $ω$ , the chemical pesticide control $u_{1}$ , and so forth. We examine the impact of optimal control profiles by implementing a Runge–Kutta fourth-order scheme on the optimality system (38). The dynamical behavior of the model, in relation to the controls, is presented. The optimal policy is achieved by finding a solution to the state system (1) and costate system (28). To find the optimal controls and respective states, we use the Runge–Kutta numerical method and the technical computing program MATLAB. As already discussed, one needs to solve four-state equations and four adjoint equations. For that, first we solve system (28) with an initial guess for the controls forward in time and then, using the transversality conditions as initial values, the adjoint system (35) is solved backwards in time using the current iteration solution of the state system. The controls are updated by using a convex combination of the previous controls and the values from (37). The process continues until the solution of the state equations at the present is very close to the previous iteration values. Precisely, in our numerical computations we use Algorithm 1. This algorithm solves a two point boundary-value problem, with divided boundary conditions at $t_{0} = 0$ and $t = t_{f}$ . The numerical solution of the optimal control problem is given in Figure 4, showing the impact of optimal control theory. We apply the control through chemical pesticide effects, bio-pesticides, and cost of advertisements for a time period of 60 days. In Figure 4, we note that, due to the effort of optimal controls $u_{1}^{*}, u_{2}^{*}, u_{3}^{*}$ , crop biomass population obtains its maximum value in 60 days, susceptible pest minimizes and infected pest is also minimized and reduced to 0 in the first 20 days. The population of pest is reduced radically with an influence of the best frameworks of universal awareness (i.e., $u_{2}^{*} λ$ ) and chemical pesticides control movement, $u_{1}^{*} γ$ . It is also seen that the susceptible pest population goes to devastation inside the earliest 50 days, due to the effort of the extremal controls, which are shown in Figure 5. Thus, the optimal control policy, by means of chemical pesticides, biological control, and global farming awareness, has a great influence in making the system free of pest and maintaining the stable nature in the remaining time period. Figure 5 shows that optimal chemical pesticides and biological control are needed to control the environmental crop biomass and to minimize the cost of cultivation with optimal awareness through global media.

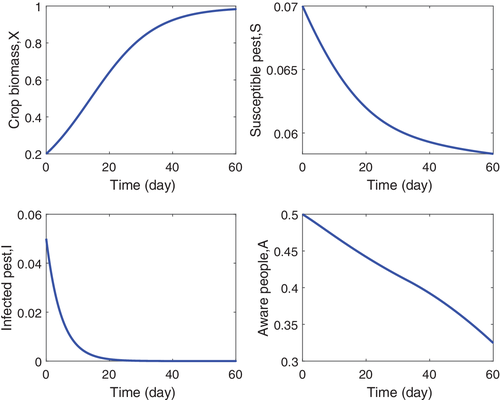
9 CONCLUSIONS

In this article, a mathematical model, described by a system of ordinary differential equations, has been developed and analyzed to plan the control of pests in a farming environment. Our model contains four concentrations, specifically, concentration of crop-biomass, density of susceptible pests, infected pests, and population awareness. The model under consideration exhibits four feasible steady state points: the crop-pest free equilibrium point, which is unstable for all parameter values; the pest free equilibrium point; the susceptible pest free equilibrium point, which may exist when the carrying capacity K is greater than the crop biomass X; and the interior equilibrium point. Local stability of the positive interior equilibrium point $E^{*}$ and local Hopf-bifurcation around it have been studied. We have shown how the dynamics changes with the parameter value $α$ (the consumption rate of pest to crops). The dynamical behavior of the system was investigated using stability theory, optimal control theory, and numerical simulations. We assumed that responsive groups take on bio-control, such as the included pest managing, as it is eco-friendly and is fewer injurious to individual health and surroundings. Neighboring awareness movements may be full as comparative to the concentration of susceptible pest available in the crop biomass. We expect that the international issues, disseminated by radio, TV, telephone, internet, and so forth, enlarge the stage of consciousness. Moreover, we have used optimal control theory to provide the price effective outline of bio-pesticides, chemical pesticide costs and a universal alertness movement. We observed the dynamical behavior of the controlled system and the effects of the three controls. This work can be extended in several ways, for example, by introducing time delays in the awareness level of farmers' attitude toward observation of fields and in becoming aware of their farm after campaigns made. Consideration of the crop population as infected and uninfected cases is also another possible extension to the present article, in order to enrich the proposed mathematical model for pest control.

ACKNOWLEDGMENTS

This work is part of first authors' PhD project, carried out at Adama Science and Technology University (ASTU), Ethiopia. Abraha acknowledges ASTU for its welcome and bear during this work, through the research grant ASTU/SP-R/027/19. Torres is grateful to the financial support from the Portuguese Foundation for Science and Technology (FCT), through CIDMA and project UIDB/04106/2020.

Biographies

Teklebirhan Abraha received his BSc degree in Applied Mathematics from the University of Gondar, Ethiopia, in July 2006, and an MSc degree in Applied Mathematics (Optimization) from Addis Ababa University, Ethiopia, in January 2011. He is currently a PhD candidate in Applied Mathematics (Optimization) at Adama Science and Technology University, Ethiopia, under the supervision of Professor Delfim F. M. Torres and Dr. Legesse Lemecha. His research interests are in the areas of applied mathematics, including optimization and optimal control, mathematical modeling of biological systems, and operations research.
Fahad Al Basir is an Assistant Professor, Department of Mathematics, Asansol Girls' College, West Bengal, India. He received BSc, MSc, and PhD degrees from Jadavpur University, Kolkata, India. He joined, as a Post-Doctoral fellow at the Department of Zoology, Visva-Bharati University, Santiniketan, India. He received Dr. D.S. Kothari Post-Doctoral Fellowship, University Grants Commission, from the Government of India. He is serving as an academic editor of Modelling and Simulation in Engineering, an Hindawi publication. He has authored and co-authored several research articles in reputed journals. His research includes mathematical modeling using ordinary and delay differential equations in disease and pest management, chemical and biochemical systems, and ecology.
Legesse Lemecha Obsu is an Associate Professor of Mathematics and a dean of Postgraduate program at Adama Science and Technology University, Ethiopia. He received MSc and PhD degrees in Mathematics from Addis Ababa University. From 1995 to 1999, he was an undergraduate student at the then Kotebe College of Teachers Education. He has authored and co-authored several research articles in reputed journals. His area of research is mainly focused on mathematical modeling, including traffic flow, epidemiology (infectious diseases), and ecology.
Delfim F. M. Torres is a Portuguese Mathematician born August 16, 1971 in Nampula, Portuguese Mozambique. He obtained a PhD in Mathematics from University of Aveiro (UA) in 2002, and Habilitation in Mathematics, UA, in 2011. He is a Full Professor of Mathematics, since March 9, 2015, Director of the R&D Unit CIDMA, the largest Portuguese research center in Mathematics, and Coordinator of its Systems and Control Group. His main research area is calculus of variations and optimal control; optimization; fractional derivatives and integrals; dynamic equations on time scales; and mathematical biology. Torres has written outstanding scientific and pedagogical publications. In particular, he is author of two books with Imperial College Press and three books with Springer. He has strong experience in graduate and post-graduate student supervision and teaching in mathematics. Twenty PhD students in Mathematics have successfully finished under his supervision. Moreover, he has been team leader and member in several national and international R&D projects, including EU projects and networks. Prof. Torres is a Highly Cited Researcher in Mathematics, having been awarded the title in 2015, 2016, 2017, and 2019. He is, since 2013, the Director of the Doctoral Programme Consortium in Applied Mathematics (MAP-PDMA) of Universities of Minho, Aveiro, and Porto. Delfim is married since 2003, and has one daughter and two sons.

REFERENCES

1Abraha T, Al Basir F, Obsu LL, Torres DFM. Pest control using farming awareness: impact of time delays and optimal use of biopesticides. Chaos Soliton Fract. 2021; 146:110869, 11 pp. doi:10.1016/j.chaos.2021.110869
10.1016/j.chaos.2021.110869
Web of Science® Google Scholar
2Abraha T, Al Basir F, Obsu LL, Torres DFM. Farming awareness based optimum interventions for crop pest control. Math Biosci Eng. 2021; 18(5): 5364-5391. doi:10.3934/mbe.2021272
10.3934/mbe.2021272
PubMed Web of Science® Google Scholar
3Chowdhury J, Al Basir F, Pal J, Roy PK. Pest control for Jatropha curcas plant through viral disease: a mathematical approach. Nonlinear Stud. 2016; 23(4): 517-532.
Google Scholar
4Chowdhury J, Al Basir F, Takeuchi Y, Ghosh M, Roy PK. A mathematical model for pest management in Jatropha curcas with integrated pesticides—an optimal control approach. Ecol Complex. 2019; 37: 24-31.
10.1016/j.ecocom.2018.12.004
Web of Science® Google Scholar
5Basir FA, Banerjee A, Ray S. Role of farming awareness in crop pest management—a mathematical model. J Theoret Biol. 2019; 461: 59-67. doi:10.1016/j.jtbi.2018.10.043
10.1016/j.jtbi.2018.10.043
PubMed Web of Science® Google Scholar
6Zhang H, Chen L, Nieto JJ. A delayed epidemic model with stage-structure and pulses for pest management strategy. Nonlinear Anal Real World Appl. 2008; 9(4): 1714-1726. doi:10.1016/j.nonrwa.2007.05.004
10.1016/j.nonrwa.2007.05.004
Web of Science® Google Scholar
7Wang X, Song X. Mathematical models for the control of a pest population by infected pest. Comput Math Appl. 2008; 56(1): 266-278. doi:10.1016/j.camwa.2007.12.015
10.1016/j.camwa.2007.12.015
Web of Science® Google Scholar
8Ghosh S, Bhattacharyya S, Bhattacharya DK. The role of viral infection in pest control: a mathematical study. Bull Math Biol. 2007; 69(8): 2649-2691. doi:10.1007/s11538-007-9235-8
10.1007/s11538-007-9235-8
CAS PubMed Web of Science® Google Scholar
9Kar TK, Ghorai A, Jana S. Dynamics of pest and its predator model with disease in the pest and optimal use of pesticide. J Theoret Biol. 2012; 310: 187-198. doi:10.1016/j.jtbi.2012.06.032
10.1016/j.jtbi.2012.06.032
CAS PubMed Web of Science® Google Scholar
10Bhattacharya DK, Karan S. On bionomic model of integrated pest management of a single pest population. Differ Equ Dyn Syst. 2004; 12(3-4): 301-330.
Google Scholar
11Al Basir F, Blyuss KB, Ray S. Modelling the effects of awareness-based interventions to control the mosaic disease of Jatropha curcas. Ecol Complex. 2018; 36: 92-100.
10.1016/j.ecocom.2018.07.004
Web of Science® Google Scholar
12Fleming WH, Rishel RW. Deterministic and Stochastic Optimal Control. Applications of Mathematics. Vol 1. Springer-Verlag; 1975.
10.1007/978-1-4612-6380-7
Google Scholar
13Pontryagin LS, Boltyanskii VG, Gamkrelidze RV, Mishchenko EF. The Mathematical Theory of Optimal Processes. Interscience Publishers John Wiley & Sons, Inc; 1962.
Web of Science® Google Scholar
14Lenhart S, Workman JT. Optimal Control Applied to Biological Models. Chapman & Hall/CRC Mathematical and Computational Biology Series. Chapman & Hall/CRC Press; 2007.
10.1201/9781420011418
Google Scholar
15Lukes DL. Differential Equations. Mathematics in Science and Engineering. Vol 162. Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers]; 1982.
Google Scholar
16Berhe HW, Makinde OD, Theuri DM. Optimal control and cost-effectiveness analysis for dysentery epidemic model. Appl Math Inf Sci. 2018; 12(6): 1183-1195. doi:10.18576/amis/120613
10.18576/amis/120613
Google Scholar
17Al Basir F, Ray S. Impact of farming awareness based Roguing, insecticide spraying and optimal control on the dynamics of mosaic disease. Ricerche Mat. 2020; 69(2): 393-412. doi:10.1007/s11587-020-00522-8
10.1007/s11587-020-00522-8
Web of Science® Google Scholar

Citing Literature

All articles

Controlling crop pest with a farming awareness based integrated approach and optimal control

Abstract

1 INTRODUCTION

2 DESCRIPTION AND MODEL FORMULATION

3 POSITIVITY OF SOLUTIONS AND THE INVARIANT REGION

4 EQUILIBRIA ASSESSMENT

5 STABILITY OF THE EQUILIBRIA

6 HOPF-BIFURCATION

7 THE OPTIMAL CONTROL PROBLEM

7.1 Existence of solution

7.2 Characterization of the solution

7.3 The method to solve the optimal control problem

8 NUMERICAL SIMULATIONS

Algorithm 1. Forward–backward sweep method

9 CONCLUSIONS

ACKNOWLEDGMENTS

Biographies

REFERENCES

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Controlling crop pest with a farming awareness based integrated approach and optimal control

Abstract

1 INTRODUCTION

2 DESCRIPTION AND MODEL FORMULATION

3 POSITIVITY OF SOLUTIONS AND THE INVARIANT REGION

4 EQUILIBRIA ASSESSMENT

5 STABILITY OF THE EQUILIBRIA

6 HOPF-BIFURCATION

7 THE OPTIMAL CONTROL PROBLEM

7.1 Existence of solution

7.2 Characterization of the solution

7.3 The method to solve the optimal control problem

8 NUMERICAL SIMULATIONS

Algorithm 1. Forward–backward sweep method

9 CONCLUSIONS

ACKNOWLEDGMENTS

Biographies

REFERENCES

Citing Literature

Figures

References

Related

Information