In Debnath et al. (2019), a tritrophic food chain model subject to a Allee effect on the prey growth and Crowley–Martin senses functional response between intermediate predator and top predator, with a top predator of sexually reproductive type is considered. It is claimed that under certain restrictions on the parameter space, the model has bounded solutions for all positive initial conditions, and is dissipative. We show that this is not true. In particular, solutions to the model can blow-up in finite time, even under the restrictions derived in Debnath et al. (2019), for sufficiently chosen initial data. We derive a new extinction boundary for the system. We also conjecture on the effect of the Allee threshold on the blow-up dynamics in the model. All of our results are validated via numerical simulations.

1 INTRODUCTION

Tritrophic food chains have been intensely investigated in ecology and applied mathematics. This started with the seminal work of Hastings and Powell, who showed that the dynamics of a three species food chain consisting of a specialist top predator depredating on a specialist middle predator, that depredates on a prey species, with Rosenzweig–McArthur functional responses, can possess chaotic dynamics.¹ This started intense investigation into chaos in ecology.^2-4 Next, Upadhyay and Rai proposed a three species food chain, where the top predator is sexually reproducing via a quadratic growth term, and is also a generalist.⁵ They model the dynamics of the top predator via a modified Leslie–Gower scheme. The Upadhyay–Rai model has since been investigated in great detail, due to the rich plethora of dynamics it possesses.^5-11 These include temporal chaos, spatio-temporal chaos, Turing patterns, and rich bifurcation structure.

Note, the Upadhyay–Rai model has also been shown to possess solutions that can blow-up in finite time, for large and small initial conditions.^{12, 13} This property has been proven for many variants of the model as well.^13-22 Thus, a recent research direction has been to modify the model and variants, via various ecological mechanisms that might prevent the blow-up, such as prey refuge, predator interference, time delay due to gestation, diffusion and mixed boundary conditions to name a few.^{20, 23-26} The most recent in this line of work,²⁷ considers two new “damping” mechanisms, (1) a Allee effect (both weak and strong) is considered in the prey and (2) the top predator's functional response is considered to be of Crowley–Martin type, although its explicit dynamics are modeled via a modified Leslie–Gower scheme.

In population dynamics, Allee effects are positive correlations between individual fitness and population density. They are said to be strong if the per capita growth rate of the population at low density is negative below a critical threshold. When the population goes below this threshold, extinction occurs.^28-31 On the other hand, they are weak when the per capita growth rate is lower at lower densities,³² but still positive. There are several mechanisms which can cause Allee effects such as difficulties in finding mates in sparse populations, predation, environmental conditioning, and inbreeding.^{33, 34} Allee effects play a critical role in the local or global extinction of populations.^{33, 35} Thus, considering this as an inhibiting mechanism, to population models that possess explosive solutions, is a worthwhile endeavor. However, a strong Allee effect in prey, and its subsequent effect on blow-up dynamics on the Upadhyay–Rai class of models, has not been considered to the best of our knowledge, before.²⁷ The strong Allee effect will clearly cause a decrease in the prey population if one is below the Allee threshold, and this will reduce recruitment into the middle predator class, so the middle predator could perhaps be kept at a lower density, via a strong Allee effect in the prey—which could work favorably in removing a blow-up solution. When the Allee effect is weak, as modeled, the growth rate of prey is lower at lower density—but again the effect on blow-up dynamics is unknown.

Note, the model as considered in Reference 27 has been considered earlier in Reference 21, without the Allee effect in the prey. Blow-up is seen there also Reference 21. The effect of interference as modeled via Crowley–Martin response, is seen to worsen the blow-up situation. In that the interference by prey handling predators alone, can cause blow-up, whilst there is global existence without this form of interference, see theorem 2.3 Reference 21. To these ends, Reference 27 claims that one has a boundedness results for the system considered therein, and that their proposed system is dissipative in $ℝ_{+}^{3}$ —under a new parametric restriction derived by them. This may seem ecologically feasible due to the complex interplay of the Allee dynamics at lowest trophic level and the Crowley–Martin response at the mid trophic level. However, one needs to investigate this claim rigorously.

In the current article we show

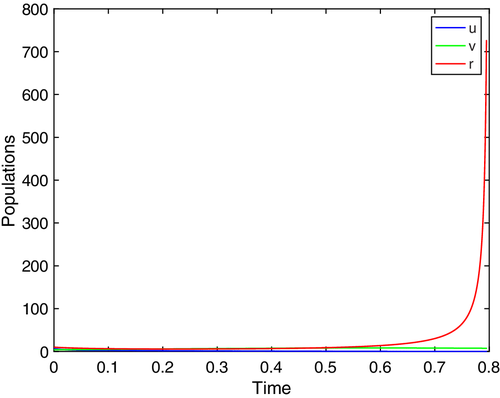
There is no boundedness for the system proposed in Reference 27, despite the Allee dynamics, and the new parametric restrictions mentioned in Reference 27. That is, there exists sufficiently large initial conditions for which the system can blow-up in finite time, see Theorem 1, see Figure 1. Thus, the system proposed in Reference 27 is not dissipative in $ℝ_{+}^{3}$ .
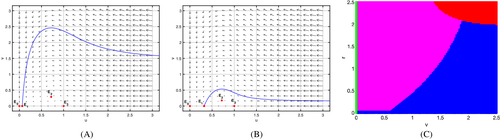
We delineate the phase space into regions of coexisting interior equilibriums versus boundary equilibriums versus blow-up solutions. Typically, the Allee threshold or “extinction boundary” as it is alluded to in the literature²⁸ delineates initial conditions that lead to persistence versus extinction. We find that in our system the boundary is more complicated, in that there are initial conditions leading to blow-up as well, see Figure 3.
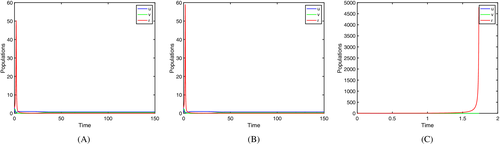
We propose via conjecture 1, and numerically verify, see Figure 2, that the weak Allee effect in bottom prey could be a stronger damping mechanism to an explosive top predator population, than a strong Allee effect. We discuss various ecological applications of these results.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Time series plot depicting finite time blow-up in r in the model (1) with initial conditions [7, 4, 10] at approximately t = 0.8. Here, $a_{2} = 0.2, α_{3} = 10, c = 1.6, δ = 0.8$ , and all other parameters are the same in (5). Note here $a_{2} + (\frac{η}{δ}) α_{1} = 0.2 + (\frac{0.802}{0.8}) 3.93 = 4.14 < \frac{10}{1.6} = 6.25 = \frac{α_{3}}{c}$ . Thus, we see that the parametric restriction (3) as claimed in Reference 27 holds, yet there is finite time blow-up

2 LACK OF BOUNDEDNESS

In Reference 27 the authors considered the following three species food chain ODE model,

\begin{array}{l} \frac{d u}{d t} = u (1 - u) (u - β) - \frac{u v}{u + a} = f_{1} (u, v, r), \\ \frac{d v}{d t} = - δ v + \frac{α_{1} u v}{u + a} - \frac{v r}{1 + a_{1} v + b_{1} r + b_{2} v r} = f_{2} (u, v, r), \\ \frac{d r}{d t} = c r^{2} - α_{3} (\frac{r^{2}}{v + a_{2}}) = f_{2} (u, v, r) \end{array}.

()

which represents a tritrophic predator-prey model with one prey and two predators with Allee effect on the growth function of the prey population u. Note, a strong Allee effect implies

0 < β \leq 1

and a weak Allee effect requires

- 1 < β \leq 0

. This prey u is fed on by an intermediate predator v, that has prey-dependent Holling type II functional response. This intermediate predator v is in turn fed on by a top predator r, via a Crowley–Martin functional response. r is sexually reproducing, and is modeled via a modified Leslie–Gower scheme.^{5, 6, 36}

In Reference 27, various results on the positivity and boundedness of the solutions to system (1) are proved, First, in order to show positivity of the solutions, the authors used the direct method. However, based on the invariant regions (see, e.g., Reference 37) we know that the region

ℝ_{+}^{3} = \{(u, v, r) \in ℝ^{3}, u \geq 0, v \geq 0, r \geq 0\},

is invariant under the following condition

f_{1} (0, v, r) \geq 0, f_{2} (u, 0, r) \geq 0, f_{3} (u, v, 0) \geq 0, for all u \geq 0, v, r \geq 0,

which is satisfied for system (1).

Second, for the boundedness of u(t), the authors studied separately, the two cases

0 < u (0) \leq 1

and

u (0) > 1

. However, we know by the same techniques based on the invariant regions, that for any positive constant M the region

\sum = \{(u, v, r) \in ℝ^{3}, 0 \leq u \leq M, v \geq 0, r \geq 0\},

is invariant (i.e., u(t) is bounded for all time t) under the following condition

f_{1} (M, v, r) \leq 0, for all u \geq 0, v, r \geq 0,

which is satisfied for system (1) for all M ≥ 1.

2.1 Boundedness of v

The authors proved that the solution components (u, v) are absorbed, before proving the global existence in time by claiming in Reference 27,

“For large values of t, we obtain $u (t) + \frac{1}{α_{1}} v (t) \leq \frac{η}{δ}$ ”

where $η = \max_{t \geq 0} \{u (1 - u) (u - β) + δ u\}$ . This cannot be claimed for such systems. Instead one should apply the following alternative (see Friedman,³⁸ Henry,³⁹ Pazy,⁴⁰ Smoller,³⁷ and Rothe⁴¹).

Proposition 1.The three-component system (1) admits a unique local in time, classical solution $(u, v, r)$ on an interval $[0, T_{\max} [$ and we have either

(i) The solution is bounded on $[0, T_{\max} [$ and it is global ( i.e., $T_{\max} = + \infty$ ).

(ii) Or

\lim_{t ↗ T_{\max}} \max \{|u (t)| + |v (t)| + |r (t)|\} = \infty,

and the solution is not global, we say that it blows-up in finite time

T_{\max}

or that it ceases to exist, where

T_{\max}

denotes the eventual blowing-up time.

Furthermore, the authors used the following differential inequality

ξ (t) = : u (t) + \frac{1}{α_{1}} v (t) \leq (u (0) + \frac{1}{α_{1}} v (0)) e^{- δ t} + \frac{η}{δ} (1 - e^{- δ t}), t > 0,

to deduce

ξ (t) \leq \frac{η}{δ},

()

which is not true, however, it is true that,

ξ (t) \leq u (0) + \frac{1}{α_{1}} v (0) + \frac{η}{δ}, 0 < t < T_{\max} .

2.2 Blow-up in finite time of r

The authors in Reference 27 claim,

“we shall prove u(t), v(t) are bounded, and if $a_{2} + (\frac{η}{δ}) α_{1} < \frac{α_{3}}{c}$ , then r(t) is bounded for any nonnegative initial condition.”

To the contrary we show,

Theorem 1.Under condition

a_{2} + (\frac{η}{δ}) α_{1} < \frac{α_{3}}{c},

()

and for large initial data, we have blow-up at finite time of the solutions to system (1).

Proof.By integrating the third equation of the (1), we have

- \frac{1}{r} + \frac{1}{r_{0}^{-}} = c t - α_{3} \underset{0}{\int^{t}} \frac{d s}{v (s) + a_{2}},

which gives

r = \frac{1}{\frac{1}{r_{0}^{-}} - c t + α_{3} \underset{0}{\int^{t}} \frac{d s}{v (s) + a_{2}}} .

If we prove that the function:

t \to ψ (t) = \frac{1}{r_{0}^{-}} - c t + α_{3} \underset{0}{\int^{t}} \frac{d s}{v (s) + a_{2}} < 0

at a time 0 < T < ∞, since

ψ (0) > 0

, then by continuity of

ψ

, and the intermediate value theorem,

ψ

must vanish at some finite time, and so the solution r will blow-up in finite time.

Since the reaction terms are continuous functions, then the solutions are classical and continuous and

\lim_{t \to 0} (\frac{1}{t} \underset{0}{\int^{t}} \frac{d s}{v (s) + a_{2}}) = \frac{1}{v_{0}^{-} + a_{2}} .

v_{0}^{-}

is sufficiently large, then there exists

δ > 0

such that

\frac{1}{t} \underset{0}{\int^{t}} \frac{d s}{v (s) + a_{2}} < \frac{c}{2 α_{3}}, for all t \in]0, δ[.

()

This is true for any c > 0, in particular for c s.t. (3) holds.

Then for all $t \in]0, δ[$ , we have

ψ (t) = \frac{1}{r_{0}^{-}} + [- c + \frac{α_{3}}{t} \underset{0}{\int^{t}} \frac{d s}{v (s) + a_{2}}] t < \frac{1}{r_{0}^{-}} - \frac{c}{2} t .

Now if

r_{0}^{-}

is sufficiently large, then we can find

T \in]0, δ[

such that

\frac{1}{r_{0}^{-}} - \frac{c}{2} T = 0^{+} .

Then the solution r of (1) blows-up in finite time for initial conditions v₀ and r₀ sufficiently large.

Remark 1.Note, the estimate via (4), holds irrespective of the value of c, and certainly holds even if c meets the requirement of (3). Thus, this parametric restriction is not sufficient to prevent blow-up if one chooses appropriately large initial conditions. Also note, the blow-up for large initial conditions clearly shows that model system (1) is not dissipative.

2.3 Effect of Allee threshold on blow-up dynamics

Herein we attempt to quantify the effect of the Allee threshold $β$ on the blow-up dynamics present in (1). To this end we conjecture,

Conjecture 1.Consider the three species food chain model (1). There is a set of positive parameters and initial data (u₀, v₀, r₀) s.t solutions blow-up in finite time, but solutions initiating from the same set of parameters with $β \leq 0$ , and the same initial data (u₀, v₀, r₀), exist globally in time.

This tells us that the transition from a strong Allee effect ( $β > 0$ ) to a weak Allee effect ( $β \leq 0$ ), can act as a damping mechanism—or rather the weak Allee effect in bottom prey, is more effective in checking explosive populations of top predators, than perhaps a strong Allee effect in bottom prey.

3 EXTINCTION BOUNDARY

The dynamics of bistable/multistable systems, even with the inclusion of Allee effects, generically consists of multiple equilibrium, interior equilibrium, and boundary equilibrium, also the extinction equilibrium. The stable manifold of the saddle (separatrix) splits the phase space into sections, delineating initial conditions from going to interior equilibrium, boundary equilibrium or extinction. Such curves are also called the extinction boundary/Allee threshold/threshold manifold in the literature.²⁸ Note, that although this curve is seen to be monotone with respect to initial conditions, its general shape (even in two species models with or without Allee effects) is an open problem in ecology.²⁸ We show that for the current system, this curve is even richer, as there exists a zone which leads to blow-up solutions. One can see this in Figure 3, if one compares the left and middle panels, with the simple extinction boundary—to the right panel, and the more complex extinction boundary.

We consider the following parameters for numerical experiments seen in Figure 3,

\{\begin{cases} β = 0.32, a = 0.85, α_{1} = 3.93, δ = 1.8, b_{1} = 0.21, b_{2} = 0.56, \\ c = 0.4, α_{3} = 0.3, a_{2} = 0.6, a_{1} = 0.54 . \end{cases}

()

4 CONCLUSION

In the current work, we show that the model as considered in Reference 27, is not bounded, even under the parametric restrictions imposed therein. In particular solutions can blow-up in finite time. We also derive a new extinction boundary, see Figure 3, which clearly delineates initial data that could go to the extinction state, a boundary equilibrium, an interior equilibrium, or to a blow-up solution. This possesses a richer structure, than standard extinction boundaries for systems, without the blow-up dynamic. Furthermore, Conjecture 1 points to an interesting albeit counter intuitive phenomenon, that the weak Allee effect in the prey, can damp the explosive top predator population perhaps more so than a strong Allee effect can. This is certainly counterintuitive as a strong Allee effect can truly cause negative density dependence, for initial data below the Allee threshold, whereas a weak Allee effect only causes the growth rate to slow, at low populations. Proving this conjecture would make for interesting future work. This also has interesting ramifications for design of conservation strategies for species. It shows that in order to control species density at the top trophic level, one could implement controls at a much lower trophic level, to achieve the desired control. One could also look into engineering a weak Allee effect in specific food chains.²⁸ Note, these results do not preclude the strong Allee effect from being a damping mechanism. But at this point we don't have a parameter set (or rigorous proof) to support this claim. This is also a possible direction of future investigation.

All in all, we caution yet again, from claiming boundedness results, for all positive initial data, for food chain models where the top predator is modeled using a modified Leslie–Gower scheme. Researchers should approach such models with care, and posit bounds on solutions, only under restrictions on the size of the initial data. It would appear from a survey of the literature where blow-up has been proved for such models, that parametric restrictions, without restricting the size of the initial data, do not suffice to yield global in time existence of solutions.

ACKNOWLEDGMENT

Eric M. Takyi and Rana D. Parshad would like to acknowledge valuable partial support from the NSF via DMS-1839993.

Biographies

Eric M. Takyi is a PhD Candidate (2021) at the Department of Mathematics at Iowa State University. His research interests include Biomathematics, Dynamical Systems, and Bifurcation theory.
Kwadwo Antwi-Fordjour is an Applied Mathematician of African diaspora and received his PhD in 2016 from the University of Alabama at Birmingham. He joined the Department of Mathematics and Computer Science at Samford University in 2018 after a 2-year Visiting Assistant Professor position at Earlham College. His professional interests lie in the area of ordinary, partial, and stochastic differential equations where he models biological, ecological, and social systems. He currently serves as an Associate Editor of the Journal of Applied Mathematics and Computing.
Said Kouachi obtained my first PHD degree in Mathematics from Paris 7 University (1985) and my second one in Applied Mathematics from University of Annaba (Algeria 1999). He has taught mathematics in several universities during 36 years. Examples of courses taught in both undergraduate and graduate levels: Linear and abstract algebra, ordinary and partial differential equations, analysis and numerical analysis, stability, dynamical systems, differential geometry, calculus 1 and 2, fluid, and continuous mechanics. He has supervised more than 45 master and PHD theses in mathematics. He has funded the post-graduation in applied mathematics and responsible of several research projects at several Saudi and Algerian Universities. He has published more than 45 International Papers in reputed Scientific Journals. Actually he is a full professor Teaching Mathematics at Khenchela University (Algeria).
Rana D. Parshad is an Assistant Professor of Mathematics at Iowa State University. His research focuses on differential equations and dynamical systems methods in population dynamics. His work has been funded by the National Science Foundation.

REFERENCES

1Hastings A, Powell T. Chaos in a three species food chain. Ecology. 1991; 72(3): 896-903.
10.2307/1940591
Web of Science® Google Scholar
2Hastings A, Hom CL, Ellner S, Turchin P, Godfray HCJ. Chaos in ecology: is mother nature a strange attractor? Annu Rev Ecol Syst. 1993; 24(1): 1-33.
10.1146/annurev.es.24.110193.000245
Google Scholar
3Upadhyay RK, Iyengar SRK, Rai V. Stability and complexity in ecological systems. Chaos Soliton Fract. 2000; 11: 533-542.
10.1016/S0960-0779(98)00112-X
Web of Science® Google Scholar
4Upadhyay RK, Iyengar SRK, Rai V. Chaos: an ecological reality? Int J Comput Math. 2010; 87: 199-214.
Google Scholar
5Upadhyay RK, Rai V. Why chaos is rarely observed in natural populations? Chaos Soliton Fract. 1997; 8(12): 1933-1939.
10.1016/S0960-0779(97)00076-3
Web of Science® Google Scholar
6Aziz-Alaoui MA. Study of a Leslie-Gower type tri-trophic population model. Chaos Soliton Fract. 2002; 14(8): 1275-1293.
10.1016/S0960-0779(02)00079-6
Web of Science® Google Scholar
7Letellier C, Aziz-Alaoui MA. Analysis of the dynamics of a realistic ecological model. Chaos Soliton Fract. 2002; 13: 95-107.
10.1016/S0960-0779(00)00239-3
Web of Science® Google Scholar
8Kumari N. Pattern formation in spatially extended tritrophic food chain model systems: generalist versus specialist top predator. ISRN Biomath. 2013; 2013:198185.
10.1155/2013/198185
Google Scholar
9Parshad RD, Upadhyay RK. Investigation of long time dynamics of a diffusive three species aquatic model. Dyn Part Differ Equat. 2010; 7(3): 217-244.
10.4310/DPDE.2010.v7.n3.a2
Web of Science® Google Scholar
10 Parshad, R.D. , Abderrahmanne, H., Upadhyay, R. K. and Kumari, N. Finite time blowup in a realistic food chain model, ISRN Biomath, 2013 ( 2013), 424062.
Google Scholar
11Upadhyay RK, Iyengar SRK, Rai V. Chaos: an ecological reality? Int J Bifurcat Chaos. 1998; 8: 1325-1333.
10.1142/S0218127498001029
Web of Science® Google Scholar
12Parshad RD, Kumari N, Kouachi S. A remark on "Study of a Leslie-Gower-type tritrophic population model" [Chaos. Soliton. Fract. 14 (2002) 1275-1293]. Chaos Soliton Fract. 2015; 71(2): 22-28.
10.1016/j.chaos.2014.11.014
Web of Science® Google Scholar
13Parshad, R. D., Quansah, E., Beauregard, M. A., & Kouachi, S. (2017). On small data blow-up in a three species food chain model. Comput Math Appl, 73(4), 576-587.
10.1016/j.camwa.2016.12.018
Web of Science® Google Scholar
14Mishra P, Raw SN, Tiwari B. Study of a Leslie-Gower predator-prey model with prey defense and mutual interference of predators. Chaos Soliton Fract. 2019; 120: 1-16.
10.1016/j.chaos.2019.01.012
Web of Science® Google Scholar
15Parshad RD, Takyi EM, Kouachi S. A remark on study of a Leslie-Gower predator-prey model with prey defense and mutual interference of predators [Chaos, Solitons & Fractals 120 (2019) 1-16]. Chaos Soliton Fract. 2019; 123: 201-205.
10.1016/j.chaos.2019.04.011
Web of Science® Google Scholar
16Parshad RD, Kumari N, Kasimov AR, Abderrahmane HA. Turing patterns and long time behavior in a three-species model. Math Biosci. 2014; 254: 83-102.
10.1016/j.mbs.2014.06.007
PubMed Web of Science® Google Scholar
17Parshad RD, Basheer A. A note on "Periodic solutions of a three-species food chain model" [Applied Math E-Notes, 9 (2009), 47-54]. Appl Math E-Notes. 2016; 16(2016): 45-55.
Google Scholar
18Parshad RD, Kouachi S, Kumari N. A comment on "Mathematical study of a Leslie-Gower type tritrophic population model in a polluted environment" [Modeling in Earth Systems and Environment 2 (2016) 1-11.]. Model Earth Syst Environ. 2016; 2(2): 1-5.
10.1007/s40808-016-0158-y
Web of Science® Google Scholar
19Parshad RD, Kouachi S, Gutierrez J. Global existence and asymptotic behavior of a model for biological control of invasive species via supermale introduction. Commun Math Sci. 2013; 11(4): 23-44.
Web of Science® Google Scholar
20Parshad RD, Bhowmick S, Quansah E, Upadhyay RK, Agrawal R. Finite time blow up in a population model with competitive interference and time delay. Int J Simulat Nonlinear Sci. 2017; 18(5): 435-450.
10.1515/ijnsns-2015-0179
Web of Science® Google Scholar
21Parshad RD, Basheer A, Jana D, Tripathi JP. Do prey handling predators really matter: subtle effects of a Crowley-Martin functional response. Chaos Soliton Fract. 2017; 103: 410-421.
10.1016/j.chaos.2017.06.027
Web of Science® Google Scholar
22Parshad RD, Upadhyay RK, Mishra S, Tiwari S, Sharma S. On the explosive instability in a three species food chain model with modified Holling type IV functional response. Math Methods Appl Sci. 2017; 40(16): 5707-5726.
10.1002/mma.4419
Web of Science® Google Scholar
23Parshad RD, Qansah E, Black K, Beauregard M. Biological control via "ecological" damping: an approach that attenuates non-target effects. Math Biosci. 2016; 273: 23-44.
10.1016/j.mbs.2015.12.010
PubMed Web of Science® Google Scholar
24Upadhyay RK, Sharma S, Parshad RD, Basheer A, Lyu J. An investigation of an explosive food chain model with interference and inhibitory effects. IMA J Appl Math. 2017; 82(6): 1209-1237.
10.1093/imamat/hxx032
Web of Science® Google Scholar
25 Parshad RD, Yao G, Li W. Another mechanism to control invasive species and population explosion: "ecological" damping continued. Differ Equat Dyn Syst. 2019;27(1):249-276. https://doi.org/10.1007/s12591-017-0402-6.
10.1007/s12591-017-0402-6
Web of Science® Google Scholar
26Parshad RD, Bhowmick S, Quansah E, Basheer A, Upadhyay RK. Predator interference effects on biological control: the "paradox" of the generalist predator revisited. Commun Nonlinear Sci Numer Simul. 2016; 39: 169-184.
10.1016/j.cnsns.2016.02.021
Web of Science® Google Scholar
27Debnath S, Ghosh U, Sarkar S. Global dynamics of a tritrophic food chain model subject to the Allee effects in the prey population with sexually reproductive generalized-type top predator. Comp Math Methods. 2019; e1079: 1-23.
Google Scholar
28 Berec L. Mathematical modeling in ecology and epidemiology. HIV/AIDS Model Control Automat. 2004.
Google Scholar
29Boukal DS, Berec L. Single-species models of the Allee effect: extinction boundaries, sex ratios and mate encounters. J Theoret Biol. 2002; 218(3): 375-394.
10.1006/jtbi.2002.3084
PubMed Web of Science® Google Scholar
30 Courchamp F, Clutton-Brock T, Grenfell B. Inverse density dependence and the Allee effect. Trends Ecol Evol. 1999; 14(10):405410.
10.1016/S0169-5347(99)01683-3
Web of Science® Google Scholar
31 Stephens PA, Sutherland WJ. Consequences of the Allee effect for behavior ecology and conservation. Trends Ecol Evolut. 1999; 14(10):401405.
10.1016/S0169-5347(99)01684-5
Web of Science® Google Scholar
32Courchamp F, Berec L, Gascoigne J. Allee Effects in Ecology and Conservation. Oxford, UK: Oxford University Press; 2008.
10.1093/acprof:oso/9780198570301.001.0001
Google Scholar
33Dennis B. Allee effects: population growth, critical density, and the chance of extinction. Natural Res Model. 1989; 3(4): 481-538.
10.1111/j.1939-7445.1989.tb00119.x
Google Scholar
34Wang M-H, Kot M. Speeds of invasion in a model with strong or weak Allee effects. Math Biosci. 2001; 171: 83-97.
10.1016/S0025-5564(01)00048-7
CAS PubMed Web of Science® Google Scholar
35Zhou SR, Liu YF, Wang G. The stability of predator-prey systems subject to the Allee effects. Theor Popul Biol. 2005; 67(1): 23-31.
10.1016/j.tpb.2004.06.007
PubMed Web of Science® Google Scholar
36Leslie PH. Some further notes on the use of matricies in population mathematics. Biometrika. 1948; 35: 213-245.
10.1093/biomet/35.3-4.213
PubMed Web of Science® Google Scholar
37Smoller JA. Shock Waves and Reaction-Diffusion Equations. New York, NY: Springer-Verlag; 1983.
10.1007/978-1-4684-0152-3
Google Scholar
38Friedman A. Partial Differential Equations of Parabolic Type. Englewood Chiffs, NJ: Prentice Hall; 1964.
Google Scholar
39Henry D. Geometric Theory of Semilinear Parabolic Equations. Lecture Notes in Mathematics. Vol 840. New-York, NY: Springer-Verlag; 1984.
Google Scholar
40Pazy A. Semigroups of Linear Operators and Applications to Partial Differential Equations. Applied Math. Sciences. Vol 44. New York, NY: Springer-Verlag; 1983.
10.1007/978-1-4612-5561-1
Google Scholar
41Roth F. Global Solutions of Reaction-Diffusion Systems. Lecture Notes in Mathematics. Vol 1072. Berlin, Germany: Springer-Verlag; 1984.
10.1007/BFb0099278
Google Scholar

Citing Literature

All articles

A remark on “ Global dynamics of a tritrophic food chain model subject to the Allee effects in the prey population with sexually reproductive generalized-type top predator” [Comp and Math Methods. 2019; E1079, pp. 1–23]

Abstract

1 INTRODUCTION

2 LACK OF BOUNDEDNESS

2.1 Boundedness of v

2.2 Blow-up in finite time of r

2.3 Effect of Allee threshold on blow-up dynamics

3 EXTINCTION BOUNDARY

4 CONCLUSION

ACKNOWLEDGMENT

Biographies

REFERENCES

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A remark on “ Global dynamics of a tritrophic food chain model subject to the Allee effects in the prey population with sexually reproductive generalized-type top predator” [Comp and Math Methods. 2019; E1079, pp. 1–23]

Abstract

1 INTRODUCTION

2 LACK OF BOUNDEDNESS

2.1 Boundedness of v

2.2 Blow-up in finite time of r

2.3 Effect of Allee threshold on blow-up dynamics

3 EXTINCTION BOUNDARY

4 CONCLUSION

ACKNOWLEDGMENT

Biographies

REFERENCES

Citing Literature

Figures

References

Related

Information