On the analysis of the fractal basins of escape in the N-body ring problem

1 INTRODUCTION

The N-body problem has seduced many researchers over the years, willing to understand the motions of the Sun, planets and other celestial bodies. In general terms, the N-body problem consists of studying the motions of a group of bodies interacting each other under the Newton's law of motion. At present, the N-body problem with a central configuration, known as the N-body ring problem, is an active field of research. This problem was first studied by Maxwell in 1859,¹ when addressing the understanding of the stability of Saturn's rings, and efficiently reformulated by Tisserand in 1889.² The N-body ring problem still focuses the interest of many other scientists throughout the years, as this configuration is used to model a wide variety of systems in Celestial Mechanics, as planetary rings, or asteroid belts.^3-5

On the other hand, the analysis of the escape geometry of a particle interacting in a dynamical system has been also a subject of interest in the scientific community in the last decades.^6-19 The interest in these type of problems is to determine the set of values of the energy of the system so that the corresponding curves of zero velocity are open. Then, for a fixed energy value among this range, the trajectory of test particles that start inside the potential well is analyzed. A particle may eventually escape from the system if it crosses, pointing outwards, any of the unstable periodic orbits that guard the openings of the potential well. These periodic orbits are called Lyapunov orbits and the sets of orbits asymptotic to them limit the set of escaping orbits.

In References 20 and 21, several numerical studies of the escape dynamics in the N-body ring problem are carried out for N = 5, analyzing the conditions of the orbits that escape from the system, and the ones that remain inside the well, or escape after a very long span of time, locating the basins of escape associated to the different openings of the potential. They use the technique of defining a surface of section²² to understand the properties of the escape from the system. In Reference 20, the escape of a set of particles starting in the interior of the potential well is examined, considering three different values of the maximum time of integration (T = 10², 10³, and 10⁴) by means of the surface of section defined by the hyperplane y = 0. One of the conclusions of this work is that a maximum time of integration of T = 10³ is adequate both for determining the proportion of orbits that leave the potential well, and for analyzing the architecture of the basins of escape. The results also show that the phase space exhibits big connected regions that give rise to the same type of escape (called “basins of escape”), but also some defined areas where the basins are mixed in an intricate manner. Indeed, the escape process presents a sensitive dependence on the initial conditions, that is, negligible changes in the initial condition of a particle can cause an escape crossing a different opening of the potential well, leading to fractal boundaries between these regions. The boundaries of the basins of escape are structured by the sets of orbits tending asymptotically to the Lyapunov orbits located at the openings of the potential well as t → ∞, whereas the shape of the sets of orbits tending asymptotically to the Lyapunov orbits as t → −∞ explains the ring and spiral structures revealed in the surface of section we have considered. Therefore, the authors conclude that the connected domains observed in the phase space provide information about the situation of the stable manifolds to each of the guardian Lyapunov orbits.

In Reference 21, the authors revisit the N-body ring system for N = 5 focusing on the use of some other surfaces of section, with a suitable fitting to the circular symmetry of the problem, in order to unveil the geometry of the escape of a particle from this system. The results of this numerical study bring out the connections between the large connected domains associated with each of the five types of escape. It turns out to be that these domains produce a repeating sequence along various diagonals of the form $\alpha =\theta +ϵ$, where $\theta$ and $\alpha$ stand for the angles of position and velocity of the test particle, respectively, and this configuration occurs at any level of scale, exhibiting a fractal structure. This fact illustrates how the projection of the sets of orbits asymptotic to the guardian Lyapunov orbits from the phase space into the $(\theta ,\alpha )$ space arrange the distribution of the basins of escape in this space.

In the present research, the aim is to extend the numerical exploration of the dynamics of test particles interacting in the N-body ring configuration for larger values of N, in order to calculate the structures of the sets of orbits that escape and the sets that are captured inside the potential well, and locate the basins of escape associated to each opening of the potential. To this purpose, we have performed this analysis for a fixed value of the Jacobi constant close to the escape value, such that the size of the openings of the potential well are approximately the same for the different values of N we have considered, which are N = 5, 6, 7, 8.

In the following, we present the details of our study and results. In Section 2, we introduce the equations of motion of a particle under the gravitational influence of the N-body ring configuration, and give some details about the numerical method we have used to integrate the system. In Section 3, we perform a exhaustive analysis of the escape properties of some sets of orbits for N = 5, 6, 7, 8, exposing in detail the results of our calculations. Finally, the last section is devoted to the conclusions and discussions of this research.

2 EQUATIONS OF MOTION

The N-body ring problem describes the motion of a particle S of negligible mass, moving under the gravitational influence of N + 1 bodies (called primaries) laid out in a planar circular configuration. A main body of mass m₀ is situated at the center of mass of the configuration, and the other N bodies, all of them with mass m, are placed at the vertexes of a regular polygon that rotates on its own plane around the center of mass with a uniform angular velocity.²³

Figures 1-3 exhibit these curves for N = 5, 6, 7, 8, $\beta =2$ and some values of the Jacobi constant C.

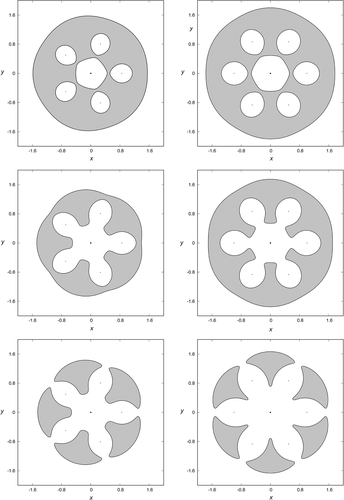
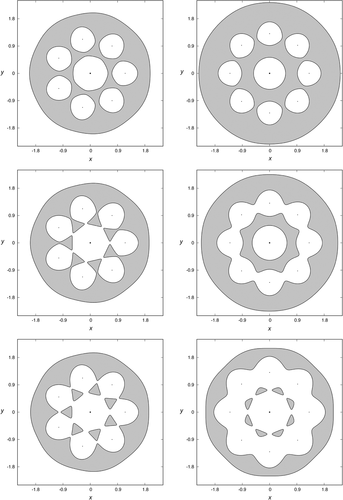
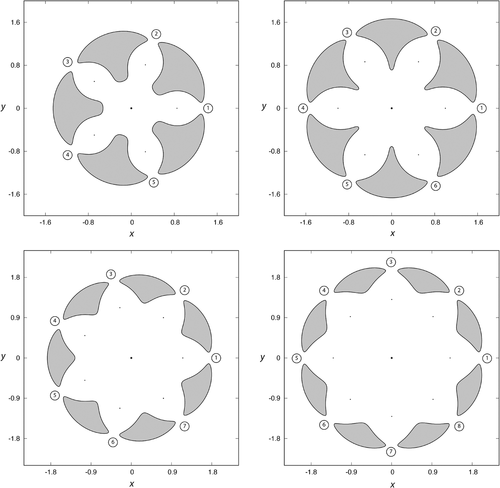
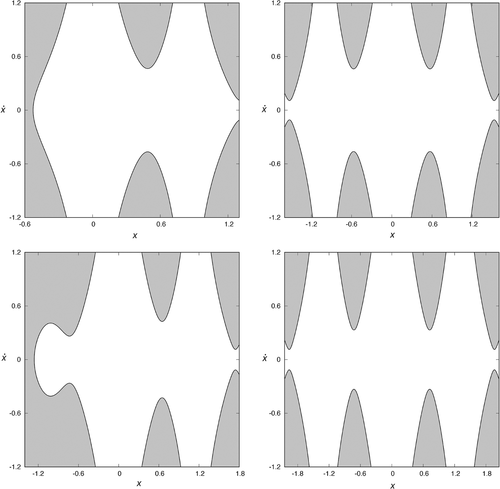
For a given value of $\beta$, there is a critical value C_e of the Jacobi constant such that, if we select a value of C smaller than C_e, the corresponding curves of zero velocity are open and test particles may escape. Besides, for each value of the Jacobi constant smaller than C_e, the well opens up at exactly N places in the configuration space (see Figure 4), and each opening is bridged by a highly unstable periodic orbit, called Lyapunov orbit. These Lyapunov orbits connect two branches of the equipotential surfaces. The main property of these orbits is that if an orbit crosses one of them outwards, then this orbit escapes from the system, as always moves outwards. Inside the domain of the configuration space limited by the Lyapunov orbits, there are orbits that escape, and also other orbits that remain trapped. In Figure 4, we show the curves of zero velocity for $\beta =2$, and N = 5 and C = 3.96 (upper left panel), N = 6 and C = 5.455 (upper right panel), N = 7 and C = 7.21 (lower left panel), and N = 8 and C = 9.22 (lower right panel). We have also numbered the exit channels of the curves of zero velocity, as well as their corresponding Lyapunov orbits (${\varphi }_{\nu }$, $\nu =1,\dots ,N$).

The critical values of the Jacobi constant, C_e, can be determined by means of the approach described by Caranicolas and Vozikis.²⁴

As we are interested in examining the escape geometry of the system, we have adopted the values C = 3.96 for N = 5, C = 5.455 for N = 6, C = 7.21 for N = 7, and C = 9.22 for N = 8, with $\beta =2$ in our computations, which are all of them values of the Jacobi constant such that the potential well is open. Moreover, these values of the Jacobi constants produce an opening in the potential well, for the different values of N, of about the same approximate size.

We have used the recurrent power series (RPS) method^{25, 26} in order to numerically integrate the equations of motion. For this numerical integration, we have set the precision to $ϵ=10^{-23}$, and the number of term series to 26, so that the Jacobi constant remains constant up to 17 decimal digits along the numerical solution to the problem.

3 ANALYSIS OF THE NUMERICAL RESULTS

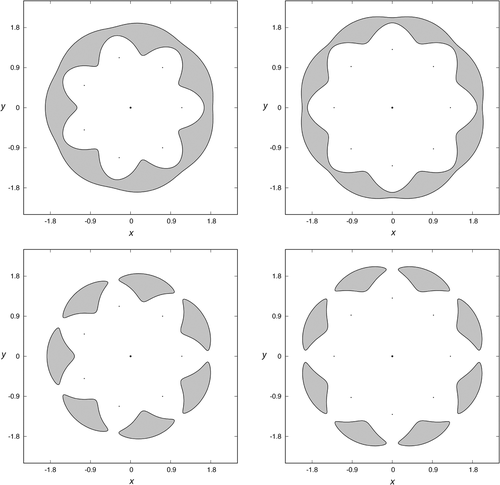
In Figure 5, we have depicted (in white) this domain, for N = 5 (upper left panel), N = 6 (upper right panel), N = 7 (lower left panel), and N = 8 (lower right panel).

According to Reference 20, we have carried out a numerical integration over a maximum period of time T = 10³ in order to study the structures of the phase space and locate the basins of escape in these configurations of the N-body ring problem.

Let us recall that the initial conditions on the surface of section $(x,\dot{x})$ leading to escape through any of the Lyapunov orbits define the corresponding basins of escape, that is, the sets of initial conditions that lead to orbits leaving the potential well through a certain escape channel. In Figure 6, we show the basins of escape considering a maximum time of numerical integration of T = 10², for N = 5, C = 3.96 (upper left panel), N = 6, C = 5.455 (upper right panel), N = 7, C = 7.21 (lower left panel), and N = 8, C = 9.22 (lower right panel). The structure of the different basins of escape is easier to see if we consider a maximum time of integration of T = 10², as there are fewer initial conditions depicted and the boundaries between the different regions are clearer. We have identified each channel of escape by using a different color, and initial conditions of colliding orbits are colored in black. For N = 5, initial conditions in forest green, light blue, dark blue, dark red, and gold correspond to orbits escaping through channels 1, 2, 3, 4, and 5, respectively. For N = 6, initial conditions in forest green, light blue, dark blue, dark red, dark salmon, and gold correspond to orbits escaping through channels 1, 2, 3, 4, 5, and 6, respectively. For N = 7, initial conditions in forest green, light blue, dark blue, dark red, dark salmon, red, and gold correspond to orbits escaping through channels 1, 2, 3, 4, 5, 6, and 7, respectively. For N = 8, initial conditions in forest green, light blue, dark blue, dark red, dark salmon, red, light green, and gold correspond to orbits escaping through channels 1, 2, 3, 4, 5, 6, 7, and 8, respectively.

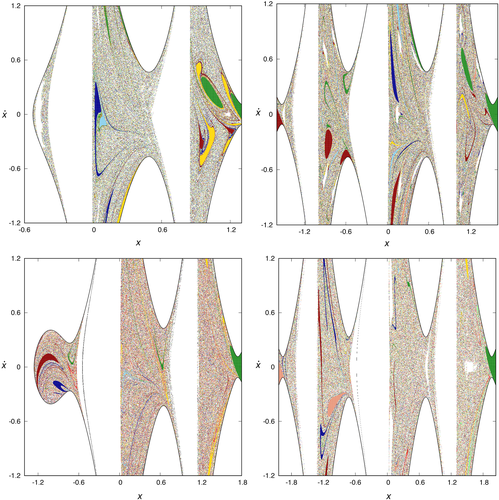
In the four plots, we can distinguish the same pattern: large connected domains, that lead to the same type of escape, and regions where the different basins are intricately mixed. In these regions, there is a very sensitive dependence on the initial conditions of the orbit behavior, that is, a slight change in the initial conditions can cause the test particle to escape through a different window.

In Reference 20, we analyzed the interrelation of the large connected domains N = 5. Due to the fact that the type of structures exhibited are analog for all the values of N considered, the conclusions of the analysis of the phase space made for N = 5 can be extrapolated to N = 6, 7, 8 peripheral bodies.

In addition, the boundaries between these regions seem to exhibit fractal structure. If we make a zoom of these plots we observe the same type of spiral structures organizing the basins of escape in the $(x,\dot{x})$ phase, for each of the values of N we have considered (see Figure 7). This fact unveils the relation between these basins and the projection of the manifolds to the guardian Lyapunov orbits on the surface of section. Due to the similarity of the structures for each of the values of N considered, we can focus our attention in studying in more detail the phase space for N = 5. In Figure 8, we show a sequence of zooms of the basins of escape for this value of N on the phase $(x,\dot{x})$, given by: (0.86, 1.1) × (−0.7, 0.1), (0.91, 0.99) × (−0.64, −0.28), (0.934, 0.95) × (−0.48, −0.36), and (0.934, 0.936) × (−0.48, −0.466), considering a maximum time of integration of T = 10².

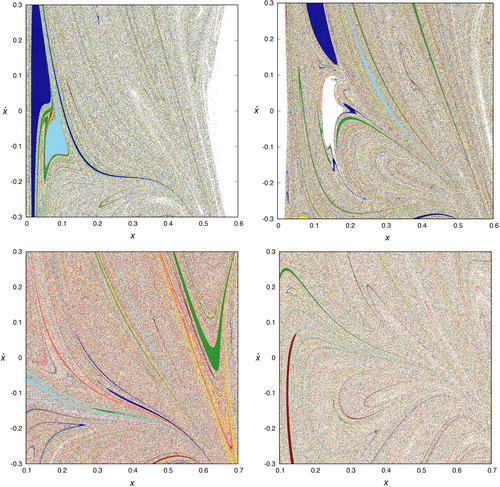
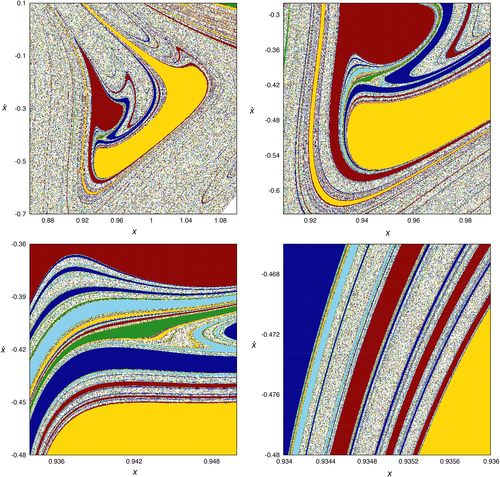
It is evident that the different basins of escape are interrelated following a fractal pattern. In the upper left panel of Figure 8, we can distinguish a primary structure colored in yellow, and a secondary formation colored in dark red infinitely spiraling around the first structure. In the second zoom (upper right panel of Figure 8), we can also detect a tertiary structure colored in dark blue spiraling around the first two structures, and also quaternary structures colored in green and light blue, infinitely spiraling around the first three structures. Indeed, two more deeper and consecutive zooms around $(x,\dot{x})\in (0.934,0.95)\times (-0.48,-0.36)$ and $(x,\dot{x})\in (0.934,0.936)\times (-0.48,-0.466)$ evidence this pattern of infinite spirals (lower left and lower right panels of Figure 8, respectively). The explanation relies on the shape of the stable and unstable manifolds to the unstable periodic orbits located at the minimum openings of the curve of zero velocity. The stable manifolds form the boundaries of the basins of escape, and the shape of the unstable manifolds is responsible for the ring and spiral structures found in the configuration space. Therefore, these connected domains observed in Figure 8 provide us information about the location of the stable manifold to the corresponding guardian periodic orbits.

4 CONCLUSIONS

This article summarizes the results of a numerical investigation of the phenomenon of escape in the N-body ring problem for N = 5, 6, 7, 8. There is a value of the Jacobi constant of the system such that for smaller values, the potential well opens and test particles may leave the potential through any of its N openings. We have studied the escape of particles from the system by using a surface of section located at the $(x,\dot{x})$ hyperplane, in order to compute the basins of escape. We have proved that in all the cases there are several large and connected regions in the surface of section leading to the same type of escape, as well as others where the escapes through the different exit channels are intricately mixed. The first connected domains are interrelated as follows: a primary structure is followed by a secondary structure infinitely spiraling around it. Then, a tertiary spiral formation tends infinitely to the two first structures, and so on and so forth. These structures reveal, on the one hand, the shape and location of the stable and unstable manifolds associated to the unstable periodic Lyapunov orbits that guard the exit channels and, on the other hand, the way these manifolds intersect in the surface of section.