Parameter estimation methods for the Weibull-Pareto distribution
Abstract
Recently there has been a growing interest to study various estimation procedures to estimate the model parameters of the Weibull Pareto distribution (WPD). It is observed that the proposed distribution can be used quite effectively to model skewed data. They also proposed a modification of the maximum likelihood method (MML) to estimate the parameters of the WPD. The proposed methods showed a better performance from the standard maximum likelihood (ML) method. However, when the shape parameter c>>1, the modified ML method showed unforgettable large bias and standard deviation. In this article, we address some new properties and propose different methods of estimation of the unknown parameters of a WPD from the frequentist point of view. We briefly describe different frequentist approaches, namely, moments estimators, L-moments estimators, percentile-based estimators, least squares estimators, method of maximum product of spacings estimators, method of Cramér-von-Mises estimators, method of Anderson-Darling estimators. Monte Carlo simulations are performed to compare the performances of the proposed methods of estimation and compare them with modified maximum likelihood estimation from the work of Alzaatreh et al (2013a). A real data set have been analyzed for illustrative purposes. Finally, bootstrap confidence intervals are obtained for the parameters of the model based on a real data set.
1 1 INTRODUCTION
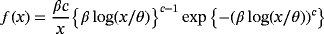 (1)
(1)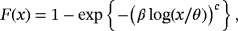 (2)
(2)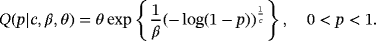 (3)
(3) (4)
(4)Alzaatreh et al6 discussed some properties of the WDP including limiting behavior, moments, and the estimation of the model parameters using different estimation strategies, in particular, ML and modified ML. In the original paper, the distribution is found to be unimodal and can be left or right skewed. The authors illustrated several applications of the WDP to real-life data sets exhibiting various types of shapes. They fitted the distribution to model data sets with long right tail, long left tail, and data with approximately symmetric characteristic. It is observed that the WDP has several properties and it can be used quite effectively to analyze skewed data. In many situations, it has been found to be performing better than the well-known generalized Weibull,7 Lagrange-gamma,8 and the exponentiated Weibull distribution.9 Furthermore, Alzaatreh et al6 pointed out that when c>1, the MLE and modified MLE show large biases and standard errors for the parameters. This motivates us to seek different methods of estimations for the WPD when the parameter c<1 and c>1.
We have a stream of estimation methods available for the parametric distribution in the literature; some of the estimation methods are well researched on theoretical aspect. We also know that the maximum likelihood estimation (MLE) and the method of moments estimation (MME) are traditional methods of estimation. Although MLE is advantageous in terms of its efficiency and has good theoretical properties, there is evidence that it does not perform well, especially, in the case of small samples. The method of moments is easily applicable and often gives explicit forms for estimators of unknown parameters. There are however cases where the method of moments does not give explicit estimators (eg, for the parameters of the Weibull and Gompertz distributions). Therefore, other methods have been proposed in the literature as alternatives to the traditional methods of estimation. Among them, the L-moments estimator (LME), least squares estimator (LSE), generalized spacing estimator (GSE), and percentile estimator (PCE) are often suggested. Generally, these methods do not have good theoretical properties, but in some cases, they can provide better estimates of the unknown parameters than the MLE and the MME. The objective of the article is to develop a guideline for choosing the best estimation method for the WPD, which we think would be of deep interest to applied statisticians.
The uniqueness of this study comes from the fact that we provide some new description of mathematical and statistical properties of this distribution with the hope that they will attract wider applications in biology, medicine, economics, reliability, engineering, and other areas of research. It is known from Alzaatreh et al6 that the rth moments exist for WPD whenever c>1. In addition, WPD has a closed-form CDF; see . Moreover, to the best of our knowledge thus far, no attempt has been made to compare all these estimators for the WPD along with mathematical and statistical properties. Additionally, all results are new, unless otherwise indicated. Comparisons of estimation methods for other distributions have been performed in the literature: Kundu and Raqab10 for generalized Rayleigh distributions, Alkasasbeh and Raqab11 for generalized logistic distributions, Teimouri et al12 for the Weibull distribution, Mazucheli et al13 for weighted Lindley distribution, and Dey et al14 for two-parameter Rayleigh distribution.
The rest of the article is organized as follows. In Section 2, different frequentist methods of parameter estimation are discussed. Simulation and real data application are presented in Section 3. Finally, in Section 4, we conclude the paper.
2 2 METHOD OF ESTIMATIONS FOR THE WDP
In this section, we obtain the estimators of the WDP parameters via different methods of estimation. For this, consider X1,X2,…,Xn as a random sample from the WDP in with observed values x1,x2,…,xn. In this paper, we consider the following methods of estimation: method of moments, method of L-moments, method of maximum product spacing, method of ordinary and weighted least-squares, percentile estimation, methods of minimum distances, and methods of Anderson-Darling and right-tail Anderson-Darling.
2.1 2.1 Method of moments estimators
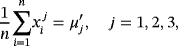 (5)
(5)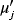 , j=1,2,3 are defined in .
, j=1,2,3 are defined in .2.2 2.2 Method of LMEs
In this section, we provide the LMEs, which can be obtained as the linear combinations of order statistics. The LMEs were originally proposed by Hosking,15 and it is observed that the LMEs are more robust than the usual moment estimators. The L-moment estimators are also obtained along the same way as the ordinary moment estimators, ie, by equating the sample L-moments with the population L-moments. L-moment estimation provides an alternative method of estimation analogous to conventional moments and have the advantage that they exist whenever the mean of the distribution exists, even though some higher moments may not exist, and are relatively robust to the effects of outliers.16
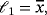 (6)
(6)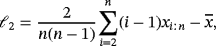 (7)
(7)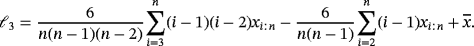 (8)
(8)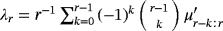 . Therefore, the first, second, and third population L-moments, respectively, are
. Therefore, the first, second, and third population L-moments, respectively, are
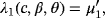 (9)
(9)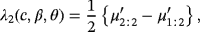 (10)
(10)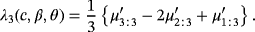 (11)
(11)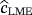 ,
,
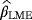 , and
, and
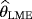 of the parameters c, β, and θ can be obtained by solving the following three equations numerically:
of the parameters c, β, and θ can be obtained by solving the following three equations numerically:
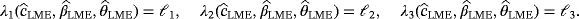
2.3 2.3 Method of maximum product spacing estimators
Cheng and Amin17, 18introduced the MPS method as an alternative to MLE for the estimation of parameters of continuous univariate distributions. Ranneby19 independently developed the same method as an approximation to the Kullback-Leibler measure of information.
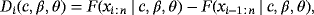
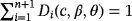 .
.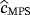 ,
,
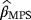 , and
, and
 of the parameters c, β, and θ are obtained by maximizing the geometric mean of the spacings with respect to c, β, and θ,
of the parameters c, β, and θ are obtained by maximizing the geometric mean of the spacings with respect to c, β, and θ,
 (12)
(12) (13)
(13) ,
,
 , and
, and
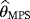 of the parameters c, β, and θ can also be obtained by solving the nonlinear equations
of the parameters c, β, and θ can also be obtained by solving the nonlinear equations
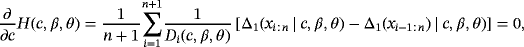 (14)
(14)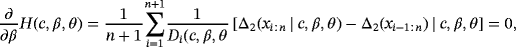 (15)
(15)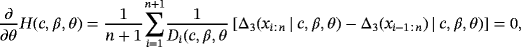 (16)
(16)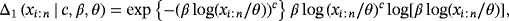 (17)
(17)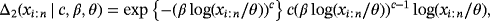 (18)
(18)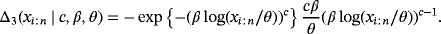 (19)
(19)2.4 2.4 Method of ordinary least-squares estimators
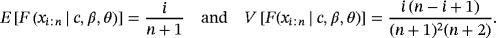 (20)
(20)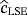 ,
,
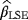 , and
, and
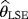 of the parameters c, β, and θ are obtained by minimizing the function:
of the parameters c, β, and θ are obtained by minimizing the function:
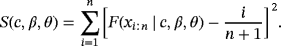 (21)
(21)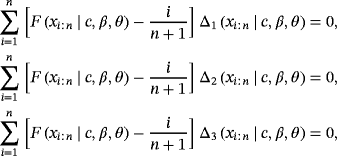
2.5 2.5 Method of percentiles estimators
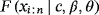 , then the PCEs
, then the PCEs
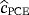 ,
,
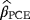 , and
, and
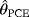 of the parameters c, β, and θ can be obtained by minimizing, with respect to c, β, and θ the function:
of the parameters c, β, and θ can be obtained by minimizing, with respect to c, β, and θ the function:
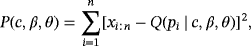 (22)
(22)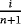 is the unbiased estimator of
is the unbiased estimator of
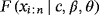 and Q(pi | c,β,θ) is defined in .
and Q(pi | c,β,θ) is defined in .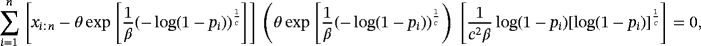
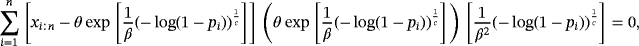

2.6 2.6 Methods of minimum distances estimators
In this subsection, we present three estimation methods for c, β, and θ based on the minimization of the goodness-of-fit statistics with respect to c, β, and θ. This class of statistics is based on the difference between the estimates of the CDF and the empirical distribution function.
2.6.1 2.6.1 Method of Cramér-von-Mises estimators
 ,
,
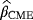 , and
, and
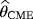 of the parameters c, β, and θ are obtained by minimizing the function C(c,β,θ) with respect to c, β, and θ:
of the parameters c, β, and θ are obtained by minimizing the function C(c,β,θ) with respect to c, β, and θ:
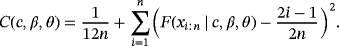 (23)
(23)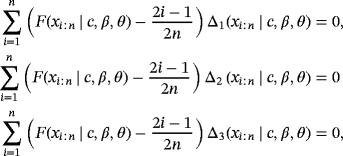
2.6.2 2.6.2 Methods of Anderson-Darling estimators
The Anderson-Darling test was developed in 1952 by Anderson and Darling22 as an alternative to other statistical tests for detecting sample distributions departure from normality. Specifically, the AD test converges very quickly toward the asymptote.23-25
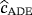 ,
,
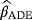 , and
, and
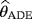 of the parameters c, β, and θ are obtained by minimizing the function A(c,β,θ) with respect to c, β, and θ, respectively,
of the parameters c, β, and θ are obtained by minimizing the function A(c,β,θ) with respect to c, β, and θ, respectively,
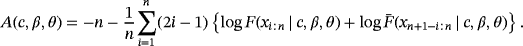 (24)
(24)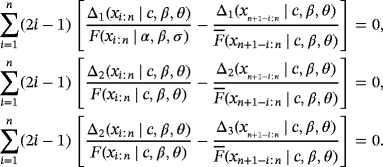
3 3 NUMERICAL COMPUTATIONS AND DISCUSSIONS
3.1 3.1 Simulation study
- When c<1, MLE for both shape and scale parameters do not exist (for reference, see the work of Alzaatreh et al6).
- When c>>1, the WPD appears to be more and more left skewed.
- In some real world data application, we are mainly interested in a WPD with a large c, as it results in heavy left-skewed data. In other words, our purpose in the current paper is to study WPD to see how well it works with negatively skewed data. In other scenarios, a WPD with a small value of c will be a good model for a heavy right-skewed data.
- As the rate parameter β decreases, the WPD becomes more and more flat (for reference, see the work of Alzaatreh et al6).
Next, we present some experimental results to evaluate the performance of the different methods of estimation discussed in the previous sections. We report only the simulation study results for the maximum spacing distance method, which (based on our results) performs the best among all other estimation methods proposed in the previous section. We conducted an extensive simulation study where we chose a different group of parameters and compare the different estimation methods based on bias (estimate-actual) and standard error for the estimates. The estimation methods that are used in the simulation study are ME (moments estimation) obtained by solving equations , LME (L-moments estimation) obtained by solving equations (28)-(30), MPS (maximum product spacing) obtained by solving equations (33)-(35), LSE (least square estimation) obtained by minimizing (43), PE (percentiles estimation) obtained by minimizing (48), CME (Cramér-von Mises estimation) obtained by minimizing (49), and ADE (Anderson-Darling estimation) obtained by minimizing (50).
Discussion. Alzaatreh et al6 proposed two estimation methods to estimate the WPD parameters. The first method is AMLE (alternative MLE) where
 , and
, and
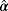 and
and
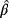 are obtained by maximizing
are obtained by maximizing
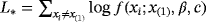 . The second method is the MMLE (modified MLE). This method applies only when c>1 and the estimates are obtained by maximizing
. The second method is the MMLE (modified MLE). This method applies only when c>1 and the estimates are obtained by maximizing
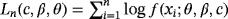 over all parameters c, β, and θ, where θ<x(1). They performed a simulation study to compare AMLE and MMLE methods. The results are reported in Tables 2–5 in their paper for sample sizes n=100 and n=500 and for different parameter values. They observed that the AMLE performed quite well when c<1. For the case c>1, AMLE showed higher bias values for the parameters c and β. In general, MMLE performed better than AMLE when c>1. However, MMLE showed higher bias and standard error values when c is large.
over all parameters c, β, and θ, where θ<x(1). They performed a simulation study to compare AMLE and MMLE methods. The results are reported in Tables 2–5 in their paper for sample sizes n=100 and n=500 and for different parameter values. They observed that the AMLE performed quite well when c<1. For the case c>1, AMLE showed higher bias values for the parameters c and β. In general, MMLE performed better than AMLE when c>1. However, MMLE showed higher bias and standard error values when c is large.
Our simulation study is based on various combination of parameter values and sample sizes of n=100 and n=500. Our objective is to compare the findings of our study with the results of Alzaatreh et al.6 We observe the following: ME and LME only exist when the parameter c>1. However, for this case, MMLE perform significantly better than ME and LME methods. Furthermore, the mean square error (MSE) values for the estimates under ME and LME are, in general, higher than the results obtained using the MMLE method. In addition, the LSE method performs equally as AMLE in most cases. Overall, we noticed that the MPS method performs better than PE, CME, and ADE. In addition, when c>1 the PE, CME, and ADE can produce higher bias values for the parameters c and β. It is noteworthy to mention that ADE provides smaller bias and MSE for the parameter θ.
From the above discussion, we observe that MPS performs better than all other estimators considered in our study. Thus, we only present simulation results on MPS to compare with MMLE methods for estimating the WPD parameters. Here, we consider the values 0.5, 1, 4, and 7 for the parameter c and the values 0.5, 1, and 3 for the parameters β and θ. The number of parameter combinations for each sample size is 36. For each parameter combination, we generate a random sample yi∼Weibull(c,1/β), i=1,…,n. Then, the random sample
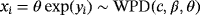 . Two different sample sizes n=100 and n=500 are considered. The process is repeated 1000 times and each time we estimate the WPD parameters using the MPS method. Tables 3 and 4 report the bias, standard deviation, and the empirical mean square error using the MPS method. In Tables 1 and 2, we report the results of the simulation study using MMLE from the work of Alzaatreh et al.6 Note that because MMLE does not exit when c>1, the results in Tables 1 and 2 show only the values of the parameter groups with c=4 and c=7.
. Two different sample sizes n=100 and n=500 are considered. The process is repeated 1000 times and each time we estimate the WPD parameters using the MPS method. Tables 3 and 4 report the bias, standard deviation, and the empirical mean square error using the MPS method. In Tables 1 and 2, we report the results of the simulation study using MMLE from the work of Alzaatreh et al.6 Note that because MMLE does not exit when c>1, the results in Tables 1 and 2 show only the values of the parameter groups with c=4 and c=7.
| Actual values | Bias | Standard deviation | MSE | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| c | β | θ |
 |
 |
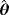 |
 |
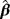 |
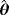 |
 |
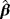 |
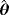 |
| 4 | 0.5 | 0.5 | 0.1423 | −0.1238 | 0.0877 | 0.9133 | 0.1153 | 0.2028 | 0.8543 | 0.028 | 0.048 |
| 1 | −0.1059 | 0.0492 | 0.1692 | 0.8724 | 0.1117 | 0.4075 | 0.7723 | 0.0149 | 0.194 | ||
| 3 | −0.1432 | 0.0498 | 0.5138 | 0.9646 | 0.1088 | 1.1955 | 0.9500 | 0.014 | 1.691 | ||
| 1 | 0.5 | 0.1311 | 0.0568 | 0.0098 | 1.3075 | 0.2551 | 0.1146 | 1.7264 | 0.068 | 0.013 | |
| 1 | −0.068 | 0.0904 | 0.0538 | 1.0991 | 0.2444 | 0.2117 | 1.2126 | 0.067 | 0.047 | ||
| 3 | 0.1152 | 0.0948 | 0.1811 | 0.9517 | 0.2179 | 0.5863 | 0.9190 | 0.055 | 0.376 | ||
| 3 | 0.5 | −0.1407 | 0.2693 | 0.0078 | 0.9301 | 0.6689 | 0.032 | 0.8848 | 0.518 | 0.001 | |
| 1 | −0.1528 | 0.2781 | 0.0161 | 0.8325 | 0.679 | 0.0632 | 0.7164 | 0.538 | 0.004 | ||
| 3 | −0.0639 | 0.2065 | 0.0263 | 1.0276 | 0.6606 | 0.1981 | 1.060 | 0.479 | 0.039 | ||
| 7 | 0.5 | 0.5 | −1.2633 | 0.1524 | 0.2709 | 1.4532 | 0.1793 | 0.3044 | 3.697 | 0.055 | 0.166 |
| 1 | −1.3581 | 0.166 | 0.3802 | 1.4926 | 0.1735 | 0.5429 | 4.048 | 0.059 | 0.439 | ||
| 3 | −1.2049 | 0.1595 | 1.3728 | 1.7056 | 0.2009 | 1.7528 | 4.347 | 0.055 | 4.958 | ||
| 1 | 0.5 | −0.425 | 0.2123 | 0.0616 | 2.7144 | 0.416 | 0.1424 | 7.520 | 0.085 | 0.0238 | |
| 1 | −1.0375 | 0.3312 | 0.2193 | 2.1728 | 0.4198 | 0.2942 | 5.784 | 0.282 | 0.134 | ||
| 3 | −1.1141 | 0.3351 | 0.5591 | 2.3534 | 0.4085 | 0.8147 | 6.754 | 0.287 | 0.975 | ||
| 3 | 0.5 | −1.8528 | 1.2261 | 0.0436 | 1.2541 | 0.9598 | 0.0303 | 4.985 | 1.669 | 0.003 | |
| 1 | 1.2936 | 1.0231 | 0.0578 | 1.4055 | 1.0194 | 0.069 | 3.631 | 2.08 | 0.008 | ||
| 3 | −0.3722 | 0.6521 | 0.0849 | 2.1807 | 1.2771 | 0.3178 | 4.890 | 2.038 | 0.108 | ||
| Actual values | Bias | Standard deviation | MSE | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| c | β | θ |
 |
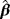 |
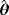 |
 |
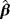 |
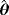 |
 |
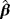 |
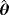 |
| 4 | 0.5 | 0.5 | 0.0053 | 0.0064 | 0.0119 | 0.3979 | 0.0424 | 0.0797 | 0.1583 | 0.1798 | 0.0064 |
| 1 | −0.0016 | 0.0063 | 0.0241 | 0.4676 | 0.0508 | 0.1947 | 0.2186 | 0.0026 | 0.0385 | ||
| 3 | −0.0143 | 0.005 | 0.0555 | 0.4024 | 0.0434 | 0.487 | 0.1621 | 0.0019 | 0.2402 | ||
| 1 | 0.5 | −0.0285 | 0.0169 | 0.0052 | 0.4173 | 0.0913 | 0.0428 | 0.1749 | 0.0086 | 0.0018 | |
| 1 | −0.0156 | 0.0141 | 0.0079 | 0.4039 | 0.0933 | 0.0863 | 0.1633 | 0.0089 | 0.0075 | ||
| 3 | −0.0612 | 0.0241 | 0.0543 | 0.4187 | 0.0952 | 0.2633 | 0.1790 | 0.0096 | 0.0722 | ||
| 3 | 0.5 | −0.0551 | 0.0783 | 0.0029 | 0.432 | 0.2732 | 0.0146 | 0.1896 | 0.0807 | 0.0002 | |
| 1 | −0.1084 | 0.1017 | 0.0079 | 0.3691 | 0.2578 | 0.0263 | 0.1479 | 0.0768 | 0.0007 | ||
| 3 | −0.0242 | 0.0437 | 0.0046 | 0.4628 | 0.3023 | 0.0942 | 0.2147 | 0.0933 | 0.0089 | ||
| 7 | 0.5 | 0.5 | −0.2417 | 0.0315 | 0.0597 | 0.6788 | 0.0836 | 0.1594 | 0.5191 | 0.0079 | 0.0289 |
| 1 | −0.1643 | 0.0265 | 0.102 | 1.011 | 0.0742 | 0.2871 | 1.0491 | 0.0062 | 0.0928 | ||
| 3 | 0.2836 | −0.0431 | 0.5019 | 0.7515 | 0.0767 | 0.8855 | 0.6452 | 0.0077 | 1.036 | ||
| 1 | 0.5 | −0.2108 | 0.0607 | 0.0214 | 1.1523 | 0.178 | 0.0822 | 1.3722 | 0.0353 | 0.0072 | |
| 1 | −0.0999 | 0.0448 | 0.0352 | 1.5578 | 0.1147 | 0.1815 | 2.4367 | 0.0151 | 0.0342 | ||
| 3 | −0.4528 | 0.0952 | 0.2354 | 0.9675 | 0.1563 | 0.4127 | 1.1410 | 0.0334 | 0.2257 | ||
| 3 | 0.5 | −0.6322 | 0.3218 | 0.0172 | 0.743 | 0.3542 | 0.0188 | 0.9517 | 0.2290 | 0.0006 | |
| 1 | −0.7231 | 0.3321 | 0.0338 | 0.7618 | 0.2236 | 0.0402 | 1.1032 | 0.1603 | 0.0027 | ||
| 3 | −0.2309 | 0.188 | 0.0383 | 1.2144 | 0.5059 | 0.1368 | 1.5280 | 0.2913 | 0.0201 | ||
| Actual values | Bias | Standard deviation | MSE | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| c | β | θ |
 |
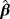 |
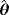 |
 |
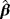 |
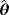 |
 |
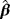 |
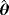 |
| 0.5 | 0.5 | 0.5 | 0.0237 | −0.0127 | 0.0291 | 0.0019 | 0.0112 | 0.0065 | 0.0006 | 0.0003 | 0.0009 |
| 0 | 1 | 0.0241 | −0.0085 | −0.0607 | 0.0020 | 0.0096 | 0.0016 | 0.0006 | 0.0002 | 0.0037 | |
| 3 | 0.0261 | −0.0331 | −0.0673 | 0.0022 | 0.0243 | 0.0057 | 0.0007 | 0.0017 | 0.0046 | ||
| 1 | 0.5 | 0.0178 | −0.0376 | −0.0192 | 0.0020 | 0.0404 | 0.0011 | 0.0003 | 0.0030 | 0.0004 | |
| 1 | 0.0191 | −0.0117 | −0.0426 | 0.0020 | 0.0399 | 0.0003 | 0.0004 | 0.0017 | 0.0018 | ||
| 3 | 0.0232 | 0.0181 | −0.0352 | 0.0019 | 0.0363 | 0.0003 | 0.0005 | 0.0017 | 0.0012 | ||
| 3 | 0.5 | 0.0204 | −0.0201 | −0.0202 | 0.0017 | 0.3455 | 0.0043 | 0.0004 | 0.1198 | 0.0004 | |
| 1 | 0.0197 | 0.0877 | −0.0368 | 0.0017 | 0.3639 | 0.0002 | 0.0004 | 0.1401 | 0.0014 | ||
| 3 | 0.0227 | −0.0310 | −0.1255 | 0.0855 | 0.3261 | 0.0015 | 0.0078 | 0.1073 | 0.0158 | ||
| 1 | 0.5 | 0.5 | 0.0416 | −0.0792 | −0.0110 | 0.0084 | 0.0021 | 0.0013 | 0.0018 | 0.0063 | 0.0001 |
| 1 | 0.0340 | −0.0083 | −0.0171 | 0.0079 | 0.0022 | 0.0050 | 0.0012 | 0.0001 | 0.0003 | ||
| 3 | 0.0416 | −0.0795 | −0.0661 | 0.0084 | 0.0021 | 0.0048 | 0.0018 | 0.0063 | 0.0044 | ||
| 1 | 0.5 | 0.0470 | 0.0260 | −0.0150 | 0.0092 | 0.0068 | 0.0043 | 0.0023 | 0.0007 | 0.0002 | |
| 1 | 0.0470 | 0.0260 | −0.0300 | 0.0092 | 0.0068 | 0.0002 | 0.0023 | 0.0007 | 0.0009 | ||
| 3 | 0.0432 | 0.0312 | −0.0991 | 0.0089 | 0.0069 | 0.0016 | 0.0019 | 0.0010 | 0.0098 | ||
| 3 | 0.5 | 0.0504 | 0.0882 | −0.0393 | 0.0101 | 0.0682 | 0.0046 | 0.0026 | 0.0124 | 0.0016 | |
| 1 | 0.0577 | 0.0595 | −0.0924 | 0.0131 | 0.0693 | 0.0018 | 0.0035 | 0.0083 | 0.0085 | ||
| 3 | 0.0439 | 0.0860 | −0.0256 | 0.0092 | 0.0570 | 0.1030 | 0.0020 | 0.0106 | 0.0113 | ||
| 4 | 0.5 | 0.5 | 0.5584 | −0.0513 | −0.0901 | 0.7552 | 0.0083 | 0.1319 | 0.8821 | 0.0027 | 0.0255 |
| 1 | 0.5584 | −0.0513 | −0.0902 | 0.7552 | 0.0083 | 0.2277 | 0.8821 | 0.0027 | 0.0600 | ||
| 3 | 0.3777 | −0.0360 | −0.4714 | 0.6465 | 0.0098 | 0.4830 | 0.5606 | 0.0014 | 0.4555 | ||
| 1 | 0.5 | 0.5584 | −0.0803 | 0.0289 | 0.7552 | 0.0334 | 0.0794 | 0.8821 | 0.0076 | 0.0071 | |
| 1 | 0.5584 | 0.0998 | 0.0578 | 0.7552 | 0.0334 | 0.0318 | 0.8821 | 0.0111 | 0.0043 | ||
| 3 | 0.5584 | 0.0498 | 0.0173 | 0.7552 | 0.0334 | 0.2860 | 0.8821 | 0.0036 | 0.0821 | ||
| 3 | 0.5 | 0.3584 | 0.1494 | 0.0279 | 0.7552 | 0.3003 | 0.0921 | 0.6987 | 0.1125 | 0.0093 | |
| 1 | 0.3584 | 0.1494 | 0.0558 | 0.7552 | 0.3003 | 0.0369 | 0.6987 | 0.1125 | 0.0045 | ||
| 3 | 0.3169 | 0.1494 | 0.0655 | 0.7637 | 0.2753 | 0.0337 | 0.6837 | 0.0981 | 0.0054 | ||
| 7 | 0.5 | 0.5 | 0.4482 | −0.1739 | −0.0346 | 0.8855 | 0.1360 | 0.2378 | 0.9850 | 0.0487 | 0.0578 |
| 1 | 0.4051 | −0.2240 | −0.0836 | 0.5640 | 0.1229 | 0.4885 | 0.4821 | 0.0653 | 0.2456 | ||
| 3 | 0.6742 | −0.2014 | −0.7405 | 0.6238 | 0.1695 | 0.5880 | 0.8437 | 0.0693 | 0.8941 | ||
| 1 | 0.5 | 0.9482 | −0.0348 | −0.0574 | 0.8855 | 0.4441 | 0.1158 | 1.6833 | 0.1984 | 0.0167 | |
| 1 | 0.8452 | −0.0698 | −0.0384 | 0.5639 | 0.3599 | 0.4692 | 1.0323 | 0.1344 | 0.2217 | ||
| 3 | 0.9452 | −0.0698 | −0.1152 | 0.5639 | 0.3599 | 0.6023 | 1.2114 | 0.1344 | 0.3760 | ||
| 3 | 0.5 | 0.3476 | −0.1633 | −0.0234 | 0.2607 | 0.5654 | 0.0143 | 0.1888 | 0.3463 | 0.0008 | |
| 1 | 0.4452 | −0.2093 | −0.0564 | 0.5639 | 0.6839 | 0.0713 | 0.5162 | 0.5116 | 0.0083 | ||
| 3 | 0.4452 | −0.2093 | −0.0169 | 0.5639 | 0.6839 | 0.0642 | 0.5162 | 0.5116 | 0.0044 | ||
| Actual values | Bias | Standard deviation | MSE | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| c | β | θ |
 |
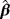 |
 |
 |
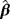 |
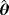 |
 |
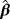 |
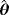 |
| 0.5 | 0.5 | 0.5 | 0.0090 | −0.0026 | 0.0042 | 0.0006 | 0.0108 | 0.0059 | 0.0001 | 0.0001 | 0.0001 |
| 1 | 0.0093 | −0.0026 | 0.0087 | 0.0006 | 0.0107 | 0.0002 | 0.0001 | 0.0001 | 0.0001 | ||
| 3 | 0.0146 | −0.0118 | 0.0082 | 0.0012 | 0.0054 | 0.0015 | 0.0002 | 0.0002 | 0.0001 | ||
| 1 | 0.5 | 0.0094 | −0.0018 | 0.0085 | 0.0007 | 0.0303 | 0.0010 | 0.0001 | 0.0009 | 0.0001 | |
| 1 | 0.0094 | −0.0018 | 0.0017 | 0.0007 | 0.0302 | 0.0002 | 0.0001 | 0.0009 | 0.0000 | ||
| 3 | 0.0099 | 0.0029 | 0.0058 | 0.0011 | 0.0314 | 0.0001 | 0.0001 | 0.0010 | 0.0000 | ||
| 3 | 0.5 | 0.0049 | −0.0193 | 0.0010 | 0.0004 | 0.1485 | 0.0024 | 0.0000 | 0.0224 | 0.0000 | |
| 1 | 0.0049 | −0.0539 | 0.0035 | 0.0004 | 0.1485 | 0.0001 | 0.0000 | 0.0250 | 0.0000 | ||
| 3 | 0.0085 | −0.0176 | 0.0018 | 0.0006 | 0.1645 | 0.0001 | 0.0001 | 0.0274 | 0.0000 | ||
| 1 | 0.5 | 0.5 | 0.0153 | −0.0038 | 0.0010 | 0.0025 | 0.0009 | 0.0006 | 0.0002 | 0.0000 | 0.0000 |
| 1 | 0.0153 | −0.0038 | 0.0021 | 0.0025 | 0.0009 | 0.0002 | 0.0002 | 0.0000 | 0.0000 | ||
| 3 | 0.0114 | −0.0036 | 0.0088 | 0.0018 | 0.0009 | 0.0005 | 0.0001 | 0.0000 | 0.0001 | ||
| 1 | 0.5 | 0.0085 | 0.0130 | 0.0007 | 0.0012 | 0.0020 | 0.0017 | 0.0001 | 0.0002 | 0.0000 | |
| 1 | 0.0063 | 0.0124 | 0.0014 | 0.0014 | 0.0019 | 0.0001 | 0.0000 | 0.0002 | 0.0000 | ||
| 3 | 0.0061 | 0.0098 | 0.0044 | 0.0016 | 0.0016 | 0.0005 | 0.0000 | 0.0001 | 0.0000 | ||
| 3 | 0.5 | 0.0199 | 0.0679 | 0.0003 | 0.0026 | 0.0361 | 0.0003 | 0.0004 | 0.0059 | 0.0000 | |
| 1 | 0.0088 | 0.0662 | 0.0007 | 0.0019 | 0.0303 | 0.0002 | 0.0001 | 0.0053 | 0.0000 | ||
| 3 | 0.0208 | 0.0557 | 0.0039 | 0.0038 | 0.0290 | 0.0018 | 0.0004 | 0.0039 | 0.0000 | ||
| 4 | 0.5 | 0.5 | −0.1382 | 0.0169 | 0.0360 | 0.4118 | 0.0034 | 0.0120 | 0.1887 | 0.0003 | 0.0014 |
| 1 | −0.1182 | 0.0169 | 0.0720 | 0.4118 | 0.0034 | 0.0478 | 0.1836 | 0.0003 | 0.0075 | ||
| 3 | −0.1280 | 0.0202 | 0.2270 | 0.2126 | 0.0023 | 0.2878 | 0.0616 | 0.0004 | 0.1343 | ||
| 1 | 0.5 | −0.2307 | 0.0498 | 0.0283 | 0.3538 | 0.0128 | 0.0036 | 0.1784 | 0.0026 | 0.0008 | |
| 1 | −0.2307 | −0.0703 | 0.0567 | 0.3538 | 0.0128 | 0.0145 | 0.1784 | 0.0051 | 0.0034 | ||
| 3 | −0.2307 | −0.0103 | 0.0170 | 0.3538 | 0.0128 | 0.1305 | 0.1784 | 0.0003 | 0.0173 | ||
| 3 | 0.5 | −0.2307 | −0.0308 | 0.0104 | 0.3538 | 0.1153 | 0.0005 | 0.1784 | 0.0142 | 0.0001 | |
| 1 | −0.2307 | −0.0308 | 0.0207 | 0.3538 | 0.1153 | 0.0019 | 0.1784 | 0.0142 | 0.0004 | ||
| 3 | −0.2307 | −0.0053 | 0.0222 | 0.3538 | 0.1153 | 0.0169 | 0.1784 | 0.0133 | 0.0008 | ||
| 7 | 0.5 | 0.5 | 0.1141 | −0.0330 | −0.0624 | 0.5839 | 0.0093 | 0.0370 | 0.3540 | 0.0012 | 0.0053 |
| 1 | 0.1211 | −0.0271 | −0.0826 | 0.2328 | 0.0132 | 0.1640 | 0.0688 | 0.0009 | 0.0337 | ||
| 3 | 0.0416 | −0.0998 | −0.3743 | 0.3502 | 0.0255 | 0.2190 | 0.1244 | 0.0106 | 0.1880 | ||
| 1 | 0.5 | −0.1705 | 0.0132 | 0.0124 | 0.2298 | 0.0226 | 0.0507 | 0.0819 | 0.0007 | 0.0027 | |
| 1 | 0.1147 | 0.0043 | 0.0095 | 0.3074 | 0.0111 | 0.0109 | 0.1076 | 0.0001 | 0.0002 | ||
| 3 | −0.0800 | 0.0118 | 0.0557 | 0.3266 | 0.0121 | 0.1064 | 0.1131 | 0.0003 | 0.0144 | ||
| 3 | 0.5 | −0.1950 | 0.0505 | 0.0028 | 0.1860 | 0.2162 | 0.0006 | 0.0726 | 0.0493 | 0.0000 | |
| 1 | 0.0115 | 0.0128 | 0.0044 | 0.3074 | 0.0995 | 0.0013 | 0.0946 | 0.0101 | 0.0000 | ||
| 3 | 0.0115 | 0.0128 | 0.0133 | 0.3073 | 0.0995 | 0.0114 | 0.0946 | 0.0101 | 0.0003 | ||
| Method of estimation | Parameter estimates | Goodness of fit | |||
|---|---|---|---|---|---|
 |
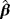 |
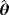 |
K-S value | P value | |
| ME | 16.0123 | 0.2246 | 0.0811 | 0.0778 | 0.9686 |
| LME | 15.7625 | 0.2105 | 0.0597 | 0.0866 | 0.9248 |
| LSE | 16.2687 | 0.2216 | 0.0781 | 0.0963 | 0.8521 |
| PE | 24.9517 | 0.1416 | 0.0060 | 0.0842 | 0.9390 |
| MPS | 18.1909 | 0.1859 | 0.0317 | 0.0809 | 0.9559 |
| CME | 15.0625 | 0.2476 | 0.1251 | 0.0879 | 0.9167 |
| ADE | 17.2488 | 0.2037 | 0.0519 | 0.0904 | 0.8990 |
| MMLE | 27.6546 | 0.1355 | 0.0043 | 0.0847 | 0.9364 |
- Abbreviations: ADE, Anderson-Darling estimators; CME, Cramer-von Mises estimators; LME, L-moments estimator; LSE, least squares estimator; ME, moments estimation; MMLE, modified maximum likelihood estimation; MPS, maximum product of spacing; PE, percentiles estimation.
- - In general, MMLE underestimates parameter c, whereas MPS in most of the cases overestimates the parameter c.
- - When c=4, in most cases the bias of the parameter c under MMLE is lower than MPS, whereas for c=7, the bias of the parameter c under MPS in general is lower than MMLE.
- - The bias of the parameter β under MPS method is lower than MMLE while the bias of the parameter θ under MMLE tends to be lower than MPS. This can be seen more clearly when n=500.
- - Furthermore, when c is large, the standard error of the parameter c using MMLE produces large standard error. This can be seen clearly from Table 1 for the cases c=4 and c=7 and from Table 2 for c=7. Besides, the standard errors of the parameters β and θ using MPS seems to be lower than the standard errors using the MMLE method.
- - Tables 3,4 show satisfactory results in terms of biases and standard errors using MPS for all values of c>0. From the above observations, it is apparent that MPS is superior to all the estimators for estimating the WPD parameters.
3.2 3.2 Real data analysis
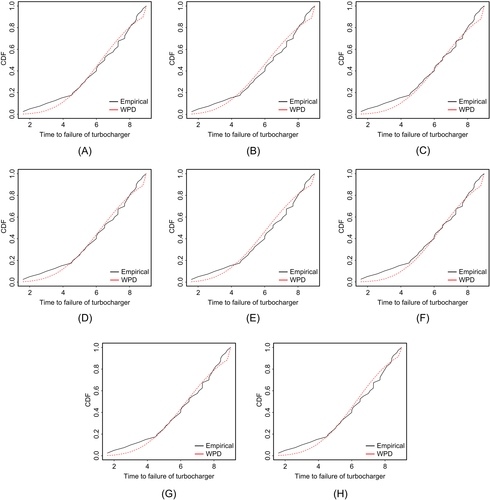
In this subsection, we show the applicability of WPD using MPS estimation method. A real data set (n=40) is taken from the work of Xu et al,26 and it represents the time to failure (103 h) of the turbocharger of one type of engine. The summary statistics from the data set are
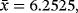 s=1.9555, skewness = −0.6542, and kurtosis = 2.5750. As it appears from the skewness value, the data set is left skewed. The data set is reported as follows:
s=1.9555, skewness = −0.6542, and kurtosis = 2.5750. As it appears from the skewness value, the data set is left skewed. The data set is reported as follows:
1.6, 2.0, 2.6, 3.0, 3.5, 3.9, 4.5, 4.6, 4.8, 5.0, 5.1, 5.3, 5.4, 5.6, 5.8, 6.00786, 6.0, 6.1, 6.3, 6.50518, 6.5, 6.7, 7.0, 7.1, 7.3, 7.3, 7.3, 7.7, 7.7, 7.8, 7.9, 8.0, 8.1, 8.3, 8.4, 8.4, 8.5, 8.7, 8.8, 9.
We fitted the WPD to the real data set using the ME, LME, LSE, PE, MPS, CME, ADE, and MMLE techniques. To use MPS, we break the ties by adding a random noise from uniform distribution on (0.001,0.0001) to the tie values. In Table 5, we report the estimated parameter values, the Kolmogorov-Smirnov (K-S) test statistic and the P value for the K-S statistic. The empirical and fitted CDFs for the data set are presented in Figure 1.
Additionally, we apply the least squares estimation method (Section 3.1) and the method of maximum likelihood method (Section 3.2), as discussed in the work of Cooray2 to this data set and make a comparison study between the two WPC (composite Weibull-Pareto) and the three-parameter WPD. The results are presented in Table 6. The associated parameter estimates and the goodness-of-fit values (Kolmogorov-Smirnov [KS] and Anderson-Darling [AD]) are provided. Furthermore, we consider average root mean square error (RMSE) and Gini statistic.
where Θ = (γ, Θ).
-
Gini statistic: Let x1,x2,…,xn be a random sample of size n drawn randomly from the population and further let x(1),x(2),…,x(n) be the order statistics obtained from the sample, and the usual estimator of the Gini index is given by

For a detailed study on the use of Gini index as a measure of goodness of fit, one is referred to the work of Noughabi.27 In their paper, the author has suggested the use of Gini index as a measure of goodness of fit for logistic distribution. We have followed the idea for our WPD as well as WPC probability models.
Here also, a smaller value of this statistic will imply that we have a better model as compared with a rival probability model.
Both the RMSE and the Gini statistic values for the two probability models (WPD and WPC) are reported in Table 7.
TABLE 6. Parameter estimates of composite Weibull-Pareto (WPC) and Weibull-Pareto distribution (WPD) for the time to failure of turbocharger data sets via the least squares (LS) and maximum likelihood (ML) methods Distribution Estimated parameters ± SE Likelihood K-S AD WPC LS 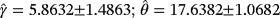
−417.348 0.0726 0.6528 ML 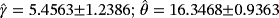
−416.23 0.0698 0.6423 WPD LS 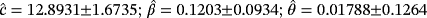
−415.03 0.0432 0.5017 ML 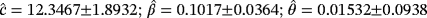
−411.06 0.0475 0.4968 - Abbreviations: AD, Anderson-Darling; K-S, Kolmogorov-Smirnov; SE, standard error.
TABLE 7. Root mean square error (RMSE) and Gini statistic values for the Weibull-Pareto distribution (WPD) and Weibull-Pareto (WPC) Distribution Method of estimation Gini RMSE WPC LS 0.1833 2.7493 ML 0.1139 2.3912 WPD LS 0.1434 1.8315 ML 0.1038 1.7937 - Abbreviations: LS, least squares; ML, maximum likelihood.
Based on the data set, it appears that WPD provides slightly better fit as compared with the WPC based on K-S and AD statistics. However, WPD provides better fit based on Gini and RMSE. In general, one cannot make a general conclusion that the former will be uniformly better than the latter. It will depend on a particular data set.
In Table 8, we report the bootstrap confidence intervals for the fitted WPD for the parameters c, β, and θ using ME, LME, LSE, PE, MPS, CME, ADE, and MMLE methods.
| Method of estimation | c | β | θ |
|---|---|---|---|
| ME | (9.2743,28.4357) | (0.1328,0.3321) | (0.0028,0.1547) |
| LME | (11.2365,26.3921) | (0.1224,0.2875) | (0.0023,0.1883) |
| LSE | (9.1187,25.3261) | (0.0966,0.2974) | (0.0129,0.1948) |
| PE | (19.4678,32.1328) | (0.0946,0.1833) | (0.0029,0.1929) |
| MPS | (13.4834,20.8112) | (0.1363,0.2819) | (0.0018,0.2009) |
| CME | (11.0937,19.8566) | (0.1529,0.3017) | (0.0912,0.2364) |
| ADE | (13.0213,24.5672) | (0.1234,0.2258) | (0.0875,0.2218) |
| MMLE | (16.7329,36.5235) | (0.0834,0.1736) | (0.0037,0.2434) |
- Abbreviations: ADE, Anderson-Darling estimators; CME, Cramer-von Mises estimators; LME, L-moments estimator; LSE, least squares estimator; ME, moments estimation; MMLE, modified maximum likelihood estimation; MPS, maximum product of spacing; PE, percentiles estimation.
4 4 CONCLUSIONS
In this paper, we study several estimation techniques for estimating the unknown parameters of the WPD. As it is not feasible to compare these methods theoretically, we have presented the results of a simulation study to identify the best method. Most importantly, the simulation result shows that the MPS method outperforms its competitors for estimating the parameters of the WPD. Combining these results with the good properties of the method such as consistency, asymptotic efficiency, normality, and invariance, we recommend its use for all practical purposes.
COMPETING INTERESTS
None of the authors has any competing interests in the manuscript.
FUNDING
This research received no specific grant from any funding agency in the public, commercial, or not-for-profit sector.
AUTHORS' CONTRIBUTIONS
The authors SD, IG, and AA with the consultation of each other carried out this work and drafted the manuscript together. All authors read and approved the final manuscript.
AVAILABILITY OF DATA AND MATERIAL
The real data set is taken from the paper of Xu et al,26 which is provided in the reference list of this paper. Therefore, it is readily available.
Biographies

Sanku Dey is currently an Associate Professor at the Department of Statistics, St. Anthony's College, Shillong, Meghalaya, India. His research interests include distribution theory, Bayesian analysis, reliability, maximum likelihood estimation, and Bayesian inference.

Ayman Alzaatreh is currently an Associate Professor at the Department of Mathematics, Nazarbayev University, Astana, Kazakhstan. His research interests include distribution theory, statistical inference, R programming, applied statistics, statistical modeling, and multivariate statistics.

Indranil Ghosh is currently an Associate Professor at the Department of Mathematics and Statistics, University of North Carolina Wilmington, Wilmington, North Carolina. His research interests include distribution theory, statistical inference, R programming, applied statistics, statistical modeling, multivariate statistics, Bayesian inference, computational statistics, mathematical statistics, classical probability theory, and statistical analysis.





