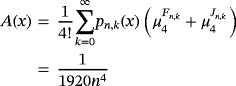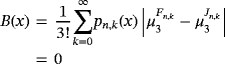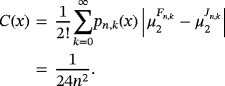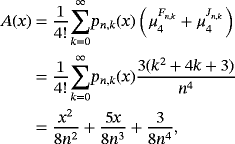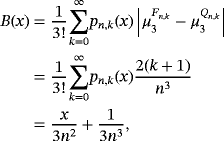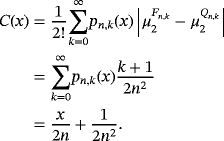General estimates for the difference of operators
Abstract
This paper deals with the quantitative estimates for the difference of operators having the same basis functions. The results essentially improve the earlier known results. In the end, some applications for the differences of Szász-Mirakyan operators with its different variants are presented.
1 DIFFERENCES OF OPERATORS
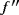 , some results have been estimated.7, 8 Let
, some results have been estimated.7, 8 Let
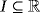 be an interval and
be an interval and
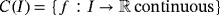 , with C (I ) containing the polynomials and CB(I ) the space of all f ∈ C(I ) such that
, with C (I ) containing the polynomials and CB(I ) the space of all f ∈ C(I ) such that
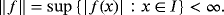
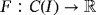 be a positive linear functional such that F (e0) = 1. Denote
be a positive linear functional such that F (e0) = 1. Denote
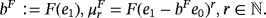
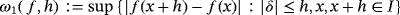
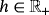 . For the functional F, the following basic results were obtained.4
. For the functional F, the following basic results were obtained.4
Lemma 1. (See the work of Acu and Raşa[4])Let f ∈ C(I ) with
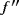 ∈ CB(I ). Then,
∈ CB(I ). Then,
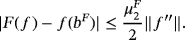
Lemma 2. (See the work of Acu and Raşa[4])Let f ∈ C(I ) with f (iv) ∈ CB(I). Then,
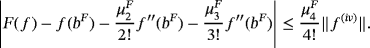
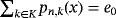 . Consider the positive linear functionals
. Consider the positive linear functionals
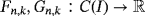 such that Fn,k(e0) = Gn,k(e0) = 1 and denote D(I ) as the set of all f ∈ C(I ) for which
such that Fn,k(e0) = Gn,k(e0) = 1 and denote D(I ) as the set of all f ∈ C(I ) for which
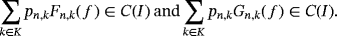
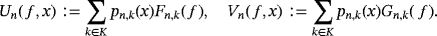
Theorem 1.If f ∈ D(I ) with
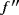 ∈ CB(I), then
∈ CB(I), then
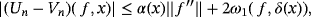
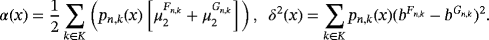
Remark 1.We may remark here that in theorem 3 in the work of Acu and Raşa4, the authors considered
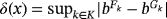 , which is true in general only when summation index K is finite, ie,
, which is true in general only when summation index K is finite, ie,
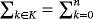 , but in case
, but in case
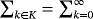 , the value of δ(x) becomes infinite. Second, for λ > 0, we know ω( f,λδ) ≤ (λ + 1)ω( f,δ). Thus, the improved conclusion of theorem 3 of Acu and Raşa4 must be considered as the following theorem.
, the value of δ(x) becomes infinite. Second, for λ > 0, we know ω( f,λδ) ≤ (λ + 1)ω( f,δ). Thus, the improved conclusion of theorem 3 of Acu and Raşa4 must be considered as the following theorem.
Theorem 2.If f ∈ D(I ) with
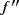 ∈ CB(I), then
∈ CB(I), then
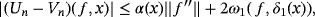
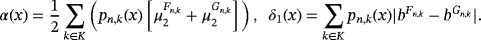
Corollary 1.If f ∈ D(I ) with
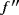 ∈ CB(I ) and both the operators Un and Vn preserve linear functions, then we have
∈ CB(I ) and both the operators Un and Vn preserve linear functions, then we have
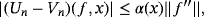
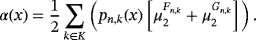
Theorem 3.If f ∈ D(I ) with
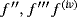 ∈ CB(I ), then for each x ∈ I, we have
∈ CB(I ), then for each x ∈ I, we have
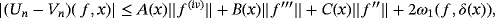
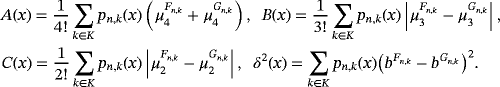
2 SOME APPLICATIONS
In this section, we provide the applications of Theorem 1 and estimate the quantitative difference estimates between Szász-Mirakyan operators and its variants.
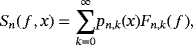 (1)
(1)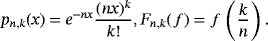
Lemma 3.The following recurrence relation holds for moments
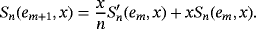
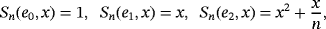
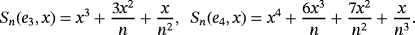
Remark 3.We have
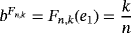
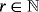 , we have
, we have
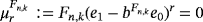
2.1 Difference with Szász-Mirakyan-Baskakov operators
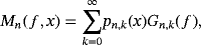 (2)
(2)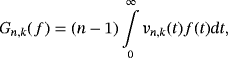
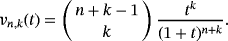
Remark 4.By definition of beta function, we have
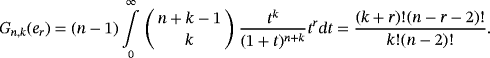

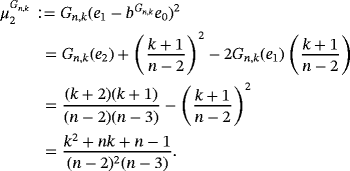
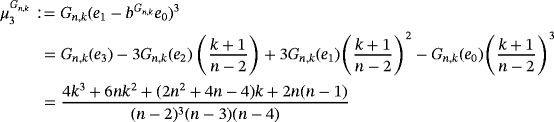
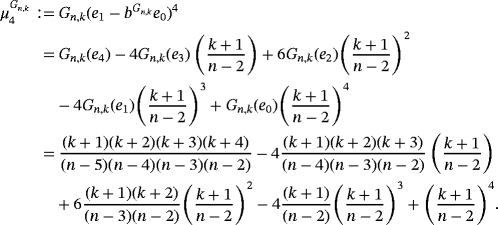
Below, we present the quantitative estimate for the difference of Szász-Mirakyan-Baskakov and Szász-Mirakyan operators.
Proposition 1.Let f (s) ∈ CB[0,∞),s ∈ {0,1,2} and x ∈ [0,∞). Then, for
 , we have
, we have
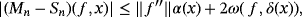
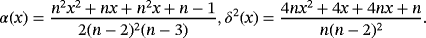
Proof.Using Remarks 3 and 4 and Lemma 3, we have
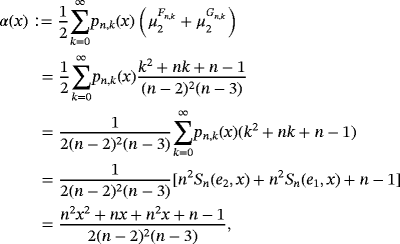
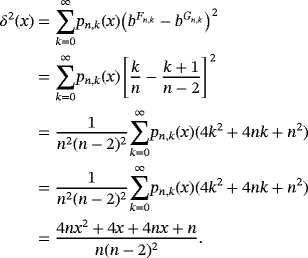
Proposition 2.Let f (s) ∈ CB[0,∞),s ∈ {0,1,2}, and x ∈ [0,∞). Then, for
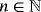 , we have
, we have
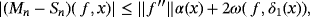
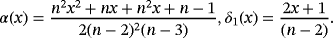
Proposition 3.Let f (s) ∈ CB[0,∞),s ∈ {0,1,2,3,4}. Then for each x ∈ [0,∞), we have
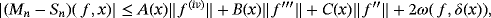
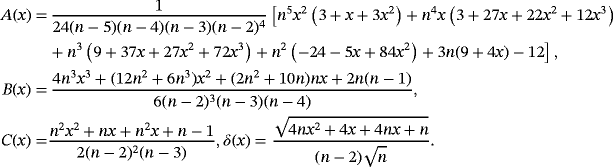
2.2 Difference with Pǎltǎnea operators
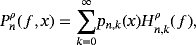 (3)
(3)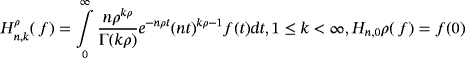
Remark 5.By definition of gamma function, we have
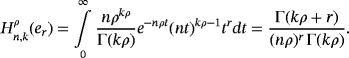
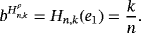
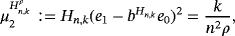
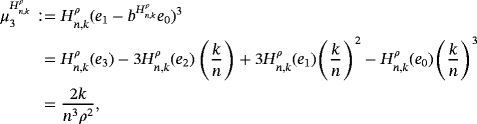
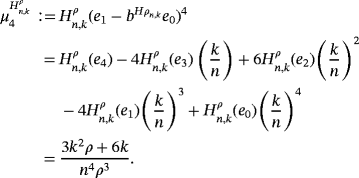
We present below the quantitative estimates for the difference of Pǎltǎnea and Szász-Mirakyan operators.
Proposition 4.Let f (s) ∈ CB[0,∞),s ∈ {0,1,2}, and x ∈ [0,∞). Then for
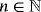 , we have
, we have
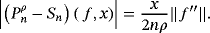
Proof.As both the operators here preserve constant and linear functions, using Corollary 1 and applying Lemma 3 and Remarks 3 and 5, we have
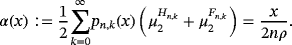
Proposition 5.Let f (s) ∈ CB[0,∞),s ∈ {0,1,2,3,4}. Then for each x ∈ [0,∞), we have
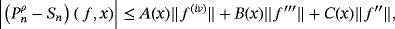
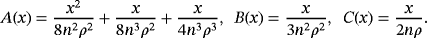
2.3 Difference with Szász-Mirakyan-Kantorovich operators
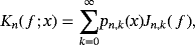 (4)
(4)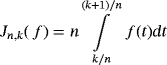
Remark 6.By simple computation, we have
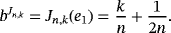
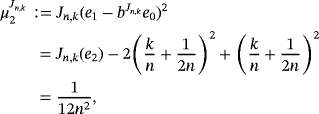
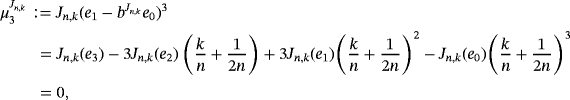
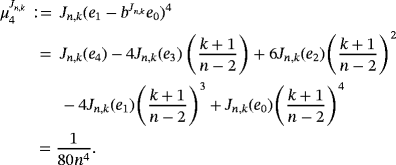
Below, we present the quantitative estimate for the difference of Szász-Mirakyan-Kantorovich and Szász-Mirakyan operators.
Proposition 6.Let f (s) ∈ CB[0,∞),s ∈ {0,1,2} and x ∈ [0,∞), then for
 , we have
, we have
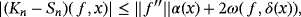
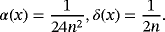
Proof.Using Remark 3, Remark 6 and Lemma 3, we have
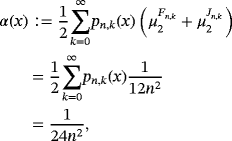
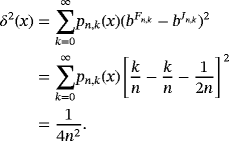
Proposition 7.Let f (s) ∈ CB[0,∞),s ∈ {0,1,2,3,4}, then for each x ∈ [0,∞), we have
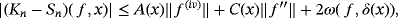
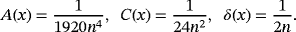
2.4 Difference with Szász-Mirakyan-Durrmeyer operators
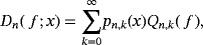 (5)
(5)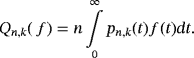
Remark 7.By simple computation, we have
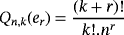
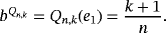
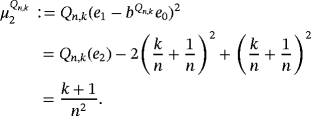
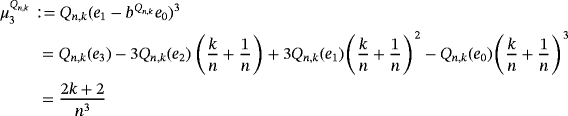
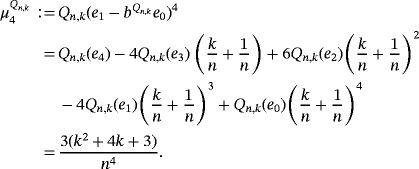
We present below the quantitative estimates for difference of Szász-Mirakyan-Durrmeyer and Szász-Mirakyan operators.
Proposition 8.Let f (s) ∈ CB[0,∞),s ∈ {0,1,2}, and x ∈ [0,∞). Then for
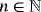 , we have
, we have
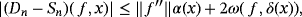
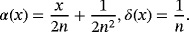
Proof.Using Remarks 3 and 7 and Lemma 3, we have
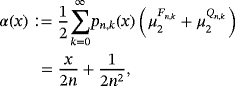
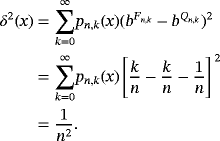
Proposition 9.Let f (s) ∈ CB[0,∞),s ∈ {0,1,2,3,4}. Then for each x ∈ [0,∞), we have
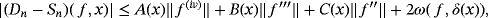
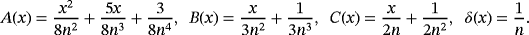
ACKNOWLEDGEMENT
The author would like to thank the referees for their valuable comments, leading to overall improvements of the paper.
Biography

Vijay Gupta PhD, is a professor at the Department of Mathematics, Netaji Subhas University of Technology (formerly, Netaji Subhas Institute of Technology), New Delhi, India. He received the PhD degree from the University of Roorkee (currently Indian Institute of Technology, Roorkee, India. His area of research is approximation theory especially on linear positive operators. He is the author of several books and book chapters, and he has over 300 research papers to his credit. He visited many universities globally on academic invitations. His present h-index is 36 (as per Google Scholar records).



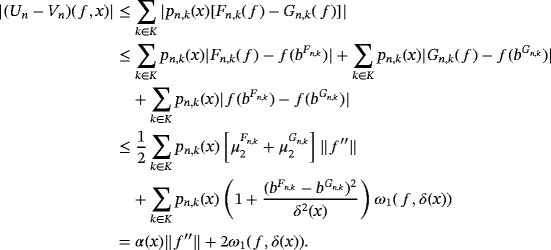
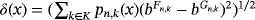 .
.

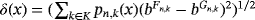 , the theorem follows.
, the theorem follows.
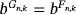 . Thus, the above theorem may be utilized for a wide range of operators.
. Thus, the above theorem may be utilized for a wide range of operators.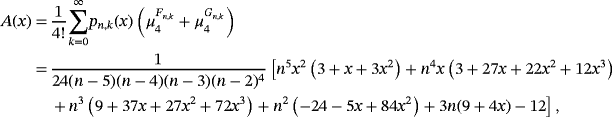
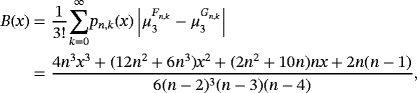
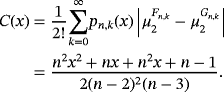
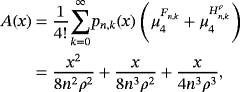
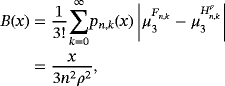
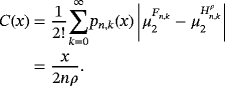
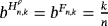 , we get δ(x) = 0; thus, the proposition follows from Theorem
, we get δ(x) = 0; thus, the proposition follows from Theorem