Numerical modeling of heat and mass transfer in the human eye under millimeter wave exposure
Abstract
Human exposure to millimeter wave (MMW) radiation is expected to increase in the next several years. In this work, we present a thermal model of the human eye under MMW illumination. The model takes into account the fluid dynamics of the aqueous humor and predicts a frequency-dependent reversal of its flow that also depends on the incident power density. The calculated maximum fluid velocity in the anterior chamber and the temperature rise at the corneal apex are reported for frequencies from 40 to 100 GHz and different values of incident power density. Bioelectromagnetics 34:291–299, 2013. © 2012 Wiley Periodicals, Inc.
INTRODUCTION
Technological developments in recent years have resulted in an increased interest in telecommunication applications in the millimeter wave (MMW) area of the electromagnetic spectrum [Xiao et al., 2008]. The formation of the Wireless Gigabit Alliance (WiGig) and the publication of its first specification whitepaper [WiGig, 2010] have given a boost to the exploitation of the 60 GHz band for indoor wireless communications. It can be expected that transmissions in this band will become ubiquitous in the future.
A decade ago, Ryan et al. [2000] reviewed the safety issues of surface heating that underlie the use of MMW radiation. Studies have focused mainly on the skin and the eyes because of the shallow penetration of radiation at this wavelength. Elder [2003] reviewed the literature for ocular effects, and other studies reported acute biological effects in the eye [Chalfin et al., 2002; Kojima et al., 2009]. However, modeling of ocular exposure has not attracted the same research interest as the skin, for which several numerical models [Walters et al., 2000; Alekseev and Ziskin, 2009; Kanezaki et al., 2010], including some highly detailed ones [Feldman et al., 2009; Shafirstein and Moros, 2011], have been constructed to study interactions with MMW radiation. A notable effort came from Foster et al. [2003], who applied a 1D thermal model to the experimental data of Chalfin et al. [2002], in order to investigate the MMW-induced damage to the primate cornea.
Several new numerical models of heat transfer in the human eye have been published that allow for the evaluation of the temperature distribution resulting from heat generation distributed in the eye tissues [Ng and Ooi, 2007; Karampatzakis and Samaras, 2010; Ooi and Ng, 2011].
In the present work, we report on thermal effects that can take place in the human eye under exposure to MMW radiation. Similar results have been reported for the rabbit eye [Papaioannou and Samaras, 2011]. However, in the latter publication, the numerical model used was a simplified one (not anatomically realistic) and consisted of only the cornea and anterior chamber that is, the frontal parts of the eye.
MATERIALS AND METHODS
Model Description
In order to study the effects of exposure to MMW radiation, the 3D model developed by Karampatzakis and Samaras [2010] was used. The model (Fig. 1) comprises six different parts (subdomains) representing anatomical structures of the eye, namely, the cornea, anterior chamber, iris, lens, vitreous humor, and sclera. The geometric properties of the model closely follow those of previous studies [Scott, 1988; Ooi et al., 2008]. The length of the pupillary axis is 25.2 mm and the length of the vertical axis is 24 mm. For the structures that are of particular interest in this study, the cornea has an average thickness of 0.57 mm, in agreement with previous modeling [Canning et al., 2002] and experimental [Liu and Pflugfelder, 2000; Jonuscheit and Doughty, 2009] studies. The anterior chamber, where the aqueous humor (AH) flows, has a volume of 232 µL, which is in the upper range of values [Rabsilber et al., 2006]. The thin layers of the choroid and retina are not modeled separately; they share the properties of the sclera. Moreover, the posterior chamber, which is a small area between the lens and the iris, is neglected for simplicity and due to computational limitations. The inflow of the AH through the pupil and its drainage via Schlemm's canal is also ignored in the current work. The thermal properties of all biological materials (which are considered homogenous and isotropic) are presented in Table 1.
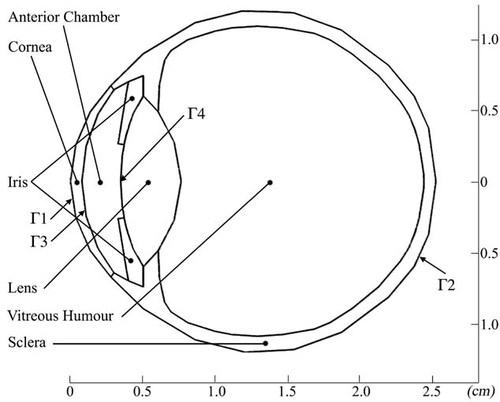
Projection of the 3D model. The six different subdomains are outlined, as well as the boundary conditions: 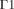 on the frontal corneal surface,
on the frontal corneal surface, 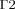 on the sclera, and
on the sclera, and 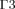 and
and  on the frontal and back surfaces of the anterior chamber, respectively.
on the frontal and back surfaces of the anterior chamber, respectively.
| Material | Thermal conductivity (W/m/°C), k | Mass density (kg/m), ρ | Specific heat (J/kg/°C), C | Blood perfusion power equivalent (W/m/°C), B | Basal metabolic heat generation (W/m), A |
|---|---|---|---|---|---|
| Cornea | 0.58 | 1050 | 4178 | – | – |
| Anterior chamber | 0.58 | 996 | 3997 | – | – |
| Iris | 0.52 | 1050 | 3600 | 35000 | 10000 |
| Lens | 0.4 | 1000 | 3000 | – | – |
| Vitreous humor | 0.603 | 1100 | 4178 | – | – |
| Sclera | 0.58 | 1050 | 3800 | 8000 | 22000 |
- * For original references see Karampatzakis and Samaras [2010].
Mathematical Formulation
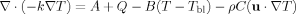 (1)
(1)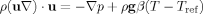 (2)
(2)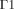 in Fig. 1) and is given by:
in Fig. 1) and is given by:
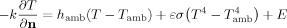 (3)
(3)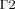 in Fig. 1); it assumes the eye to be embedded in a homogenous region with constant blood temperature (Tbl), and is given by:
in Fig. 1); it assumes the eye to be embedded in a homogenous region with constant blood temperature (Tbl), and is given by:
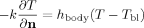 (4)
(4)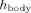 is the heat transfer coefficient between the eye and the surrounding tissues. The values of the boundary equation parameters are shown in Table 2.
is the heat transfer coefficient between the eye and the surrounding tissues. The values of the boundary equation parameters are shown in Table 2.| Parameter | Description | Value |
|---|---|---|
| Tbl | Blood temperature, °C | 37 |
| Tamb | Ambient temperature, °C | 23 |
| hbody | Body heat transfer coefficient, Wm−2 °C−1 | 65 |
| hamb | Ambient heat transfer coefficient, Wm−2 °C−1 | 10 |
| E | Evaporation rate, Wm−2 | 40 |
| σ | Stefan-Boltzmann constant, Wm−2 K−4 | 5.67 × 10−8 |
| ε | Emissivity of cornea surface | 0.975 |
- * For original references see Karampatzakis and Samaras [2010].
Equations (3) and (4) define the boundary conditions for Equation (1). In order to set the boundaries for solving Equation (2), the anterior and posterior surfaces of the anterior chamber (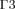 and
and 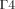 , respectively, in Fig. 1) are considered as impermeable and incompressible walls and set to a no-slip condition that is the AH has zero velocity relative to these boundaries.
, respectively, in Fig. 1) are considered as impermeable and incompressible walls and set to a no-slip condition that is the AH has zero velocity relative to these boundaries.
The electromagnetic absorption of MMW radiation was modeled as in Papaioannou and Samaras [2011] that is, an exponential decay of the electric field was assumed inside the tissues [Gandhi and Riazi, 1986; Alekseev and Ziskin, 2009]. Energy was assumed to be dissipated and turned into heat only within the cornea, since for the frequencies of interest the penetration depth is comparable to its thickness (Table 3). The width of the incident beam was assumed wide enough to include the whole cornea. The propagation direction was parallel to the pupillary axis of the eye. The waves were refracted at the air–cornea interface, traveling normal to it after having entered in the cornea. As explained and verified numerically with the use of the finite-difference time-domain technique [Papaioannou and Samaras, 2011], this approach gives a very good approximation.
| Frequency (GHz) | Conductivity (S/m) | Relative permittivity | Penetration depth (mm) |
|---|---|---|---|
| 40 | 40.76 | 16.41 | 0.590 |
| 60 | 48.92 | 11.65 | 0.423 |
| 80 | 53.77 | 9.32 | 0.347 |
| 100 | 57.04 | 7.99 | 0.302 |
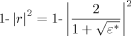 (5)
(5)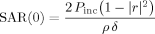 (6)
(6)Numerical Technique
The geometry was created and the coupled problem was solved using Comsol Multiphysics FEM software (Version 3.5a, COMSOL, Stockholm, Sweden). The mesh consists of about 66000 tetrahedral elements, which are quadratic in the case of the heat transfer problem and linear for the fluid dynamics equations. A direct algorithm (SParse Object Oriented Linear Equations Solver—SPOOLES) is used for solving the equation system with a convergence criterion at a relative tolerance of 10−6.
NUMERICAL RESULTS
In our previous study, we showed that consideration of the AH flow leads to a non-symmetrical temperature distribution in the eye [Karampatzakis and Samaras, 2010]. It is also known that the velocity field of the flow is strongly affected by temperature gradients in the anterior parts of the eye that is between the posterior surface of the cornea (endothelium) and the anterior surface of the lens/iris.
The model was tested for exposure to 40, 60, 80, and 100 GHz MMW over a range of power density values. The temperature at the cornea apex (Tcornea), the magnitude of maximum velocity of the AH (umax), and the flow direction inside the anterior chamber are included in Table 4. Counter-clockwise (CCW) flow that rises near the back of the anterior chamber and falls toward the front is normal [Canning et al., 2002], while clockwise (CW) flow is in the reverse direction.
| Pinc (Wm−2) | 40 GHz | 60 GHz | 80 GHz | 100 GHz | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Tcornea (°C) | umax (10−4 m s−1) | Direction | Tcornea (°C) | umax (10−4 m s−1) | Direction | Tcornea (°C) | umax (10−4 m s−1) | Direction | Tcornea (°C) | umax (10−4 m s−1) | Direction | |
| 100 | 34.7 | 2.95 | CCW | 34.8 | 2.93 | CCW | 34.8 | 2.91 | CCW | 34.8 | 2.90 | CCW |
| 200 | 35.1 | 2.49 | CCW | 35.2 | 2.44 | CCW | 35.2 | 2.39 | CCW | 35.2 | 2.36 | CCW |
| 300 | 35.5 | 1.97 | CCW | 35.6 | 1.87 | CCW | 35.6 | 1.80 | CCW | 35.6 | 1.75 | CCW |
| 400 | 35.9 | 1.38 | CCW | 36.0 | 1.24 | CCW | 36.1 | 1.14 | CCW | 36.1 | 1.07 | CCW |
| 500 | 36.4 | 0.74 | CCW | 36.4 | 0.56 | CCW | 36.5 | 0.44 | CCW | 36.5 | 0.35 | CCW |
| 600 | 36.8 | 0.23 | CCW | 36.8 | 0.34 | CW | 37.0 | 0.51 | CW | 37.0 | 0.64 | CW |
| 700 | 37.2 | 0.77 | CW | 37.3 | 1.04 | CW | 37.4 | 1.23 | CW | 37.5 | 1.37 | CW |
| 800 | 37.6 | 1.43 | CW | 37.8 | 1.70 | CW | 37.9 | 1.89 | CW | 37.9 | 2.03 | CW |
| 900 | 38.0 | 2.01 | CW | 38.2 | 2.29 | CW | 38.3 | 2.48 | CW | 38.3 | 2.61 | CW |
| 1000 | 38.4 | 2.52 | CW | 38.6 | 2.80 | CW | 38.7 | 2.99 | CW | 38.8 | 3.12 | CW |
| 1100 | 38.8 | 2.98 | CW | 39.0 | 3.25 | CW | 39.1 | 3.44 | CW | 39.2 | 3.57 | CW |
| 1200 | 39.2 | 3.38 | CW | 39.4 | 3.65 | CW | 39.5 | 3.84 | CW | 39.6 | 3.97 | CW |
| 1300 | 39.6 | 3.74 | CW | 39.8 | 4.02 | CW | 39.9 | 4.20 | CW | 40.0 | 4.33 | CW |
| 1400 | 40.0 | 4.07 | CW | 40.2 | 4.35 | CW | 40.3 | 4.53 | CW | 40.4 | 4.67 | CW |
| 1500 | 40.3 | 4.38 | CW | 40.6 | 4.65 | CW | 40.7 | 4.84 | CW | 40.8 | 4.97 | CW |
| 1600 | 40.7 | 4.65 | CW | 40.9 | 4.93 | CW | 41.1 | 5.12 | CW | 41.2 | 5.25 | CW |
Effect of Incident Power Density
Figure 2 shows the temperature distributions in the mid-sagittal plane for incident power densities of 0, 400, 800, and 1600 Wm−2 at 40 GHz. It is clear that in the unexposed model warmer AH masses move toward the top of the anterior chamber, leaving the coolest area inferior to the pupillary axis. Previous studies have neglected the AH flow, thus predicted a symmetrical distribution [Ng and Ooi, 2007; Sharon et al., 2008]. In the case of incident power densities of 800 Wm−2 and higher, the direction of the AH flow is reversed and forms a CW rotational flow, mainly due to the change in the temperature gradient profile between the two surfaces of the anterior chamber. In the unexposed model, the temperature in the posterior surface of the cornea is lower than the temperature of the lens and the iris, however, this situation is inverted with the absorption of MMW radiation in the cornea. Table 4 shows that in the case of 40 GHz radiation, and for power densities of about 700 Wm−2 and above, the corneal temperature becomes higher than the blood temperature; the temperature of the sclera can be assumed to remain the same, that is, that of blood. The inversion of temperature gradients along the pupillary axis is also shown in Figure 3. The temperature at the cornea apex increases in an almost linear fashion with the incident power density at a rate of about 0.4 °C/100 Wm−2. However, the time needed to reach a steady state depends on the frequency, power density, and boundary conditions, and is on the order of 1/2 to 2 min, which is in agreement with the experimental measurements in a rabbit eye by Koike et al. [2011].
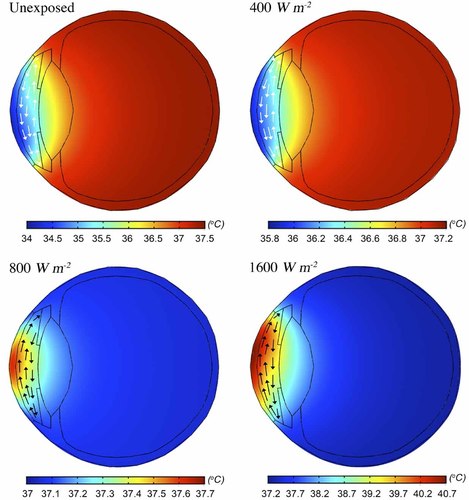
Temperature distribution on the mid-sagittal plane for exposure at 40 GHz and power densities of 0 (unexposed), 400, 800, and 1600 Wm−2. Aqueous humor flow is depicted by the arrows (not to scale); white arrows denote a counter-clockwise direction and black a clockwise one.

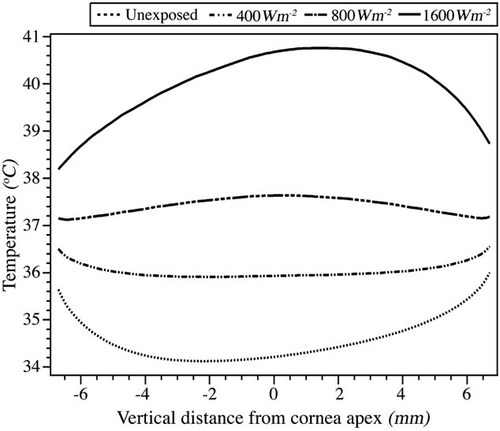
Temperature distribution plots along the pupillary axis for exposure at 40 GHz and power densities of 0 (unexposed), 400, 800, 1200, and 1600 Wm−2. The temperature distribution for the unexposed model is drawn with a dashed line, while the one for 800 Wm−2, where reversal of the flow has already occurred, with a bold one. The temperature distributions for the rest of the power density values are drawn with regular solid lines.
For the unexposed model, we have shown that when the AH flow is considered, the coolest area of the outer corneal surface is inferior to its geometric center by 2 mm, and the temperature variation on the corneal surface is 1.7 °C [Karampatzakis and Samaras, 2010], in excellent agreement with ocular thermographs [Morgan et al., 1993; Tan et al., 2009]. The temperature variation along the vertical midline of the corneal surface for 40 GHz and various power densities is given in Figure 4. The AH flow cools the lower part of the corneal surface for power densities that significantly heat the central region. For example, the hottest spot on the cornea (40.8 °C) for the eye exposed to 40 GHz and 1600 Wm−2 is 1.4 mm above the geometric center. Furthermore, as power densities increase, the hottest spot appears to be moving away from the geometric center of the cornea toward the upper limbus as a result of the increasing velocity of the AH rotational flow. Under the above irradiation conditions (1600 Wm−2 at 40 GHz), a reversed (CW) flow profile with a maximum velocity of 0.465 mm/s is predicted. For the interest of comparison, it is mentioned that in the unexposed model a normal (CCW) flow profile with a maximum velocity of 0.336 mm/s was calculated [Karampatzakis and Samaras, 2010].
Temperature variation along the vertical midline of the anterior corneal surface for exposure at 40 GHz and power densities of 0 (unexposed), 400, 800, and 1600 Wm−2. The starting point of the abscissa is the lower limbus.
Effect of Frequency
It is well known that penetration depth is inversely proportional to the frequency of radiation. Taking into account the frequency-dependent transmission coefficients, it can be seen that by increasing the frequency of the incident radiation, (slightly) larger increases in the temperature of the corneal apex are observed, irrespective of the flow direction (Fig. 5; Table 4). This is in agreement with the results of Foster et al. [1978], who predicted larger temperature increases in tissue irradiated at higher frequencies.
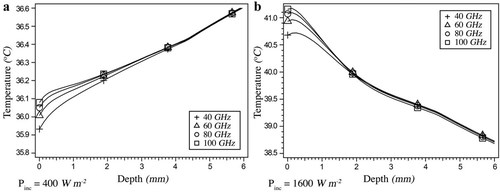
Temperature distribution along the outermost 6 mm of the pupillary axis for exposure at 40, 60, 80, and 100 GHz and power densities of (a) 400 Wm−2 and (b) 1600 Wm−2. In the latter case, AH flow reversal has occurred. See Figure 3 for the temperature distribution of an unexposed eye for visual comparison.
As depicted in Figure 6, the power density threshold for reversing the AH flow is expected to be higher for lower frequencies. It should be noted that the aim of the current study was not to provide a definite value for the incident power density that would initiate a reversal in AH flow, but to demonstrate the possibility of its occurrence. This is why no parametric study or uncertainty budget with respect to the numerical technique was performed.
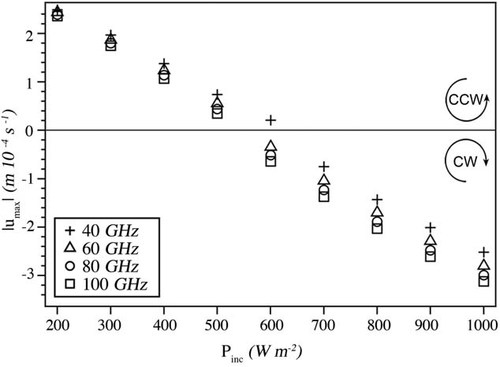
Maximum AH flow velocities and direction for exposure at 40, 60, 80, and 100 GHz and power densities ranging from 200 to 1000 Wm−2. The threshold for flow reversal is marked by the horizontal line.
DISCUSSION
The AH acts as a blood surrogate for the eye. It provides nutrition, removes excretory products, transports neurotransmitters, and contributes to the regulation of the homeostasis of ocular tissues [Goel et al., 2010]. The AH is in constant motion inside the anterior chamber. Due to temperature gradients that affect its density, for a standing subject the fluid appears to be rising (i.e., opposing gravity) near the back of the anterior chamber and falling toward the front, with little or no lateral movement [Canning et al., 2002]. In the rabbit eye, a temperature difference between the front and back surfaces of the anterior chamber as small as 0.02 °C was sufficient to induce circulation of the AH [Kumar et al., 2006]. The AH also permits inflammatory cells and mediators to circulate in the eye in pathological conditions, as well as drugs to be distributed to different ocular structures [Goel et al., 2010]. Therefore, its rotational flow has greater importance when particulate matter is considered inside the anterior chamber, for example, as a result of eye trauma or disease. Red or white blood cells may be present or pigment particles may have been detached from the iris. Canning et al. [2002] performed an analysis showing that thermally driven flow can provide a powerful mechanism for the distribution of particles within the anterior chamber, competing with gravity-induced settling, to determine the final distribution of particulate matter for patients with hyphema or Krukenberg's spindle.
The reversal of flow in the anterior chamber of the rabbit eye under MMW illumination was demonstrated experimentally by Koike et al. [2011], who reported a threshold at 500 Wm−2 incident power density at 75.4 GHz, which is in excellent agreement with the values predicted here for the human eye at 80 GHz (Table 4; Fig. 6). Koike et al. [2011] reported velocities of the AH about one order of magnitude greater than the ones calculated in the present work. They measured a velocity of about 4 mm/s at 75.4 GHz and 1500 Wm−2, compared to our estimates of 0.48 mm/s at 80 GHz and 1500 Wm−2 (Table 4). The experimental velocity values in the rabbit eye are closer to the theoretical ones obtained by Canning et al. [2002], who correlated the maximum velocity with the temperature difference between the frontal and back surfaces of the anterior chamber. In the present study, the predicted temperature rise for the human eye was lower than the temperature rise computed for the rabbit eye, consistent with a lower velocity and different threshold for flow reversal between the rabbit and the human eyes. Finally, it should be noted that the experimental results for the rabbit eye [Koike et al., 2011] were obtained with the use of a dielectric lens antenna [Kojima et al., 2009], which results in a non-uniform SAR distribution and a higher corneal temperature rise compared with plane wave exposure with the same average incident power [Sasaki et al., 2011].
The effect of non-uniformity in radiation absorption and the resulting limitations have been discussed by Foster et al. [2003], notably the effects on several anatomical structures comparable in dimensions to the radiation wavelength, such as the eyelids and eyelashes.
Eye closure, both voluntary and involuntary, i.e., the blinking reflex, was ignored in the present study. Schwartz [1964] showed that closing the eyelids tends to eliminate the temperature gradient between the cornea and the posterior chamber of the eye because of the boundary conditions imposed at the frontal surface of the cornea. Consequently, prolonged eyelid closure is a mechanism that would change the flow pattern inside the eye of a standing person. In terms of the physiological impact of eye blinking, continuous evaporation was assumed in the model; that is the tear film deposition by blinking was not accounted for. Therefore, spontaneous eye blinking is unlike to contribute to the effects modeled except to delay their appearance. On the contrary, intentional eyelid closure due to cornea irritation (e.g., upon sensing a high temperature) might prevent flow reversal due to the thickness of the eyelid skin (42% thicker than the cornea [Hwang et al., 2006]), which would absorb most of the incident MMW radiation.
CONCLUSIONS
We have shown that it is possible to induce a reversal of the AH flow inside the anterior chamber of the eye if the appropriate incident power density is used. This is a biophysical effect with unknown potential health implications, if any. The threshold incident power density for the induction of AH flow reversal may exceed the levels occurring in practical applications of MMW fields. However, current exposure guidelines allow for a relaxation of the basic limit up to 20-fold when the averaging area is reduced from 20 to 1 cm2 [ICNIRP, 1998]. This means that the occupational limit becomes 1000 Wm−2, for which flow reversal could be observed in the event that the eyelid remains open. However, intentional eyelid closure upon heat sensing could avert the effect.
Acknowledgements
The authors wish to thank the anonymous reviewers for their valuable comments.




