Generic Axion Maxwell Equations: Path Integral Approach
Abstract
The low energy interactions between axions and electromagnetic fields that arise in models with heavy dyons charged under a spontaneously broken global axial U(1) symmetry are derived using the path integral approach. Hence, generic axion-Maxwell equations relevant for experimental searches are obtained. It is found that the structure of the axion Maxwell equations can be significantly different compared to what is normally assumed in the literature, as the derived equations feature new axion-dependent terms including CP-violating ones. The new terms can reconcile the Peccei–Quinn solution to the strong CP problem with astrophysical axion hints, as well as give unique signatures in light-shining-through-wall and haloscope experiments. Moreover, via the latter signatures, these experiments can indirectly probe the existence of heavy dyons.
1 Introduction
Note that by definition, background fields and satisfy free Maxwell equations. It is essential that these fields are treated as external. Indeed, close to the sources, which have to be treated as point-like in a classical theory with both electric and magnetic charges,[19, 20] the latter fields diverge and the classical weak field approximation used in Equations (5)–(8) is no longer valid.
While in ref. [10] we focused primarily on explaining the loophole in the previous theoretical works on the axion-photon coupling and investigated the new electromagnetic couplings of axions in the effective field theory (EFT) approach, in this article we would like to give a detailed derivation of the general axion Maxwell equations (Equations (5)–(8)) in the path integral framework. The path integral approach is very instructive when dealing with the quantum field theory (QFT) that includes both electric and magnetic charges: indeed, the only exhaustive proof of the Lorentz-invariance of such QFT was obtained in the path integral framework.[20, 21] Moreover, in the path integral approach, it is easier to understand how the peculiarities of the corresponding classical theory, such as Dirac vetos, originate and why they do not signal any inconsistencies.
This article is structured as follows: In Section 2, we review the path integral formulation of the QFT describing the interactions between electric and magnetic charges as well as discuss the general distinctive features of this QFT; in Section 3, we introduce the dyon-philic axion models in the path integral approach, transform the integral over the heavy dyon field into the integral over the dyon proper time parameter, and calculate the effective low energy Lagrangian that describes the interactions of dyon-philic axions with the electromagnetic field by performing an exact non-perturbative calculation; in Section 4, we derive the general axion Maxwell equations (Equations (5)–(8)) and briefly discuss their experimental implications; finally, in Section 5, we conclude.
2 Quantum Field Theory with Magnetic Charges and Its Path Integral Formulation
There exist several equivalent formulations of the QFT with magnetic charges, see, for example, refs. [22, 23] and the exhaustive review.[24] All these formulations necessarily share a common feature that drastically distinguishes them from the theory of Quantum Electrodynamics (QED). This feature is non-locality:[25] Any QFT with both electric () and magnetic () charges is actually a theory of the interaction of two-particle irreducible states.[26-28] Indeed, an asymptotic state of two particles for which constitutes an entangled “pairwise” state. Each such state is characterized by a pairwise helicity variable, which corresponds to the asymptotically non-vanishing angular momentum of the electromagnetic field. Note that the Dirac–Schwinger–Zwanziger (DSZ) quantization condition follows naturally from the quantization of this angular momentum. Asymptotic irreducible two-particle states obviously violate the cluster decomposition principle, which is another way to understand why any QFT with magnetic charges is fundamentally different from QED, for which the cluster decomposition is a well-established property (see e.g., ref. [29], pp. 252–254). While one can introduce magnetic monopoles in QED as external sources, to study the creation or annihilation of real and virtual monopoles, one has to work in a substantially different framework.
We explained why the classical equations of the Zwanziger theory are -independent. It remains to be shown that the full quantum theory shares this property. The respective proof was given in refs. [20, 21]. We will briefly return to their arguments after presenting the path integral formulation of the theory. Before this, let us note that at each finite order of the formal perturbation theory applied to the Zwanziger theory, the resulting approximation is not -independent and is therefore ill-defined. This means that the theory is essentially non-perturbative. A very important point is that this non-perturbativity is associated to the -dependence and thus to the non-locality feature described earlier, but not necessarily to the presence of a large expansion parameter. Indeed, the effective expansion parameter can be made small for some particular processes,[33-35] however this does not justify applying perturbation theory: the latter is still ill-defined and can give wrong results as explained in ref. [36].
The known proof of the Lorentz-invariance of the Zwanziger QFT[20, 21] relies essentially on the path integral representation of the theory. Let us briefly explain the main ideas behind this proof. First of all, to establish the Lorentz-invariance of the theory, it is sufficient to show the Lorentz-invariance of the generating functional (Equation (18)). Second, it is easy to notice that the Lorentz-invariance in this case is equivalent to -independence. Finally and most importantly, one has to remember that the functional integrals over the charged matter fields can be represented as series involving integrals over point-particle trajectories.[20, 41-43] It then turns out that the only -dependence remains in the interactions between particles (real or virtual) of a different electric–magnetic type and that the -dependent part basically counts the number of times the trajectory of one particle intersects some oriented -dependent three-surface associated to the trajectory of another particle, which is simply an integer but for some exceptional trajectories that form a measure zero subset and can therefore be omitted in the integral over all the trajectories. The part associated to the -dependent integer does not contribute to the generating functional after imposing the DSZ quantization condition on the charges of all the possible pairs of dyons, since in this case the -dependent contribution to the action is always equal to which obviously does not contribute to the path integral (Equation (18)).
Note that both in the classical case and in the full quantum relativistic case, the -independence crucially depends on the point-particle representation of charged matter, as opposed to the usual continuum approximation in field theory where the distribution of charged matter is continuous. In fact, the classical field theory of magnetic charges, that is, the theory where charges and currents are by definition continuously distributed in space, is always inconsistent, as the Jacobi identity for the gauge covariant derivatives is necessarily violated in this case.[19, 20] While the failure of the continuum approximation seems to be against the usual local-field-theoretic intuition , one has to remember that one of the key features of the QFT with magnetic charges is its non-locality. As -vector in the Zwanziger theory is responsible for capturing the non-locality, it is not surprising that the point-particle, as opposed to the continuous, distribution of charge is crucial for -independence of the gauge-invariant observables. Finally, let us note that the same feature of non-locality invalidates the conventional decoupling principle applied to the theories with both electric and magnetic charges: A given heavy charged particle cannot be fully integrated out at the energy scales below its mass since it contributes a non-local angular momentum to the electromagnetic field, which is felt by other particles even in the deep infrared (IR), compared with Equations (10) and (11). This means that even if all the magnetically charged particles are very heavy, and their effect on the low energy interactions is indirect, the low energy theory describing the interactions of light electrically charged particles is not given by a QED-like theory, but still by a theory the structure of which is similar to the QFT with magnetic charge. Simply put, in this case, we still need Zwanziger-like (or any equivalent) description of the electromagnetic field even at low energies.
3 Electromagnetic Interactions of Dyon-Philic Axions
3.1 Outline of the Model
Let us now consider the dyon-philic axion models[10, 13, 14] in the path integral framework of the previous section. In these models, similarly to the KSVZ axion model,[11, 12] one introduces at least one new heavy vector-like quark ψ charged under the global U(1)PQ symmetry, as well as the PQ complex scalar field Φ which gives mass to the new quark(s) in the phase where the U(1)PQ is spontaneously broken due to a non-zero vacuum expectation value . A new heavy quark can in general be charged under the electromagnetic U(1)EM subgroup of the gauge group of the Standard Model. Moreover, there is no reason to assume that it carries only an electric, but no magnetic charge, given that the existence of heavy magnetically charged particles is currently regarded as a necessity for obtaining a consistent quantum gravity theory.[16-18] According to the discussion of the previous section, to describe all the effects of magnetically charged particles, one has to work in the framework of the QFT with magnetic charges. In particular, we chose to work with a particular realization of the QFT with magnetic charges given by the Zwanziger formalism quantized via the path integral methods outlined in the previous section.
3.2 Proper Time Representation of the Heavy Fermion Path Integral
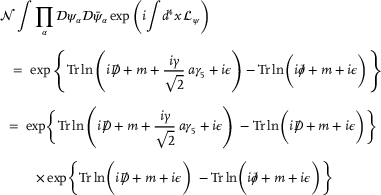 (23)
(23)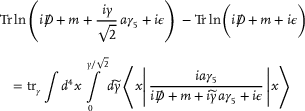 (24)
(24)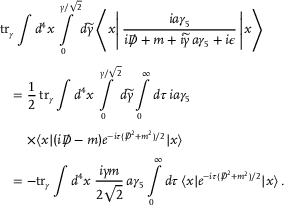 (25)
(25)3.3 Role of the Non-Local Terms
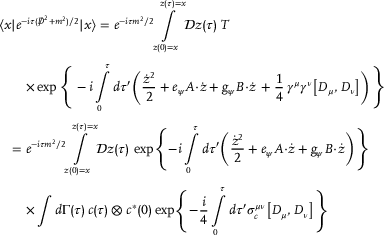 (26)
(26)Let us now show that the non-local terms from Equations (10) and (11), which arise whenever one rewrites in terms of physical electric and magnetic fields, contribute nothing more than an additional () term to the action (Equation (29)). Such additional term of course does not contribute to the dynamics of the system, since in Equation (26) and thus there is no change to the functional integrals in Equations (23) and (22).
3.4 Integration over the Heavy Fermion Intermediate State
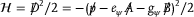 (38)
(38)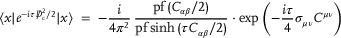 (39)
(39)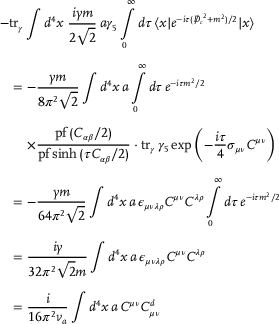 (40)
(40)4 Axion Maxwell Equations
4.1 Derivation of the Axion Maxwell Equations
It is important that the low energy approximation we used to derive the effective Lagrangian (Equation (44)) works only for sufficiently weak fields F. On the other hand, as we mentioned in the end of Section 2, the classical field theory featuring magnetic charges is inconsistent for continuous distribution of charges and currents due to the violation of the Jacobi identity for the gauge covariant derivatives. Therefore, the classical charges must be modeled as point-like, which means that the classical electromagnetic field F necessarily becomes large in the neighborhood of each of the charges. Thus, the only way to keep the classical weak field approximation consistent is to restrict the support of the axion-dependent terms in Equations (45) and (46) so that it excludes the short-distance neighborhoods of the charges. Note that such prescription is no more than a mathematical formality: The low energy experiments for which the classical Equations (45)–(47) are written probe only long-distance physics, anyway. Importantly, however, the latter prescription implies in Equations (45) and (46). As the terms featuring these derivatives are multiplied by another power of , we can safely omit them in our low energy approximation.
4.2 Implications of the Axion Maxwell Equations
The phenomenological consequences of Equations (61)–(64) were discussed in refs. [10, 47-51]. Here, we would like to review the main results, without going into details.
First, let us note that Equations (62) and (63) show that there can appear effective magnetic charges and currents in the presence of axions in external electromagnetic fields. This means that Faraday's law and the no-magnetic-monopoles law can be violated in a given experiment with external or field assuming there exists some cosmic abundance of axion-like particles. As these laws cannot be violated in the case where no magnetic monopoles exist,[52, 53] one can experimentally test the existence of heavy magnetic monopoles and dyons. Such indirect probe of heavy dyons would complement the numerous experiments searching for cosmic magnetic monopoles,[54] as it does not depend on the cosmic abundance of monopoles and dyons.
Second, note that due to the DSZ quantization condition applied to Equations (56)–(58), one expects . Indeed, the electric charge of the electron is small while its magnetic charge is zero, so substituting these charges into the DSZ quantization condition applied to the pair of particles — an electron and a given heavy dyon ψ — we see that () for every dyon. Then, the DSZ quantization condition applied to dyons can be solved as an equation for the electric charges of the dyons: (where , while is the CP-violating parameter), which assuming gives . Therefore, one can expect and thus , as mentioned previously. Because of this, the effective axion-induced magnetic current is expected to dominate over the effective axion-induced electric current in a given axion detection experiment, which significantly changes the response of the system to the axion dark matter signal compared to the normally considered case described by Equations (1)–(4). For instance, this means that in the case where the axion wavelength is much larger than the size of the detector, the dominant effect is given by the axion-induced electric field , as opposed to . This represents a clear distinction from the conventional case (cf. Equations (1)–(4)) where the dominant axion-induced field in the long-wavelength case is . In the case of resonant haloscope experiments, it turns out that the DC magnetic field normally used yields a system which is not sensitive to the dominant and couplings in the non-relativistic limit . On the contrary, applying DC electric field to a cavity resonator, one can achieve sensitivity to the latter two couplings. In general, the new couplings and provide a lot of unique signatures; the corresponding effects can be easily distinguished from the effects of the conventional coupling in a wide range of experiments.
Third, the hierarchy has important implications for the searches for the QCD axion, that is, the axion which solves the strong CP problem. In this case, the axion decay constant , , is fixed in terms of the axion mass , which means that the axion couplings (Equations (56)–(58)) can be plotted as functions of , with uncertainties given by the anomaly coefficients N, E, M, and D. The hierarchy of the couplings implies that at a given mass , the effects of the and couplings are much stronger compared to the effects of the conventional coupling. This means that our current experiments, if adapted to look for the new couplings, can be much more sensitive to the electromagnetic couplings of the QCD axion than previously thought. Moreover, it turns out that the coupling of the QCD axion can explain the anomalous TeV transparency of the Universe[55-57]—an issue which was hypothesized to be resolved by an axion-like particle with only the coupling in many investigations, but which could not be explained in the framework of conventional QCD axion models with only the coupling, since in the KSVZ and DFSZ models, the value of the coupling is too small in the relevant range of masses . Even more, the coupling, required to explain the anomalous TeV transparency, can also account for another astrophysical axion hint, which was derived from studying the cooling of horizontal branch stars in globular clusters.[58] Note that this latter hint cannot be explained within the KSVZ and DFSZ models assuming the mass range – the axion-photon coupling calculated in these models is too small.
Fourth, the coupling violates CP. Note that the conventional coupling is necessarily CP-conserving, since in general, QED preserves CP. In the QFT with dyons, however, there exists a possible source of CP violation associated to the charge spectrum of dyons of the theory. This means that the CP violation in the electromagnetic interactions of axions is a clear signature of the existence of heavy dyons. Moreover, such CP violation would imply that the spectrum of heavy dyons is CP-violating, that is, in Equation (58). Experimentally, one can probe the coupling in light-shining-through-wall experiments by varying the polarization of the incoming light,[10] as well as in haloscope experiments.[48, 59]
Finally, let us note that the axion Maxwell equations (Equations (61)–(64)) become trivial in the case of a constant and homogeneous axion field . This means that there is no Witten-effect induced interaction[60] between the axion and the currents of charged particles and in the model we consider. In particular, charged particles do not obtain extra charges proportional to θ from their interaction with the axion field. Contrary to the misconception which sometimes appears in the literature, the Witten-effect induced interactions of axions are not a general feature of axion electrodynamics.[61] The Witten-effect induced interactions arise only in particular ultraviolet models which feature an extra rotor (instanton) degree of freedom in the IR, see ref. [10] for a detailed discussion.
5 Summary
Using the path integral approach, we gave a detailed step-by-step derivation of the axion Maxwell equations in dyon-philic axion models, that is, in hadronic axion models where heavy PQ-charged quarks are allowed to carry magnetic charges. The form of the derived axion Maxwell equations (Equations (61)–(64)) fully agrees with the one derived by us in the EFT approach in a previous publication.[10] In particular, we confirmed that there can exist additional axion-photon couplings and along with the normally considered axion-photon coupling . As these new couplings change the structure of the axion Maxwell equations significantly, we predict unique signatures in haloscope and light-shining-through-wall experiments. In particular, the detection of the effective axion-induced magnetic charges or currents in a haloscope would represent an indirect evidence for the existence of magnetically charged matter. Moreover, the new electromagnetic couplings of axions can reconcile the Peccei–Quinn solution to the strong CP problem with astrophysical axion hints, such as the anomalous TeV transparency of the Universe and the anomalous energy loss of horizontal branch stars in globular clusters.
Through an example of a particular UV-complete dyon-philic axion model, the path integral approach allowed us to illustrate and explain in detail some peculiarities of the low energy description of QFTs with magnetic charges, namely the impossibility to fully integrate out heavy dyons and the ensuing continuity prescriptions for the fields in the IR. Also, by analyzing the electromagnetic interactions of axions in the dyon-philic axion models, we found that in these models, there are no Witten-effect induced interactions between axions and charged particles. Thus, we confirmed that the axion-photon couplings and the Witten-effect induced couplings need not coincide: an important fact discussed in detail in ref. [10].
Acknowledgements
A.S. was funded by the UK Research and Innovation grant MR/V024566/1. A.R. acknowledges support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany's Excellence Strategy - EXC 2121 Quantum Universe - 390833306. This work was partially funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation)—491245950.
Conflict of Interest
The authors declare no conflict of interest.
Appendix A: θ-Term in U(1) Gauge Theories
However, we are interested in studying the U(1) gauge theory in the presence of a magnetic monopole, which yields a completely different scenario: In this case, the topology of M has to be modified. Indeed, suppose there exists a static magnetic monopole at the origin of the spatial coordinates , and consider any sphere with the centre at . By definition of the monopole, the magnetic flux , which due to the identity means that there cannot exist a global projection of the principal connection A onto the sphere and therefore onto the base space M. The obstruction to the triviality of the principal bundle is described by the relevant characteristic class, which for the principal U(1)-bundle is the first Chern class valued in the second cohomology group of M with integer coefficients. Since the corresponding Chern form, that is, the invariant polynomial is simply , and , the magnetic flux is quantized: , , which of course yields the Dirac quantization condition for the charges. Now, we see exactly why the topology of M should be modified: The second cohomology group is always non-trivial in the presence of a magnetic charge, and therefore our space actually has a hole: .
Note that due to the hole in the base space M, it is meaningless to assign any value to F at : this point is simply excluded from our space. For example, within the U(1) gauge theory reviewed in the previous paragraphs, it does not make sense to write : The support of the distribution falls exactly into the hole invalidating the statement. Of course, one could choose a different, more complete theoretical framework, such as Dirac's classical relativistic theory of magnetic charges[19] or Zwanziger's (Schwinger's) quantum relativistic theory of magnetic charges,[22, 23] where no such holes arise; however, in the latter theories, one has to introduce the magnetic charges directly into the Lagrangian, as well as to modify the structure of the U(1) gauge theory significantly, as it was illustrated in Section 2 by the example of the Zwanziger theory. In ref. [10], we give a description of the Witten effect (as well as the Rubakov–Callan effect) within the Zwanziger theory.
In the end of this Appendix, let us analyze whether there could arise any non-trivial effects from the surface terms in the variation of the action (Equation (A3)). Although within the Euler–Lagrange method, we put the variations of fields at the boundaries to zero, it is known that in non-Abelian gauge theories, semi-classical (finite-action) IR processes are possible which yield (non-zero, but a pure gauge), where is the non-Abelian four-potential.[64] These processes called instantons can modify the IR dynamics of the non-Abelian theory. However, no similar effects arise in the U(1) gauge theory case under consideration. Indeed, due to the finiteness of the action, the field strength F has to fall faster than at infinity, while the four-potential falls as , where . This means that the integral of K over the infinity three-surface equals zero in the limit : no instanton solution exists. Also, this is clear from the topology of the U(1) group, since , and no non-trivial winding is possible.
To conclude, we showed that the total variation of the action (Equation (A2)) does not depend on θ, including any possible surface terms. This means that the saddle point of the path integral of the theory also has no θ-dependence, and so the θ-term (Equation (A1)) has no influence on the physical processes at least at leading order. This means that there does not exist any no-go theorem saying that in the presence of the θ-term in a U(1) gauge theory, there cannot exist magnetic monopoles without extra electric charge of . Whereas we presented a detailed analysis in this Appendix, this conclusion could actually be easily guessed from the very beginning. Indeed, within the U(1) gauge theory presented earlier, a magnetic monopole is an external source and one only studies the electromagnetic theory in its background. It is not surprising that one cannot change the properties of the external source, such as its electric charge, by adding extra terms into the Lagrangian: In the end, by definition of the external source all its degrees of freedom are independent of the dynamics of the theory and therefore of the Lagrangian. The Witten effect arising for example in the case of the ′t Hooft–Polyakov monopoles can of course easily be accounted for in this theory: one should give the magnetic monopole an electric charge proportional to by definition. If the mass of such monopole (i.e., unification scale) is high enough, no low energy dynamics can change the value of this charge as well as its motion. If one wants to incorporate the monopoles into the theory as dynamical sources, then one has to use a more complete theoretical framework, as it was done in the main body of this article while studying a particular axion model. The implementation of the Witten effect as well as the Rubakov–Callan effect into such more complete theoretical framework, where the monopoles are allowed to be dynamical, was discussed by us in ref. [10].
Open Research
Data Availability Statement
Data sharing is not applicable to this article as no new data were created or analyzed in this study.




