Free-Electron Tomography of Few-Cycle Optical Waveforms
Abstract
Ultrashort light pulses are ubiquitous in modern research but the electromagnetic field of the optical cycles is usually not easy to obtain as a function of time. Field-resolved pulse characterization requires either a nonlinear-optical process or auxiliary sampling pulses that are shorter than the waveform under investigation and pulse metrology without at least one of these two prerequisites is often thought to be impossible. Here is reported how the optical field cycles of laser pulses can be characterized with field-linear sensitivity and no ultrashort probe events. A free-space electron beam is let to cross with the waveform of interest. Randomly arriving electrons interact by means of their elementary charge with the optical waveform in a linear-optical way and reveal the optical cycles as the turning points in a time-integrated deflection histogram. The sensitivity is only limited by the electron-beam emittance and can reach the level of thermal radiation and vacuum fluctuations. Besides overturning a common belief in optical pulse metrology, the idea also provides practical perspectives for in situ characterization and optimization of optical waveforms in higher-harmonics experiments, ultrafast transmission electron microscopes, laser-driven particle accelerators, free-electron lasers, or generally any experiments with waveform-controlled laser pulses in a vacuum environment.
1 Introduction
Ultrashort light pulses with a controlled electromagnetic waveform are central to modern research, because such pulses provide access to the time-dependent response of complex materials on the level of a single cycle of light with a time resolution of attoseconds or less.[1, 2] For example, few-cycle pulses can control chemical reactions[3] and photoionization processes,[4] produce high-order harmonic radiation,[5-9] trigger electron emission from nanostructures,[10-12] shape free-electron beams into attosecond pulses,[13, 14] steer and visualize field-induced currents in complex materials,[15-17] and accelerate particles with laser light.[18, 19] Also, a substantial amount of energy can be concentrated into a subcycle time interval, providing unprecedented field strengths and intensities for rapid material processing or high-field experiments.[18, 19]
Essential for almost all such experiments with few-cycle light is a profound knowledge of the electromagnetic waveform in space and time, in order to relate the measured observables to the forces that produce them. It is a common belief in optics that almost any pulse characterization method requires either a nonlinear-optical process or a probe pulse of even shorter duration than the pulse to be determined, or both. For example, pulse characterization techniques like intensity autocorrelation,[20] frequency-resolved optical gating,[21, 22] spectral phase interferometry for direct electric-field reconstruction,[23] or dispersion-scan[24] rely on a nonlinear-optical effect such as second-harmonic generation, difference frequency mixing, higher-order harmonic generation, or optical-parametric conversion. Methods like electro-optic sampling,[25, 26] photoelectron streaking,[27, 28] petahertz nonlinear optical mixing,[29] all-optical cathode-ray oscilloscopes,[30-34] or direct-current metrology in optoelectronic device[35, 36] are all based on test pulses or controllable events that are as short or shorter than the field cycles of interest. Linear-optical methods only provide relative quantities with respect to reference light, for example, with spectral interferometry.[37, 38] Consequently, it is a widespread notion in ultrafast optics that a purely linear characterization of the electromagnetic field of a light wave with long probe pulses may be impossible, or at least unrealistic.
2 Free-Electron Tomography of Optical Waveforms
Here, we show how an optical waveform can be determined by neither using a nonlinear interaction nor an ultrashort sampling process. The idea is based on the use of free electrons instead of photons or bound electrons as a probe. As elementary particles in free space, beam electrons are directly and immediately accelerated in the electric field of laser light via the Lorentz force and therefore offer a linear-optical and instantaneous response to the optical waveform.[13, 14, 31, 33, 34, 39-47] Figure 1a depicts our approach. The unknown optical waveform (red) and an electron beam (blue) interact with each other in an angled geometry in which the electric field of the waveform accelerates the electrons in a sideways direction. A modulation element (black), for example, a mirror, provides momentum and energy conservation.[14, 45, 48-50] The temporally long electron beam continuously covers the entire optical waveform in time, and a time-integrating detector therefore records an incoherent accumulation of deflections in form of a histogram of the field cycles. The electron beam does not have to be pulsed. It can be a continuous beam, provided that enough electrons randomly coincide in time with the optical waveform within a realistic integration time.
Both pictures show that high-energy beam electrons are deflected by the cycles of an optical waveform as a function of their arrival time in a very similar way as the bound electrons of an atom when ionized by attosecond high-energy photons under presence of an optical field.[57] However, by replacing the bound electrons with the swift free electrons in a beam, by substituting the atomic core with our macroscopic mirror membrane, we obtain an instantaneous and field-linear light–electron interaction without the need for an ultrashort probe event (i.e., attosecond ionization). The time resolution of our waveform sampling is limited only by the time it takes for a beam electron to pass though the membrane, which is less than 0.3 fs in this experiment.
3 Experiment and Results
In the experiment, the few-cycle laser pulses centered at 6.9 µm (50 kHz repetition rate) to be measured are produced by optical parametric amplification[58] and focused under p-polarization onto a 20 nm thick aluminum foil coated on a freestanding 20 nm thick silicon nitride membrane (0.5 × 0.5 mm2). The carrier-envelope phase (φCE) of the few-cycle pulse is passively stable to better than 200 mrad (rms) h−1[57] and can be shifted continuously under preservation of all other pulse parameters by simply changing the relative delay between the seed pulses and the pump pulses in our optical parametric amplifier.[8] The estimated peak field strength in the optical focus is 0.4 V nm−1. An electron beam is generated at a kinetic energy of 70 keV and a velocity of 0.5c by laser-triggered photoemission and subsequent electrostatic acceleration.[46] The diameter of the collimated electron beam (100 µm, flat top shape) is smaller than the diameter of the laser focus (≈400 µm, 1/e2) in order to measure a local field. The duration of the electron pulses is ≈500 fs, much longer than the optical pulses, and the entire optical waveform of interest is therefore covered with electrons at a nearly constant rate. A continuous electron beam would work as well, provided that a sufficient number of electrons randomly fall into the time range of the optical pulses within the experimental integration time.
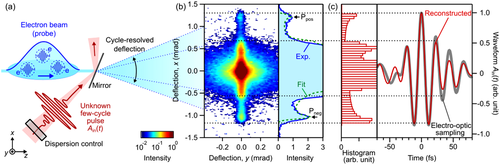
Figure 1b depicts a typical measurement result. The direct electron beam initially hits the screen at , but in presence of the optical field, it is elongated into a line shape along the x-axis. This streaking direction is parallel to the electric field vector of the optical waveform, and the magnitude of deflection is directly proportional to the electromagnetic field strength (Figure S1, Supporting Information). The electrons around x = 0 are not helpful for waveform reconstruction (see below) and can thus be blocked. Figure 1b is deflection data in which φCE was adjusted to give the largest deflection toward +x. Interestingly, the measured pattern shows several special points where there are either maximum intensities (for example, at Ppos and Pneg) or where there are abrupt, stepwise intensity decreases (cutoffs). The dotted lines mark four such special points at −1.2, −0.6, +0.7, and +1.4 mrad. Note that the measured pattern is highly asymmetric: all cutoffs and also the four accumulation points do not have the corresponding points at opposite x; for example, Ppos is at 1.2 mrad and Pneg at −1.0 mrad. The right panel of Figure 1b shows an integration along the y-axis into which no streaking is induced. We see again the asymmetric peaks Ppos and Pneg as well as the four cutoffs of the deflection signal (dotted lines).
Given the linear relation of beam deflection to the optical waveform according to Equations (1) and (2), electrons accumulate on the detector mainly at such deflection angles where the optical waveform has a turning point, that is, an approximately constant field as a function of time. In other words, each local maximum or minimum of the waveform produces a cutoff in the streaking pattern at a deflection value given by the local peak field strength. The measured four cutoff points (dotted lines) therefore reveal that the optical waveform is a few-cycle pulse with two particular field crests in positive direction and two particular field crests in negative direction. The intensity of Pneg is 2.1 times higher than Ppos, suggesting that Pneg is induced by two temporally separated negative peaks of the optical waveform. We therefore conclude, so far without any numerical analysis, on a cosine-shaped waveform that consists of one positive maximum and two similar negative extrema at adjacent times. Although the precise timing of the field cycles is not yet determined, we see that the qualitative nature of an optical waveform including its carrier-envelope phase and sequence of cycles can be deduced.
In order to confirm this assessment, we plot in the right panel of Figure 1c the results of an electro-optical sampling measurement of our pulses.[8, 58] In order to account for the sampling of a Ain(t) in our experiment [see Equations (1) and (2)], we adjust the carrier-envelope phase to give a cosine-shaped waveform. The result is shown in Figure 1c as a gray line. Indeed, the optical waveform with its asymmetric shape has a complex series of field cycles at the positions and field strengths that have been deduced (dotted lines).
3.1 Waveform Reconstruction
The waveform is then determined by the three leading parameters φCE (the carrier-envelope phase, CEP), φGDD (the group delay dispersion, GDD), and φTOD (the third-order dispersion, TOD). φGD describes a group delay and only shifts the entire waveform in time. More coefficients are typically not significant for few-cycle pulses but can be incorporated if required. We now retrieve the optical waveform from a single deflection histogram by fitting Equations (1), (3), and (4) to the measurement results. We note that a retrieval of is, in principle, possible without the use of the optical spectrum, but at least ω0 has to be given in order to map the reconstructed waveform crests to timing information via the cycle period; we recall that all of our data are taken without scanning a delay time. There remains only an ambiguity in sign, to be resolved as described below.
In the measured data of Figure 1b, a cosine-like waveform has been set up in our pulse source[58] by simply maximizing the highest positive deflection (Ppos). Therefore, we assume and only optimize the two remaining parameters φGDD and φTOD via a least square fitting algorithm to the observed deflection signal of Figure 1b. The green curve in Figure 1b and the red squares in Figure 1c show the fitting result and the retrieved field-cycle histogram, respectively. The red curve in Figure 1d shows the reconstructed waveform. We see that it is nearly identical to the waveform obtained by the electro-optical sampling reference (gray) except small details at weaker cycles. Also, the reconstructed waveform corresponds well to the direct guess of the peak amplitudes from the raw data alone (dotted lines).
3.2 Tomography Scans
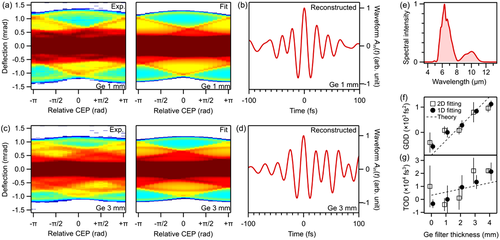
In order to test the robustness and universality of our procedure, and to remove the time-axis ambiguity, we now scan the carrier-envelope phase (φCE) of the laser waveform and record a series of static, not-time-resolved electron deflection histograms as a function of φCE. Figure 2a shows in the left panel the raw data in the form of a series of deflection patterns (integrated along y). We stress again that no time delay is scanned, and each column in Figure 2a is a single time-integrated image for a particular φCE. We call such data a tomographic scan, because we record a series of “time-collapsed” optical waveforms under variation of φCE in a very analogous way to X-ray tomography, where one accumulates a series of “depth-collapsed” projection images under variation of an illumination angle. In Figure 2a, we see several curved lines (e.g., dark blue, orange, red, dark red) with complex near-sinusoidal shapes as a function of φCE. These changes of cutoffs and peaks correspond to gradually changing field strengths of the different optical cycles. Deflection signals at are nearly identical with those at when flipped upside down, as expected from the change of a cosine-shaped to a minus-cosine-shaped waveform. The extreme cutoffs at maximum positive and negative deflections (dark blue) go in parallel, indicating the simultaneous loss and gain of the highest positive and lowest negative waveform crest as a function of φCE. Figure 2c shows such a scan for the case of an intentionally chirped optical waveform. We now see more peaks and fringes, as expected from the multiple field cycles that are now involved. Also, the dependency on φCE becomes more complex than that without the chirp. In particular, the result becomes sensitive to time reversal.
For analyzing such tomographic scans, we simply optimize the three parameters φCE, φGDD, and φTOD with a global fit. The right panel of Figure 2a shows the simulated tomography signal and Figure 2b depicts the reconstructed waveform. All the features are well reproduced. The reconstruction of the chirped pulse data of Figure 2c is depicted in Figure 2d. Also, here, the tomography image is well reproduced, and the reconstructed waveform now reveals an asymmetric shape in time due to the influences of third-order dispersion.
3.3 Consistency Checks with Dispersion Control
In another experiment, we record electron beam deflection data as a function of a varying dispersion of the optical waveform, produced by introducing four different germanium windows into the optical beam path. Each time, we record a single waveform shadow at like in Figure 1a and then evaluate the optical waveform according to Equation (4). The black circles in Figure 2f,g show the obtained GDD (φGDD) and TOD (φTOD), respectively. When using a complete tomography scan under variation of φCE for all four dispersions, followed by four global fits, we obtain the black open squares. Both analyses provide nearly the same results. All measured dispersion values scale approximately linear with the window thickness and the slopes are consistent with the literature values[59] (dotted lines).
The general similarity of all experimental and simulation data in Figure 2a,c in combination with the agreement to electro-optical sampling and recorded dispersion data establish the accuracy of free-electron tomography to capture electromagnetic few-cycle waveforms of almost arbitrary shape. Essentially, we require neither a nonlinear optical process nor an ultrashort probe event.
4 Multidimensional Space-Time Tomography with Electron Microscopy
Figure 3a depicts a proof-of-concept experiment for a combination of the above reported free-electron tomography with transmission electron microscopy. The spatiotemporal optical waveform to be determined is guided onto a large mirror membrane (gray) under an incidence angle of 45° in the -plane with help of a parabolic mirror. The laser focus is set to about 3 mm behind the crossing point with the electron beam in order to produce a nontrivial waveform in space and time. A large-diameter electron beam is converted into a nearly linear shape with help of a slit aperture (orange). Consequently, our detector screen measures time-integrated free-electron streaking along the x-axis that is spatially resolved as a function of the position along the y-axis. Postspecimen quadrupole magnets (not depicted) provide special resolution along the y-axis while maintaining angular resolution in the streaking direction along x.
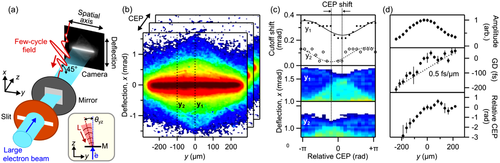
As illustrated in Figure 3b, we observed a series of 2D tomography images as a function of φCE. Again, no ultrashort probe event is applied, and no delay time is scanned. For each y (horizontal direction), a waveform is reconstructed as demonstrated above. Figure 3c shows in the two lower panels the measured tomographic signals as a function of φCE for two example positions y1 and y2. We see at least two special lines (dark blue and turquoise) with sinusoidal dependencies on φCE, but their minima and maxima are shifted substantially; see the upper panel of Figure 3c. This observation is direct evidence for a change of the carrier-envelope phase as a function of position along y.
Each tomography dataset produces values for the overall waveform amplitude and the spectral phases of Equations (3) and (4) as a function of the position y. Because φGD can never be revealed in our non-time-resolved experiment, we determine it with a scan of the macroscopic electron-laser delay at a fixed CEP and subsequent search for the maximum deflection angles. This measurement is the only data in this report where a time delay is scanned. Figure 3d shows the combined results. The upper panel shows the absolute field amplitude of the waveform. It reveals a Gaussian function that corresponds to the optical beam profile. The middle panel shows the group delay of the optical field. We see a nearly linear increase (dotted line) and a slight curvature at the beam center. The slope of 0.5 fs µm−1 reveals that the laser pulses travel on the mirror surface at a surface speed of 2 µm fs−1 or 6.7c, indicating an incidence angle of in the yz-plane; see inset of Figure 3a. The curvature of the group delay at the beam center is attributed to the curved wave front of a converging beam outside the focus; see inset of Figure 3a. The dispersions φGDD and φTOD are not substantially changing as a function of y (see Appendix D, Supporting Information). However, the lower panel in Figure 3d shows the carrier-envelope phase φCE as a function of y. We see a change of ≈π over the beam size and also a substantial curvature. These observations are incompatible with the Gouy phase shifts of a perfect monochromatic Gaussian beam and demonstrate the presence and significance of the focal phases[60, 61] of realistic few-cycle fields that are, for example, essential for strong-field experiments.[62] More experimental results on few-cycle waveforms before, at, and after the nominal focus position are reported in Appendix D, Supporting Information.
5 Sensitivity
We assess the generality and applicability of our method to weak and special waveforms. In principle, there are two aspects of resolution that are related. On the one hand, the deflection caused by the optical waveform must exceed the intrinsic divergence angle of the electron beam. This divergence is limited by the source brightness and the size of the optical focus. On the other hand, a minimum accumulated amount of electrons must coincide with each optical cycle in the time domain to make it visible in the data. This coverage is limited by the electron beam current. Together, we see that the brightness of the electron source is the essential factor for our waveform tomography.
How many electrons are needed? We estimate from simulations that at least a number of electrons must fall into each optical cycle. With an average current I of the electron beam, a waveform repetition rate ν, and the center frequency ω0 of the optical cycles, the needed experimental integration time Ttot becomes . For example, a continuous electron beam in a transmission electron microscope has a typical current of 10 nA. Assuming a laser repetition rate of 100 kHz and a center frequency of 273 THz at 6.9 µm wavelength, the total integration time becomes 0.7 s per deflection histogram, eventually to be multiplied by the needed numbers of parameters for a complete tomography, if desired. We see that the ability of our cycle tomography to measure optical waveforms is not restricted to pulsed electron sources and can work with a continuous electron beam as well.
Assuming enough electrons, we now ask, how long optical pulses can still be measured appropriately? In too long pulses, adjacent cycles will produce an indistinguishable deflection and the histogram will smear out beyond the point of cycle-based information. Mirror membranes can produce a deflection angle of approximately up to[45] , where E0 is the electric field amplitude and λL is the central wavelength of the optical field. In order to distinguish a certain field cycle from an adjacent one, this deflection should be different enough. Assuming a Fourier-transform-limited pulse of a duration τFWHM, the deflection angle by the second-strongest peak is . The two cycles can be distinguished if the two deflection signals αdeflect and αdeflect, 2nd are well separated with respect to αbeam, the intrinsic divergence of the electron beam, that is, . We see that only the quality of the electron beam limits the achievable dynamic range of pulses to be determined. For the conditions of the experiment ( mrad, E0 = 0.4 V nm−1, λL = 6.9 µm), we obtain 130 fs (≈5.6 cycles). For a near-infrared femtosecond source with λL = 780 nm and V nm−1 (≈1012 W cm−2),[63] we obtain 14 fs (≈5.4 cycles). The limiting factor is solely the emittance of the electron beam, which can be made 100–1000 times better than in our experiment,[64] if required.
Assuming a single-cycle waveform, how weak fields can still be detected? The angle αdeflect must be larger than the intrinsic angle spread αbeam. Using an electron beam with an emittance ε focused down to a diameter of , we obtain . Setting and assuming an electron beam[64] with 2 pm rad−1 at 0.5c, we obtain 105 V m−1. Such values are not too far away from the typical electric field strength of thermal radiation (see Appendix E, Supporting Information) or vacuum fluctuations[65] and correspond to optical pulses with merely femtojoule of pulse energy, the same or less than in recent results with the on-chip waveform sampling.[36] In principle, the emittance of an electron beam for tomography purposes can be almost arbitrarily improved with apertures or other filters at cost of electron flux, so further advancements can be conceived. For example, it should be possible to assess electric-field fluctuations or squeezing by observing correlations in the deflection data on basis of detecting single-electron events.
In many high-field experiments with short laser pulses, it is essential to know the amount of pulse energy that is within the main peak in comparison to a background-like intensity around it. Our waveform tomography could be well suited to measure this ratio simply by relating the total amount of deflected electrons above a certain angle (defined by the definition of pulse width) with respect to all other electrons that are deflected less. In the experiment, we have resolved the intrinsic time ambiguity of a single deflection histogram by rotating the CEP by 2π, but any other controllable laser parameter that breaks the temporal symmetry of the optical cycles will be useful as well. The theoretical framework of Section 2 and appendices A and B allow to predict the achievable level of sensitivity for a given question and set of laser parameters in a rather straightforward way. If the experiment is repeated on a single-shot/single-electron basis, we will also become sensitive to fluctuations and classical or nonclassical statistics of the optical field with subcycle time resolution.
6 Conclusion and Outlook
The concept and experimental results reported in this work establish the ability to measure optical waveforms without the need for either a nonlinear-optical phenomenon or an ultrafast time resolution. The origin of this capability is the elementary charge of the electron and its large velocity in a free-space beam. High-energy beam electrons can be focused down to sub-nanometer dimensions and a transmission electron microscope without particular time resolution is therefore useful for measuring electromagnetic waveforms of almost any optical wavelength in space and time. The reported unification of few-cycle laser science with free-space electron beams and non-time-resolved electron microscopy may therefore open up novel research directions in the fields of nanophotonics, metamaterials, nonlinear optics, high-field physics, free-electron quantum optics, dielectric particle acceleration, and many more.
Acknowledgements
The authors thank Simon Stork for help with mirror preparation and Ferenc Krausz for laboratory infrastructure. Y.M. acknowledges Peter Hommelhoff for general support. The authors acknowledge funding from the German Science Foundation via SFB 1432, the Dr. K. H. Eberle Stiftung, the Vector Stiftung, and the FAU Emerging Talent Initiative.
Open access funding enabled and organized by Projekt DEAL.
Conflict of Interest
The authors declare no conflict of interest.
Open Research
Data Availability Statement
All relevant data are available from the corresponding authors upon reasonable request.




