Absolute humidity and the human nose: A reanalysis of climate zones and their influence on nasal form and function
Abstract
Objectives
Investigations into the selective role of climate on human nasal variation commonly divide climates into four broad adaptive zones (hot-dry, hot-wet, cold-dry, and cold-wet) based on temperature and relative humidity. Yet, absolute humidity—not relative humidity—is physiologically more important during respiration. Here, we investigate the global distribution of absolute humidity to better clarify ecogeographic demands on nasal physiology.
Methods
We use monthly observations from the Climatic Research Unit Timeseries 3 (CRU TS3) database to construct global maps of average annual temperature, relative humidity and absolute humidity. Further, using data collected by Thomson and Buxton (1923) for over 15,000 globally-distributed individuals, we calculate the actual amount of heat and water that must be transferred to inspired air in different climatic regimes to maintain homeostasis, and investigate the influence of these factors on the nasal index.
Results
Our results show that absolute humidity, like temperature, generally decreases with latitude. Furthermore, our results demonstrate that environments typically characterized as “cold-wet” actually exhibit low absolute humidities, with values virtually identical to cold-dry environments and significantly lower than hot-wet and even hot-dry environments. Our results also indicate that strong associations between the nasal index and absolute humidity are, potentially erroneously, predicated on individuals from hot-dry environments possessing intermediate (mesorrhine) nasal indices.
Discussion
We suggest that differentially allocating populations to cold-dry or cold-wet climates is unlikely to reflect different selective pressures on respiratory physiology and nasal morphology—it is cold-dry, and to a lesser degree hot-dry environments, that stress respiratory function. Our study also supports assertions that demands for inspiratory modification are reduced in hot-wet environments, and that expiratory heat elimination for thermoregulation is a greater selective pressure in such environments.
1 INTRODUCTION
The critical role of the nasal complex in heating and humidifying inspired air in preparation for entry to the lungs is well established (Elad, Wolf, & Keck, 2008; Keck, Leiacker, Heinrich, Kühnemann, & Rettinger, 2000b; Keck, Leiacker, Riechelmann, & Rettinger, 2000a, 2000b; Wolf, Naftali, Schroter, & Elad, 2004). Further, numerous analyses of nasal function have demonstrated that variation in nasal morphology influences the overall efficacy of this air conditioning process (Churchill, Shackelford, Georgi, & Black, 2004; Keck et al., 2000a, 2000b; Naftali, Rosenfeld, Wolf, & Elad, 2005). As demands for heat and moisture exchange during respiration are largely governed by the external environment (Walker, Wells, & Merrill, 1961), anthropologists have long argued that ecogeographic associations between nasal morphology and climate are the result of natural selection on adaptive respiratory function (Carey & Steegmann, 1981; Cottle, 1955; Crognier, 1981a, 1981b; Davies, 1932; Evteev, Cardini, Morozova, & O'higgins, 2014; Franciscus, 1995; Franciscus & Long, 1991; Franciscus & Trinkaus, 1988; Harvati & Weaver, 2006; Hiernaux & Froment, 1976; Hubbe, Hanihara, & Harvati, 2009; Noback, Harvati, & Spoor, 2011; Roseman, 2004; Roseman & Weaver, 2004; Thomson, 1913; Thomson & Buxton, 1923; Weiner, 1954; Woo & Morant, 1934; Yokley, 2009).
The actual physics of heat and moisture exchange in the human nose are remarkably simple (see Walker et al., 1961, for a detailed review). Inspired air, which is typically below body core temperature, enters the nasal passages and comes in contact with the warm, moist respiratory mucosa that lines the passage walls. The ensuing temperature gradient initiates heat transfer from the warm mucosa to the cooler air via convection. The amount of moisture that air can hold increases with temperature (Barry & Chorley, 2009; Salby, 2012), so warming the inspired air and providing a source of moisture facilitates a concurrent transfer of water from mucosa to air via evaporation. While the vast majority of inspiratory heat and moisture exchange occurs within the nose (Keck et al., 2000a, 2000b), the process of heating and humidifying inspired air continues in the pharynx, larynx, and trachea, until air reaches the “isothermic saturation boundary” (Dery, 1973; Williams, 1998) of body core temperature (37°C) and 100% water vapor saturation (44 g/m3) prior to entering the lungs. Upon expiration, the heat and moisture exchange process works in reverse. Warm, moist air leaves the lungs and enters the posterior portion of the nasal passages where it comes in contact with the respiratory mucosa that was cooled during inspiration. Here, the temperature gradient is reversed from the one formed on inspiration, and as a result, convective heat flows in the opposite direction, from expired air to mucosa. As the expired air cools, it is forced to give up some of its moisture, which condenses on the mucosal surface. The transfer of heat and moisture to inspired air thus protects upper respiratory tract and lung tissues from thermal damage, desiccation, and infection, while modification of expired air aids in the regulation of heat and water loss from the body (Cole, 1982; Franciscus, 1995; Proetz, 1953; Sahin-Yilmaz & Naclerio, 2011; Walker et al., 1961; Yokley, 2006, 2009).
From this brief physiological overview, it becomes readily apparent that respiratory function is dependent on two primary factors: temperature and absolute humidity (the actual amount of water vapor present in a given volume of air). These factors thus differ from those overwhelmingly used in studies of human climatic adaptation: temperature and relative humidity (the percentage of actual water vapor in the air relative to the maximum amount of water vapor that air can potentially hold) (Salby, 2012; Wiederhold, 1997). Importantly, relative humidity can theoretically vary independently from temperature (Barry & Chorley, 2009). As a consequence, two geographic localities with similarly high temperatures can exhibit either high or low relative humidities, as can two localities with similarly low temperatures. This has resulted in a common convention of assigning populations from various geographic locals to either hot-dry, hot-wet, cold-dry, or cold-wet climatic regimes (see Butaric, 2015 for a discussion). Conversely, absolute humidity is directly constrained by temperature, as the amount of water vapor that air can hold decreases exponentially with reductions in temperature (Salby, 2012; Wiederhold, 1997). Thus, because hot air has the capacity to hold large amounts of water (but does not always do so), absolute humidity can vary considerably among geographic localities with high temperatures (Figure 1 top row). In contrast, as cold air is incapable of containing large amounts of water, all localities with low temperatures are restricted to exhibiting low absolute humidities (Figure 1 bottom row). Indeed, a high relative humidity value in a cold climate simply conveys that the air contains a large percentage of whatever small amount of water that air is actually capable of holding (Figure 1 bottom left).
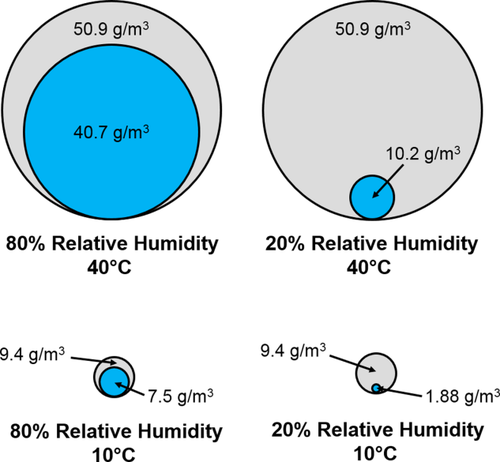
Diagram depicting the maximum saturation humidity (gray circle) and actual absolute humidity (blue circle) based on given temperature and relative humidity values for hypothetical “hot-wet” (top left), “hot-dry” (top right), “cold-wet” (bottom left), and “cold-dry” (bottom right) climates.
Fortunately, if the temperature and absolute humidity for a given locale can be determined, the amount of modification required to maintain homeostatic respiratory function can easily be calculated by subtracting the temperature and moisture content of inspired air from those of the isothermic saturation boundary (37° C, 44 g/m3) (Williams, 1998). Moreover, given the vast range of climates that humans inhabit, the amount of modification required can vary drastically (Beall, Jablonski, & Steegmann, 2012; Lieberman, 2011; Walker et al., 1961). For example,1 air inspired in a tropical environment with a temperature of 35°C and absolute humidity of 35.6 g/m3 requires considerably less modification (+2°C, +8.4 g/m3) than air inspired in an Arctic environment with a temperature of −25°C and absolute humidity of 0.63 g/m3 (+62°C, +43.37 g/m3). The selective pressures created by this wide range of heat and moisture demands are almost certainly a primary driver of variation in modern human nasal morphology (Evteev et al., 2014; Franciscus & Long, 1991; Noback et al., 2011; Yokley, 2009).
Some of the potential problems involved in investigating climatic adaptation in nasal morphology without reference to absolute humidity have previously been noted by Weiner (1954), who demonstrated a much higher correlation between the nasal index and absolute humidity (R = 0.82) than relative humidity (R = 0.42). However, while clearly demonstrating a strong correlation between absolute humidity and nasal morphology, Weiner's (1954) brief study did not provide any information regarding the distribution of absolute humidity around the globe. Possibly as a consequence, subsequent studies on human nasal function and adaption (e.g., Beals, 1972; Butaric, McCarthy, & Broadfield, 2010; Guglielmino-Matessi, Gluckman, & Cavalli-Sforza, 1979; Hanida et al., 2013; Naftali, Schroter, Shiner, & Elad, 2005; Naftali et al., 2005; Noback et al., 2011) have continued to use hot-wet, hot-dry, cold-wet, and cold-dry regimes irrespective of the actual amount of breathable moisture present in the air. Yet, such climatic assignments appear unlikely to accurately reflect selective pressures on human nasal anatomy and physiology, as in particular, the constraints of temperature on absolute humidity suggest that “cold-wet” air is a climatological impossibility.
Accordingly, this study seeks to build upon the earlier work of Weiner (1954) by more fully investigating the global distributions of temperature and absolute humidity to test the validity of ascribing populations to “cold-wet” environments, and to facilitate a better understanding of actual climatic pressures imposed on the noses of ecogeographically distributed modern human populations.
2 MATERIALS AND METHODS
To more fully visualize and interpret the global patterning of temperature, relative humidity and absolute humidity, distribution maps were first created using data from the Climate Research Unit (CRU) TS v 3.22 dataset (Harris, Jones, Osborn, & Lister, 2014). This gridded dataset includes monthly average values for temperature and vapor pressure at 0.5° resolution for the years 1901–2013. Relative humidity was determined for each month using vapor pressure in conjunction with saturation vapor pressure calculated from temperature values (WMO, 2008). Absolute humidity was calculated from monthly vapor pressure values using the ideal gas law and taking the individual gas constant for water vapor as 461.5 joules per kilogram per kelvin (WMO, 2008). All monthly values of temperature, relative humidity, and absolute humidity from 1901 to 2013 were averaged to produce climatological annual average values. These annual values thus reflect average climatic conditions over the last 113 years. Furthermore, numerous studies (e.g., Betti, Balloux, Amos, Hanihara, & Manica, 2009; Harvati & Weaver, 2006; Roseman, 2004) have demonstrated that recent climatic conditions provide reasonable proxies for climates faced by earlier modern human populations. Robinson projection maps presenting these data were plotted with the Basemap 1.0.8 add-on for Python (Whitaker, 2011). Note that climatic data derived from the CRU dataset were exclusively used in the construction of global maps and were not used in subsequent analyses.
Subsequently, to further investigate the temperatures and absolute humidities experienced by actual modern human populations, we reconstructed Weiner's (1954) analysis, which used data collected by Thomson and Buxton (1923) on climate and nasal dimensions for over 15,000 living adult individuals from 147 geographic localities around the globe (Table 1 and Supporting Information). Following Weiner (1954), we used the average annual temperature value provided by Thomson and Buxton (1923) for each geographic locality to calculate the corresponding maximum absolute (saturation) humidity value for that temperature (see Goff, 1957; Wiederhold, 1997; and Supporting Information for conversion formulae). We then used this saturation humidity value in conjunction with the relative humidity values provided by Thomson and Buxton (1923) to determine the approximate absolute humidity for each locality (i.e., the absolute humidity value corresponding to the given relative percentage of the saturation value). It should be noted here that, for our analyses, we have corrected two apparent climatic misclassifications within the Thomson and Buxton dataset (which delineates between hot/cold climates at 16°C and between wet/dry climates at 62% relative humidity). Specifically, we have reassigned Thomson and Buxton's Tibetan sample (12.6°C, 79% relative humidity) from hot-wet to cold-wet and their Egyptian “Bishareen” sample (24.3°C, 55% relative humidity) from hot-wet to hot-dry, as the given average annual temperature/relative humidity values clearly align these samples with other cold-wet or hot-dry populations in the dataset (see Supporting Information).
| Geographic sample | Number of populations |
|---|---|
| Hot-Wet | 61 |
| Indian Subcontinent | 27 |
| Middle East | 3 |
| North America (USA) | 1 |
| South America (Argentina) | 1 |
| Southeast Asia | 15 |
| Sub-Saharan Africa | 14 |
| Cold-Wet | 40 |
| Arctic Circle (Greenland) | 1 |
| Europe | 16 |
| Himalayas | 8 |
| Middle East | 10 |
| North America | 4 |
| South America (Chile) | 1 |
| Hot-Dry | 32 |
| Indian Subcontinent | 21 |
| Middle East | 3 |
| North Africa | 7 |
| Southern Europe (Sicily) | 1 |
| Cold-Dry | 15 |
| Indian Subcontinent (India) | 1 |
| Middle East | 13 |
| North America (USA) | 1 |
Thomson and Buxton (1923) also provide mean living nasal index (nasal breadth/nasal height ×100) values for each of their 147 populations, providing the opportunity to investigate the potential influences of temperature and absolute humidity on an aspect of human nasal morphology widely argued to evince climatic adaptation (Beall et al., 2012; Churchill et al., 2004; Evteev et al., 2014; Franciscus & Long, 1991; Lieberman, 2011; Noback et al., 2011; Yokley, 2009). While Thomson and Buxton's 147 living populations encompass most of the human geographic distribution, this sample lacks representatives from one of the most extreme climates inhabited by humans: the Arctic Circle. Given the importance of Arctic samples in discussions of human nasal adaptation (Butaric, 2015; Evteev et al., 2014; Noback et al., 2011), we have thus included data for an Arctic population drawn from Thomson and Buxton's smaller dataset derived from dry crania (the other geographic locales in this cranial sample being largely redundant with those comprising the living sample). Absolute humidity values for this Arctic population were calculated in the same fashion as previously discussed for the living populations (i.e., from the temperature and relative humidity values provided by Thomson and Buxton for this sample). However, the inclusion of this sample required conversion of the mean skeletal nasal index provided by Thomson and Buxton into a living nasal index value to facilitate comparisons to the other 147 populations in the study. While living and cranial nasal index measurements are not directly convertible at the individual level (Davies, 1999; Thomson & Buxton, 1923), Davies (1932) has previously demonstrated a strong relationship (R2 = 0.996) between the two measurements when based on population mean values. Accordingly, we used Davies (1932) regression formula (mean living nasal index = mean skeletal nasal index × 2.33 – 37.9) to convert the mean skeletal nasal index value for the Arctic sample into an equivalent mean living nasal index value. While this conversion procedure may introduce a small degree of error, we contend the value of extending the geographic/climatic distribution of the study to include the Arctic Circle warrants this possibility (with any error restricted exclusively to analyses involving nasal indices).
These climatological and nasal index data were subsequently used in multiple statistical analyses, all of which were conducted in the NCSS software package (Hintze, 2015). When Thomson and Buxton's (1923) hot-wet (n = 61), hot-dry (n = 40), cold-wet (n = 32), and cold-dry (n = 15) groups were analyzed separately, the raw data for temperature, relative humidity, and absolute humidity all exhibited deviations from normality and equal variances. These climatic data were thus log10 transformed, which, for each group, equalized all variances but failed to adequately normalize the data. As a consequence, non-parametric Kruskal–Wallis one-way ANOVAs and Dunn's post hoc tests were used to test for significant group differences in average annual temperature, relative humidity and absolute humidity. Subsequently, bivariate least squares regression2 was used to assess the relationship between living nasal index and each of the three climatic variables across the pooled sample. Multiple regression was then used to evaluate the nasal index regressed against temperature combined with either relative or absolute humidity as predictor variables.
3 RESULTS
Global average annual temperature, relative humidity and absolute humidity maps are presented in Figure 2. As expected from well-known climatological principles (Lydolph, 1985), average annual temperature is generally greater near the equator with fairly constant reductions in temperature at higher latitudes. Global relative humidity patterns show little coordination with temperature, with high relative humidities notably found in both equatorial (hot) and circumpolar (cold) regions. In contrast, global absolute humidity values largely follow temperature gradients, with higher temperatures generally accompanied by higher absolute humidity values and lower temperatures accompanied by lower absolute humidities. While this trend between temperature and absolute humidity appears consistent in areas with low temperatures (i.e., no region presents an unusually high absolute humidity in conjunction with a low temperature), deviations from this trend are apparent in geographic regions characterized by high temperatures. For example, areas such as North Africa and the Arabian Peninsula exhibit notably lower absolute humidities compared to other areas with similarly high temperatures such as West Africa and the Amazon Basin. It is worth noting, however, that these classic “hot-dry” regions still exhibit greater absolute humidity values than high latitude regions with extremely low temperatures, indicating that the air in these hot deserts actually contains more breathable water than that of Arctic and sub-Arctic areas.
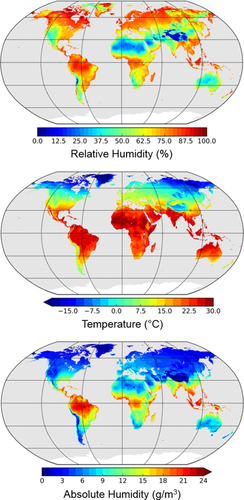
Robinson projection maps for mean annual relative humidity (top), temperature (middle), and absolute humidity (bottom) for the years 1901–2013.
Mean annual absolute humidity values for 148 human populations calculated from mean annual temperature and relative humidity values collected by Thomson and Buxton (1923) are provided in the Supporting Information. Results of Kruskal–Wallis tests conducted on average annual temperature, relative humidity, and absolute humidity values for human populations classified as inhabiting hot-wet, hot-dry, cold-wet, and cold-dry climates reveal significant differences among the four climatic groups for temperature (X2 = 105.6, p < .0001), relative humidity (X2 = 96.3, p < .0001), and absolute humidity (X2 = 126.8, p < .0001). Subsequent Dunn's post hoc tests (Table 2) indicate significant pairwise differences in temperature between “hot” and “cold” groups, with no significant differences in temperature between hot-wet/hot-dry or cold-wet/cold-dry categories. Conversely, Dunn's test results for relative humidity reveal significant pairwise differences between “wet” and “dry” groups, with no detectable differences between the hot-wet/cold-wet or hot-dry/cold-dry categories. For absolute humidity, however, significant differences exist between all climates except between the cold-wet and cold-dry groups. These results are readily interpretable in a bivariate plot of absolute humidity on temperature (Figure 3 bottom), where the statistically indistinguishable absolute humidities experienced by populations inhabiting cold-wet and cold-dry environments are particularly evident, especially in comparison to a plot of the relative humidity and temperature values on which Thomson and Buxton (1923) based the climatic groupings (Figure 3 top). Furthermore, in conjunction with our previous absolute humidity map findings, it is also worth noting that absolute humidity values for hot-dry climates are generally greater than that of either cold-dry or cold-wet environments (Figure 4).
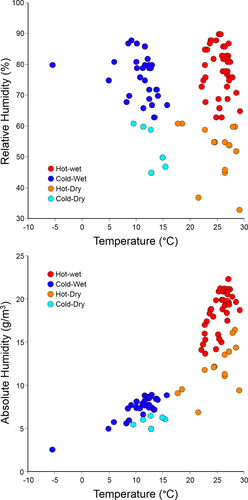
Bivariate plots of mean annual relative humidity (top) and absolute humidity (bottom) on temperature for the 148 populations employed in this study. Note that, due to identical values, a large number of populations overlap.
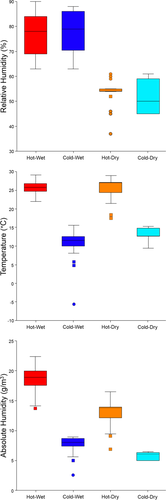
Box plots displaying the median, interquartile ranges, mild (squares), and extreme (circles) outliers for mean annual relative humidity (top), temperature (middle), and absolute humidity (bottom) across the four climatic zone samples.
| Hot-Wet | Cold-Wet | Hot-Dry | Cold-Dry | |
|---|---|---|---|---|
| Temperature (C°) | ||||
| Hot-Wet | – | 8.5440 | 1.0829 | 4.8620 |
| Cold-Wet | 8.5440 | – | 8.3260 | 1.1133 |
| Hot-Dry | 1.0829 | 8.3260 | – | 5.2334 |
| Cold-Dry | 4.8620 | 1.1133 | 5.2334 | – |
| Relative Humidity (%) | ||||
| Hot-Wet | – | 0.2755 | 7.7203 | 6.5531 |
| Cold-Wet | 0.2755 | – | 6.8688 | 6.0527 |
| Hot-Dry | 7.7203 | 6.8688 | – | 0.6503 |
| Cold-Dry | 6.5531 | 6.0527 | 0.6503 | – |
| Absolute Humidity (g/m3) | ||||
| Hot-Wet | – | 9.4117 | 4.8053 | 8.5539 |
| Cold-Wet | 9.4117 | – | 3.6513 | 1.8179 |
| Hot-Dry | 4.8053 | 3.6513 | – | 4.5264 |
| Cold-Dry | 8.5539 | 1.8179 | 4.5264 | – |
- Z-values significant at alpha = 0.05 indicated in Bold.
- Regular Test (top triangle): significantly different if z-value > 1.9600.
- Bonferroni Test (bottom triangle): significantly different if z-value > 2.6383.
Mean living nasal index data for all 148 of Thomson and Buxton's (1923) populations used in this study are also provided in the Supporting Information. Detailed results of regression analyses between living nasal index and climatic variables are presented in Table 3. Bivariate regression of living nasal index on each of the three climatic variables indicates statistically significant relationships between the index and each of the predictor variables. Specifically, leptorrhine (relatively narrow) nasal indices are generally associated with lower temperature, relative humidity, and absolute humidity values, while platyrrhine (relatively wide) nasal indices are typically associated with higher temperatures, relative and absolute humidities (Figure 5). However, only absolute humidity (R2 = 0.69, p < .0001) permits predication of living nasal index with any degree of accuracy, with temperature (R2 = 0.45, p < .0001) and relative humidity (R2 = 0.19, p < .0001) each representing poor predictor variables. Moreover, two multiple regression analyses using temperature combined with either relative humidity or absolute humidity as independent variables each return a coefficient of determination value of 0.72 (p < .0001), only slightly higher than absolute humidity alone. Standardized regression coefficients (β) for the multiple regression analysis involving temperature (β = 0.7304) and relative humidity (β = 0.5240) indicate both predictor variables are contributing substantially to the regression equation. For the second multiple regression analysis, temperature (β = −0.3398) contributes relatively little to the predictive equation compared to absolute humidity (β = 1.1382).
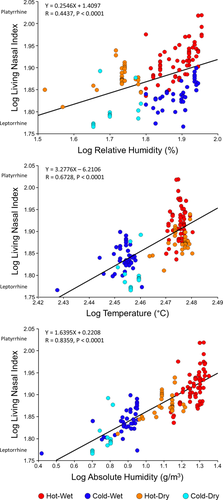
Least squares regression of log10 nasal index on log10 mean annual relative humidity (top) temperature (middle) and absolute humidity (bottom) for the 148 populations employed in this study.
| Measurement | R | R2 | Slope | 95% CI | p-Value |
|---|---|---|---|---|---|
| Temperature | 0.6728 | 0.4527 | 3.2776 | 2.6882–3.8671 | <.0001 |
| Relative humidity | 0.4437 | 0.1969 | 0.2546 | 0.1705–0.3387 | <.0001 |
| Absolute humidity | 0.8359 | 0.6987 | 0.2208 | 0.1970–0.2445 | <.0001 |
| Measurements | R | R2 | Adjusted R2 | F-ratio | p-Value |
| Temperature & relative humidity | 0.8508 | 0.7239 | 0.7201 | 190.121 | <.0001 |
| Temperature & absolute humidity | 0.8501 | 0.7227 | 0.7189 | 188.995 | <.0001 |
4 DISCUSSION
The results of this study clearly indicate that breathing in all cold climates requires a substantial amount of moisture be transferred to inspired air, with individuals traditionally assigned to “cold-wet” environments requiring similar levels of humidification as those from “cold-dry” environments. Indeed, our study found no significant difference in absolute humidity values between these two climatic categories, despite significant differences in relative humidity values. This result further supports arguments that relative humidity is minimally informative when assessing respiratory function in cold climates (Burch, 1945; Butaric, 2015; Walker et al., 1961; Weiner, 1954; Wolpoff, 1968). Moreover, while absolute humidity values can vary in cold environments, our analyses suggest that this variation is effectively negligible relative to the amount of water that must be added to inspired air to achieve the isothermic saturation boundary. For example, the corresponding range of absolute humidity values for 15°C air is 0.0 to 12.8 g/m3. While this range may initially appear substantial, when compared to the 44 g/m3 of water required to maintain homeostatic respiratory function, it becomes clear that all air at 15°C is exceedingly water deficient, requiring the respiratory system to contribute at least 70% of the water required for each breadth. In other words, compared to the internal conditions of the lungs, 15°C air is always relatively dry, even when saturated with as much water as it can possibly hold. Accordingly, our results strongly suggest that all cold air is inherently dry air (see also Burch, 1945; Noback et al., 2011; Walker et al., 1961), and thus, differentially allocating populations to cold-dry or cold-wet climates is unlikely to reflect substantially different selective pressures on respiratory physiology and morphology.
Given their importance in studies of modern human nasal adaptation (see Butaric, 2015; Evteev et al., 2014; Noback et al., 2011), we intentionally incorporated a sample from the Arctic Circle in this study. This sample, perhaps better than any other, demonstrates the potentially erroneous conclusions regarding respiratory demands that may be inferred from assessments of climate based exclusively on temperature and relative humidity. Thomson and Buxton (1923) relay a low average annual temperature (−5.6°C) and high average annual relative humidity (80%) for the environment of this Arctic sample, values that are concordant with our global maps of temperature and relative humidity (see Figure 2). Based on these temperature and relative humidity values, Thomson and Buxton (1923) designate this population as inhabiting a “cold-wet” environment, noting the ready availability of moisture in such coastal environments. However, while the high relative humidity reported for this Arctic environment may initially appear to suggest an ample supply of moisture for respiratory purposes, this relative humidity value belies the fact that air at −5.6°C is maximally capable of holding only 3.3 g/m3 of water as breathable vapor. This, consequently, necessitates the respiratory system to contribute 40.7 g/m3 (92.5%) of the water necessary for each breath to attain the 44 g/m3 required by the lungs at a core body temperature of 37°C. Thus, at only 80% of this maximal value (2.6 g/m3), our results reveal that the air typically breathed by this “cold-wet” Arctic sample is, in fact, the driest of any sample included in the study, including populations assigned to both cold-dry and hot-dry environments (despite these latter environments being characterized by much lower relative humidity values). Accordingly, evidence for strong climatic signatures in the nasal morphology (and surrounding midface) of Arctic populations (Butaric, 2015; Butaric & Maddux, 2016; Evteev et al., 2014; Harvati & Weaver, 2006; Hubbe et al., 2009; Noback et al., 2011; Roseman, 2004; Roseman & Weaver, 2004) appears likely attributable to physiological demands for both heat and moisture exchange in Arctic environments, rather than exclusively driven by temperature as suggested by a “cold-wet” climatic assignment.
Another important finding highlighted by both our global absolute humidity map and our Kruskal–Wallis test results is that “hot-dry” climates are generally characterized by greater absolute humidities than colder environments. A comparison of two populations from our dataset effectively illustrates this point. Thomson and Buxton (1923) report the average annual climatic conditions for the “hot-dry” M'zab region of Algeria in the northern Sahara Desert as 29°C with 33% relative humidity. This corresponds to an average annual absolute humidity of 9.5 g/m3, slightly greater than the 9.0 g/m3 for the “cold-wet” costal region of Landes in southwestern France, characterized by an average annual temperature of 12.8°C and relative humidity of 80%. While this example reiterates the lack of air moisture in cold environments, it also demonstrates that hot air is capable of containing comparatively large amounts of water vapor at low relative humidities. This is possible because the amount of water vapor that air can hold increases exponentially with increased temperature (Salby, 2012; Wiederhold, 1997; Williams, 1998). Thus, as the air of the M'zab region is actually capable of holding nearly 29 g/m3 of water vapor, even a third of this total capacity provides more breathable water vapor than is typically available in a relatively “humid” region of Europe.
Cold-dry: requiring extensive warming and humidifying of inspired air, along with maximum recuperation of both heat and moisture during expiration. Expiration always results in some loss of heat and moisture to the external air (Cole, 1982). In cold environments, where retention of body heat is a thermoregulatory imperative (Holliday, 1997; Ruff, 1991, 1993, 1994), mucosal recuperation of heat and moisture during expiration not only facilitates preparation for the next bout of inspiratory air modification (Walker et al., 1961; Yokley, 2009) but also reduces the total amount of body heat lost to the external environment (Cole, 1982; Melville, Josenhans, & Ulmer, 1970).
Hot-dry: requiring minimal warming but substantial humidification of inspired air, as well as considerable recuperation of moisture during expiration. Recovery of moisture during expiration will also result in the transfer of latent heat to the mucosa (Cole, 1982; Walker et al., 1961), but pressure to eliminate heat during expiration is likely mitigated by the superiority of sweating as a thermoregulatory cooling mechanism in hot environments with low relative humidities (Frye & Kamon, 1983; Lieberman, 2015; Ruff, 1991, 1993, 1994).
Hot-wet: requiring only minimal warming and/or humidification during inspiration but maximal elimination of heat during expiration. While ambient air conditions reduce pressure for inspiratory modification (Burch, 1945; Noback et al., 2011; Walker et al., 1961; Williams, 1998), the reduced efficacy of sweating as a means of thermoregulation in hot-humid environments (Dennis & Noakes, 1999; Frye & Kamon, 1983; Havenith, 2005; Ruff, 1994) likely requires increased use of the respiratory system as mechanism for heat dissipation (Cabanac & White, 1997; Franciscus & Long, 1991; Mariak, White, Lewko, Lyson, & Piekarski, 1999; Noback et al., 2011).
While these three climatic zones may be broadly defined in terms of temperature and absolute humidity, there are factors that must be considered when applying these regimes. First, both temperature and absolute humidity are arrayed continuously, thus there may be little actual climatic difference between two environments falling just above or below values used to delineate different regimes. Second, and perhaps more importantly, many geographic localities experience considerable variability in temperature and/or absolute humidity due to seasonality (Barry & Chorley, 2009; Lydolph, 1985; Salby, 2012).
While the problematic issue of seasonality on respiratory function has been discussed in the literature related to human nasal morphology (Davies, 1932; Thomson & Buxton, 1923), it is generally agreed that natural selection is likely acting upon the most extreme climatic condition faced by the respiratory tracts of individuals inhabiting a particular geographic locale (Evteev et al., 2014; Franciscus, 2003; Steegmann, 1975; Walker et al., 1961). Our study suggests that, for most areas of the world, this respiratory extreme is likely to coincide with the lowest absolute humidity, regardless of whether this low absolute humidity is being driven by low temperature (as in cold environments) or occurring independent of temperature (as in hot-dry environments). However, our data also suggest that in some tropical areas (those that are never particularly cold or dry), the most extreme condition is actually likely to be found in conjunction with high absolute humidity values. This may not necessarily be because high absolute humidities are actually a major respiratory pressure (see Melville et al., 1970), but because high absolute humidities can only occur at high temperatures, which, due to the reduced efficiency of other thermoregulatory cooling mechanisms (i.e., sweating) in humid conditions (Dennis & Noakes, 1999; Frye & Kamon, 1983; Havenith, 2005), may require the respiratory system to maximize elimination of heat (Cabanac & White, 1997; Franciscus & Long, 1991; Walker et al., 1961; White, Greiner, & McDonald, 2011). In the face of these opposing selective pressures, neither maximum nor minimum seasonal values would appear to fully reflect selective pressures across all populations, as seasonal minimums (e.g., lowest annual temperature/absolute humidity) would be unlikely to drive nasal adaptation in hot-wet environments and seasonal maximums unlikely to influence morphology in cold and hot-dry environments. Such a possibility highlights the importance of Weiner's (1954) influential study on the relationship between average annual absolute humidity and the nasal index.
Although the degree to which climate influences the nasal index has been debated (Hoyme, 1965; Hoyme and Işcan, 1989; Wolpoff, 1968), it is widely viewed that, as a basic measurement of nasal aperture shape, the nasal index broadly reflects climate-mediated adaptations for modulating nasal airflow3 during respiration (Beall et al., 2012; Churchill et al., 2004; Evteev et al., 2014; Franciscus & Long, 1991; Lieberman, 2011; Noback et al., 2011). The findings of Weiner (1954), who demonstrated statistically significant relationships between living nasal index and average annual relative humidity (R = 0.42), temperature (R = 0.63), and especially absolute humidity (R = 0.82), are commonly cited in support of this view. However, beyond simply attributing the higher correlation with absolute humidity to the physiological importance of inspiratory humidification, Weiner (1954) did not actually investigate the underlying structure of the variables driving this result. Our bivariate plot of living nasal index regressed on average annual absolute humidity (Figure 5) clearly demonstrates that Weiner's finding is related to two factors we have previously discussed: (a) the similarly low absolute humidities experienced by populations from all cold environments, and (b) the intermediate absolute humidities experienced by populations in hot-dry environments (which are generally greater than those living in cold climates yet lower than populations living in similarly hot but more humid environments). It is this second factor that appears to have predominantly contributed to Weiner finding a higher correlation between the nasal index and absolute humidity than with temperature: a conclusion supported by our multiple regression analyses. While the high coefficient of determination result for our multiple regression using temperature and relative humidity might initially appear to undermine Weiner's argument, it must be recognized that relative humidity, when combined with a corresponding temperature, provides an alternative measure of absolute humidity (i.e., the percentage of water vapor relative to the maximum amount possible for that temperature). This is almost certainly why the coefficients of determination for this analysis and the second multiple regression using temperature and absolute humidity are virtually identical. In this second analysis, absolute humidity overwhelmingly drives nasal index prediction, which appears attributable to the fact that temperature and absolute humidity both predict similar nasal index values for cold and hot-wet populations, but only absolute humidity accurately predicts intermediate (mesorrhine) nasal index values for populations from hot-dry environments (with temperature predicting relatively wide nasal apertures for populations inhabiting all hot environments).
While our findings highlight the importance of hot-dry populations to Weiner's (1954) finding of a strong association between the nasal index and absolute humidity, it also emphasizes a limitation of the Thomson and Buxton (1923) dataset used by Weiner. As noted by Davies (1932), a geographic bias is evident among Thomson and Buxton's (1923) hot-dry populations, as these derive almost entirely from North Africa, the Middle East, and the Indian subcontinent. In Weiner's (1954) study, we have shown that the mesorrhine nasal indices of these populations correlate strongly with the intermediate absolute humidity values of the hot-dry environments they inhabit. However, it must be recognized that indigenous populations exhibiting exceedingly platyrrhine nasal indices, such as South African Khoisan and Aboriginal Australians (Davies, 1932; De Villiers, 1968; Franciscus, 1995), are known to inhabit hot-dry areas with high temperatures and intermediate absolute humidities (Figure 2; see also Noback et al., 2011). As a consequence, the high correlation between the nasal index and absolute humidity found by Weiner (1954) may have been unduly influenced by a limited sampling of nasal morphologies found among populations living in hot-dry environments. Future studies using samples from a broader range of hot-dry environments are clearly needed to further evaluate this possibility.
Even if absolute humidity is eventually found to be a less powerful predictor of nasal aperture morphology, virtually all researchers recognize that it is internal components of the human nose that are primarily responsible for heat and moisture exchange during respiration (Cole, 1982; Elad et al., 2008; Franciscus, 2003; Franciscus & Long, 1991; Hanida et al., 2013; Inglestedt, 1956; Keck et al., 2000b; Naftali et al., 2005; Noback et al., 2011; Walker et al., 1961; Yokley, 2009). Accordingly, our findings related to the lack of moisture in all cold climates, and the relatively intermediate absolute humidities in hot-dry environments, may actually be more relevant to future studies of internal nasal fossa morphology. For example, our results lead us to suggest that the internal nasal morphology of humans inhabiting hot-wet areas may be under different selective pressures compared to individuals from other climatic regimes. Specifically, we suggest that, unlike cold and hot-dry environments where demands for inspiratory modification likely drive internal nasal morphology, in hot-wet environments the internal nose may be predominantly adapted for eliminating heat during expiration. Tentative support for this contention can be drawn from the findings of Noback et al. (2011), who studied nasal cavity morphology in ten ecogeographically diverse samples. In contrast to individuals from other climatic regimes, these authors found individuals from hot-humid environments to exhibit nasal cavities that progressively widen from the choanae to anterior nasal aperture. Noback et al. (2011) suggest this anterior widening would reduce contact between ambient air and the nasal mucosa during inspiration while simultaneously facilitating evaporative cooling during expiration. Such morphology appears consistent with our hypothesis of reduced demands for inspiratory modification and increased demands for expiratory heat elimination in hot-wet environments.
Furthermore, the capacity for the nasal complex to facilitate heat loss under conditions of hyperthermia has been reliably demonstrated (Carbanac & White, 1997; Hanson, 1974; Mariak et al., 1999; White & Carbanac, 1995, 1996), and it is generally recognized that hot-wet environments present the greatest risk of hyperthermia due to the reduced efficacy of sweating as a mechanism for shedding heat in hot-humid conditions (Frye & Kamon, 1983; Havenith, 2005; Taylor, 2006a, 2006b). As a consequence, while hot-wet environments are often considered “low stress” respiratory environments, due to the minimal amount of inspiratory modification required to prepare air for entry into the lungs (Noback et al., 2011; Walker et al., 1961), thermoregulatory demands for increased heat dissipation in these environments may actually represent a strong selective pressure on nasal morphology (Franciscus & Long, 1991; Lieberman, 2015). Accordingly, cold-dry and hot-wet environments may actually represent two respiratory extremes, with cold-dry environments requiring extensive inspiratory modification and hot-wet environments requiring maximal shedding of heat during expiration. In such a scenario, hot-dry environments would actually appear to be the least physiologically demanding, with lower demands for inspiratory modification and expiratory cooling compared to cold-dry and hot-wet environments respectively. Reduced selective pressure on the nasal complex in hot-dry environments may explain the apparent range of nasal index values among populations inhabiting hot-dry areas discussed previously (e.g., North Africa/Middle East vs. Khoisan/Australia). However, additional studies are needed to evaluate whether the internal nasal morphologies of these populations are as variable as their nasal index values.
ACKNOWLEDGMENTS
The authors thank P. Ellison and two anonymous reviewers for helpful comments that improved this manuscript. We also thank T. Holliday, L. Butaric, B. Auerbach, L. Cowgill, and K. Middleton for insightful discussions related to this project.




