Quantifying lateral femoral condyle ellipticalness in chimpanzees, gorillas, and humans
Abstract
Articular surfaces of limb bones provide information for understanding animal locomotion because their size and shape are a reflection of habitual postures and movements. Here we present a novel method for quantifying the ellipticalness (i.e., departure from perfectly circular) of the lateral femoral condyle (LFC), applying this technique to hominid femora. Three-dimensional surface models were created for 49 Homo sapiens, 34 Pan troglodytes and 25 Gorilla gorilla femora. Software was developed that fit separate cylinders to each of the femoral condyles. These cylinders were constrained to have a single axis, but could have different radii. The cylinder fit to the LFC was allowed to assume an elliptical cross-section, while the cylinder fit to the medial condyle was constrained to remain circular. The shape of the elliptical cylinder (ratio of the major and minor axes of the ellipse) was recorded, and the orientation of the elliptical cylinder quantified as angles between the major axis of the ellipse and the anatomical and mechanical axes of the femur. Species were compared using analysis of variance and post hoc multiple comparisons tests. Confirming qualitative descriptions, human LFCs are more elliptical than those of chimpanzees and gorillas. Human femora exhibit a narrow range for the angle between the major axis of the elliptical cylinder and femoral axes. Conversely, the chimpanzee sample is bimodal for these angles, exhibiting two ellipse orientations, while Gorilla shows no preferred angle. Our results suggest that like modern human femora, chimpanzee femoral condyles have preferentially used regions. Am J Phys Anthropol, 2012. © 2012 Wiley Periodicals, Inc.
Animal movement remains an area of principle interest for biologists and paleontologists alike because of the pivotal role that locomotion plays in the evolutionary success of terrestrial animals, affording access to the critical resources of food, water, safety, and potential mates. Aspects of the cranial and postcranial skeleton provide clues as to the locomotor adaptations of animals, both living and extinct (Stern and Susman,1983; Spoor and Zonneveld,1998; Ruff,2002; Patel,2010). Analyses of limb bones can contribute to our understanding of animal locomotion by exploring the relationship between skeletal form, limb function, and locomotor behavior. The articular surfaces of limb bones are especially informative because their size and shape appear to be related to habitual postures and movements (Jungers,1991). More precisely, the size and shape of articular surfaces reflect the functional requirements for joint strength, mobility, and stability, demands which must be met for successful locomotion (Hamrick,1996). Joint mobility is the potential range of motion allowed at an articulation without suffering soft tissue damage, while joint stability is the ability of a joint to resist motion outside normal kinematics and joint dislocations. Joint strength is the magnitude and frequency of force a joint can withstand without incurring damage to the bone and articular cartilage. These are critical features of articulations because damage to overall joint integrity, the avascular articular cartilage, or subchondral bone can impede normal joint function and negatively affect locomotor behaviors.
The knee has received a great deal of attention, not only from functional morphologists, but also clinically oriented researchers (i.e., biomedical engineers and orthopedists), because of its critical weight-bearing role in terrestrial locomotion (Tardieu,1979, 1981; Iwaki et al.,2000; Pinskerova et al.,2000; Lovejoy,2007; Sylvester et al.,2011). Knee joint articular surfaces must be of the size and shape to accommodate normal locomotor demands, and therefore, provide information about locomotor adaptations. Here we quantify the shape of the lateral femoral condyle (LFC) of humans, chimpanzees, and gorillas to explore the relationship between this aspect of lower limb morphology and knee function. There has been a great deal of interest in the shape of the LFC of large bodied hominids, especially within the context of the evolution of hominin bipedalism (Johanson et al.,1976; Tardieu,1979, 1998; Lague,2002; Lovejoy,2007). Given the importance and interest in primate locomotion, and the potential information contained within the LFC for studies of human evolution, there were three goals for this project. The first was to develop a novel method of quantifying the degree of ellipticalness (departure from perfectly circular) of the LFC that does not require an a priori assumption about bone orientation, but rather is guided by bone morphology alone. The second was to use this metric to determine the degree of ellipticalness in modern humans (Homo sapiens), chimpanzees (Pan troglodytes), and gorillas (Gorilla gorilla) to quantify the range of variation in this morphology, both between and within species. We expected the human LFC to be more elliptical than either that of Gorilla or Pan as has been qualitatively described previously (Heiple and Lovejoy,1971). Finally, we also measured the orientation of the ellipse that describes the LFC relative to anatomical and mechanical axes of the femur. In this measure, we expected that the long axis of the ellipse describing the modern human LFC will orient roughly 90 degrees relative to the anatomical and mechanical axes of the femur as predicted by Heiple and Lovejoy (1971). In Pan and Gorilla, we did not anticipate finding a preferred orientation (Lovejoy et al.,1999).
Abbreviations
-
- AIC
-
Akaike information criterion
-
- ANOVA
-
analysis of variance
-
- BIC
-
Bayesian information criterion
-
- cTEA
-
clinical transepicondylar axis
-
- GMM
-
Gaussian mixture model
-
- ICP
-
iterative-closest-point
-
- LFC
-
lateral femoral condyle
-
- MFC
-
medial femoral condyle
-
- sTEA
-
surgical transepicondylar axis
DISTAL FEMORA OF HUMANS, CHIMPANZEES, AND GORILLAS
Because of the insight provided for understanding the origin of hominin bipedalism, much attention has been paid to the knees of the chimpanzee, gorilla, and modern human. Features that appear unique to humans and their bipedal ancestors include an anteriorly projecting lateral lip of the patella surface, a valgus knee, and an elliptical LFC (Aiello and Dean,1990). The human valgus knee is important for bipedal progression because it positions the leg and foot closer to the sagittal midline of the body, which facilitates balancing during the single support phase of walking and running. This feature is the result of biomechanical loading during ontogeny and does not develop in humans that never walk (Shefeldbine et al.,2002). The projecting lateral lip of the patellar surface is functionally linked to the valgus knee (Tardieu et al.,2006). Contraction of the quadriceps femoris muscle tends to dislocate the patella laterally because of the angle formed between the tibia and the femur. This movement is counteracted by the projecting lateral lip of the patellar surface, as well as the patellar retinaculum (Heegaard et al.,1994; Farahmand et al.,2004).
The shape of the LFC (as viewed from a lateral perspective) has been used to differentiate bipedal modern humans from quadrupedal chimpanzees and gorillas (Heiple and Lovejoy,1971; Tardieu,1979). The human LFC has been described as being elliptical, with the long axis of the ellipse oriented perpendicular to the anatomical axis of the femur, which is the major axis of the femoral shaft (Heiple and Lovejoy,1971; Tardieu,1979; Lovejoy,2007). The shape of the human LFC has also been quantified geometrically using two circles fit to a single sagittal section through the middle of the condyle (Iwaki et al.,2000; Pinskerova et al.,2000; Freeman and Pinskerova,2004). One circle describes the shape of the posterior portion of the LFC, while a second larger circle is used to describe the more anterior/inferior portion. Such a technique, however, may be of limited use for comparison with other mammals as the radius of curvature may change in different ways requiring more (or fewer) circles for adequate description. Both the qualitative and geometric descriptions of the human LFC indicate, however, that the portion of the LFC in contact with the tibia at full knee extension, and in early flexion, has a larger radius of curvature than the rest of the condyle (Weber and Weber,1836; Albrecht,1876; Lindahl and Movin,1967). This increased radius of curvature increases the contact area between the femoral and tibial condyles in this position thereby reducing pressures within the joint during bipedal walking (Kettlekamp et al.,1972; Maquet et al.,1975; Maquet,1976).
In contrast to modern humans, the LFC of chimpanzees and gorillas have been described as being circular in profile. Heiple and Lovejoy (1971) found that the LFC of non-human primates “closely approximates” the arc of a circle, while Tardieu (1981) simply stated that the LFC of non-human primates are circular. Lovejoy et al. (1999) argued that the circular chimpanzee LFC does not reflect any particular knee angle with increased cartilage contact, presumably because their locomotion is more varied (i.e., less stereotypical) than human walking. Chimpanzees and gorillas are known to use a diverse locomotor repertoire including vertical climbing, quadrumanous scrambling, and suspensory behaviors, all of which must be accommodated by joint structures. The vast majority of locomotion, however, in both apes is quadrupedalism (terrestrial and arboreal), making up over 95% of all locomotion in gorillas and 85–95% in chimpanzees (Doran,1996).
Lovejoy (2007) created a metric to quantify the ellipticalness of the LFC and to demonstrate the difference between chimpanzee and humans, which confirmed earlier visual assessments. Lovejoy (2007) took lateral photographs of the LFC (with the femoral shaft positioned vertically) and then measured the length of two tangent lines, using them to create a shape ratio (Fig. 1). This metric is, however, deficient for the purpose of defining a unique ellipse. Five parameters are required to define a unique ellipse: accounting for the position of the center (2), lengths of the major and minor axes (2), and orientation (1). Thus, a unique ellipse can then be defined with five (x, y) coordinate data points along the perimeter, as long as any three of these points are not collinear. A special case exists in which all five parameters can be derived from two points along the perimeter of an ellipse, if these points are known to be the ends of the major and minor axes. While Lovejoy (2007) measured the vertical line to the point of tangent with the posterior portion of the LFC (thus providing the position of the end of the major axis), the horizontal line was measured to the meniscal groove. The vertical distance from the end of the horizontal tangent line to the meniscal groove was not measured and as a result these measurements are insufficient for defining the five parameters of a unique ellipse or the four parameters of an ellipse where the orientation is known (Fig. 2).
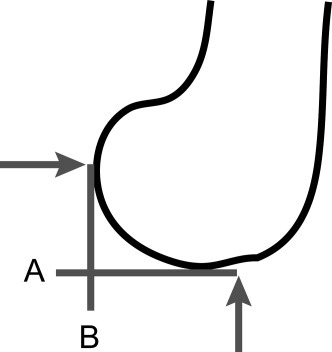
Created after Lovejoy (2007). Measurements used to create a LFC shape ratio. The vertical line B was measured from the intersection with horizontal line A to the tangent point with the posterior point on the condyle. The horizontal line A was measured from the intersection to the point below the meniscal groove. The ratio of these two measurements was used as a shape ratio.
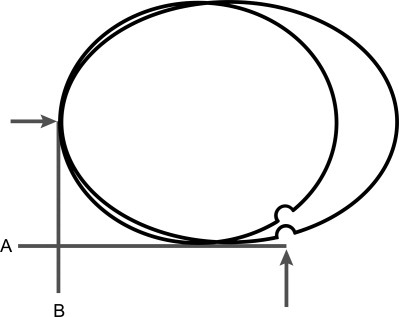
Two idealized LFC outlines are presented along with measurements described by Lovejoy (2007). Notches in ellipses above the vertical arrow represent the meniscal groove. Using Lovejoy's (2007) metric, these two ellipses would have the same shape ratio (i.e., classified as the same shape), despite the fact that they are very differently shaped ellipses.
Any procedure that measures the shape of the femoral condyles must do so with respect to the axis of knee flexion-extension. Recent work challenges the persistent conventional wisdom that the knee flexion-extension axis moves during knee rotation, demonstrating instead that knee flexion-extension occurs about a fixed axis (Berger et al.,1993; Hollister et al.,1993; Churchill et al.,1998; Eckhoff et al.,2003; Asano et al.,2005). Because of clinical applications, a great deal of work has been devoted to estimating this fixed axis in humans, and several axes have been proposed, including the clinical transepicondylar axis (cTEA), the surgical transepicondylar axis (sTEA), and the geometric axis of the condyles (Berger et al.,1993; Eckhoff et al.,2003; Asano et al.,2005). The lateral landmark for the cTEA and sTEA is the prominence of the lateral epicondyle, while the medial is, respectively, the prominence and sulcus of the medial epicondyle. The geometric axis is either achieved by fitting cylinders to the posterior portion of the femoral condyles (Eckhoff et al.,2003, 2005; Miranda et al.,2010) or circles to sagittal profiles of the condyles (Churchill et al.,1998; Asano et al.,2005). These axes are similar in approximating the axes of knee flexion-extension.
FUNCTIONAL ALIGNMENT
An additional complication when comparing the shapes of human and non-human primate distal femora, is finding a functionally equivalent alignment. “Alignment” is defined as the placement of all specimens in a common position and orientation, and is a critical step prior to the analysis of shape. The difficulty inherent in achieving proper alignment is a well-understood problem in geometric morphometrics, with several procedures available for the alignment of specimens for geometric morphometric analyses. Of these procedures, Procrustes Superimposition (which also removes size) is the most widely used in the analysis of landmark data (Mitteroecker and Gunz,2009). For functional analyses however, alignments such as Procrustes Superimposition, which minimize overall shape differences, may not be the most appropriate. This is because to understand functional shape differences, specimens should be in functionally equivalent orientations, that is, orientations that represent how they perform functionally equivalent tasks (Lovejoy,2007). While the anatomical lateral surface of the femur can be identified and would provide an equivalent anatomical orientation, this does not necessarily provide a functional equivalent. Previous analyses of the knee have relied upon mathematically derived orientations (e.g., Lague,2002) or have assumed functional orientations from anatomical ones (Lovejoy,2007). The measurement technique created here to quantify the ellipticalness of the LFC is dictated by the morphology of the condyles alone, and is invariant to bone position and orientation.
The changing radius of curvature of the human LFC, as captured by an ellipse, reflects the preferential use of certain regions near full knee extension (Kettlekamp et al.,1972; Maquet et al.,1975; Maquet,1976). Regions of lower curvature increase the contact between the femoral and tibial condyles, thus attenuating transarticular forces. Using an elliptical model demonstrates the presence of a change in curvature and areas of relatively low curvature, indicating non-uniform use patterns. Knowing the orientation of the ellipse allows the areas of low curvature to be located relative to the whole bone, so that this information can then be related to stereotypical joint position during locomotion and postures.
MATERIAL AND METHODS
Sample and data collection
The sample consists of the femora of 108 extant African hominids, and includes Homo sapiens (n = 49), Gorilla gorilla (n = 25) and Pan troglodytes (n = 34) (Table 1). The modern human specimens are parts of the Pöch Collection (Khoisan) curated by the Department of Anthropology at the University of Vienna (Vienna, Austria), and the William M. Bass Skeletal Collection (20th c. North Americans, largely of European and African ancestry) curated by the Department of Anthropology at The University of Tennessee (Knoxville, TN). The gorilla and chimpanzee femora derive from collections housed at the Max Planck Institute for Evolutionary Anthropology (Leipzig, Germany), the University of Vienna (Vienna, Austria), the Museum für Naturkunde (Berlin, Germany) and the National Museum of Natural History (Smithsonian Institute, Washington, D.C.). All bones are from adult individuals and free of pathology.
| Species | Female | Male | Unknown |
|---|---|---|---|
| Pan troglodytes verus | 13 | 7 | 2 |
| Pan troglodytes subsp. | 2 | 6 | 4 |
| Gorilla gorilla gorilla | 4 | 4 | 1 |
| Gorilla gorilla subsp. | 1 | 1 | |
| Gorilla beringei beringei | 5 | 7 | |
| Gorilla beringei graueri | 2 | 2 | |
| Khoisan (Pöch Collection) | 8 | 12 | |
| William M. Bass Collection | 15 | 14 |
Virtual models of all femora were generated using one of two different procedures. The modern human femora from the William M. Bass Skeletal Collection were scanned using a GE Lightspeed 16 Slice CT scanner, resulting in DICOM image stacks with 0.625 mm cubic voxels. These femora were manually segmented from the DICOM images in commercially available software, and used to generate triangulated mesh models. All other femora were scanned using a Breuckmann optoTop-HE white light surface scanner which directly produces triangulated mesh surface models.
Surface models were imported into a virtual workspace and the articular surfaces of both femoral condyles were trimmed from the rest of the surface models. The femoral condyles of the primate femur have overlapping regions that accommodate patellar and tibial articulations (Lovejoy,2007). As our goal was to quantify the LFC with respect to knee flexion (and hence, its tibial articulation), we selected regions of the femoral condyles that do not also accommodate patellar motion. To do this, we created a color-coded local curvature map of each distal femur (Fig. 3, Supporting Information Figs. 1-3), to facilitate identification of functionally separate regions of the condyles as described by Lovejoy (2007). One region of the LFC accommodates both patellar and tibial motion, and comprises the medial portion of the LFC (bordering the intercondylar notch) and is the inferior continuation of the patellar surface. The second region of the LFC accommodates the tibial articulation, and is separated from the first by a ridge of relatively high curvature running anteroposteriorly across the anterior portion of the LFC and can be visualized on the using the color-coded curvature maps. The lateral border of the LFC was selected as the ridge of curvature that is both equal to that separating the two previously described functional regions of the condyle and is parallel to the articular margin. An analogous procedure was used to delimit the portion of the medial femoral condyle (MFC) that articulates with the tibia. In all cases, the anterior extent of the articular surface was delimited by one of two features. In humans, the anterior extent was the meniscal groove, which is an impression in the articular surface left by the meniscus. In the chimpanzee and gorilla samples, the lateral and medial borders of the tibial contact area often converge anteriorly. The posterior extent of the articular surface in all specimens was the articular margin. Although the anterior extent of the articular surface is not always well defined, the algorithm used to estimate the axis of knee flexion-extension is robust to moderate variation in the amount of articular surface included. The number of vertices used to represent each condyle was then reduced to approximately 275–300 vertices to decrease the computation time of the following steps.
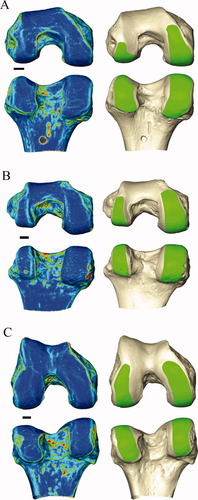
Local curvature maps (left column) and articular surface for accommodating tibial motion (right column) for Pan (A), Gorilla (B), and Homo (C). Black bars between distal (upper row within species) and posterior (lower row with species) views represents 1 cm and in all images lateral is left and medial is right. In these color-coded curvature maps, local three-dimensional curvature (maximum curvature) is converted to a color spectrum where cooler colors (violet/blue) represent regions of low curvature and warmer colors (red) represent regions of greater curvature. These maps allow for the identification of a ridge of high curvature that separates the portions of the articular surface that articulate exclusively with the tibia from the portions of the condyles that also accommodate patellar motion. In the right column of images, the green represents the portion of the condyle used in this study.
Quantifying the shape of the lateral condyle
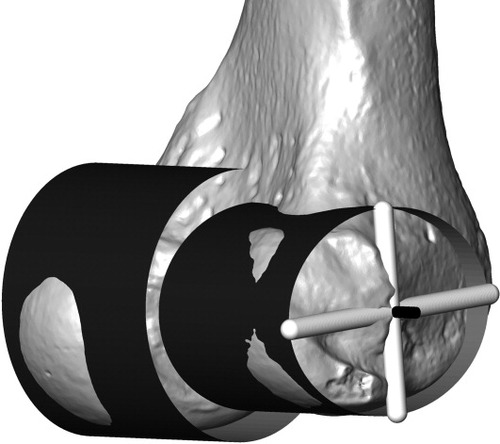
To quantify the degree of ellipticalness of the LFC, we fit each condyle pair (trimmed MFC and LFC) simultaneously with two cylinders (termed here “dual-cylinder”) using a procedure similar to that described by Eckhoff et al. (2003), and conceptually similar to other work (Asano,2005). The two cylinders were allowed to differ in their radii, but were constrained to have a common axis (Fig. 4). This axis has been shown to provide a good estimate of the axis of knee flexion-extension (Morrison,1970; Penncock and Clark,1990; Churchill et al.,1998; Asano et al.,2005; Miranda et al.,2010), intersecting the medial and lateral epicondyles at the attachment points for the medial and lateral collateral ligaments. In addition, the cylinder that was fit to the LFC was permitted to be elliptical in cross-section while the cylinder fit to the MFC was required to remain circular. Thus, the total shape space (free from scale, orientation and location) of the dual-cylinder can be described by two parameters. The first is a ratio of the major and minor axes of the elliptical cylinder, and the second is the ratio of the radius of the cylinder fit to the MFC, to the minor axis of the elliptical LFC cylinder. The dual-cylinder was long enough to extend well beyond the width of all distal femora and did not need to be estimated. The cylinder fit to the MFC was not permitted to be elliptical because computation time is a power function where the number of estimated parameters is the exponent. Estimating the two parameters used here took approximately 4 h per specimen on an eight-processor work station, and the addition of one parameter would increase computation time to 5 days per specimen.

An example of a dual-cylinder. The dual-cylinder was permitted to have different radii, and the cylinder fit to the LFC (picture here as the left cylinder) was also permitted to be elliptical in cross-section.
To find the best fitting dual-cylinder for a given pair of condyles, a recursive algorithm searched through a predefined region of the total dual-cylinder shape space. During each round of the recursive search, approximately 400 different dual-cylinders were fit to the condyles using an iterative-closest-point (ICP) surface fitting algorithm (described below). The radius of the MFC cylinder was allowed to be between 0.5 and 2 times the minor axis of the LFC cylinder. The major axis of the elliptical could be 0.5–2 times that of the minor axis. The best fit dual-cylinder of each set was then used as a starting value for the next round of the recursive search in which a smaller sub-region of dual-cylinder shape space was searched with a higher resolution. The resolution of the last round of the recursive search was 0.0001 for both shape parameters.
An ICP surface fitting algorithm was used to fit each of the dual-cylinders. A starting position for the dual-cylinder is found by “manually” fitting (i.e., translating, rotating, and scaling) an exemplar dual-cylinder to the two condylar surfaces in a virtual environment. The first step of the surface fitting algorithm is to fit each potential dual-cylinder to the starting position, orientation and size of the manually fit exemplar dual-cylinder. From the starting position, the ICP algorithm then proceeds by projecting the vertices representing the femoral condyles onto their closest position anywhere on the surface of the dual-cylinder. This creates point correspondences between the condyles and the surface of the dual-cylinder. The Arun (Arun et al.,1987) method then provides the least-squares solution (solving for translation, rotation, and scale) to fit the projected vertices to the vertices representing the condyles. The resulting rotation, translation and scale transformations are then applied to the dual-cylinder itself. Following this transformation, a new set of point-to-surface correspondences are calculated and another transformation carried out. These two steps (point projection/correspondence creation and least-squares transformation) continue until the dual-cylinder achieves a stable position, orientation, and scale (Fig. 5).
Example of the final position of a dual-cylinder fit to a chimpanzee femur. White lines represent major and minor axes of the ellipse. Small black line at the intersection of the white lines is the central axis of the dual-cylinder.
To quantify the degree of ellipticalness of the LFC, we recorded the ratio of the major and minor axes of the elliptical cylinder fit to the LFC. In addition, we also calculated the angle between the major axis of the elliptical cylinder and the anatomical and mechanical axes of the femur (Fig. 6). The anatomical axis of the femur was calculated by fitting a single cylinder to the vertices representing the diaphysis of the femur (from below the lesser trochanter to beginning of the popliteal swell). The mechanical axis was defined as a line connecting the center of the femoral head to the midpoint along the axis of the dual-cylinder between the two femoral condyles. We calculated the femoral head center by fitting a sphere to the vertices representing the articular surface of the femoral head.

Measurements used to quantify the orientation of the LFC elliptical cylinder. Angle A is the angle between the major axis of the ellipse and mechanical axis of the femur. Angle B is the angle between the major axis of the ellipse and the anatomical axis of the femur.
Analysis
Species were compared for all metrics using analysis of variance and Games-Howell post hoc tests for multiple comparisons. To determine whether morphologically distinct groups existed within any of the species (e.g., resulting from sexual dimorphism) we employed Gaussian mixture model (GMM) analyses using the expectation-maximization algorithm. Gaussian mixture modeling is a clustering technique that identifies subpopulations within a larger heterogeneous population. The technique provides maximum likelihood estimates of the parameters (means, variances, and mixing proportions) for multiple normal distributions fit to the observed data (Dong,1997). The best mixture model (i.e., which includes the best number of normal distributions) was identified using the Bayesian Information Criterion (BIC) and the Akaike Information Criterion (AIC). These criteria are relative and are used to select among potential models, with lower values indicting a better model fit, and can be used to calculate a probability for each model (Akaike,1981; Burnham and Anderson,2004).
To determine whether body size had any effect on the shape of the LFC (degree of ellipticalness) or the angle of the major axis of the ellipse relative to the axes of the femur, we regressed both metrics against femoral head diameter within species and within the sexes of each species. Although body mass is the preferred metric to quantify body size (Jungers,1985), this was unfortunately unavailable for most of the specimens in our sample. As a result we selected femoral head diameter as it has been shown to be highly correlated with body mass in the species examined here (Jungers,1991; Ruff et al.,1991, 1997; McHenry,1992; Grine et al.,1995; Ruff,2003). None of the regression analyses revealed statistically significant relationships and therefore are not reported, but the lack of correlation is discussed.
RESULTS
Summary statistics for all species are provided in Table 2. Both the chimpanzee and the gorilla LFCs are very close to circular (mean value = 1.07), with ellipse ratios that range from essentially perfectly circular (1.001) to values at the low end of the human range (1.20). Only nine of the 59 chimpanzees and gorillas, however, had ellipse ratios above 1.10. The human LFC is much more elliptical, ranging from 1.17 to 1.60, with a mean value of 1.33. The LFC of the human femur is significantly more elliptical than either that of the gorilla (P < 0.001) or the chimpanzee (P < 0.001), although the latter two do not differ from each other. Results for all Games-Howell post hoc comparison tests are provided in Table 3.
| Ellipse ratio | Angle B (Ellipse- anatomical axis angle) | Angle A (Ellipse- mechanical axis angle) | ||
|---|---|---|---|---|
| Pan | Mean | 1.07 | 69.79 | 73.87 |
| St dev. | 0.05 | 41.84 | 41.61 | |
| Range | 1.00–1.20 | 15.24–141.05 | 18.76–145.37 | |
| Gorilla | Mean | 1.07 | 77.19 | 80.94 |
| St dev. | 0.03 | 45.13 | 45.38 | |
| Range | 1.01–1.13 | 5.88–147.46 | 11.77–150.81 | |
| Homo | Mean | 1.33 | 93.45 | 97.44 |
| St dev. | 0.10 | 7.27 | 7.00 | |
| Range | 1.17–1.60 | 78.6–107.66 | 82.85–109.95 | |
| Ellipse ratio | Ellipse— Anatomical axis angle | Ellipse—Mechanical axis angle | |
|---|---|---|---|
| Pan–Gorilla | 0.098 | 0.983 | 0.814 |
| Pan–Homo | <0.001 | <0.001 | 0.007 |
| Gorilla–Homo | <0.001 | <0.001 | 0.188 |
Angles between the major axis of the LFC elliptical cylinder and the femoral mechanical and anatomical axes were found to be highly correlated in all species (R2 > 0.97 for all species), with the mechanical axis angle being slightly larger (5–10 degrees) than the anatomical axis angle. Because the two angle measures are so highly correlated and similar in value, further discussions will be restricted to the anatomical axis angle. In humans, the angle between the elliptical dual-cylinder and the anatomical axis of the femur falls within a narrow range (79–108 degrees), with a mean of 93 degrees. In chimpanzees and gorillas, the angle between the LFC ellipse major axis and the anatomical axis of the femur nearly covers the entire possible range of motion (approximately 140 degrees). While the angle appears to be uniformly distributed in Gorilla, the GMM analysis suggests that the distribution is bimodal in chimpanzees, indicating two separate orientations for the ellipse (Table 4 and Fig. 7). One of ellipse orientations forms an average angle of 38.85 degrees with the anatomical axis of the femur (standard deviation = 11.34 degrees), while the other has a mean value of 119.76 (standard deviation = 13.94 degrees).
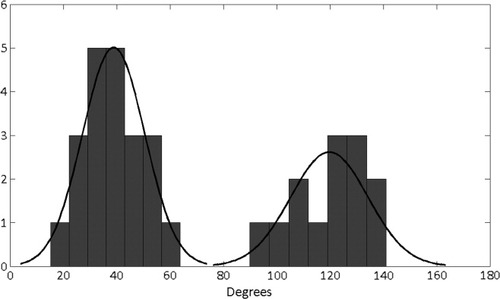
Histogram of angle B for Pan. Normal distributions are fit to the data as separated by the GMM.
| Componentsa | AIC (probability) | BIC (probability) |
|---|---|---|
| 1 | 353.38 (<0.01) | 356.43 (<0.01) |
| 2 | 322.19 (0.93) | 329.83 (0.99) |
| 3 | 327.39 (0.07) | 339.00 (0.01) |
| 4 | 332.62 (<0.01) | 349.41 (<0.01) |
- a Number of normal distributions fit to the observed data.
DISCUSSION
Although the mammalian knee follows a basic pattern of morphology (Haines,1942; Dye,1987), there is tremendous variation in mammalian knee morphology, reflecting different locomotor adaptations (see Salton and Sargis,2009, for a review). Features that have been used to distinguish climbing, digging, cursorial, and leaping mammals include the shape of the patellar groove, the shapes and relative sizes of the femoral condyles, the shape and position of the tibial tuberosity, and the sizes and shapes of the tibial spines, crest, and condyles. For instance, Tardieu (1981) demonstrated that in both digitigrade and plantigrade animals, the patellar surface and the femoral condyles form a single continuous surface, while in unguligrade animals there is a gap between these surfaces. Taylor (1976) noted that more cursorial forms of Viverridae have deeper patellar grooves relative to the other species. In a comprehensive analysis of 61 mammalian genera, Carrano (1997) established that the patellar groove of digitigrade mammals is deeper than that of plantigrade forms. Argot (2002) showed that climbing marsupials have less posteriorly projecting tibia condyles than do terrestrial marsupials. Elton (2001) observed that cercopithecoid species that differ in their use of arboreal and terrestrial environments can be distinguished based on the relative lengths and widths of the femoral condyles, while Organ and Ward (2006) demonstrated that the lateral tibial condyle can be used to distinguish bipedal and quadrupedal hominids.
Here for the first time, we quantitatively assess the difference in shape of the LFC in chimpanzees, gorillas and modern humans. The method confirms earlier qualitative descriptions finding modern humans to be much more elliptical than chimpanzees and gorillas (Heiple and Lovejoy,1971). In addition, our measurement in modern humans of the angle between the major axis of the LFC elliptical cylinder and the femoral anatomical axis is very close to 90 degrees as predicted by Heiple and Lovejoy (1971). The present study also confirms the quantitative “two-circle” description of the human LFC (Iwaki et al.,2000; Pinskerova et al.,2000; Freeman and Pinskerova,2004). In the two-circle description, one circle describes the shape of the posterior portion of the LFC, while a second larger circle is used to describe the more anterior/inferior portion. In humans, these two circles also represent two functional regions of the LFC (and there are parallel distinctions for the MFC). The more anterior/inferior circle, which has a larger radius of curvature, is known to represent the early portion of knee flexion (full extension to approximately 20 degrees), while the smaller more posterior circle represents the rest of active knee flexion (Pinskerova et al.,2000). The larger radius of curvature of the anterior portion of the LFC increases the contact between the tibia and femur in early portions of knee flexion (Kettlekamp et al.,1972; Maquet,1975), as used during walking. The degree of ellipticalness of the human LFC demonstrated here confirms the change in the radius of curvature across the human LFC, and the orientation of the ellipse confirms a smaller radius at the posterior portion of the LFC which increases moving anteriorly across the surface. While the “two-circle” model is useful for comparing among modern humans, this model would be more difficult to implement and compare across species because all species do not necessarily share the same basic pattern (e.g., more or fewer circles could be required).
Our results also confirm the visual description of a circular LFC for gorillas (Heiple and Lovejoy,1971; Tardieu,1981). The ellipse ratio for the LFC of gorilla indicates that the major axis is at most only 13% larger than the small axis, and thus it does approximate a circular cylinder in shape. In addition, the lack of any particular discernible angle between the ellipse major axis and the axes of the femur (anatomical or mechanical) suggests that the gorilla LFC does not contain functionally distinct regions. There are two possible explanations for the observed pattern. First, as offered by Lovejoy (2007) for chimpanzees, gorillas may not preferentially use any particular portion of the range of knee motion (and hence of the LFC surface). This would result in an LFC that is essentially circular and thus the ellipse model used here would not detect a particular angle of orientation. The second possible reason is unequal load transmission in the two femora condyles. The MFC is much larger than the LFC in the gorilla to accommodate the greater load borne by the MFC during quadrupedal walking (Preuschoft,1971; Preuschoft and Tardieu,1996). If this is the case, then any preferred knee position may not be demonstrable in the gorilla LFC as sufficient loading does not occur.
The LFC of the chimpanzee femur is also very nearly, on average, circular in profile. While five chimpanzees showed an ellipse ratio above 1.10, most were much closer to circular. Although the shape of the chimpanzee LFC is not nearly as elliptical as in humans, the particular patterning of the angle between the elliptical cylinder and the shaft of the femur suggests that there are areas of the chimpanzee LFC that are used preferentially. If no particular portion was used preferentially, one would expect, as with the gorilla, that the angle between the major axis of the ellipse and the shaft would be randomly and uniformly distributed through the possible range. Among the chimpanzee LFC, however, two clusters of angles were discovered. One possibility is that there are two separate chimpanzee LFC morphologies, each with its own region of decreased curvature. Inspection of group memberships resulting from the clustering analysis did not provide any obvious explanation for morphologically distinct groups (e.g., sex, subspecies, collection etc.), and regression against femoral head diameter (used as a surrogate for body mass) did not reveal any significant relationships. A second possibility, and the one favored here, is that all chimpanzee femora have two regions of the LFC with increased radius of curvature, and these two regions are nearly equal in size. Because the elliptical cylinder can only assume a single orientation, it might align with one of the areas of lower curvature in some femora, and in other femora align with the second area.
Only a more detailed analysis of the curvature of the LFC would be able to distinguish between these (and other potential) possibilities. Still, it is interesting to note the angles of the two different orientations of the LFC elliptical cylinder relative to the anatomical axis of the femur (Fig. 8). One is close to 40 degrees while the other is approximately 120 degrees. These angles indicate the orientation of the major axis of the ellipse; however, it is the minor axis that indicates the region of decreased curvature. Since the major and minor axes differ by 90 degrees, the minor axes of the ellipse orientations are approximately 130 degrees and 30 degrees relative to the anatomical axis of the femur. The smaller angle (30 degrees) may indicate full knee flexion that results from squatting behavior. Squatting with fully flexed knees (and hips) makes up almost 30 percent of all chimpanzee positional and locomotor activities (Hunt,1992), and is known to leave areas of reduced curvature on this region of the femoral condyles of modern humans (Trinkaus,1975). Alternatively, this region of lower curvature may be the impression left by the popliteus muscle. The larger angle (130 degrees) appears to indicate a knee position that is close to that reported for midstance knee angle during bonobo walking (D'Août et al.,2002). Thus, our analysis does not support the visual assessment that the chimpanzee LFC is circular in profile, and furthermore suggests that chimpanzee femora do have portions of the LFC that are used preferentially.
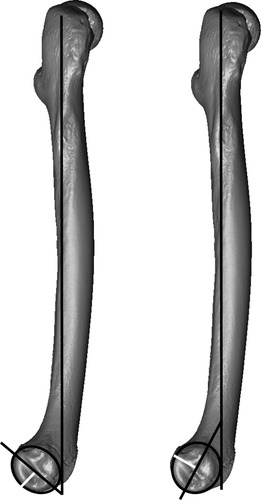
Two femora demonstrating the two groups (angle between ellipse major axis and anatomical axis of the femur) of Pan discovered using the GMM. On the left, the major axis of the ellipse forms an angle of approximately 40 degrees relative to the anatomical axis of the femur (vertical black line). The white line indicates the orientation of the minor axis (130 degrees relative to the anatomical axis) and the region of low curvature. On the right, the major axis of the ellipse forms an angle of approximately 120 degrees with the anatomical axis of the femur (vertical black line). The white line indicates the orientation of the minor axis (30 degrees relative to the anatomical axis) and the region of low curvature.
Femoral head diameter, used as a surrogate for body mass, did not exhibit a relationship with either the ellipse ratio or the angle of orientation of the ellipse relative to the rest of the femur, either within species or within sexes (also within species). If the angle of the ellipse orientation reflects typical joint position, then it is perhaps not surprising that this metric does not show a relationship with body mass. While changes in joint positions have been noted across species (Biewener,1989), joint angles are certain to be less variable within species. Such levels of variation may be difficult to detect morphologically, and may be affected by more than body mass. Femoral head diameter also did not show a relationship with the ratio of the major and minor axes of the ellipse. The chondral modeling hypothesis (Frost,1979, 1994, 1999; Hamrick,1999) has been proposed as the mechanism leading to the distal flattening of the human femoral condyles (Plochocki et al.,2009), predicting that high levels of hydrostatic pressure within a frequently loaded region of articular cartilage inhibits chondrocyte mitosis and articular cartilage growth. Adjacent regions experiencing lower loading would not be inhibited and this differential growth leads to changes in joint curvature. Under this hypothesis, it might be expected that larger individuals within a species would experience greater joint loading leading to more joint flattening (Latimer et al.,1987; Latimer and Lovejoy,1989). Joint loading, however, is more than a product of body mass alone and includes individual behavior, which may in part explain the lack of correlation found here.
The main limitation of the approach used here is that the elliptical cylinder can only represent the dominant shape of the LFC. If multiple areas of low curvature are present on an articular surface, the ellipse model can only identify one of them because it can only assume a single position, orientation, and size. Another complication is the greater capacity for internal/external rotation of the knee in chimpanzees (and presumably gorilla) compared to humans as demonstrated by Tardieu (1986a, b). The larger range of knee internal/external rotation in chimpanzee knees likely changes the contact point between the lateral femoral and tibial condyles for a given knee flexion position. This opens the possibility that the regions of low curvature in the non-human ape condyles detected by the ellipse model do not indicate stereotypical knee flexion/extension position as they do humans. The difference in LFC shapes may also reflect known differences in lateral meniscus morphology (Tardieu,1986a, b) further complicating the direct interpretation of the ellipse model used here. Although non-human apes certainly use a more varied locomotor repertoire than modern humans, their locomotor behavior is dominated by quadrupedalism (Doran,1996). Consequently, we do not think the correlation between the regions of low curvature detected by the ellipse model and typical knee positions (midstance and squatting) in chimpanzees is coincidental. Regardless, it is clear that a more detailed approach to mapping articular surface curvature, relative to the axis of joint rotation, is desirable to obtain finer-grained information about joint curvature, and especially changes in joint curvature across a single surface. Such detailed mapping could be combined with kinematic data to strengthen our understanding of the connection between articular surface morphology, joint function, and locomotor behavior. Although sophisticated approaches for understanding three-dimensional shape currently exist (i.e., geometric morphometrics (Bookstein,1989; Rholf and Slice,1990; Gunz et al.,2005, 2009), such techniques do not quantify curvature per se and certainly not with respect to specific functional axes. As a result novel methods will be required.
CONCLUSION
Understanding the connection between skeletal form and function remains a primary task of functional morphologists. Here we provide a novel orientation-free method for quantifying an important aspect of knee morphology—the shape of the LFC, and for the first time provide quantitative values for the degree of ellipticalness in chimpanzees, gorillas, and modern humans. Our analyses confirm, and quantitatively support previous qualitative analyses (Heiple and Lovejoy,1971; Tardieu,1981) which argued that modern human LFC are significantly more elliptical than that of chimpanzees and gorillas. We also confirmed the pattern of the change in the radius of curvature in the modern human LFC, which indicates a preferential use of the most anterior portions of the LFC during walking and standing. Surprisingly, we found that chimpanzee LFC are also slightly elliptical, and that these ellipses are clustered around two particular angles which appear to correlate with common locomotor and postural positions.
Acknowledgements
The authors thank Patricia A. Kramer for comments during the development of this project and manuscript, and Alexander Stöβel and K. Lindsay Eaves for critique and suggestions. They are also indebted to Dr. Lee Jantz and Dr. Richard Jantz (The University of Tennessee), Linda Gordon (National Museum of Natural History, Washington D.C.), Nora Lange and Dr. Frieder Mayer (Museum für Naturkunde, Berlin), and Maria Teschler-Nicola and Barbara Herzig (Naturhistorisches Museum Wien), and Uta Olbrich-Schwarz (Max Planck Institute for Evolutionary Anthropology) for access to collections in their care. Finally, they also thank the associate editor and two anonymous reviewers for helpful comments and critiques that substantially improved this work.




