Social networks dynamics revealed by temporal analysis: An example in a non-human primate (Macaca sylvanus) in “La Forêt des Singes”
Abstract
This study applied a temporal social network analysis model to describe three affiliative social networks (allogrooming, sleep in contact, and triadic interaction) in a non-human primate species, Macaca sylvanus. Three main social mechanisms were examined to determine interactional patterns among group members, namely preferential attachment (i.e., highly connected individuals are more likely to form new connections), triadic closure (new connections occur via previous close connections), and homophily (individuals interact preferably with others with similar attributes). Preferential attachment was only observed for triadic interaction network. Triadic closure was significant in allogrooming and triadic interaction networks. Finally, gender homophily was seasonal for allogrooming and sleep in contact networks, and observed in each period for triadic interaction network. These individual-based behaviors are based on individual reactions, and their analysis can shed light on the formation of the affiliative networks determining ultimate coalition networks, and how these networks may evolve over time. A focus on individual behaviors is necessary for a global interactional approach to understanding social behavior rules and strategies. When combined, these social processes could make animal social networks more resilient, thus enabling them to face drastic environmental changes. This is the first study to pinpoint some of the processes underlying the formation of a social structure in a non-human primate species, and identify common mechanisms with humans. The approach used in this study provides an ideal tool for further research seeking to answer long-standing questions about social network dynamics.
1 INTRODUCTION
Primates mainly live in perennial social groups (Aron, Passera, & Pasteels, 2009). Although group living provides individuals with many advantages (Alados, 1985; Avilés & Tufino, 1998; Mann, 2000), it is dependent upon the use of mechanisms to maintain the homeostasis between individuals (i.e., a trade-off between individual costs and benefits). Individuals establish relationships with their congeners using different types of behaviors (Kutsukake, 2009). These include tolerance behaviors (which allow conspecific to gather), agonistic behaviors (used for the management of conflicts), and affiliative behaviors, which enable the construction of a cohesive social structure (Aureli & de Waal, 2000). Several authors have already underlined the crucial importance of gaining an understanding of the evolutionary processes and adaptive mechanisms via which social cohesion in animal societies is maintained (Kanngiesser, Sueur, Riedl, Grossmann, & Call, 2011; Lusseau, 2003; Manno, 2008; Sosa, 2014). Affiliative behaviors are known to allow group cohesion (i.e., reciprocal mutualism) (Clutton-Brock, 2009), and also to enable the creation of coalition relationships between individuals (e.g., allogrooming behavior) (De Waal, 1997; De Waal & van Roosmalen, 1979; Seyfarth & Cheney, 1984), consequently influencing rank acquisition (De Waal, 1997; De Waal & Roosmalen, 1979; Flack, Girvan, De Waal, & Krakauer, 2006; Seyfarth & Cheney, 1984).
Given the multitude of functions of affiliative relationships described above, and their clear fitness consequences, it is important to pinpoint the rules that govern their formation and maintenance (Silk, Alberts, & Altmann, 2003; Silk et al., 2010). In doing so, we may highlight individual strategies for forming coalition relationships and thereby shed new light on the complex processes underpinning the development of a hierarchical and multi-behavioral social structure. Social network analytical (or SNA) techniques are well-suited tools to unravel the complex patterning of affiliative relationships in primate societies because they facilitate a global approach to behavioral analysis. In particular, the multi-level approach of SNA allows a more thorough analysis of group behaviors than the study of dyadic relationships, and provides a global picture of complex social structure (Sueur, Jacobs, Amblard, Petit, & King, 2011).
To date, social network analysis applications have focused on static networks when addressing social behavioral questions. Yet animal societies are dynamic systems in which social relationships are constantly changing through events such as deaths, births, migration, environmental variations (seasonal or not), and so on. This makes the temporal study of animal social networks an essential step in understanding how these complex social systems handle such dynamic processes. For example, through the study of the overall network structure, we can understand how it influences the transmission of information and/or diseases (Romano et al., 2016), revealing how evolution may shape animal societies to optimize species resilience (Kanngiesser et al., 2011; Lusseau, 2003; Sosa, 2014). Other studies aimed to understand how animal groups handle environmental variations such as meteorological changes and prey density variations over several years (Ilany, Booms, & Holekamp, 2015). A dynamic SNA approach also makes it possible to study the way groups handle demographic variations through natural processes of migration (Borgeaud, Sosa, Sueur, Bshary, & van de Waal, 2016), or when experiencing a massive loss of individuals (Boucherie, Sosa, Pasquaretta, & Dufour, 2016). Another interesting aspect raised by the SNA approach is the presence of some dynamic interactional patterns that seem to be common in many social systems. The triadic closure process is one such example, and has been identified in humans (Scholz, Atzmueller, Kibanov, & Stumme, 2014), crows (Boucherie et al., 2016), hyenas (Ilany et al., 2015), and non-human primates (Borgeaud et al., 2016). These common patterns are interesting not only from a comparative perspective but also at an evolutionary level, as it is closely linked to reciprocal altruism.
These results provide part of this picture by revealing the existence of certain interactional patterns that could provide information about (i) how an individual structures his own social network (ego-network) and (ii) how such patterns shape the global structure of a specific network. Depending on the type of structure concerned, it could then be possible to identify certain intrinsic characteristics (resilience, the optimization of information transfer, etc.). This approach may, therefore, be a valid tool to assess how a network (whether individual or global) varies over time and deals with events such as the loss of individuals or the transmission of diseases.
Network growth through the preferential attachment process (GPA) (Barabási & Albert, 1999) is one such example. In this process, the most connected individuals are more likely to receive new connections, allowing the emergence of scale-free networks. This type of structure is characterized by a small number of extremely central individuals that are indispensable to the group, as their disappearance leads to the fragmentation, and, therefore, the destruction, of the network. Of course, this structure is important from an epidemiologic perspective regarding the spread of disease (Pastor-Satorras & Vespignani, 2001). This process also highlights a phenomenon of attraction to central individuals, which may be related to the attractiveness of high-ranking individuals, as described in numerous studies (see Schino, 2001 for a meta-analysis) and put forward by Seyfarth (1977) then the market theory (Noë & Hammerstein, 1995) with respect to allogrooming. This PA process may also be present in non-human primates, possibly characterized by indegree popularity micro-motifs. Here, we assume that this micro-motif could also be present in Barbary macaque societies, given the attractiveness of high-ranking individuals.
Another example is (TC) (Banks & Carley, 1996), that describes the fact that individuals preferably create links with individuals who are connected to individuals they already know. This dynamical behavioral pattern is generally described as follows: “the friend of my friend is my friend” and is characterized in networks by transitive triplet micro-motifs. This process highlights how individuals extend their network and underlines the importance of the first individual connections for future network expansion. Moreover, previous studies have shown that the TC process produces strongly interconnected networks (Skvoretz, 1991), and potentially facilitating cooperation within a group (Banks & Carley, 1996; Buskens, 2002; Coleman, 1988; Lou, Tang, Hopcroft, Fang, & Ding, 2013; Righi & Takacs, 2014; Walker, Kogut, & Shan, 1997; Watts, 1999). In a recent study, Righi and Takacs (2014) created an agent-based model in which an agent plays the prisoner's dilemma with peers, and showed that cooperation disappears without triadic closure process, regardless of whether strategies can be used. Similar results were obtained for the free rider problem (Coleman, 1988), in which individuals have to deal with a costly but collectively advantageous choice. These data evidenced that the triadic micro-structure is the only one featuring a “trust transitivity” property (if A trusts B and B trusts C, A is more likely to trust C). As reciprocity is a well-known phenomenon in primates (non-human and human) (Clutton-Brock, 2009; Kappeler & Van Schaik, 2006), it would not be surprising to find evidence of TC process in the primate order. From a biological perspective, triadic motifs could be explained by several well-known mechanisms. For example, non-human primates are known to be capable of transitive inference (deducing that A>C from observing that A>B and B>C) (Addessi, Mancini, Crescimbene, Padoa-Schioppa, & Visalberghi, 2008), which should allow them to build transitive triplets. Nepotism is also a widely known phenomenon observed not only among macaques but in most primate species (Silk, 2001), whereby young individuals create preferential bonds with closely related congeners. This simple phenomenon alone constitutes the TC process. We, therefore, assume that this micro-motif is present in Barbary macaque societies, enabling individuals to facilitate and accelerate the extension of their ego-networks and allowing them rapid access to a more central position within the group. Enhanced centrality in the group ensures that an individual is better informed and facilitates coalitional relationships (Sueur, Petit et al., 2011). Moreover, as this process is intimately linked to reciprocal altruism, it is likely generated by evolution.
Another interesting aspect is the analysis of homophily (Lazarsfeld & Merton, 1954). This process describes preferential interactions between individuals sharing common attributes. It is crucial to understand how individuals interact according to their own attributes (gender, age, matriline, and hierarchical rank) and those of others before attempting to build a picture of how they build their ego-networks. Moreover, extensive research on human homophily has stressed that it is a major mechanism in stranger cooperation (Haun & Over, 2015), social learning (Buttelmann, Zmyj, Daum, & Carpenter, 2013), and the transmission of culture and norms (Chudek & Henrich, 2011). Determining the presence or absence of this mechanism can, therefore, be crucial in many aspects of social cognition and evolutionary cognitive psychology. Homophily has already been demonstrated in many animal species: cetaceans (Lusseau & Newman, 2004), fishes (Croft et al., 2005), marmots (Wey & Blumstein, 2010), non-human primates (Cords, 2002; Silk, 2001; Sosa, 2016), and humans (McPherson, Smith-Lovin, & Cook, 2001). The present study examines whether a temporal approach can reveal the presence of homophily in a non-human primate species. We assume that, for example, males tend to preferentially interact with males in order to create or consolidate their coalitional network. In the same way, we can expect females to preferentially interact with females due to the well-known female kinship phenomenon (Silk, 2001). As previously explained, such mechanisms are also widely involved in several evolutionary aspects.
The study presumes that from a purely strategic perspective, an individual will attempt to (i) have preferential affiliative interactions with central individuals (PA process); (ii) extend its ego-network through preferential interactions with “friends of his friends” (TC process); (iii) preferentially interact with individuals with same attributes (homophily process). These processes should also reveal the main individual behavioral strategies involved in affiliative networks. These individual strategies strongly affect the coalitional system and thus, in turn, the hierarchical structure and the global affiliative network structure. It is, therefore, vital to consider these processes if we wish to obtain a holistic perspective of the complex systems in animal societies.
2 DESCRIPTION
This study focuses on three dynamic micro-structural mechanisms (TC, PA, and homophily) and the role they play in the formation of an affiliative social structure of a social group of Macaca sylvanus over a 3-year period. This was achieved by using the advanced Social Network Analysis (SNA) tool call SIENA (Simulation Investigation for Empirical Network Analysis) (Snijders, 2001) to infer the processes involved in the observed evolutionary pattern of three affiliative social networks (allogrooming, sleep in contact and triadic interaction) over time by creating new connections or removal of existing connections.
SIENA (Snijders, 2001) is a log-linear dynamic model based on Markov processes that allows longitudinal network analysis. SIENA proposes a statistical model for longitudinal data analysis that requires at least two observations of the state of a network at two consecutive moments (in the Markov process, the first observation is the predictor and the second one the predicted). The model assumes that some observations are missing between the two moments and that changes occur on a linear time basis through small steps between the two states observed. SIENA also allows to consider demographic changes over time by estimations through the “Method of Moments.” SIENA builds a predictive model that detects link changes within the network by testing multiple hypotheses and selecting the best model according to the likelihood. For more details on SIENA model, see Ripley, Snijders, and Preciado (2014). SIENA provides a dichotomous analysis of inter-individual connections. This model aims to explain the emergence, pattern and evolution of all individuals’ relations within the network. It describes the changes occurring in these relations over time, according to the influence of different factors. Three such factors are examined in this paper, namely the dynamic micro-structural mechanisms triadic closure (TC), preferential attachment (PA), and homophily.
SIENA is based on several postulates. The model is based on the purposive action of individuals: actors are considered to be aware of the state of the network as a whole (i.e., they are informed of the different relationships between other group members). They make choices consciously and can opt to create, maintain, or remove an association in order to optimize their position within the group. These choices are made independently (i.e., at each time step, each actor makes a choice considering the state of the network) but can be constrained by exogenous factors (e.g., individual attributes) and random effects. Individuals can create or delete a link at each step.
First, two potential structural effects were tested to explain the network changes over time: the “TransTrip” (transitive triplets) and “InPop” (indegree popularity) effects, which respectively indicate the presence of triadic closure (TC) and preferential attachment (PA) processes. In order to control kinship in the triadic closure process, we added the “sameXTransTrip” effect that examines if transitive triplets are between same-attribute individuals (in our case, close relatives). Moreover, in order to control attractiveness to high-ranking individuals, we added the “AltX” effect which determines whether actors with higher values of their attributes tend to be more appealing to others and hence have higher indegrees.
We also built a second model using the “SimX” effect. It calculates the similarity scores between too individuals according to a covariate. This covariate can be an attribute, which allowed us to examine the presence of homophily according to age, gender, and hierarchical rank.
As suggested by Snijders (2001), density and reciprocity effects were included in all models. Calculation details for all the effects are described in Table 1. Further information can be found in the SIENA manual (Snijders, Steglich, Schweinberger, & Huisman, 2008).
| Model | Formula | Description |
|---|---|---|
| TransTrip (i.e., TC) | 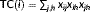 |
Analyzes individuals’ transitive triplets. It describes the «friends of my friends are my friends» phenomenon. |
| TC(i) is the number of transitive triplets in the ego-network of i, i.e., i is linked to j and h, which are also linked together. | ||
| Here Xij in {0, 1} denotes a link from i to j. | ||
| InPop (i.e., PA) | 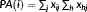 |
Analyzes individuals’ popularity. This effect disclose individual’ preference to be linked to popular individual (i.e., individual with highest degrees receive more incoming links [indegree]) |
| PA(i) is defined, for individual i, as the number of relation received by individual j whom i is linked to. | ||
| Here xij in {0,1} denotes a link from i to j. | ||
| SimX (i.e., homophily) | 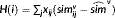 |
Analyzes individuals’ homophily, i.e., the tendency for two individuals to be linked if they share similar attributes. |
| with | H(i) is the sum of centered similarity scores 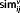 between i and j according to the covariate v (i.e., age, gender, and hierarchical rank). between i and j according to the covariate v (i.e., age, gender, and hierarchical rank). |
|
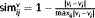 |
Here xij in {0,1} denotes a link from i to j and 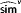 is the mean value of all similarity scores. The similarity scores are computed as the normalized difference between the two covariates vi and vj. is the mean value of all similarity scores. The similarity scores are computed as the normalized difference between the two covariates vi and vj. |
|
| AltX (i.e., attractiveness according to attribute X) | 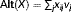 |
Covariate-related popularity, defined by the sum of the covariate over all actors to whom i has a tie. |
The model computes the occurrence of each process tested (PA and TC) to explain the observed dynamics. A Wald-type test was carried out for each parameter to evaluate the probability of obtaining the observed relationship between process and the network dynamics by chance alone. The t-ratio parameter indicates the convergence of the algorithm (deviation between simulated values and observed values), with values below 0.1 and an overall maximum convergence ratio of 0.25 (see Ripley, Snijders, et al., 2014 for more information). All analyses were performed with 1,000 permutations using RSIENA (Ripley, Boitmanis, & Snijders, 2014).
3 EXAMPLE
3.1 Study site and subjects
The study took place in “La Forêt des Singes,” Rocamadour, France, a zoological park created in 1974 for the conservation of several groups of M. sylvanus. The 141 individuals of the park are divided into three semi-free ranging groups living in a 20-hectare forest. The individuals are fed in designated foraging areas and water is provided ad libitum. For more details on the management of the park, see de Turckheim and Merz (1984). As we performed simple observations without any type of intervention, we did not require any authorization from the CCNE (French National Advisory Ethics Committee). Moreover, this research adhered to the American Society of Primatologists principles for the ethical treatment of primates.
This study was carried out on one of the three groups. The observations were conducted over 3 periods, namely a first period of four months from July to October 2011 (the post-natal period), 3 months from April to June 2012 (the birth period and pre-mating season), and finally a 4-month period from November 2012 to February 2013 (the mating season). The social network data resulting from these observations over the three periods was used to analyze the dynamics of these networks over time. Three affiliative behaviors were examined, namely allogrooming, sleep in contact, and triadic interactions.
Triadic interaction (Deag, 1974) is a species-specific affiliative behavior. It is the interaction between two adult or sub-adult individuals, one of which is carrying a baby and heading for the other receptive individual. During the interaction, both individuals display teeth chattering, one holding the baby's hind legs and smelling its ano-genital area, and the other holding the front legs and smelling the baby's face. The baby also shows teeth chattering. This behavior solely occurs in affiliative contexts and favors the consolidation affiliative and coalitional bonds between two adult individuals. To clearly distinguish between triadic closure phenomenon and triadic interaction in this paper, the term “infant-mediated behavior” will be used to describe triadic interaction.
For the first period, the number of focal individuals in the group was N = 51 (24 females and 27 males). The four individuals that were born during this period were added to the network at the age of 1 (they were not considered to be actively involved in social interactions until they reached this age). Following the death of one individual between the first period and the second period, the number of focal individuals in the second period was N = 54 (25 females and 29 males). The number of focal individuals remained unchanged for the third period (N = 54). No migrant individuals joined the group during the observation periods. Focal individuals were between 1 and 26 years old. We decided to run the analysis across the entire group to reveal any possible common interactional patterns among the individuals of a non-human primate society.
3.2 Behavioral observations
Observations took the form of repeated focal samplings (Chase, Bartolomeo, & Dugatkin, 1994) of 30 min per individual, with a total observation time of 1,905 hr. Observed interactions included 3,320 allogrooming interactions, 1,372 infant-mediated behaviors, and 2,779 sleep-in-contact behaviors. These three types of behaviors are all affiliative behaviors. The behavioral observations were performed using an iPad 1 (Inc, 1976) and the application What I See 2.0 (Heuser, 2009) to register the individuals involved, and the direction and duration of the behaviors.
3.3 Statistical analysis
3.3.1 Calculation of relative frequencies
As the total number of observations per individual varies slightly in each period, we adjusted the matrices frequencies by dividing each interaction frequency between two individuals during a given period by the total number of observations for the two individuals. The resulting tables represent the average number of allogrooming, infant-mediated and sleep-in-contact behaviors per observation for each pair of individuals. This number is hereafter referred to as the relative frequency (RF) (Overdorff, Erhart, & Mutschler, 2005).
3.3.2 Binary matrices transformation
The statistical model used to analyze the dynamics of social interactions uses binary networks (i.e., the presence or absence of a connection between two individuals). The mean + 1.96 * standard deviation of RF was chosen as the threshold for a given behavior and time period. Below this threshold, links were deleted and only the strongest links of the network were retained for analysis (Fedurek, Machanda, Schel, & Slocombe, 2013; Levé, Sueur, Petit, Matsuzawa, & Hirata, 2016). This method of network binarization was used by Fedurek (2013) to study social networks.
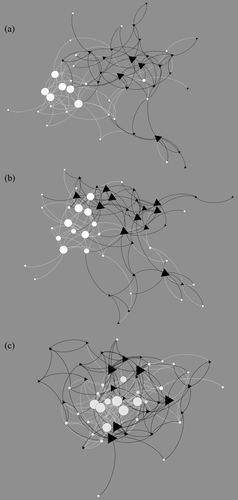
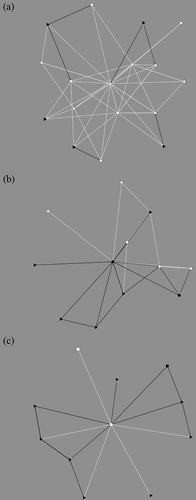
The nine resulting networks were analyzed to identify the social mechanisms governing the creation of new connections or the removal of existing connections over time. The density of these affiliative networks over time can be found in Table 2. See Figure 1 for an example of social (allogrooming) network dynamics over the three periods.
| Allogrooming | Sleep in contact | Triadic interaction | |
|---|---|---|---|
| Period 1 | 0.044 | 0.043 | 0.039 |
| Period 2 | 0.058 | 0.046 | 0.030 |
| Period 3 | 0.072 | 0.052 | 0.030 |
4 RESULTS
Both the allogrooming and the infant-mediated behavior networks show a clear pattern of transitive triplets (allogrooming: χ2 = 25.768, p < 0.001; infant-mediated behavior: χ2 = 8.926, p < 0.001). This confirms the occurrence of triadic closure in such networks. Controlling for kinship in this transitive triplets does not give significant results (allogrooming: χ2 = 0.040, p > 0.05; infant-mediated behavior: χ2 = 0.013, p > 0.05), and indicates that this process is not ruled through nepotism. We also note that the density of the network is relatively low, so TC process cannot be a side effect of high density, and this remains unlikely as the SIENA model also controls for the density of the network through the density effect. See Figure 2 for the ego-networks of some individuals to highlight triadic bounds.
Indegree popularity effect is only significant for infant-mediated behaviors (χ2 = 25.109, p < 0.01), revealing the presence of preferential attachment in this network. This points to the presence of highly central individuals with greater attractiveness for new incoming interactions. Controlling for attractiveness to high-ranking individuals did not produce significant results (χ2 = 0.038, p > 0.05).
Tests for attractiveness to high-ranking individuals with AltX effect for the allogrooming behavior revealed a significant effect (χ2 = 12.11, p < 0.01). This result is in line with both Seyfarth's prediction (1977) and the market theory (Noë & Hammerstein, 1995). When considered alongside the non-significant indegree popularity results obtained for allogrooming behavior, this result shows that individuals with a high degree do not necessarily have a high indegree and thus are not necessarily high-ranking.
Homophily is significant for infant-mediated behavior only with gender attribute (χ2 = 32.027, p < 0.01). When the homophily analysis is run on the first two periods only (period 3 is excluded as it corresponds to the mating season), we obtain significant homophily by gender for allogrooming (χ2 = 78.618, p < 0.01) and sleep-in-contact behaviors (χ2 = 12.292, p < 0.01), disclosing seasonal changes in this micro-structural pattern (see Figure 1 for the allogrooming network showing homophily by gender for the first two periods (Figure 1a,b).
Homophily effect for age and hierarchical rank is not significant over the three periods. It could not be tested for the first two periods alone, as SIENA can only test the effect of variables with values changing over time for three or more periods. There is, therefore, no confirmation that this effect exists outside the mating season.
See Tables 3-5 for a synthesis of the results of the models.
| Siena model | Wald-type test | |||||
|---|---|---|---|---|---|---|
| Estimate standard error | Estimate standard error | t-Ratio | χ2 | df | p-Value | |
| Structural effects | ||||||
| Constant (from periods 1 to 2) | 7.87 | 1.14 | −0.07 | |||
| Constant (from periods 2 to 3) | 19.91 | 3.25 | −0.05 | |||
| Density | −1.79 | 0.09 | −0.03 | 399.708 | 1 | 0.000 |
| Reciprocity | 0.99 | 0.12 | −0.02 | 70.215 | 1 | 0.000 |
| Transitive triplets | 0.25 | 0.06 | −0.04 | 25.768 | 1 | 0.000 |
| Indegree popularity | 0.01 | 0.02 | −0.03 | 0.072 | 1 | 0.789 |
| Transitive triplets same kinship | 0.14 | 0.7 | −0.05 | 0.040 | 1 | 0.839 |
| Indegree popularity hierarchy | 0 | 0 | 0.00 | 12.116 | 1 | 0.000 |
| Overall maximum coverage ratio: 0.1039 | ||||||
| Attributes effects | ||||||
| Constant (from periods 1 to 2) | 7.24 | 1 | 0.07 | |||
| Constant (from periods 2 to 3) | 20.07 | 3.77 | 0 | |||
| Density | −1.68 | 0.06 | 0.06 | 756.864 | 1 | 0.000 |
| Reciprocity | 1.07 | 0.12 | −0.03 | 78.618 | 1 | 0.000 |
| Same gender | 0.09 | 0.07 | 0.02 | 1.649 | 1 | 0.199 |
| Hierarchy similarity | −0.3 | 0.2 | 0.02 | 2.11 | 1 | 0.146 |
| Homophily by gender for the two first periods only | ||||||
| Constant (from periods 1 to 2) | 8.89 | 1.16 | 0.04 | |||
| Density | −2.14 | 0.12 | −0.03 | 28.369 | 1 | 0.000 |
| Reciprocity | 0.57 | 0.24 | −0.03 | 756.864 | 1 | 0.000 |
| Same gender | 0.57 | 0.15 | −0.04 | 78.618 | 1 | 0.000 |
| Overall maximum coverage ratio: 0.1039 | ||||||
- Constant (period I), Constant (period 2), Outdegree (density), and Reciprocity are parameters that have to be included in the model but do not need to be interpreted (see Snijders et al., 2008 for more information).
- Values for notable significant effects are in bold.
| Effects | Estimate | Standard error | t-Ratio | χ2 | df | p-Value |
|---|---|---|---|---|---|---|
| Structural effects | ||||||
| Constant (from periods 1 to 2) | 11.93 | 2.58 | 0.03 | |||
| Constant (from periods 2 to 3) | 42.06 | 19.25 | 0.04 | |||
| Density | −2.01 | 0.51 | 0.0.3 | 15.555 | 1 | 0.000 |
| Reciprocity | 0.91 | 0.13 | 0.05 | 46.876 | 1 | 0.000 |
| Transitive triplets | 0.26 | 1024.61 | 0.07 | 0.000 | 1 | 1.000 |
| Indegree popularity | 0.05 | 0.11 | 0.07 | 0.209 | 1 | 0.647 |
| Overall maximum convergence ratio: 0.1761 | ||||||
| Attributes effects | ||||||
| Constant (from periods 1 to 2) | 9.65 | 1.45 | ||||
| Constant (from periods 2 to 3) | 34.37 | 17.22 | ||||
| Density | −1.78 | 0.07 | 0.12 | 696.944 | 1 | 0.000 |
| Reciprocity | 0.99 | 0.14 | 0.01 | 48.050 | 1 | 0.000 |
| Same gender | 0.04 | 0.08 | 0.07 | 0.185 | 1 | 0.667 |
| Same age | −0.29 | 0.27 | 0.05 | 1.099 | 1 | 0.294 |
| Hierarchy similarity | −0.24 | 0.20 | 0.05 | 1.455 | 1 | 0.228 |
| Overall maximum convergence ratio: 0.1723 | ||||||
| Homophily bygender for the two first periods only | ||||||
| Constant (from periods 1 to 2) | 12.63 | 2.580 | ||||
| Density | −2.24 | 0.130 | −0.010 | 315.539 | 1 | 0.000 |
| Reciprocity | 1.31 | 0.230 | −0.110 | 33.097 | 1 | 0.000 |
| Same gender | 0.49 | 0.140 | 0.020 | 12.292 | 1 | 0.000 |
| Overall maximum convergence ratio: 0.1619 | ||||||
- Constant (period I), Constant (period 2), Outdegree (density), and Reciprocity are parameters that have to be included in the model but do not need to he interpreted (see Snijders et al., 2008 for more information).
- Values for notable significant effects are in bold
| Siena model | Wald-type test | |||||
|---|---|---|---|---|---|---|
| Effects | Estimate | Standard error | t-Ratio | χ2 | df | p-Value |
| Structural effects | ||||||
| Constant (from periods 1 to 2) | 8.17 | 1.56 | −0.02 | |||
| Constant (from periods 2 to 3) | 8.75 | 2.05 | 0.04 | |||
| Density | −2.48 | 0.13 | 0.02 | 382.705 | 1 | 0.000 |
| Reciprocity | 0.25 | 0.33 | 0.01 | 0.607 | 1 | 0.436 |
| Transitive triplets | 0.52 | 0.17 | 0.05 | 8.926 | 1 | 0.003 |
| Indegree popularity | 0.11 | 0.02 | 0.07 | 25.109 | 1 | 0.000 |
| Transitive triplets same Kinship | 3.6748 | 32.0091 | −0.0807 | 0.013 | 1 | 0.908 |
| Indegree popularity hierarchy | −0.0004 | 0.0018 | 0.0016 | 0.038 | 1 | 0.8453 |
| Overall maximum convergence ratio: 0.1101 | ||||||
| Attributes effects | ||||||
| Constant (from periods 1 to 2) | 7.62 | 1.11 | 0.03 | |||
| Constant (from periods 2 to 3) | 8.61 | 1.16 | −0.01 | |||
| Density | −2.34 | 0.11 | −0.09 | 475.652 | 1 | 0.000 |
| Reciprocity | 0.17 | 0.3 | −0.04 | 0.34 | 1 | 0.56 |
| Same gender | 0.69 | 0.12 | −0.06 | 32.027 | 1 | 0.000 |
| Same age | −1.23 | 0.73 | −0.03 | 2.827 | 1 | 0.093 |
| Hierarchy similarity | −0.19 | 0.29 | 0.03 | 0.42 | 1 | 0.517 |
| Overall maximum convergence ratio: 0.1303 | ||||||
- Constant (period 1), Constant (period 2), Outdegree (density), and Reciprocity are parameters that have to he included in the model but do not need to be interpreted (see Snijders et al., 2008 for more information).
- Values for notable significant effects are in bold.
5 DISCUSSION
Current knowledge on primate capability of transitive inference (Addessi et al., 2008), market theory (Noë & Hammerstein, 1995) and previous research on animal homophily (Silk, 2001; Lusseau & Newman, 2004) lead us to expect the presence of some processes (TC, PA, and homophily) in three social affiliative networks in a non-human primate species, M. sylvanus. Revealing their presence helps us to better understand how individuals living in a same group maintain and rearrange affiliative relationships. This also highlights some interesting evolutionary aspects of animal societies, as will be discussed in the following paragraphs.
More specifically, we demonstrated the involvement of the triadic closure (TC) process in allogrooming and infant-mediated behavior networks. Such behaviors are known to play a critical role in the establishment of support relationship between two individuals (Deag, 1974; De Waal, 1997; De Waal & van Roosmalen, 1979; Seyfarth & Cheney, 1984). Alternatively, the fact that TC is not found in the sleep-in-contact network may reflect the low contribution of this behavior in the creation of friendship bonds. It may involve individuals who were already connected and who selected their interaction with other individuals, with infrequent changes of partners. Unfortunately, very little is known about sociality and sleep-in-contact in non-human primates (McNamara, Barton, & Nunn, 2010) and further research is needed to better understand these issues.
The TC phenomenon highlights the existence of local network motifs that describe how individuals interact in a preferential way with specific partners. This simple rule enables us to predict short-scale network variations in the network, which cannot be accomplished at a dyadic level. This process can play an important role in the construction of ego-networks by young individuals (i.e., juveniles and sub-adults). However, we do not observe any involvement of kinship in the establishment of this process. The fact that primates are known to be capable of transitive inference allows us to assume that this cognitive process could be involved in the TC process, enabling individuals to facilitate and accelerate the extension of their ego-networks, and allowing them rapid access to a more central position within the group which eventually improves their fitness (Clutton-Brock, Albon, & Guinness, 1984; Ellis, 1995).
From a more global and evolutionary perspective, it is increasingly accepted that local network motifs can be elements in the construction of complex networks with specific properties (Mangan & Alon, 2003; Milo et al., 2002). The main topological effect of TC mechanism is the clusterization (i.e., subgroups inside the network) of the network or the emergence of cohesive groups, leading to reciprocity and cooperation. These phenomena engender adaptive value (increased fitness) (Coleman, 1988; Lion & Baalen, 2008). TC has been observed in other species, including spotted hyenas (Ilany et al., 2015), rooks (Boucherie et al., 2016), and vervet monkeys (Borgeaud et al., 2016). However, this theory does not make it possible to determine whether triadic closure is the evolutionary consequence or the prerequisite of cooperation. More studies are needed to understand whether triadic closure is a by-product of social network or relatedness, or whether it is a social strategy leading to improved cooperation between multiple partners. Finally, the TC process may also be a mechanism enabling network assortativity (i.e., individuals interact in a preferential way with individuals of the same degree) (Lusseau et al., 2006), which is a key element in social network resilience (Newman, 2002, 2003), and thus has implications on an ecological and evolutionary level.
Concerning PA process, it is only observed in the infant-mediated behavior network. This process can also provide information about strategic aspects driving social interactions, highlighting an individual inclination to interact with high-degree individuals. It seems reasonable to assume that interacting with the latter, which could be considered “central” and “key” due to their connection to a high number of individuals in the group, could enable group members to build themselves a larger social network, which could subsequently be extended through TC processes. Interestingly, the PA process was only observed in the infant-mediated behavior social network in this study. This species-specific behavior allows the consolidation of inter-individual alliances, and indicates the presence of key individuals in the network that sustain the hierarchical structure through coalition phenomena. Nonetheless, the PA process in infant-mediated behavior does not seem to target high-ranking individuals, revealing that the most central individuals in this network are not the highest ranking ones. On the contrary, while the PA process is not observed in allogrooming behavior, we do observe attraction to high-ranking individuals. This finding reveals that although high-ranking individuals are not the most central members of the group (regarding the individual degree), yet they are preferred partners for allogrooming interactions (regarding the individual indegree). These two points are consistent with previous literature. Indeed, Sueur, Petit et al. (2011) reports that the centrality of high ranking individuals varies according to the dominance style in macaques, with lower centrality observed for top-ranking individuals in tolerant species (including M. sylvanus). Moreover, top-ranking individuals are thought to be the most efficient service providers in primate societies. Individuals should thus be expected to aim to create affiliative links with higher ranking individuals, as indicated by Seyfarth (1977) and the market theory (Noë & Hammerstein, 1995). This phenomenon has already been observed in many non-human primate species (Kanngiesser et al., 2011; Sueur, Petit et al., 2011; Watts, 2000).
Again, from a more global perspective, the growth preferential attachment (GPA) process is commonly considered as a process that shapes a specific network structure (related to scale-free network) (Barabási & Albert, 1999). This type of structure indicates the presence of few highly connected individuals and many poorly connected individuals. This topology of link distribution can help to determine if these networks contain highly central individuals that play a crucial role in maintaining network cohesion. It is difficult to reveal such network topology in animal societies, as it necessitates the use of degree distribution analysis. The main issue when studying degree distribution in an animal social network is the large sample size required for reliable statistical analyses (Brent, Lehmann, & Ramos-Fernández, 2011; Croft, James, & Krause, 2010). SIENA could be a means to reveal the presence of network mechanisms such as GPA that enable the emergence of a specific network typology. This study demonstrates the presence of PA, which could induce GPA. We cannot confirm the occurrence of GPA due to the limitations of our data set (i.e., the small number of individuals entering the network). However, we hope that this approach will encourage primatologists to apply this approach for groups with greater demographic variation over a longer timescale.
The homophily process sheds light on how and with whom an individual creates its affiliative network. In this case, individuals connect mainly with same-gender individuals for allogrooming and sleep in contact behaviors. To reach higher hierarchical ranks and thus improve their fitness, males have to create coalitions through affiliative behaviors, which could lead them to preferentially interact with males (except during the mating season) (Sosa, 2016). The well-known female kinship phenomenon (Silk, 2001) may largely explain the preferential interactions between females, enabling them to consolidate their matrilineal clan.
As for the TC phenomenon, the homophily process enables the establishment of clusters within the group. These clusters consist of individuals with one common attribute, thus facilitating cooperation between them (Croft et al., 2006; Lusseau & Newman, 2004). This phenomenon, like TC and PA, directly impacts the very structure of the affiliative network. Recent studies argue that homophilic preferences may explain the gap between animals and humans regarding stranger cooperation (Haun & Over, 2015), social learning (Buttelmann et al., 2013), cultural and norms transmission (Chudek & Henrich, 2011). Here, we demonstrate that the homophily process can be subject to seasonal dynamics and should, therefore, be taken into account when conducting comparative research in psychology.
SIENA also evidenced seasonality by revealing that the homophily process is only present in the two first periods outside mating season for the allogrooming and sleep-in-contact behavior (see models for homophily by gender for the two first periods in Tables 3 and 4). SIENA can, therefore, be an interesting analytical approach for revealing seasonal changes in interactional patterns. This could be a new avenue for future research. Unlike gender homophily, the TC process is not influenced by seasonal variation. This reveals the perenniality of this mechanism and underlines the particularly important role it plays in the network.
In this study, we demonstrated that these three dynamic processes are not only interesting from a biological perspective, as these behavioral patterns can be linked to behavioral strategies, but they also describe the underlying network dynamics and show how network interactions evolve and shape the global network structure (Barabási & Albert, 1999). In this light, they are of crucial importance in the study of animal societies. This stresses the great potential of this approach in the study of primate societies and, more broadly, animal societies. For example, our analysis focused on the entire group to reveal common interactional patterns among the individuals of a non-human primate society. Previous research showed that individuals’ interactional patterns (Fedigan, 1982), their role and position within the network (Sosa, 2016; Wey & Blumstein, 2010) can differ according to their attributes. Therefore, one interesting future approach this analytical protocol enables is the study of the differences between inter-individual micro-motif patterns according to individual attributes.
In summary, this study used the stochastic model SIENA to highlight some of the interactional dynamical structuring and endogenous processes involved in the affiliative network of a non-human primate species. We successfully adopted a multilevel approach that simultaneously considered individual attributes (endogenous factors) and structural dynamics (structuring factor). Taking into account these different factors, we were able to explain the creation and fluctuation of the interactional dynamics that shape local motifs which, in turn, affect the global structure. From a purely evolutionary perspective, the intrinsic properties of this global structure carry an adaptive value which could have encouraged the establishment of reciprocal altruism. Determining how individuals interact affiliatively will contribute to our understanding of how a complex and structured society is created and maintained. We also know that these different interaction patterns provide information about the formation processes of the affiliative networks that underlie several aspects of hierarchical structure (coalition phenomena) (De Waal, 1997; Flack et al., 2006; Seyfarth & Cheney, 1984) and network resilience (Newman, 2002, 2003). These dynamic characteristics are ideal tools for a comparative approach, as they exist in different animal species and in humans.
6 COMPARISON AND CRITIQUE
This study aimed to highlight the benefits of dynamical SNA tools, such as SIENA, and pinpoint the roles played by micro-structural mechanisms and seasonal changes in a non-human primate affiliative network. We hope that this work will encourage further research to assess the suitability of SNA tools for use in other animal species and/or for longer timescales to widen our understanding of temporal dynamics in animal social networks. This is why we provide in Appendix I the description of the script used for analyzing the infant-mediated behavior network, in the hope of promoting such approach.
Biologists are currently limited when it comes to analyzing dynamic networks. GLMM with permutation approach can be an interesting tool, as explained by Croft, Madden, Franks, and James (2011). This approach allows scientists to study the link between network metrics (degree, eigenvector, clustering coefficient, etc.) and individual attributes (sex, hierarchical rank, age, etc.) or environmental factors (demographic, meteorological, resource variation, etc.). However, GLMM is limited to individual role and position within the network and consequently is not appropriate for the study of individual interactional patterns.
At present, only exponential random graph models (ERGM), including SIENA, are suitable for the analysis of individual interactional patterns. Although these models do entail constraints such as the need to binarize the data, occasioning a loss of information, they nevertheless offer biologists and primatologists interesting new means to determine which individual interactional patterns allow the emergence and the durability of one specific global network. To date, the SNA approach has mainly been used by sociologists, who have identified the presence of such individual interactional patterns in different human social structures. SNA is, therefore, an interesting comparative analytical tool for primatologists and anthropologists alike. Our example also illustrates that seasonal variations can be identified in individual interactional patterns. This provides ecologists with a very useful tool to understand resilience in animal societies or animal ecosystems. For all these reasons, we truly believe that this approach may be a vital tool enabling biologists and primatologists to widen their knowledge of animal societies.
ACKNOWLEDGMENTS
First of all, I would like to formulate special thanks to Francesc Salvador Beltran and Vicenç Quera for guiding and advising me throughout this investigation. Many thanks to Ellen Merz who allowed me to lead the research field work at “La Forêt des Singes” and provided me the demographic data; I sincerely thank her for her advice. I would also like to thank the American Journal of Primatology reviewers for their helpful suggestions, which were crucial to the improvement of this work. Finally, thanks to all those who have encouraged me and enabled me to achieve this work.
APPENDIX A
R script for infant-mediated behavior network analysis
-
library(RSiena)
-
library(RSienaTest)
-
library(network)
-
library(sna)
-
library(xtable)
-
siena07ToConvergence <- function(alg, dat, eff, ans0=NULL, …){
-
numr <- 0
-
ans <- siena07(alg, data=dat, effects=eff, prevAns=ans0, …)
-
repeat {
-
numr <- numr+1
-
tm <- ans$tconv.max
-
cat(numr, tm,“\n“)
-
if (tm < 0.25) {break}
-
if (tm > 8) {break}
-
if (numr > 100) {break}
-
ans <- siena07(alg, data=dat, effects=eff, prevAns=ans, …)
-
}
-
if (tm > 0.25)
-
{
-
cat(“Warning: convergence inadequate.\n“)
-
}
-
ans
-
}
-
# Importing networks
-
Tfriend.data.w1 <- as.matrix(read.table(“try1.csv“))
-
Tfriend.data.w2 <- as.matrix(read.table(“try2.csv“))
-
Tfriend.data.w3 <- as.matrix(read.table(“try3.csv“))
-
# Importing individuals attributes
-
Kinship<-as.matrix(read.table(“Kinship.csv“))
-
Hierarchy<- as.matrix(read.table(“Ds.csv“))
-
Gender<- as.matrix(read.table(“Genre.csv“))
-
Age<- as.matrix(read.table(“Age.csv“))
-
Hierarchy<- as.matrix(read.table(“Ds.csv“))
-
Gender<- coCovar(Gender[,1])
-
Age<- varCovar(Age)
-
Hierarchy<- varCovar(Hierarchy)
-
Hierarchy<- varCovar(Hierarchy)
-
Kinship<-coCovar(Kinship[,1])
-
# First model (structural effects)
-
# Siena objects
-
Tfriendship <- sienaDependent(array(c(Tfriend.data.w1, Tfriend.data.w2, Tfriend.data.w3),dim = c(55, 55, 3)))
-
Tmydata <- sienaDataCreate(Tfriendship,Kinship,Hierarchy)
-
#adding effects
-
Tmyeff <- includeEffects(Tmyeff,transTrip,inPop)
-
Tmyeff <- includeEffects(Tmyeff,sameXTransTrip,interaction1 = “Kinship“)
-
Tmyeff <- includeEffects(Tmyeff,alterX,interaction1 = “Hierarchy“)
-
Tmyeff
-
Tmyalgorithm <- sienaAlgorithmCreate(projname = 'Tryade structural effect',cond=FALSE)
-
ans1 <- siena07ToConvergence(Tmyalgorithm,Tmydata,Tmyeff,returnDeps = TRUE)ans1
-
# Wald-type tests & results
-
TDensity<-Multipar.RSiena(ans1,3)
-
TReciprocity<-Multipar.RSiena(ans1,4)
-
TTransTrip<-Multipar.RSiena(ans1,5)
-
TInPop<-Multipar.RSiena(ans1,6)
-
TXTransTrip<-Multipar.RSiena(ans1,7)
-
alterX<-Multipar.RSiena(ans1,8)
-
TDensity
-
TReciprocity
-
TTransTrip
-
TInPop
-
TXTransTrip
-
alterX
-
# Second model (homophily effects)
-
# Siena objects
-
THfriendship <- sienaDependent(array(c(Tfriend.data.w1, Tfriend.data.w2, Tfriend.data.w3),dim = c(55, 55, 3)))
-
THmydata <- sienaDataCreate(THfriendship,Gender,Age,Hierarchy)
-
THmyeff <- getEffects(THmydata)
-
THmyeff<- includeEffects(THmyeff,sameX, interaction1 = “Gender“)
-
THmyeff<- includeEffects(THmyeff,sameX, interaction1 = “Age“)
-
# Siena model and estimation
-
THmyeff<- includeEffects(THmyeff,simX, interaction1 = “Hierarchy“)
-
THmyalgorithm <- sienaAlgorithmCreate(projname = 'Tryade Attributs effects',cond=FALSE)
-
ans2 <- siena07ToConvergence(THmyalgorithm,THmydata,THmyeff,returnDeps = TRUE)
-
ans2
-
# Wald-type tests & results
-
ThDensity<-Multipar.RSiena(ans2,3)
-
ThReciprocity<-Multipar.RSiena(ans2,4)
-
ThGender<-Multipar.RSiena(ans2,5)
-
ThAge<-Multipar.RSiena(ans2,6)
-
ThHie<-Multipar.RSiena(ans2,7)
-
ThDensity
-
ThReciprocity
-
ThGender
-
ThAge
-
ThHie
-
# Third model (Final model with only significant effects)
-
T3.friendship<- sienaDependent(array(c(Tfriend.data.w1, Tfriend.data.w2, Tfriend.data.w3),dim = c(55, 55, 3)))
-
T3.mydata <- sienaDataCreate(T3.friendship,Gender,Age,Hierarchy,Kinship)
-
T3.myeff <- getEffects(T3.mydata)
-
T3.myeff <- includeEffects(T3.myeff,transTrip,inPop)
-
T3.myeff <- includeEffects(T3.myeff,sameX, interaction1 = “Gender“)
-
T3.myeff
-
# Siena model and estimation
-
T3.myalgorithm <- sienaAlgorithmCreate(projname = 'Tryade final model',cond=FALSE)
-
ans3 <- siena07ToConvergence(T3.myalgorithm,T3.mydata,T3.myeff,returnDeps = TRUE,nbrNodes=7)
-
ans3
-
# Wald-type tests & results
-
T3.Density<-Multipar.RSiena(ans3,3)
-
T3.Reciprocity<-Multipar.RSiena(ans3,4)
-
T3.Transtrip<-Multipar.RSiena(ans3,5)
-
T3.Inpop<-Multipar.RSiena(ans3,6)
-
T3.Gender<-Multipar.RSiena(ans3,7)
-
T3.Density
-
T3.Reciprocity
-
T3.Transtrip
-
T3.Inpop
-
T3.Gender
-
xtable(ans3, type='html',file='infant-mediated behavior model.html')




