Genetic linkage and association studies in bipolar affective disorder: A time for optimism
Abstract
Genetic research on complex diseases is beginning to bear fruit, with the successful identification of candidate susceptibility genes in diabetes, asthma, and other illnesses. Similar success is on the horizon for bipolar affective disorder (BPAD), but significant challenges remain. In this review, we outline the basic concepts of linkage and association mapping for complex phenotypes. We point out important caveats inherent in both approaches, and review guidelines on the interpretation of linkage statistics and significance thresholds. We then apply these concepts to an evaluation of the present status of genetic linkage and association studies in BPAD. The challenges posed by locus heterogeneity, phenotype definition, and sample size requirements are given a detailed treatment. Despite these challenges, we argue that the way ahead remains firmly rooted in linkage studies, complemented by association studies in linked regions. This is the only truly genome-wide approach currently available; it has succeeded in other complex phenotypes, and it is the surest strategy for mapping susceptibility genes in BPAD. Once these genes are identified, genetic mapping methods will yield to the other methods of 21st-century molecular biology as we begin to elucidate the pathophysiology of BPAD. © 2003 Wiley-Liss, Inc.
INTRODUCTION
In this review of linkage and association studies in bipolar affective disorder (BPAD), we attempt to give an overview of some of the developing issues in the field along with a summary of linkage and association methods in complex genetics. Several reviews of linkage and association findings in BPAD have been published quite recently [Berrettini, 2001; Craddock and Jones, 2001; Craddock et al., 2001; Jones and Craddock, 2001; Kato, 2001; Prathikanti and McMahon, 2001; Baron, 2002; Schumacher et al., 2002; Sklar, 2002]. Rather than review these findings again in detail, we discuss the problem of achieving consistent findings in BPAD genetics. We outline reasons for optimism, given the success of linkage and association studies in other complex disorders, promising findings in BPAD and other mental illnesses, rapid increases in the available sample sizes, and improvements in genome technology. We show how increasing attention to ascertainment methods, phenotype characterization, and sample size can lead to increased consistency between study designs and results. Finally, we outline a way forward that uses all available tools in a mutually complementary manner to achieve the final goal of mapping genes involved in BPAD and understanding their function.
DEFINITIONS AND BASIC CONCEPTS
Genetic Linkage Studies
General principle
Two genetic loci (i.e., sites on a chromosome) are said to be “linked” when they are not transmitted independently to offspring. The traditional measure of genetic linkage is the recombination fraction theta (θ). Theta values range from 0 (complete linkage) to 0.5 (unlinked loci on the same or different chromosomes) [Pericak-Vance, 1998; Nyholt, 2000; Risch, 2000].
Classically, linkage studies relied on visible traits, which themselves might be clinically variable and uninformative in many families. The discovery of polymorphic markers, i.e., molecular variations in DNA that are directly measurable in the laboratory [Botstein et al., 1980; Weber and May, 1989], led to the widespread use of linkage studies for mapping human disease loci.
The procedure is rather straightforward: 1) collect a series of families containing multiple cases of illness; 2) genotype the family members using a set of polymorphic markers spanning the genome; and 3) perform statistical tests to determine which markers are inherited along with the disease in families. The application and interpretation of these statistical tests is not so straightforward. We address these in the next section.
Parametric LOD score method
The original statistical method that has been successfully applied to localize genes for numerous monogenic, Mendelian disorders is the LOD score method [Morton, 1955]. The LOD score is the log10 of the odds of linkage. More precisely, the LOD score is the log10 of the ratio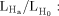 
the likelihood 
of the observed constellation of disease and marker data assuming linkage (θ < 0.5), compared to the likelihood 
of observing the same data assuming no linkage (θ = 0.5). The traditional LOD score approach is considered parametric, since the values for several variables have to be specified, including affection status and mode of inheritance (dominant, recessive) along with the frequency and penetrance of the disease allele, i.e., the probability of being ill, given one carries the allele. Testing for the largest LOD score over varying degrees of θ produces the so-called maximum LOD score. Parametric LOD score analysis is primarily a two-point analysis that tests for linkage between a single marker locus and a presumed disease locus, but can be extended to include information from neighboring markers. An extension to the traditional LOD score method adds locus heterogeneity (i.e., the possibility that the same disease can be caused by variations in different genetic loci) as an additional parameter, creating a so-called HLOD.
Nonparametric methods
The LOD score method is a very powerful approach when the parameters discussed above are known. Parameters are generally known for monogenic disorders, but for complex diseases like BPAD, the parameters are not at all clear. Individuals deemed unaffected might develop the disease later in life, and the mode of inheritance, gene penetrances, and disease allele frequencies cannot be specified with certainty.
There are several approaches to address this problem. One can perform parametric analyses over a range of likely parameters and then correct for the number of independent analyses performed. This approach may be advantageous under many circumstances [Abreu et al., 1999; Durner et al., 1999], but is less popular than so-called nonparametric linkage analysis.
Nonparametric linkage (NPL) analysis is now the most common approach to address the lack of knowledge about inheritance parameters.
Nonparametric linkage analysis is now the most common approach to address the lack of knowledge about inheritance parameters.
Nonparametric linkage analysis does not require specification of a genetic model, but is based instead on the comparison of observed vs. expected sharing of the same alleles—known as identity by descent (IBD)—between pairs of affected relatives. The most widely used method is the affected sib pair (ASP) method. Under the assumption of no linkage between a disease and a marker locus, affected siblings are expected to share zero (z0), one (z1), or two (z2) alleles, with probabilities of 25%, 50%, and 25%, respectively. Since actual IBD sharing cannot always be determined unequivocally from the data, likelihood ratio methods have been developed [Hinds and Risch, 1996; Hauser et al., 1996]. These methods use an expectation-maximization (EM) algorithm [Dempster et al., 1977] to maximize observed sharing probabilities, producing a kind of LOD score known as the MLS [Holmans, 1993]. Both two-point and multipoint analyses can be performed, but the latter is now the standard since it uses information from all markers. This method has been implemented in the widely used analysis tools ASPEX (ftp://lahmed.stanford.edu/pub/aspex/index.html) [Hinds and Risch, 1996; Hauser et al., 1996] and SAGE (http://darwin.cwru.edu/octane/sage/sage.php) [S.A.G.E., 2001].
Another major allele-sharing test allows for the analysis of allele sharing between more distant relatives [Lander and Green, 1987; Kruglyak et al., 1996]. It has been implemented in the GENEHUNTER (http://www.fhcrc.org/labs/kruglyak/Downloads/index.html) [Kruglyak et al., 1996] family of software packages. The IBD probabilities at each point along the chromosome are estimated, using information from all markers. This inheritance information can then be used to examine allele sharing between any set of affected relatives. Next the inheritance information is tested for linkage, either in pairs (Spairs statistic) or in the full set of affected relatives in a family (Sall statistic). The statistics are averaged over all feasible inheritance patterns, normalized to a Z score, and weighted by family, with larger families assigned greater weight. These scores are most commonly known as NPL scores. They are not LOD scores, cannot be added across studies as LOD scores can, and differ in other ways as well (see boxed text “What Is an NPL Score?”).
Interpreting the significance of LOD, ASP MLS, and NPL scores
The above methods are perhaps the most widely used approaches in human genetic linkage mapping today. Because of differences in the ways the various linkage statistics are calculated, however, conventional thresholds of statistical significance vary among them (Fig. 1). Furthermore, because of the large number of independent hypotheses that are actually tested in a genome-wide scan for linkage, we have come to recognize that the conventional thresholds of statistical significance themselves are too liberal and must be adjusted in order to achieve a true experiment-wise type I error rate of no more than 5%.
Relationship between linkage score and significance level. Nomogram illustrating the significance levels of commonly used linkage statistics. P values for LOD scores and MLS are calculated as detailed in Nyholt [2000]. P values for NPL scores are estimated using the normal approximation [Kruglyak et al., 1996].
Lander and Kruglyak [1995] performed a simulation analysis of a fully informative map of markers. The simulations showed that the traditional LOD score threshold of 3.0 needed to increase to 3.3 in order to achieve a true genome-wide significance, that is, statistical evidence expected to occur 0.05 times in a genome scan by chance alone. They further recommend that a LOD score of 1.9 be considered suggestive evidence for linkage, since values of this magnitude are expected to occur randomly about once per genome scan. For designs based on ASP, the corresponding scores (MLS) are 3.6 and 2.2, respectively. Table I summarizes the recommended statistical thresholds with the corresponding P values. For the confirmation of a prior finding, Lander and Kruglyak [1995] suggested a nominal P value of 0.01.
| Method | Genomewide suggestive linkagea | Genomewide significant linkageb | |
|---|---|---|---|
| LOD | P value | 1.7 × 10−3 | 4.9 × 10−5 |
| Score | 1.9 | 3.3 | |
| ASP-MLS | P value | 7 × 10−4 | 2 × 10−5 |
| Score | 2.2 | 3.6 |
- * Adapted from Lander and Kruglyak [1995].
- a Occurs at random once per genome scan.
- b Occurs at random 5 times per 100 genome scans (0.05).
Some have criticized these thresholds as overly conservative [Witte et al., 1996]. Whether or not one accepts the rather stringent criteria of Lander and Kruglyak [1995], it should be clear that different analysis methods can lead to different results. A LOD score larger than 3 is not always the gold standard, especially if the algorithm does not produce true LOD scores [Nyholt, 2000]. The P values generated by standard statistical tests are asymptotic, and thus it is unjustified to put too much weight on the difference between a P value of 0.001 and a P value of 0.00001. Both are significant in the usual sense, but neither gives a good sense of the true significance of the finding: the magnitude of the effect of genetic variation on the phenotype (see boxed text “Effect Size Does Matter”).
Association Studies: Basics
Association testing compares the frequencies of alleles between a control sample and a sample that suffers from a disease. Thus linkage analysis deals with loci on a family level, while association analysis deals with alleles on a population level.
Genetic association testing can be considered in two major subgroups: case-control and family-based approaches [for review, see Schulze and McMahon, 2002]. Family-based approaches have gained popularity since they are less prone to false findings that arise from unrecognized mismatching of cases and controls, a problem known as population stratification. Population stratification, sometimes called structure or substructure, implies the existence of genetically different groups in the population under study.
The principle of family-based methods is that controls and cases are drawn from the same population, namely, the same family. The cardinal example of this approach is the transmission-disequilibrium test
The principle of family-based methods is that controls and cases are drawn from the same population, namely, the same family. The cardinal example of this approach is the transmission-disequilibrium test.
(TDT) [Spielman et al., 1993], which compares the transmission vs. nontransmission of marker alleles from parents to affected offspring. Because of its design, the TDT is immune to population stratification, but this is not true of all family-based association methods [Dudbridge et al., 2000; Zhao et al., 2000]. Since family-based designs are less powerful, genotype for genotype, than case-control designs using unrelated controls [Morton and Collins, 1998; Risch and Teng, 1998; Teng and Risch, 1999], methods that attempt to control for stratification in case-control samples [Devlin and Roeder, 1999; Pritchard et al., 2000] have recently been introduced.
Association studies in a complex disorder like BPAD may be used for a variety of purposes. One can choose genetic polymorphisms in genes that by virtue of their supposed physiological function or expression pattern can be considered promising candidates. This is the so-called candidate gene approach. Association testing can also be used in a more focused way as a follow-up procedure in a region showing evidence of linkage. For this purpose, one can perform testing on genes identified in the region (positional candidate genes) or screen the region systematically with densely spaced markers, without regard to the gene positions, an approach we will refer to as linkage disequilibrium mapping.
In any case, a positive association finding may result when the marker under study is itself the causal variant or when the marker lies so close to the causal variant that little or no recombination has occurred over time between them. (The latter situation is referred to as linkage disequilibrium (LD)). This is an important distinction, with implications for what can be expected in subsequent studies and in replication work. For example, if the associated marker is the causal variant, the same allele should show association in other populations. If the associated marker is merely in LD with the causal variant, however, then different alleles may show association in other populations, even though the same causal variant is present.
LINKAGE STUDIES IN BPAD: A MANIC DEPRESSIVE HISTORY OR THE NATURAL HISTORY OF A COMPLEX DISEASE?
It has been argued that the history of linkage studies in BPAD is itself manic depressive, with the exuberance elicited by positive findings leading inevitably to disappointment when these findings are not supported by subsequent studies [Risch and Botstein, 1996]. The early years were indeed punctuated by findings that could not be supported by subsequent work [Baron, 1977; Egeland et al., 1987]. But this is not a problem confined to BPAD [Compston, 2000; Hopper, 2001; Crook, 2002; Menzel, 2002], and these false starts [Robertson, 1989] do not mean that the journey is doomed. Rather, they have served as a stimulus to learn from what went wrong. Genome-wide scans using dense maps of polymorphic markers in small pedigrees are now the standard, and we now realize that linkage analysis cannot safely be based on a particular set of parameters or on the clinically unaffected status of probands' relatives. Still, highly significant, widely replicated linkage findings remain elusive. The main reason for our ongoing difficulty most likely lies in three mundane problems: locus heterogeneity, phenotype definition, and sample size.
Locus Heterogeneity and Ascertainment
In the field of genetics the term heterogeneity has two different dimensions, known as locus and allelic heterogeneity. Locus heterogeneity refers to the possibility that clinically similar phenotypes may be referable to different genes. Alzheimer disease provides a good example: clinically (and neuropathologically) similar cases are referable to one of several distinct loci [Burke and Roses, 1991; Goate et al., 1991; Martin et al., 2001b]. Allelic heterogeneity describes the same phenotypic outcome for different alleles (i.e., different kinds of genetic variation) within the same gene. Marfan syndrome, an inherited disorder of connective tissue, is a good example of this: while all cases of Marfan syndrome are referable to the fibrillin gene on chromosome 15, very few affected families carry the same mutation [Dietz et al., 1995].
Allelic heterogeneity does not pose a problem for linkage analysis, since linkage to the same chromosomal region will still be detected regardless of the specific variation present. Allelic heterogeneity is a problem for association analysis, since association tests generally depend on cases sharing the same allele. The situation is almost reversed for locus heterogeneity. The presence of several different genes with the same phenotypic outcome will generally defeat linkage analysis, unless there is some way to select individual large pedigrees or large sets of smaller pedigrees in which most cases are affected for the same genetic reason. Locus heterogeneity is less of a problem for association analysis, but does lead to reduced power [Gershon and Goldin, 1986; Risch and Merikangas, 1996].
The problem of locus heterogeneity in linkage analysis has been recognized for some time. Suarez et al. [1994] simulated a complex disease phenotype partially caused by six equally frequent, unlinked genes. A locus detected in one sample was unlikely to be replicated in another sample unless the second sample was much larger. This is because different samples are very likely to contain differing proportions of families linked to particular loci.
Several approaches to the problem of locus heterogeneity have been proposed. Some have advocated collecting families from genetically isolated populations, where the number of different susceptibility genes may be smaller [for review, see Escamilla, 2001]. Another approach focuses on familial patterns of illness, with the assumption that different patterns could point to different susceptibility genes [McMahon et al., 1997, 2001; MacKinnon et al., 1998; Potash et al., 2001]. Yet another approach seeks families that are enriched for clinically severe phenotypes, assuming that these families may be more homogeneous [NIMH Genetics Initiative Bipolar Group, 1997].
All of these approaches have one emphasis in common: ascertainment—how families that will be studied are located, identified, and enrolled. Ascertainment is a fundamental principle of epidemiology, but genetic studies of BPAD vary widely in their attention to this issue.
Ascertainment is a fundamental principle of epidemiology, but genetic studies of BPAD vary widely in their attention to this issue.
Most pedigree samples have been collected opportunistically, thus excluding from study a set of families that are difficult to recapture or describe. Remarkably, no two of the more than 20 genome-wide linkage scans in BPAD have used the same ascertainment scheme [Prathikanti and McMahon, 2001]. While uniformity of ascertainment will probably not eliminate the problem of locus heterogeneity, failure to ascertain samples uniformly may increase locus heterogeneity across samples. This may be one reason why widespread replication of linkage findings in BPAD has been so difficult. Variable ascertainment may also contribute to the difficulty that meta-analysis studies have encountered in attempting to identify convergent sets of linked loci when multiple samples are considered together [Badner and Gershon, 2002; Segurado et al., 2003].
Comparing the BPAD situation with schizophrenia, another point can be made: several major schizophrenia samples [Pulver and Bale, 1989; Pulver et al., 1996; Kendler et al., 1996a, 1996b; Blouin et al., 1998], with strong and replicated linkage regions that have recently led to the identification of candidate susceptibility genes [Straub et al., 2002; Chumakov et al., 2002], were collected through a population-based ascertainment scheme that systematically samples all families present in a defined region. This strategy has not been used in most of the large BPAD collections.
Phenotype Definition
Another major issue in BPAD genetics that has been receiving increasing attention recently is phenotype definition. The ideal phenotype for linkage studies of bipolar disorder remains unclear. This is because twin and family studies indicate that several clinically distinct forms of mood disorder typically occur within the same family [Bertelsen et al., 1977; Gershon et al., 1982]. Some of these mood disorders, such as major depression, are also quite common in the population, raising concerns that at least some cases of major depression in families collected through probands with bipolar disorder are not affected for the same genetic reason as the probands; i.e., they are phenocopies or are expressing alternative risk loci. Attempts to identify, using clinical features, cases of major depression among relatives that are actually expressing the same risk locus that causes bipolar disorder in the proband have been unsuccessful [Blacker et al., 1996]. Accordingly, many in the field have decided to define the affected phenotype as narrowly as possible, for example, studying only families with multiple cases of bipolar I disorder. This approach assumes that the most clinically homogeneous form of disease is also the most genetically homogeneous, but can introduce biases if the narrow form of the phenotype clusters in only a minority of families or requires multiple hits to become manifest clinically [McMahon et al., 2001].
Although current concepts of BPAD are reassuringly conjunctive and highly reliable, this is no guarantee of validity. In other words, we cannot be sure that everyone—or even most people—who carry the diagnosis of BPAD share the same underlying biology. This is also true for other common complex disorders. For this reason, attempts have been made to discover so-called endophenotypes, clinical entities associated with a disease but closer to the underlying biology than the symptoms usually used to define a case. Endophenotypes attempt to go beyond the usual approaches to clinical subtyping based on symptom picture, age at onset, comorbidity, treatment response, etc. Endophenotype studies have increased our understanding of the clinical picture in schizophrenia (e.g., prepulse inhibition [Adler et al., 1982]), panic disorder (e.g., sensitivity to lactate infusion [Gorman et al., 1990]), and alcoholism (e.g., evoked potentials) [Porjesz et al., 2002], but have so far not led to the same kinds of insights in BPAD.
The potential value of an endophenotype for genetic mapping purposes depends on the degree to which the endophenotype aggregates in families. Endophenotypes that are less familial than the disease they putatively underlie offer no advantage in gene mapping, no matter how interesting they may be in other contexts.
The potential value of an endophenotype for genetic mapping purposes depends on the degree to which the endophenotype aggregates in families. Endophenotypes that are less familial than the disease they putatively underlie offer no advantage in gene mapping, no matter how interesting they may be in other contexts.
Risch [1987, 1990a] offered a straightforward method for estimating familiality, known as lambda, the ratio of the prevalence of illness among relatives of a case vs. the prevalence of illness in the population. Risch [1990b] further demonstrated that this intuitive measure is directly related to the power to detect linkage. A related measure, gamma, is directly related to the power to detect association [Risch and Merikangas, 1996]. Future studies of potential endophenotypes for BPAD will need to systematically study relatives if they are to accurately estimate familiality and identify those endophenotypes most likely to facilitate gene mapping.
Sample Sizes
The final mundane problem still facing linkage and association studies in BPAD is sample size. To date, no genome scan for linkage and no candidate gene association study has been based on the kind of sample size we now know is necessary to cope with the complex genetics of BPAD.
To date, no genome scan for linkage and no candidate gene association study has been based on the kind of sample size we now know is necessary to cope with the complex genetics of BPAD.
How do we know the sample sizes have been inadequate? In a widely cited paper, Risch and Merikangas [1996] estimated the sample sizes needed to identify a disease locus in linkage and association studies. They found that the reliable detection of a locus with a frequency of 50% that led to a twofold increase in disease risk would require about 2,500 ASP families for linkage analysis, but only 340 families for association analysis.
The latter estimate is a minimum since most association studies will test marker loci, not the disease locus. The required sample size increases very rapidly with increasing distance between marker and disease locus, by a factor of 1/r2, where r2 is a measure of the LD between marker and disease alleles [Kruglyak, 1999]. The required sample sizes increase further when markers used are not completely informative [Hauser et al., 1996]. Mapping a locus by linkage methods to a narrow region requires even more families [Lander and Kruglyak, 1995].
Some promising linkages have been detected despite small sample sizes, and meta-analytic methods may overcome some of the limitations of small samples [Levinson et al., 2003], but the simple fact that all published findings are based on inadequate sample sizes may itself explain much of the apparent inconsistency in findings to date. Large samples are currently being studied under the auspices of the NIMH Genetics Initiative and other collaborations [reviewed in Merikangas et al., 2002].
ASSOCIATION STUDIES IN BPAD
The apparent advantage in statistical power has propelled genetic association studies into a major position in all fields of complex genetics. Association studies in regions of genetic linkage have been instrumental in identifying susceptibility genes for non-insulin-dependent diabetes mellitus (NIDDM) [Horikawa et al., 2000], Crohn disease [Rioux et al., 2001], asthma [Van Eerdewegh et al., 2002], and other complex diseases. Candidate gene association studies have contributed to the discovery of genes that are involved in thrombotic disease [Bertina et al., 1994; Svensson and Dahlback, 1994], Alzheimer disease [Corder et al., 1993], and several other disorders. These successes have established association methods as a leading strategy in complex genetics.
At the same time, we have witnessed many positive association studies that could not be replicated. Ioannidis et al. [2001] evaluated 370 studies investigating 36 genetic associations for various diseases, including BPAD. They found that the results of an initial positive study correlated only modestly with subsequent replication attempts. The main reasons cited for nonreplication were overestimation of effect size by the original study (see boxed text “Effect Size Does Matter”) and underestimation of sample size by replication efforts.
Candidate gene association methods have been widely used in BPAD genetics [for review, see Jones and Craddock, 2001]. There have been no widely replicated findings so far, but some evidence implicates the genes encoding the serotonin transporter (on chromosome 17q11-12) and catechol-o-methyl-transferase (COMT), on chromosome 22q11. None of the published studies reaches the threshold of genome-wide significance recommended for candidate gene studies [Risch and Merikangas, 1996].
Methodological problems tarnish many candidate gene studies in BPAD. Most studies are based on small sample sizes, making them very susceptible to the problems highlighted by Ioannidis et al. [2001]
Methodological problems tarnish many candidate gene studies in BPAD. Most studies are based on small sample sizes, making them very susceptible to [overestimation of effect size].
Few studies attempt to sample all of the common genetic variation in the gene of interest, and many use older, relatively uninformative markers. Some studies focus appropriately on genetic variation that has potential consequences on gene function, but the evidence for actual functional effects of that variation in vivo may not be clear. Several studies attempt to increase power by splitting the sample into clinically defined subgroups, but this requires statistical correction for multiple testing and it is not always clear how best to do this. Since association studies are relatively easy to carry out, many negative studies are probably never published [Easterbrook et al., 1991; Ioannidis et al., 2001]. Because of these limitations, the vast majority of potentially important candidate gene markers have yet to be confidently excluded from a role in BPAD.
The larger problem with candidate gene association studies is that good candidate genes for BPAD are hard to define. We do not yet know enough about the biochemical pathways underlying BPAD symptoms—much less the large groups of genes and even larger number of genetic variants involved—to make a truly educated guess in selecting candidate genes for study. Unless the prior probability is reasonably high (better than ∼1 in 1,000) that a particular gene polymorphism is in fact causally related to the disease, Bayes' theorem shows that most statistically significant association findings at the P = 0.001 level will actually be false positives. If we assume that there are about 30, 000–60,000 human genes and that any could be a candidate for BPAD, then the prior probability that a particular gene is a disease gene is no better than one in 30,000. If we only consider those genes expressed in the central nervous system (CNS), the denominator might be cut in half, but the odds are still long [Sullivan et al., 2001]. We cannot even confidently exclude the possibility that disease-relevant variants do not lie within genes at all, but rather in intergenic regions, the functional importance of which we still are far from comprehending fully.
A WAY AHEAD
With all of its limitations, genetic linkage mapping remains the only systematic, genome-wide approach to the study of complex diseases like BPAD. All other available approaches, whether based on association analysis, gene expression studies, or detection of cytogenetic abnormalities, are limited to particular genes or chromosomal regions. While genome-wide association studies have been advocated by some authorities, the number of genotypes required for even the most optimistic scenarios remain impractically large, and the statistical problems posed by a genome-wide association study remain formidable [Risch, 2000; Terwilliger et al., 2002]. Despite the issues we have discussed, genetic linkage studies of BPAD have indeed identified chromosomal regions where the evidence, while not in itself conclusive so far, provides a solid basis for additional linkage and association mapping. At least a few loci are supported by several linkage or association studies. These include loci on chromosomes 12q [Craddock et al., 1994], 13q [Detera-Wadleigh et al., 1999], 18q [Stine et al., 1995], and 22q [Kelsoe et al., 2001]. Results of ongoing genome scans in large samples, such as the NIMH Genetics Initiative, will likely implicate other loci that could not be reliably detected in smaller samples.
For the foreseeable future, linkage studies will remain the starting point for systematic molecular genetic research in BPAD. In addition, the challenges of complex genetic diseases like BPAD require that all available tools be brought to bear on the problem. Association studies in linked regions are a natural complement to linkage studies, providing independent support for a linkage finding and helping to narrow the implicated chromosomal region to the point that individual genes and regulatory sequences can be intensively studied. Yet even the most successful genetic mapping experiments will never tell the whole pathophysiologic story. Genetic mapping work must be further complemented with gene expression studies, studies in model organisms, and, ultimately, basic neurobiology before the true promise of genetic research—revolutionary improvements in diagnosis and treatment—can be fully realized.
Acknowledgements
We gratefully acknowledge critical input from Nancy Cox, Sevilla Detera-Wadleigh, and Doug Levinson.
What Is an NPL Score?
The NPL is not a LOD score, although unfortunately it is sometimes handled as such. In principle, an NPL score is a Z-score, corresponding to a point along the standard normal distribution.
The statistical significance (P value) of the NPL score can be estimated in at least two ways: When the sample size is large, the P value can be obtained directly from the normal distribution. This strategy is referred to as the normal approximation [Kruglyak et al., 1996]. The program GENEHUNTER [Kruglyak et al., 1996] assesses the significance by means of an exact distribution based on a so-called perfect data approximation. Kong and Cox [1997] showed that this approach can be overly conservative when some data are missing.
All of these significance levels are based on statistical theory that might not accurately capture the true type I error rate of a given study design. Thus it has become standard in complex genetics to supplement nominal P values with those determined by computer simulation, providing an empirical estimate of statistical significance.
Effect Size Does Matter
An overemphasis on P values is problematic, since P values tell us little about the magnitude of the genetic effect that is actually being detected. This value is really the key finding in any linkage or association study, with immediate implications for reproducibility of the finding (not to mention clinical significance). In an association study, the effect size is most simply estimated by the odds ratio (OR), where a value of 1.0 corresponds to no effect. (In family-based designs, the ratio of transmissions to nontransmissions of the associated allele approximates the OR under the assumption of a multiplicative model [Altshuler et al., 2000].) Typical OR values in complex genetics are <3. (Compare this to the OR of >40 in the association between smoking and lung cancer.)
No simple measure of effect size exists for a linkage study, beyond the usual linkage statistics such as the LOD score, which also reflects sample size. In an ASP linkage study, genetic effect size can be estimated with the value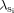 
obtained by dividing the observed proportion of sibling pairs sharing no alleles identical by descent (z0) by the expected proportion of 0.25 [Risch, 1987]. Genetic effect sizes are strong predictors of the likelihood that a subsequent study can replicate the original finding. In general, OR and 
values much less than 2 are very difficult to replicate. The effect size estimated by one particular study may not be a good measure of the true effect size. An initial positive study will generally overestimate an initial positive study will overestimate effect size, in much the same way that the winner of an auction will have paid a bit too much for the object sold: studies that came up with smaller effect sizes may not have reached statistical significance and may never have been published. This is unfortunate, since it means that replication efforts will not have as good a chance of success as the initial, upwardly biased, estimate of the effect size might suggest [Ioannidis et al., 2001].
Some Practical Issues
Assuming a first-stage genome scan has identified several linkage peaks, the next step should be to perform a second-stage analysis of the most promising regions. For this purpose, a dense microsatellite marker map is needed. High-resolution genetic maps [Kong et al., 2002] and genome sequence information [Lander et al., 2001; Venter et al., 2001] should be used to guarantee correct marker order. Rigorous screening for likely genotyping errors (i.e., double recombinants) should be applied to prevent possible inflation in the linkage evidence due to genotyping errors [Feakes et al., 1999]. We recently described such an approach for the BPAD susceptibility region on 18q22 [Schulze et al., 2003]. Methods to further delineate linkage regions may include the use of covariates [Goddard et al., 2001], stratification on phenotypic characteristics [Goate et al., 1991; Froguel et al., 1993; McMahon et al., 2001; Rioux et al., 2001], and multilocus approaches [Cox et al., 1999]. After these procedures have been exhausted, one should focus on the most promising region(s) as the target for fine mapping by association analysis. When the sequence information in the region is complete and all genes have been described, methods that rely on studying markers in and near genes may be the most efficient. When this is not the case, methods that rely on detecting LD between marker and disease alleles may be used. Given that the success of association mapping hinges on the detectability of LD between marker and disease allele, knowledge about intermarker LD (background LD) patterns in the candidate region should help estimate the initial marker density needed for association screening [Escamilla et al., 1999; Schulze et al., 2002].
Fine mapping should be based on accurate and reliable genotyping methods [Akula et al., 2002]. Either case-control or family-based approaches can be used, but findings that arise consistently out of both approaches are desirable. Power calculations [Chen and Deng, 2001; Fallin et al., 2002; Lange and Laird, 2002] should take into account multiple testing and the possibility that disease alleles will be very common. The possibility of false positive results should be addressed appropriately. In TDT samples, transmission ratio distortion [Spielman and Ewens, 1996] and genotyping errors [Gordon et al., 2001] can increase the type I error rate. In case-control samples, strategies that detect and correct for population stratification [Devlin and Roeder, 1999; Pritchard et al., 2000] should be used. Association studies in regions of genetic linkage signals should assess how well putative association findings partition the evidence of linkage in the original sample [Horikawa et al., 2000; Myers et al., 2002]. Convergence of results is the key indicator of true findings.
Care must also be taken in the selection of statistical analysis methods and software. All statistical tests are based on specific assumptions; usage that violates these assumptions may lead to uninterpretable results. Most software packages for genetic linkage analysis have now been successfully vetted in the field and further developed to address weaknesses. The same cannot yet be said of all software packages for association mapping. Many of the novel association methods, while intriguing and potentially useful, must be considered unproven until widely used in a variety of settings. Available methods vary widely in their assumptions, robustness to population stratification, correction for nonindependence among relatives, and quality of haplotype estimation [Clayton, 1999; Dudbridge et al., 2000; Martin et al., 2000, 2001a; Zhao et al., 2000; Schaid et al., 2002]. Careful and critical application of statistical methods is perhaps more important than ever before.
