A coalescent simulation of marker selection strategy for candidate gene association studies†
Please cite this article as follows: Cole SM, Long JC. 2007. A Coalescent Simulation of Marker Selection Strategy for Candidate Gene Association Studies. Am J Med Genet Part B 147B:86–93.
Abstract
Recent efforts have focused on the challenges of finding alleles that contribute to health-related phenotypes in genome-wide association studies. However, in candidate gene studies, where the genomic region of interest is small and recombination is limited, factors that affect the ability to detect disease-susceptibility alleles remain poorly understood. In particular, it is unclear how varying the number of markers on a haplotype, the type of marker (e.g., single nucleotide polymorphism (SNP), short tandem repeat (STR)), including the causative site (cs) as a genetic marker, or population demographics influences the power to detect a candidate gene. We evaluated the power of association tests using coalescent-modeled computer simulations. Results show that an effective number of markers on a haplotype is dependent on whether the cs is included as a marker. When the analyses include the cs, highest power is achieved with a single-marker association test. However, when the cs is excluded from analyses, the addition of more nonfunctional SNPs on the haplotype increases power to a certain point under most scenarios. We find a rapidly expanding population always has lower power compared to a population of constant size; although utilizing markers with a frequency of at least 5% improves the chance of detecting an association. Comparing the mutational properties of a nonfunctional SNP versus an STR, multi-allelic STRs provide more or comparable power than a bi-allelic SNP unless SNP frequencies are constrained to 10% or more. Similarly, including an STR with SNPs on a haplotype improves power unless SNP frequencies are 5% or more. © 2007 Wiley-Liss, Inc.
INTRODUCTION
The search for alleles that contribute to health-related phenotypes using statistical association methods is proceeding on two different scales, genome-wide and candidate gene [Goldstein et al., 2003]. In response to large-scale initiatives such as the International HapMap Project [Gibbs, 2003], many recent studies have focused on the challenges presented in genome-wide scans. However, candidate gene studies present with different obstacles compared to genome-wide studies and approaches developed to meet the challenges of scanning the genome may not be ideal for the needs of candidate gene analysis. Recombination is the dominant force on linkage disequilibrium on the genome-wide scale. Whereas in the small genomic regions occupied by candidate genes, recombination is less important and the processes of mutation and genetic drift are paramount in determining patterns of linkage disequilibrium. The primary interest in selecting markers for genome-wide scans is to reduce the genotyping burden by selecting an informative subset of SNPS to tag specific regions [Zhang et al., 2002]. Some candidate gene studies share this goal, but candidate gene studies are also interested in testing functional hypotheses that relate a particular marker allele to a disease phenotype. There is no guarantee that the same set of markers will serve both purposes equally well.
The potential for success of both genome-wide and candidate gene studies critically depends on the genetic markers chosen for analysis. Genome-wide scans use single nucleotide polymorphisms (SNPs) almost exclusively, because of their abundance throughout the genome, their low mutation rate, and their amenability to high-throughput genotyping platforms. In contrast, candidate gene studies use many different kinds of genetic markers, often with different mutational properties, in order to extract all of the information available from the region of interest. In addition to SNPs, both variable number tandem repeat (VNTR) and short tandem repeat (STR) loci appear as markers in substance abuse candidate genes. For example, Anney et al. 2004 tested for association between nicotine dependence and a tetranucleotide repeat in the tyrosine hydroxylase gene. Zhang et al. 2004b investigated whether polysubstance abuse was associated with a trinucleotide repeat in the cannabinoid receptor type 1 gene. Li et al. 2004 tested for association between methamphetamine abuse and a heptanucleotide repeat in exon III and a 120-bp promoter VNTR in the dopamine D4 receptor gene. Contini et al. 2006 tested whether alcohol dependence and antisocial behavior were associated with a 30-bp VNTR in the promoter region of the monoamine oxidase A gene.
Moreover, investigators have used haplotypes composed of mixtures of repeat polymorphisms and SNPs to perform tests for association between candidate genes and substance abuse phenotypes. Sullivan et al. 2001 investigated association between haplotypes composed of two SNPs and one dinucleotide repeat in the dopamine D5 receptor gene and smoking initiation and nicotine dependence. Goldman et al. 1997 tested whether alcoholism and substance abuse were associated with a three-locus haplotype composed of a STR and two SNPs in the dopamine D2 receptor gene.
Despite the use of various types of markers in association tests, it is not clear how the mutational properties of different polymorphisms affect the power to detect a causative variant. In particular, how does a bi-allelic SNP compare to a multi-allelic STR? Generally, SNP markers have such a low mutation rate that the probability of a recurrent mutation is unlikely and allelic identity is likely to be by descent. In contrast, STRs, which are characterized by step-wise mutations, have a high mutation rate [Valdes et al., 1993; Weber and Wong, 1993]. The back and forth nature of STR mutations could disrupt associations because allelic identity may be by state rather than by descent [Valdes et al., 1993; Di Rienzo et al., 1994]. The question as to which type of marker provides more statistical power in association tests has been investigated in terms of genome-wide scans [Chapman and Wijsman, 1998; Xiong and Jin, 1999]; however, the issue is poorly understood in low-recombining candidate gene systems.
The optimum number of markers for a candidate gene analysis is an open question. A computer simulation study found that a large number of markers improves the power of association analyses on a genomic scale where recombination is likely [Long and Langley, 1999]. In these simulations, many markers were necessary to achieve high power because recombination broke linkage disequilibrium over moderate genetic map distances. However, we postulate that there is a limit to the number of markers necessary in gene regions with low recombination. We expect that information will be saturated beyond a threshold number of markers.
In the present study, we used coalescent-modeled computer simulations of population-based sampling to investigate factors that influence the ability to detect association between a phenotype and markers at a candidate locus. We investigated the composition of optimal marker sets with respect to three genomic factors (1) the kind of marker (e.g., SNP, STR), (2) using haplotypes composed of mixtures of SNP and STR markers, and (3) inclusion of the causative variant in the marker set. We also investigated these variables under differing demographic variables.
METHODS
The power to detect a candidate gene was investigated under several scenarios that differed with respect to the effect of the candidate gene on the phenotype and the composition of a set of genetic markers. Under each scenario, we generated a large number of replicate data sets, tested each data set for association, and tabulated the percentage of datasets for which the effect of the candidate gene was statistically significant.
Simulation of Candidate Gene DNA Sequences
DNA sequences were simulated using the coalescent model [Hudson, 1990, 1993]. (1) The genealogy of a sample of DNA sequences at a candidate gene locus was simulated by pairing sequences at random until all sequences in the sample linked back to a common ancestral sequence. (2) A set number of mutations was randomly placed on the genealogy to define polymorphic sites within the candidate locus. (3) One mutated site was chosen to contribute to variability to a quantitative trait. Hereafter, this site is referred to as the causative site (cs). The remaining mutated sites were assigned nonfunctional roles and their alleles served only as markers in the association analyses. In some analyses, the alleles at the cs also served as markers for testing association between the candidate gene and the quantitative trait. Each simulated DNA sequence was stored as a haplotype consisting of one allele at the cs and one allele at each polymorphic nonfunctional site. (4) Diploid individuals were created by randomly pairing simulated haplotypes.
Quantitative Trait Values
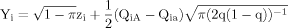
 in which zi is a standard normal random variable and π is the proportion of the quantitative trait variance that is due to the cs. The genetic component of the quantitative trait is contributed by
in which zi is a standard normal random variable and π is the proportion of the quantitative trait variance that is due to the cs. The genetic component of the quantitative trait is contributed by  , where one cs allele is arbitrarily designated “A” and the other cs allele is designated “a.” QiA is the number of “A” alleles in the ith individual's genotype and Qia is the number of “a” alleles. The letter q denotes the frequency of the “a” allele.
, where one cs allele is arbitrarily designated “A” and the other cs allele is designated “a.” QiA is the number of “A” alleles in the ith individual's genotype and Qia is the number of “a” alleles. The letter q denotes the frequency of the “a” allele.Association Test—Multiple Regression
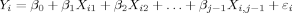
Power to Detect Association
The power to detect association was estimated as the proportion of 1,000 replicate simulations for which the regression null hypothesis was rejected at the α = 0.05 level of significance.
Simulation Models
The sample size was set at 250 diploid individuals in all simulation models. The proportion of total phenotypic variation accounted for by the cs was varied from 1% to 25%. For haplotype-based analyses, we selected the most ancient mutation from all polymorphic sites as the cs. For genetic markers analyzed individually, the cs allele frequency was set at 50%. In preliminary analyses, the power to detect an association was similar when the frequency of the cs allele was set at 30, 40, or 50%, thus for simplicity all results are reported for a cs allele frequency equal to 50%.
To investigate how varying the number of markers in a haplotype affects the power to detect an association, we varied the number of polymorphic sites on a haplotype. Depending on the analysis, 2, 5, 10, 15, or 20 SNPs were superimposed on the gene-genealogy. SNPs were distributed on the genealogy according to a random uniform variable and the total branch length of the tree [Hudson, 1993].
To study how the mutational property of a STR polymorphism affects the power of an association test, one STR locus was generated in the coalescent model. The stepwise mutation approach was applied which assumes that the STR mutation is single-step and reversible. The number of mutations on a branch in the genealogy was a Poisson random variable with parameter λ = µt, where µ is the mutation rate and t is the branch length. The STR mutation rate was set at 10−4.
RESULTS
Number of Markers in a Haplotype
Causative SNP (cs) excluded from haplotype
Figure 1 presents the effect of varying the number of markers on a haplotype when the cs is not in the marker-set. Each panel evaluates the performance of haplotypes composed of 2, 5, 10, 15, or 20 nonfunctional SNPs as a function of the % of total phenotypic variance contributed by the cs. The four panels represent combinations of population size (constant, growing) and allele frequency constraint (no minimum, 5% or over). As expected, in all panels power is higher with an increasing contribution of the cs to total phenotypic variation. Power also increases universally with more SNPS in the haplotypes. However, the benefit of increasing the number of markers eventually plateaus. In the case of constant population size and no minimum allele frequency, 10, 15, and 20-marker haplotypes have considerably more power than 2- and 5-marker haplotypes (Fig. 1a). The benefit of adding markers approaches saturation with 10 markers on a haplotype and completely plateaus with 15- and 20-marker haplotypes. In contrast, if marker allele frequencies are 5% or greater, then fewer markers are necessary to achieve comparable power (Fig. 1b). The power of a 5-marker haplotype increases considerably and resembles the power of a 10-marker haplotype from Figure 1a. The power of 10, 15, and 20 markers is virtually identical, and only modestly higher than a 5-marker haplotype. In the case of rapid population expansion with no allele frequency constraints (Fig. 1c), power continues to increase with 15- and 20-marker haplotypes rather than reaching a plateau. Despite higher power with additional markers, the probability of detecting a candidate gene remains under 60% unless the cs accounts for 25% of the total phenotypic variance. The situation improves, however, if allele frequencies are at least 5% (Fig. 1d). In this scenario, power increases considerably, although it remains lower than the constant population size model shown in Figure 1b.
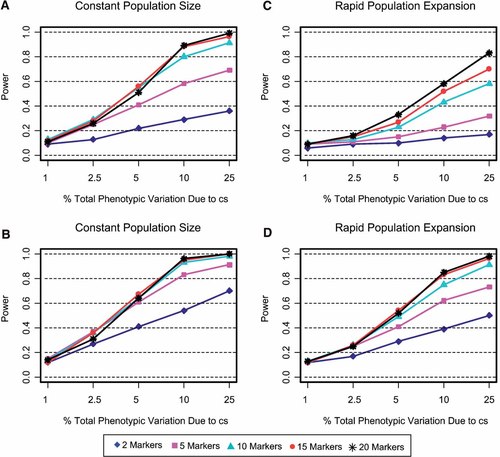
A–D: The effect of varying the number of markers on a haplotype when the cs is excluded from analyses. Haplotypes are composed of 2, 5, 10, 15, or 20 nonfunctional SNPs as a function of the % total phenotypic variance contributed by the cs. The power to detect a significant association was evaluated for population size, (constant, expanding) and SNP allele frequency constraints, no minimum (A,C) and 5% or over (B,D). [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
Thus, when haplotypes do not contain the cs, 10–15 nonfunctional markers have more power to detect an association compared to a smaller number of markers. In most scenarios, power plateaus with 15 markers in a haplotype. The one exception is the case of population expansion with no allele frequency constraints. Here, power increased with 20 markers, however, more power can be obtained with fewer markers if allele frequencies are at least 5%.
cs included in haplotype
The effect of varying the number of markers in a haplotype when the cs is in the marker-set is shown in Figure 2. The two panels present the power of haplotypes composed of 2, 5, or 10 nonfunctional SNPs as a function of the % of total phenotypic variance contributed by the cs. Two elements of population size, constant versus growth and a minimum allele frequency of at least 5% were evaluated in simulations. If the cs is included in the haplotype, then power decreases as more nonfunctional markers are added to the marker-set regardless of population history (Fig. 2a,b). Highest power is obtained when the cs is analyzed alone, however, power is only slightly lower with a 2-marker haplotype (data not shown). Thus, if a marker is strongly believed to be functional, then nonfunctional markers should not be used in the analyses.
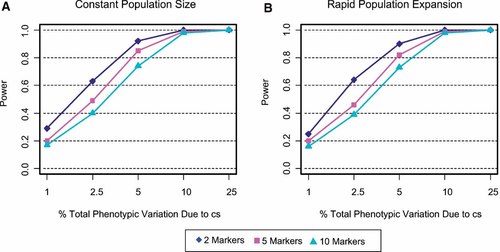
A,B: The effect of varying the number of markers on a haplotype when the cs is included in the analyses. In addition to the cs, haplotypes are composed of 2, 5, or 10 nonfunctional SNPs as a function of the % total phenotypic variance contributed by the cs. The power to detect a significant association was evaluated for two conditions of population size, constant (A) and expanding (B). For all simulations, SNP allele frequencies were at least 5%. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
STR Versus SNP Markers
Figure 3 presents the power of a single STR relative to that of a single nonfunctional SNP. Single-locus tests were evaluated as a function of the % of total phenotypic variance contributed by the cs. The six panels are distinguished by various configurations of population size (constant, growing) and heterozygosity levels (no minimum, 9.5% or more, 18% or more). In all panels, power is higher when the cs accounts for a greater proportion of the total phenotypic variation. Moreover, a STR polymorphism provides either comparable or higher power than a SNP unless the SNP is common in the population. Under the scenario of a constant population size with no heterozygosity constraints, a STR has considerably more power than a SNP (Fig. 3a). If SNP and STR locus heterozygosity is at least 9.5%, then the STR has only modestly higher power compared to the SNP (Fig. 3b). With a more rigorous heterozygosity threshold of 18%, the power of a SNP and STR is similar (Fig. 3c). Under conditions of population growth and no heterozygosity constraints, a STR has more power compared to a SNP (Fig. 3d). The difference between the power of a SNP and a STR somewhat resembles the pattern shown in Figure 3a, however, here, overall power is lower. In the case where heterozygosity is least 9.5%, the power of a SNP and STR is identical (Fig. 3e). If heterozygosity is 18% or more, then a SNP outperforms a STR (Fig. 3f) and approaches the level of power found in a constant population size model (Fig. 3c).
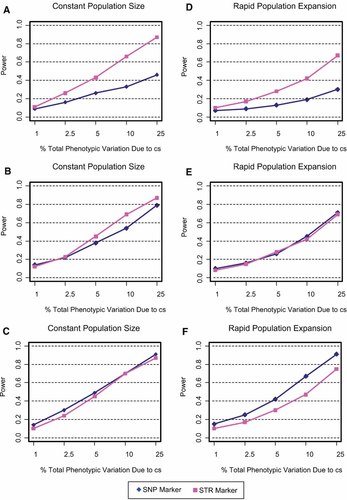
A–F: The power of a single STR relative to a single nonfunctional SNP as a function of the % total phenotypic variance contributed by the cs. The power to detect a significant association was evaluated for population size, (constant, expanding) and heterozygosity constraints, no minimum (A,D), 9.5% or over (B,E), and 18% or over (C,F). [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
Regardless of population demographics, locus heterozygosity constraints had virtually no effect on the power of a STR, whereas the power of a SNP improved substantially with stricter allele frequency cutoffs. These findings show that the multi-allelic nature of a STR is advantageous relative to a bi-allelic SNP, unless SNP frequencies are at least 10%.
STR and SNP Haplotype Marker-Sets
The power of haplotypes composed of two nonfunctional SNPs and one STR or three nonfunctional SNPs is presented in Figure 4. Haplotypes were evaluated as a function of the % of total phenotypic variance contributed by the cs under conditions of population size (constant, growing), and heterozygosity constraints (no minimum, 9.5% or more). In the case of constant population size and no heterozygosity constraints, 1-STR/2-SNP haplotypes have more power than 3-SNP haplotypes (Fig. 4a). However, if heterozygosity is at least 9.5%, then power is essentially identical between 1-STR/2-SNP and 3-SNP haplotypes (Fig. 4b). When simulation conditions are modified to account for population expansion, we find trends similar to those found when the population size is constant, albeit, overall power is reduced (Fig. 4c,d). Thus, haplotypes composed of a mixture of a STR and SNP markers provide either comparable or more power compared to haplotypes constructed entirely of SNPs.
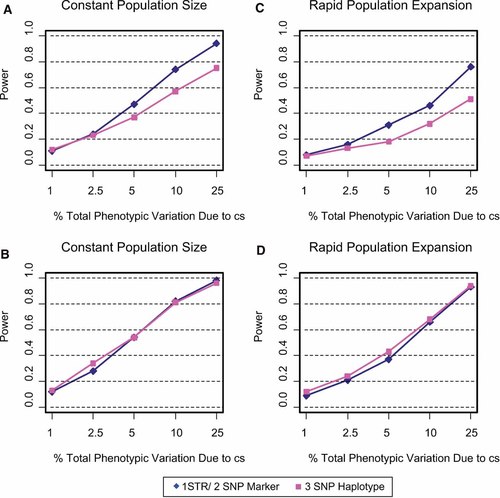
A–D: The power of haplotypes composed of one STR and two nonfunctional SNPs or three nonfunctional SNPs as a function of the % total phenotypic variance contributed by the cs. The power to detect a significant association was evaluated for population size, (constant, expanding) and heterozygosity constraints, no minimum (A,C) and 9.5% or over (B,D). [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
DISCUSSION
There are different obstacles to overcome when considering marker selection in a candidate gene versus a genome-wide association study. On a genome-wide scale, recombination plays a prominent role influencing linkage disequilibrium; while mutation and genetic drift are the predominant forces generating linkage disequilibrium in candidate genes. SNPs are the primary marker used in genome-wide scans, whereas, numerous types of markers with different mutational properties are used in candidate gene studies. There is a considerable effort to develop marker-selection strategies for large genome segments [Bader, 2001; Byng et al., 2003; Huang et al., 2003; Stram et al., 2003; Weale et al., 2003; Halldorsson et al., 2004]; however, it is not clear how well such strategies apply to small, low-recombining regions such as candidate genes. In this study, we used coalescent-based computer simulations to investigate factors that influence the power to detect a candidate gene.
The following factors were evaluated in a nonrecombining candidate gene system: (1) the number of markers in a haplotype, (2) whether or not the cs is included in the haplotype, (3) polymorphisms with different mutational mechanisms (STR vs. SNP), (4) allele frequency constraints, (5) haplotypes composed of different types of polymorphisms, and (6) population demographics. However, these are not the only factors that determine the power of a study. We did not investigate the contribution of sample size because there is no question that larger samples have more power. Also, we did not examine the effect of inferring haplotype phase from diplotype data. This is because the conditions of our simulations, that is, common polymorphisms in nonrecombining regions, enable accurate inference of haplotype phase using the EM algorithm [Excoffier and Slatkin, 1995; Hawley and Kidd, 1995; Long et al., 1995]. Therefore, adding a haplotype inference step to our simulations would have needlessly increased computations. We did not investigate the issue of correction for multiple tests because the regression procedure that we used accounts for multiple haplotypes at a locus. Of course, if one were evaluating multiple candidate genes, a multiple test correction such as Bonferroni's would be necessary. Lastly, evaluating the power to detect the effect of a haplotype that carries more than one cs [Hamon et al., 2004, 2006] was beyond the scope of this study. It would be a suitable objective for a subsequent study.
We began by investigating the power to detect association as a function of the number of markers on a haplotype. We found that the answer differed depending on whether or not the marker-set included the cs. When the cs is included in the analysis, the highest power is achieved when the cs is the only marker. The possibility of this phenomenon was suggested by Zhang et al. 2002, 2004a. The placement of more nonfunctional markers on the haplotype decreases the power. Power is lost because non-cs markers spread the cs over etiologically identical haplotype classes, and thereby, needlessly inflate the degrees of freedom associated with the F test. We conclude that analyzing strong candidate polymorphisms alone will achieve the highest power. This supports the recent recommendation to prioritize markers by function in association studies [Tabor et al., 2002; Rebbeck et al., 2004]. Functionally irrelevant markers dampen the signal of strong candidates. However, a two-marker haplotype (the cs and one nonfunctional SNP) does not compromise power much and will increase the power if the candidate gene is correct but the wrong functional marker has been selected.
Association analyses performed without the cs in the marker-set present a very different picture with respect to the optimal number of markers on a haplotype. We find that adding markers now enhances the power to detect association. This is because each marker increases the chance that at least one marker will be in strong linkage disequilibrium with the cs. Nonetheless, the power reaches a plateau. As shown (Fig. 1), 15 markers are sufficient to saturate the power curve in several scenarios; however, the actual number of makers needed is sensitive to the population demographics. Growing populations require more markers on haplotypes than do stable populations. This is because in growing populations most mutations creating markers appear in the terminal branches of the genealogy and are thus rare. Our result agrees with Zollner and von Haeseler 2000 who found a lower amount of linkage disequilibrium in an expanding population compared to a population of constant size.
A marker site with a rare allele does not increase power. Regardless of cs allele frequency, high linkage disequilibrium is only possible with a common marker allele. With unselected SNPs, more markers on a haplotype are necessary because the chance that there is a higher frequency allele in linkage disequilibrium with the cs is lower. Choosing markers with minor allele frequencies of at least 5% increases the chance that at least one marker is in strong disequilibrium with the cs. This finding supports a recommendation that selecting SNPs with a frequency of at least 5% will improve the success of a candidate gene association study [Tabor et al., 2002]. Constraining allele frequencies to higher values is especially critical for an expanding population (Fig. 1c). When SNP allele frequencies are 5% or more, power is higher with fewer markers on a haplotype reaching a plateau at 15 markers (Fig. 1d).
In a previous family-based association analysis of Alzheimer disease with SNPs surrounding the apolipoprotein E (APOE) gene, Martin et al. 2000 found that haplotype analyses offered little advantage over single-marker analyses when the causative APOE-4 allele was included. However, excluding the APOE-4 allele changed the situation and haplotypes were more powerful for detecting the effect of APOE than SNPs analyzed individually. Our results extend their findings by showing that (1) increasing the number of nonfunctional markers on a haplotype that contains the cs leads to a steady decline of power and (2) when the cs is excluded from the analyses, the addition of nonfunctional markers increases the power of haplotypes to a certain point.
The next set of questions that we addressed dealt with the power of a STR to detect association relative to the power of a SNP. A potential concern of using a STR polymorphism in association analyses is that the underlying mutational process creates new alleles that are indistinguishable from existing alleles. The overall effect of these “parallel” mutations is to randomize the pairing of STR and causative alleles. To address this problem, we chose to use a pure single-step process to model mutation at STR loci. This process imposes the most regularity on the generation of new alleles [Valdes et al., 1993; Di Rienzo et al., 1994]; it constitutes a worse case scenario for STRs because it maximizes the production of new alleles that are identical to existing alleles [Slatkin, 1995].
We find that the power of a STR is higher than a single randomly chosen nonfunctional SNP. The multiple STR alleles provide a greater chance that a high frequency allele is associated with the cs. In contrast, the bi-allelic nature of a SNP results in fewer instances of a high frequency allele in linkage disequilibrium with the cs. When SNP frequency thresholds are set at 5% or 10%, the power of a SNP either resembles or surpasses a STR. SNP frequency constraints have a considerable influence on power by eliminating rare alleles. On the other hand, constraining STR locus heterozygosity in our simulations has little to no effect on power, because generally, STR heterozygosity is higher than the minimum threshold of 18%. These results demonstrate the effectiveness of a STR in detecting a candidate gene.
We then evaluated whether markers with different mutational mechanisms can be effectively combined on haplotypes in association studies. We find that including a STR on a haplotype with randomly chosen nonfunctional SNPs improves power. 1-STR/2-SNP haplotypes have more power than 3-SNP haplotypes when allele frequencies are not constrained. As we discussed above, a multi-allelic STR is advantageous because there is greater chance of a higher frequency allele associated with the cs. However, when rare SNPs are excluded from analysis with a minimum allele frequency threshold, the power of 1-STR/2-SNP and 3-SNP haplotypes are comparable.
In conclusion, we have identified several novel considerations when selecting markers for detecting association between phenotypes and candidate genes. First, the number of markers on a haplotype necessary to optimize the power of an association test depends on whether the cs is included in the analysis. When the cs is used in an association analysis, a single-marker test provides the highest power. Moreover, including nonfunctional markers with the cs reduces statistical power. However, when the haplotype marker-set is exclusively comprised of nonfunctional markers, more markers provide higher power. Even then, the benefit of adding markers plateaus. Second, STR polymorphisms are powerful markers for candidate gene association studies. We find STRs provide comparable or greater statistical power over a SNP. For haplotype association analysis, a STR provides more statistical power than randomly chosen SNPs, and comparable power to high frequency SNPs. A STR provides important information for detecting an association and should be used if it occurs in a candidate gene region.
Acknowledgements
This work was supported by a postdoctoral fellowship T32DA 07267 (to S.M.C) from the National Institute of Drug Abuse, National Institutes of Health.