Molecular mechanism of aggregation-induced emission
Abstract
Deep understanding of the inherent luminescence mechanism is essential for the development of aggregation-induced emission (AIE) materials and applications. We first note that the intermolecular excitonic coupling is much weaker in strength than the intramolecular electron-vibration coupling for a majority of newly termed AIEgens, which leads to the emission peak position insensitive to excitonic coupling, hence the conventional excitonic model for J-aggregation cannot effectively explain their AIE phenomena. Then, using multiscale computational approach coupled with our self-developed thermal vibration correlation function rate formalism and transition-state theory, we quantitatively investigate the aggregation effect on both the radiative and the nonradiative decays of molecular excited states. For radiative decay processes, we propose that the lowest excited state could convert from a transition dipole-forbidden “dark” state to a dipole-allowed “bright” state upon aggregation. For the radiationless processes, we demonstrate the blockage of nonradiative decay via vibration relaxation (BNR-VR) in harmonic region or the removal of nonradiative decay via isomerization (RNR-ISO) or minimum energy crossing point (RNR-MECP) beyond harmonic region in a variety of AIE aggregates. Our theoretical work not only justifies a plethora of experimental results but also makes reliable predictions on molecular design and mechanism that can be experimentally verified. Looking forward, we believe this review will benefit the deep understanding about the universality of AIE phenomenon and further extending the scope of AIE systems with novel applications.
INTRODUCTION
Over the years, organic electroluminescence plays a continuously important role in the development of science and technology and the improvement of people's life. Especially, for recent decades, it has been widely applied in flexible displays, solid-state lighting, organic lasers, and chemical/biological sensors, etc.[1-6] For practical applications, these organic materials are required to have a high luminescence quantum efficiency in solid phase. Traditionally, organic molecules with extended π-conjugation can emit bright light in solution; however, they always suffer from an annoying concentration- or aggregation-caused quenching of luminescence.[7] One hence got accustomed to focusing on the investigation of organic systems with strong fluorescence in solution for a long time, which largely limited the development and innovation of organic luminescent materials in solid phase. In 2001, Tang et al. coined the term aggregation-induced emission (AIE) to describe a phenomenon of organic molecules showing a substantial increase in luminescence upon aggregation,[8] which opened up a broad vision to rethink the design strategy of high-efficiency solid-phase organic systems. Since then, numerous of AIEgens have been synthesized and a wide variety of applications have been exploited.[9] Deep understanding of the inherent microscopic mechanism of AIE can pave ways into the design of novel AIEgens and the development of their applications.
In organic aggregates, the intermolecular interactions are diverse, including π–π, cation–π, anion–π+, dipole–dipole, ion–dipole, hydrogen bonding, halogen bonding and π–halogen bonding, etc., and the nature of such forces varies from electrostatic, dispersion, exchange (repulsion) to induction (polarization).[11, 12] The interactions can change the molecular geometric and electronic structures, and affect the excited-state energy dissipation pathways, which is complicated and system-dependent.[13] The traditional J-aggregation with strong excitonic coupling was first proposed independently by Scheibe and Jelley, in which the transition dipole moment is enlarged owing to the in-phase quantum superposition, was regarded as the major cause for the enhancement of solid-phase luminescence for a long time.[14] However, it cannot effectively explain the phenomena of the majority of newly synthesized AIEgens, of which the intermolecular excitonic coupling is generally much weaker than the intramolecular electron–vibration coupling. The plausible intermolecular quantum phase led by aggregation will be hindered owing to the flexible intramolecular motions in these AIEgens.[9] As a result, a variety of explanations have been proposed for AIE phenomena for different organic systems, such as restriction of the intramolecular rotation (RIR),[8, 10] restriction of intermolecular motion (RIM)[15] and blocking of nonradiative decay channels,[16] the restriction of E/Z isomerization process,[17] the excited-state intramolecular proton transfer,[18] the blockage of access to dark state via isomerization,[19] restricted access to conical intersection[20] crystalline-induced reversal from dark to bright state,[21, 22] Herzberg-Tell vibronic coupling induced emission,[23] and so on.[9, 10] Nevertheless, a clear and comprehensive picture is not yet to be drawn for the microscopic AIE mechanism, the corresponding relationship between photophysical property and mechanism, and general principles of aggregation behavior modulation.
Upon photoexcitation, there are three decay pathways from the excited state (ES) (singlet S1 or triplet T1) to the ground state (GS) S0 (Figure 1): (i) radiative decay process (), for which the simplest two-level Einstein spontaneous rate reads: (in s−1), where f is the dimensionless oscillator strength and is the vertical transition energy in unit of wavenumber. It could slightly vary with temperature if vibrational structures are considered. Typically, is in 107–9 s−1 for singlet and in 101–6 s−1 for triplet emissions; (ii) the nonradiative decay induced by vibration relaxation (NR-VR), which requires the equilibrium positions of ES and GS close each other. Such process could be approximated as harmonic oscillator relaxation which we term as harmonic region (); (iii) the nonradiative decay via isomerization (NR-ISO) or a minimum energy crossing point (NR-MECP) in which the molecular geometry in the ES undergoes large conformation change. We term these two situations as “beyond harmonic region” (). According to Kasha's excitonic theory, excitonic coupling leads to different optical spectrum in aggregates with respect to that of single molecules, namely, blueshifted/enhanced absorption and redshifted/quenched emission for H-aggregates and redshifted/strengthened for absorption and emission in J-aggregates (middle panel of Figure 1). The intermolecular quantum coherence could be hindered due to both intramolecular and intermolecular static and dynamic disorders. In this case, the emission still stems from single molecule and the surrounding molecules act as environment that influences ES decay rates.
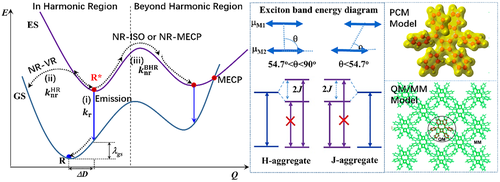
In this review, we first comparatively investigate the effect of excitonic coupling on the optical spectra in conventional H- and J-aggregates and newly reported AIEgens. We find the emission property of typical AIEgens is hardly influenced by the intermolecular excitonic coupling (J) owing to strong intramolecular electron–vibration coupling (λ) and relatively weak J with J/λ< 0.17 at room temperature. Then, we quantitatively predict the rate constants of three microscope processes (radiative, NR-HR, and NR-BHR) and luminescence quantum yield (ΦLQY) of a variety of organic molecules in different environments by combining quantum chemistry calculations and TVCF theory developed by our group.[24-27] The solution and aggregation effects are considered by polarizable continuum model (PCM) and quantum mechanics/molecular mechanics approach (QM/MM), respectively (the computational models are shown in right panel of Figure 1). Importantly, we systematically analyze the dependence of key physical parameters on the intermolecular interactions and disclose the microscopic mechanisms of the inversion from a dipole-forbidden “dark” state to a dipole-allowed “bright” state upon aggregation, the blockage of nonradiative decay channels via vibration relaxation (NR-VR) in harmonic region, and the removal of isomerization (NR-ISO) or minimum energy crossing points (NR-MECP) beyond harmonic region in a plethora of systems, in close comparison with the corresponding experiments. This provides a very comprehensive photophysical picture to deeply understand the emission phenomena of organic systems in different environments. We emphasize the molecular mechanism for AIE.
EFFECTS OF EXCITONIC COUPLING AND ELECTRON–VIBRATION COUPLING ON OPTICAL SPECTRA OF AGGREGATES
The middle panel of Figure 1 displays the electronic structure of the original Davydov's molecular excitonic model for H- and J-aggregates without considering electron–vibration coupling. The spectrum can be very different if vibrationally resolved structures are taken into accounts. Therefore, we here systematically calculate the vibrationally resolved spectra of the conventional H- and J-aggregates in close comparison with the AIEgens, with and without considering intermolecular electrostatic interaction and excitonic coupling, and analyze the origin of these spectra.[28]
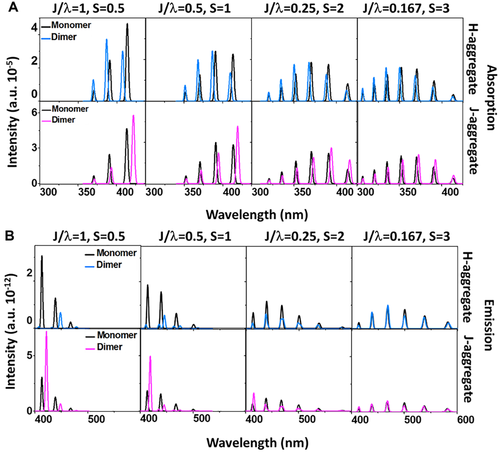
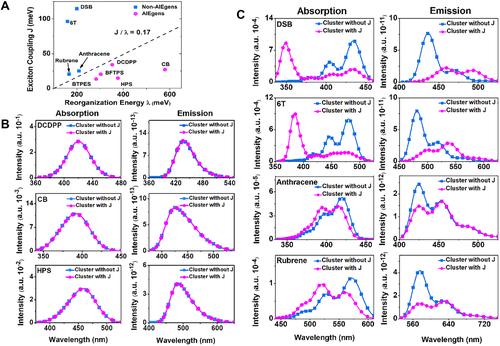
Bearing this in mind, we made extensive quantum chemistry computations considering all the molecular vibrational modes and the corresponding Huang–Rhys factors for both AIEgens and non-AIEgens. The intermolecular J is calculated based on crystal structures. The magnitude of J/λ and the optical spectra with and without electrostatic interaction and excitonic coupling of a series of fluorophores are depicted in Figure 3, including four conventional non-AIEgens (DSB, 6T, Anthracene, Rubrene) and five AIEgens (DCDPP, CB, HPS, BFTPS, BTPES) as shown in Scheme 1. Here, the electrostatic interaction is taken into account for the geometrical optimizations and frequency calculations of these compounds via QM/MM method. It is interesting to note that J/λ for non-AIEgens are always greater than 0.17 while those of AIEgens are all less than 0.17 as shown in Figure 3A. Accordingly, the spectra of the non-AIEgens change significantly before and after taking excitonic coupling into consideration while the ones of AIEgens are almost unchanged, which fully confirms the competition between intermolecular excitonic coupling and electron–vibration coupling in determining the emissive property of the aggregates, and the validity of the critical J/λ value to judge the effect of excitonic coupling. The spectra of DSB and 6T experience the largest variaion owing to very large J/λ, namely, sharply blue-shifted and significantly intensity-enhanced absorption spectra and red-shifted and intensity-reduced emission spectra from solution to aggregate. The ones of anthracene and rubrene exhibit slight variance because of relatively small J/λ. The spectra of the AIEgens are independent of the excitonic coupling because of smaller J/λ caused by weak intermolecular excitonic coupling and strong intramolecular electron–vibration interaction. This indicates the excitonic couplings can be neglected when we calculate the excited state decay rate constants of these investigated AIEgens and similar systems.
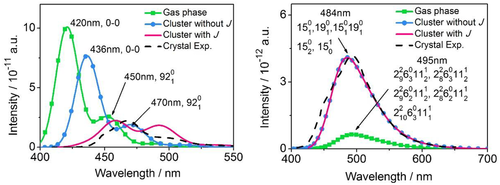
We take DSB and HPS as examples to compare the optical spectra of the isolated molecule and those of aggregates with and without considering intermolecular electrostatic interaction and excitonic coupling in Figure 4, together with available experimental results. It is found that the emission spectra consist of two significant peaks which are 0–0 transition and 0–1 transition of mode ∼1650 cm−1 for isolated DSB and solid-phase DSB without considering J, respectively. Moreover, the solid-phase spectrum is red-shifted with respect to the isolated molecules owing to the decreased ΔE. After considering J, the 0–0 peak noticeably slumps and the 0–1 peak becomes dominant owing to oppositely oriented transition dipole–dipole interaction in H-aggregate, which generates pronounced red-shift as observed in experiment. Different from DSB, the emission spectrum of HPS is a broad band without fine structure owing to the participation of a large number of vibration states, namely 2–8, 2–9, and 2–10 transitions of the 2nd mode with low frequency but large Huang–Rhys factor, 0–3 and 0–2 transitions of the 6th mode, and 1–1 and 1–2 transitions of the 11th mode for isolated HPS, and 0–1, 0–2, and 1–0 transitions of the 15th and 19th for solid-phase HPS. More strikingly, the emission spectrum of HPS is greatly enhanced in intensity and significantly blue-shifted upon aggregation, and remains almost unchanged before and after taking J into account. This indicates the remarkable change of the emission spectrum upon aggregation is mainly caused by the electrostatic interaction other than the excitonic coupling for the investigated AIEgens. Therefore, the excitonic coupling (whether H or J-type) will no longer be included in the following sections.
EMERGENCE OF THE LOWEST STATE S1 AS BRIGHT STATE UPON AGGREGATION
The radiation from molecule requires electric transition dipole moment between ES and GS, . Thus, the nature of wave function, including shape, symmetry, and spatial distribution, is essential to transition dipole moments, and thereupon several selection rules are generated: (i) spin-allowed if the multiplicities of the two states are identical, (ii) symmetry-allowed if the transition happens between a gerade state and a ungerade state, and (iii) overlap-allowed if the wave functions of two states are not completely separated in space.[7] For luminescent materials (for instance with π→ π* transition), the radiative decay from the lowest excited state is always transition dipole-allowed in both solution and aggregate phase.[20] Nevertheless, recently, it is found that the “dark” state with n → π* or σ→ π* or fully charge-transfer (CT) or symmetry-forbidden transitions can convert to a “bright” state owing to electrostatic interactions in some organic compounds when going from solution to aggregation phase.[21, 22, 31] Moreover, a “dark” state with symmetry-forbidden transition is also found to emit bright light owing to the Herzberg-Teller vibronic coupling in 5, 10-diphenylphenazine (DPhPZ) aggregate.[23] As a result, the novel cores/backbones of AIEgens are exploited which provides a new stage to tremendously broaden the scope of excellent AIEgens. Several examples are presented in the following subsections.
Aggregation-induced reversal from dark n–π* to bright π–π*state
A typical aromatic diacid, terephthalic acid (TPA, Scheme 1) was reported to exhibit a unique phenomenon of strong fluorescence, delayed fluorescence and phosphorescence upon crystallization, relative to extremely weak visible light in solution and amorphous phases.[32] To find out the morphology dependence of luminescence property, we here comparatively analyze the geometrical and electronic structures of the low-lying excited states of the isolated and crystalline TPA at hybrid CASPT2 (8e, 8o)/ANO-RCC-VDZP/AMBER level by interfacing MOLCAS[33] and TINKER[34] packages.[21] It is found that electrostatic interaction from the surrounding molecules in crystal can largely lift the excited state with n → π* transition and slightly lower the excited state with π→ π* transition in energy as seen in Figure 5. The n-orbital is sensitive to the electrostatic forces owing to the charge concentrating on the oxygen that gives a separation of charge, while the π-orbital is insensitive due to uniform charge distribution of the charge. Thus, upon crystallization the 1(π,π*) state is reduced to be the lowest excited state S1 (4.76 eV) from the second lowest excited state S2 (4.99 eV) in the gas phase, whereas the 1(n,π*) state is lifted to be S2 state (5.05 eV) from S1 (4.81 eV) in the gas phase. These findings reinforce that crystallization induces the conversion from dark 1(n, π*) to bright 1(π,π*) for the S1 state in TPA, recovering the strong emission in light of Kasha's rule. The resultant transition dipole moment of S1 is largely increased from 4.97 × 10−4 to 5.28 × 10−2 Debye upon aggregation, which meet the necessary requirement for fluorescence or phosphorescence .[21]
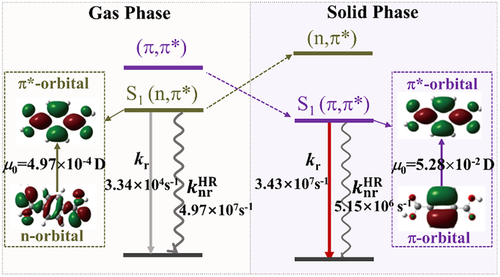
More excitingly, the electrostatic interaction not only plays a role for a faster radiative decay via changing the energetic order of the low-lying excited state, but also introduces a slower nonradiative decay via weakening electron–vibration coupling of S1→S0 upon crystallization. The rate constants of the radiative and nonradiative decay from S1 to S0 are calculated via TVCF method in our home-built MOMAP program.[24-26, 35, 36] The resultant is greatly increased by three orders of magnitudes from 3.34 × 104 s−1 to 3.43 × 107 s−1 and the is decreased by one order of magnitude from 4.97 × 107 s−1 to 5.15 × 106 s−1, as TPA goes from the gas phase to crystalline phase. The enhancement of radiative decay rate and the reduction of nonradiative decay rate together lead to the occurrence of strong fluorescence and phosphorescence upon crystallization, which rationalize the mechanism of the crystallization-induced double emission phenomenon as observed in experiment.
Crystallization-induced reversal from dark (n+σ)–π* to bright π–π* state
A unique squaraine (SQ) derivative (CIEE-SQ, Scheme 1) is found to emit brighter and brighter light from in crystal to cocrystal with CIEE-SQ:CHCl3 = 1 with respect to very weak emission in solution, which have rarely been observed in previous reported SQ derivatives.[22] To unveil the inherent micromechanism, we comparatively investigated the geometrical and electronic structures of the CIEE-SQ in isolated, crystalline and cocrystalline phases using ONIOM approach with two layers TD/M062X/6-31G*/UFF implemented in Gaussian 16.[37] It should be noted that there are three conformations (C1, C2, and C3) in CIEE-SQ crystal, which are calculated and discussed in details in reference.[22] Here we take C2 as a representative to illustrate the changes of the geometrical and electronic property from isolated to aggregated CIEE-SQ. It is first found that the geometry of S0 state (S0-geometry) of the isolated CIEE-SQ is similar to that of the aggregated CIEE-SQ, which is confirmed by the analogous absorption spectra in dilute solution and crystalline phase as observed in experiment. Second, there occurs dramatic geometric change to the S1-geometry upon excitation. The S1-geometry of the isolated molecule tends to extend as much as possible with the decrease of θ angle from 54.80o of S0 to 18.48o of S1 state, while that of the crystalline structure becomes more distorted with the increase of θ angle from 58.20o to 71.52o and ϕ angle from 3.70o to 15.66o (see Figure 6A), which is expected to bring about their distinct electronic transition property in both phases. Third, as seen in Figure 6B, the calculated oscillator strength of the S1 state is zero because the transition is forbidden from mixed n- and σ-orbital to π*-orbital, while that of the S2 state is 0.8900 owing to its dipole-allowed transition from π- to π*-orbitals for the isolated CIEE-SQ. These results lead to extremely weak fluorescence in dilute solution based on Kasha's rule, as observed in experiment. On the contrary, the energetic order of the low-lying excited states for C2 happens to be reversed upon aggregation, that is, the S1 state turns to be bright 1(π, π*) with f = 0.8454 while the S2 state is converted to be a dark state, which justifies the recovery of luminescence from in solution to aggregate in experiment.
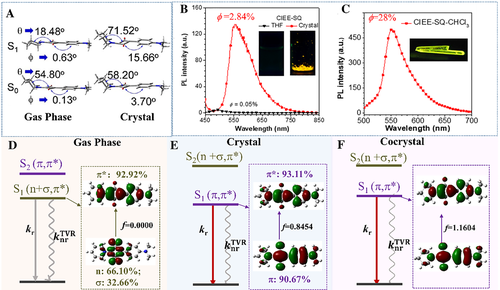
Except for the radiative decay, the nonradiative decay simultaneously takes place to dissipate the excited state energy. As it is known from previous investigations, the geometrical relaxation energy (λ), also called as reorganization energy or electron–vibration coupling, can properly characterize the rate of nonradiative decay process.[13, 38] The λ of the isolated molecule and C2 in crystal are calculated to be 4928.78 cm−1 and 3273.53 cm−1, respectively, which indicates that the rigid environment in crystal significantly suppress λ to restrict the nonradiative decay to some extent and facilitate the radiative decay. Considering the fact that the electrostatic interaction can stabilize 1(π, π*) and restrict the intramolecular motions to a greater extent, we introduce chloroform (CHCl3) into CIEE-SQ crystal to form a more compact co-crystal conformation. As expected, the participation of chloroform further stabilizes the 1(π, π*) state with f increasing from 0.8454 to 1.1604 and λ decreasing from 3273.53 to 870.80 cm−1 when going from crystal to co-crystal, greatly boosting the fluorescence, which agrees with the measurements quite well, that is, the quantum efficiency improved from 2.84% to 28.0%. Overall, crystallization or cocrystallization induces the conversion from dark 1(n + σ, π*) state to bright 1(π, π*) state to generate significantly fast radiative decay rate and simultaneously suppress the nonradiative decay rate, boosting fluorescence. More importantly, a novel type of AIEgens without typical π-conjugation feature have been exploited for high-performance solid-phase luminescence, which inspires researchers to design excellent solid-phase fluorophores via excited-state manipulation.
HINDRANCE OF NONRADIATIVE CHANNELS IN AGGREGATES
The quantitative calculation of quantum luminescence yield
As seen in Figure 1, the NR-VR in harmonic region and NR-ISO/NR-MECP beyond harmonic region presumably occur simultaneously and compete with each other in organic systems, that is, either the former is dominant or the latter becomes the rate-determining step of the whole nonradiative processes. Such issue has raised open discussions for a long time. In 1923, predissociation phenomenon of O2 found by Henri was regarded as the earliest nonradiative transition phenomenon observed in experiment.[39] In 1932, Zener theoretically suggested that molecules can undergo nonradiative transition through nonadiabatic crossing of energy levels.[40] In 1937, Teller extended the nonradiative transition to polyatomic molecules with conical intersection (CI) of potential surfaces of two electronic states with identical symmetry.[41] In 1950, Huang and Rhys proposed nonradiative transition theory in F-centers based on displaced harmonic oscillator model.[42] From 1961 to 1965, Robinson, Frosch, and Ross treated the internal conversion (IC) as a tunneling process, during which the crossing of potential surfaces rarely occurred, and the IC rate constant is the product of the square of perturbation matrix time the FC factor.[43] In 1966, Lin wrote the general expression of nonradiative transition rate constant considering the Boltzmann distribution of temperature based on Fermi-golden rule and displacement harmonic oscillator model.[44] On this basis, Englman and Jortner derived the energy gap law for the nonradiative transition in large molecules by adopting weak-coupling approximation, followed by Fischer and Schneider via adding an anharmonic term to the formula in 1971.[45] Lin discussed Duschinsky rotation effect of several vibrational modes on the transition rate in 1998.[46] In 2007, Peng and Shuai derived an analytical expression based on time-dependent formalism by considering Duschinsky rotation effect of all vibration normal modes via the thermal vibration correlation function (TVCF).[24] Islampour and Miralinaghi also obtained similar formalism by employing generation function independently in the same year.[47] In 2008, applying TVCF approach, Niu and Shuai further got a more general analytical formalism via abandoning the promoting-mode approximation,[26] and starting from second-order perturbation, Peng et al. derived an analytical formalism combining spin-orbit coupling and nonadiabatic coupling for nonradiative decay rate constant between triplet and singlet states.[25] Marian et al. investigated the effect of spin-vibronic coupling on the intersystem crossing rate.[48] In 2017, Peng and Shuai further took the excitonic coupling into account for nonradiative transition rate of molecule-in-aggregate under a primitive split operator approximation.[49] The conical intersections are also widely discussed as an important transition pathway in a number of nonemissive photochemical processes.[50]
From the perspective of dynamics theory, the molecular quantum nonadiabatic dynamics simulation in principle can provide an accurate picture of the real systems regardless of the nonradiative transition induced by VR or ISO or MECP. However, the typical time scale of the best currently available nonadiabatic dynamics simulation is the order of ∼fs or ∼ps,[51] which is about 3–4 orders of magnitude smaller than the radiative/nonradiative decay rate constant of ca. 10 ns for strongly luminescent organic systems. Moreover, the favored organic molecules for practical applications in the field of light-emitting devices have dozens to hundreds of atoms, which are far beyond the computational ability of quantum dynamics simulations. Therefore, the kinetic TVCF formalism for of a VR-induced transition in harmonic region[52] (channel II in Figure 1) and transition state theory (TST) for of a MECP or isomerization one beyond harmonic region[53] (channel III in Figure 1) should be considered as practical alternatives for quantitatively predicting luminescence quantum yield ().
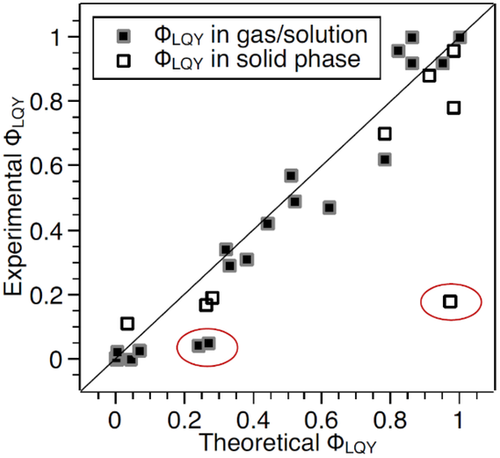
In order to check the reliability and practicability of TVCF approach for the prediction of , we first compare the experimental and theoretical ones via combining TVCF formulism and quantum chemistry calculations for a variety of organic systems (Scheme 1), as given in Figure 7, as well as the values of the radiative and nonradiative rate constants listed in Tables 1 and 2. Here, The radiative decay rate constant was evaluated via TVCF formulism as .[36] The is approximated to be IC rate constant by neglecting the insignificant S → T ISC rate constants for these systems, which is evaluated as with corresponding to the TCVF and referring to nonadiabatic coupling and being the paritition function for the initial state parabola.[26] From Figure 7, it is obvious that TVCF formulism has achieved a big success in quantitatively predicting for organic systems either in the gas phase, solution or in solid phase according to the good linear relationship between the calculated and experimental .
| Molecule | ||||
|---|---|---|---|---|
| BDP-1Aa | 1.90 × 108 | 0.32 × 108 | 0.86 | 0.92 |
| BDP-1Ca | 2.67 × 108 | 4.44 × 108 | 0.38 | 0.31 |
| BDP-1Da | 2.20 × 108 | 0.11 × 108 | 0.95 | 0.92 |
| BDP-1Fa | 2.18 × 108 | 0.36 × 108 | 0.86 | 1.00 |
| BDP-1Ga | 1.17 × 108 | 3.73 × 108 | 0.24 | 0.04 |
| BDP-1Ha | 1.12 × 108 | 3.09 × 108 | 0.27 | 0.05 |
| BDP-1Ia | 1.65 × 108 | 3.29 × 108 | 0.33 | 0.29 |
| BDP-2Aa | 1.87 × 108 | 0.52 × 108 | 0.78 | 0.62 |
| BDP-2Ca | 2.32 × 108 | 2.12 × 108 | 0.52 | 0.49 |
| BDP-2Da | 2.59 × 108 | 1.60 × 108 | 0.62 | 0.47 |
| BDP-2Ia | 2.52 × 108 | 0.56 × 108 | 0.82 | 0.96 |
| BDP-2Ka | 2.07 × 108 | 4.35 × 108 | 0.32 | 0.34 |
| BDP-3Aa | 2.30 × 108 | 2.17 × 108 | 0.51 | 0.57 |
| tt-DPBb | 9.58 × 108 | 11.9 × 108 | 0.44 | 0.42 |
| Perylenec | 0.91 × 108 | 0.72 × 103 | 1.00 | 1.00 |
| DCDPPd | 0.93 × 107 | 4.45 × 109 | 2.09 10−3 | 1.50 10−4 |
| 1,2,3,4-TPBDb | 4.80 × 108 | 1.09 × 1010 | 4.20 10−2 | 1.10 10−3 |
| DMTPSe | 1.20 × 108 | 1.80 × 1011 | 6.66 10−4 | 2.20 10−4 |
| HPDMCbf | 0.86 × 108 | 1.31 × 1011 | 6.59 10−4 | 1.7 10−3 |
| TPSg | 0.93 × 106 | 1.62 × 1010 | 1.0 10−4 | 2.0 10−4 |
| HPSg | 4.98 × 107 | 2.53 × 108 | 2.0 10−3 | 2.2 10−3 |
| BTPESg | 6.76 × 107 | 2.66 × 108 | 2.5 10−3 | 2.3 10−2 |
| BFTPSg | 1.22 × 108 | 1.66 × 109 | 6.86 10−2 | 2.6 10−2 |
| APPEFh | 0.47 × 108 | 1.27 × 108 | 3.69 10−3 | 1.10 10−3 |
| Molecule | ||||
|---|---|---|---|---|
| COTha | 6.05 × 105 | 1.87 × 107 | 0.031 | 0.11 |
| HPDMCbb | 7.95 × 105 | 2.29 × 107 | 0.78 | 0.70 |
| TPSc | 1.15 × 106 | 3.32 × 106 | 0.26 | 0.17 |
| HPSc | 7.43 × 107 | 1.56 × 106 | 0.98 | 0.78 |
| BTPESc | 6.57 × 107 | 1.93 × 106 | 0.97 | 0.18 |
| BFTPSc | 1.14 × 108 | 1.07 × 107 | 0.91 | 0.88 |
| CPEId | 2.17 × 108 | 5.64 × 108 | 0.28 | 0.19 |
| (CAACAd)CuCle | 7.83 × 105 | 1.47 × 104 | 0.98 | 0.96 |
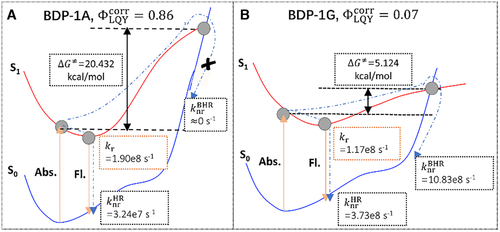
As seen in Figure 7, three large deviations are found in two molecules in solution (BDP-1G and BDP-1H), and one in solid phase (BTPES), of which the calculated are significantly larger than the experimental counterparts. In terms of the excited state decay processes illustrated in Figure 1 and analyzed above, from equilibrium point of S1 to MECP should be considered besides, and in this case should become . We here choose BDP-1A and BDP-1G as “good” and “bad” representatives, respectively, to quantitatively compare the contribution from and to the whole nonradiative decay rate constants.[54] We first locate the S1/S0 MECPs of both systems by using the penalty function method developed by Levine et al.[55] at spin-flip TDDFT (SF-TDDFT) level in Q-CHEM program.[56] The obtained MECP-geometry of BDP-1G is very close to that determined at CASPT2 level in reference,[57] indicating the reliability of SF-TDDFT in describing the MECP for such systems. The is evaluated by TST approach as with denoting the Gibbs free energy of activation from the FC point to MECP-geometry along the reaction path in the S1 state, and the calculated results are presented in Figure 8. The S1/S0 MECP of BDP-1A lies much higher than the FC point in energy and the resultant is approximately vanishing due to an extremely large ΔG⧧ = 20.432 kcal mol–1. It should be noted that ΔG⧧ is the energy difference between the S1 states at the S0-geometry and MECP-geometry as plotted in Figure 8 because there is no transition state along the reaction path. Thus, the calculated including only and is in good consistence with experimental values for BDP-1A compound, as shown in Figure 7. On the contrary, (10.83 × 108 s−1) of BDP-1G is 2∼3 times larger than (3.73 × 108 s−1), which results in a significant decrease of from 0.24 to 0.07, much approaching to the experimental value (0.04). Therefore, in this case of BDP-1A, both and should be taken into consideration and the resultant luminescence yield is in line with the experimentally measured value. Given the fact that is around 107–9 s−1 for typical organic molecules, NR-MECP can be fully neglected when ΔG⧧ > 10 kcal mol–1 (< 106 s–1). Otherwise it would play an important role in the nonradiative decay processes, especially when ΔG⧧ < 6 kcal mol–1 (> 108 s−1).
Taking these microprocesses into mind and considering the effect of molecular aggregation on the processes, the mechanism of aggregation-induced emission is naturally revealed for the AIEgens. By quantitatively investigating and via TVCF approach of a series of AIEgens in different environments, including temperatures, gas phase, solution and solid phase, Shuai's group confirmed that the nonradiative decay channels are significantly blocked due to the decrease of electron–vibration coupling (reorganization energy) and the vibration–vibration decoupling (Duschinsky rotation effect) in rigid environmental conditions.[15, 58-60] Blancafort et al. claimed that strong fluorescence is caused by the removal of MECP from solution to aggregates for some AIEgens.[20, 61] The elimination of photoisomerization is found to lead to the occurrence of AIE phenomenon from solution to aggregate.[62] Other groups declare the photo-induced ring-closed nonradiative process in TPE by nonradiative dynamic method.[63] These indicate that the two kinds of nonradiative decay processes are system-dependent and environment-dependent, and they sometimes coexist and compete with each other, or one of them is dominant and rate-controlling step. How to probe and confirm the micromechanism for certain systems? Although the nonradiative decay process cannot be visualized via experiments, the related photophysical property and signals are likely to behave selectively and specifically for different mechanisms. In the following sections, we review the quantitative description of these nonradiative decay pathways, disclose different AIE mechanisms of some typical AIEgens and present unique characteristics of the photophyscial behaviors corresponding to different mechanisms.
Blockage of nonradiative decay via vibration relaxation in harmonic region
Quantitative description of the blockage of NR-VR
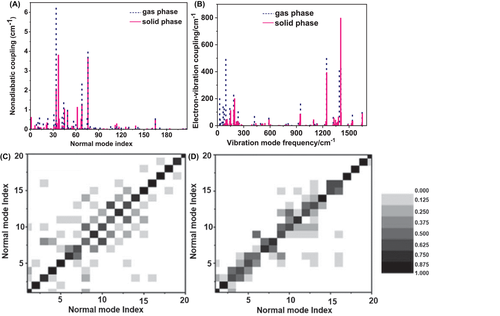
As seen from the comparison between the radiative and nonradiative decay rate constants summarized in Tables 1 and 2 for AIEgens in the gas phase/solution and solid phase, it is easily found that the radiative decay rate constant is almost independent from the environment, while the nonradiative decay rate constants greatly decrease from solution to aggregate, which leads to the occurrence of strong fluorescence in aggregates. Taking HPS an example, we disclose the origin of the change of the nonradiative decay rate by analyzing the nonadiabatic coupling, electron–vibration coupling and vibration–vibration mode mixing (Duschinsky rotation effect, DRE) during the excited state decay process in Figure 9.[66] The nonadiabatic coupling provide the driving force of internal conversion from S1 to S0, whose coupling matrix elements are calculated by based on the first-order perturbation theory; the electron–vibration coupling characterizes the ability of molecular vibrations to accept the electronic excited-state energy during the internal conversion, which is computed via for the ith normal mode; the mode mixing corresponds to multichannel internal conversion of a vibration mode of S1 to many modes of S0, in which Duschinsky rotation matrix (DRM) is obtained via (Li(f) is the normal mode with mass weighted in the initial (final) electronic states. From Figure 9, it can be seen that the nonadiabatic coupling is insensitive to the environment. While the electron–vibration coupling and the degree of mode mixing are very susceptible to aggregation: (i) the low-frequency vibration modes are significantly blue-shifted with the number of modes with energy less than 100 cm−1 decreased from 15 to 6; (ii) the electron–vibration couplings are notably weakened, especially those of the low-frequency modes; and (iii) many modes are segregated from each other with many vanishing off-diagonal terms from Figure 8C to 8D (when the off-diagonal element of DRM is not zero, the corresponding two modes are mixing each other) when going from solution to aggregate. These changes slow down the nonradiative decay from S1 to S0, recovering strong light-emitting in aggregate.
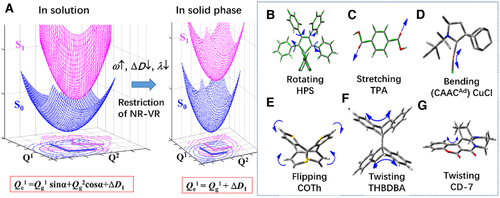
Based on the above analysis, we propose the micromechanism of these investigated AIEgens and plot the change feature of the potential energy surface from solution to aggregate in Figure 10. In light of the important contribution of low-frequency modes to the AIE of HPS, we present the PESs of S0 and S1 of two low-frequency modes as a representative. In solution, the PESs of S0 and S1 are very flat and far apart from each other. Moreover, each mode of S1 is mixing with many modes of S0 (taking two modes an example). At room temperature, many vibrational modes with high quantum numbers are activated to dissipate the excited-state owing to strong electron–vibration coupling, and a lot of nonradiative channels are opened due to effective mode-mixings. Both of these two processes highly speed up the nonradiative decay rate. When going to aggregate, the PESs become very steep because the intramolecular vibrational motions are restricted by the intermolecular interactions in compact molecular-packing aggregate. Accordingly, the number of activated vibration states and the nonradiative decay channels are decreased because of the weak electron–vibration couplings and subtle mixing among modes. Consequently, the nonradiative decays rate is sharply decreased. Theoretical investigations of a tremendous amount of systems demonstrate that aggregation can effectively attenuate the couplings between electron and a great variety of vibration modes, including rotating,[15, 58-60, 66] twisting,[15, 68] stretching,[21] bending,[69] and flipping[70] vibrations by virtue of their special intermolecular interactions (see Figures 10B–G), which all significantly restrict the molecular geometrical relaxation and slow down the nonradiative decay, thus inducing strong fluorescence upon aggregation. These findings provide sound theoretical evidences for the RIR, RIV and RIM mechanism proposed by Tang's group from the perspective of molecular conformations.[8, 9, 14, 68] So far, theoretical calculation have drawn a clear picture to demonstrate the change of electron–electron, electron–vibration, vibration–vibration coupling, and the effect of them on the nonradiaitive decay rate constants from solution to aggregate, which unravels deep insights of various experimental phenomena.
Experimental verifications of the theoretical predictions
The AIE mechanism revealed above focused on the change of electron–vibration coupling and vibration–vibration mixing upon aggregation. In order to visualize the theoretical parameters in experiments to confirm their contributions to AIE, we bridge the theoretically calculated parameters and experimentally measurable physical parameters.
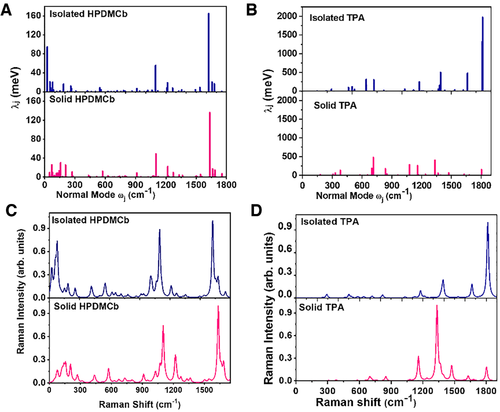
Resonance Raman spectroscopy (RRS) is a spectroscopic technique to characterize molecular excited-state dynamics, including but not limited to molecular vibrational redistribution and electron–vibration couplings.[71, 72] Because the intensity of the RRS signal from the jth normal mode is proportional to the product of electron–vibration coupling and frequency () under the FC approximation and the resonance condition,[72] we proposed that the RRS can be used as an effective tool to detect the aggregation effect on the λ, validating the AIE mechanism revealed above.[73]
Taking two AIEgens HPDMCb and TPA as examples, their calculated RRS intensity (σ) and electron–vibration coupling (λ) are plotted in Figure 11 in isolated and solid phases. Comparing σ and λ of HPDMCb and TPA, it is clearly found that their distribution features among vibration modes are almost identical in both phases. For HPDMCb, the low-frequency peaks have remarkable blue-shift with sharply decreased RRS intensity while the high-frequency peaks are almost unresponsive in both position and intensity. Different from HPDMCb, the low-frequency peaks of TPA are insensitive to the environment while the high-frequency peaks have changed significantly in intensity. The intensity of the peak corresponding to C = O stretching vibration is largely decreased while that of the peak from C = C stretching vibration is remarkably increased when TPA going from solution to aggregate owing to the appearance of hydrogen bonding interaction. All these findings indicate that the RRS can rationally reflect the change of the electron–vibration coupling in different environments, which fully confirm the contribution of electron–vibration coupling to the AIE process. The AIE mechanism are thoroughly validated as the fact that the decoupling between the transition electrons and low-frequency vibrations in HPDMCb and high-frequency vibrations in TPA significantly slows down the nonradiative decay rate, making strong fluorescence appear upon aggregation.
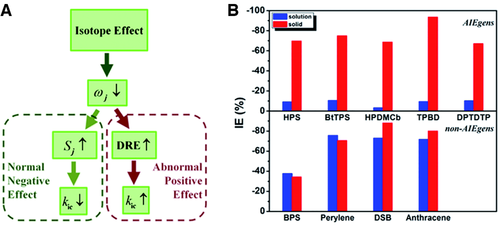
Isotope effect (IE) has been widely applied to probe the nonradaitive decay process.[74, 75] Herein, deuteration is always used an effective mean to decrease the nonradiative decay rate so as to greatly improve the luminescence efficiency for conventional luminogens. Conventional luminogens are mostly rigid π-conjugated systems, which obey the Fermi-golden rule under displaced harmonic oscillator model for the nonradiative decay rate.[76] In this case, the nonradiative decay rate constant is proportional to, in which S can be determined by . is equal to the difference of the excitation energies at the equilibrium S0-geomtery and S1-geometry, which is unchanged due to the same geometrical and electronic structures after deuteration. Thus, S is increased owing to the decrease of frequency, which consequently decreases the nonradiative decay rate based on the exponentially proportional relation between the rate constant and S as given above.
Differently, the flexible AIEgens in solution are beyond the description of the displaced harmonic oscillator model because the mixing among vibrational modes or DRE is severe in the excited-state decay process. Especially, in the AIEgens with large reorganization energy introduced from low-frequency modes, the DRE becomes more serious for much more activated low-frequency vibration states after deuteration, which sharply accelerate the nonradiative decay rate. Hence, the deuteration brings up two contradictory effects on the nonradiative decay rate, the negative effect through increased S and the positive effect via strengthened DRE. When the latter outstrip the former, there would be abnormal positive isotope effect, and vice versa. We define the isotope effect as and calculate the isotope effect of a series of AIE-active systems and non-AIE ones by combining TVCF rate formulism in MOMAP program and (TD) DFT with PCM for solution and ONIOM approach in Gaussian 09 program for solid as seen in Figure 1.[60] It is expectedly seen that AIEgens in solution exhibit abnormal positive isotope effect owing to strong vibration–vibration coupling, while the AIEgens in solid phase recover normal negative isotope effect because of the decoupling of the vibration–vibration upon aggregation, as analyzed above. The isotope effects of non-AIEgens are independent from the environment owing to marginally vibration–vibration mixing. Overall, for AIEgens, a more remarkable IE exists in solid phase than in solution, while for non-AIEgens, high IE happens in both solid and solution phases. So far, these fully prove the important contribution of DRE or vibration–vibration coupling on the AIE. At the same time, the isotope effect can be used as a mean to probe the AIE property at the molecular level.
Removal of nonradiative channels beyond harmonic region
Restricted access to a MECP and experimental visualization
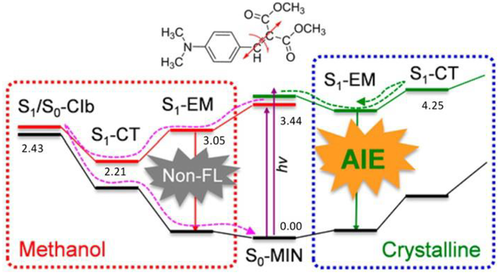
As analyzed above, the nonradiative decay via MECP is sometimes a dominant factor to quench emission in solution, and its removal leads to strong fluorescence in aggregate. Li and Blancafort first proposed restricted access to a conical intersection (RACI) to rationalize the AIE phenomenon of diphenyl dibenzofulvene (DPDBF).[20] Since then, RACI has been used for the explanation of the AIE phenomenon for many AIEgens.[77-82] We here illustrate the RACI mechanism via an example of 4-diethylamino-2-benzylidene malonic acid dimethyl ester (BIM) with AIE activity, whose fluorescence quenching in solution and fluorescence enhancement in crystal are investigated by Liu group via QM (TDDFT and CASSCF) and ONIOM (QM:MM) calculations.[80] The calculated S1 potential energy surface along the torsion coordinate of the styrene double bond in solution shows that upon excitation, BIM first initiates a FC-like local minimum (S1-EM), then experiences a barrierless relaxation to a low-energy intermediate with charge-transfer character (S1-CT), then reaches a S1/S0 conical intersection (S1/S0-CIb), and finally nonradiatively comes back to S0 via the CIb, as depicted in Figure 13. The barrier to access S1/S0-CIb is very small from S1-EM, which indicate that S1/S0-CIb is responsible for the fluorescence quenching of RIM in methanol. In the crystalline phase, the rigid environment precludes the torsion of the styrene double bond, which restricts the access to a conical intersection with much higher energy. As a result, RIM is trapped in the S1-EM and the S1-EM emits strong fluorescence.
How to prove the occurrence of nonradiative decay via VR (), or CI or MECP (), or both them? We here call the temperature dependence of the nonradiative decay rate to mind. Because for organic fluorophores, the nonradiative decay via MECP always needs to cross over an energy barrier, either to a transition state (TS) or to a high-energy MECP, is likely to be very sensitive to temperature and have a sudden growth when energy reaching the mutation point at certain temperature. On the contrary, the nonradiative decay via VR is a decay process from high-energy excited state to low-energy ground state without an energy barrier, is not as sensitive to temperature as and behaves a monotonically slight increase with the increase of temperature. Consequently, the excited-state lifetime and luminescence quantum efficiency combining the two nonradiative processes will exhibit nonmonotonic behaviors with a “knee point” as temperature increases. Keeping this in mind, we exemplify fac-Ir(F2ppy)(ppz)2 (ppy = 2-phenylpyridine and ppz = phenylpyrazole) with comprehensive photophysical data from experiments[83] to quantitatively investigate the , , and and excited-state lifetime τ at different temperatures in THF solution.[84] The emissive state of fac-Ir(F2ppy)(ppz)2 is a triplet excited state. We first construct the PES of T1 and S0 by locating the minimum point of S0 (S0-geometry) and the local minimum point of T1 with metal–ligand charge transfer transition (3MLCT) in the harmonic region, and TS and local minimum with metal–center transition (MC) and MECP between T1 and S0 (MECP) beyond harmonic region, as seen in Figure 14A. Herein, the optimizations except for the MECP are performed at the level of B3LYP with LANL2DZ for Iridium atom and 6–31G (d,p) basis set for the others in Gaussian 09 package. The MECP is optimized using Harvey's algorithm at the B3LYP/ECP-60-mwb/def2-SVP level and its activation energy is corrected by PWPB95-D3/ECP-60-mwb/def2-SVP in the ORCA package.[85] From Figure 14A, it is easily seen that the emissive 3MLCT can directly radiatively decay to S0 as light (), directly nonradiative decay to S0 via vibration relaxation (), and indirectly nonradiative decay to S0 by a two-step reaction of . In the two-step reaction, the barrier to populate the TS plays a decisive role because the largest geometrical variation takes place from the 3MLCT (pseudo-octahedral) to the 3MC (trigonal bipyramid) point (3MLCT → 3MC) via the broken of one Ir-N bond and the rotation of relative ligand.[86]
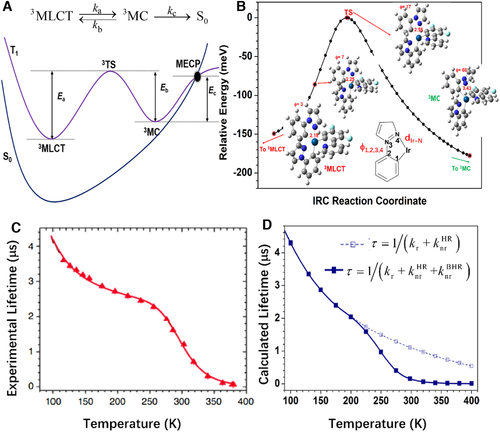
Based on the obtained geometrical and electronic structure information, kr is calculated with the Einstein relationship by considering Boltzmann population of three substates of triplet state; is computed with the TVCF approach in MOMAP program; and is obtained by adapting the kinetic model in reference 86, in which 3MLCT → 3MC is the rate limiting step and the equilibration between 3MLCT and 3MC is considered and the rate constant can be simply calculated as under steady state approximation. Here, A0 is a temperature-dependent prefactor and; A stands for the pre-exponential factor obtained by canonical variational transition state theory (CVT) implemented in POLYRATE program[87]; and Ea, Eb, Ec are the activation energies marked in Figure 14A. Figures 14C and 14D show the experimentally measured and theoretically calculated plot of the excited state lifetime of) versus temperature, as well as the calculated) for comparison, and the detailed data are collected in Table 3. The sigmoid-like dependency is well reproduced by the calculated results. Three distinct regimes are depicted in Figure 14D, that is, a slight lifetime decrease at 77–220 K and a second more significant drop at 220–320 K, and a third almost unchanged tendency at temperature higher than 320 K. The two key inflexion points are at ca. 220 and 320 K, which are very close to experimentally observed values, that is, 250 and 340 K. It is easily understood that kr slightly grows up owing to the increasing population of the substates with the largest kr value among the three substates from 3MLCT observed at 77–130 K, and then it is almost unchanged when T > 130 K because the thermally activated vibrations always largely broaden and redshift the spectrum lineshape (instead of the integral area). is expected to slightly increase because of small relaxation energy that exclusively comes from high-frequency stretching and in-plane deformation vibrations.[84] At the low-temperature regime, only kr and components contribute to the lifetime because the temperature cannot provide enough energy to reach the barrier for proceeding significant . Therefore, the temperature effect is not obvious at low temperature. However, when temperature reaches to a certain point, the molecule has enough energy to cross over the barrier to produce the transform 3MLCT → TS → 3MC. becomes significant only when temperature going above ca. 230 K and hugely influences the quantum efficiency and lifetime by directly competing with radiative decay at room temperature, and then evolves into the most prominent deactivation channel that significantly quenches the luminescence at high temperatures. The relevance of is further illustrated in Figure 14D by switching off its contribution to lifetime of ) (dashed line in Figure 14D). The sigmoid-like temperature-dependence is fully lost without taking into consideration, which is not consistent with the experimental observation. At the same time, this work provides a criterion for judgment whether the MECP occur in the excited-state decay processes both in solution and aggregates.
| Temperature (K) | kr (s−1) | (s−1) | (s−1) | τ (μs) | |
|---|---|---|---|---|---|
| 77 | 1.60 × 104 | 1.78 × 105 | 4.43 × 10−12 | 5.16 | 0.08 |
| 100 | 3.99 × 104 | 1.93 × 105 | 1.92 × 10−6 | 4.29 | 0.17 |
| 130 | 8.23 × 104 | 2.16 × 105 | 4.31 × 10−2 | 3.35 | 0.28 |
| 150 | 1.13 × 105 | 2.36 × 105 | 3.67 × 100 | 2.86 | 0.32 |
| 175 | 1.52 × 105 | 2.66 × 105 | 2.26 × 102 | 2.39 | 0.36 |
| 196 | 1.82 × 105 | 2.97 × 105 | 4.93 × 103 | 2.04 | 0.38 |
| 225 | 2.22 × 105 | 3.53 × 105 | 5.37 × 104 | 1.59 | 0.35 |
| 250 | 2.52 × 105 | 4.16 × 105 | 3.62 × 105 | 0.97 | 0.25 |
| 275 | 2.80 × 105 | 4.96 × 105 | 1.72 × 106 | 0.40 | 0.11 |
| 298 | 3.03 × 105 | 6.00 × 105 | 5.69 × 106 | 0.15 | 0.05 |
| 320 | 3.23 × 105 | 7.07 × 105 | 1.52 × 107 | 0.06 | 0.02 |
| 340 | 3.40 × 105 | 8.38 × 105 | 3.33 × 107 | 0.03 | 0.01 |
| 360 | 3.55 × 105 | 1.00 × 106 | 6.67 × 107 | 0.02 | 0.005 |
| 380 | 3.70 × 105 | 1.20 × 106 | 1.24 × 108 | 0.008 | 0.003 |
| 400 | 3.83 × 105 | 1.46 × 106 | 2.17 × 108 | 0.005 | 0.002 |
Aggregation-dispelled isomerization and experimental confirmation
Except for the MECP, photoexcited isomerization is another nonradiative decay channel to quench luminescence beyond the harmonic region, termed as NR-ISO. Generally, most AIEgens have twist/rotor structures while aggregation-caused quenching (ACQ) molecules possess planar conjugated structures. However, Huang's group found six planar molecules with analogous structure that show completely differen emission behaviors in experiment. 1,2-di(2-selenophenyl)-ethene (SVS), 1,2-Di(2-thienyl)-ethene (TVT), and (E)-1,2-bis(thieno[3,2-b]thiophen-2-yl)ethane (TTVTT) molecules exhibit typical ACQ phenomena, while SVS(OEt), TVT(OEt), and TTVTT(OEt) show interesting AIE behavior.[62] Therefore, it is very meaningful to investigate the mechanism of their completely different emission behaviors from their similar planar structures.
We choose TTVTT and TTVTT(OEt) as representatives and first construct the PESs of S0 and S1 by a relaxed scan at the level of (TD)B3LYP/6-31G(d, p) in Gaussian 09 package, as seen in Figures 15A and B. It is obvious that the PESs of the two compounds both have double wells, corresponding to cis- and trans-geometries, respectively. The trans-geometry is more stable owing to its lower energy than that of cis-geometry, which is in line with the single-crystal X-ray structure. The isomerization barriers from trans to cis are very high for TTVTT(OEt) (1.26 eV) and TTVTT (1.23 eV) in the S0 state. However, the barriers sharply reduce in the S1 state up to 0.45 eV of TTVTT(OEt) and 0.67 eV of TTVTT. Thus, the introduction of -OCH3 destabilizes the planar conformation and facilitates the occurrence of isomerization from trans- to cis-TTVTT(OEt) in the S1 state.[88]
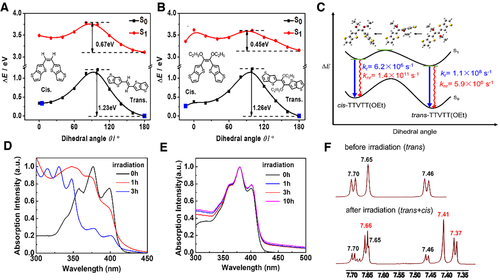
We further compare the luminescence property of trans- and cis-TTVTT(OEt) by computing their and in the harmonic range of locally optical transition using the TVCF approach in MOMAP program. It is found that of trans-TTVTT(OEt) (1.1 × 108 s−1) is two orders of magnitude larger than that of cis-TTVTT(OEt) (6.2 × 106 s−1), which mainly stems from larger transition dipole moment of trans-TTVTT(OEt) (18.56 Debye) with a more planar conjugated structure than that of cis-TTVTT(OEt) (6.42 Debye) with twisted conformation. On the contrary, of trans-TTVTT(OEt) (5.9 × 106 s−1) is five orders of magnitude smaller than that of cis-TTVTT(OEt) (1.4 × 1011 s−1), which is caused by the rigidity of trans-TTVTT(OEt) and flexibility of cis-TTVTT(OEt). Consequently, trans-TTVTT(OEt) emits very bright fluorescence with > > whereas cis-TTVTT(OEt) shows dark with < < in the gas phase. Overall, the whole photophyscial process in solution is described as the following: after absorbing a phonon the stable trans-TTVTT(OEt) first jumps from S0 to S1, then transforms to cis-TTVTT(OEt) along the S1-PES, and finally nonradiaitively goes back to S0 of cis-TTVTT(OEt) without generating visible fluorescence. The lifetime of cis- TTVTT(OEt) is calculated to be 7.1 ps, being consistent with the experimental one (<30 ps). When going in aggregate, the isomerization from trans-TTVTT(OEt) to cis-TTVTT(OEt) are inhibited, resulting in a strong fluorescence from trans-TTVTT(OEt). Therefore, the aggregation-dispelled photoisomerization from bright state (trans-conformation) to dark state (cis-conformation) is responsible for the unusual AIE activity of these highly planar molecules.
To confirm the photoisomerization mechanism proposed above, a series of measurements are performed, including UV−Vis and 1H NMR before and after irradiated by an UV lamp for TTVTT(OEt) in THF, and the results are shown in Figures 15D–F. As expected, after a period of irradiation, a new set of absorption bands start to appear and the intensity is gradually increased, while the intensity of original bands is contrarily decreased (Figure 15D), which indicates the generation of a new compound. A new set of peaks (7.66, 7.41, 7.37 ppm) in 1H NMR also arise after 3-hour irradiation, which underlines that the new compound is cis-TTVTT(OEt). By this time, the mixture of cis- and trans-TTVTT(OEt) exhibit nonemissive characteristics in solution, which verify the dark S1 state of cis-TTVTT(OEt) with < <. However, the UV–vis spectra of TTVTT (Figure 15E) are almost identical before and after irradiation for 10 hours, suggesting photoisomerization barely happened in TTVTT solution. The solid-phase TTVTT(OEt) upon UV light irradiations also displays unchanged UV–vis spectrum before and after irradiation, indicating the hindrance of photoisomerization. These perfectly confirm the mechanism of aggregation-dispelled isomerization in TTVTT derivatives, which can be extended to explain a series of systems.
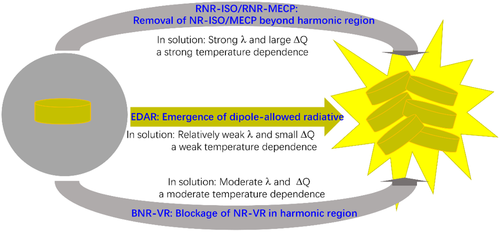
Thus far, the microscope mechanism of molecular luminescence has been clearly illustrated by one example after another. To sum up, the bright emissions in aggregates are induced by the emergence of dipole-allowed radiation (EDAR) owing to the change of the composition, symmetry, and spatial distribution of electronic states, or the blockage of the nonradiation via vibration relaxation (BNR-VR) in harmonic region, or the removal of the nonradiation via an isomerization/a minimum energy crossing point (RNR-ISO/RNR-MECP) beyond harmonic region, as seen in Chart 1. In aggregates, all of the investigated AIEgens have weak electron–vibration coupling λ and small changes in geometry structures ΔQ during the excited-state decay processes. However, the AIEgens with different AIE mechanisms exhibit distinct features during excited-state decay processes in solution. The ones with EDAR always have relatively small λ and ΔQ, and their spectra and decay rates are merely affected by temperature. The ones with RNR-MECP always behave the largest λ and ΔQ, and the NR rates are abruptly increased as temperature rises to a key point. The emission properties of the ones with RNR-ISO strongly depend on the relative competition between the original compound and isomer. And the ones with BNR-VR exhibit moderate λ and ΔQ, and their spectra and rates also greatly change with the increase of temperature. More importantly, it is keenly realized that the microscope mechanism is system-dependent due to great individual characteristics in organic molecules. However, looking from the other side, it is conducive to the expansion of AIEgens, and AIE is experiencing the development from exotic phenomena in individual systems to universal phenomenon in a variety of systems. In addition, the relationship among AIE compound, AIE mechanism predicted by theoretical calculations, and the computational method are summarized in Table 4, which is helpful to design the AIE molecules from first principles.
| AIEgens | Computational method | AIE mechanism | Ref. |
|---|---|---|---|
| TPA | CASPT2 (8e, 8o)/ANO-RCC-VDZP/AMBER | EDAR | [21] |
| CIEE-SQ | TD/M062X/6-31G*/UFF | EDAR | [22] |
| HPS | TD/M062X/6-31G*/UFF | BNR-VR | [67] |
| COTh | TD/B3LYP/SV(P)/GAFF | BNR-VR | [70] |
| HPDMCb | TD/PBE0/SV(P)/GAFF | BNR-VR | [73] |
| TPS | TD/B3LYP/SV(P)/GAFF | BNR-VR | [67] |
| BTPES | TD/B3LYP/SV(P)/GAFF | BNR-VR | [67] |
| BFTPS | TD/B3LYP/SV(P)/GAFF | BNR-VR | [67] |
| CPEI | TD/B3LYP/SV(P)/GAFF | BNR-VR | [38] |
| (CAACAd)CuCl | TD/M06/LANL2DZ/6-31G(d)/UFF | BNR-VR | [69] |
| DPDBF | CASSCF/CASPT2/UFF TD-CAM-B3LYP/UFF | RNR-MECP | [20] |
| BIM | CASSCF/ TD/PBE0/UFF | RNR-MECP | [80] |
| TTVTT(OEt) | TD/B3LYP/6-31G(d, p) | RNR-ISO | [62] |
CONCLUSION AND PERSPECTIVES
In this review, starting from the discussion of the effect of excitonic coupling (J) on the optical spectra of the traditional H- and J-aggregate systems and newly reported AIEgens, we noted that the AIE phenomena cannot be reasonably explained via Kasha's J-aggregation picture because these AIEgens have strong intramolecular electron–vibration coupling (λ) and weak intermolecular excitonic coupling (J), namely J/λ < 0.17, which results in the optical spectra insensitive to excitonic coupling. That is to say, the intermolecular quantum decoherence occurs in the excited states of the AIEgens and the excitionic coupling can be neglected.
Then we focus on the molecular mechanism of AIE. From the microscopic perspective, there are three common decay pathways of an excited molecule, that is, radiative decay of rate constant , nonradiative decay via vibration relaxation in harmonic region (NR-VR) of rate constant and nonradiative decay via isomerization or a MECP beyond harmonic region (NR-ISO, NR-MECP) of rate constant . Here we quantitatively evaluated the rate constants of three processes and the quantum luminescence yield in different environments for a variety of organic molecules by combining multiscale approaches with thermal vibration correlation function (TVCF) rate formalism and canonical variational transition state theory (CVT).
The resultant radiative, NR-VR, and NR-MECP exhibit different sensitivity to temperature, aggregation, etc. for distinct systems. We illustrated the aggregation-induced inversion from transition dipole-forbidden dark state to transition dipole-allowed bright state in AIEgens with n–π* or σ–π* transition feature, which triggers the fluorescence. This might be used to explain the recovery of fluorescence in aggregate for AIEgens with charge-transfer, high-symmetry and other transition dipole-forbidden properties. Through constructing the potential energy surface and comparing the dynamic rate constants, two nonradiative decay processes, NR-VR and NR-MECP, may coexist and compete each other, and the former happens in harmonic region with relatively small geometrical modifications while the latter appear beyond harmonic region with much large geometrical modifications.
In NR-VR dominated cases of AIEgens, the restriction of NR-VR is realized by the decoupling of electron–vibration and vibration–vibration among various kinds of normal modes, such as rotating, stretching, bending, flipping, and twisting vibrations, which are confirmed via experimentally visualizable signals. When the NR-VR is superior, the lifetime of excited state exhibits a monotonic decreasing with the increase of temperature. Once the NR-MECP appears, it acquires a sigmoid-like dependency of lifetime on the temperature with two key inflexion points, as observed in experiment. This is because the NR-MECP process is more sensitive to temperature than NR-VR. When going from solution to aggregate, the barrier of MECP grows higher owing to intermolecular interaction in rigid aggregate, which significantly inhibits NR-MECP and hence largely enhances the luminescence. Altogether, a clear physical image is presented, depicting the microcosmic mechanism of aggregation-induced emission of organic compounds.
Looking forward, accurate description of the electronic structure and decay processes of an excited state molecule is still a long-term computational challenge owing to complicated electron–electron correlation and electron–vibration coupling which are required to be considered, let alone the excited state of an aggregate.[89] There are a lot of processes and effects that have not been discussed in the calculations of the investigated systems. (i) The intersystem crossing through VR or MECP between S1 and Tn(n≥1) are not considered because of insignificant spin-orbit coupling and large singlet-triplet splitting energy[90]; (ii) the anharmonic effect is not involved in TVCF method. Because tremendous amount of normal modes in the systems with large number of atoms share the excess excitation energy which sharply decrease the anharmonic effect of potential energy surface[91]; (iii) only one molecule is dealt with QM calculation without taking intermolecular excitonic coupling and charge transfer into consideration it is found that the excitonic coupling has very minor effect on the optical spectra and NR-VR rate constant in the typical AIEgens[28, 49]; and (iv) the polarizable force field is not used in QM/MM protocol for these systems are not charge-transfer ones.[92] However, these aspects might play an important role in the excited-state decay processes for some systems, which should be carefully checked and handled. These issues have been actively pursued in our group.
In addition, from the perspective of experimental phenomena, this review has not covered the room temperature phosphorescence of purely organic systems,[10, 13] the aggregation-induced delayed fluorescence,[93] clusterization-triggered emission of nonaromatic molecules,[94] mechanochromic luminescence of organic aggregates,[95, 96] aggregation-induced circularly polarized luminescence,[97] multicolor of a single molecule in aggregate,[98] and so on,[99] which are developed recently and become one of the research hotspots in the field of organic luminescence. It is eagerly demand to demystify the microcosmic mechanism behind the newly interesting experimental phenomena with different categories.
ACKNOWLEDGMENTS
This work is supported by the National Natural Science Foundation of China (Grant Nos. 21788102, 21973099 and 21973043) and the Ministry of Science and Technology of China through the National Key R&D Plan (Grant No. 2017YFA0204501). Contributions from the following collaborators are greatly acknowledged: Shiwei Yin, Yingli Niu, Qunyan Wu, Tian Zhang, Yujun Xie, Huili Ma, Ping-an Yin, Xu Zhang, Qi Ou, Ben Zhong Tang, Zhen Li, Anjun Qin, Zhiming Wang, Xingui Gu, Hui Huang, and many more.
CONFLICT OF INTEREST
The authors declare that is no conflict of interest.
Biographies

Qian Peng received her PhD from the Institute of Chemistry of the Chinese Academy of Sciences in 2008 supervised by Prof. Z. Shuai. Then she joined the Key Laboratory of Organic Solids in the Institute as a research assistant and she was promoted as associate professor in 2010 and full professor in 2019 there. In 2020, she joined the School of Chemical Sciences, University of Chinese Academy of Sciences. Her research interests are theoretical investigations into the molecular aggregation effects on the light-emitting phenomena with excited state decay processes involving nonadiabatic and spin-orbit couplings, photophysical mechanisms of various luminescence phenomena in organic optoelectronic materials and theoretical design of light-emitting molecules.

Zhigang Shuai received his PhD in theoretical physics from Fudan University in 1989. He accepted a full professor position under the “Hundred-Talent Program” in 2000 in the Institute of Chemistry of the Chinese Academy of Sciences after working as postdoc and research scientist for 11 years at the University of Mons, Belgium. He moved to Tsinghua University as a Changjiang Scholar Professor in 2008. His research interests focus on development and application of theoretical modeling methods for the electronic processes in organic optoelectronic materials.




