Conflicts, Choices, and Solutions: Informing Risky Choices
Abstract
This article deals with key aspects of informing decision making of what may be the optimal choice, given a set of potential choices, unpredictable events, the value of the consequences (positive or negative) associated with each choice, and criteria for making the choice. This article introduces some of those criteria, methods and measures that can be used to inform policy maker relative to the set of options included in the analysis, and provides examples.
In managing risky activities, decision makers (DMs) may have different available choices, payoffs or utilities (see Utility Function) for outcomes, as well as cultural expectations and ethical or moral values constraining how they believe they should behave. For example, a confrontation occurs in an international forum, such as in the development of certain terms for a convention or a treaty, where some stakeholders want to determine their best payoff, while minimizing that of another, before or during their negotiations (see Considerations in Planning for Successful Risk Communication; Role of Risk Communication in a Comprehensive Risk Management Approach). Similarly, an industry may assess what it can pay, before a fee or penalty schedule is codified. In these and many other situations, it is advantageous to describe alternatives or choices; positive or negative outcomes associated with each choice; probable effects of each choice, modeled by evaluating the probable consequences of different combinations of choices made by the DMs or stakeholders. The study of strategies and counterstrategies clarifies what a solution to a conflict (or partial conflict) situation is, when one exists, whether it is unique, why and whether it is stable (so that it is not plausible for players to deviate from it), conditions under which communicating with an opponent is or is not advisable, and ways to systematically change assumptions to test the sensitivity of results to those changes.
This article deals with key aspects of decisions by one or two stakeholders that confront alternative choices. In this confrontation, a strategy is a feasible act or option (including decision rules specifying what to do contingent upon information available at the time a choice must be made). Each stakeholder is assumed to have a discrete set of possible strategies that are mutually exclusive and fully exhaustive; these strategy sets are assumed to be common knowledge. A measure of value associated with each outcome is the payoff that each of the individuals has. Payoffs can be measured in units of money (usually transferable), utility (not necessarily transferable among players), or physical units (e.g., number of deaths or life-years lost), depending on the application.
1 Framework for Analysis
1.1 A Decision Maker with a Single Objective
Table 1 shows a problem with three mutually exclusive and collectively exhaustive choices (the rows) that a single DM must choose from. However, Nature—representing all factors over which the DM has no control—may affect the net gains or losses (in the cells of the table, the cij) by either taking on state 1 (s1) or state 2 (s2), with probability 0.50 each in this example. Note that the two states are mutually exclusive and collectively exhaustive: exactly one occurs. We can account for uncertainty by assigning probabilities to each of these two states, perhaps using historical data or expert judgment. The last column of Table 1 shows the calculation of the expected values of the acts/rows (defined by adding the values for each possible outcome, weighted by their respective probabilities). According to these calculations, a single DM who seeks to maximize expected value should choose act a2.
States of Nature |
|||
|---|---|---|---|
Decision maker's alternative actions |
s1 (pr = 0.50) |
s2 (pr = 0.50) |
Expected values |
No action, a1 |
c11 = 200 |
c12 = −180 |
(0.5)(200) + (0.5)(−180) = 10 |
Low cost intervention, a2 |
c21 = 100 |
c22 = −20 |
(0.5)(100) + (0.5)(−20) = 40 |
High cost intervention, a3 |
c31 = 0 |
c32 = 0 |
(0.5)(0) + (0.5)(0) = 0 |
Before making a final choice, it is useful to measure the value of payoffs that might result from each choice. One obvious choice of scale is money. Another is von-Neumann–Morgenstern (NM) utility, which justifies the use of expected values (i.e., expected utilities) to choose among acts.
1.2 Two or More Decision Makers with Different Objectives
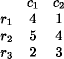
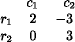
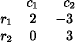
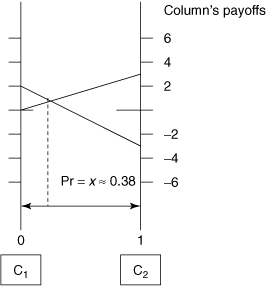
Graphical solution of two-person games: finding Row's probabilities
The solution (obtained algebraically) is 0.375 and thus Row 1 should be played with probability 0.375 and Row 2 with probability 0.625. Column will play strategy 1 with a probability that equals 0.75 and strategy 2 with probability that equals 0.25. Observe that the original game did not have a saddle; the approach requires assessing that the 2 × 2 game does not have either a saddle or dominance by a strategy, and then proceed as developed. The importance of this technique is that it allows for the solution of n × k zero-sum games by assessing mixed strategies in 2 × 2 subgames of the original n × k game (a result that is guaranteed by the minimax theorem (Straffin (3)), due to John von Neumann).
1.3 Beyond the 2 × 2 Game

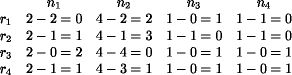
Because different decision criteria lead to different optimal choices, several axioms have been developed to guide their selection. Some of those axioms are summarized in Table 2 and are related to the criteria for justifying that choice.
Axiom |
Description |
Criterion met by |
Criterion not met by |
|---|---|---|---|
Symmetry |
Permuting rows or columns should not change the best choice |
Maximin, expected value, regret |
NRb |
Dominance |
When every row element is greater than another, the latter is inferior and can be ignored |
Maximin, expected value, regret |
NR |
Linearity |
Multiplying by a positive constant and/or adding a constant to all entries in the payoff matrix should not change the best choice |
Maximin, expected value, regret |
NR |
Duplication of columns |
Repeating columns should not change the best choice |
Maximin, regret |
Expected value |
Addition of row |
Repeating row or rows should not change the best choice |
Maximin, expected value |
Regret |
Invariance to a change in utility |
A constant amount of utility or disutility does not change the choice |
Expected value, regret |
Maximin |
Comparability |
Adding a weakly dominated row should not change the best choice of act |
Expected value, regret |
Maximin |
- a Adapted from Straffin (3)
- b Not reported
2 Searching for a Common Ground: Nash Equilibrium
The process of understanding rational decisions can be shown by the same normal form representation of strategies, Si, j, consequences, Ci, j, and probabilities adopted in the previous section with the added understanding of the possibility of choices of strategies that are optimal. We use 2 × 2 games in which DMs can either cooperate or not. Some games do not allow sequential choices, while others do. Strategies, as course of actions, say cooperate, defect, attack, retreat, and so on, can be either pure (no probabilistic assessment is used: deterministic numbers are used) or mixed (probabilities play a role in assessing the eventual outcome from the situation confronting the DMs). A 2 × 2 game has two strategies per DM: for example, either defect or cooperate, but not both. We will discuss games that are effectuated simultaneously; further information is given in Burkett (5).
2.1 Pure Strategy Games
We begin with situations in which pure strategies are used to study what might happen. Consider, for example, the following situation in which DM1 and DM2 cannot cooperate—speak to one another (Table 3). The consequences (outcomes or payoffs) for two DMs are measured by numbers such that a number of large magnitude is preferred to one of smaller magnitude (for example, 3 is preferred to 2). If the numbers were to represent disbenefits, then the opposite interpretation is true. The first number in a cell is that for DM1 and the second is that for DM2:
Decision maker 1 |
|||
|---|---|---|---|
S1 |
S2 |
||
Decision maker 2 |
S1 |
4, 4 |
0, 6 |
S2 |
6, 0 |
3, 3 |
|
What would these two DMs do in this situation? They would most likely select their dominant strategies. The dominant strategy for DM1 is S2 = 6, 3 and the dominant strategy for DM2 is S2 = 6, 3. DM1 and DM2 are aware of the consequences and, because they do not know what the other will do, will settle for the strategy that dominates as seen from the vantage point of the individual DM. Thus the solution will be 3, 3: neither of the two will be induced to deviate form his/her choice of dominant strategy. Clearly, however, the optimal solution is 4, 4; if the two DMs could communicate, they would select S1 as their solution to the game.
The solution identified by the couple 3, 3 is known as the Nash equilibrium for this game: it is the strategy that does not provide any incentive to move elsewhere from that solution. For the example, it is a unique Nash equilibrium. Some games have no Nash equilibrium while others can have multiple Nash equilibriums. Consider the game in Table 4:
Decision maker 1 |
|||
|---|---|---|---|
S1 |
S2 |
||
Decision maker 2 |
S1 |
Profits, does not profit |
Does not profit, profits |
S2 |
Does not profit, profits |
Profits, does not profit |
|
This situation does not have a Nash equilibrium because the two DMs can switch strategy as there is no incentive to maintain a strategy regardless of what the other does.
2.2 Mixed Strategy Games
The distinguishing feature of mixed strategies is that each is characterized by probabilities. Continuing with the 2 × 2 representation, if strategy for DM1 has two outcomes, then one outcome has probability pr and the other has probability (1 − pr). For the other DM, however, we label the probabilities as q and (1 − q). Consider the earlier game as in Table 5.
Decision maker 1 |
|||
|---|---|---|---|
S1 |
S2 |
||
Decision maker 2 |
S1 |
4, 4 |
0, 6 |
S2 |
6, 0 |
3, 3 |
|
-
For DM2 and S1: (pr)(4) + (1 − pr)(0) = (pr)(4). For DM2 and S2: (pr)(6) + (1 − pr)(3) = (pr)(3) + 3.
-
For DM1 and S1: (q)(4) + (1 − q)(0) = (pr)(4). For DM2 and S2: (q)(6) + (1 − q)(3) = (q)(3) + 3.
-
For DM2 and S1: (0.5)(4) + (1 − 0.5)(0) = (pr)(4). For DM2 and S2: (0.5)(6) + (1 − 0.5)(3) = (0.5)(3) + 3 = 4.5.
-
For DM1 and S1: (0.5)(4) + (1 − 0.5)(0) = (0.5)(4). For DM2 and S2: (0.5)(6) + (1 − 0.5)(3) = (0.5)(3) + 3 = 4.5.
Decision maker 1 |
|||
|---|---|---|---|
S1 |
S2 |
||
Decision maker 2 |
S1 |
Profits = 1, does not profit = 0 |
Does not profit = 0, profits = 1 |
S2 |
Does not profit = 0, profits = 1 |
Profits = 1, does not profit = 0 |
|
-
For DM2 and S1: (0.5)(1) + (1 − 0.5)(0) = 0.5. For DM2 and S2: (0.5)(1) + (1 − 0.5)(0) = 0.5.
-
For DM1 and S1: (0.5)(0) + (1 − 0.5)(1) = 0.5. For DM2 and S2: (0.5)(0) + (1 − 0.5)(1) = (0.5)(3) + 3 = 0.5.
The concepts of sequential games (5), where the choices made by the DMs account for the evolution of the choices, can be illustrated (Figure 2) as a decision tree in which the lines are the branches of the tree:
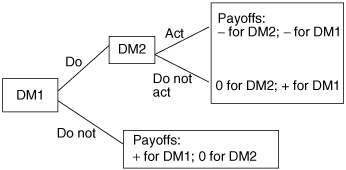
Simple example of sequential decision making involving two decision makers and two binary choices
Each branch identifies a possible strategy that can be taken by a DM. This tree identifies simple binary choices and payoffs, which can be positive (+), negative (−), or zero (0). Reading the tree from left to right leads to an understanding of how the two DMs can behave and their possible final choices. DM1 would probably do, while DM2 might try to change the game, if it were possible.
3 Discussion
-
The structure of a game is unambiguously described.
-
The payoffs, either inutilities or other suitable units, are quantitative expressions of each stakeholder's attitude.
-
The methods for solving these games are theoretically sound and replicable.
-
The criteria for choosing an alternative strategy over another consider both stakeholders.
-
The resolution of some of the ambiguities inherent to such games may exist and be unique to that game.
-
The difference between individual and societal choices can be shown in a coherent framework.
In the end, it is preferable to have more information than less (not necessarily, e.g., mutual insurance can be destroyed by free information, reducing everyone's expected utility); thus, anticipating the outcomes of a dispute provides useful information by orienting and informing a choice.
How does this theoretical framework compare with actual behavior? The basis for game theory is that DMs optimize their choices and seek more utility, rather than less. Although this basis is theoretically sound, there have been many cases of violations in simple, practical situations. Some, for example, Kahneman and Tversky (1979) found that actual behavior affects decision making to the point that the theory, while sound, required modifications, thus resulting in prospect theory. Camerer and Fehr (6) have also found that DMs inherently act altruistically and thus are not money maximizers.
Glimcker (7) reports the following. He uses the game work or shirk in a controlled setting: the employer faces the daily decision of going to work; the employer has the choice to inspect the employee's performance. For example consider Glimcker [(7)] (with change in terminology). The two stakeholders incur daily monetary costs and benefits in unstated monetary units, as shown in Table 7.
Employer checks attendance |
Employer does not check |
|
|---|---|---|
Employee works |
Wage – leisure, revenue – wage – inspection cost (100 – 50 = 50, 125 – 100 – 50 = 25) |
Wage – leisure, revenue – wage (50, 25) |
Employee shirks |
0, –inspection cost (0, –50) |
Wage, –wage (100, –100) |
In general, because inspection cost is high, the employer will be allowed some shirking. If the inspection cost was lower, they could result in more inspection and thus lead to decreasing rates of shirking: the result is Nash's equilibrium. For the employer, the hazard rates are (shirk) = ($inspection/$wage); (inspect) = ($leisure/$wage). The Nash equilibrium is (the result is obtained by solving for the probabilities, e.g., 50 × x + (1 − x) × 50 = 100 − 100 × x; thus x = 0.5) shirk 50% of the time and inspect 50% of the time [(7), p. 304]. Students (unfamiliar with game theory) were enrolled in the shirk–inspect game to assess if their behavior was consistent with this theoretical equilibrium. In the first 100 (out of approximately 140) tests, the stakeholders modified their outcomes and tended toward the Nash equilibrium. When the payoffs were changed, the results changed as well.
The shirk-work game discussed in Glimcker (7) provides some interesting insights on the sequential choices made between either working or shirking, when deciding which alternative to take by the worker who is initially contemplating the choice of either working or shirking work. The results show that the worker (in an experiment involving 150 trials) appears to be acting randomly and thus keeps the employer guessing as to what course of action she will actually take. This author reports that the choices, made in 150 games, has the results as in Figure 3.

Decision tree depicting the alternatives in the wage-shirking work game
The decision tree shows the chronology of the decision. The initial choices are to either work or shirk. The second decision, conditioned (the conditionalization is symbolized by the symbol “|”), is to work | work, shirk | work, and so on, as depicted by the tree. It appears that the worker is acting randomly and thus keeps the employer guessing!
Clearly, individual choices cannot be divorced from the fact that those choices are made in the brain. Interestingly, it is now increasingly apparent that humans have (8) … at least two systems working when making moral judgments …. There is an emotional system that depends on (the ventromedial prefrontal cortex) … and another that performs more utilitarian cost–benefit analyses which in these people is intact. When that region is damaged, individuals opt for choices that are different from those not damaged. For example, in a relatively small sample of respondents, only approximately 20% of normal individuals answered yes, while approximately 80% of individuals with damaged brain answered yes, to the following question:
You have abandoned a sinking cruise ship and are in a crowded lifeboat that is dangerously low in the water. If nothing is done it will sink before the rescue boats arrive and everyone will die. However, there is an injured person who will not survive in any case. If you throw the person overboard, the boat will stay afloat and the remaining passengers will be saved. Would you throw this person overboard in order to save the lives of the remaining passengers?
Now consider a different choice (Carey (8)): having to divert a train by flipping a switch, to save five workers, knowing that such diversion would kill one other worker for sure. The research shows that those with the brain injury, normal individual, and those with a different type of brain injury would divert the train. When that certainty of killing the single worker was not apparent, all of the three groups rejected the trade-off. Moreover, if the action did not comport flipping a switch but, rather, the act was equivalent to pushing that single individual to certain death to save several others at risk, the results by all of the three groups were still different: those with the ventromedial injury were about twice as likely as other participants to say that they would push someone in front of the train (if that were the only option …). Although the brain injury is uncommon, the responses may make some think twice about the implications of either answer.



