The skin effect in vibrating systems with many concentrated masses

We address the asymptotic behaviour of the vibrations of a body occupying a domain \documentclass{article}\usepackage{amsfonts}\begin{document}\pagestyle{empty}$\Omega\subset\mathbb{R}^n, n=2,3$\end{document}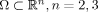. The density, which depends on a small parameter $\varepsilon$\nopagenumbers\end , is of the order $O(1)$\nopagenumbers\end out of certain regions where it is $O(\varepsilon^{-m})$\nopagenumbers\end with $m>2$\nopagenumbers\end. These regions, the concentrated masses with diameter $O(\varepsilon)$\nopagenumbers\end, are located near the boundary, at mutual distances $O(\eta)$\nopagenumbers\end, with $\eta=\eta(\varepsilon)\rightarrow 0$\nopagenumbers\end. We impose Dirichlet (resp. Neumann) conditions at the points of $\partial\Omega$\nopagenumbers\end in contact with (resp. out of) the masses. We look at the asymptotic behaviour, as $\varepsilon\rightarrow 0$\nopagenumbers\end, of the eigenvalues of order $O(1)$\nopagenumbers\end, the high frequencies, of the corresponding eigenvalue problem. We show that they accumulate on the whole positive real axis and characterize those giving rise to global vibrations of the whole system. We use the fact that the corresponding eigenfunctions, microscopically, present a skin effect in the concentrated masses. Copyright © 2001 John Wiley & Sons, Ltd.