Priority search with outside options
Abstract
This paper examines the welfare implications of priority service in a frictional search environment with heterogeneous outside options. Priority search facilitates expedited matching with public options in the market by charging a service premium. Our main analysis demonstrates that a profit-maximizing priority search program always induces the efficient level of market participation. The key insight underpinning our results is the non-monotonic relationship between the priority service premium and market participation, which is driven by the nonexclusivity of priority search. This finding extends to several market design details and elucidates how to generate revenue and regulate congestion simultaneously in the presence of matching frictions.
1 Introduction
Priority service programs are prevalent in many markets with search frictions or congestion, whereby individuals who pay for premium service are matched more quickly than regular participants. Notable examples of priority search include advanced booking of train tickets by waiting lists during peak travel seasons (Hakimov, Heller, Kübler, and Kurino (2021)), guaranteed tips on ride hailing platforms during rush hours (Ashkrof, de Almeida Correia, Cats, and van Arem (2022)), express toll lanes on congested highways (Hall (2018)), expedited COVID-19 testing during the pandemic (Yang, Cui, and Wang (2022)), and a variety of premium memberships for services, such as amusement parks, hotels, airlines, and job matching platforms (Cui, Wang, and Yang (2020), Gurvich, Lariviere, and Ozkan (2019)).1 In these marketplaces, the underlying goods or services (e.g., public transportation or healthcare) often operate inclusively. In other words, the priority service provider does not prevent agents from entering the market due to institutional constraints or regulatory considerations. Instead, the service provider creates a channel for expedited matching.2
A common feature of these congested marketplaces is that individuals differ in their access to options outside the market, which is often their private information.3 Unequal outside opportunities may be driven by differences in transaction or participation costs, heterogeneous waiting costs, or the availability of alternatives (Akbarpour, Kapo, Neilson, van Dijk, and Zimmerman (2022), Gershkov and Winter (2023)). For instance, in a transportation setting, business travelers have the flexibility to book air tickets at full price without discounts, while the alternatives for budget or leisure travelers are low-speed trains or long-distance buses (Orhun, Guo, and Hagemann (2022)). In labor markets, job candidates may conduct an on-the-job or off-the-job search (Delacroix and Shi (2006), Faberman, Mueller, Şahin, and Topa (2022), Shi (2009)).
This paper examines the welfare implications of priority service in an environment with search frictions and unequal outside options. The model is deliberately stylized to be broadly relevant to many applications of priority search, although it is not intended to capture the details of any specific marketplace. Our analysis elucidates how to regulate congested markets in the presence of matching frictions, such as medical resource rationing during pandemics, job hunting, and ride hailing during peak times. In our framework, each public option inside the market involves a homogeneous indivisible good. Each agent with unit demand has a common value for the public option and access to a private outside option. Agents simultaneously and independently decide whether to search for public options in the market or to opt for their heterogeneous outside options.
In a laissez faire situation, referred to as the baseline search, each public option is allocated through random rationing among those who visit it. In equilibrium, too many agents enter the market relative to the efficient level. The reason is that an agent's decision to switch from a private outside option to a public option neglects the potential crowding-out effect of existing matches in the market. Consequently, congestion emerges due to search frictions and coordination failure, which has detrimental effects on total welfare.
As a natural intervention to alleviate congestion, public options may be managed by an intermediary service provider (e.g., a platform or a third party), which charges a fee for each entry. We refer to this arrangement as the entry fee scheme. We show that the revenue-maximizing entry fee scheme overcorrects the congestion issue in the baseline search and results in underparticipation relative to the efficient level of market entry. Intuitively, as the entry fee decreases, the marginal loss in surplus extractable for the service provider is greater than the marginal social cost. The main reason is that the former accounts for the loss in revenue from both existing and new (if any) matches, while the social cost reflects only the forgone outside option value of the marginal agent. Accordingly, the service provider tends to overcharge and thereby raise the bar for market entry, which undermines social welfare.
Motivated by several practical market designs mentioned above, we introduce the priority search program to fix these issues. Under this program, the allocation of public options in the market is administered by a priority service provider, who facilitates expedited matching with public options by charging a priority membership fee. Before searching in the market, an agent can pay a fee to become a priority member, which grants him or her a greater probability of being matched when a public option is visited by multiple agents. Essentially, priority service reduces competition for public options by increasing the cost of searching in the market both directly for priority members and indirectly for nonpriority members. Note that the indirect cost to nonpriority members is embedded in their disadvantaged matching probability relative to priority members.
Importantly, the priority search program is nonexclusive, allowing agents to freely enter the market and search without priority, in contrast to the entry fee scheme. By and large, this setup accommodates both practical manifestations of the priority search program and the strategic considerations of the service provider. On the one hand, the nonexclusivity of priority search largely reflects the inclusivity of the underlying public options in our motivating examples, such as public transportation or healthcare.4 On the other hand, the literature suggests various incentives for priority service providers to offer free service to nonpriority members, including leveraging network effects to create a thick market (Boudreau, Jeppesen, and Miric (2022), Shi, Zhang, and Srinivasan (2019)), establishing market dominance and creating barriers to entry (Caillaud and Jullien (2003)), enhancing user acquisition, engagement and retention (Belo and Li (2022)), and extracting surplus through user data collection (Fainmesser, Galeotti, and Momot (2023)).
Priority search leads to three types of equilibrium behavior by agents, contingent on the priority membership fee. Specifically, if membership is relatively inexpensive, all agents who search for public options opt for priority service since the marginal benefit of becoming a priority member exceeds the direct cost of the membership fee. This essentially means that no one has priority. When the fee is moderate, market entrants adopt a mixed strategy when making their priority membership decisions, which endogenously creates a two-tier service queue in the matching process. This novel type of equilibrium arises due to the nonexclusivity of the priority search program, in contrast to the exclusivity of the entry fee scheme.5 With a sufficiently high membership fee, none of the agents becomes a priority member, which degenerates to the case of the baseline search.
Based on the different types of equilibrium behavior, we first establish that the impact of the priority membership fee on market entry is nonmonotonic. In the case of low fees, priority service deters market entry monotonically as the direct cost of market entry increases. However, as the membership fee increases, fewer market entrants become priority members, which reduces the indirect cost of market entry for nonpriority members, thereby encouraging greater market entry. This important insight underpins our main result that a revenue-maximizing priority search program induces the efficient level of market participation.
Intuitively, the trade-off faced by the priority service provider centers on charging a higher membership fee versus incentivizing membership enrollment, where the latter is closely aligned with, but not equivalent to, encouraging broader market entry. Notably, the monopolistic service provider's market power is constrained by the nonexclusivity of the priority service in that agents may enter without priority membership and potentially obtain a public option at no cost. When the membership fee is sufficiently low such that every entrant opts for priority, the priority search program operates similarly as the entry fee scheme and, hence, the service provider can increase revenue by charging a higher fee. However, due to the nonexclusivity of priority search, a higher membership fee triggers nonpriority search where more agents enter without purchasing priority membership. With declining membership enrollment, the service provider cannot further boost revenue by increasing the fee. As a result, the presence of nonpriority search mitigates the monopolist's incentive to extract additional surplus. At the threshold for triggering nonpriority search, the marginal agent is indifferent among three choices, namely, entering the market with priority, entering without priority, or taking the outside option. In particular, the expected payoff of an agent entering without priority is determined by the likelihood of a public option not visited by priority members, which also represents the marginal social benefit of an additional entry. Consequently, the revenue-maximizing priority membership fee, which is equal to the difference in the expected payoff of searching with priority and that without priority at the triggering threshold, fully internalizes the marginal social cost of market entry and thereby implements the socially efficient level of participation.
Our main results apply to a wide range of settings regardless of the distribution of outside options. In a richer environment where agents are heterogeneous in both their outside options and their valuations of public options, our analysis suggests that the priority search program improves entry efficiency and social welfare more than alternative market interventions with entry fees do. In several extensions, we show that the welfare-improving property of the priority search program is robust to the matching technology, the market size, and the timing of membership fee payment.
Overall, our findings indicate that the priority search program is more advantageous than the entry fee scheme in terms of simultaneously regulating the market density and improving social welfare. Essentially, under the priority search program, the monopolistic service provider has less market power characterized by a smaller range of realizable revenue relative to its counterpart under the entry fee scheme, which prevents the priority service provider from overcharging on the membership fee. In this regard, the priority search program provides a potential channel for simultaneously generating revenue and regulating congestion, which is a well recognized challenge that service providers face when managing service systems (Feldman and Segev (2022)). Moreover, our finding that the optimality of priority search is achievable by a monopoly, regardless of the market details, has important antitrust policy implications and provides novel regulatory insights. Note that by imposing a proper price cap on the entry fee scheme, entry efficiency can also be achieved. However, such a price regulation would require the market designer or regulator to obtain precise information about the market primitives, such as the market size and the distribution of outside options. These details may change frequently and are often less accessible to regulators than to monopolists (Guo and Shmaya (2024)). Hence, our study provides novel insights into the classic and challenging problem of monopoly regulation (Baron and Myerson (1982)) by considering implementable mechanisms rather than imposing price constraints (Armstrong (1999), Galenianos, Kircher, and Virág (2011), Lewis and Sappington (1988a,b)).
The remainder of this paper is organized as follows. In the rest of this section, we discuss the related literature and our contributions. Section 2 presents the model and baseline analysis. We analyze the priority search program in Section 3. Section 4 generalizes our framework to accommodate heterogeneous preferences for public options and examines a multi-tier priority search program. We explore several extensions in Section 5. Finally, we offer concluding remarks in Section 6. All proofs are provided in the Appendix A.
1.1 Related literature and contributions
This paper contributes to a large body of economics research on rationing and priority service design by analyzing their welfare implications in a search environment with unequal outside options. The classic works of Harris and Raviv (1981), Chao and Wilson (1987), and Wilson (1989) examine priority pricing in environments with uncertain supply or demand. More recent studies have focused on the effect of priority service on consumer surplus in a queuing framework (Gershkov and Winter (2023)) and the role of priority pricing as an instrument for a durable goods monopolist to mitigate the inability to commit to future prices (Correia-da Silva (2021)). Our paper also connects to a parallel line of operations research literature on pay-for-priority schemes in queuing, where customers who pay a premium price gain priority over those who do not (Afèche, Baron, Milner, and Roet-Green (2019), Cui, Wang, and Yang (2020), Gurvich, Lariviere, and Ozkan (2019), Mendelson and Whang (1990)).
Priority services sometimes manifest as informal or illegal market arrangements, such as speed money or bribery (Kleinrock (1967), Lui (1985)).6 For instance, in the allocation of scarce public resources, market participants face long waiting times, leading to congestion under the rationing-by-waiting system (Barzel (1974), Nichols, Smolensky, and Tideman (1971), Polterovich (1993), Sah (1987)). In these marketplaces, the effects of introducing a fee-based priority service into the system remain controversial and are often context dependent. For instance, Kulshreshtha (2007) finds that speed money reduces the cost of waiting and improves allocation efficiency. In contrast, Budish, Cramton, and Shim (2015) and Hakimov et al. (2021) argue that existing priority-based services in the form of high-frequency trading arms races in financial exchanges and black markets for appointments in online booking systems represent a flawed market design. Our study contributes to these discussions by providing the novel insight that efficient market entry in a frictional search environment can be achieved by a monopolistic priority service provider.
Our paper also complements recent market design literature advocating non-fee-based priority systems in markets without monetary transfers. For instance, in health care, rationing by priority is effective in promoting aggregate incentives to register as deceased organ donors and enhancing social welfare (Kessler and Roth (2012), Kim and Li (2022), Kim, Li, and Xu (2021)) as well as reducing organ wastage in transplantation (Tunç, Sandıkçı, and Tanrıöver (2022)). Priority systems are also useful in the allocation of vaccines, ventilators, and other scarce health resources (Akbarpour, Budish, Dworczak, and Kominers (2024), Pathak, Sönmez, Ünever, and Yenmez (2020)), and in the design of COVID-19 testing queues (Yang, Cui, and Wang (2022)).
A distinct feature of our framework, compared to the extant literature broadly related to priority services, is the consideration of priority search in the presence of unequal outside options. A growing body of research has underscored that heterogeneity in outside options is important in many classical settings and crucially affects standard results. Board and Pycia (2014) find that when buyers have an outside option that they may exercise each period, the idea of negative selection that drives the Coase conjecture fails. Hwang and Li (2017) study the effect of the transparency of outside options in bilateral bargaining.7 Akbarpour et al. (2022) examine the welfare implications of unequal outside options in centralized school choice.8 Other studies have shown that the presence of outside options substantially changes the optimal selling mechanism (Chang (2021)).9 We advance this line of research by studying the welfare implications of priority search in the presence of heterogeneous outside options.
Finally, the matching process in our model relates to the substantial literature on search with capacity and mobility constraints, e.g., Peters (1984, 1991), Montgomery (1991), Acemoglu and Shimer (1999), Burdett, Shi, and Wright (2001), and Lester (2011). By embedding priority-based allocation mechanisms into a frictional search environment, our study provides novel insights into analyzing and improving welfare in frictional and congested marketplaces using a market design approach. More broadly, our focus on entry efficiency in markets with search and matching frictions is related to the widely discussed Hosios condition (Hosios (1990), Mangin and Julien (2021), Mortensen and Wright (2002)), which characterizes the condition for efficient market participation in a competitive search framework. The distinctive feature of our study is that we use a market design approach to resolve the inefficiency problem through the priority search program. More interestingly, optimality is achieved mostly by the tangency condition in previous studies, whereas the optimum occurs at a kink in our paper, which has no analog in the literature.
2 Model and baseline analysis
There is a continuum of agents with measure α and a unit mass of public options.10 Each public option involves one unit of a homogeneous indivisible good. Each agent has a unit demand, which can be satisfied through either a public option inside the market or the agent's private outside option. Agents simultaneously and independently decide where to visit, namely, whether to stay outside and opt for private outside options or to enter the market and search for a public option, thus forgoing outside options. Along the line of Burdett, Shi, and Wright (2001), we assume that there is no coordination among agents and focus on symmetric equilibrium throughout the analysis. Specifically, agents follow a symmetric threshold for market entry, and upon entry, all entrants adopt a symmetric mixed strategy of visiting each public option with equal probability.11
If agent i stays with his or her private outside option, his or her utility gain is , which is independently and identically distributed (iid) on with a smooth cumulative distribution function (CDF), denoted by , and probability density function (PDF), denoted by . If he or she obtains a public option, his or her utility gain is normalized to .12 Otherwise, he or she gains zero utility.
2.1 Baseline search equilibrium
In the laissez faire situation, referred to as the baseline search, there is no restriction on market entry, and upon entry, there is no expedited matching service. If a public option is visited by only one agent, this agent obtains the market good. When multiple agents search for the same public option, conflicts emerge and random rationing is applied; that is, one agent is randomly and uniformly selected to receive the market good. In this regard, the aggregate meeting process is essentially a limiting case of the canonical urn–ball matching environment13 and the matching functions are as specified in the following lemma.
Lemma 1.Consider a measure of m agents who enter the market and search for public options. Under symmetric mixed strategies, the (conditional) matching probability for each entrant is if and , and a public option in the market remains unmatched with probability .
2.2 Efficient market entry
To understand this optimal condition, we consider the social consequences associated with the entry decision by a marginal agent, who has an outside option value . If this agent enters the market and searches for public option j, he or she makes a positive contribution to the social surplus only if j is still available, that is, if none of the other entrants visits j, which occurs with probability based on Lemma 1. If this agent stays outside the market, he or she receives , which captures the social cost of his or her entry. Equation (3) essentially means that the expected social surplus is optimized when the social benefit and cost associated with the entry decision are equal. The following proposition compares the level of market entry in the baseline equilibrium with the efficient level.
Proposition 1. (Congestion in the Baseline Equilibrium)The baseline search results in market congestion relative to the efficient level of market participation, that is, .
Proposition 1 indicates that the baseline search intensity of the agents is higher than the efficient level. This result holds regardless of market tightness, that is, whether there is a shortage or abundance of market goods. Intuitively, when agent i enters the market and searches for public option j while forgoing his or her outside option, the individual opportunity cost is simply the outside option value . However, due to possible conflicts with other agents in the market, the associated social cost additionally accounts for the expected loss from crowding out a possible match between j and another agent . In other words, individual entry decisions fail to account for the negative externalities imposed on other agents in the market. Both the individual and social benefits are captured by the enlarged matching opportunity with a public option for the entering agent i. Hence, the misalignment between the social cost and the private cost of market entry triggers coordination failure among market participants, which leads to overparticipation and market congestion under the baseline search.
2.3 Entry fee scheme
To alleviate congestion, a first natural intervention is to impose an entry fee. We refer to such a practice as the entry fee scheme and assume that the fee is charged by a third-party intermediary or a platform that facilitates the matching service for the public options. The time line is as follows. The service provider first sets an entry fee . After observing p, agents simultaneously and independently decide whether to search for a public option in the market by paying p or to accept their private outside options. Thereafter, the matching process is governed by random rationing, similar to that in the baseline environment. Throughout the analysis, the fee is treated as a transfer from the agents to the service provider. Hence, the entry fee scheme does not introduce any direct welfare effect.
Proposition 2 states that under the entry fee scheme, the threshold for entry induced by the revenue-maximizing fee , denoted by , is always lower than the efficient level of market entry. This result indicates that the entry fee scheme overcorrects the congestion issue under the baseline search, leading to underparticipation. Figure 1 illustrates the results for Propositions 1 and 2.
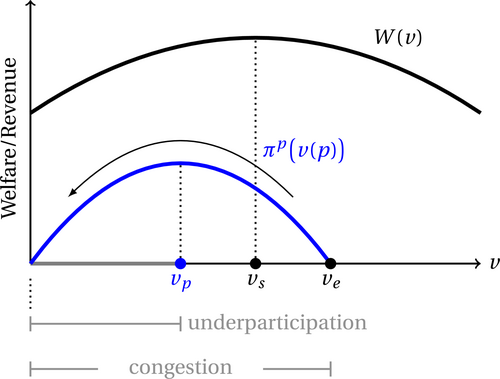
Overcorrection of the entry fee scheme. This figure plots the service provider's revenue πp(v(p)) under the entry fee scheme and the total welfare W(v). The horizontal axis represents the threshold value of market entry, which indicates that agents whose outside option value is lower than the threshold search in the market for public options. Specifically, vp and ve denote the equilibrium thresholds under the entry fee scheme and the baseline search, respectively, where vs is the threshold of efficient market entry.
Proposition 2. (Overcorrection of the Entry Fee Scheme)Compared to the efficient level of market entry, the revenue-maximizing entry fee scheme leads to underparticipation, that is, .
To understand the intuition behind this result, we first observe that based on (4), the threshold for market entry is decreasing in p. Indeed, a higher entry fee makes the public option less attractive. Thus, from the service provider's perspective, choosing p is strategically equivalent to choosing , as in (5). Next we consider the trade-off faced by the service provider. On the one hand, by increasing p, or equivalently, raising the barrier to market entry, fewer agents enter the market; hence, each public option is less likely to be matched with an agent. On the other hand, a higher p means that each entrant obtains a lower expected payoff, which, in turn, from the service provider's perspective, indicates a gain in surplus extractable from the remaining entrants.
These countervailing forces behind the service provider's incentive pinpoint the key force at work in Proposition 2. To illustrate the intuition, we examine the impacts of a marginal decrease in the entry threshold at the efficient level , i.e., a higher p. The marginal cost of the service provider is captured by the decrease in surplus extractable from the trading with the marginally exiting agents. Specifically, it is the difference between the lost matching opportunities and the expected payoff of the marginal agents exiting the market. The service provider's marginal benefit comes from the increase in surplus extractable from the remaining entrants. From a welfare perspective, the social loss, captured by the lost matching opportunities with public options, is exactly compensated by the associated social benefit, derived from the outside option value of marginal agents who stay out of the market. Regarding the trading surplus generated from each trade, because the compensation guaranteed to each entrant exactly matches his or her outside option value based on (4), the marginal cost to the service provider is zero; hence, his or her marginal net benefit is positive when decreasing v at . Accordingly, the extra benefit to the service provider, captured by the gain in surplus extractable from the remaining entrants, induces him or her to further increase p and, hence, lower the entry threshold at . Therefore, the revenue-maximizing fee induces a lower threshold for market entry relative to the efficient level.
3 Priority search
The priority search program facilitates expedited matching with the public option and proceeds in two stages. First, the priority service provider sets a priority membership fee . In the second stage, after observing r, each agent decides whether to enter the market to search for a public option and to pay the fee to become a priority member (PM).16 Based on the entry decisions and priority membership statuses, a public option is first allocated among the PMs (if any) uniformly and randomly, and then among all the non-PMs in the market. In other words, under priority search, a PM has a greater chance of being matched than a non-PM does. Moreover, within the same priority status group, the good is allocated through random rationing. Essentially, the priority search program operates as a tie-breaking device by differentiating the agents in terms of matching probabilities.
Using backward induction, our analysis begins by deriving agents' decisions on market entry and priority membership under different levels of priority fees in the second stage of the game. Thereafter, we consider the optimal priority membership fee set by the priority service provider who aims to maximize total revenue. Similar to the previous discussion, the priority membership fee, as a transfer, does not introduce any direct welfare effect.
3.1 Agents' decisions
We use and to denote the probabilities of being matched with a public option for the PMs and the non-PMs upon market entry, respectively, which are endogenously determined by agents' equilibrium strategies. Since PMs are prioritized over non-PMs during the matching process under priority search, we must have . Given a fixed priority membership fee r, the payoff of agent i contingent on his or her priority membership status and entry decision is specified as
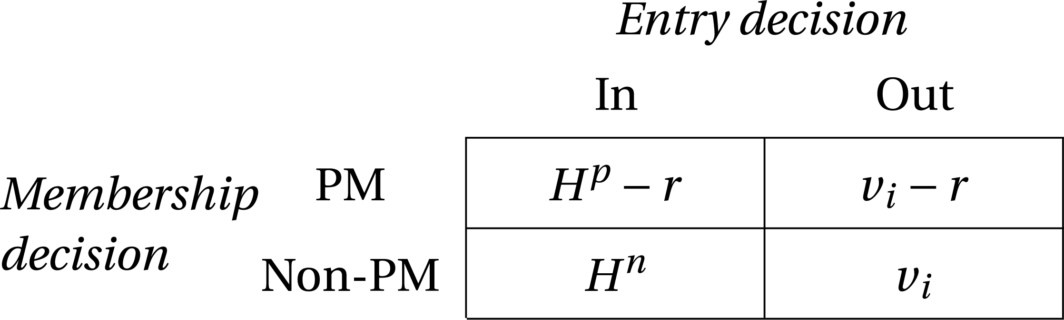
where and denote the expected payoffs of entering the market as a PM and non-PM, respectively, and and are the payoffs of the agent choosing his or her outside option as a PM and a non-PM, respectively. Alternatively, the payoff functions of agent i as a PM and a non-PM can be expressed as and , respectively.
To analyze agents' behavior, we focus on a symmetric equilibrium of agents' decisions concerning market entry and priority membership. The following observations based on the payoff functions are useful for characterizing the equilibrium behavior of the agents. First, it is a dominated strategy to stay outside the market and become a PM. Second, agents with attractive outside options, i.e., a high , will not enter the market. Third, conditional on entering the market, an agent's payoff no longer depends on his or her outside option.
Accordingly, for each fixed r, the equilibrium entry decisions are determined by a threshold outside option value, denoted by , below which agents choose to search for a public option. Additionally, the decisions regarding priority membership hinge on the relative sizes of and , as illustrated in Figure 2. Intuitively, when the priority membership fee r is relatively small, every market entrant has an incentive to become a PM to gain an advantage in the matching process. In contrast, agents tend to enter the market without priority membership when r becomes substantially large.
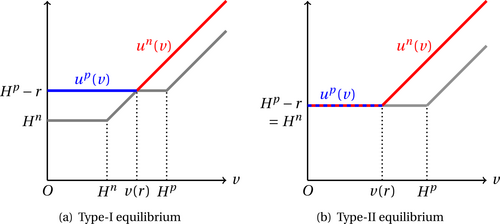
Different types of equilibrium under priority search.
When the priority fee is at an intermediate level, the market entrants are indifferent between becoming a PM and not. Interestingly, the priority fees that support the intermediate case, i.e., Figure 2(b), do not constitute a measure-zero set, as shown in our subsequent analysis. These discussions suggest that in equilibrium, an agent's priority membership decision is captured by the likelihood of becoming a PM conditional on entering the market, denoted by .
Given a priority fee r, the second-stage equilibrium is characterized by the threshold for market entry and the likelihood of becoming a PM .17 In equilibrium, an agent enters the market if and only if his or her outside option value is less than , and conditional on entry, he or she purchases the priority membership with probability . Due to coordination failure, agents in the market visit each public option with equal probability, regardless of their membership status. The probability of an agent searching for a public option as a PM is , whereas that for an agent entering without priority membership is . The matching probabilities contingent on membership status are as follows.
Lemma 2. (Membership-Contingent Matching Probabilities)Let v denote the threshold for market entry and let θ represent the proportion of market entrants with priority membership. When , the conditional matching probability for the PMs is
The PMs compete only within their own priority group under priority search; hence, the demand–supply ratio is , which immediately implies (6). To understand (7), we decompose its right-hand side into two parts. First, for non-PMs, a necessary condition for having a positive chance of being matched with a public option is that this option is not visited by any priority member, which occurs with probability based on Lemma 1. In other words, the public option must “survive” the competition among PMs before being considered by non-PMs. Second, conditional on a public option being still available, the demand–supply ratio becomes among non-PMs, which leads to a matching probability of . Accordingly, the marginal benefit of becoming a PM for an entrant is .18
An immediate observation from Lemma 2 is that for any v. This observation is intuitive because when all the market entrants have the same priority membership status, i.e., either they are all PMs or they are all non-PMs, the conditional matching probability with a public option is the same as that under the baseline search. Accordingly, , which follows from the baseline equilibrium in (1). In the limiting case of , namely, no agent purchases a priority membership, as long as an agent becomes a PM, he or she always obtains a market good, regardless of which public option he or she visits. Thus, . At the other extreme with , that is, when everyone else in the market is a PM, a marginal entrant without priority membership can be matched with a public option if and only if that option has not yet been visited by anyone else. Hence, we have . Accordingly, it follows from the efficient entry in (3) that .
Based on the cost and benefit of becoming a PM, there are three types of priority search equilibrium classified by the fraction of entrants with priority membership . When r is relatively small, every agent who enters the market purchases priority membership. As r increases, only a fraction of the entrants opt for priority membership, while the remainder enter the market without priority. When r becomes sufficiently large, none of the entrants chooses to obtain priority membership.
Based on these equilibrium conditions, we derive the following comparative statics for the equilibrium variables with respect to the priority membership fee r.
Proposition 3. (Comparative Statics)Consider a symmetric priority search equilibrium characterized by . If it satisfies the type-I equilibrium condition (L1), then
Proposition 3 establishes that the effect of the priority membership fee on the degree of crowdedness in the market, as measured by , is not monotonic. Intuitively, both a free priority service and a substantially expensive service induce the same threshold for market entry. This fact also follows from the indifference equations under conditions (L1) and (L3) since . As r increases, the priority search equilibrium transitions from type I to type II and then to type III. Specifically, when r is relatively small, it induces a type-I equilibrium with , in which case the market becomes less congested as r increases. This result occurs because the priority membership fee directly increases the cost of market entry by inducing every participant to pay the fee, which reduces the propensity to compete for public options. In this regard, the type-I equilibrium under the priority search program is analogous to the entry fee scheme analyzed in Section 2.3. When r increases further, the equilibrium becomes type II. In this case, more agents enter the market with a larger v, whereas fewer market entrants become PMs with a smaller θ as the priority membership fee escalates. This outcome stands in contrast to the entry fee scheme because the priority service provider cannot prevent non-PMs from entering the market and being matched with a public good. A sufficiently large r leads to a type-III equilibrium, which is essentially equivalent to the baseline equilibrium. In such a scenario, no agents opt for priority membership and, hence, r no longer has an impact on market entry.
To determine the regions of equilibrium, it follows from the above analysis that the boundaries of the three types of equilibrium correspond to the type-II equilibrium at and . When in a type-II equilibrium, , which coincides with the efficient entry characterized by (3). Hence, we have when . Similarly, when , , which suggests that based on (1). Accordingly, the boundaries of the different types of equilibrium are determined by the relative gain in becoming a PM over a non-PM at and , that is, and with . These arguments lead to an important observation that for all three types of equilibrium. In other words, the effective domain of the entry threshold induced by the priority search program is bounded below and above by the agents' equilibrium behavior. This critical insight underpins our ensuing analysis of the priority service provider's optimal decision.
Proposition 4 establishes the existence and uniqueness of a priority search equilibrium and provides a unified indifference condition for market entry.
Proposition 4. (Priority Search Equilibrium)For each fixed priority membership fee , there exists a unique symmetric equilibrium under priority search, which is characterized by the threshold entry type v and the fraction of priority members . As r increases, the optimal decisions of agents follow
- the type-I equilibrium with and v determined by condition (L1) if
- the type-II equilibrium with θ and v determined by condition (L2) if
- the type-III equilibrium with and v determined by condition (L3) if ,
where . In each type of priority search equilibrium, we have
In (8), the two sides represent the threshold entrant's ex ante cost and benefit of entering the market. Specifically, on the left-hand side, v, as the threshold outside option value, is the opportunity cost of entering the market, and θr is the expected payment of the priority membership fee. The right-hand side of (8) represents the expected matching benefit for an agent searching for a public option, which is contingent on his or her membership status, i.e., . Alternatively, it can be regarded as the conditional matching probability when all other agents have the same priority membership status, i.e., .
3.2 Service provider's decision
Theorem 1 states our main result that the optimal priority membership fee is at the margin between the type-I equilibrium and the type-II equilibrium, which induces the efficient threshold for market entry. This result suggests that for any degree of market tightness, introducing a monopolistic priority service provider can always remedy the congestion problem. More crucially, this intervention induces the efficient level of market entry. A direct implication is that the aggregate surplus under the entry fee scheme analyzed in Section 2.3 is lower than that under the priority search program.
Theorem 1. (Optimality of Priority Search)The revenue-maximizing priority membership fee under the priority search program satisfies . Accordingly, market participation reaches the efficient level, i.e., .
Compared to the baseline search, providing differentiated services for agents in terms of matching probabilities increases the cost of market entry for PMs directly and for non-PMs indirectly. The reason is that agents who enter the market as PMs need to pay the additional priority membership fee, whereas the additional costs for the non-PMs are the disadvantaged matching probability relative to the PMs. Hence, introducing the priority search program can reduce participation and mitigate congestion. From the service provider's perspective, the trade-off is between a higher priority membership fee and more priority members along with increased market entry, as shown in the comparative statics of Proposition 3. Therefore, the service provider's optimal decision is to set the membership fee equal to the priority benefit enjoyed by the PMs over the non-PMs, which corresponds to the enlarged matching probability, i.e., . This fee induces the type-II equilibrium in the second stage of the game. As discussed earlier, the implied range of the entry threshold is . Based on Proposition 2, the revenue function is maximized at and, hence, it decreases when . Therefore, the optimal priority membership fee induces with .
This optimal priority membership fee, on the one hand, represents the net benefit of an agent becoming a PM relative to entering the market without priority membership when all the agents in the market are PMs. On the other hand, it also measures the degree of negative externality introduced by this agent's participation in the market. To demonstrate this fact, we refer to the agent as i and to the public option he or she searches for as j. Note that represents agent i's expected payoff from visiting j. As long as agent i obtains the good, he or she crowds out another agent who makes the same attempt. That is, is also the expected loss of another agent who is in direct conflict with agent i when visiting j. The only exception is when agent i is the only agent visiting j, which occurs with probability . Therefore, the effective social loss induced by agent i successfully being matched with public option j is , which coincides with the revenue-maximizing priority membership fee . In this regard, the revenue-maximizing priority search program successfully internalizes the social cost of market entry and, in particular, the extra cost of crowding out other agents. Hence, it fully corrects the congestion problem under the baseline search without leading to underparticipation and maximizes aggregate welfare.
Figure 3 provides an illustration of the social welfare and revenue functions to facilitate comparisons between the priority search and entry fee schemes. When the fees, i.e., p and r, are relatively low, the revenue functions under entry scheme and priority search program overlap in . However, as the fees increase further, while the enforcement power of the entry fee scheme remains the same, the priority search program can no longer induce all market entrants to enroll in priority membership. Instead, as membership becomes more expensive, agents are more likely to enter as non-PMs, consistent with the type-II equilibrium under priority search. In particular, when agents' behavior follows the type-I equilibrium under priority search, an increase in r discourages market entry, and increases as v declines from to . When agents' behavior enters the type-II equilibrium regime, the threshold for market entry rises again and, hence, the revenue decreases, returning to the initial levels. This “backtracking” pattern, similar to a “U-turn,” is driven mainly by the fact that the priority search program does not exclude agents from entering markets as non-PMs due to institutional constraints or regulatory considerations. Consequently, in contrast to the entry fee scheme, under the priority search program, the service provider has no market power to further increase the fee from to extract more surplus from agents. The nonexclusivity feature of the priority search program prevents the service provider from earning more revenue than his or her counterpart under the entry fee scheme, which nonetheless addresses the underparticipation issue and results in efficient market participation.
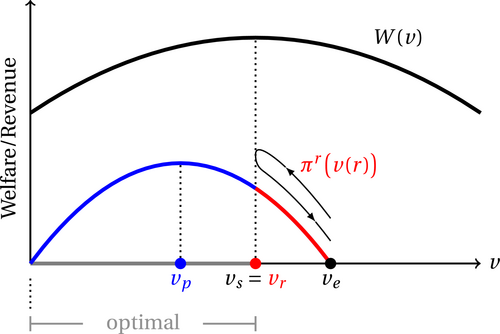
Optimality of the priority search program. This figure plots the priority service provider's revenue πr(v(r)), represented by the red segment of the parabola, and the total welfare W(v). The horizontal axis represents the threshold value of market entry, which indicates that agents with outside option values lower than the threshold search in the market for public options. Specifically, vp, vr, and ve denote the equilibrium thresholds under the entry fee scheme, the priority search program, and the baseline search, respectively, where vs is the threshold of efficient market entry.
4 Heterogeneous preferences for public options
This section introduces heterogeneity in the valuations of public options and examines the welfare implications of priority search in this richer environment.20 For simplicity and tractability, we consider binary types of public option values, denoted by . Each agent's valuation of a public option is with probability and with probability . The valuations of outside and public options, i.e., and , respectively, are private information and are independent of each other. We assume that the distribution of outside options is regular; that is, is log concave. Throughout the analysis, we focus on a modest level of δ such that all the mechanisms under consideration serve both types of agents in equilibrium, which therefore captures the inclusivity feature of the public options.21
4.1 Priority search program
Given the heterogeneous preferences for public options, it is natural for the service provider to design differentiated priority levels by setting high and low membership fees , resembling “platinum” and “gold” memberships in practice. An agent, if entering the market, decides whether to enroll in priority membership and, if so, which tier of the priority service to choose. Agents who pay are matched before agents who pay , and the latter are prioritized over non-PMs. Accordingly, the multi-tier priority search program separates the market entrants into three groups with high, low, and no priority, denoted by . For notational simplicity in the subsequent analysis, we set , which essentially represents the inclusiveness of the priority search program.
Given , an agent's strategy in the second stage is contingent on his or her valuation of the public option. Specifically, a type-τ agent's entry decision is determined by a threshold , above which an agent stays outside the market. Let denote the vector of entry thresholds. Accordingly, the measures of high- and low-type entrants are and , respectively. Upon entry, a type-τ agent's decision regarding priority membership is represented by , where denotes the probability of subscribing to ρ-level priority and for .22 We use to denote the priority membership decisions of both the high and low types.
By examining the optimal choice(s) of ρ for maximizing , we can characterize different types of equilibrium behavior for priority membership decisions among the agents. According to the previous analysis with homogeneous market value in Section 3.1, as the membership fee increases, the priority search program induces three types of equilibrium with decreasing rates of membership, from full subscription to partial subscription and then to null subscription. With heterogeneous market values and multiple tiers of priority, different combinations of and result in considerably more types of equilibrium. Table 1 and Figure 4 present the different types of equilibrium in which both the high- and low-priority levels receive subscriptions.23 Specifically, type h entrants may always pay to become platinum members or adopt a mixed strategy between paying and . We refer to the former and latter as HP and HM, respectively, indicating that high-type agents adopt a pure or mixed strategy in their membership decisions. Similarly, for low-type agents, a pure strategy for membership decisions is denoted by LP. There are several cases of mixed strategies, referred to as LM, in which indifference may occur between high and low priority, between low and no priority, or among all three priority levels.
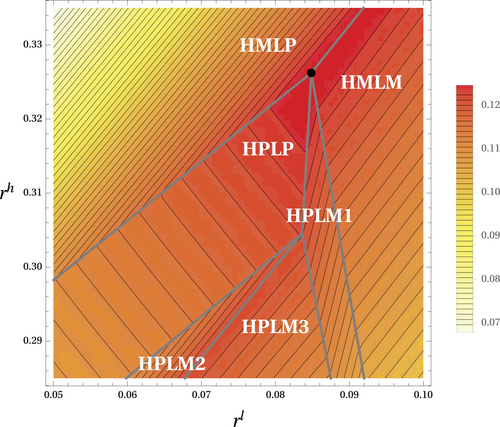
Regions of priority search equilibrium with heterogeneous market values. The figure plots the regions of different types of priority search equilibrium in which both the high- and low-priority levels receive subscriptions and the isoprofit curves of the service provider with varying membership fees. The black dot represents the maximum of the service provider's profit. The parameter values are set as (α,β,δ)=(2,0.5,0.1) and v ∼ U[0,2].
|
High-Type Agents |
Low-Type Agents |
|||||
|---|---|---|---|---|---|---|
|
|
|
|
|
|
|
|
|
HPLP |
1 |
0 |
0 |
0 |
1 |
0 |
|
HPLM1 |
1 |
0 |
0 |
0 |
(0,1) |
(0,1) |
|
HPLM2 |
1 |
0 |
0 |
(0,1) |
(0,1) |
0 |
|
HPLM3 |
1 |
0 |
0 |
(0,1) |
(0,1) |
(0,1) |
|
HMLP |
(0,1) |
(0,1) |
0 |
0 |
1 |
0 |
|
HMLM |
(0,1) |
(0,1) |
0 |
(0,1) |
(0,1) |
0 |
- Note: The table presents the priority membership decisions of high- and low-type agents under different types of priority search equilibrium, in which both the high- and low-priority levels receive subscriptions. For and , denotes the probability of type-τ agents getting ρ-level priority.
The first part of Proposition 5 establishes that the revenue-maximizing priority search program induces a fully separating equilibrium, namely, the HPLP equilibrium, in which the high- and low-type agents always choose high and low priority, respectively. The service provider's optimal strategy is to induce all entrants to subscribe to a priority service, similar to our main analysis with homogeneous market value. Moreover, the multi-tier priority search program has a sorting effect on the matching process because agents' decisions regarding priority membership perfectly reveal their preferences for public options. Accordingly, the service provider's decision problem can be transformed into choosing two threshold values for market entry. The second part of Proposition 5 characterizes the optimal entry thresholds under the priority search program.
Proposition 5. (Optimal Priority Search Program)The revenue-maximizing priority search program induces a separating equilibrium such that and . Under the optimal priority search program, the entry thresholds satisfy
4.2 Entry fee scheme
With binary types of public option value, the service provider under the entry fee scheme sets high and low entry fees . Market entrants must pay either or , where those who pay enjoy a higher matching probability than those who pay . In this regard, the entry fee scheme is equivalent to an “entry-priority” mechanism, where all agents must pay for entry and each entrant can further purchase priority membership to enjoy an expedited matching service over those who pay only the entry fee.
Due to the exclusivity of the entry fee scheme, there are only two groups of entrants, , classified by the entry fee paid. Accordingly, in the second stage, an agent's strategy is characterized by the entry threshold values and the decisions on entry fee , where represents the probabilities of paying and for entry by type-τ agents and for . Upon entry, the matching probabilities contingent on the entry fee payment, with , are defined in the same way as those under the priority search program.
Proposition 6. (Optimal Entry Fee Scheme)The revenue-maximizing entry fee scheme induces a separating equilibrium such that and . Under the optimal entry fee scheme, the entry thresholds satisfy
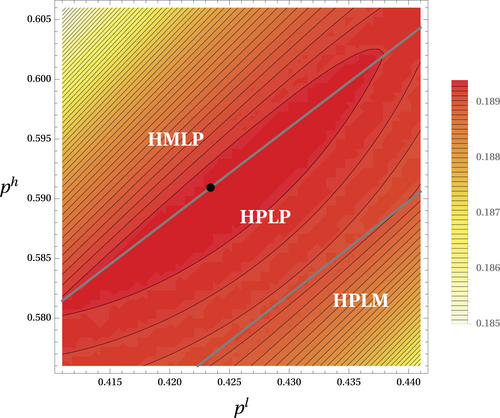
Regions of entry fee equilibrium with heterogeneous market values. The figure plots the regions of different types of entry fee equilibrium in which both high and low entry fees are chosen by some entrants and the isoprofit curves of the service provider with varying entry fees. The black dot represents the maximum of the service provider's profit. For the equilibrium labels, HPLP indicates that both types of agents employ a pure strategy on their entry fee decision with θh = (1,0) and θl = (0,1). HMLP indicates that the high-type agents employ a mixed strategy between ph and pl with θh = (θ,1 − θ), where θ ∈ (0,1) and θl = (0,1). HPLM indicates that the low-type agents employ a mixed strategy between ph and pl with θh = (1,0) and θl = (θ,1 − θ), where θ ∈ (0,1). The parameter values are set as (α,β,δ)=(2,0.5,0.1) and v ∼ U[0,2].
4.3 Comparison with the baseline search and efficient entry
Aggregate participation is measured by the total number of high- and low-type market entrants, and is denoted by , where . Theorem 2 establishes that the priority search program mitigates the underparticipation issue under the entry fee scheme, although both mechanisms result in less market entry than the efficient level.
Theorem 2. (Comparisons of Entry Efficiency and Welfare)With heterogeneous preferences for public options, the aggregate levels of market entry under the entry fee scheme (), priority search program (), efficient entry (), and baseline search () satisfy
Intuitively, the priority search program corrects underparticipation in the entry fee scheme because it does not restrict agents' entry. With heterogeneous market values, the monopolistic service provider aims to extract more rent from the high type, which lowers market entry under priority search compared to the efficient level. Specifically, for , we have for both the priority search and efficient entry. Thus, under the priority search program, the participation level of the low type would be efficient if there were no distortions in high-type participation. However, because of the potential adverse selection problem with information asymmetry, the service provider must guarantee incentive compatibility for high-type agents. Hence, compared to , the additional term in is , which is smaller than that at the efficient level. Hence, underparticipation of the high type indirectly results in a higher entry threshold for the low type than the efficient level. In aggregate, the direct effect on the high type dominates, which leads to an overall lower participation level than the efficient level. In comparison, under the entry fee scheme, since the service provider can exclude agents from entering the market by imposing a cost on all entrants, the underparticipation problem is more severe than that under the priority search program.
Regarding the social surplus, Theorem 2 indicates that the relative rankings of different mechanisms in terms of entry efficiency apply mostly to welfare implications. Specifically, compared with the entry fee scheme, the priority search program increases the social surplus whereby both mechanisms underperform compared to efficient entry. Notably, the overparticipation of low-type agents and underparticipation of high-type agents under priority search results in more public options being allocated to those who value them less. Consequently, the welfare loss under priority search is partly driven by such a distortion in allocation. While it is analytically infeasible to compare the welfare under different market interventions with the laissez faire situation, our simulation results in Figure 6 suggest that the priority search program consistently generates greater social surplus than the baseline level. In contrast, the entry fee scheme may either underperform or overperform the baseline search.
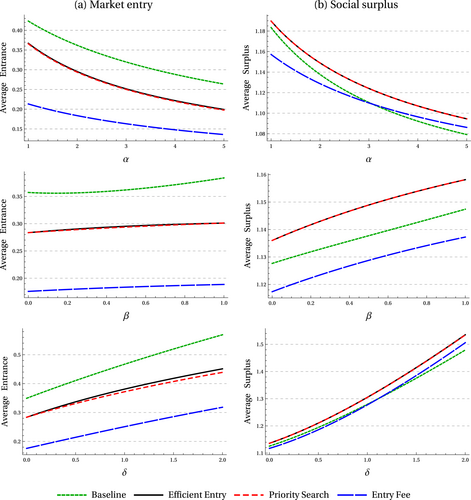
Comparisons of entry efficiency and welfare with heterogeneous market values. The figure plots the average market entry and social surplus under different mechanisms, calculated as the aggregate market entry and aggregate welfare divided by the total measure of agents. In each set of simulations, we separately vary the market tightness (α), the proportion of high-type agents (β), and the relative valuation for a public option by high-type agents (δ). The parameter values, if not varied along the horizontal axis, are set as (α,β,δ)=(2,0.5,0.1) and v ∼ U[0,2].
To complement the theoretical analysis, we conduct a series of numerical simulations to examine the market entry and social surplus under different mechanisms by varying several key model parameters, as shown in Figure 6.26 These simulation results not only illustrate the qualitative performance of the priority search compared to the entry fee scheme but also provide quantitative evaluations of the priority search relative to efficient entry. Under different sets of parameters, we consistently observe that the priority search program is approximately efficient in the sense that both market entry and social surplus are very close to efficient levels, especially compared to those under the entry fee scheme or the baseline search. This finding of approximate efficiency is robust to model primitives, including market tightness α, the proportion of high-type agents β, and the relative valuation of a public option by high-type agents δ.
5 Discussion and extension
Our main analysis demonstrates that the congestion issue in a laissez faire situation with a baseline search can be remedied by the revenue-maximizing priority search program but not by the entry fee scheme. This section discusses several extensions to explore the robustness of our findings. For simplicity, the extensions are based on our main model with homogeneous preferences for the public option.
5.1 General matching function
The first extension explores whether our results apply to other matching functions. Let and denote the trading probabilities for the agents and public options, respectively. Similarly, we use to denote the probability that a public option is not matched to any agent. We assume that and satisfy the following properties, which are standard in the literature (Galenianos and Kircher (2012)).
Assumption 1.For , (i) , ; (ii) , ; and (iii) .
Corollary 1.Under general matching functions that satisfy Assumption 1, the intensities of market participation under the baseline search (), the entry fee scheme (), and efficient entry () always satisfy .
Under the priority search program, to rule out any direct efficiency consequences, we assume that upon entry, the aggregate matching efficiency is not affected by the priority service. In other words, for a fixed number of market entrants, the expected matching probability for agents is independent of the share of priority members, denoted by . Specifically, the membership-contingent matching probabilities under the priority search, denoted by and , satisfy the following property.
Assumption 2.For and , we have .
Essentially, measures the expected matching probability for each entrant when agents enter the market and each entrant opts for priority membership with probability θ, and represents the matching probability for each entrant when all entrants have the same priority status. This assumption ensures that the two-tier matching process under the priority search program does not introduce direct efficiency gains compared to the baseline search or the entry fee scheme.
A large class of matching functions featuring both coordination failure and additional frictions, summarized by Petrongolo and Pissarides (2001), satisfy the above assumption. For instance, in addition to the urn–ball matching process described in our main analysis, each agent who visits a public option may additionally experience a match-specific qualification shock such that he or she is qualified with probability . This situation yields , , and , which satisfy Assumptions 1 and 2. More generally, the matching processes for PMs and non-PMs may even be different. Corollary 2 establishes the optimality of the priority search program under general matching functions using ideas similar to our main analysis.
5.2 Finite market
5.3 Deferred payment
In the priority search program with deferred payment, agents who sign up for the priority service pay the membership fee only after being successfully matched with a public option, instead of providing upfront or immediate payment.28 The matching process is operated in the same way as in our main setup. The priority service provider charges a (deferred) priority membership fee , which sets the expected payment of the priority fee under the deferred payment scheme equal to the priority membership fee under the immediate payment scheme. The expected payoff functions of an agent with outside option , contingent on his or her priority membership status, are and . It follows that the second-stage equilibrium behavior of the agents can be characterized by the same set of conditions as those in (L1)–(L3). Intuitively, agents are indifferent to the timing of the priority membership fee payment as long as the expected amount of the payment remains the same. For the priority service provider's optimal decision, we have . Hence, the deferred and immediate payment schemes are strategically equivalent. More generally, our framework can accommodate many alternative payment schemes. For instance, a downpayment scheme, where agents first pay a deposit for priority service and obtain a full refund if not matched, leads to the same outcome as the deferred payment and immediate payment schemes.
6 Conclusions
How to simultaneously generate revenue and regulate congestion is a well known challenge that service providers face when managing service systems. This paper studies the priority search program in an attempt to resolve the overparticipation issue in a laissez faire situation and improve market entry efficiency. Our analysis focuses on a stylized search framework with heterogeneous outside options that is broadly relevant to various marketplaces.
Under priority search, a monopolistic priority service provider facilitates expedited matching with public options by charging a priority membership fee, which raises the cost of entry directly for agents who opt for priority membership and indirectly for other entrants by lowering their chances of obtaining public options. Our main analysis establishes that a revenue-maximizing priority search program always induces the efficient level of market participation and is superior to alternative market interventions involving entry fees. By allowing agents to enter the market without paying the priority membership fee, the priority search program prevents the monopolist from overcharging on the service fee and inducing underparticipation relative to the entry fee scheme.
Our study provides important insights for regulating congested markets, such as medical resource rationing, job hunting, ride hailing, and train ticket rationing during peak seasons. In the presence of heterogeneous outside options, simple fixes that impose a mandatory entry fee or a uniform transaction cost for public options are not fully effective and are not desirable if they are operated by a profit-maximizing platform or third party. The priority search program is an effective resolution since it induces the efficient level of market participation. More importantly, it can be flexibly designed with respect to the matching technology, market size, and timing of the membership fee payment.
Appendix A: Proofs
Proof of Lemma 1
Proof of Proposition 1
Proof of Proposition 2
Proof of Lemma 2
Proof of Proposition 3
Finally, we derive the relation between v and θ based on the second equality in condition (L2), that is, . Because both and are decreasing in v and is decreasing in θ, it follows that v is decreasing in θ. With v increasing in r, we conclude that θ is decreasing in r, that is, .
Proof of Proposition 4
Next, we derive the regions corresponding to each type of equilibrium and show the existence and uniqueness of the equilibrium by investigating conditions (L1)–(L3) one by one. Based on condition (L1), the range of r that supports the type-I equilibrium satisfies , which is equivalent to based on Lemma 2. This inequality holds when according to (3). Hence, it follows from the first part of Proposition 3 that we must have . In the type-I equilibrium, . Since decreases in v and is bounded above by 1 but not bounded below, it follows that the equilibrium threshold v always exists for any fixed . Furthermore, the type-I equilibrium (when it exists) is unique because v is decreasing in , as established in Proposition 3.
For the type-II equilibrium, we have established in the proof of Proposition 3 that the range of r supporting the equilibrium is . According to (L2), we have . Since the left-hand side of the equation decreases in v and is bounded above by 1 but not bounded below, it follows that a unique v always exists for any . Similarly, based on (8), a unique v always exists for any . Because v is increasing in r, whereas θ is decreasing in r, as established in the second part of Proposition 3, it follows that for each fixed , there exists a unique pair of v and θ satisfying condition (L2).
For the type-III equilibrium, based on condition (L3) and (1), . Hence, the range of r that supports the type-III equilibrium is . It then follows from the proof of Proposition 1 that for any fixed , a unique equilibrium threshold v always exists and satisfies .
To complete the proof, we note that the above analysis, on the one hand, shows that within each range of r, the respective type of priority search equilibrium exists and is unique. On the other hand, the ranges corresponding to each type of equilibrium form a partition of the set of nonnegative real numbers, which guarantees the existence and uniqueness of a priority search equilibrium for any given .
Proof of Theorem 1
The main idea of the proof is to establish that in the type-I equilibrium, the service provider's revenue is increasing in , whereas in the type-II equilibrium, the revenue is decreasing in . Note that in the type-III equilibrium, the revenue is always 0 since no agents choose the priority service with when . Hence, we only need to focus on the type-I and type-II equilibrium.
Proof of Proposition 5
To determine the equilibrium conditions of agents' behavior, we establish the following result for membership decisions.
Lemma A.1.Let denote the lowest priority level with . Then, for any higher priority level with , we have .
Proof.Suppose that for some with . Then, for low-type agents,
Lemma A.2.With and under priority search, (i) condition (IRh) is always slack, and (ii) conditions (ICh) and (ICl) cannot be binding simultaneously. Hence, conditions (ICh)–(IRl) are equivalent to
Proof.To prove (i), we have
To prove (ii), we rewrite (ICh) and (ICl) as
Finally, to prove A.2, we substitute into (ICh) to obtain and substitute into (ICl) to obtain . □
Based on Lemma A.1, when and , we have the following six types of equilibrium, classified by the agents' priority membership decisions. In the labels of equilibrium, “H” and “L” represent agents with high and low market values, respectively, whereas “P” and “M” represent “pure” and “mixed” strategies, respectively.
- I. HPLP: , .
- II. HPLM1: , with .
- III. HPLM2: , with .
- IV. HPLM3: , with and .
- V. HMLP: , with .
- VI. HMLM: , with .
Next, we characterize and rule out the type-II–VI equilibria by examining the optimal decision of the priority service provider. Specifically, for each type of equilibrium involving mixed strategies, we find a profitable deviation for the service provider.
II. HPLM1
Case 1. If (ICl) is slack, then a profitable adjustment for the service provider is to decrease while keeping unchanged. This adjustment is feasible for the following reasons. Obviously, the adjustment will not affect (II-a). To satisfy (II-c), θ needs to increase since decreases in both θ and . When both and decrease, increases and, hence, must decrease such that increases. To satisfy (II-b), we need to adjust only. For (ICh), since increases and decreases, must decrease, which satisfies condition (ICh).
III. HPLM2
Case 2. If , then the service provider's payoff becomes , and since . Hence, a profitable adjustment for the service provider is to decrease while satisfying (III-a)–(III-c) and . This outcome can be achieved through the following series of changes. When decreases, we need to increase , which implies that and increase. Furthermore, (III-a) and (III-b) imply that and must both increase. To satisfy (III-c), we need to adjust only.
IV. HPLM3
V. HMLP
Case 1. If (IRl) is slack, it is profitable for the service provider to decrease both and , which is feasible for the following reasons. Equation (V-a) can be satisfied by adjusting . To further satisfy (V-b) and (V-c), we may decrease and increase . Since decreases in θ, we need θ to increase.
VI. HMLM
In the following analysis, we examine the possibilities with or . Based on Lemma A.1, there are two remaining cases as follows.
In the final part of the proof, we show that both (ICh) and (IRl) are binding under the optimal priority search program. First, we note that the three inequality conditions, i.e., (ICh), (ICl), and (IRl), cannot all be slack. Otherwise, and under the optimal priority search program, which would imply that , violating (IRl).
Proof of Proposition 6
First, we note that the result in Lemma A.1 applies similarly to the entry fee scheme. That is, if high-type agents choose the low membership fee with a positive probability, i.e., , then the low-type agents will never choose the high membership fee, i.e., .
Similar to the analysis in Proposition 5, we first consider the possible types of second-stage equilibria where the high-type (low-type) agents subscribe to the high (low) priority membership with a positive probability, i.e., and . Accordingly, we have the following three possible types of equilibria.
- I. HPLP: , .
- II. HPLM: , with .
- III. HMLP: , with .
In the following analysis, we show that the type-II equilibrium and the type-III equilibrium are never optimal for the service provider.




