Location Sorting and Endogenous Amenities: Evidence From Amsterdam
Abstract
This paper shows the endogeneity of amenities plays a crucial role in determining the welfare distribution of a city's residents. We quantify this mechanism by building a dynamic model of residential choice with heterogeneous households, where consumption amenities are the equilibrium outcome of a market for non-tradables. We estimate our model using Dutch microdata and leveraging variation in Amsterdam's spatial distribution of tourists as a demand shifter, finding significant heterogeneity in residents' preferences over amenities and in the supply responses of amenities to changes in demand composition. This two-way heterogeneity dictates the degree of horizontal differentiation across neighborhoods, residential sorting, and inequality. Finally, we show the distributional effects of mass tourism depend on this heterogeneity: following rent increases due to growing tourist demand for housing, younger residents—whose amenity preferences are closest to tourists—are compensated by amenities tilting in their favor, while the losses of older residents are amplified.
1 Introduction
Socioeconomic inequality is tightly linked to residential choice, both across and within cities (Moretti (2013)). Higher socioeconomic status households can afford to live in locations with more desirable amenities. Furthermore, amenities improve as residential composition changes, reinforcing the desirability of locations. This response of a location's amenities to demographic sorting has been shown to be a quantitatively important mechanism for amplifying welfare inequality (Guerrieri, Hartley, and Hurst (2013), Diamond (2016)). However, relatively little is understood about the nature of these endogenous amenities, as they are typically modeled as a one-dimensional object summarizing a wide variety of a location's characteristics.
It is natural to think different types of households have diverse tastes for different types of consumption amenities, and that firms providing such amenities cater to this heterogeneity (George and Waldfogel (2003)). For example, when neighborhoods gentrify, the initial increase in the share of young, college-educated households is typically accompanied by an increase in the presence of bars and restaurants, and a reduction in mom-and-pop stores. While providing tractability, aggregating amenities into a single index does not allow for the horizontal differentiation of neighborhoods on the demand side, nor for differential supply-side responses to consumer heterogeneity. Moreover, if this heterogeneity plays an important distributive role, understanding its sources is crucial to design policies that alleviate urban inequality. For example, incumbent low-income residents living in gentrifying neighborhoods may not only suffer from higher housing prices, but also from the changes in neighborhood characteristics associated with the increase in higher-income households. Therefore, in this paper, we ask: How does preference heterogeneity over multiple endogenous consumption amenities shape within-city residential sorting and inequality?
To answer our research question, we build and estimate a dynamic spatial equilibrium model of a city with heterogeneity in household preferences over a bundle of endogenous amenities, whose supply caters to each neighborhood's demographic composition. To estimate our model, we use restricted-access microdata from the Centraal Bureau voor de Statistiek (CBS), the statistics bureau of the Netherlands. From these data, we construct an annual panel of residential location choices for the universe of residents in the Netherlands. We complement these data with an annual panel of establishment counts, allowing us to track consumption amenities across time and space. Apart from the availability of high-quality data, Amsterdam provides an ideal laboratory to study the link between residential composition and endogenous amenities, as it has undergone significant changes due to the impact of mass tourism on local housing and amenity markets.
We start by showing the expansion of tourism across Amsterdam is significant enough to affect housing and local amenity markets. The number of overnight tourist stays went from 8 million in 2008 to nearly 16 million in 2017, along with a stark increase in housing units converted to short-term rentals (STR), primarily through the Airbnb platform. In contrast to hotels, which tend to spatially cluster in the city center, STR growth sprawled across all neighborhoods, reaching over 5% of the city-wide rental market and exceeding 20% in some central neighborhoods. Next, we show STR expansion is sizable enough to impact rent prices. We continue by showing amenities catering to tourists increase in nearly every neighborhood, and their presence is negatively correlated with amenities catering exclusively to locals, such as nurseries/daycare facilities, which decline in more than half of neighborhoods at a median rate of −32%. Finally, we show different demographic groups respond differently to these neighborhood changes through their residential choices, suggesting different valuations for the changes in amenities.
In our model, residential choices and amenities are jointly determined equilibrium outcomes. We model the residential choices of local residents with a dynamic discrete choice setup—they are forward-looking, change locations subject to heterogeneous moving costs, and hold heterogeneous preferences over location attributes. We also specify a static model of how tourists choose the location where they book their STR. Hence, a location's total demand for housing and amenities is shaped by the location choices of both locals and tourists.
On the housing supply side, we assume atomistic absentee landlords supply housing to locals on traditional, long-term leases or to tourists on short-term leases. On the amenity supply side, monopolistically competitive firms provide a variety of consumption amenities that differentially cater to different types of locals and tourists. Compared to settings where amenities are collapsed to a one-dimensional quality index, introducing multiple types of amenities allows neighborhoods to endogenously become horizontally differentiated, because residents can trade off one type of amenity for another. This implies households of different income levels may disagree on which neighborhoods are most desirable, therefore decoupling income inequality from welfare (i..e, amenity-adjusted) inequality.
Because our microdata track the residential locations of households, we can accommodate forward-looking behavior and state-dependent moving costs in our estimation of locals' residential choices. These dynamic elements of our model are motivated by two features of our data. First, moving decisions are infrequent, suggesting significant moving costs. Second, we observe the probability of moving is state-dependent: it decreases in the time a household has been living in its current location. We capture these features of the data by (i) including standard distance-adjusted moving costs, and (ii) allowing agents to accumulate location capital that is lost upon moving, which introduces a dynamic, state-dependent component to moving costs. Failure to account for these dynamic elements is known to lead to biased estimates (Bayer, McMillan, Murphy, and Timmins (2016), Traiberman (2019)).
We estimate our dynamic location choice model by building upon the Euler Equation in Conditional Choice Probability (ECCP) methodology (Aguirregabiria and Magesan (2013), Scott (2013), Kalouptsidi, Scott, and Souza-Rodrigues (2021b)). We use an instrumental variable approach to address the endogeneity of rental prices and consumption amenities. Our demand estimates reveal preference parameters that correlate with demographics in reasonable ways. For example, households without children value restaurants the most, consistent with having the most leisure time among all groups. By contrast, households with children value nurseries the most. The highest income and most educated households dislike touristic amenities.
On the amenity supply side, we also estimate reasonable supply responses of different amenity categories to different demographics. We find the presence of tourists mainly drives the entry of touristic amenities, restaurants, and non-food retail, but does not affect the entry of nurseries. Instead, the supply of nurseries responds most strongly to households with children, while younger households incentivize the entry of restaurants. The supply of grocery stores is the most homogeneous across household types, consistent with the notion they provide a service that is demanded similarly across socioeconomic strata.
We use our estimated model to run counterfactuals highlighting how preference heterogeneity and the endogeneity of amenities interact to determine sorting and inequality. In our first counterfactual, we compare the equilibrium outcome of our baseline specification with heterogeneous preferences to one with homogeneous preferences. We show that heterogeneous preferences lead to more spatial sorting, as households have more neighborhood dimensions along which to sort. However, although heterogeneous preferences and endogenous amenities can reinforce each other to generate more sorting, they can also reduce welfare inequality across household types. Intuitively, if preferences over amenities are misaligned between two demographic groups, then they sort into different locations. This sorting increases the supply of their most preferred amenities, making neighborhoods more differentiated, such that the two groups avoid competing for housing in the same location. Thus, there are two mechanisms reducing the welfare gap across groups when preferences are heterogeneous and amenities are endogenous: tailored amenities and lower rental prices. Our findings complement the existing literature on spatial sorting and inequality by introducing two-way heterogeneity in the relationship between households and amenities.
In our second counterfactual, we evaluate the effect of STR entry on local residents' welfare. We disentangle these effects into (i) the direct effects on rent via the reduction in housing supply, and (ii) the indirect effects on amenities via the endogenous response of amenity supply to the increased tourist population. The key insight behind our results is that while all residents lose from higher rents, their losses may be compensated or amplified depending on how they value the changes in amenities the tourists bring along. Moreover, we show the correlation between income and preferences for the amenities tourists bring determines how regressive STR entry is. If the lowest-income (highest-income) groups dislike the amenities that tourists bring, then STR entry is more regressive (progressive). Finally, in our third counterfactual, we compare different forms of regulating mass tourism: through housing markets or amenity markets. Specifically, we compare a tax on short-term rentals to a tax on touristic amenities and show how the distributional impact of each policy lever depends on heterogeneity on both demand and supply sides of the amenities market.
Related Literature
Spatial equilibrium models date back to Rosen (1979) and Roback (1982) and are a benchmark to study spatial inequality across and within cities (Moretti (2013), Diamond (2016), Couture and Handbury (2020)). A subset of the literature focuses on the within-city margin, but typically remains silent on the exact mechanisms through which specific amenities are provided (Bayer, Ferreira, and McMillan (2007), Guerrieri, Hartley, and Hurst (2013), Ahlfeldt, Redding, Sturm, and Wolf (2015), Davis, Hartley, and Gregory (2019), Su (2022)). Recent studies impose structure on amenity provision, but often lack heterogeneity in residents' preferences over amenities or collapse amenities into a single quality index (Couture, Gaubert, Handbury, and Hurst (2024), Hoelzlein (2020), Miyauchi, Nakajima, and Redding (2021)). We contribute by allowing for preference heterogeneity over multiple and differentiated amenities, whose supply is microfounded through a market mechanism. We build upon the notion of “preference externalities”: demand-side preference heterogeneity can translate into differences in the variety of products supplied (George and Waldfogel (2003), Handbury (2021)). Similarly, we interpret neighborhoods as differentiated products where amenities play the role of endogenous product attributes, and highlight the implications for residential sorting and inequality.
Our paper also contributes to the literature on the STR industry, as well as tourism more broadly. There is extensive work on the effects of STR entry on the housing market (Sheppard and Udell (2016), Koster, Van Ommeren, and Volkhausen (2021), Garcia-López, Jofre-Monseny, Martínez-Mazza, and Segú (2020), Barron, Kung, and Proserpio (2021)) and hotel revenue (Zervas, Proserpio, and Byers (2017)). Farronato and Fradkin (2022) studied the effect of STR entry on competing hotel sector. Calder-Wang (2021) studied the distributional effects on the New York City rental market, focusing on rent effects but abstracting from amenity effects. Faber and Gaubert (2019) showed the importance of tourism in the economic development of the Mexican coastline. Finally, Allen, Fuchs, Ganapati, Graziano, Madera, and Montoriol-Garriga (2021) studied the effects of seasonal tourism on prices of goods and amenities borne by residents of Barcelona. We complement their work by simultaneously studying the effects of tourism on both residential and amenity markets, showing how they interact to shape urban inequality.
In terms of methods, we use discrete choice tools from the empirical industrial organization literature and show how they can be applied to urban residential markets (McFadden (1974), Berry (1994), Berry, Levinsohn, and Pakes (1995), Rust (1987)). Specifically, our dynamic estimation uses the Euler Equation in Conditional Choice Probabilities (ECCP) estimator (Hotz and Miller (1993), Arcidiacono and Miller (2011), Aguirregabiria and Magesan (2013), Scott (2013), Kalouptsidi, Scott, and Souza-Rodrigues (2021b)). The method has been applied to several contexts where dynamics are first order: agricultural markets (Scott (2013), Hsiao (2021)), occupational choice (Traiberman (2019), Humlum (2021)), and residential choice (Diamond, McQuade, and Qian (2019), Davis, Hartley, and Gregory (2019), Davis, Gregory, Hartley, and Tan (2021)).
2 Data
Individual-Level Data: Residential Histories and Socioeconomic Characteristics
Our individual-level microdata are from the statistical bureau of the Netherlands, Centraal Bureau voor de Statistiek (CBS). The key data set for our dynamic model is the residential cadaster, from which we construct a panel of residential history for the universe of individuals in the Netherlands. We also observe household-level demographics from tax return data: income, educational attainment, employment status, household composition, and ethnic background. We classify households as low-, medium-, or high-skill using educational attainment bins. Because we do not observe workplace nor occupations, our analysis focuses on residential market, rather than labor market outcomes. Further details are in Supplemental Appendix A.2.1 (Almagro and Domínguez-Iino (2025)).
Housing Unit Data: Tax Valuations, Tenancy Status, Physical Characteristics, Rental Prices, and Transaction Values
First, we obtain property values from a CBS tax appraisal panel for the universe of residential housing units for 2006–2020, which also includes geo-coordinates, quality measures, and the occupant's tenancy status (owner-occupied, rental, social housing). For the subset of these properties that are transacted, we can confirm that their tax appraisals are highly correlated with transaction prices (we observe all housing sale transactions in the Netherlands). Second, we obtain rental prices from a CBS national rent survey for 2006–2019. Since the survey does not cover the universe of tenants, we impute rental prices by linking it to the universe of tax appraisal valuations and employing a random forest, which outperforms traditional linear hedonic models (Mullainathan and Spiess (2017)). Imputation details are in Supplemental Appendix A.2.4.
Neighborhood-Level Data: Amenities, Demographic Changes, Tourist Inflows
We use two levels of geographic units based on Amsterdam's administrative divisions: 99 “wijk” (neighborhoods) that belong to 25 larger “gebied” (districts). An average wijk had roughly 8540 inhabitants as of 2018. After dropping unpopulated or industrial-use-only neighborhoods, we end up with 95 neighborhoods and 22 districts. We observe annual neighborhood-level outcomes from Amsterdam City Data (ACD) from 2008 to 2018. These outcomes include demographics (e.g., ethnic, income, and skill composition) and a rich set of consumption amenities. We also obtain city-level tourist inflows from ACD. The ACD wijk-level and Tourism data are publicly available at ACD BBGA (https://onderzoek.amsterdam.nl/dataset/basisbestand-gebieden-amsterdam-bbga) and ACD Tourism (https://data.amsterdam.nl/dossiers/dossier/toerisme/fdcc54a1-5aa7-4ddf-af16-1c28a99b8c5f/?term=toerisme).
For our estimation procedure and counterfactuals, we narrow down the set of amenities to six: restaurants, bars, food stores, non-food stores, nurseries, and “touristic amenities.” First, we chose these categories because they are available at a granular spatial unit for the whole time period in our sample (many categories are not reported every year nor at every administrative subdivision). Second, these categories likely vary in the extent to which they cater to tourists versus different types of locals. “Touristic amenities” is a category defined by ACD that includes tourist-oriented business such as travel agencies, cultural/recreational establishments, and lodging. We remove lodging from the original ACD definition because we treat hotels separately in our analysis—we consider them solely as accommodation for tourists rather than as a consumption amenity that could potentially be valued by both tourists and locals. Thus, our final measure of touristic amenities consists of consumption services that some locals may value, such as cultural/recreational establishments. Bars includes pub-style establishments that serve only alcohol, as well as cafe-style establishments that serve both coffee and alcoholic drinks, without being full-fledged restaurants. Food stores refers to establishments that sell food without service, such as a grocery or convenience store. Non-food stores refers to non-food commercial retail, such as clothing stores. Restaurants and nurseries are self-explanatory.
Short-Term Rental Listings
Airbnb holds over 80% of the STR market share in Amsterdam. Hence, throughout the paper, we use Airbnb and STR interchangeably. Our Airbnb data are from Inside Airbnb (http://insideairbnb.com/), an independent website providing monthly web-scraped listings data for many cities. Our data consist of listing-level observations with information such as geo-coordinates, prices per night, calendar availability, and reviews. We use this information to separately identify “active” from “dormant” STR listings, and to flag commercially-operated listings—those likely to be permanently rented to tourists, thus reducing housing supply for locals. We define commercial listings as entire-home listings with booking activity above a threshold. Classification details are in Supplemental Appendix A.2.7.
Final Sample: Time Period and Geographic Unit of Analysis
We construct an annual panel of location choices and characteristics for 2008–2018. For our dynamic model of locals' residential choices, we aggregate 95 neighborhoods (wijk) into 22 districts (gebied). Using larger geographical units allows us to estimate more precise conditional choice probabilities that feed into the estimation of the dynamic model. Because demand is at the district level, we also use districts in the estimation of amenity supply. Our estimation of housing supply and tourist demand only requires unconditional choice probabilities. Thus, for those cases, we use the smaller neighborhoods as spatial units, allowing us to obtain more precise estimates.
3 Stylized Facts
We present the stylized facts of our empirical setting and how they motivate our model's key features. We show tourism volume and STR penetration have grown over time and across neighborhoods, and how such growth correlates with our outcomes of interest: rental prices, consumption amenities, and the socioeconomic composition of residents. The role these tourism-induced compositional changes have in shaping local amenities, and how local residents respond to such amenity changes by moving, is what motivates our overarching question of how endogenous amenities interact with sorting across neighborhoods.
Fact 1: Tourists and STR Listings Have Grown Dramatically and Sprawled Across Amsterdam
Amsterdam has one of the highest tourist-to-local ratios in the world, above Florence and slightly below Venice (source: ESTA (https://www.official-esta.com/information/reports/cities-with-most-tourists)). Figure 1 shows that, between 2008 and 2017, the number of overnight stays per resident doubled, hotel capacity grew from approximately 22,000 to to 31,000 rooms, while STR listings grew from zero to over 25,000. The figure also shows the evolution of commercially-operated listings, which are available year-round and therefore comparable to hotel rooms in terms of nights-availability. By 2017, there were approximately 7000 of these listings, which is equivalent to 25% of the city's stock of hotel rooms.
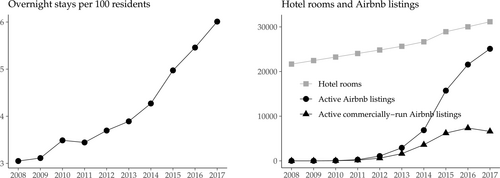
Overnight stays per resident, hotel rooms, and STR listings (2008–2017). Note: On the left, “overnight stays per 100 residents” is constructed as annual overnight stays (in hotels and STR) divided by population, and multiplied by 100—a value of 5 means that on an average night there are 5 tourists per 100 residents. On the right, active and commercial Airbnb listings are constructed from Inside Airbnb data using the procedure described in Supplemental Appendix A.2.7. Hotel, stay, and population data are from ACD Tourism (https://onderzoek.amsterdam.nl/dossier/toerisme?term=toerisme) and ACD BBGA (https://data.amsterdam.nl/datasets/rl6-35tFAw2Ljw/basisbestand-gebieden-amsterdam-bbga/).
Figure 2 shows commercial listings have sprawled to cover most of the city. By contrast, the spatial distribution of hotels remains mostly unchanged and clustered in the city center. This is partly due to zoning regulations that apply to hotels but not to the STR segment. At the aggregate level, commercially-operated STR listings represented 6% of the rental market in 2017, exceeding 20% in some central neighborhoods. These trends suggest the increasing presence of tourists as part of the city's population is significant enough to alter local housing and amenity markets.
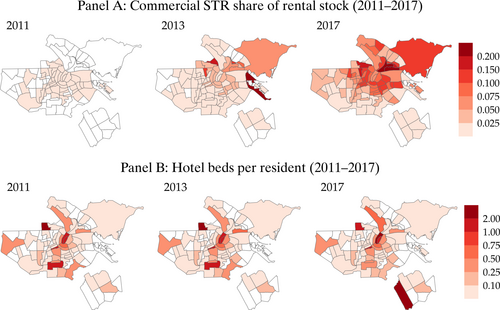
STR share of rental stock and hotel beds per resident (2011–2017). Note: Maps show neighborhood- (“wijk”) level outcomes. We construct commercial STR listings from Inside Airbnb data, using the procedure described in Supplemental Appendix A.2.7. Rental housing stock, hotel beds, and population data are from ACD BBGA (https://data.amsterdam.nl/datasets/rl6-35tFAw2Ljw/basisbestand-gebieden-amsterdam-bbga/). The rental stock corresponds to private market rental stock (i.e., we exclude social housing rentals).
Fact 2: Rents Have Increased More in Neighborhoods With More STR Entry
Table I shows the intensity of STR penetration is positively correlated with housing market outcomes. OLS regressions in the top panel show a 1% increase in a neighborhood's commercial STR listings is associated with a rent increase between 0.06–0.11%. These magnitudes are sizable given rents grew at an annualized rate of 1.02% between 2009–2019, and are also in line with recent studies estimating the effect of STR on housing market prices. For example, Barron, Kung, and Proserpio (2021) estimated an STR elasticity of rent of 0.018. The bottom panel of Table I repeats the regression exercise for sale prices, finding a 1% increase in commercial STR listings is associated with a house sale price increase between 0.04–0.11% in OLS specifications.
|
Ln (Rent/m2) |
||||||
|---|---|---|---|---|---|---|
|
OLS |
IV |
OLS |
IV |
OLS |
IV |
|
|
Ln (commercial Airbnb listings) |
0.065 |
0.091 |
0.051 |
0.114 |
0.109 |
0.205 |
|
(0.008) |
(0.021) |
(0.006) |
(0.021) |
(0.018) |
(0.093) |
|
|
Control variables |
X |
X |
X |
X |
||
|
District-year FE |
X |
X |
||||
|
First-stage F-stat |
586.89 |
384.21 |
69.66 |
|||
|
Observations |
770 |
770 |
763 |
763 |
763 |
763 |
|
Ln (House Sale Price) |
||||||
|---|---|---|---|---|---|---|
|
OLS |
IV |
OLS |
IV |
OLS |
IV |
|
|
Ln (commercial Airbnb listings) |
0.109 |
0.290 |
0.034 |
0.149 |
0.037 |
0.326 |
|
(0.016) |
(0.030) |
(0.006) |
(0.016) |
(0.022) |
(0.102) |
|
|
Control variables |
X |
X |
X |
X |
||
|
District-year FE |
X |
X |
||||
|
First-stage F-stat |
572.02 |
370.87 |
65.9 |
|||
|
Observations |
738 |
738 |
737 |
737 |
737 |
737 |
- Note: Observations are at the wijk (neighborhood) level. A “district” is a larger spatial unit than a neighborhood. Rent prices are neighborhood-average long-term rental prices constructed from CBS rent surveys. House sale prices are neighborhood average transaction values, constructed from CBS data covering the universe of housing transactions. Commercial Airbnb listings are constructed from the Inside Airbnb data (see Supplemental Appendix A.2.7 for construction details). Neighborhood-level control variables are: housing stock, average income, high-skill population share, all from ACD BBGA (https://data.amsterdam.nl/datasets/rl6-35tFAw2Ljw/basisbestand-gebieden-amsterdam-bbga/). Standard errors are clustered at the wijk level in parentheses.
The main endogeneity concern from the OLS results is that time-varying neighborhood-level unobservables correlate with both STR penetration and housing market prices, leading to biases that depend on the sign of such correlations. For example, if neighborhoods that are becoming more attractive to tourists are becoming less attractive to locals, then such areas will have more STR and lower rent, leading to downward-biased OLS estimates. Beyond including controls that likely correlate with such unobservables, we address these concerns with a shift-share instrument (Goldsmith-Pinkham, Sorkin, and Swift (2020), Borusyak, Hull, and Jaravel (2022)), a common research design in the literature measuring the impact of STR on housing markets (Barron, Kung, and Proserpio (2021), Garcia-López et al. (2020)).
The “shift” part of the instrument exploits time variation in worldwide demand for STR, as proxied by online search activity for Airbnb. The “share” part constructs neighborhood-level exposure to tourism by using the spatial distribution of historic monuments. Our exclusion restriction requires both factors to be orthogonal to time-varying and neighborhood-level unobservables, conditional on the rest of the covariates. First, Airbnb's worldwide popularity is unlikely to be informative of neighborhood-specific trends. Second, the spatial distribution of monuments determined centuries ago is unlikely to be informative of current trends affecting housing prices. Our results indicate the OLS estimates are downward-biased. This is consistent with the unobservables being positively correlated with Airbnb presence and negatively correlated with housing market prices, that is, they are likely dis-amenities for local residents.
Finally, note the reduced-form results from Table I capture the total impact of STR. This is a combination of (i) less housing supply for locals, which raises rents, and (ii) changes in amenities, which can raise or lower rents depending on how locals value such amenities. This limitation of the reduced-form analysis is what motivates our model, with which we aim to disentangle these two channels.
Fact 3: Amenities Have Tilted Toward Tourists and Away From Locals
Beyond the impact of STR on the housing market, the amenities surrounding the housing units have also changed as tourists become an increasing share of the city's population.
Figure 3 shows touristic amenities have grown across nearly all neighborhoods, although at different intensities, while amenities catering exclusively to locals, such as nurseries, have declined in most locations. Figure 4 confirms touristic amenities indeed locate in neighborhoods with high tourist intensity, and that their growth is negatively correlated with amenities that are clearly targeted to locals, such as nurseries. Overall, these patterns are consistent with tourists having different preferences over amenities than locals. As for the other four amenities displayed in Figure 3, they are likely in between the two extremes of touristic amenities and nurseries in the sense they would not a priori seem to cater solely to locals or solely to tourists, but likely to both. The purpose of our amenity supply model is to estimate the extent to which amenities such as these lie in between the two extremes, given the observed trends can be explained by both an increasing number of tourists arriving to the city and specific types of local residents departing.
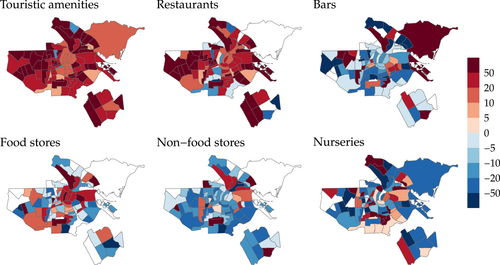
Evolution of consumption amenities (2011–2017 pp changes). Note: Maps show percentage point changes between 2011–2017 for each amenity sector. Data are from ACD BBGA (https://data.amsterdam.nl/datasets/rl6-35tFAw2Ljw/basisbestand-gebieden-amsterdam-bbga/).
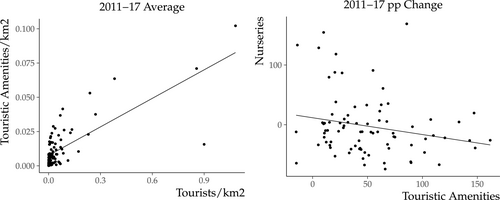
Spatial correlation between tourist-oriented and local-oriented amenities. Note: Left figure plots the 2011–2017 average tourist intensity versus touristic amenity intensity, for each neighborhood. Right figure plots the 2011–2017 percentage point change for nurseries versus touristic amenities, for each neighborhood. Nurseries decline in 58% of neighborhoods, with a median decline of −32%. Data are from ACD BBGA (https://data.amsterdam.nl/datasets/rl6-35tFAw2Ljw/basisbestand-gebieden-amsterdam-bbga/).
Fact 4: The Composition of Residents Has Changed Heterogeneously Across Neighborhoods
Figure 5 shows how socioeconomic composition has evolved in each neighborhood by displaying changes in the population shares of various demographic groups. The top panel shows a falling share of residents with Dutch background in most neighborhoods, except those around the city center. By contrast, the share of non-European immigrants has increased in a few central neighborhoods and mostly in the periphery. In terms of income heterogeneity, the middle panel shows the share of residents in the top 20% of the national income distribution has grown in central neighborhoods but not in the outskirts, indicating a rise in income inequality between the core and periphery. The bottom panel shows heterogeneity along household composition: households with children have become increasingly outnumbered by those without in most neighborhoods.1 To summarize, the heterogeneity in the socioeconomic make-up of neighborhoods and in their evolution over time motivates the heterogeneity in our model's demand primitives: rent elasticities, moving costs, and valuation of amenities.
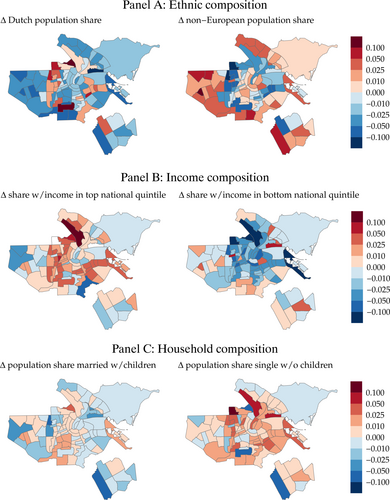
Changes in socioeconomic composition of neighborhoods (2011–2017). Note: Maps show changes in neighborhood population share of each group. Data are from ACD BBGA (https://data.amsterdam.nl/datasets/rl6-35tFAw2Ljw/basisbestand-gebieden-amsterdam-bbga/).
4 A Dynamic Model of an Urban Rental Market
Motivated by the previous facts, we build a dynamic model of a city's rental market that consists of (i) heterogeneous households and tourists making location decisions, (ii) landlords who can rent their units to locals or tourists, and (iii) a market for amenities that microfounds how the composition of amenities endogenously responds to the composition of locals and tourists.
Notation
We present the model in three steps. First, Section 4.1 shows how amenities are endogenously determined by the population composition . Second, Sections 4.2 and 4.3 show the reverse mapping—how population composition adjusts to amenities through location choices. Third, Section 4.4 brings the two mappings together by providing an equilibrium definition through which population composition and amenities are jointly determined.
4.1 Endogenous Amenities
This section shows how amenities are endogenously determined by residential composition. We present main results, relegating derivations to Supplemental Appendix A.3.1.
Demand for Amenities
Supply of Amenities
Equilibrium Amenities
4.2 Housing Supply
Let denote the total housing stock, measured in units of floor space, in location j and year t. We assume housing stock is inelastic in the short run and follows an exogenously determined path over time.3
Housing Supply in Each Location
4.3 Housing Demand
Demand for housing is composed of the demand from local residents and the demand from tourists staying in short-term rental units.
4.3.1 Demand From Locals
At the beginning of each period t, a household i chooses a residential location . Locations inside the city are indexed , while the outside option of leaving the city is denoted .
Moving Costs and Location Tenure
Individual State Variables
We denote as the vector of individual state variables that are observable to the econometrician: location and tenure . Households also face a vector of unobservable idiosyncratic preference shocks for each location, .
Aggregate State Variables
Flow Utility and Value Function
Location Choice and Evolution of the Population
Housing Demand From Locals in Each Location
4.3.2 Demand From Tourists
There is an exogenous number of tourists arriving into the city and choosing to stay in a short-term rental or a hotel.
Tourists in Short-Term Rentals
Tourists in Hotels
Housing Demand From Tourists in Each Location
4.4 Equilibrium
Definition. (Stationary Population Distribution)Given a vector of rental prices and a matrix of amenities , a stationary population distribution over locations and tenure is a vector for each type k that satisfies
Definition. (Stationary Equilibrium)A stationary equilibrium is:
- 1. a vector of long-term rental prices and a vector of short-term rental prices ,
- 2. a matrix of amenities , where is the vector defined in (2),
- 3. a stationary population distribution of locals over locations and tenure for each type k, which through (22) delivers the type-k population count across locations for ,
- 4. a vector of tourist population in short-term rentals,
such that:
- 1. the long-term rental market clears for every location,
where is long-term housing supply defined in (9) and is long-term housing demand defined in (15),
- 2. the short-term rental market clears for every location,
where is short-term housing supply, defined residually from the long-term market as in (10), and is short-term housing demand from tourists defined in (17),
- 3. the amenities market clears, by satisfying the mapping defined in (8),
where is the population composition of location j, consisting of local types 1 through K and tourists. The tourist population includes both those staying in short-term rentals as well as the (exogenous) tourist population staying in hotels, defined in (18) as .
A useful interpretation of the equilibrium definition is that conditions 1–2 determine the population distribution of locals and tourists through the clearing of rental markets, for a given distribution of amenities. On the other hand, condition 3 determines the distribution of amenities—as firms enter to clear amenities markets—while taking the population distribution as given. Hence, by combining conditions 1–2 with 3, the population, rents, short-term rental prices, and amenities are jointly and endogenously determined in equilibrium.
In models such as ours, where population composition can have local spillovers, equilibrium uniqueness is not guaranteed. Hence, we use the observed value of prices and amenities as the starting point of our equilibrium solver as a selection rule. In Supplemental Appendix A.4.2, we numerically show the equilibrium is locally unique under this rule.
5 Estimation
5.1 Defining Household Heterogeneity
We first classify households into three categories based on modal tenancy status: homeowners, private market renters, and social housing renters. First, ex ante classification step is motivated by the fact that the average household belongs to its modal category more than 90% of the time, suggesting this margin of adjustment is minor in our context. Second, it allows us to abstract away from the transition between renting and home-ownership. Third, it allows us to separately quantify welfare effects on homeowners and renters in our counterfactual analysis. Hence, we assume tenancy status is determined outside our model and constant over time.
After the first classification step, we classify households further into “types” using a k-means algorithm on demographics. Existing studies typically classify households into groups based on income or skill, while others incorporate additional dimensions, such as race, due to evidence that sorting does not only happen across income levels (Bayer et al. (2016), Davis, Hartley, and Gregory (2019)). When the set of demographic characteristics is large, the practitioner faces a variance-bias trade-off in defining such groups: having more groups captures more heterogeneity but results in fewer observations per group, leading to noisier estimates of choice probabilities. The k-means approach allows us to solve this trade-off in a data-driven manner by exploiting correlations across observables to reduce dimensionality. Further implementation details are in Supplemental Appendix A.6.1.
Results
Table II shows the six household types that result from our classification and summary statistics of their average characteristics. We give each group a label based on how prominent their characteristics are. For example, the “Students” group is characterized by being the youngest and lowest-income, while also being high-skilled and unlikely to have children. Among household types likely to have children, social housing tenants have the lowest income and are less likely to have a Dutch ethnic background. Moving up the income distribution, we have a group of middle-aged homeowners that do not have children, which we label as “Singles.” Next, we have a group of renters that are slightly older and wealthier, but have substantially more children, which we label as “Younger Families.” Finally, the highest-income group consists of older homeowners likely to have children, which we label as “Older Families.” Overall, the six types vary substantially along income, share with children, and age.
|
Group |
Homeowners |
Renters |
Social Housing Tenants |
|||
|---|---|---|---|---|---|---|
|
Older Families |
Singles |
Younger Families |
Students |
Immigrant Families |
Dutch Low Income |
|
|
Age |
44.59 |
37.84 |
40.56 |
28.42 |
55.12 |
38.52 |
|
Share with Children |
0.93 |
0.12 |
0.65 |
0.13 |
0.53 |
0.43 |
|
Share Low-Skilled |
3.20% |
2.42% |
6.08% |
5.40% |
99.91% |
0.02% |
|
Share Medium-Skilled |
3.01% |
5.87% |
2.28% |
11.33% |
0.09% |
16.95% |
|
Share High-Skilled |
93.79% |
91.71% |
91.65% |
83.27% |
0.00% |
83.02% |
|
Share Dutch Indies |
6.92% |
6.59% |
4.12% |
4.07% |
13.22% |
12.41% |
|
Share Dutch |
64.41% |
58.74% |
53.13% |
61.44% |
24.86% |
49.36% |
|
Share Non-Western |
18.76% |
21.43% |
21.64% |
19.48% |
57.96% |
30.37% |
|
Share Western |
9.91% |
13.23% |
21.12% |
15.01% |
3.96% |
7.87% |
|
Household Income (€) |
62,031.39 |
30,611.41 |
47,441.08 |
16,821.48 |
21,243.24 |
27,714.85 |
|
Income Pctl. |
77.04 |
45.59 |
64.64 |
0.23 |
33.41 |
42.17 |
|
Per Capita Income (€) |
40,155.65 |
27,609.21 |
35,058.39 |
15,162.83 |
15,167.45 |
21,179.13 |
|
Income Pctl. per Person |
73.42 |
52.84 |
65.83 |
26.34 |
26.69 |
42.10 |
|
Number of Households |
106,388 |
78,561 |
105,712 |
124,112 |
83,117 |
174,203 |
- Note: Table presents the groups resulting from k-means classification on mean demographic characteristics. We report average characteristics across households in each group. “Low-,” “medium-,” and “high-skilled” correspond to high school or less, vocation/selective secondary education, and college and above, respectively. Group names are chosen to serve as an easy-to-remember label and are not an outcome of the data.
Household Types Used in Estimation and Counterfactuals
We estimate the housing demand of local residents, presented in Section 4.3.1, for the first three groups: “Older Families,” “Singles,” and “Younger Families.” The reason for excluding “Students” and the two social housing types is that their residential choices are driven by non-market forces outside the scope of our model. The location choices of “Students” are largely determined by university policy. As for social housing tenants, their units are assigned through a centralized application system.
Despite the exclusion of these three groups in the housing demand estimation, we include all six groups—along with tourists in hotels and in short-term rentals—in the estimation of the amenity supply model described in Section 4.1. The reason is that while residential choices might not be primarily determined by market mechanisms for all groups, as indicated in the prior paragraph, the decisions of firms supplying consumption amenities do take into account all groups regardless of how they make their housing choices. Throughout this Section 5, we show our procedure estimates housing demand and amenity supply in separate and independent blocks: estimating amenity supply only requires neighborhood-level data on population composition, so our sample restriction on the microdata for estimating housing demand does not affect our amenity supply estimates.
Finally, for our counterfactuals, we include all six types of locals and tourists as part of our equilibrium definition. Because we do not have preference estimates for students and the two social renter types, we take their location choices as exogenously fixed to levels observed in the baseline data. Given we do not estimate preferences for these groups, we do not make any statements about their welfare effects in our counterfactuals. Our interpretation of keeping the locations of these groups fixed in counterfactuals is that their residential outcomes are determined by an allocation mechanism that does not respond to market forces. Therefore, our counterfactuals should be interpreted as addressing equilibrium responses from the part of the housing market that is determined through market mechanisms.
5.2 Amenities
Identification
First, similarly to Couture et al. (2024), we calibrate η. We solve our fully estimated model for a range of , which is based on the range of supply elasticities from Saiz (2010). We choose since it delivers the best model fit, corresponding to a housing supply elasticity of 0.66, the estimate for San Francisco in Saiz (2010).5 In Supplemental Appendix A.7.1, we show that the main takeaways from our counterfactuals are robust to the full range of .
The main identification problem in identifying from (24) is simultaneity arising from the equilibrium conditions. The expenditures by household type for a given location, , are the outcome of residential choices made based on the availability of amenities . Hence, any unobservable firm costs affecting will also affect (and thus ) in equilibrium. Because is an amenity supply shock, we require instruments that act as amenity demand shifters.
Implementation
Results
Our estimates for the parameters are shown in Table III and broadly align with expected differences in consumption patterns across demographic groups. First, the supply of Nurseries, which is likely the amenity most targeted to locals—and specifically those with children—responds most positively to the three family groups and least to Singles and Tourists. Second, Touristic Amenities respond strongly to Tourists, as expected, but also to Students and Singles that might plausibly have similar consumption patterns to those of Tourists. Third, Restaurants respond mostly to Singles, Students, and Tourists, while Bars respond mostly to Tourists. Fourth, Food Stores estimates are the most homogeneous in that they respond to all groups in similar magnitude. This is consistent with the notion that they provide products (groceries) that are demanded homogeneously across all socioeconomic strata. In terms of magnitudes, our parameter estimates imply an exogenous increase in the number of tourists city-wide by 10% would increase the number of firms in Touristic Amenities, Restaurants, Bars, Food Stores, Non-food Stores, and Nurseries by 2.3%, 0.5%, 2.3%, 0.9%, 2.9%, and 0%, respectively.
|
Touristic Amenities |
Restaurants |
Bars |
Food Stores |
Non-Food Stores |
Nurseries |
|
|---|---|---|---|---|---|---|
|
Older Families |
195.132 |
7.623 |
0.0 |
4.875 |
11.872 |
997.282 |
|
[0.0,507.572] |
[0.0,42.708] |
[0.0,0.0] |
[0.0,43.249] |
[0.0,59.013] |
[276.57,1933.37] |
|
|
Singles |
379.284 |
94.408 |
0.0 |
100.327 |
13.254 |
0.0 |
|
[0.0,2050.842] |
[0.0,394.792] |
[0.0,0.0] |
[0.0,387.739] |
[0.0,337.327] |
[0.0,0.0] |
|
|
Younger Families |
0.0 |
0.936 |
11.284 |
51.769 |
194.102 |
627.542 |
|
[0.0,0.0] |
[0.0,42.092] |
[0.0,52.539] |
[0.0,155.976] |
[34.436,367.68] |
[0.0,1605.014] |
|
|
Students |
968.243 |
396.4 |
22.944 |
125.976 |
2.652 |
226.429 |
|
[0.0,2332.0] |
[151.408,753.73] |
[0.0,147.192] |
[0.0,361.108] |
[0.0,151.533] |
[0.0,2292.879] |
|
|
Immigrant Families |
0.241 |
7.621 |
25.798 |
95.523 |
126.253 |
503.976 |
|
[0.0,0.0] |
[0.0,93.355] |
[0.0,82.216] |
[0.0,289.614] |
[0.0,428.495] |
[0.0,2176.451] |
|
|
Dutch Low Income |
109.857 |
8.142 |
0.0 |
7.607 |
0.204 |
0.0 |
|
[0.0,582.268] |
[0.0,88.955] |
[0.0,0.0] |
[0.0,100.956] |
[0.0,9.849] |
[0.0,0.0] |
|
|
Tourists |
758.024 |
397.5 |
211.574 |
137.194 |
718.797 |
0.0 |
|
[448.195,1062.898] |
[294.627,502.675] |
[142.194,292.815] |
[59.974,218.708] |
[536.993,958.326] |
[0.0,0.0] |
- Note: This table reports bootstrap results for coefficients from equation (24) using a three-way panel of 22 districts in Amsterdam for 2008–2018 over 500 draws. Parameters and fixed effects and are estimated via GMM, where we restrict parameters to be weakly positive as implied by the microfoundation of the amenity model in Supplemental Appendix A.3.1. The estimation procedure is outlined in Section 5.2 following a Bayesian-bootstrap with random Dirichlet weights. Total expenditure is measured in thousands of euros. Top rows indicate average estimates of the bootstrap samples. Results inside square brackets indicate 95% confidence intervals. We omit estimates of the location and time fixed effects.
Observe that, of the 42 coefficients in Table III, we have several zeros because our constrained optimization problem places some coefficients on the lower bound of zero. Our interpretation is that if a coefficient hits the lower bound, then it means the supply of sector-s amenities does not respond to the presence of type-k residents. Through the lens of our amenity demand model from Section 4.1, this non-response occurs because a coefficient of implies type-k agents do not spend any of their income on sector-s amenities. Choosing a lower bound larger than zero would ensure and thus guarantee positive amenity expenditure shares, but we choose not to do so because this would restrict the parameter space.
Finally, while we cannot directly test the exclusion restriction of equation (25), we can provide suggestive evidence that our instrument is uncorrelated with the unobservable component of fixed costs faced by firms. To the best of our knowledge, the main change in amenity regulations during 2008–2018 was a restriction in the operating hours of restaurant outdoor dining space in residential areas. These restrictions were imposed at the precinct level, a spatial unit larger than the districts at which we implement our estimation. Hence, we can use precinct-year fixed effects to control for the unobservable costs imposed by such regulations on the firms supplying amenities. In Supplemental Appendix A.7.2, we show that including precinct-year fixed effects does not significantly change our estimates from Table III. We interpret this as suggestive evidence that our instruments are not significantly correlated with the unobservable fixed costs faced by firms: if they were, the precinct-year fixed effects would have changed our results significantly, given we know that amenity regulations were indeed modified at the precinct level during this period.
5.3 Housing Demand
5.3.1 Housing Demand From Locals
We estimate preference parameters of local residents using the “Euler Equations in Conditional Choice Probabilities” (ECCP) estimator, building on Aguirregabiria and Mira (2010), Scott (2013), and Kalouptsidi, Scott, and Souza-Rodrigues (2021b). The method allows us to recover parameters without taking a stance on beliefs, computing value functions, or solving the equilibrium, thus reducing computational burden. We proceed to describe the assumptions required for the estimation procedure.
Assumptions
We assume the state variables follow a Markov process, along with the following standard assumptions:
- 1. Atomistic agents: the market-level state ω evolves according to a Markov process that is unaffected by individual-level decisions j or states ,
- 2. Conditional independence: the transition density for the Markov process factors as
- 3. Payoff to outside option: the flow payoff of living outside the city is normalized to zero, .6
Our ECCP estimator is a two-step estimator. First, we estimate conditional choice probabilities (CCP) directly from the data, using a multinomial logit that exploits information about the conditional state. We show in Supplemental Appendix A.6.4 that this approach reduces the finite sample bias relative to a non-parametric approach that estimates CCP using frequency estimators. Second, the CCP are plugged into a regression equation that relates differences in the likelihood of two different residential histories to differences in their flow payoffs. To derive this regression equation, we first introduce the concept of renewal actions.
Renewal Actions
Two paths of actions are said to exhibit finite dependence if after a finite number of periods, the distribution of future states is the same (Arcidiacono and Miller (2011)). In our model, finite dependence appears whenever two households living in different initial locations, j and , choose to move to the same new location . We call such an action a renewal action, because the location tenure is reset and the distribution of future states is the same for both households. Because expectations of future payoffs are unobservable to the econometrician, a key difficulty in estimating dynamic models is disentangling variation in current payoffs from continuation values. Renewal actions separate these two components by equalizing continuation values, thus leaving differences in choice probabilities being solely a function of differences in flow payoffs.
Concretely, let be the function that maps action j and state to current location capital. Consider the following path represented by Figure 6: let j and denote actions chosen at state , reaching states and , respectively, and let be a renewal action chosen at time .
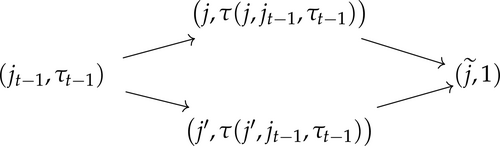
Depiction of path combinations used in the estimation.
The key observation is that at time , when two agents of the same type k choose the renewal action , they both move to the same individual state and hence their future expected payoffs are the same. Therefore, the value functions from each path cancel each other out at and disappear from equation (26), which states that differences in the likelihood of path relative to path are explained solely by differences in flow utility.
Parametric Assumptions on Flow Utility
Implementation
In practice, the locations in our empirical application are Amsterdam's 22 districts (“gebied”) and our sample period is 2008 to 2018. We define the outside option as any location outside Amsterdam, and our market as households that have lived in Amsterdam at least once between 2008 and 2020. We set our discount value β equal to 0.85 (De Groote and Verboven (2019), Diamond, McQuade, and Qian (2019)). We discretize the location tenure space similarly to Rust (1987), defining two bins of location capital: less than three years of tenure or more than four. Supplemental Appendix A.6.2 shows the technical details of the discretization of the state space. Overall, each group has a total of 46 states per year (23 past locations times two location capital states). We focus on the first three groups—Older Families, Single Households, and Younger Families—because their location choices are primarily driven by market forces, in contrast to households living in social housing or university housing. Note our Older Families and Singles groups are homeowners. In treating their location decisions in the same way as those of renters, we are implicitly assuming they are renting to themselves.
Identification
Results
Table IV shows estimates of the preference parameters in (29) over moving costs, location capital, rent, and consumption amenities for our main three groups. All groups exhibit that moving is costly, with costs that increase with distance between past and current location. All households benefit from the accumulation of location capital. Estimates for rent are negative throughout.
|
Dependent Variable: Relative Likelihood of Renewal Paths |
|||
|---|---|---|---|
|
Older Families |
Singles |
Younger Families |
|
|
High Location Capital |
0.187 |
0.210 |
0.264 |
|
(0.017) |
(0.013) |
(0.014) |
|
|
Intra-City Moving Cost |
−5.916 |
−5.337 |
−5.384 |
|
(0.015) |
(0.011) |
(0.012) |
|
|
Bilateral Moving Cost |
−0.067 |
−0.059 |
−0.041 |
|
(0.000) |
(0.000) |
(0.000) |
|
|
In/Out of City Moving Cost |
−4.407 |
−4.012 |
−4.043 |
|
(0.012) |
(0.009) |
(0.010) |
|
|
Log Rent |
−10.886 |
−2.310 |
−1.964 |
|
(1.205) |
(0.999) |
(1.028) |
|
|
Log Touristic Amenities |
−1.319 |
−0.496 |
0.317 |
|
(0.215) |
(0.182) |
(0.177) |
|
|
Log Restaurants |
0.288 |
0.735 |
−0.280 |
|
(0.346) |
(0.305) |
(0.286) |
|
|
Log Bars |
−0.757 |
−0.528 |
−0.104 |
|
(0.099) |
(0.085) |
(0.086) |
|
|
Log Food Stores |
−1.695 |
−1.216 |
−0.540 |
|
(0.327) |
(0.281) |
(0.282) |
|
|
Log Non-food Stores |
0.427 |
1.533 |
1.383 |
|
(0.356) |
(0.311) |
(0.302) |
|
|
Log Nurseries |
1.631 |
0.044 |
0.246 |
|
(0.173) |
(0.143) |
(0.147) |
|
|
N |
233,772 |
233,772 |
233,772 |
- Note: This table presents regression results of preference parameters for a dynamic location choice model for 22 districts for 2008–2019. We estimate preference parameters separately for three groups via two-step optimal GMM. The dependent variable is differences in path likelihoods after normalizing with respect to the outside option. After this normalization, each type has 46 possible states (23 past locations and two location capital categories), 22 possible actions, and 21 possible renewal actions over 11 years, which leads to 233,772 possible states and two-step path combinations. We omit exogenous controls—the log of social housing units and the log of the average apartment in square meters—for exposition. Two-step efficient GMM standard errors in parentheses.
Moving on to preferences over amenities, note the coefficients from (29) capture the sum of (i) a positive effect from the direct consumption of the amenity, and (ii) indirect spillovers that the amenity brings along (e.g., noise from bars) which can be negative. As discussed when we analyzed equation (28), this explains why the signs of the coefficients in Table IV can be negative.
Moving beyond the interpretation of the sign of the amenity coefficients, comparing the intensity of preferences across household types requires translating the estimates from Table IV into willingness to pay (WTP) measures. Concretely, the WTP of group k for amenity sector s is computed as the ratio . Using our WTP measure, the coefficients from Table IV imply that the two family groups are willing to increase their rent by roughly 0.14% in exchange for a 1% increase in the number of nurseries, while the WTP of singles for nurseries is only 0.02%. Restaurants show a positive and significant coefficient for Singles, with a WTP of 0.3% more in rent for a 1% increase in the number of restaurants. For the other groups, the WTP for restaurants is closer to zero. The first two groups perceive a net negative payoff from Touristic Amenities, while the Younger Families exhibit a positive one. In terms of economic magnitude, the first two groups have a WTP of 0.1% and 0.2% more in rent to avoid a 1% increase in Touristic Amenities, respectively. Non-food stores are positively valued by all groups, with the highest WTP for Younger Families. Coefficients for bars are negative for all groups, suggesting the presence of negative spillovers associated with these amenities, such as noise, that outweigh their consumption benefits. Finally, coefficients for food stores are negative for all groups. Despite the signs being negative, the ordering is fairly intuitive: the WTP of the family groups for food stores is higher (i.e., less negative) than for singles.
5.3.2 Housing Demand From Tourists
|
Dependent Variable: |
||||
|---|---|---|---|---|
|
Baseline |
Controlling for Reviews |
|||
|
Log Price Per Guest |
−2.723 |
(0.819) |
−2.659 |
(0.759) |
|
Log Touristic Amenities |
1.008 |
(0.377) |
0.837 |
(0.394) |
|
Log Restaurants |
0.048 |
(0.259) |
0.017 |
(0.243) |
|
Log Bars |
0.051 |
(0.154) |
0.056 |
(0.164) |
|
Log Food Stores |
−0.000 |
(0.300) |
0.037 |
(0.323) |
|
Log Nonfood Stores |
−0.229 |
(0.417) |
−0.185 |
(0.407) |
|
Log Nurseries |
−0.233 |
(0.137) |
−0.229 |
(0.136) |
|
Log Review Scores |
4.761 |
(3.696) |
||
|
N |
371 |
370 |
||
|
R2 |
0.529 |
0.537 |
||
- Note: Table reports estimates of tourists' preference for neighborhood (wijk-level) characteristics for a static model of location choice, using neighborhood-level data for 2015–2018. Construction of Airbnb supply and prices is described in Supplemental Appendix A.2. Wijk-level clustered standard errors in parentheses.
5.3.3 Connecting Amenity Demand and Supply Estimates to Equilibrium Sorting
Our model predicts several co-location patterns between household types and amenity sectors. If and , our model predicts positive assortative patterns between type-k households and the amenity s sector. On the contrary, if and , there is a negative assortative pattern: not only do type-k households move away from locations with amenity s, but their presence does not lead to amenity s entry. These two cases also create incentives of type k to co-locate together and, thus, act as an agglomeration force. The intermediate case in which and is analytically ambiguous in terms of sorting patterns. Moreover, in such a case, the endogeneity of amenities can be thought of as a congestion force similar to rent that makes type-k households disperse across locations. Given our range of estimates for and in Tables III and IV, we should see Older Families positively sort with Nurseries, Non-food Stores, and Restaurants. Singles should positively sort with Restaurants and Non-food Stores. Younger Families should positively sort with Nurseries and Non-food Stores. Finally, Tourists positively sort with Touristic Amenities and Bars.
5.4 Housing Supply
Instruments
OLS estimation leads to simultaneity bias from regressing quantities on prices. The solution is an instrument that shifts relative demand for short- versus long-term units. We use predicted tourist demand from a shift-share instrument: the “shift” part of the instrument exploits time variation in worldwide demand for STR as proxied by online search volume (Barron, Kung, and Proserpio (2021)), while the “share” part constructs neighborhood-level exposure to the shift from the historic spatial distribution of touristic attractions. The relevance condition is straightforward: higher predicted demand of tourists raises short- relative to long-term rental prices. The exclusion restriction holds as long as changes in the predicted tourist demand are uncorrelated with changes in the unobservable costs driving landlords' decisions. Intuitively, the exposure measure is unlikely to be correlated with changes in landlords' relative costs of renting short versus long term.
Results
For this section, we end our estimation sample in 2017 because by the end of this year the Amsterdam municipality began to restrict the number of nights that landlords could rent to tourists. We do this to estimate our housing supply elasticity during a period with a stable policy environment, thus avoiding changes in supply that are responding to regulatory changes rather than price changes. Table VI presents estimates for α, the landlord's marginal utility of income. OLS estimates are downward-biased compared to IV, as expected with simultaneity bias. Our preferred specification is the IV with two-way fixed effects, despite it being less significant than the others, which likely occurs due to little within-neighborhood variation in a short panel. Reassuringly, though, IV estimates are fairly stable across all specifications. In terms of economic significance, the results imply that an increase in the gap between STR prices and long-term rental prices of one standard deviation—which is equivalent to a 29% increase—would raise the market share of the short-term relative to the long-term segment by 13.6%.12
|
Dependent Variable: ln (LT Share) − ln (ST Share) |
||||
|---|---|---|---|---|
|
OLS |
IV |
IV |
IV |
|
|
LT price-ST price |
0.242 |
0.287 |
0.309 |
0.385 |
|
(0.099) |
(0.086) |
(0.091) |
(0.639) |
|
|
Year FE |
X |
X |
||
|
Wijk FE |
X |
|||
|
First-stage F-stat |
65.68 |
61.62 |
3.24 |
|
|
Observations |
275 |
275 |
275 |
275 |
- Note: Table reports estimates of landlords' marginal utility of income for a discrete choice model between the short- and long-term rental markets. Data are a panel with 92 locations 2015–2017. Prices are instrumented using a shift-share instrument (Barron, Kung, and Proserpio (2021)) that proxies for demand shocks. Wijk-level clustered standard errors in parentheses.
5.5 Model Fit
To wrap up our estimation section, we show how our model fits the data by simulating a stationary equilibrium for 2017. We assume agents have perfect foresight, we impose the demand shocks in steady state, we take our housing supply estimate from Section 5.4, and we calibrate landlords' differential costs to match the STR tourists in each location in 2017. Simulation details are in Supplemental Appendix A.4.1. Figures 7 and 8 plot the simulated endogenous objects—rents and amenities—against the observed objects in the data, showing our model explains a large portion of the variation in rent, STR prices, and amenities by only using variation in observable characteristics, as the unobservable components of our demand model, , are set equal to zero. Moreover, the slope of our simulated equilibrium objects and their data counterparts are not statistically different from 1 with the exception of Food and Non-food stores. We take these results as evidence that our model, estimated parameters, and equilibrium assumptions are a good approximation of the economic forces reflected in the data.
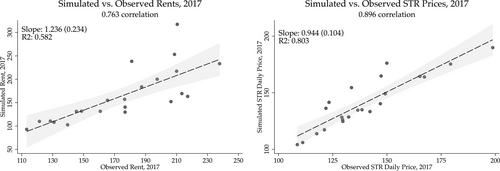
Model fit: rents and STR prices. Note: The figure presents scatter plots, linear fit, and 95% confidence intervals of simulated rents and STR prices, against observed rents and prices for 22 districts. Rents are in euros/m2 per year. STR prices are average daily prices.
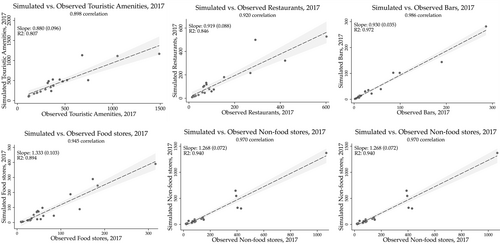
Model fit: amenities. Note: The figure presents scatter plots, linear fit, and 95% confidence intervals of the simulated number of amenities against the observed number of amenities for 22 districts. All units are levels.
6 Counterfactuals
6.1 Role of Preference Heterogeneity for Sorting and Inequality
First, we evaluate how preference heterogeneity interacts with the endogeneity of amenities to determine spatial sorting and inequality across residents. We solve the model using the estimates of our baseline heterogeneous preference specification and then compare equilibrium outcomes to those of a homogeneous preference specification. For the homogeneous case, we set preference parameters for consumption amenities to the average value across all household types, weighted by the size of groups.13 We measure sorting with the entropy index, a common measure of residential segregation across household types, with higher values corresponding to more segregation. We measure inequality as the ratio of the highest consumer surplus household (in euros) to that of the lowest consumer surplus household, with higher values corresponding to more inequality. Our qualitative insights are robust to other measures of inequality.
The left panel of Figure 9 shows segregation is higher when households have heterogeneous preferences for amenities, as they have more neighborhood dimensions along which to sort. The right panel of Figure 9 shows that, despite increased sorting, inequality is lower when preferences are heterogeneous. This empirical result is one of our main takeaways: although heterogeneous preferences and endogenous amenities reinforce each other to generate more spatial sorting, they can also reduce welfare inequality across household types. The intuition is that heterogeneous preferences lead to more sorting, which is amplified as amenities respond and make neighborhoods more differentiated. Household inequality can fall if preferences for amenities are heterogeneous because high-income groups do not compete with low-income groups for the same locations, allowing low-income groups to obtain their preferred amenities without having the high-income groups bid up their rents. Table VII conveys the neighborhood differentiation mechanism by showing that all amenities, except one, become more spatially clustered when preferences are heterogeneous, resulting in more differentiated neighborhoods.
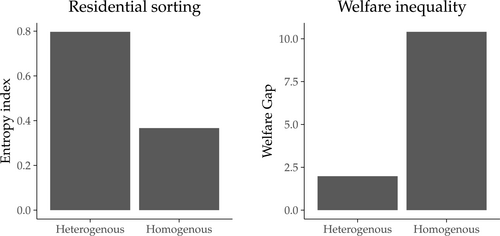
Role of preference heterogeneity for spatial sorting and inequality across households. Note: The left panel reports the entropy index, a measure of spatial segregation of household types: higher values indicate more segregation (see Supplemental Appendix A.5.6 for a formal definition). The right panel reports the ratio of the highest consumer surplus household (in euros) to that of the lowest household: higher values indicate more inequality.
|
Amenity |
Gini index for each preference specification |
HE-HO |
|
|---|---|---|---|
|
Homogeneous (HO) |
Heterogeneous (HE) |
||
|
Touristic amenities |
0.35 |
0.37 |
0.02 |
|
Restaurants |
0.43 |
0.56 |
0.13 |
|
Bars |
0.59 |
0.67 |
0.08 |
|
Food stores |
0.32 |
0.58 |
0.26 |
|
Non-food stores |
0.53 |
0.67 |
0.14 |
|
Nurseries |
0.51 |
0.41 |
−0.10 |
- Note: Columns “Homogeneous” and “Heterogeneous” report the Gini index for each amenity sector: how concentrated the number of establishments in each sector is across locations. Higher values indicate most of the sector's establishments are clustered in a few locations. Column HE-HO reports the difference between the “Heterogeneous” and “Homogeneous” columns. Positive values in the HE-HO column indicate the spatial distribution of the amenity becomes more clustered across space when preferences are heterogeneous.
6.2 Decomposing Welfare Effects of the Short-Term Rental Industry
In analyzing STR entry, our goal is to disentangle the welfare effects for residents into two components: the increase in rent due to the reduction in housing supply, and changes in amenities due to changes in the composition of amenity demand. To separate these effects, we proceed in three steps. First, we remove the landlords' STR option and solve for equilibrium rents and amenities , which we interpret as the pre-entry equilibrium. Second, we allow landlords to have an STR option but keep amenities fixed at the baseline , and only solve for rents and STR prices, r and p—the post-entry equilibrium with exogenous amenities. Finally, we allow landlords to have the STR option and simultaneously solve for rents , STR prices , and amenities —the post-entry equilibrium with endogenous amenities.
The left panel of Figure 10 shows the welfare effects from STR entry measured in consumption equivalent (CE) terms: how much extra income a household must be given in the pre-entry equilibrium to be as well off as in the counterfactual post-entry.14 Therefore, positive values indicate welfare gains from STR entry. The dark bars show that, under exogenous amenities, every household loses because STR entry reduces housing supply and raises rents. The magnitudes of the losses are similar across household types and equivalent to an income tax between 1–2%. The light bars show the welfare effects when amenities are allowed to endogenously respond to residential composition. The key insight is that while all residents lose due to higher rent, their losses may be compensated or amplified depending on how they value the changes in amenities tourists bring along. Older Families lose more than when amenities were exogenous because, on top of facing higher rent, they also lose the amenities they value most. On the other hand, Singles and Younger Families now obtain welfare gains because they face an increase in the amenities they like, offsetting losses from higher rent. This mechanism is clearest by looking at the right panel of Figure 10, which plots the correlation between a household type's preferences for amenities and the amenity changes they are exposed to following STR entry. The negative slope for Older Families implies they are losing access to the amenities they value most. The positive slope for the other groups implies they are gaining access to the amenities they value most.
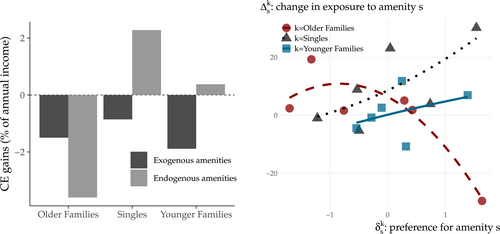
Decomposition of welfare effects from STR entry. Note: On the left panel, the consumption equivalent (CE) gains on the vertical axes are computed as how much extra income a household must be given in the baseline equilibrium to obtain the same utility as in the counterfactual equilibrium. Therefore, positive values indicate welfare gains due to STR entry. Details in Supplemental Appendix A.5.5. On the right panel, the horizontal axis shows preference parameters for amenity sectors. The vertical axis shows the change in exposure to amenity s after STR entry for a type-k household, defined as , where ΔNsj is the change in sector-s amenities in location j after STR entry, weighted by , location j's share of the city-wide population of type k before STR entry. Hence, is type k's exposure to location j.
Finally, Figure 11 maps the changes in amenities across space and the baseline exposure of each household type to such changes. Note touristic amenities and bars expand the most in locations originally populated by Older Families, and that this group ranks these two amenities among its three least desirable, which explains this group's negative slope in the right panel of Figure 10.
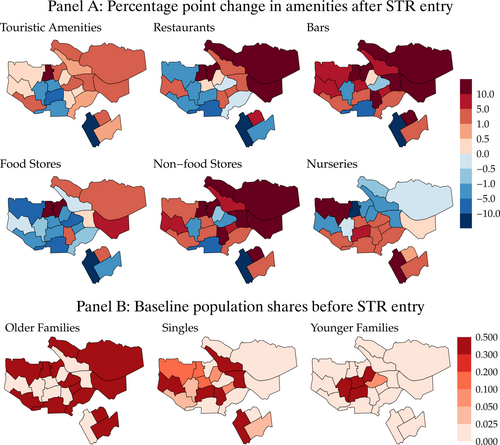
Effect of STR entry on amenities and baseline distribution of households. Note: Panel A shows changes in the number of establishments by amenity sector after STR entry. Panel B shows the baseline neighborhood population share of each household type before STR entry, that is, a measure of exposure to the amenity changes from Panel A. To facilitate comparison between equilibria, we always initialize our equilibrium solver from Supplemental Appendix A.4.1 with the observed vectors of rents and amenities.
As a final takeaway, note Older Families are the highest-income group and are subject to a welfare loss equivalent to a 4% income tax according to Figure 10. Singles and Younger Families, which are poorer, are subject to welfare gains ranging between 1–2% of their income. In this sense, STR entry is progressive because the higher-income group is implicitly taxed at a higher rate. Note this progressive pattern did not hold with exogenous amenities, since the implicit tax was highest on Younger Families, the middle-income group. In this sense, accounting for the endogeneity of amenities can matter for incidence qualitatively, not just quantitatively.
6.3 Policy Implications for Targeting of Amenities
Given our model has both amenity and housing markets, we can compare urban policies that operate separately through each of them. For the purposes of regulating mass tourism, consider two policy levers: a short-term rental (STR) tax or a touristic amenities (TA) tax. The STR tax is a housing policy: its goal is to increase housing supply for locals and improve welfare through rent reductions. The TA tax is an amenity-market policy: it targets certain amenities without directly altering others, but may do so indirectly through equilibrium effects.
Figure 12 shows how welfare changes as we gradually increase the tax rate, for each type of tax. First, note that the welfare of all groups is monotonically increasing in the STR tax because the policy reduces rent, and all groups agree they prefer lower rent. However, the rate at which welfare increases is highest for Older Families, since the reduction in STR units also leads to fewer tourists and touristic amenities, and they especially dislike touristic amenities relative to the other groups.
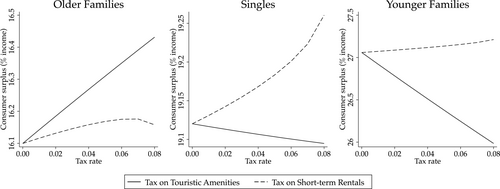
Welfare effects: short-term rental tax versus touristic amenity tax. Note: The figure reports consumer surplus (measured as % of income) for each household type under each tax rate.
Second, the shared monotonicity of the tax rate does not hold for the TA tax because the groups disagree on this amenity's desirability. While the welfare of Older Families is increasing, the welfare the other groups is decreasing. This is because Older Families especially dislike touristic amenities and Younger Families value them positively. The case of Singles is more nuanced because they dislike touristic amenities yet somehow lose as the TA tax is increased. The reason is they highly value restaurants, which tend to co-locate with touristic amenities. To see this, note from our amenity supply estimates in Table III that the supply of touristic amenities and restaurants coincide in that they respond strongly to Singles and Tourists. Taxing touristic amenities leads to fewer Tourists, lowering the supply of restaurants, thus hurting Singles. This highlights the importance of understanding heterogeneity in supply responses of amenities in addition to preference heterogeneity.
To conclude, the incidence of regulating the housing or the amenity market hinges on both preference heterogeneity and supply-side heterogeneity. Therefore, the choice of which policy lever to use depends on the interaction between preference and supply correlations and the distributional objectives of a regulator.
7 Concluding Remarks
We study the role of preference heterogeneity over a set of endogenous location amenities in shaping within-city sorting and welfare inequality. To do so, we build a model of residential choice where heterogeneous, forward-looking households consume a bundle of amenities provided by firms in a market for non-tradables. In contrast to work that collapses amenities into a one-dimensional index, we microfound how different consumption amenities arise in equilibrium, endogenizing the extent to which neighborhoods become horizontally differentiated.
Our empirical findings suggest substantial heterogeneity in the preferences of residents for different amenities, as well as in the supply responses of different types of amenities to local demographics. We find that while the endogeneity of amenities reinforces sorting across space, it has ambiguous effects on inequality across households. Concretely, inequality can fall when neighborhoods become horizontally differentiated through the endogenous response of amenities to the sorting of households. Thus, low-income households may sort into neighborhoods only they find desirable, without high-income households bidding up their rents. We also show how the distributional incidence of urban policies depends on heterogeneity on both the demand and supply side of the amenities market. While our model is rich in many dimensions, it is tailored to answer a specific set of questions while remaining silent on others. In our concluding remarks, we discuss the limitations of our analysis and potential extensions for future work.
Amenity Quality
We do not consider quality differences within an amenity sector because we do not have the firm-level data required to incorporate this dimension. Hence, in our model, amenities are only differentiated horizontally. If we had quality data, then the nature of differentiation across amenities would be a mix of horizontal and vertical dimensions. How would this affect our takeaways? Note our counterfactual in Section 6.1 speaks to this because it shows how the degree of horizontal differentiation (measured as the degree of preference heterogeneity) matters for sorting and inequality. To the extent adding amenity quality is a way of dampening horizontal in favor of vertical differentiation, because quality is desired by all groups, we would expect our results to qualitatively change in the direction of the case of homogeneous preferences—there would be less scope to reduce inequality through sorting and the horizontal differentiation of neighborhoods.
Non-Stationarity and Transitional Dynamics
The role of our model's dynamic elements is to estimate unbiased preference parameters (Bayer et al. (2016), Traiberman (2019)). To highlight economic mechanisms, our counterfactuals focus on stationary equilibria. The reason is that we are interested in long-run changes that result from the interaction between preference heterogeneity and endogeneity of amenities. It is the cross-sectional correlation between preferences over amenities and supply responses of amenities to demographics that is at the core of our economic mechanisms. It is unclear a priori that introducing transitional dynamics would significantly change the qualitative nature of our mechanisms, beyond separately quantifying short- versus long-run impacts. Given the stationary analysis already imposes substantial technical complexity, as well as conceptual complexity in understanding how each model ingredient contributes to economic mechanisms, we leave transitional dynamics as an interesting avenue for future research.
Consuming Amenities Outside the Residential Location
We assume consumers only access amenities in their residential location. An empirical application that relaxes this assumption requires data on consumption trips across neighborhoods, which we do not have for Amsterdam. Note that our mechanisms are driven by the positive correlation between residential location and amenity consumption. Under our assumption of no commuting to consume, the correlation is perfect. Allowing for commuting would weaken this relationship, but part of the correlation would survive as long as commuting costs depend on distance from home. While we cannot quantify such costs in our setting due to data limitations, smartphone-based evidence from other cities suggests urban residents tend to consume amenities located near their home (Miyauchi, Nakajima, and Redding (2021), Allen et al. (2021)). To the extent this positive correlation between residential location and amenity consumption is also valid in our setting, we expect our main qualitative insights to hold. Finally, abstracting away from the commuting-to-consume margin is likely to be less problematic for the fairly large spatial units used in our analysis, although it is worth noting the use of larger units may reduce the scope for horizontal differentiation.




