Strong Duality in Monopoly Pricing
Abstract
The main result in Daskalakis, Deckelbaum, and Tzamos (2017) establishes strong duality in the monopoly problem with an argument based on transportation theory. We provide a short, alternative proof using linear programming.
The question of how a monopoly should sell its wares to maximize profit is, mathematically, an optimization program in infinite dimensions because the optimization variable, the selling mechanism, is a function of the buyer's valuations, a continuum. When private information is one-dimensional, the answer was provided, famously, by Myerson (1981): the form of the optimal mechanism is independent of the seller's prior distribution of buyer's valuations. When private information is multi-dimensional, as is usual when the monopoly has multiple objects to sell, the form of the optimal mechanism depends fundamentally on the prior distribution (Manelli and Vincent (2007)). This highlights the need for methods to identify the optimal mechanism for classes of prior distributions. Daskalakis, Deckelbaum, and Tzamos (2017), henceforth DDT, is an important contribution in this regard. Their main result, Theorem 2, establishes that the value of the primal program equals the value of its dual; that is to say, strong duality holds. Their proof is complex and long; its outline follows the proof of the Monge–Kantorovich duality presented in Villani (2009), with technical variations due to convexity constraints.
We provide an alternative proof of strong duality as a direct consequence of duality in linear programming. To this end, we use a result in Gretsky, Ostroy, and Zame (2002). In the rest of this essay, we present the economic environment, introduce preliminaries, set the primal and dual programs, state and prove our theorem, and conclude with remarks.
First, we offer a sketch of the economic question and its formalization. A fuller treatment can be found in McAfee and McMillan (1988) and in Rochet and Choné (1998). The N-vector of buyer's valuations 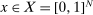 , one valuation per available good, is private information of the buyer and distributed according to a density function f that is continuous and differentiable with bounded derivative. The buyer's preferences are linear in value and money. The seller maximizes her expected revenue. A direct revelation mechanism is a pair of functions specifying probabilities of trade and a transfer payment for every possible buyer's report such that the buyer's optimal choice is to report valuations truthfully. Using a well-known characterization of incentive compatibility (for instance, Rochet (1987), Rochet and Choné (1998)), a mechanism may be defined by a continuous, convex utility function
, one valuation per available good, is private information of the buyer and distributed according to a density function f that is continuous and differentiable with bounded derivative. The buyer's preferences are linear in value and money. The seller maximizes her expected revenue. A direct revelation mechanism is a pair of functions specifying probabilities of trade and a transfer payment for every possible buyer's report such that the buyer's optimal choice is to report valuations truthfully. Using a well-known characterization of incentive compatibility (for instance, Rochet (1987), Rochet and Choné (1998)), a mechanism may be defined by a continuous, convex utility function 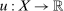 whose gradient
whose gradient 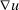 , where defined, is the vector of probabilities of trade for each of the N goods. As a vector of probabilities,
, where defined, is the vector of probabilities of trade for each of the N goods. As a vector of probabilities, 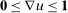 . Hence u is non-decreasing and satisfies a 1-Lipschitz constraint,
. Hence u is non-decreasing and satisfies a 1-Lipschitz constraint, 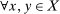 ,
, 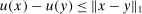 . The function
. The function 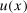 is the buyer's expected utility when her valuation is x. Individual rationality, the requirement of a non-negative utility for every type of buyer, is captured by the equation
is the buyer's expected utility when her valuation is x. Individual rationality, the requirement of a non-negative utility for every type of buyer, is captured by the equation 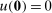 which also implies that no unnecessary surplus will be left for the buyer. The seller's revenue when the buyer reports x is
which also implies that no unnecessary surplus will be left for the buyer. The seller's revenue when the buyer reports x is 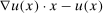 .
.
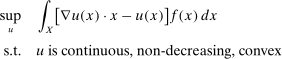 (1)
(1) (2)
(2)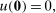 (3)
(3)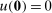 suffices to guarantee individual rationality, wrote
suffices to guarantee individual rationality, wrote 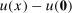 in the objective function and maximized over all continuous, convex, non-decreasing functions u. We chose instead to include
in the objective function and maximized over all continuous, convex, non-decreasing functions u. We chose instead to include 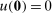 in the feasible set.) Per DDT equations (2), (3), and DDT Theorem 1, there is a signed Radon measure μ on X such that
in the feasible set.) Per DDT equations (2), (3), and DDT Theorem 1, there is a signed Radon measure μ on X such that 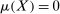 and for all u satisfying (1)–(3),
and for all u satisfying (1)–(3),
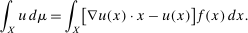 (4)
(4)Second, we introduce the relevant spaces, an order on each space, and functions to represent the constraints. Let 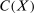 be the space of continuous, real-valued functions on X with the sup norm
be the space of continuous, real-valued functions on X with the sup norm  . Let
. Let 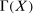 be its dual, the space of signed Radon measures with the variation norm
be its dual, the space of signed Radon measures with the variation norm 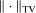 . Bilinear forms are represented by
. Bilinear forms are represented by 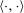 .
.
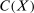 ,
, 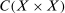 ,
, 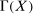 , and
, and 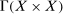 respectively:
respectively:
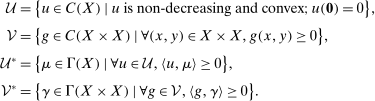
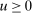 if
if 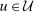 ,
, 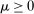 if
if 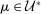 ,
, 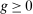 if
if 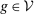 , and
, and 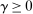 if
if 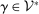 . (In contrast to DDT's use of the same symbol, our definition of
. (In contrast to DDT's use of the same symbol, our definition of 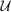 includes the constraint
includes the constraint 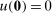 . This difference is immaterial in the seller's problem and we will show later that it is equally inessential in the dual program.)
. This difference is immaterial in the seller's problem and we will show later that it is equally inessential in the dual program.)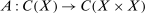 and
and 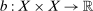 defined by
defined by
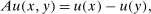 (5)
(5)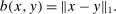 (6)
(6)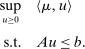 (7)
(7)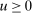 means
means 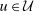 and captures (1) and (3); and (7) is the 1-Lipschitz constraint (2). Thus, this program is the seller's problem and corresponds to DDT Theorem 1-(4).
and captures (1) and (3); and (7) is the 1-Lipschitz constraint (2). Thus, this program is the seller's problem and corresponds to DDT Theorem 1-(4).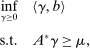 (8)
(8)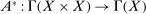 is the adjoint of A. This is the dual in DDT Theorem 2. To see this, consider first the objective function. Recall that
is the adjoint of A. This is the dual in DDT Theorem 2. To see this, consider first the objective function. Recall that 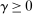 means
means 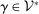 . The set
. The set 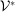 is the set of positive measures Dunford and Schwartz (1988, p. 262) which DDT denoted by
is the set of positive measures Dunford and Schwartz (1988, p. 262) which DDT denoted by 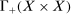 . The function b is defined in (6). Thus, our objective function is the function in the right side of DDT Theorem 2-(5). We now show that (8) is equivalent to the convex domination constraint in DDT. For any
. The function b is defined in (6). Thus, our objective function is the function in the right side of DDT Theorem 2-(5). We now show that (8) is equivalent to the convex domination constraint in DDT. For any  ,
,  ,
,
 and
and 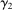 are the marginal distributions of γ, that is, for any measurable
are the marginal distributions of γ, that is, for any measurable 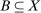 ,
, 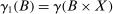 and
and 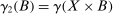 ; and the last two lines are notation. We conclude that
; and the last two lines are notation. We conclude that 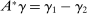 and hence (8) can be written as
and hence (8) can be written as 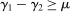 . By definition of the relevant order, this means
. By definition of the relevant order, this means
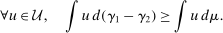 (9)
(9)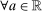 ,
, 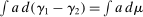 because
because 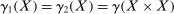 and
and 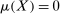 . Since (9) holds for any
. Since (9) holds for any 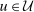 and for any constant function u, it holds for any continuous, non-decreasing, convex u even if
and for any constant function u, it holds for any continuous, non-decreasing, convex u even if 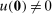 . This is precisely
. This is precisely 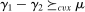 in DDT's notation.
in DDT's notation.Fourth, we state and prove our theorem.
Theorem.The value of the dual equals the value of the primal and both primal and dual have an optimal solution.
To prove the theorem, we parameterize the primal. For 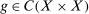 , define
, define 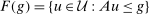 and
and 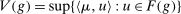 . Thus,
. Thus, 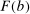 and
and 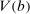 are the primal's feasible set and value.
are the primal's feasible set and value.
We establish first that 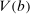 is finite and there exists
is finite and there exists 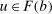 such that
such that 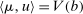 . The set
. The set 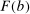 is non-empty since it contains
is non-empty since it contains 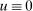 . It is equicontinuous and uniformly bounded because every
. It is equicontinuous and uniformly bounded because every 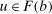 is 1-Lipschitz by equation (7) and
is 1-Lipschitz by equation (7) and 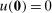 . It is closed because uniform convergence preserves continuity, convexity, and monotonicity. The Arzelà–Ascoli theorem (Dunford and Schwartz (1988, Theorem IV.6.7)) implies that it is compact. Since the objective function is continuous, it attains a maximum.
. It is closed because uniform convergence preserves continuity, convexity, and monotonicity. The Arzelà–Ascoli theorem (Dunford and Schwartz (1988, Theorem IV.6.7)) implies that it is compact. Since the objective function is continuous, it attains a maximum.
It remains to prove that there is no duality gap and that the dual has an optimal solution. Theorem 1 in Gretsky, Ostroy, and Zame (2002) establishes that this is so if and only if the subdifferential of 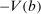 at b is non-empty. (Gretsky, Ostroy, and Zame defined the primal as a minimization, and thus its value function is convex. We chose to represent the primal as a maximization given its underlying economic interpretation. It is therefore
at b is non-empty. (Gretsky, Ostroy, and Zame defined the primal as a minimization, and thus its value function is convex. We chose to represent the primal as a maximization given its underlying economic interpretation. It is therefore 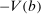 that is convex and that must have a non-empty subdifferential at b.) The lemma completes the proof of the theorem.
that is convex and that must have a non-empty subdifferential at b.) The lemma completes the proof of the theorem.
Lemma.The subdifferential of 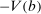 at b is non-empty.
at b is non-empty.
Proof.It suffices to show that 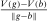 is bounded above (Condition 3, page 266 in Gretsky, Ostroy, and Zame (2002)). To this end, for any
is bounded above (Condition 3, page 266 in Gretsky, Ostroy, and Zame (2002)). To this end, for any 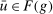 , we construct
, we construct 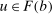 such that
such that 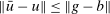 .
.
Given 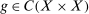 and
and 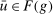 , define, for
, define, for 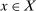 ,
,
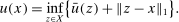 (10)
(10)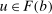 . By Theorem 1 in Rockafellar (1974), u is convex because
. By Theorem 1 in Rockafellar (1974), u is convex because 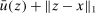 is convex in
is convex in 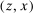 .
.For the remainder of the proof, fix any 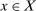 . Since
. Since 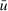 is continuous, the infimum is attained in (10). Therefore, pick
is continuous, the infimum is attained in (10). Therefore, pick 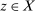 so that
so that 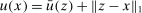 . Then
. Then
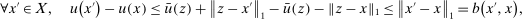
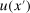 , and the second one by the triangle inequality. This shows that
, and the second one by the triangle inequality. This shows that 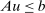 .
.To see that u is non-decreasing, note that, for any 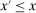 ,
,
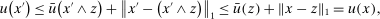
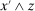 is the componentwise minimum of
is the componentwise minimum of 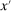 and z. The first inequality follows by (10) for
and z. The first inequality follows by (10) for 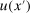 . The second inequality follows because
. The second inequality follows because 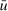 is non-decreasing and because
is non-decreasing and because 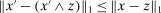 (if
(if 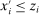 ,
, 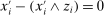 ; if
; if 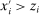 , then
, then 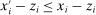 since
since 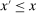 ).
).Since 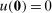 , we have verified that
, we have verified that 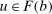 .
.
Finally, 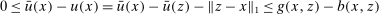 , where the first inequality follows by (10) for
, where the first inequality follows by (10) for 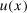 and the second one because
and the second one because 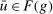 and
and 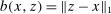 . This shows that
. This shows that 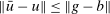 . Since μ is bounded,
. Since μ is bounded, 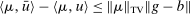 and thus
and thus 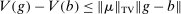 . Hence,
. Hence, 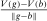 is bounded above and the subdifferential of −V is non-empty at b. □
is bounded above and the subdifferential of −V is non-empty at b. □
Last, we conclude with some comments.
A well-known sufficient condition for strong duality is the existence of 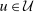 such that
such that  lies in the interior of
lies in the interior of 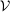 (see, for instance, Luenberger (1969, Theorem 1, page 217)). In some programs, this interiority condition fails because the analogue of the cone
(see, for instance, Luenberger (1969, Theorem 1, page 217)). In some programs, this interiority condition fails because the analogue of the cone 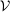 has an empty interior. In our application,
has an empty interior. In our application, 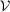 has a non-empty interior but the condition still fails because the operator A places Au on the boundary of
has a non-empty interior but the condition still fails because the operator A places Au on the boundary of 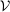 :
: 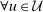 ,
, 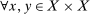 with
with 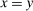 ,
, 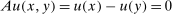 .
.
Some of the ideas in Gretsky, Ostroy, and Zame (2002) appear in Rockafellar (1974, Theorems 7 and 16), which characterize strong duality in general convex programs using variational methods, and in Theorem 18, which states sufficient conditions for strong duality. Mitter (2008) also considered general convex programs and provided, among other things, sufficient conditions for strong duality based on perturbations along feasible directions.
With the inclusion of 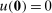 in the definition of
in the definition of 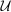 ,
, 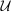 becomes a pointed cone, and therefore Gretsky, Ostroy, and Zame (2002) may be applied directly. Shapiro (2010, Proposition 2.5), obtains an analogous result to Gretsky, Ostroy, and Zame's for linear programs with cone constraints where the cones need not be pointed.
becomes a pointed cone, and therefore Gretsky, Ostroy, and Zame (2002) may be applied directly. Shapiro (2010, Proposition 2.5), obtains an analogous result to Gretsky, Ostroy, and Zame's for linear programs with cone constraints where the cones need not be pointed.
The measure μ in the objective function of the primal was derived from economic primitives. Our theorem applies to any signed Radon measure μ, not just those obtained from economic primitives.




