The Macroeconomic Impact of Microeconomic Shocks: Beyond Hulten's Theorem
Abstract
We provide a nonlinear characterization of the macroeconomic impact of microeconomic productivity shocks in terms of reduced-form nonparametric elasticities for efficient economies. We also show how microeconomic parameters are mapped to these reduced-form general equilibrium elasticities. In this sense, we extend the foundational theorem of Hulten (1978) beyond the first order to capture nonlinearities. Key features ignored by first-order approximations that play a crucial role are: structural microeconomic elasticities of substitution, network linkages, structural microeconomic returns to scale, and the extent of factor reallocation. In a business-cycle calibration with sectoral shocks, nonlinearities magnify negative shocks and attenuate positive shocks, resulting in an aggregate output distribution that is asymmetric (negative skewness), fat-tailed (excess kurtosis), and has a negative mean, even when shocks are symmetric and thin-tailed. Average output losses due to short-run sectoral shocks are an order of magnitude larger than the welfare cost of business cycles calculated by Lucas (1987). Nonlinearities can also cause shocks to critical sectors to have disproportionate macroeconomic effects, almost tripling the estimated impact of the 1970s oil shocks on world aggregate output. Finally, in a long-run growth context, nonlinearities, which underpin Baumol's cost disease via the increase over time in the sales shares of low-growth bottleneck sectors, account for a 20 percentage point reduction in aggregate TFP growth over the period 1948–2014 in the United States.
1 Introduction
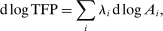
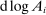 is a shock to producer i and
is a shock to producer i and 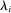 is its sales share or Domar weight.
is its sales share or Domar weight.Hulten's theorem is a cornerstone of productivity and growth accounting: it shows how to construct aggregate TFP growth from microeconomic TFP growth, and provides structurally-interpretable decompositions of changes of national or sectoral aggregates into the changes of their disaggregated component industries or firms. It also provides the benchmark answers for counterfactual questions in structural models with disaggregated production.
The surprising generality of the result has led economists to de-emphasize the role of microeconomic and network production structures in macroeconomic models. After all, if sales summarize the macroeconomic impact of microeconomic shocks and we can directly observe sales, then we need not concern ourselves with the details of the underlying disaggregated system that gave rise to these sales. Since it seems to imply that the very object of its study is irrelevant for macroeconomics, Hulten's theorem has been something of a bugbear for the burgeoning literature on production networks.
Are these conclusions warranted? Even at a purely intuitive level, there are reasons to be skeptical. Take, for example, shocks to Walmart and to electricity production. Both Walmart and electricity production have a similar sales share of roughly 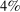 of U.S. GDP. It seems natural to expect that a large negative shock to electricity production would be much more damaging than a similar shock to Walmart. Indeed, this intuition will be validated by our formal results. Yet it goes against the logic of Hulten's theorem which implies that, because the two sectors have the same Domar weight, the two shocks should have the same impact on aggregate output.
of U.S. GDP. It seems natural to expect that a large negative shock to electricity production would be much more damaging than a similar shock to Walmart. Indeed, this intuition will be validated by our formal results. Yet it goes against the logic of Hulten's theorem which implies that, because the two sectors have the same Domar weight, the two shocks should have the same impact on aggregate output.
In this paper, we challenge the view that the macroeconomic importance of a microeconomic sector is summarized by its sales share and, more broadly, the notion that the microeconomic details of the production structure are irrelevant for macroeconomics. The key is to recognize that Hulten's theorem only provides a first-order approximation. Nonlinearities can significantly degrade the quality of the first-order approximation for large enough shocks. To capture these nonlinearities, we provide a general second-order approximation by characterizing the derivatives of Domar weights with respect to shocks. The second-order terms are shaped by the microeconomic details of the disaggregated production structure: network linkages, microeconomic elasticities of substitution in production, microeconomic returns to scale, and the degree to which factors can be reallocated.
Our results are general in that they apply to any efficient general equilibrium economy. They suggest that Cobb–Douglas models, commonly used in the production-network, growth, and multi-sector macroeconomics literatures, are very special: the Domar weights, and more generally the whole input–output matrix, are constant and can be taken to be exogenous, the first-order approximation is exact, the model is log-linear, and as a result, the microeconomic details of the production structure are irrelevant.1 These knife-edge properties disappear as soon as one deviates from Cobb–Douglas: the Domar weights, and more generally the whole input–output matrix, respond endogenously to shocks, and the resulting nonlinearities are shaped by the microeconomic details of the production structure.
- 1. Using a calibrated structural multi-industry model with realistic complementarities in production, we find that nonlinearities amplify the impact of negative sectoral shocks and mitigate the impact of positive sectoral shocks.2,3 Large negative shocks to crucial industries, like “oil and gas,” have a significantly larger negative effect on aggregate output than negative shocks to larger but less crucial industries such as “retail trade.” Nonlinearities also have a significant impact on the distribution of aggregate output: they lower its mean and generate negative skewness and excess kurtosis even though the underlying shocks are symmetric and thin-tailed. Nonlinearities in production generate significant welfare costs of sectoral fluctuations, ranging from
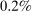 to
to 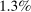 depending on the calibration. These are an order of magnitude larger than the welfare costs of business cycles arising from nonlinearities in utility (risk aversion) identified by Lucas (1987).
depending on the calibration. These are an order of magnitude larger than the welfare costs of business cycles arising from nonlinearities in utility (risk aversion) identified by Lucas (1987). - 2. We derive and use a simple nonparametric formula, taking into account the observed change in the Domar weight for crude oil, to analyze the impact of the energy crisis of the 1970s up to the second order. We find that nonlinearities almost tripled the impact of the oil shocks from
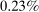 to
to 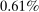 of world aggregate output.
of world aggregate output. - 3. We show that the nonlinearities are also important for long-run growth in the presence of realistic complementarities across sectors. They cause the Domar weights of bottleneck sectors with relatively low productivity growth to grow over time and thereby reduce aggregate growth, an effect identified as Baumol's cost disease (Baumol (1967)). We calculate that nonlinearities have reduced the growth of aggregate TFP by 20 percentage points over the period 1948–2014 in the United States.4
The outline of the paper is as follows. In Section 2, we derive a general formula describing the second-order impact on aggregate output of shocks in terms of nonparametric sufficient statistics: reduced-form general equilibrium elasticities of substitution and input–output multipliers.5 We explain the implications of this formula for the impact of correlated shocks and for the average performance of the economy. In Section 3, we use two special illustrative examples to provide some intuition for the roles of the general equilibrium elasticities of substitution and of the input–output multipliers and for their dependence on microeconomic primitives. In Section 4, we fully characterize second-order terms in terms of microeconomic primitives for general nested-CES economies with arbitrary microeconomic elasticities of substitution and network linkages. In Section 5, we further generalize the results to arbitrary (potentially non-CES) production functions. In Section 6, we provide some illustrations of the quantitative implications of our results.
Related Literature
Gabaix (2011) used Hulten's theorem to argue that the existence of very large, or in his language granular, firms can be a possible source of aggregate volatility. If there exist very large firms, then shocks to those firms will not cancel out with shocks to much smaller firms, resulting in aggregate fluctuations. Acemoglu, Carvalho, Ozdaglar, and Tahbaz-Salehi (2012), working with a Cobb–Douglas model in the spirit of Long and Plosser (1983), observed that in an economy with input–output linkages, the equilibrium sizes of firms depend on the shape of the input–output matrix. Central suppliers will be weighted more highly than peripheral firms, and therefore, shocks to those central players will not cancel out with shocks to small firms.6 Carvalho and Gabaix (2013) showed how Hulten's theorem can be operationalized to decompose the sectoral sources of aggregate volatility.7
Relatedly, Acemoglu, Ozdaglar, and Tahbaz-Salehi (2017) deployed Hulten's theorem to study other moments of the distribution of aggregate output. They argued that if the Domar weights are fat-tailed and if the underlying idiosyncratic shocks are fat-tailed, then aggregate output can exhibit non-normal behavior. Stated differently, they showed that aggregate output can inherit tail risk from idiosyncratic tail risk if the distribution of the Domar weights is fat-tailed. Our paper makes a related but distinct point. We find that, for the empirically relevant range of parameters, the response of aggregate output to shocks is significantly asymmetric. Therefore, the nonlinearity inherent in the production structure can turn even symmetric thin-tailed sectoral shocks into rare disasters endogenously. This means that the economy could plausibly experience aggregate tail risk without either fat-tailed shocks or fat-tailed Domar weights.
In a recent survey article, Gabaix (2016), invoking Hulten's theorem, wrote “networks are a particular case of granularity rather than an alternative to it.” This has meant that researchers studying the role of networks have either moved away from efficient models, or that they have retreated from studying aggregate output and turned their attention to the microeconomic implications of networks, namely, the covariance of fluctuations between different industries and firms.8,9 However, our paper shows that except in very special cases, models with the same sales distributions but different network structures only have the same aggregate-output implications up to a fragile first order of approximation. Their common sales distributions produce the same linearization, but their different network structures lead to different nonlinearities. Hence, in the context of aggregate fluctuations, networks are neither a particular case of granularity nor an alternative to it. It is simply that the sales distribution is a sufficient statistic for the network at the first order but not at higher orders.
2 General Framework
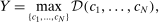
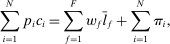
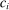 is the representative household's consumption of good i,
is the representative household's consumption of good i, 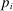 is the price and
is the price and 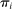 is the profit of producer i,
is the profit of producer i, 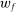 is the wage of factor f which is in fixed supply
is the wage of factor f which is in fixed supply 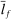 . The two sides of the budget constraint coincide with nominal GDP, using respectively the final expenditure and income approaches.
. The two sides of the budget constraint coincide with nominal GDP, using respectively the final expenditure and income approaches.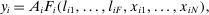
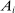 is Hicks-neutral technology,
is Hicks-neutral technology, 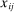 are intermediate inputs of good j used in the production of good i, and
are intermediate inputs of good j used in the production of good i, and 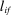 is labor type f used by i. The profits earned by the producer of good i are
is labor type f used by i. The profits earned by the producer of good i are
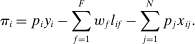
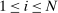 and factors
and factors 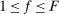 are
are
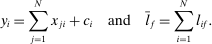
We interpret Y as a cardinal measure of (real) aggregate output and note that it is the correct measure of the household's “standard of living” in this model. We implicitly rely on the existence of complete financial markets and homotheticity of preferences to ensure the existence of a representative consumer. Although the assumption of a representative consumer is not strictly necessary for the results in this section, it is a standard assumption in this literature since it allows us to unambiguously define and measure changes in real aggregate output without contending with the issue of the appropriate price index.
We assume that the production function 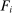 of each good i has constant returns to scale, which implies that equilibrium profits are zero. This assumption is less restrictive than it may appear because decreasing returns to scale can be captured by adding fixed factors to which the corresponding profits accrue.10 A similar observation applies to the assumption that shocks are Hicks-neutral: we can represent a productivity shock augmenting a specific input by adding a new producer that produces this input and hitting this new producer with a Hicks-neutral shock.11 Note also that although we refer to each producer as producing one good, our framework actually allows for joint production by multi-product producers: for example, to capture a producer i producing goods i and
of each good i has constant returns to scale, which implies that equilibrium profits are zero. This assumption is less restrictive than it may appear because decreasing returns to scale can be captured by adding fixed factors to which the corresponding profits accrue.10 A similar observation applies to the assumption that shocks are Hicks-neutral: we can represent a productivity shock augmenting a specific input by adding a new producer that produces this input and hitting this new producer with a Hicks-neutral shock.11 Note also that although we refer to each producer as producing one good, our framework actually allows for joint production by multi-product producers: for example, to capture a producer i producing goods i and 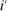 using intermediate inputs and factors, we represent good
using intermediate inputs and factors, we represent good 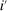 as an input entering negatively in the production and cost functions for good i.12 Finally, note that goods could represent different varieties of goods from the same industry, goods from different industries, or even goods in different time periods, regions, or states of nature.13
as an input entering negatively in the production and cost functions for good i.12 Finally, note that goods could represent different varieties of goods from the same industry, goods from different industries, or even goods in different time periods, regions, or states of nature.13
Define  to be the equilibrium aggregate output as a function of the exogenous technology levels. Throughout the paper, and without loss of generality, we derive results regarding the effects of shocks in the vicinity of the steady state, which we normalize to be
to be the equilibrium aggregate output as a function of the exogenous technology levels. Throughout the paper, and without loss of generality, we derive results regarding the effects of shocks in the vicinity of the steady state, which we normalize to be 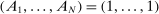 . All the relevant derivatives are evaluated at that point.
. All the relevant derivatives are evaluated at that point.
Theorem 1. ([Hulten] ([1978]))The first-order macroeconomic impact of microeconomic shocks is given by14
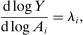 (1)
(1)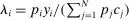 the sales of producer i as a fraction of GDP or Domar weight.
the sales of producer i as a fraction of GDP or Domar weight.
Hulten's theorem can be seen as a consequence of the first welfare theorem: since this economy is efficient,  is also the social planning optimum and prices are the multipliers on the resource constraints for the different goods. Applying the envelope theorem to the social planning problem delivers the result.
is also the social planning optimum and prices are the multipliers on the resource constraints for the different goods. Applying the envelope theorem to the social planning problem delivers the result.
Hulten's theorem has the powerful implication that, to a first order, the underlying microeconomic details of the structural model are completely irrelevant as long as we observe the equilibrium sales distribution: the shape of the production network, the microeconomic elasticities of substitution in production, the degree of returns to scale, and the extent to which inputs and factors can be reallocated, are all irrelevant.
We now provide a characterization of the second-order effects in terms of reduced-form elasticities. We need to introduce two objects: GE elasticities of substitution, and the input–output multiplier. Later on, we show how these reduced-form elasticities arise from structural primitives using a structural model.
 , the Morishima (1967) elasticity of substitution is
, the Morishima (1967) elasticity of substitution is
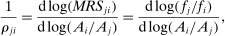
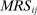 is the ratio of partial derivatives with respect to
is the ratio of partial derivatives with respect to 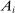 and
and 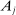 , and
, and 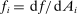 .15
.15When the homothetic function f corresponds to a CES utility function and 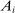 to quantities,
to quantities, 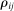 is the associated elasticity of substitution parameter. However, we do not impose this interpretation, and instead treat this object as a reduced-form measure of the curvature of isoquants. By analogy, we define a pseudo elasticity of substitution for non-homothetic functions in a similar fashion.
is the associated elasticity of substitution parameter. However, we do not impose this interpretation, and instead treat this object as a reduced-form measure of the curvature of isoquants. By analogy, we define a pseudo elasticity of substitution for non-homothetic functions in a similar fashion.
Definition 1.For any smooth function 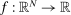 , the pseudo elasticity of substitution is
, the pseudo elasticity of substitution is
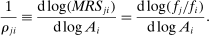
The pseudo elasticity of substitution is a generalization of the Moroshima elasticity of substitution in the sense that whenever f is homogeneous of degree 1, the pseudo elasticity is the same as the Moroshima elasticity of substitution.
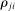 is interesting because it measures changes in the relative sales shares of j and i when there is an exogenous shock to i. This follows from the fact that
is interesting because it measures changes in the relative sales shares of j and i when there is an exogenous shock to i. This follows from the fact that
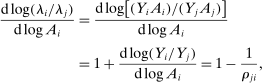
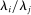 to increase when
to increase when 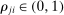 , and to decrease otherwise. We say that a j is a GE-complement for i if
, and to decrease otherwise. We say that a j is a GE-complement for i if 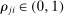 , and a GE-substitute otherwise. When f is a CES aggregator, this coincides with the standard definition of gross complements and substitutes. As usual, when f is Cobb–Douglas, i and j are neither substitutes nor complements. In general, GE-substitutability is not reflexive.
, and a GE-substitute otherwise. When f is a CES aggregator, this coincides with the standard definition of gross complements and substitutes. As usual, when f is Cobb–Douglas, i and j are neither substitutes nor complements. In general, GE-substitutability is not reflexive.An important special case is when the shock 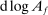 hits the stock of a factor. In that case, Hulten's theorem implies that
hits the stock of a factor. In that case, Hulten's theorem implies that 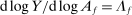 , where
, where 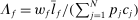 is the share of factor f in GDP. Since
is the share of factor f in GDP. Since 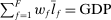 , Euler's theorem implies that the aggregate output is homogeneous of degree 1 in the supplies of the factors. This implies that the general equilibrium pseudo elasticity of substitution between two factors can be interpreted as a genuine elasticity of substitution between these factors in general equilibrium.16
, Euler's theorem implies that the aggregate output is homogeneous of degree 1 in the supplies of the factors. This implies that the general equilibrium pseudo elasticity of substitution between two factors can be interpreted as a genuine elasticity of substitution between these factors in general equilibrium.16
Next, we introduce the input–output multiplier.
Definition 2.The input–output multiplier is
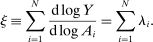
When 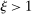 , total sales of the shocked quantities exceed total income, an indication that there are intermediate inputs. When
, total sales of the shocked quantities exceed total income, an indication that there are intermediate inputs. When 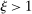 , the impact of a uniform technology shock is correspondingly amplified due to the fact that goods are reproducible. The input–output multiplier ξ captures the percentage change in aggregate output in response to a uniform one-percent increase in technology. Loosely speaking, it captures a notion of returns-to-scale at the aggregate level. Changes
, the impact of a uniform technology shock is correspondingly amplified due to the fact that goods are reproducible. The input–output multiplier ξ captures the percentage change in aggregate output in response to a uniform one-percent increase in technology. Loosely speaking, it captures a notion of returns-to-scale at the aggregate level. Changes 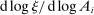 in the input–output multiplier can be interpreted as another kind of GE elasticity of substitution, namely, the substitution between the underlying factors (whose payments are GDP) and the reproducible goods (whose payments are sales).17
in the input–output multiplier can be interpreted as another kind of GE elasticity of substitution, namely, the substitution between the underlying factors (whose payments are GDP) and the reproducible goods (whose payments are sales).17
Having defined the GE elasticities of substitution and the input–output multiplier, we are in a position to characterize the second-order terms. We start by investigating the impact of an idiosyncratic shock.
Idiosyncratic Shocks
Theorem 2. (Second-Order Macroeconomic Impact of Microeconomic Shocks)The second-order macroeconomic impact of microeconomic shocks is given by18
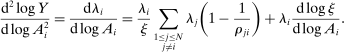 (2)
(2)The second-order impact of a shock to i is equal to the change in i's sales share 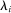 . The change in i's share of sales is the change in the aggregate sales to GDP ratio, minus the change in the share of sales of all other industries. The former is measured by the elasticity of the input–output multiplier ξ, while the latter depends on the GE elasticities of substitution. Collectively, the sales shares
. The change in i's share of sales is the change in the aggregate sales to GDP ratio, minus the change in the share of sales of all other industries. The former is measured by the elasticity of the input–output multiplier ξ, while the latter depends on the GE elasticities of substitution. Collectively, the sales shares 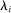 , the reduced-form elasticities
, the reduced-form elasticities 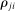 , and the reduced-form elasticity of the input–output multiplier
, and the reduced-form elasticity of the input–output multiplier 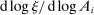 are sufficient statistics for the response of aggregate output to to productivity shocks up to a second order.
are sufficient statistics for the response of aggregate output to to productivity shocks up to a second order.
This result implies that Hulten's first-order approximation is globally accurate if reduced-form elasticities are unitary 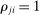 for every j and if the input–output multiplier ξ is independent of the shock
for every j and if the input–output multiplier ξ is independent of the shock 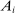 . We shall see that this amounts to assuming Cobb–Douglas production and consumption functions where sales shares, and more generally the whole input–output matrix, are constant. The model is then log-linear.
. We shall see that this amounts to assuming Cobb–Douglas production and consumption functions where sales shares, and more generally the whole input–output matrix, are constant. The model is then log-linear.
Outside of this special case, there are nonlinearities, and the quality of the first-order approximation deteriorates as the shocks become bigger. The deterioration can be extreme, with the aggregate output function becoming nearly non-smooth, when 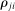 approaches 0 for any j, either from above or from below. As we shall see, these arise in the cases of extreme microeconomic complementarities with no reallocation or extreme microeconomic substitutabilities with full reallocation. In these limiting cases, the first-order approximation is completely uninformative, even for arbitrarily small shocks. Similar observations apply when
approaches 0 for any j, either from above or from below. As we shall see, these arise in the cases of extreme microeconomic complementarities with no reallocation or extreme microeconomic substitutabilities with full reallocation. In these limiting cases, the first-order approximation is completely uninformative, even for arbitrarily small shocks. Similar observations apply when 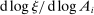 approaches infinity. Therefore, although the Cobb–Douglas special case is very popular in the literature, it constitutes a very special case where the second-order terms are all identically zero.19
approaches infinity. Therefore, although the Cobb–Douglas special case is very popular in the literature, it constitutes a very special case where the second-order terms are all identically zero.19
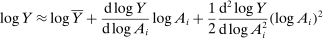
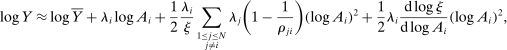
 is Y evaluated at the steady-state technology values. When goods are GE-complements, the second-order terms amplify the effect of negative shocks and attenuate the effect of positive shocks relative to the first-order approximation. Instead, when goods are GE-substitutes, the second-order approximation attenuates the negative shocks and amplifies the positive shocks instead. A similar intuition holds for the input–output multiplier: if the input–output multiplier is increasing, then the second-order approximation amplifies positive shocks and dampens negative shocks, and if this multiplier is decreasing, then the opposite is true.
is Y evaluated at the steady-state technology values. When goods are GE-complements, the second-order terms amplify the effect of negative shocks and attenuate the effect of positive shocks relative to the first-order approximation. Instead, when goods are GE-substitutes, the second-order approximation attenuates the negative shocks and amplifies the positive shocks instead. A similar intuition holds for the input–output multiplier: if the input–output multiplier is increasing, then the second-order approximation amplifies positive shocks and dampens negative shocks, and if this multiplier is decreasing, then the opposite is true.Correlated Shocks
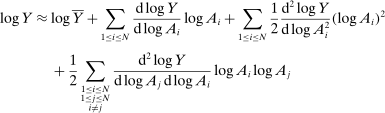
Proposition 3. (Correlated Shocks)The second-order macroeconomic impact of correlated microeconomic shocks is given by
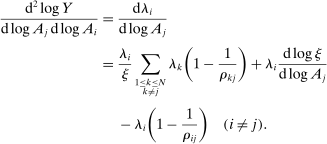 (3)
(3)The second-order effect of a common shock to i and j is not simply the sum of the second-order impacts of the idiosyncratic shocks to i and to j, and instead there are interactions between the two shocks.20 In Section 4, we provide an explicit characterization of the Hessian in terms of microeconomic primitives.
Macro Moments
We can use the second-order terms to approximate an economy's macroeconomic moments. To illustrate this intuition while preserving expositional simplicity, we consider shocks to a single producer i which are log-normal with mean log 0 and variance 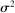 .21
.21
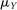 , for which a Taylor approximation yields
, for which a Taylor approximation yields
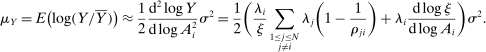
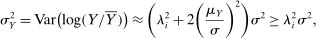
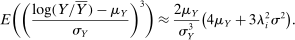
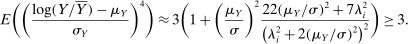
The importance of all these effects increases with the variance 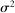 of the shocks because they are driven by nonlinearities, and because the importance of nonlinearities increases with the size of the shocks.
of the shocks because they are driven by nonlinearities, and because the importance of nonlinearities increases with the size of the shocks.
Welfare Costs of Sectoral Shocks
For the majority of the paper, we focus on 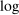 aggregate output, which can be characterized with unitless elasticities. With complementarities, we have argued that sector shocks lower the mean of
aggregate output, which can be characterized with unitless elasticities. With complementarities, we have argued that sector shocks lower the mean of 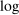 aggregate output, an effect which we can interpret as the welfare cost of sectoral shocks. One may imagine that the losses from uncertainty that we identify depend on the concavity of the
aggregate output, an effect which we can interpret as the welfare cost of sectoral shocks. One may imagine that the losses from uncertainty that we identify depend on the concavity of the 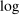 function. A consumer with
function. A consumer with 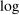 utility prefers a mean-preserving reduction in uncertainty even when the aggregate output function is linear. However, as shown by Lucas (1987), the corresponding losses are extremely small in practice in business-cycle settings. The much larger effects that we identify originate in nonlinearities in production, and they are present even when the utility function is linear in aggregate consumption.
utility prefers a mean-preserving reduction in uncertainty even when the aggregate output function is linear. However, as shown by Lucas (1987), the corresponding losses are extremely small in practice in business-cycle settings. The much larger effects that we identify originate in nonlinearities in production, and they are present even when the utility function is linear in aggregate consumption.
The following proposition formalizes this intuition and shows that the Lucas-style welfare losses due to nonlinearities in the utility function in the form of risk aversion and the losses due to nonlinearities in production do not interact with one another up to a second-order approximation.22
Proposition 4. (Welfare Cost of Sectoral Shocks)Let 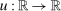 be a utility function and let
be a utility function and let 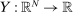 be the aggregate output function. Suppose that
be the aggregate output function. Suppose that 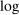 productivity shocks have mean 0 and a diagonal covariance matrix with kth diagonal element
productivity shocks have mean 0 and a diagonal covariance matrix with kth diagonal element 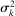 . Then
. Then
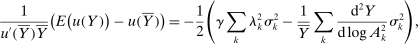 (4)
(4) .
.
The first term on the right-hand side, which is quantitatively small, is the traditional Lucas-style cost arising from curvature in the utility function. The second term, which is quantitatively large, is due to the curvature inherent in production and does not depend on the coefficient of relative risk aversion.23
Mapping From Micro to Macro
Theorem 2 implies that the GE elasticities of substitution  and the elasticity of the input–output multiplier
and the elasticity of the input–output multiplier  are sufficient statistics for the second-order impact of shocks. However, these sufficient statistics are reduced-form elasticities, and unlike
are sufficient statistics for the second-order impact of shocks. However, these sufficient statistics are reduced-form elasticities, and unlike 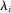 and ξ, they are not readily observable. Furthermore, since they are general equilibrium objects, they cannot be identified through exogenous microeconomic variation. So, while careful empirical work can identify micro-elasticities, the leap from micro-estimates to macro-effects can be hazardous.
and ξ, they are not readily observable. Furthermore, since they are general equilibrium objects, they cannot be identified through exogenous microeconomic variation. So, while careful empirical work can identify micro-elasticities, the leap from micro-estimates to macro-effects can be hazardous.
In this paper, we provide the mapping from structural micro parameters to the reduced-form GE elasticities. This general characterization can be found in Section 4 for general nested-CES economies, and in Section 5 for arbitrary economies. However, rather than stating these results up front, we build up to the general characterization using some important special cases in Section 3.
3 Illustrative Examples
In this section, we work through two special cases to illustrate and isolate some intuition for how the GE elasticities of substitution and the input–output multiplier affect the shape of the aggregate output function. After working through these examples, we provide a generic characterization of the second-order terms in Sections 4 and 5.
3.1 GE Elasticities of Substitution
To start with, we focus on the GE elasticities of substitution by considering a simple example of a horizontal economy with no intermediate inputs. The input–output multiplier is constant and equal to 1, and so deviations from Hulten's theorem are only due to non-unitary GE elasticities of substitution. We emphasize how the GE elasticities of substitution depend not only on the micro-elasticities of substitution, but also on the degree to which labor can be reallocated across uses and on the returns to scale in production. Throughout all the upcoming examples, variables with overlines denote steady-state values.
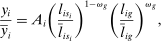
 and
and 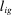 are the amounts of the specific and general labor used by producer i. The specific labor of type i can only be used by producer i and the general labor can be used by all producers.
are the amounts of the specific and general labor used by producer i. The specific labor of type i can only be used by producer i and the general labor can be used by all producers.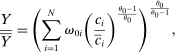
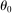 is the microeconomic elasticity of substitution in consumption and
is the microeconomic elasticity of substitution in consumption and 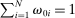 .
.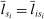 and
and 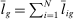 . The market-clearing conditions are
. The market-clearing conditions are
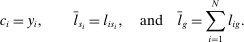
Different degrees of labor reallocation can be expected depending on the degree of aggregation. The time horizon is also important since we might expect labor to be more difficult to adjust at short horizons than at long horizons. Some of these dynamic effects can be captured by performing comparative statics with respect to  , where
, where  represents an economy where labor cannot be reallocated, and
represents an economy where labor cannot be reallocated, and  an economy where labor can be fully reallocated.
an economy where labor can be fully reallocated.
Proposition 5.In the horizontal economy, the sales shares are given by 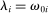 , the input–output multiplier is constant with
, the input–output multiplier is constant with  and
and  . The GE elasticities of substitution are all equal and are given by
. The GE elasticities of substitution are all equal and are given by
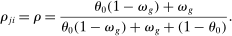
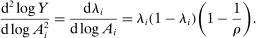
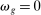 and with full reallocation where
and with full reallocation where 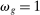 . We start with the no-reallocation case where
. We start with the no-reallocation case where 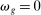 . Because labor cannot be moved across producers, it is as if there were a fixed endowment of each good and so aggregate output is given by
. Because labor cannot be moved across producers, it is as if there were a fixed endowment of each good and so aggregate output is given by
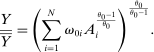
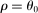 . Since
. Since 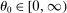 , we have
, we have 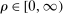 . The second-order macroeconomic impact of microeconomic shocks is given by
. The second-order macroeconomic impact of microeconomic shocks is given by
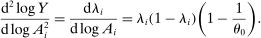
In the Cobb–Douglas case 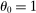 , second-order terms are identically equal to zero and the first-order approximation of Hulten's theorem is globally accurate. The quality of the first-order approximation deteriorates as we move away from
, second-order terms are identically equal to zero and the first-order approximation of Hulten's theorem is globally accurate. The quality of the first-order approximation deteriorates as we move away from 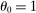 in both directions. The second-order term is negative when
in both directions. The second-order term is negative when 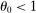 and positive when
and positive when 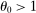 . Relative to the first-order approximation, the second-order approximation amplifies negative shocks and mitigates positive shocks in the former case and the reverse the latter case.
. Relative to the first-order approximation, the second-order approximation amplifies negative shocks and mitigates positive shocks in the former case and the reverse the latter case.
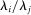 of i versus j changes in response to a shock to i:
of i versus j changes in response to a shock to i:
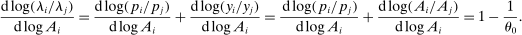
Because there is no reallocation, the relative quantity 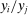 moves one-for-one with the shock to i. In the Cobb–Douglas case
moves one-for-one with the shock to i. In the Cobb–Douglas case 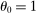 , the relative price
, the relative price 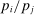 moves one-for-one in the opposite direction, and so the relative share
moves one-for-one in the opposite direction, and so the relative share 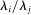 remains constant. When
remains constant. When 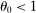 , the relative price moves more than one-for-one with the shock, and so the relative share increases when the shock is negative, and increases when it is positive. When
, the relative price moves more than one-for-one with the shock, and so the relative share increases when the shock is negative, and increases when it is positive. When 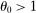 , the relative price moves less than one-for-one with the shock, and so the relative share decreases when the shock is negative, and increases when it is positive.
, the relative price moves less than one-for-one with the shock, and so the relative share decreases when the shock is negative, and increases when it is positive.
Consider the Leontief limit 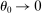 . In this limit, deviations from the first-order approximation become so large that the first-order term becomes completely uninformative. Following a negative shock to i, the relative price
. In this limit, deviations from the first-order approximation become so large that the first-order term becomes completely uninformative. Following a negative shock to i, the relative price 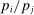 jumps to infinity, and so does the relative share
jumps to infinity, and so does the relative share 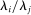 . Following a positive shock, the relative price jumps to zero and so does the relative share. The associated amplification of negative shocks and mitigation of positive shocks is extreme.
. Following a positive shock, the relative price jumps to zero and so does the relative share. The associated amplification of negative shocks and mitigation of positive shocks is extreme.
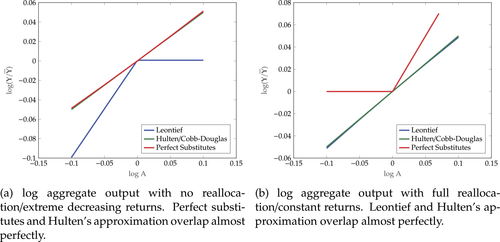
Let us now consider the perfect-substitutes limit 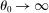 . Positive shocks are amplified and negative shocks are mitigated, but the effect is not nearly so dramatic. In fact, because goods are perfect substitutes, the relative price
. Positive shocks are amplified and negative shocks are mitigated, but the effect is not nearly so dramatic. In fact, because goods are perfect substitutes, the relative price 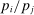 is constant. Therefore, the relative share
is constant. Therefore, the relative share 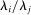 moves one-for-one with the shock to i. The situation is depicted graphically in Figure 1a.
moves one-for-one with the shock to i. The situation is depicted graphically in Figure 1a.
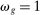 . Solving out the allocation of labor to each producer and replacing leads to the following expression for aggregate output:
. Solving out the allocation of labor to each producer and replacing leads to the following expression for aggregate output:
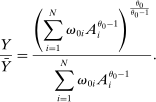
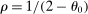 . Because
. Because 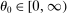 , we have
, we have 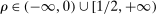 . The second-order macroeconomic impact of microeconomic shocks is given by
. The second-order macroeconomic impact of microeconomic shocks is given by
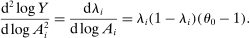
As above, in the Cobb–Douglas case 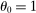 , second-order terms are identically equal to zero and the first-order approximation of Hulten's theorem is globally accurate. The second-order term is negative when
, second-order terms are identically equal to zero and the first-order approximation of Hulten's theorem is globally accurate. The second-order term is negative when 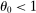 and positive when
and positive when 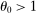 . Relative to the first-order approximation, the second-order approximation amplifies negative shocks and mitigates positive shocks in the former case and the reverse in the latter case. However, this time, the second-order term becomes singular when the goods are highly substitutable rather than when they are highly complementary.
. Relative to the first-order approximation, the second-order approximation amplifies negative shocks and mitigates positive shocks in the former case and the reverse in the latter case. However, this time, the second-order term becomes singular when the goods are highly substitutable rather than when they are highly complementary.
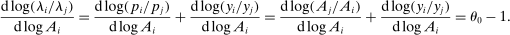
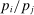 always moves inversely one-for-one with the shock to i. In the Cobb–Douglas case, the relative quantity
always moves inversely one-for-one with the shock to i. In the Cobb–Douglas case, the relative quantity 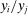 moves one-for-one with the shock to i, and the relative share
moves one-for-one with the shock to i, and the relative share 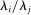 remains constant. When
remains constant. When 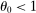 , the relative quantity moves less than one-for-one with the shock as labor is reallocated toward i if the shock is negative and away from i if the shock is positive. As a result, the relative share increases when the shock is negative, and increases when it is positive. When
, the relative quantity moves less than one-for-one with the shock as labor is reallocated toward i if the shock is negative and away from i if the shock is positive. As a result, the relative share increases when the shock is negative, and increases when it is positive. When 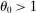 , the relative quantity moves more than one-for-one with the shock as labor is reallocated away from i when the shock is negative and toward i when it is positive. As a result, the relative share decreases when the shock is negative, and increases when it is positive.
, the relative quantity moves more than one-for-one with the shock as labor is reallocated away from i when the shock is negative and toward i when it is positive. As a result, the relative share decreases when the shock is negative, and increases when it is positive.Contrary to what one may have assumed, a near-Leontief production function is not sufficient for generating large deviations from Hulten's theorem, as long as factors can be reallocated freely, precisely because this reallocation is successful at reinforcing “weak links.” In the Leontief limit, the relative quantity 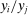 is invariant to the shock, and so the relative sales share
is invariant to the shock, and so the relative sales share 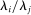 moves inversely one-for-one with the shock to i. Relative to the first-order approximation, the second-order approximation still amplifies negative shocks and mitigates positive shocks, but the corresponding magnitudes are much smaller than in the case where labor cannot be reallocated.
moves inversely one-for-one with the shock to i. Relative to the first-order approximation, the second-order approximation still amplifies negative shocks and mitigates positive shocks, but the corresponding magnitudes are much smaller than in the case where labor cannot be reallocated.
In the perfect-substitutes limit, labor is entirely allocated to the most productive producer. In response to a positive shock to i, the relative quantity 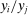 jumps to infinity, and so does the relative share
jumps to infinity, and so does the relative share 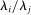 . In response to a negative shock, the relative quantity drops to zero, and so does the relative share. Relative to the first-order approximation, the second-order approximation still amplifies positive shocks and mitigates negative shocks, but the corresponding magnitudes are now much larger than in the case where labor cannot be reallocated. The situation is depicted graphically in Figure 1b.
. In response to a negative shock, the relative quantity drops to zero, and so does the relative share. Relative to the first-order approximation, the second-order approximation still amplifies positive shocks and mitigates negative shocks, but the corresponding magnitudes are now much larger than in the case where labor cannot be reallocated. The situation is depicted graphically in Figure 1b.
Finally, note that both when labor can or cannot be reallocated, the second-order term scales in 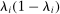 as a function of the size
as a function of the size 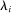 of the shocked producer i. Its absolute value is therefore hump-shaped in
of the shocked producer i. Its absolute value is therefore hump-shaped in 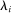 : it goes to zero when
: it goes to zero when 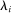 is close to 0 or 1, and reaches a maximum when
is close to 0 or 1, and reaches a maximum when 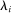 is intermediate at 1/2. That the term is small when
is intermediate at 1/2. That the term is small when 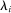 is close to 0 is intuitive. That it is small when
is close to 0 is intuitive. That it is small when 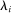 is close to 1 makes sense since then the economy behaves much like producer i and aggregate output is then close to being proportional to
is close to 1 makes sense since then the economy behaves much like producer i and aggregate output is then close to being proportional to 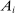 . The second-order term can only be significant for intermediate values of
. The second-order term can only be significant for intermediate values of 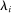 .
.
To recap, with complementarities: a negative shock can cause a large downturn when labor cannot be freely reallocated, but the ability to reallocate labor largely mitigates these effects; positive shocks have a lesser impact. By contrast, with substitutabilities: a positive shock can cause a big boom when labor can be reallocated, but the inability to reallocate labor mitigates these effects; negative shocks have a lesser impact. Cobb–Douglas stands as a special case where the macroeconomic impact of microeconomic shocks is symmetric independently of whether or not labor can be reallocated (since the equilibrium allocation of labor across producers is constant even when labor can be reallocated).24 These effects are less pronounced when the size of the shocked producer is very small or very large, and are more pronounced when it is intermediate.
3.2 Input–Output Multiplier
In the previous example of a horizontal economy, the input–output multiplier ξ is constant and deviations from Hulten's theorem are due to non-unitary GE elasticities of substitution. We now focus on a different example, that of a roundabout economy, where deviations from Hulten's theorem are driven purely by variability in ξ, and the GE elasticities of substitution play no role.
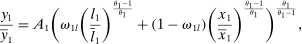
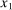 is the amount of good 1 used as an intermediate input. The supply of the factor is inelastic at
is the amount of good 1 used as an intermediate input. The supply of the factor is inelastic at 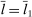 . Final output
. Final output 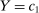 is produced one-to-one from good 1.
is produced one-to-one from good 1.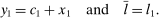
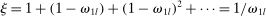
 and increases with the intermediate input share
and increases with the intermediate input share  . Hulten's theorem implies that
. Hulten's theorem implies that
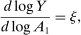
Proposition 6. (Variable IO Multiplier)In the roundabout economy, the input–output multiplier is given by 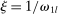 and its elasticity is given by25
and its elasticity is given by25
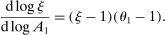
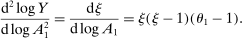
Hulten's approximation is exact only when there are no intermediate inputs so that 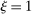 or when the economy is Cobb–Douglas so that
or when the economy is Cobb–Douglas so that 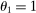 . Otherwise, the second-order term is increasing in
. Otherwise, the second-order term is increasing in 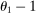 and in a network term
and in a network term 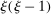 .26
.26
Intuitively, this results from the fact that output is used as its own input. When 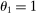 , the input–output multiplier remains constant. When
, the input–output multiplier remains constant. When 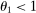 , the input–output multiplier increases if the shock is negative, and decreases if it is positive. When
, the input–output multiplier increases if the shock is negative, and decreases if it is positive. When 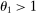 , the input–output multiplier decreases if the shock is negative, and increases if it is positive. The larger is the steady-state input–output multiplier, the larger is the effect.
, the input–output multiplier decreases if the shock is negative, and increases if it is positive. The larger is the steady-state input–output multiplier, the larger is the effect.
Figure 2 plots 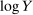 as a function of
as a function of 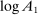 for the case where
for the case where 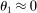 ,
, 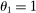 , and
, and 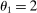 . In the limit
. In the limit 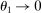 , output is linear in productivity (rather than log-linear) with slope
, output is linear in productivity (rather than log-linear) with slope 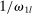 . When
. When 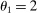 , output is hyperbolic in productivity.27
, output is hyperbolic in productivity.27
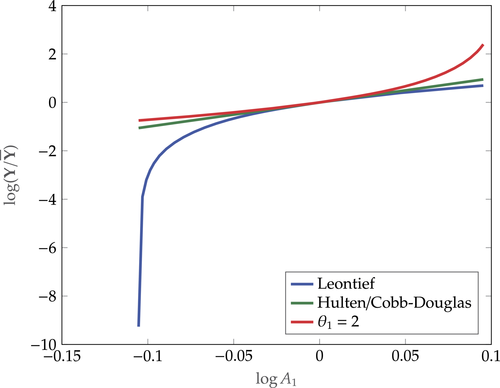
Output as a function of productivity shocks 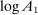 with variable input–output multiplier effect with steady-state input–output multiplier ξ = 10.
with variable input–output multiplier effect with steady-state input–output multiplier ξ = 10.
4 General Nested-CES Networks
We now characterize the second-order terms for a general nested-CES economy (encompassing the examples in Section 3). Throughout this section, variables with over-lines are normalizing constants equal to the values in steady state.28
Any nested-CES economy with a representative consumer, an arbitrary numbers of nests, elasticities, and intermediate input use, can be rewritten in what we call standard form, which simply means that each CES aggregator corresponds to a node in the production network with a 1 node-specific elasticity of substitution. Through a relabeling, this structure can represent any nested-CES economy with an arbitrary pattern of nests and elasticities. Intuitively, by relabeling each CES aggregator to be a new producer, we can have as many nests as desired.
Formally, a nested-CES economy in standard form is defined by a tuple 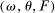 and a set of normalizing constants
and a set of normalizing constants 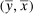 . The
. The 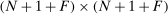 matrix ω is a matrix of input–output parameters where the first row and column correspond to household sector, the next N rows and columns correspond to reproducible goods, and the last F rows and columns correspond to factors. What distinguishes factors from goods is that factors cannot be produced. The
matrix ω is a matrix of input–output parameters where the first row and column correspond to household sector, the next N rows and columns correspond to reproducible goods, and the last F rows and columns correspond to factors. What distinguishes factors from goods is that factors cannot be produced. The 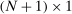 vector θ is a vector of microeconomic elasticities of substitution. For convenience, we use number indices starting at 0 instead of 1 to describe the elements of ω and θ.29
vector θ is a vector of microeconomic elasticities of substitution. For convenience, we use number indices starting at 0 instead of 1 to describe the elements of ω and θ.29
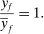
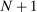 goods are reproducible with production functions
goods are reproducible with production functions
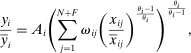
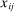 are intermediate inputs from j used by i. Producer 0 represents final demand and its production function is the final-demand aggregator so that
are intermediate inputs from j used by i. Producer 0 represents final demand and its production function is the final-demand aggregator so that
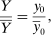
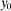 is the final good.
is the final good.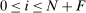 are
are
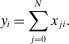
To state our results, we need the following definitions.
Definition 3.The 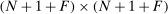 input–output matrix Ω is the matrix whose ijth element is equal to the steady-state value of
input–output matrix Ω is the matrix whose ijth element is equal to the steady-state value of
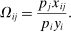
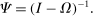
Intuitively, the ijth element 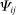 of the Leontief inverse is a measure of i's total reliance on j as a supplier. It captures both the direct and indirect ways through which i uses j in its production.30
of the Leontief inverse is a measure of i's total reliance on j as a supplier. It captures both the direct and indirect ways through which i uses j in its production.30
Definition 4.The input–output covariance operator is
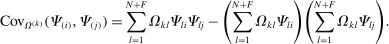 (5)
(5)It is the covariance between the ith and jth column of the Leontief inverse using the kth row of the input–output matrix as the distribution. The input–output covariance operator plays a crucial role in our results.
We consider arbitrary CES network structures (in standard form), starting with a single factor and then generalizing to multiple factors. As previously mentioned, a one-factor model is equivalent to a model where primary factors are equivalent and can be fully reallocated. To model limited factor reallocation or decreasing returns, we need to have multiple factors.
4.1 One Factor
Proposition 7. (Second-Order Network Centrality)Consider a nested-CES model in standard form with a single factor. The second-order macroeconomic impact of microeconomic shocks is given by
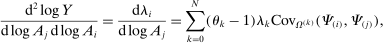 (6)
(6)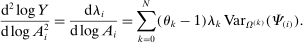 (7)
(7)Equations (6) and (7) have a simple intuition. Let us focus first on equation (6). The change in the sales share of i, in response to a shock to j, depends on how the relative demand expenditure for i changes. Changes in the demand expenditure for i arise from the substitution by the different nodes k and are captured by the different terms in the sum on the right-hand side.31
Consider, for example, the effect of a negative productivity shock 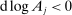 to j. The change in the vector of prices of the different producers is proportional to the vector of direct and indirect exposures to the shock, which is simply the jth column
to j. The change in the vector of prices of the different producers is proportional to the vector of direct and indirect exposures to the shock, which is simply the jth column 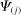 of the Leontief inverse. Now consider a given producer k. If
of the Leontief inverse. Now consider a given producer k. If 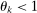 , producer k increases its expenditure share on inputs whose price increases more, that is, inputs that are more exposed to the shock to j, as measured by
, producer k increases its expenditure share on inputs whose price increases more, that is, inputs that are more exposed to the shock to j, as measured by 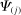 . This increases the relative demand expenditure for i if those inputs are also relatively more exposed to i, as measured by the ith column of the Leontief inverse
. This increases the relative demand expenditure for i if those inputs are also relatively more exposed to i, as measured by the ith column of the Leontief inverse 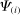 . The overall effect is stronger, the higher is the covariance
. The overall effect is stronger, the higher is the covariance 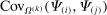 , the larger is the size of producer k as measured by
, the larger is the size of producer k as measured by 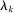 , and the further away from 1 is the elasticity of substitution
, and the further away from 1 is the elasticity of substitution 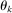 as measured by
as measured by  .
.
Equation (7) is a particular case of equation (6) and so the intuition is identical. The change in the sales share of i depends on substitution by all producers k. The extent to which substitution by producer k matters depends on how unequally k is exposed to i through its different inputs, on how large k is, and on how far away from 1 is the elasticity of substitution in production of k. If k is small, or is exposed in the same way to i through all of its inputs, then the extent to which it can substitute amongst its inputs is irrelevant. If the elasticity of substitution of k is equal to 1, then the direct and indirect relative demand expenditure for i arising from k does not change in response to shocks. Equation (7) can be seen as a centrality measure which combines structural microeconomic elasticities of substitution and features of the network.32
The Cobb–Douglas specification is the knife-edge special case where all the second-order terms are equal to zero and where the first-order approximation is globally accurate. This occurs because sales shares, and more generally, the whole input–output matrix, are constant and can be taken to be exogenous. Away from the Cobb–Douglas case, sales shares and the input–output matrix respond endogenously to shocks, and this is precisely what gives rise to the nonlinearities which are captured by the second-order approximation.
GE Elasticities of Substitution
A Network-Irrelevance Result
To build more intuition, we provide a benchmark irrelevance result where the deviation from Hulten's approximation does not depend on the network structure.33 The key assumptions required for obtaining this irrelevance result are: (1) productivity shocks are factor-augmenting; (2) the structural microeconomic elasticities of substitution are all the same.
Once the economy is written in standard form, the shocks are factor-augmenting if they only hit producers i which have the primary factor as their only input, i.e. if 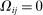 for every
for every 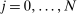 . In other words, the productivity shocks
. In other words, the productivity shocks 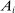 hitting producers i which do not have the primary factor as their only input are kept at their steady-state values of
hitting producers i which do not have the primary factor as their only input are kept at their steady-state values of 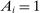 .
.
Corollary 1. (Network Irrelevance)Consider a nested-CES model in standard form with a single factor, uniform elasticities of substitution 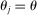 for every j, and with factor-augmenting shocks. Aggregate output is given by the closed-form expression
for every j, and with factor-augmenting shocks. Aggregate output is given by the closed-form expression
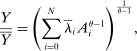
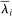 is the steady-state Domar weight of i. The second-order macroeconomic impact of factor-augmenting microeconomic shocks is given by
is the steady-state Domar weight of i. The second-order macroeconomic impact of factor-augmenting microeconomic shocks is given by
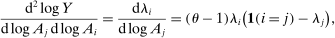
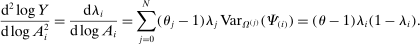
In words, if we consider factor-augmenting shocks, and if all microeconomic elasticities of substitution are the same, then the network structure remains irrelevant, even though there are deviations from Hulten's approximation. In this special case, the Domar weights and the structural microeconomic elasticities of substitution are sufficient statistics for the second-order effects.In fact, the result is true not only locally, but also globally.
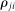 which are uniform and constant
which are uniform and constant
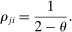
Energy Example—One Factor
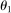 :
:
 :
:
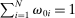 .
.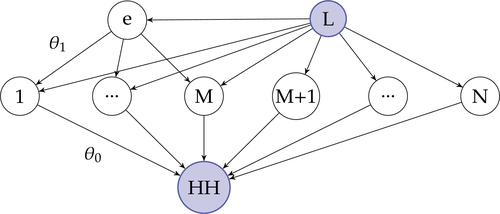
An illustration of the economy with a near-universal intermediate input which we call energy. Each downstream producer substitutes across labor and energy with elasticity θ1 < 1. The household can substitute across final goods with elasticity of substitution θ0 > θ1. Energy is produced from labor with constant returns.
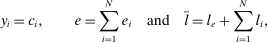
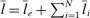 .
.Producer i's steady-state sales share is 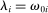 , the intermediate input share of industry i is
, the intermediate input share of industry i is 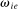 , and the sales share of energy is
, and the sales share of energy is 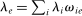 .
.
We simplify the example further by supposing that all final sectors are equally sized with 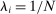 , and that
, and that 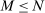 producers use energy with the same steady-state intermediate input share
producers use energy with the same steady-state intermediate input share  , while the other
, while the other 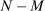 producers use no energy at all so that
producers use no energy at all so that 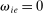 . We set
. We set 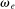 to ensure that
to ensure that 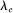 stays constant. We take
stays constant. We take 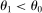 and
and 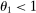 .
.
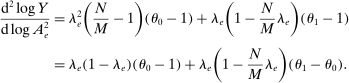
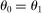 as in Corollary 1. The second term is a network-dependent correction that takes into account the fact that
as in Corollary 1. The second term is a network-dependent correction that takes into account the fact that 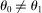 .
. , these equations become
, these equations become
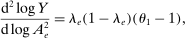
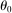 drops out completely. The fact that
drops out completely. The fact that 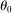 is irrelevant when
is irrelevant when 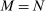 is a manifestation of the general principle stated in Proposition 7. When
is a manifestation of the general principle stated in Proposition 7. When 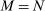 , energy is a universal input and hence
, energy is a universal input and hence 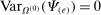 . In this case, the household is symmetrically exposed to shocks to energy via the different downstream producers, and so the elasticity of substitution in consumption
. In this case, the household is symmetrically exposed to shocks to energy via the different downstream producers, and so the elasticity of substitution in consumption 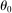 is irrelevant.
is irrelevant.When  instead,
instead,  matters, with a weight that decreases with N. Through the lens of Proposition 7,
matters, with a weight that decreases with N. Through the lens of Proposition 7, 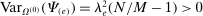 is decreasing in M: as heterogeneity in energy intensity across downstream producers increases, the ability of the household to substitute across these producers matters more and more.
is decreasing in M: as heterogeneity in energy intensity across downstream producers increases, the ability of the household to substitute across these producers matters more and more.
Because 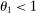 , when
, when 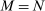 , the second-order approximation magnifies negative the macroeconomic impact of negative shocks to energy compared to the first-order approximation. As M decreases, this effect becomes weaker, since a lower M means that energy is less of a universal input, and so it becomes easier to substitute away from it further downstream across producers with different energy intensities. The sign of the effect can even flip if M is low enough and if
, the second-order approximation magnifies negative the macroeconomic impact of negative shocks to energy compared to the first-order approximation. As M decreases, this effect becomes weaker, since a lower M means that energy is less of a universal input, and so it becomes easier to substitute away from it further downstream across producers with different energy intensities. The sign of the effect can even flip if M is low enough and if 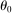 is high enough above 1.
is high enough above 1.
Macro-Influence—One Factor
A final implication of Proposition 7 is that it is only the producer's role as a supplier that matters, not its role as a consumer.34
Proposition 8. (Macro-Influence)Consider a nested-CES model in standard form with a single factor. Suppose that all producers k have the same expenditures on producers i and j so that 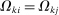 for all k. Then
for all k. Then
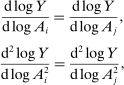
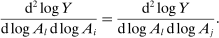
The intuition is that, in a one-factor model, we can normalize the wage to 1, and then aggregate output, which is equal to real factor income, depends only on the prices of final goods. A change in the size of the ith industry does not affect its price. Hence, a productivity shock travels downstream from suppliers to their consumers by lowering their marginal costs and hence their prices, but it does not travel upstream from consumers to their suppliers. This result fails whenever there are multiple factors, and by implication when the model does not feature constant returns to scale.35
4.2 Multiple Factors
We now generalize the results of the previous section to allow for multiple factors of production. This in turn opens the door to modeling limited-reallocation and decreasing-returns-to-scale via producer and industry-specific fixed factors.
We sometime use separate uppercase indices to denote the producers that correspond to factors, and lowercase indices to denote all other producers. For example, we sometime use  to denote the Domar weight, or income share, of factor f, and Λ to denote the
to denote the Domar weight, or income share, of factor f, and Λ to denote the 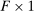 vector of factor shares.
vector of factor shares.
Proposition 9. (Second-Order Network Centrality With Multiple Factors)Consider a nested-CES model in standard form. Then
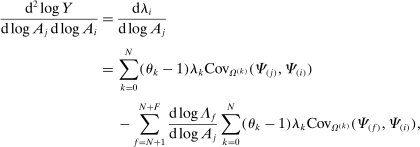 (8)
(8)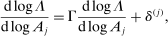 (9)
(9)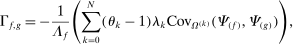
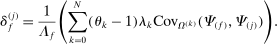
Note that we can rewrite equation (8) as a function of 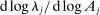 using the identity
using the identity 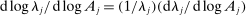 . Proposition 9 can then be seen as a full characterization of the elasticities of the Domar weights of the different producers to the different shocks.
. Proposition 9 can then be seen as a full characterization of the elasticities of the Domar weights of the different producers to the different shocks.
The intuition is the following. The first set of summands on the right-hand side of equation (8) are exactly those in equation (6) in Proposition 7: these terms capture how substitution by downstream producers k in response to a shock to j changes the sales share of i. The second set of summands in equation (8) take into account the fact that, when there are multiple factors, the shock also changes relative factor prices, and substitution in response to changes in factor prices in turn affects the sales share of i.
Consider, for example, a negative shock 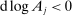 to producer j. Imagine that this shock increases the price of factor f relative to the prices of other factors, so that
to producer j. Imagine that this shock increases the price of factor f relative to the prices of other factors, so that 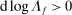 . Now consider the response of a producer k to this change. If
. Now consider the response of a producer k to this change. If 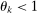 , producer k increases its expenditure share on producers that are more exposed to factor f as measured by
, producer k increases its expenditure share on producers that are more exposed to factor f as measured by 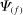 . If these producers are also more exposed to i, as measured by
. If these producers are also more exposed to i, as measured by 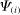 , then the substitution increases the sales share of i. These changes must be cumulated across producers k and factors f. The total effect on the relative demand expenditure for producer i, and hence on its sales share, is the sum of the effect of substitutions in response to the initial impulse
, then the substitution increases the sales share of i. These changes must be cumulated across producers k and factors f. The total effect on the relative demand expenditure for producer i, and hence on its sales share, is the sum of the effect of substitutions in response to the initial impulse 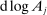 , as well as the substitutions in responses to changes in relative factor prices captured by
, as well as the substitutions in responses to changes in relative factor prices captured by 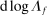 .
.
Equation (9) in turn determines how factor shares 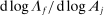 respond to different shocks. For a given set of factor prices, a shock to j affects the relative demand expenditure for each factor, and hence the factor income shares, as measured by the
respond to different shocks. For a given set of factor prices, a shock to j affects the relative demand expenditure for each factor, and hence the factor income shares, as measured by the 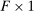 vector
vector 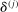 . This change in the factor income shares then causes further substitution through the network, leading to additional changes in relative factor shares and prices. The impact of the change in the relative share or price of factor g on the relative demand expenditure for factor f is measured by the fgth element of the
. This change in the factor income shares then causes further substitution through the network, leading to additional changes in relative factor shares and prices. The impact of the change in the relative share or price of factor g on the relative demand expenditure for factor f is measured by the fgth element of the 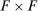 matrix
matrix  . Crucially, the matrix
. Crucially, the matrix  does not depend on which producer j is being shocked.
does not depend on which producer j is being shocked.
We can verify that we get back Proposition 7 when there is only a single factor, since in that case the exposure vector  , corresponding to the unique factor, is equal to a vector of all ones, and so the second set of summands in equation (8) is identically zero.
, corresponding to the unique factor, is equal to a vector of all ones, and so the second set of summands in equation (8) is identically zero.
Just like in the case of a single factor and for the same reasons, the Cobb–Douglas specification is the knife-edge special case where all the second-order terms are equal to zero and where the first-order approximation is globally accurate because sales shares, and more generally the whole input–output matrix, are constant and can be taken to be exogenous.
GE Elasticities of Substitution
A Network-Irrelevance Result
In the special case where all microeconomic elasticities of substitution are the same, we once again obtain a network-irrelevance result. However, because there are multiple factors, it is not enough to consider factor-augmenting shocks as we did in the case of a single factor, and we must instead focus on shocks that increase the overall quantities of the different factors.
Corollary 2. (Network Irrelevance)Consider a nested-CES model in standard form with uniform elasticities of substitution  for every j, and shocks
for every j, and shocks  to the supplies of the different factors f. Aggregate output is given by the following closed-form expression:
to the supplies of the different factors f. Aggregate output is given by the following closed-form expression:
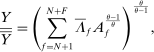
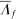 is the Domar weight of f at steady state. The second-order macroeconomic impact of microeconomic shocks to the supplies of factors is given by
is the Domar weight of f at steady state. The second-order macroeconomic impact of microeconomic shocks to the supplies of factors is given by
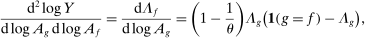
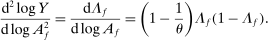
In this special case, the Domar weight and the structural microeconomic elasticities of substitution are sufficient statistics for the second-order effects. In fact, the result is true not only locally, but also globally.
A consequence of this corollary is that whenever all the micro-elasticities of substitution are the same and equal to θ, the GE elasticity of substitution 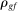 between any two factors f and g is also equal to θ.
between any two factors f and g is also equal to θ.
Energy Example—Multiple Factors
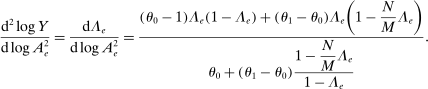
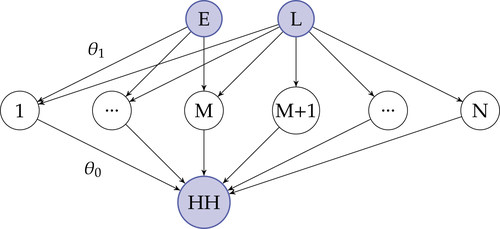
An illustration of the economy with a near-universal input which we treat as energy. Each industry has different shares of labor and energy and substitutes across labor and energy with elasticity θ1 < 1. The household can substitute across goods with elasticity of substitution θ0 > θ1. Labor and energy are in fixed supply.
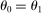 , the shape of the network becomes irrelevant. Additionally, in the extreme case where energy becomes a universal input
, the shape of the network becomes irrelevant. Additionally, in the extreme case where energy becomes a universal input 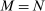 , the elasticity
, the elasticity 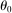 drops out of the formula because producers are uniformly exposed to energy:
drops out of the formula because producers are uniformly exposed to energy:
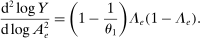
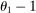 instead of
instead of 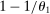 . This reflects the aforementioned fact that in contrast to the case of a single factor, labor cannot be reallocated to the production of energy following a negative shock to energy, which further amplifies the negative impact of the energy shock.
. This reflects the aforementioned fact that in contrast to the case of a single factor, labor cannot be reallocated to the production of energy following a negative shock to energy, which further amplifies the negative impact of the energy shock.Macro-Influence—Multiple Factors
In contrast to the case of a single factor, shocks to prices now propagate downstream and upstream. The result derived in Proposition 8 when there is only one factor breaks down when there are multiple factors: two producers with identical demand chains do not necessarily have the same importance. This is because they might have different direct and indirect exposures to the different factors. As a result, the role of a producer as a consumer matters in addition to its role as a supplier.
5 Beyond CES
The input–output covariance operator defined in equation (5) is a key concept capturing the substitution patterns in economies where all production and utility functions are nested-CES functions. In this section, we generalize this input–output covariance operator in such a way that allows us to work with arbitrary production functions.
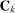 , we define the Allen–Uzawa elasticity of substitution between inputs x and y as
, we define the Allen–Uzawa elasticity of substitution between inputs x and y as
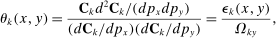
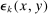 is the elasticity of the demand by producer k for input x with respect to the price
is the elasticity of the demand by producer k for input x with respect to the price 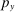 of input y, and
of input y, and 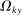 is the expenditure share in cost of input y.
is the expenditure share in cost of input y.Note the following properties. Because of the symmetry of partial derivatives, we have 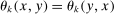 . Because of the homogeneity of degree 1 of the cost function in the prices of inputs, we have the homogeneity identity
. Because of the homogeneity of degree 1 of the cost function in the prices of inputs, we have the homogeneity identity 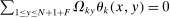 .
.
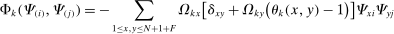 (11)
(11)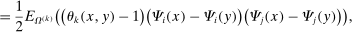 (12)
(12)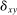 is the Kronecker delta,
is the Kronecker delta, 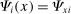 and
and 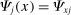 , and the expectation on the second line is over x and y. The second line can be obtained from the first using the symmetry of Allen–Uzawa elasticities of substitution and the homogeneity identity.
, and the expectation on the second line is over x and y. The second line can be obtained from the first using the symmetry of Allen–Uzawa elasticities of substitution and the homogeneity identity.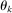 , all the cross Allen–Uzawa elasticities are identical with
, all the cross Allen–Uzawa elasticities are identical with 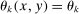 if
if 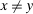 , and the own Allen-Uzawa elasticities are given by
, and the own Allen-Uzawa elasticities are given by 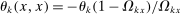 . It is easy to verify that we then recover the input–output covariance operator:
. It is easy to verify that we then recover the input–output covariance operator:
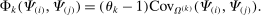
Even outside the CES case, the input–output substitution operator shares many properties with the input–output covariance operator. For example, it is immediate to verify that:  is bilinear in
is bilinear in  and
and  ;
; 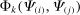 is symmetric in
is symmetric in 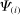 and
and 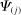 ; and
; and 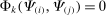 whenever
whenever 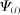 or
or 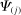 is a constant.
is a constant.
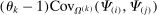 by
by 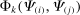 . For example, equation (8) in Proposition 9 becomes
. For example, equation (8) in Proposition 9 becomes
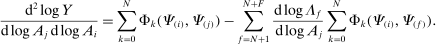
Intuitively, 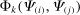 captures the way in which k redirects demand expenditure towards i in response to proportional unit decline in the price of j. To see this, we make use of the following observation: the elasticity of the expenditure share of producer k on input x with respect to the price of input y is given by
captures the way in which k redirects demand expenditure towards i in response to proportional unit decline in the price of j. To see this, we make use of the following observation: the elasticity of the expenditure share of producer k on input x with respect to the price of input y is given by 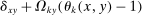 . Equation (11) requires considering, for each pair of inputs x and y, how much the proportional reduction
. Equation (11) requires considering, for each pair of inputs x and y, how much the proportional reduction  in the price of y induced by a unit proportional reduction in the price of j causes producer k to increase its expenditure share on x (as measured by
in the price of y induced by a unit proportional reduction in the price of j causes producer k to increase its expenditure share on x (as measured by 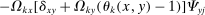 ) and how much x is exposed to i (as measured by
) and how much x is exposed to i (as measured by 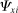 ).
).
Equation (12) says that this amounts to considering, for each pair of inputs x and y, whether or not increased exposure to j as measured by 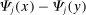 , corresponds to increased exposure to i as measured by
, corresponds to increased exposure to i as measured by 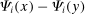 , and whether x and y are complements or substitutes as measured by
, and whether x and y are complements or substitutes as measured by 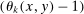 . If x and y are substitutes, and
. If x and y are substitutes, and 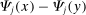 and
and 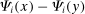 are both positive, then substitution across x and y by k, in response to a shock to a decrease in the price of j, increases demand for i.
are both positive, then substitution across x and y by k, in response to a shock to a decrease in the price of j, increases demand for i.
6 Quantitative Illustration
In this section, we develop some illustrative quantitative applications of our results to gauge the practical importance of the nonlinearities that we have identified. We perform three exercises focusing on macroeconomic phenomena at different frequencies. First, we calibrate a multi-sector business-cycle model with sectoral productivity shocks. We match the observed input–output data, and use the best available information to choose the structural (micro) elasticities of substitution, and we match the volatility of sectoral shocks at business-cycle frequencies. We compare the outcome of the nonlinear model to its first-order approximation. In the second exercise, we study the macroeconomic impact of the energy crisis of the 1970s using a nonparametric generalization of Hulten (1978) that takes second-order terms into account. In the third and final exercise, we investigate the importance of nonlinearities which underpin Baumol's cost disease for long-run aggregate TFP growth. All our exercises suggest that production is highly nonlinear.
6.1 A Quantitative Multi-Sector Business-Cycle Model With Sectoral Productivity Shocks
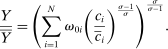
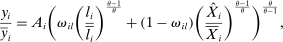
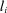 and intermediate inputs
and intermediate inputs 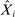 .
.We consider two polar opposite possibilities for the labor market: the case where each labor type is specific to each industry and cannot be reallocated, and the case where there is a common factor which can be reallocated across all industries. In light of increasing evidence (see, e.g., Acemoglu, Autor, Dorn, Hanson, and Price (2016), Autor, Dorn, and Hanson (2016), Notowidigdo (2011)) that labor is not easily reallocated across industries or regions after shocks in the short run, we view the no-reallocation case as more realistic for modeling the short-run impact of shocks, and the full-reallocation case as better suited to study the medium- to long-run impact shocks.38
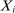 is given by
is given by
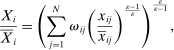
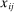 are intermediate inputs from industry j used by industry i.
are intermediate inputs from industry j used by industry i.Data and Calibration
We work with the 88 sector U.S. KLEMS annual input–output data from Dale Jorgenson and his collaborators, dropping the government sectors. The data set contains sectoral output and inputs from 1960 to 2005. We use the sector-level TFP series computed by Carvalho and Gabaix (2013) using the methodology of Jorgenson, Gollop, and Fraumeni (1987).
We calibrate the expenditure share parameters to match the input–output table, using 1982 (the middle of the sample) as the base year. We specify sectoral TFP shocks to be log-normally distributed so that  , where
, where  is the sample variance of log TFP growth for industry i. We work with uncorrelated sectoral shocks since the average correlation between sectoral growth rates is small (less than
is the sample variance of log TFP growth for industry i. We work with uncorrelated sectoral shocks since the average correlation between sectoral growth rates is small (less than 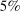 ). Our results are not significantly affected if we matched the whole covariance matrix of sectoral TFP instead.
). Our results are not significantly affected if we matched the whole covariance matrix of sectoral TFP instead.
We consider shocks at annual and quadrennial horizons, the latter corresponding to the average period of a business cycle. The average standard deviation at a quadrennial frequency is about twice its value at an annual frequency. In fact, it is the only difference between the annual and quadrennial calibrations. Nonlinearities, which matter more for bigger shocks, are more important at a quadriennal frequency than at an annual frequency.
Our specification assumes only three distinct structural microeconomic elasticities of substitution. This is because estimates of more disaggregated elasticities are not available. For our benchmark calibration, we set 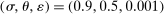 . We set the elasticity of substitution in consumption
. We set the elasticity of substitution in consumption 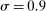 , following Atalay (2017), Herrendorf, Rogerson, and Valentinyi (2013), and Oberfield and Raval (2014), all of whom used an elasticity of substitution in consumption (across industries) of slightly less than 1. For the elasticity of substitution across value-added and intermediate inputs, we set
, following Atalay (2017), Herrendorf, Rogerson, and Valentinyi (2013), and Oberfield and Raval (2014), all of whom used an elasticity of substitution in consumption (across industries) of slightly less than 1. For the elasticity of substitution across value-added and intermediate inputs, we set 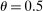 . This accords with the estimates of Atalay (2017), who estimated this parameter to be between 0.4 and 0.8, as well as Boehm, Flaaen, and Pandalai-Nayar (2017), who estimated this elasticity to be close to zero. Finally, we set the elasticity of substitution across intermediate inputs to be
. This accords with the estimates of Atalay (2017), who estimated this parameter to be between 0.4 and 0.8, as well as Boehm, Flaaen, and Pandalai-Nayar (2017), who estimated this elasticity to be close to zero. Finally, we set the elasticity of substitution across intermediate inputs to be 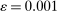 , which matches the estimates of Atalay (2017).
, which matches the estimates of Atalay (2017).
Owing to uncertainty surrounding the estimates for 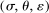 , we include many robustness checks in Tables IV–VII in Appendix D of the Supplemental Material. In the main text in Table I, we focus on four sets of elasticities
, we include many robustness checks in Tables IV–VII in Appendix D of the Supplemental Material. In the main text in Table I, we focus on four sets of elasticities 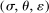 : our benchmark calibration
: our benchmark calibration 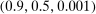 ; a calibration with lower but still plausible elasticities
; a calibration with lower but still plausible elasticities 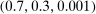 ; a calibration with higher elasticities
; a calibration with higher elasticities 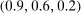 ; and a (close to) Cobb–Douglas calibration
; and a (close to) Cobb–Douglas calibration 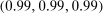 . In Appendix D of the Supplemental Material, we report robustness checks for different values of these elasticities on a grid with
. In Appendix D of the Supplemental Material, we report robustness checks for different values of these elasticities on a grid with 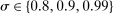 ,
, 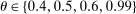 , and
, and 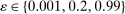 . Our results in Table I are not sensitive to the exact value of
. Our results in Table I are not sensitive to the exact value of 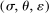 provided that the elasticities are collectively low enough that the calibration matches the observed volatility of the Domar weights.
provided that the elasticities are collectively low enough that the calibration matches the observed volatility of the Domar weights.
|
|
Mean |
Std |
Skew |
Ex-Kurtosis |
|
|---|---|---|---|---|---|
|
Full Reallocation—Annual |
|||||
|
(0.7, 0.3, 0.001) |
−0.0023 |
0.011 |
−0.10 |
0.1 |
0.090 |
|
(0.9, 0.5, 0.001) |
−0.0022 |
0.011 |
−0.08 |
0.0 |
0.069 |
|
(0.9, 0.6, 0.2) |
−0.0020 |
0.011 |
−0.05 |
0.0 |
0.056 |
|
(0.99, 0.99, 0.99) |
−0.0013 |
0.011 |
0.01 |
0.0 |
0.001 |
|
No Reallocation—Annual |
|||||
|
(0.7, 0.3, 0.001) |
−0.0045 |
0.012 |
−0.31 |
0.4 |
0.171 |
|
(0.9, 0.5, 0.001) |
−0.0034 |
0.012 |
−0.18 |
0.1 |
0.115 |
|
(0.9, 0.6, 0.2) |
−0.0024 |
0.011 |
−0.11 |
0.1 |
0.068 |
|
(0.99, 0.99, 0.99) |
−0.0011 |
0.011 |
0.00 |
0.0 |
0.001 |
|
Full Reallocation—Quadrennial |
|||||
|
(0.7,0.3,.0.001) |
−0.0118 |
0.026 |
−0.4 |
0.4 |
0.307 |
|
(0.9, 0.5, 0.001) |
−0.0113 |
0.026 |
−0.28 |
0.4 |
0.176 |
|
(0.9, 0.6, 0.2) |
−0.0100 |
0.026 |
−0.23 |
0.2 |
0.133 |
|
(0.99, 0.99, 0.99) |
−0.0058 |
0.025 |
0.01 |
0.0 |
0.003 |
|
No Reallocation—Quadrennial |
|||||
|
(0.7, 0.3, 0.001) |
−0.0270 |
0.037 |
−2.18 |
12.7 |
0.404 |
|
(0.9, 0.5, 0.001) |
−0.0187 |
0.030 |
−1.11 |
3.6 |
0.267 |
|
(0.9, 0.6, 0.2) |
−0.0129 |
0.027 |
−0.44 |
0.7 |
0.154 |
|
(0.99, 0.99, 0.99) |
−0.0057 |
0.025 |
0.00 |
0.0 |
0.002 |
|
Annual Data |
– |
0.015 |
– |
– |
0.13 |
|
Quadrennial Data |
– |
0.030 |
– |
– |
0.27 |
- a For the data, we use the demeaned growth rate of aggregate TFP. For the model, we use the sample moments of log output. The simulated moments are calculated from 50,000 draws. Skewness and kurtosis of the data are impossible to estimate with enough precision and so we do not report them.
Since the volatility of Domar weights is a measure of the size of the second-order terms in the model, we use the volatility of Domar weights as a sanity check for our calibration. Specifically, we target 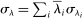 , where
, where 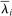 is the time-series average of the ith Domar weight and
is the time-series average of the ith Domar weight and 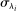 is the time-series standard deviation of industry i's log-differenced Domar weight. In our data, at annual frequency,
is the time-series standard deviation of industry i's log-differenced Domar weight. In our data, at annual frequency, 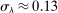 , and for quadrennial frequency,
, and for quadrennial frequency, 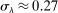 . With no labor reallocation, our baseline calibrations match these numbers relatively well; the lower-elasticity calibrations overshoot; the higher-elasticity calibrations undershoot; and the Cobb–Douglas calibrations deliver zero volatility of the Domar weights. Allowing for labor reallocation reduces the volatility of the Domar weights.39
. With no labor reallocation, our baseline calibrations match these numbers relatively well; the lower-elasticity calibrations overshoot; the higher-elasticity calibrations undershoot; and the Cobb–Douglas calibrations deliver zero volatility of the Domar weights. Allowing for labor reallocation reduces the volatility of the Domar weights.39
Results
Table I displays the mean, standard deviation, skewness, and excess kurtosis of log aggregate output for various specifications. For comparison, the table also shows these moments for aggregate TFP growth in the data.40 In addition, we also report the volatility of the Domar weights, both in the model and in the data. Since we have too few annual (and even fewer quadrennial) observations of aggregate TFP, we do not report the skewness and excess kurtosis: the implied confidence intervals for these estimates would be so large as to make the point estimates uninformative. In Appendix D of the Supplemental Material, we report results for numerous other permutations of the elasticities of substitution for robustness.
Overall, given our elasticities of substitution, the model with full reallocation is unable to replicate the volatility of the Domar weights at either annual or quadrennial frequency, suggesting that this model is not nonlinear enough to match the movements in the Domar weights as arising from sectoral productivity shocks. On the other hand, the model without reallocation is able to match the volatility of the Domar weights, which is consistent with the intuition of Section 3.
Let us consider each moment in turn, starting with the mean. For our benchmark calibration 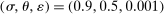 , the model without reallocation matches the volatility of Domar weights at both annual and quadrennial frequency. The reductions in the mean are around
, the model without reallocation matches the volatility of Domar weights at both annual and quadrennial frequency. The reductions in the mean are around 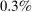 at annual and just under
at annual and just under 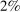 at quadrennial frequency. Since our log-normal shocks are calibrated to have a mean of 1 in levels, as we increase the variance, the mean of the log declines. We can net out this mechanical effect by subtracting the average loss in performance from the ones in the log-linear Cobb–Douglas model. At an annual frequency, this results in a loss from nonlinearities of
at quadrennial frequency. Since our log-normal shocks are calibrated to have a mean of 1 in levels, as we increase the variance, the mean of the log declines. We can net out this mechanical effect by subtracting the average loss in performance from the ones in the log-linear Cobb–Douglas model. At an annual frequency, this results in a loss from nonlinearities of 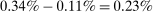 , and at a quadrennial frequency, the loss from nonlinearities is
, and at a quadrennial frequency, the loss from nonlinearities is 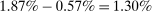 . These numbers, which identify the welfare costs of sectoral shocks arising from concavity in production, can be compared with the welfare costs of fluctuations à la Lucas (1987) arising from concavity in utility, which are around
. These numbers, which identify the welfare costs of sectoral shocks arising from concavity in production, can be compared with the welfare costs of fluctuations à la Lucas (1987) arising from concavity in utility, which are around 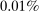 and
and 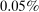 , respectively, in these calibrations. The reduction in the mean increases as we pump up the degree of nonlinearity, and so do the corresponding losses from nonlinearities.
, respectively, in these calibrations. The reduction in the mean increases as we pump up the degree of nonlinearity, and so do the corresponding losses from nonlinearities.
A qualitatively similar pattern holds for the model with full reallocation. In that case, the reductions in the mean are smaller: 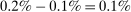 at an annual frequency and
at an annual frequency and 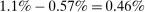 at a quadrennial frequency. Unsurprisingly, the approximately Cobb–Douglas model behaves similarly regardless of the mobility of labor—this follows from the fact that Hulten's theorem holds globally for a Cobb–Douglas model where no labor reallocation takes place in equilibrium whether or not it is allowed.
at a quadrennial frequency. Unsurprisingly, the approximately Cobb–Douglas model behaves similarly regardless of the mobility of labor—this follows from the fact that Hulten's theorem holds globally for a Cobb–Douglas model where no labor reallocation takes place in equilibrium whether or not it is allowed.
At an annual frequency, both models undershoot a bit on the overall volatility of aggregate TFP. One reason why the model undershoots on standard deviation, particularly at annual frequency, is that we restrict the industry-level productivity shocks to be independent, whereas in the data, particularly at higher frequencies, they feature some correlation. At a quadrennial frequency, the model better matches the volatility of aggregate TFP. The degree of nonlinearity makes little difference for the volatility of aggregate TFP at an annual frequency.41 Nonlinearities matter more for the volatility of aggregate TFP at a quadrennial frequency because the shocks are larger.
Finally, the models with and without reallocation both generate negative skewness and some positive excessive kurtosis (in fact, a very high amount for the quadrennial specifications without reallocation). The skewness and excess kurtosis fatten the left tail of the distribution, providing an endogenous explanation for “rare disasters.” Unlike Acemoglu, Ozdaglar, and Tahbaz-Salehi (2017) or Barro (2006), to achieve rare disasters, we do not need to assume fat-tailed exogenous shocks nor rule out “rare bonanzas” a priori. Instead, these features are endogenously generated by the nonlinearities in the model. This can be seen in Figure 5, where we plot the histograms for the benchmark calibrations with no reallocation (which match the volatility of Domar weights) and for a log-linear approximation subject to the same shocks. As expected, nonlinearities are more important at a quadrennial frequency than at an annual frequency because the shocks are larger (more volatile).
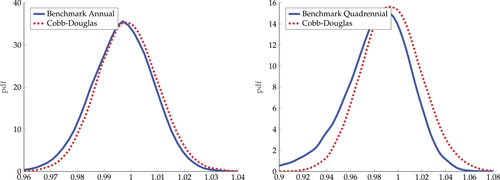
The left panel shows the distribution of aggregate output for the benchmark model and log-linear model at an annual frequency. The right panel shows these for shocks at a quadrennial frequency. The difference between the two frequencies is that shocks are larger (their volatility is higher) at a quadrennial than at an annual frequency. The benchmark model has (σ,θ,ε)=(0.9,0.5,0.001) and no labor reallocation. Note that the scales are different in these two figures.
We also consider the response of aggregate output to shocks to specific industries, using our benchmark calibration. It turns out that for a large negative shock, the “oil and gas” industry produces the largest negative response in aggregate output, despite the fact it is not the largest industry in the economy. Figure 6 plots the response of aggregate output for shocks to the oil and gas industry as well as for the “retail trade (excluding automobiles)” industry. The retail trade industry has a similar sales share, and therefore, to a first order, both industries are equally important. As expected, the nonlinear model amplifies negative shocks and mitigates positive shocks. However, whereas output is roughly log-linear for shocks to retail trade, output is highly nonlinear with respect to shocks to oil and gas.
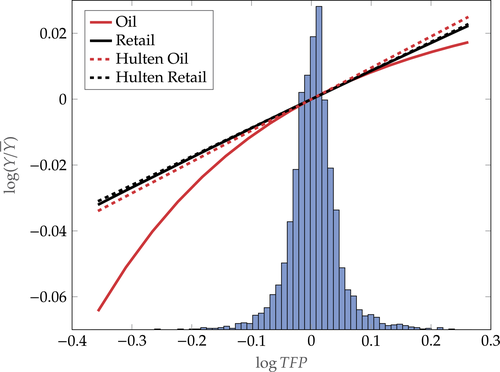
The effect of TFP shocks to the oil and gas industry and the retail trade industry. Both industries have roughly the same sales share, and so they are equally important up to a first-order approximation (dotted line). The nonlinear model is more fragile to both shocks than the log-linear approximation. The “oil and gas” industry is significantly more important than “retail trade” for large negative shocks. The histogram is the empirical distribution of sectoral annual TFP shocks pooled over the whole sample. The model has (σ,θ,ε)=(0.9,0.5,0.001) with no labor reallocation and no adjustment costs.
The intuition for this asymmetry comes from the examples in Figures 3 and 4. “Oil and gas” is an approximately universal input, so that the downstream elasticity of substitution (in consumption) σ is less relevant and the upstream elasticity of substitution (in production) θ is more relevant. Since 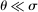 in our calibration, this means that output is more nonlinear in shocks to “oil and gas” than in shocks to “retail trade.” Furthermore, “oil and gas” have a relatively low share of intermediate input usage. As a result, in response to a negative shock, resources cannot be reallocated to boost the production of oil and gas. This means that we are closer to the economy depicted in Figure 4 than the one in Figure 3, with a correspondingly lower GE elasticity of substitution between oil and gas and everything else due to the lack of reallocation.
in our calibration, this means that output is more nonlinear in shocks to “oil and gas” than in shocks to “retail trade.” Furthermore, “oil and gas” have a relatively low share of intermediate input usage. As a result, in response to a negative shock, resources cannot be reallocated to boost the production of oil and gas. This means that we are closer to the economy depicted in Figure 4 than the one in Figure 3, with a correspondingly lower GE elasticity of substitution between oil and gas and everything else due to the lack of reallocation.
The strong asymmetry between the effects of positive and negative shocks is consistent with the empirical findings of Hamilton (2003) that oil price increases are much more important than oil price decreases.42
6.2 The Effect of Oil Shocks
In this section, we use the oil shocks of the 1970s to demonstrate the way nonlinearities can amplify the macroeconomic impact of industry-level shocks.43 To recap the history, starting in 1973, coordinated action by OPEC caused the price of crude oil to increase from 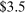 per barrel in 1972 to
per barrel in 1972 to 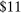 per barrel in 1974. In 1979, OPEC implemented a second round of quantity restrictions which caused the price of crude to soar to
per barrel in 1974. In 1979, OPEC implemented a second round of quantity restrictions which caused the price of crude to soar to 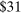 per barrel. Shortly after this, the Iranian revolution of 1979 and the ensuing Iraqi invasion of Iran caused further disruptions to global crude oil supply. The price peaked at
per barrel. Shortly after this, the Iranian revolution of 1979 and the ensuing Iraqi invasion of Iran caused further disruptions to global crude oil supply. The price peaked at 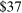 in 1980. Starting in the early 1980s, with the abdication of the Shah, OPEC's pricing structure collapsed and, in a bid to maintain its market share, Saudi Arabia flooded the market with inexpensive oil. In real terms, the price of crude oil declined back to its pre-crisis levels by 1986.
in 1980. Starting in the early 1980s, with the abdication of the Shah, OPEC's pricing structure collapsed and, in a bid to maintain its market share, Saudi Arabia flooded the market with inexpensive oil. In real terms, the price of crude oil declined back to its pre-crisis levels by 1986.
We adopt a nonparametric approach which allows us to account for the second-order macroeconomic impact of microeconomic shocks using ex post data. Instead of trying to predict how Domar weights change in response to a shock as would be required for a counterfactual exercise, we can simply observe it. Formally, we rely on the following result.
Proposition 10.Up to the second order in the vector 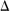 , we have
, we have
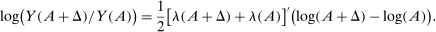
The idea of averaging weights across two periods is due to Törnqvist (1936). Proposition 10 relates the macroeconomic impact of microeconomic shocks to the size of the shock and the corresponding Domar weights before and after the shock.44
We measure the price of oil using the West Texas Intermediate Spot Crude Oil price from the Federal Reserve Database. Global crude oil production, measured in thousand tonne of oil equivalents, is from the OECD. World GDP, in current USD, is from the World Bank national accounts data. The choice of the pre and post Domar weight is not especially controversial. Crude oil, as a fraction of world GDP, increased from 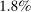 in 1972 to
in 1972 to 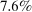 in 1979. Reassuringly, the Domar weight is back down to its pre-crisis level by 1986 (see Figure 7). This means that, taking the second-order terms into account, we need to weight the shock to the oil industry by
in 1979. Reassuringly, the Domar weight is back down to its pre-crisis level by 1986 (see Figure 7). This means that, taking the second-order terms into account, we need to weight the shock to the oil industry by 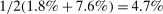 . Hence, the second-order terms amplify the shock by a factor of
. Hence, the second-order terms amplify the shock by a factor of 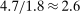 .
.
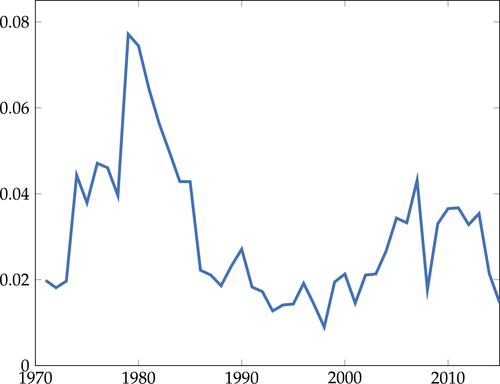
Global expenditures on crude oil as a fraction of world GDP.
Calibrating the size of the shock to the oil industry is more tricky, since it is not directly observed. If we assume that oil is an endowment, then we can simply measure the shock via changes in the physical quantity of production. To do this, we demean the log growth rate in global crude oil production, and take the shock to be the cumulative change in demeaned growth rates from 1973 to 1980, which gives us a shock of 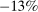 .45
.45
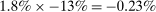
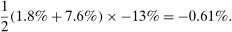
6.3 Baumol's Cost Disease and Long-Run Growth
Our final empirical exercise looks to quantify the importance of nonlinearities on long-run productivity growth. For this exercise, we use World KLEMS data for the United States from 1948 to 2014.
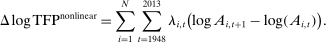
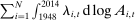 .
.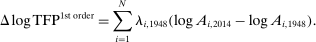
By comparing actual aggregate TFP growth and TFP growth in the counterfactual log-linear economy, we quantify the importance of Baumol's cost disease (Baumol (1967)): the notion that over time, because of complementarities, the sales shares of low-productivity-growth industries increase while those of high-productivity-growth industries decrease, thereby slowing down aggregate TFP growth.
By the end of the sample, aggregate TFP growth in the counterfactual log-linear or Cobb–Douglas economy is around 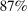 whereas actual TFP grew by
whereas actual TFP grew by 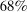 . Hence the presence of nonlinearities slowed down aggregate TFP growth by around 19 percentage points over the sample period.
. Hence the presence of nonlinearities slowed down aggregate TFP growth by around 19 percentage points over the sample period.
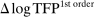 is a first-order approximation of actual aggregate TFP growth. A second-order approximation, which captures some of the nonlinearities, is given by
is a first-order approximation of actual aggregate TFP growth. A second-order approximation, which captures some of the nonlinearities, is given by
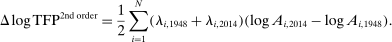
In Figure 8, we plot aggregate TFP growth using the nonlinear, first-order, and second-order measures. The gap between the nonlinear measure and the first-order approximation is sizeable, but that between the nonlinear measure and the second-order approximation is much smaller.
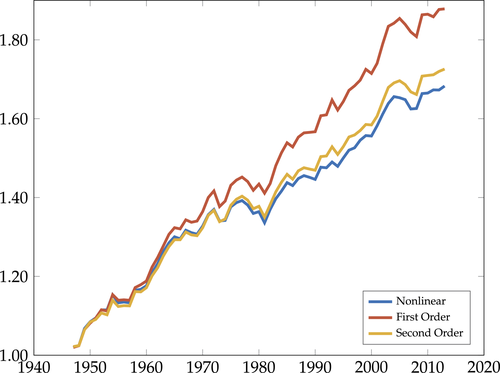
Cumulative change in TFP: nonlinear (actual), first-order approximation, and second-order approximation.
These findings are in some sense more general than Baumol's hypothesized mechanism. Traditionally, the mechanism for Baumol's cost disease is through prices: because of complementarities, as the prices of high-productivity-growth industries fall, their shares in aggregate output fall, resources are reallocated away from them, thereby reducing aggregate TFP growth. Alternative stories for structural transformation emphasize other mechanisms, principally, non-homotheticities whereby as real income increases, consumers increase their expenditures on industries that happen to have lower productivity growth.47 From the perspective of our framework, non-homotheticities and complementarities are both nonlinearities. Our calculations of the impact of nonlinearities encompass both types of mechanisms.48,49
7 Conclusion
The paper points to many unanswered questions. For instance, it shows that the macroeconomic impact of a microeconomic shock depends greatly on how quickly factors can be reallocated across production units. Since our structural model is static, we are forced to proxy for the temporal dimension of reallocation by resorting to successive comparative statics. In ongoing work, we investigate the dynamic adjustment process more rigorously and find that although we can think of the no-reallocation and perfect-reallocation cases as the beginning and end of the adjustment, the speed of adjustment also greatly depends on the microeconomic details. This means that the dynamic response of aggregate output to different shocks is greatly affected by issues like geographic or sectoral mobility of labor, even with perfect and complete markets that allow us to abstract from distributional issues. Our structural application also lacks capital accumulation and endogenous labor supply, and incorporating these into the present analysis is an interesting area for future work.
Furthermore, in this paper, we have focused exclusively on the way shocks affect aggregate output. In Baqaee and Farhi (2018a), we focused on how shocks affect factor shares and derived characterizations of the macroeconomic elasticities of substitution between factors and of the macroeconomic bias of technical change. In Baqaee and Farhi (2018b), we took up the related question of how shocks affect non-aggregate outcomes, namely, how shocks propagate from one producer to another, and how microeconomic variables comove with one another in a production network.
In addition, this paper assumes that aggregate final demand is homothetic. Non-homothetic aggregate final demand can arise from non-homothetic individual final demand or from the aggregation of heterogeneous but homothetic individual demands. In Baqaee and Farhi (2018b, 2019), we showed how to take these elements into account. In particular, in Baqaee and Farhi (2018b), we show how to combine input–output production networks with heterogeneous agents and non-homothetic final demand in closed economies. In Baqaee and Farhi (2019), we showed how to take these elements into account in trade models.
Finally, this paper assumes away non-technological frictions, but the forces we identify do not disappear in richer models with inefficient equilibria. Non-unitary elasticities of substitution in networks can amplify or attenuate the underlying distortions. In Baqaee and Farhi (2018c), we undertook a systematic characterization of these effects. We showed that in inefficient models, the “second-order” terms that we characterize in this paper can become first order.
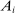 is a factor-augmenting shock, the relevant
is a factor-augmenting shock, the relevant 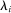 corresponds to a producer's bill for this factor as a share of GDP. This is because if we relabel the labor input of producer i as a new producer, we can represent a factor-augmenting shock to i's labor as a Hicks-neutral shock to this new producer.
corresponds to a producer's bill for this factor as a share of GDP. This is because if we relabel the labor input of producer i as a new producer, we can represent a factor-augmenting shock to i's labor as a Hicks-neutral shock to this new producer.
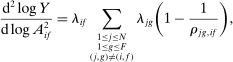
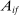 is a shock-augmenting factor f in the production of good i,
is a shock-augmenting factor f in the production of good i, 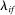 is the share of factor f in GDP arising from its use by producer i, and
is the share of factor f in GDP arising from its use by producer i, and 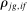 is the GE elasticity of substitution between factor f in the production of good i and factor g in the production of good j.
is the GE elasticity of substitution between factor f in the production of good i and factor g in the production of good j.
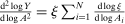 . So, for aggregate shocks, deviations from Hulten's theorem can only come from the input–output multiplier.
. So, for aggregate shocks, deviations from Hulten's theorem can only come from the input–output multiplier.
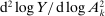 , but we can use these results to compute the welfare cost in Proposition 4 by noting that
, but we can use these results to compute the welfare cost in Proposition 4 by noting that 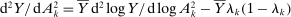 .
.
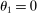 , we have
, we have 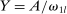 , where
, where 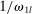 is the steady-state input–output multiplier. Therefore, although Hulten's approximation fails in log terms, Hulten's theorem is globally accurate in linear terms. This is a consequence of the fact that there is only one good. In Appendix B of the Supplemental Material, we generalize this example to multiple goods, and show that output can be very strongly nonlinear even with full labor reallocation.
is the steady-state input–output multiplier. Therefore, although Hulten's approximation fails in log terms, Hulten's theorem is globally accurate in linear terms. This is a consequence of the fact that there is only one good. In Appendix B of the Supplemental Material, we generalize this example to multiple goods, and show that output can be very strongly nonlinear even with full labor reallocation.
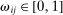 ,
, 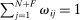 for all
for all 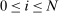 ,
, 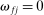 for all
for all 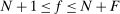 ,
, 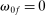 for all
for all 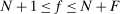 , and
, and  for all
for all  .
.
 to a factor industry g. The productivity shock is then just a shock to the endowment of the factor. For example, we have
to a factor industry g. The productivity shock is then just a shock to the endowment of the factor. For example, we have
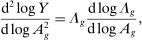
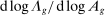 is the gth element of the vector
is the gth element of the vector 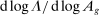 which solves the linear system
which solves the linear system
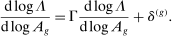 (10)
(10)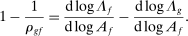
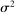 , whereas that of the nonlinear terms scales in
, whereas that of the nonlinear terms scales in 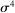 .
.
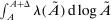 , and our formula approximates this integral by performing a first-order (log) approximation of the Domar weight
, and our formula approximates this integral by performing a first-order (log) approximation of the Domar weight 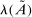 , or equivalently, a second-order (translog) approximation of aggregate output. In theory, if TFP is a continuous diffusion, then one can disaggregate time periods and compute the impact of shocks over a time period
, or equivalently, a second-order (translog) approximation of aggregate output. In theory, if TFP is a continuous diffusion, then one can disaggregate time periods and compute the impact of shocks over a time period  as
as 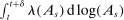 which can be seen as a repeated application of Hulten's theorem at every point in time over infinitesimal intervals of time. However, when TFP has jumps, then this decomposition no longer applies. In any case, even when it does apply, and when the required high-frequency data regarding TFP shocks and Domar weights are available, it can only be useful ex post to assess the changes in aggregate output over an elapsed period of time due to the TFP shocks
which can be seen as a repeated application of Hulten's theorem at every point in time over infinitesimal intervals of time. However, when TFP has jumps, then this decomposition no longer applies. In any case, even when it does apply, and when the required high-frequency data regarding TFP shocks and Domar weights are available, it can only be useful ex post to assess the changes in aggregate output over an elapsed period of time due to the TFP shocks 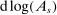 to a given sector given the observed path of Domar weight
to a given sector given the observed path of Domar weight 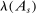 . It is of no use ex ante to predict how these future shocks will affect aggregate output because one would need to know how the Domar weight will change over time as a result of the shocks, and hence of no use to run counterfactuals. This latter part is precisely what the second-order approximation at the heart of our paper accomplishes.
. It is of no use ex ante to predict how these future shocks will affect aggregate output because one would need to know how the Domar weight will change over time as a result of the shocks, and hence of no use to run counterfactuals. This latter part is precisely what the second-order approximation at the heart of our paper accomplishes.
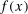 can be extended into a constant-returns function
can be extended into a constant-returns function 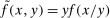 where
where 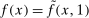 . Then, non-homotheticity in f is equivalent to a non-unitary elasticity of substitution between x and y in
. Then, non-homotheticity in f is equivalent to a non-unitary elasticity of substitution between x and y in 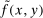 .
.
Appendix A: Proofs
Proof of Theorem 1.Since the first welfare theorem holds, the equilibrium allocation solves
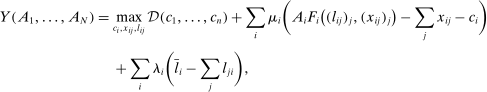
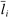 is the endowment of each labor type, and
is the endowment of each labor type, and 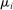 and
and 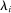 are Lagrange multipliers. The envelope theorem then implies that
are Lagrange multipliers. The envelope theorem then implies that
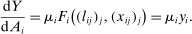
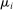 is equal to the price of i in the competitive equilibrium, then we are done.
is equal to the price of i in the competitive equilibrium, then we are done.Meanwhile, for each good j, either there exists another producer i using that good as an input, or the household must consume that input (otherwise, the input is irrelevant and has a price of zero). Hence, in a competitive equilibrium, we must have either
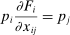 (13)
(13)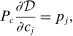 (14)
(14) is the ideal price index associated with
is the ideal price index associated with  (which we can take to be the numeraire). The expression above uses the fact that
(which we can take to be the numeraire). The expression above uses the fact that  is constant-returns-to-scale.
is constant-returns-to-scale.On the other hand, the first-order conditions of the social planners problem implies that for each j, either
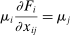 (15)
(15)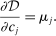 (16)
(16)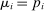 for every i. □
for every i. □
Proof of Theorem 2.Differentiate 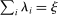 to get
to get
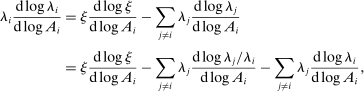
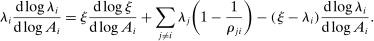
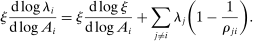 (17)
(17)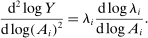
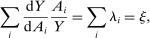
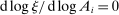 . □
. □
Proof of Proposition 4.We prove a slightly more general formulation with arbitrary variance covariance matrix and an arbitrary twice-differentiable utility function:
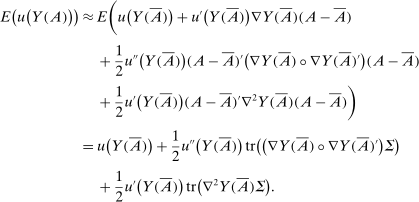
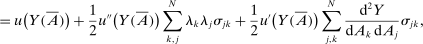
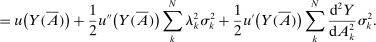
Proof of Proposition 3.
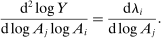 (18)
(18)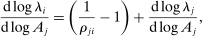 (19)
(19)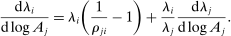 (20)
(20)
Proof of Proposition 5.The allocation for labor is
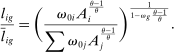
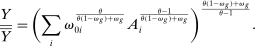
Then, for this economy,
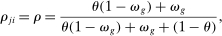
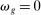 corresponds to
corresponds to
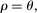
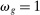 ,
,
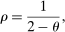
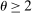 . For
. For 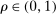 , we get something in between the perfectly reallocative and no-reallocation special cases. □
, we get something in between the perfectly reallocative and no-reallocation special cases. □
Proof of Proposition 6.Consumption is given by
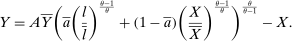
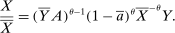
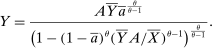
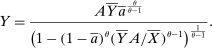
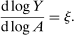
Proof of Proposition 7.This follows as a special case of Proposition 9. □
Proof of Corollary 1.The proof is similar to that of Corollary 2. □
Proof of Proposition 8.Denote the ith standard basis vector by  . Then, by assumption,
. Then, by assumption,  and
and 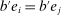 . Repeated multiplication implies that
. Repeated multiplication implies that 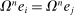 . This then implies that
. This then implies that 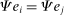 so that, in steady state,
so that, in steady state, 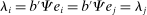 . So the first-order impact of a shock is the same. Furthermore, substitution into (7) shows that the second-order impact of a shock is also the same. □
. So the first-order impact of a shock is the same. Furthermore, substitution into (7) shows that the second-order impact of a shock is also the same. □
Proof of Proposition 9.Denote the 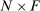 matrix corresponding to
matrix corresponding to 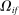 by
by 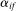 . By Shephard's lemma,
. By Shephard's lemma,
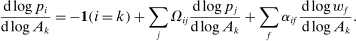 (21)
(21)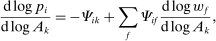 (22)
(22)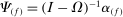 . Note that
. Note that 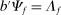 .
.Denote the household's final demand expenditure share  by
by 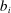 . Then, for a factor L, we have
. Then, for a factor L, we have
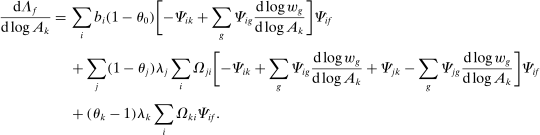
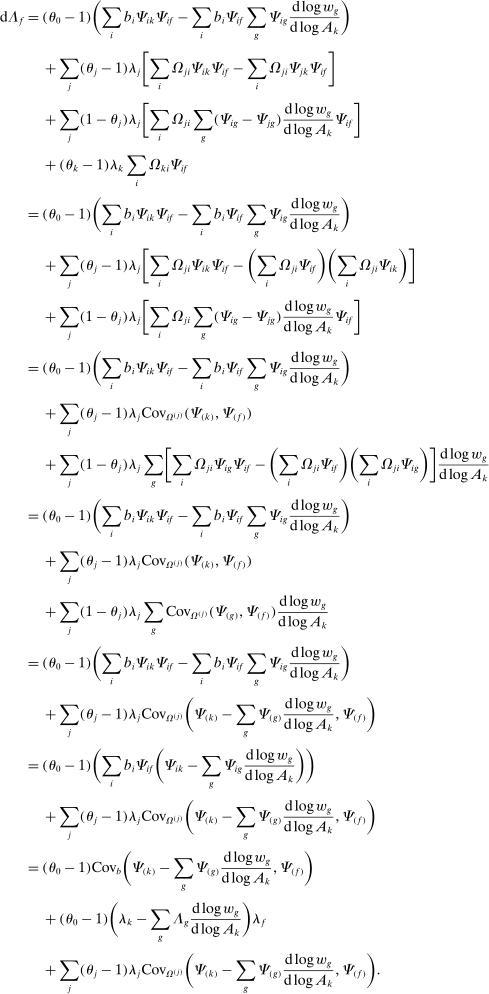
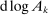 , letting
, letting 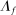 be demand for factor f, we have
be demand for factor f, we have
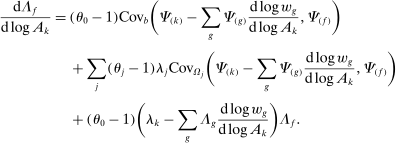 (23)
(23)We have
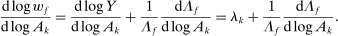 (24)
(24)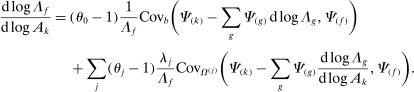 (25)
(25)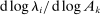 is similar. □
is similar. □
Proof of Corollary 2.Note that since 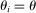 for every i, market clearing for a good i (neglecting the normalizing constants and setting the household's price index to be the numeraire) is
for every i, market clearing for a good i (neglecting the normalizing constants and setting the household's price index to be the numeraire) is
 (26)
(26)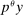 denote the vector whose ith element is
denote the vector whose ith element is 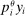 and
and  , we can write
, we can write
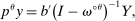 (27)
(27) is the matrix of
is the matrix of  raised to θ elementwise. Let
raised to θ elementwise. Let 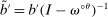 . This is reminiscent of the supplier centrality defined by Baqaee (2018).
. This is reminiscent of the supplier centrality defined by Baqaee (2018).Furthermore, market clearing for labor type k is
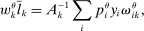 (28)
(28)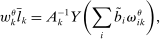 (29)
(29)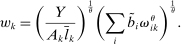 (30)
(30)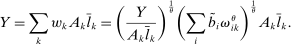 (31)
(31)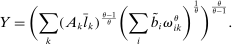 (32)
(32)



 aggregate output as a function of productivity
aggregate output as a function of productivity  in the economy with full reallocation/constant returns for different values of θ0. This example consists of two equally sized industries using labor as their only input. The economies depicted in Figures
in the economy with full reallocation/constant returns for different values of θ0. This example consists of two equally sized industries using labor as their only input. The economies depicted in Figures 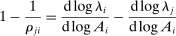
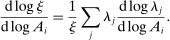
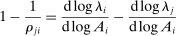
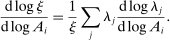
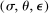
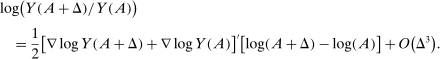
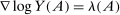 and
and 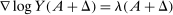 . □
. □

