Development and Laboratory Evaluation of a Bioenergetics Model for Subadult and Adult Smallmouth Bass
Present address: Department of Wildlife and Fisheries, South Dakota State University, Brookings, South Dakota 57007, USA.
Abstract
A previously developed bioenergetics model for smallmouth bass Micropterus dolomieu (Hewett and Johnson 1992) was originally constructed with data exclusively from age-0 fish but has since been used to predict growth and food consumption for both age-0 and older fish, including adults. We developed a bioenergetics model for subadult and adult smallmouth bass and compared the abilities of the two models to predict growth and food consumption for fish weighing from 100 to 270 g. Model-independent laboratory growth and food consumption data for individual subadult and adult fish were used to evaluate the performance of both models. Experimental fish were subjected to three consecutive 3-week feeding regimes: an ad libitum ration at 22°C, a ration of 2.5% wet body weight/d at 22°C, and a ration of 2% wet body weight/d at 27°C. Overall, the bioenergetics model developed for subadult/adult smallmouth bass produced significantly greater accuracy in estimates of relative growth rate and cumulative consumption for subadult and adult fish than did the age-0 model. The subadult−adult model tracked observed changes in mean fish weight more closely than did the model developed for age-0 fish, and the mean percentage errors in predicting cumulative consumption were consistently lower for the subadult−adult model. Our findings are consistent with previous studies, which have also found that bioenergetics models developed for a particular life stage of a species can yield substantially inaccurate predictions of growth and consumption for other life stages of that species. The model developed for subadult and adult fish produced better agreement with observed growth and food consumption by subadult and adult smallmouth bass than the model developed for age-0 fish and is recommended for applications involving fish weighing more than 50 g.
Introduction
Bioenergetics models have been constructed for at least 20 fish species (Hanson et al. 1997) and are frequently used by fisheries scientists and managers. However, these models are rarely corroborated, primarily due to the difficulty in acquiring data for estimating the required model input and output parameters in field settings. Most evaluations of bioenergetics models have been conducted with field estimates of growth, food consumption, diet composition, energy densities of predators and prey, water temperature, and activity (e.g., Rice and Cochran 1984; Beauchamp et al. 1989; Wahl and Stein 1991; Peterson and Ward 1999; Schaeffer et al. 1999). However, uncertainty associated with field estimates of food consumption and other required model inputs complicates the interpretation of model performance when model predictions and field data disagree (Hewett and Johnson 1992). In addition, model and field estimates of growth and consumption could show good agreement but both be inaccurate, thereby yielding misleading corroboration (Ney 1993). Other evaluations of bioenergetics models have been conducted in laboratory settings (Whitledge and Hayward 1997; Whitledge et al. 1998; Madenjian and O'Connor 1999), which can eliminate much uncertainty regarding daily food consumption, growth, and fish thermal experience and can potentially control energetic costs associated with activity.
An existing bioenergetics model for smallmouth bass Micropterus dolomieu (Hanson et al. 1997) was developed with data taken exclusively from age-0 fish (Shuter and Post 1990), although the age specificity of this model is not indicated in the software or manuals (Hewett and Johnson 1992; Hanson et al. 1997). This model has not been independently corroborated and has been used to predict growth and food consumption for age-0 fish and, in at least three cases, older fish. Bioenergetics models for at least six other species use different sets of parameters depending on fish age (Hanson et al. 1997), because allometric and water temperature functions, as well as optimum and maximum temperatures for respiration and consumption, can vary substantially with fish age (Post 1990; Hanson et al. 1997). Thus, bioenergetics models developed for a particular life stage of a species may yield highly inaccurate predictions of growth and consumption for other life stages of that species. For example, a bioenergetics model for adult walleyes Stizostedion vitreum was a poor predictor of growth and food consumption by age-0 walleyes (Madon and Culver 1993). The objectives of our study were to develop a bioenergetics model for subadult and adult smallmouth bass and to test the ability of this model and that of the existing age-0 model to predict growth and food consumption for subadult and adult smallmouth bass at two feeding levels at 22°C and one feeding level at 27°C. Models were evaluated with independent data from a laboratory setting in which water temperature, daily ration, and resultant growth were all known.
Methods
Derivation of model parameters
We developed parameters for a Wisconsin-type bioenergetics model (Kitchell et al. 1977) for subadult and adult smallmouth bass, namely,

where growth rate (G, defined as grams of weight gained or lost per gram of body weight per day) is a function of the specific rates of food consumption (C), respiration (R, including inactive, active, and specific dynamic action), egestion (F), and excretion (E). Each variable is described by weight- and temperature-dependent functions. The equation for determining consumption rate (C, grams of prey consumed per gram of body weight per day) is
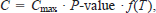
where Cmax is the maximum specific consumption rate, P-value is the proportion (range, 0–1.0) of Cmax exhibited by the fish, and f(T) is the water temperature dependence function. We used water temperature dependence equation (2) from Hewett and Johnson (1992), which is typically used for warmwater fishes and requires the following parameters: optimum water temperature for consumption (CTO), maximum water temperature for consumption (CTM, the temperature above which consumption ceases), and a water temperature dependence coefficient (CQ). The maximum specific consumption rate is defined as an allometric function of fish weight, that is,
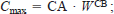
where W is fish weight (g) and CA and CB are the intercept and slope of the allometric function, respectively. Data for deriving parameters describing weight and temperature dependence of consumption for subadult and adult smallmouth bass (weight range, 43.4–200.1 g; mean weight, 114 g) were obtained from Zweifel et al. (1999). A value of −0.31 was assigned to CB, corresponding to the average of 30 such values reported by Hewett and Johnson (1992) and to the value used by Zweifel et al. (1999) to weight-standardize daily consumption rates for subadult and adult smallmouth bass. A value for CA was then calculated with the above value for CB, a value of 0.78 for Cmax (the highest value for mean daily consumption observed by Zweifel et al. 1999), and a value of 114 g for W, the weight to which consumption data from Zweifel et al. (1999) were standardized. The resulting value for CA was 0.339, which is within the range of values reported for other species by Hewett and Johnson (1992); CTO was set at 22°C, the temperature at which mean daily consumption was highest for subadult and adult smallmouth bass (Zweifel et al. 1999); CTM was set at 37°C to approximate an incipient upper lethal temperature for subadult and adult smallmouth bass (Wrenn 1980). After values were assigned to CA, CB, CTO, and CTM, CQ was adjusted until specific consumption rates calculated with a P-value of 1.0 matched the mean weight-specific maximum daily consumption rates at 18, 22, 26, and 30°C reported by Zweifel et al. (1999). Due to a decrease in the rate at which maximum daily consumption declined at temperatures greater than 26°C (Zweifel et al. 1999), two values of CQ were required to match predicted maximum daily consumption rates with observed values; one CQ value was used for water temperatures lower than 26°C (CQ = 4.2) and another for water temperatures higher than 26°C (CQ = 1.95). Specific daily consumption rates calculated for a hypothetical 114-g fish with CA, CB, CTO, CTM, and CQ values as described above and a P-value of 1.0 were nearly identical to the mean values for maximum specific daily consumption rates reported by Zweifel et al. (1999) (Figure 1A).
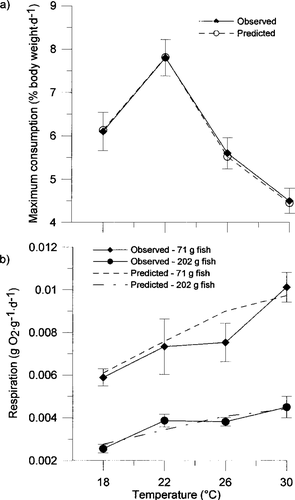
Mean observed maximum daily consumption rates (% body weight/d ± SE) for a 114-g smallmouth bass at 18, 22, 26, and 30°C (Zweifel et al. 1999) and mean daily consumption rates predicted for a hypothetical 114-g fish based on consumption equation (2) in Hewett and Johnson (1992), with consumption parameter values developed for adult smallmouth bass and a P-value of 1.0; (b) mean observed resting respiration rates (g O2·g−1·d−1 ± SE) for 71-g and 202-g smallmouth bass at 18, 22, 26, and 30°C (Whitledge et al. 2002) and mean resting respiration rates predicted for fish of the same sizes based on respiration equation (2) in Hewett and Johnson (1992), with respiration parameter values developed for adult smallmouth bass and the value of the multiplicative increment for active metabolism (ACT) set at 1
The equation for determining respiration rate is

where R and Rs are the respiration and resting metabolic rates (g O2·g−1·d−1), ACT is the multiplicative increment for active metabolism, and f(T) is the water temperature dependence function. We again used Hewett and Johnson's (1992) water temperature dependence equation (2), which requires the following parameters: optimum water temperature for respiration (RTO, i.e., the temperature at which respiration is highest), maximum water temperature for respiration (RTM, the upper incipient lethal temperature), and a water temperature dependence coefficient (RQ). The resting metabolic rate is defined as an allometric function of fish weight, that is,
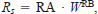
where RA and RB are the intercept and slope, respectively, of the allometric function at the optimum water temperature. Data for deriving parameters describing weight and temperature dependence of resting metabolism for subadult and adult smallmouth bass (weight range, 48.7–304.8 g; mean weight, 136.7 g) were obtained from Whitledge et al. (2002). Values for RA and RB were determined by fitting a power function to data relating specific resting metabolic rate to fish weight (g) at 30°C (RTO), the temperature at which metabolic rate was highest. The fitted allometric equation was Rs = 0.244 · W−0.756 (r² = 0.97, P < 0.0001); RTM was set at 37°C to approximate an upper lethal temperature for smallmouth bass (Wrenn 1980), as suggested by Hewett and Johnson (1992). After values were assigned to RA, RB, RTO, and RTM, RQ was adjusted until specific respiration rates calculated with a value of 1 for ACT closely matched mean resting metabolic rates at 18, 22, 26, and 30°C for each of the two size-classes of fish (mean weights, 71 and 202 g) measured by Whitledge et al. (2002). The resulting value for the RQ was 1.8. Specific daily respiration rates calculated for hypothetical 71-g and 202-g fish with values for RA, RB, RTO, RTM, and RQ as described above and a value of 1 for ACT were within 1 SE of the mean specific daily respiration rates for fish of these sizes determined by Whitledge et al. (2002), with the exception of the value for a 71-g fish at 26°C (Figure 1B).
Data regarding rates of egestion and excretion as functions of temperature and ration for adult smallmouth bass were unavailable. Therefore, we used the egestion−excretion equation set 1 in Hewett and Johnson (1992), with values for the proportion of ingested energy that is egested (FA) and the proportion of assimilated energy that is excreted (UA) identical to those used in the existing bioenergetics models for age-0 smallmouth bass and largemouth bass M. salmoides (Hanson et al. 1997). Model predictions of growth and food consumption are generally insensitive to changes in these parameters (Bartell et al. 1986).
Growth and consumption data
Model-independent fish growth data in response to known daily consumption and temperature regimes were generated for individual subadult and adult smallmouth bass in the laboratory to test bioenergetics model predictions. Seven smallmouth bass (mean weight 140 g) were collected from a central Missouri stream and acclimated to the laboratory environment for several weeks. Fish were held individually in perforated, 8-L plastic chambers submerged in 945-L tanks equipped with water recirculation and biofiltration systems. For at least 7 d prior to the beginning of the study, fish were kept at 22 ± 0.5°C under a photoperiod of 12 h light: 12 h dark and were fed live fathead minnows Pimephales promelas ad libitum, with once-daily prey introduction. The presence of live fathead minnows in all chambers on all days subsequent to feeding confirmed that smallmouth bass were fed ad libitum.
Daily ration and growth of each fish were monitored over three consecutive 3-week periods in the laboratory. Fish were held individually in the chambers described above at 22 ± 0.5°C and were fed live fathead minnows ad libitum once daily for the first 3 weeks. Fish were then held at 22 ± 0.5°C for 3 additional weeks and were fed live fathead minnows once daily at 2.5–3.0% of wet body weight. During the final 3 weeks, fish were held at 27 ± 0.5°C and were fed once daily at about 2% of wet body weight. The photoperiod was 12 h light: 12 h dark throughout the experiment. Daily consumption was determined from the difference between the wet weights of minnows presented as food and those that were uneaten after 24 h. Smallmouth bass were weighed weekly to the nearest 0.1 g (wet weight).
Bioenergetics modeling
We predicted daily ration (% body weight), cumulative consumption (CC [g]), the relative growth rate (RGR [g·g−1·d−1), and changes in body weight (g) for individual fish with both our subadult−adult smallmouth bass bioenergetics model and the existing model developed for age-0 fish. Simulations were run in the microcomputer program of Hanson et al. (1997), which is an upgrade of an earlier model (Hewett and Johnson 1992). Physiological parameters for the subadult−adult smallmouth bass model and the existing age-0 smallmouth bass model are shown in Table 1. For the age-0 model, two sets of growth and consumption predictions were made, one based on a value of 2 for ACT (the value assigned by the age-0 model; Hanson et al. 1997) and another based on a value of 1 for ACT. Completion of a second set of simulations for the age-0 model with an ACT value of 1 allowed us to assess the extent to which differences in predictive ability of the age-0 and subadult−adult models might be due exclusively to different default values for ACT. A value of 1 for ACT is likely more representative of activity costs for fish in this study, as fish were held individually in relatively small chambers that limited mobility and reduced potential energy costs from social interaction. A value of 1 for ACT was used in a previous laboratory study (Whitledge and Hayward 1997), which corroborated a bioenergetics model for largemouth bass under the same conditions used in the present study. We used an energy density of 4,184 J/g wet weight for smallmouth bass, which is the value used for centrarchids in all bioenergetics models (Hewett and Johnson 1992). Fathead minnows were assigned an energy density of 3,853 J/g wet weight, which was the mean value (± 32 J/g wet weight [SE]) determined by bomb calorimetry for three successive batches of prey fish used in this study. Predator and prey energy densities were assumed to remain constant throughout the study in all models. For each model, P-values were fit to both observed final weight and observed CC for individual fish for each of the three 3-week periods in the growth and consumption test data set. This was done so that P-values would reflect changes in daily rations among the 3-week periods. Each model's predictions of body weight change during each 3-week period were then calculated for individual fish with P-values fit to CC during the same time period. Predictions of daily ration and cumulative food consumption for individual fish during each 3-week period were then made with P-values fit to the weights of individual fish at the end of each 3-week period.
Model evaluation
We compared the mean values observed for CC and RGR over each 3-week period and weekly changes in mean body weight (g) for smallmouth bass with the corresponding values predicted by our subadult−adult smallmouth bass model, the age-0 fish model with ACT set at 2, and the age-0 fish model with ACT set at 1. For each model, absolute differences between predicted and observed values for both RGR and CC were calculated for individual fish during each 3-week period as
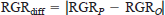
and
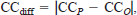
where RGRO and CCO are observed values for RGR and CC, respectively, RGRP and CCP are the corresponding predicted values, and RGRdiff and CCdiff are the absolute differences between the predicted and observed values for RGR and CC. Absolute differences between predicted and observed values were used to evaluate model performance so that large positive and negative errors in model predictions in different 3-week experimental periods would not offset and yield false indications of good overall model performance. Intermodel differences in the means for RGRdiff and CCdiff were assessed by means of analysis of variance (ANOVA) in a randomized complete-block design with a 3 × 3 factorial arrangement and individual fish as the blocking unit. The least-squares-means (LSMEANS) procedure in the Statistical Analysis System (SAS Institute 1990) was then used to assess the significance of intermodel differences in RGRdiff and CCdiff within each of the three experimental periods. To determine whether model predictions of mean RGR and CC were significantly different from observed values, we also used the LSMEANS procedure to test whether the values of RGRdiff and CCdiff for each model within each 3-week period were significantly different from zero. The percentage errors in predicting the body weights of individual fish at the end of each week of the experiment and cumulative food consumption by each fish during each 3-week period were also calculated for each model as

where PRED is the predicted value of fish weight or CC and OBS is the corresponding observed value.
Results
The mean body weights of smallmouth bass predicted by the subadult−adult model closely followed the trajectory of observed weights and were within 1 SE of the observed mean values at the end of 8 of the 9 weeks of the experiment (Figure 2A). Mean weights predicted by the age-0 model with an ACT value of 2 deviated slightly more from the trajectory of observed weights than the predictions of the subadult−adult model, but both models' predicted mean fish weights remained within 2 SEs of the observed values at the end of each week. The mean errors in predicting fish weight were always less than 8% for the subadult−adult model (Figure 2B). For the age-0 model with an ACT value of 2, the mean errors ranged from 2% to 14%. The mean weights predicted by the age-0 model with an ACT value of 1 diverged from observed values and fell more than 2 SEs beyond the observed mean weights on several dates (Figure 2A). The mean errors were as high as 34% for the age-0 model with ACT set at 1 (Figure 2B).
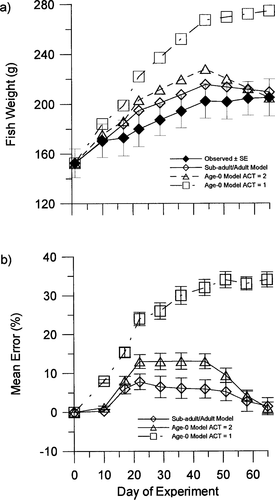
Mean (±SE) observed fish weights and mean weights predicted by the subadult−adult model, the age-0 model with ACT set at 2, and the age-0 model with ACT set at 1 (alues are shown at approximately weekly intervals); (b) mean errors (%) of predicted fish weights at the end of each week of the experiment for the subadult−adult model, the age-0 model with ACT set at 2, and the age-0 model with ACT set at 1. Negative error values indicate underestimation of fish weight, positive values overestimation
Overall, the mean RGRdiff was significantly lower for the subadult/adult model than for the age-0 models with ACT set at 2 or 1 (P < 0.05). During the first 3-week period, all models overestimated mean RGR, and mean RGRdiff values were significantly different from zero for each model (P < 0.05; Table 2). During this period, mean RGRdiff was significantly lower for the subadult−adult model than for both of the age-0 models (P < 0.05) and was significantly lower for the age-0 model with ACT set at 2 than for the age-0 model with ACT set at 1 (P < 0.05). During the second 3-week period, mean RGRdiff values for the subadult−adult model and the age-0 model with an ACT of 2 were not significantly different from zero (P ≥ 0.05). However, the age-0 model with an ACT value of 1 overestimated mean RGR during the second 3-week period, and its mean RGRdiff was significantly different from zero (P < 0.05). Mean RGRdiff values for the subadult−adult model and the age-0 model with ACT set at 2 were not significantly different (P ≥ 0.05) during the second 3-week period, but both of these models had significantly lower RGRdiff values than did the age-0 model with ACT set at 1 (P < 0.05). During the third 3-week period, mean RGRdiff values were significantly different from zero for all three models (P < 0.05), with the subadult/adult model and the age-0 model with an ACT value of 2 underestimating mean RGR and the age-0 model with an ACT value of 1 overestimating mean RGR. During this period, mean RGRdiff was significantly higher for the age-0 model with ACT set at 2 compared with the results of the other two models (P < 0.05).

The mean CCdiff for the subadult/adult model during the second 3-week period did not differ significantly from zero (P ≥ 0.05; Table 3); all other mean CCdiff values for each model during each 3-week period differed significantly from zero (P < 0.05). The age-0 model with ACT set at 1 underestimated mean CC by 26–49% during each 3-week period. The age-0 model with ACT set at 2 overestimated mean CC during the third 3-week period by 42% and underestimated mean CC by 28% during the first period and 9% during the second period. Mean percentage errors of CC predictions during each 3-week period ranged from 1% to 17% for the subadult−adult model.
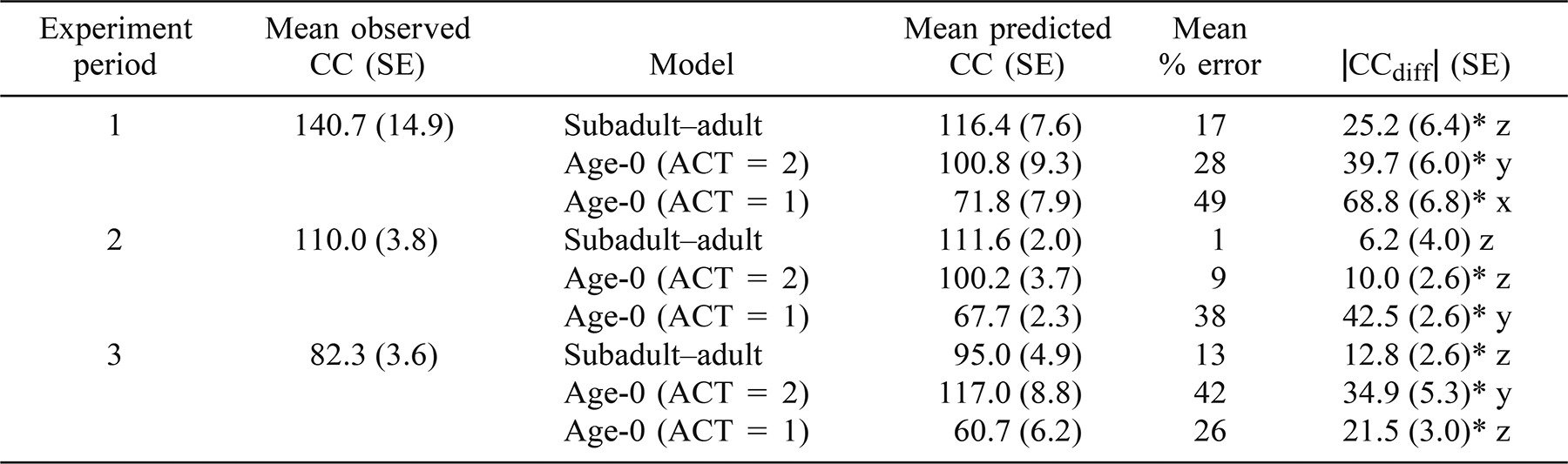
Overall, the mean CCdiff for the subadult−adult model was significantly lower than those of the age-0 models with ACT set at 2 or 1 (P < 0.05). During the first 3-week period, the mean CCdiff was significantly lower for the subadult−adult model than for both of the age-0 models (P < 0.05; Table 3) and was significantly lower for the age-0 model with ACT set at 2 than for the age-0 model with ACT set at 1 (P < 0.05). Mean CCdiff values for the subadult−adult model and the age-0 model with an ACT of 2 were not significantly different (P ≥ 0.05) during the second 3-week period, but both models had significantly lower CCdiff values during this period than did the age-0 model with an ACT of 1 (P < 0.05). During the third 3-week period, the mean CCdiff was significantly higher for the age-0 model with ACT set at 2 than for the subadult−adult model and the age-0 model with ACT set at 1 (P < 0.05).
Discussion
Overall, the bioenergetics model developed for subadult and adult smallmouth bass produced significantly greater accuracy in estimates of RGR and cumulative food consumption for subadult and adult fish than did the model previously developed with data from age-0 fish (Shuter and Post 1990) under the temperature and feeding conditions used in this study, regardless of the ACT value used in the age-0 model. The subadult−adult model's predictions of RGR and CC during each of the 3-week periods were consistently as accurate as or significantly more accurate than corresponding predictions of the age-0 models with ACT set at 1 or 2. The mean percentage errors in predicting fish weight were nearly always lower for the subadult−adult model than either of the two age-0 models, and the mean percentage errors in predicting cumulative consumption were consistently lowest for the subadult−adult model. The relatively low error achieved by the age-0 model (ACT = 2) for the final mean fish weight resulted from that model's significant overestimation of RGR during the first 3-week period and its significant underestimation of RGR during the final 3-week period, indicating greater systematic error in predicting growth rates for fish in this study. The age-0 model with ACT set at 1 yielded poor estimates of growth and food consumption, even though a value of 1 for ACT is likely more appropriate than an ACT value of 2 for subadult and adult fish under the experimental conditions of this study. Fish were held individually in relatively small chambers that limited movement and eliminated energy-expending social interactions. Whitledge and Hayward (1997) also used a value of 1 for ACT in their evaluation of the largemouth bass model under conditions which were identical to those in the present study. Thus, the poor performance of the age-0 model with ACT set at 1 likely reflects the inadequacy of that model's consumption and respiration parameter values for describing allometric and temperature-dependence functions for consumption and resting metabolism by subadult and adult fish. That the performance of the subadult−adult model was significantly better than both of the age-0 models indicates that differences in default ACT values were not solely responsible for differences in predictive abilities of the subadult−adult model and the age-0 model. Our results indicate that the model developed for subadult and adult fish produced significantly better overall agreement with observed growth and food consumption than did the model developed for age-0 fish, particularly when ACT values for the two models were identical. The model developed for subadult and adult fish is recommended for applications involving fish weighing approximately 45–300 g, corresponding to the range of sizes used to derive growth and consumption parameters for the subadult−adult model.
Our results indicate that bioenergetics models developed for a particular life stage of a fish species can yield inaccurate predictions of growth and consumption for other life stages of that species. The bioenergetics model previously developed with data from age-0 smallmouth bass was less accurate in predicting growth and food consumption for subadult and adult fish than our model, which was developed with consumption and respiration data from subadult and adult fish. These findings are consistent with those of Madon and Culver (1993), who found that a bioenergetics model developed for adult walleyes yielded inaccurate predictions of growth and consumption by age-0 walleyes. Post (1990) also found that a bioenergetics model for adult yellow perch Perca flavescens underestimated food consumption rates for age-0 yellow perch. Bioenergetics models for several other species also use different parameter sets depending on fish age because allometric and water temperature functions, along with optimum and maximum temperatures for respiration and consumption, can vary substantially with fish age (Hanson et al. 1997). Bioenergetics model users should not assume that a model for a particular species will accurately predict growth and consumption for all sizes and ages of that species. The age-0 smallmouth bass model may yield substantial over- or underestimates of growth and consumption when applied to older juveniles and adult fish. Consumption and respiration parameters in the subadult−adult smallmouth bass model were derived from data for fish weighing about 45–300 g, and the model was evaluated with fish ranging from about 100 to 280 g wet weight. Our evaluation was also limited to two feeding levels at 22°C and one feeding level at 27°C. Further evaluation is recommended before the subadult−adult smallmouth bass model is applied to larger or smaller fish or at temperatures substantially beyond the range of those used in this study.
This study highlights the utility of housing fish individually during laboratory evaluations of bioenergetics models. Laboratory evaluations can eliminate much of the uncertainty inherent in field evaluations regarding daily food consumption, growth, and fish thermal experience and may be able to control the energetic costs associated with activity. The adequacy of model parameters, equations, and assumptions can be tested in a laboratory setting with relative quickness and ease for a variety of temperatures and feeding levels. The holding of fish individually permits direct determination of food consumption rates and increases statistical power by enabling comparisons of observed and predicted growth and consumption rates for each fish in the study. Ideally, bioenergetics models should first be evaluated in the laboratory and then corroborated in the field (Brandt and Hartman 1993; Ney 1993). If a model yields sufficiently accurate predictions of growth and consumption under controlled laboratory conditions, then field evaluations should be conducted to ensure that allometric and temperature-dependence functions for consumption, respiration, and egestion−excretion are applicable to noncaptive fish.
Acknowledgments
This study was supported by funds and equipment provided by the Missouri Department of Conservation, the Missouri Agricultural Experiment Station, and the Missouri Cooperative Fish and Wildlife Research Unit (Biological Resources Division of the U.S. Geological Survey, Missouri Department of Conservation, University of Missouri, and Wildlife Management Institute cooperating). We thank Mark Ellersieck for assistance with statistical analyses and Eric Nelson, Ray Wright, Debra Whitledge, Sharon Whitledge, and Lara Gawenis for their assistance in the laboratory.