Assessing the Threshold of Need for Supplemental Damping in Seismic Base Isolation of Multistory Buildings
Abstract
The comprehension of the threshold for the need of supplemental dampers in the base isolation of multistory buildings could be beneficial in the advancement of the application of base isolation to achieve seismic safety. In this study, stick models of 1-, 4-, 7-, 10-, 13-, 16-, and 19-story buildings were designed in fixed-base, simply base-isolated, and damping-assisted base-isolated scenarios. The isolation system considered is the well-known friction pendulum system, with supplemental damping provided by widely used viscous dampers. Time history analyses were conducted using seven far-fault accelerograms and seven near-fault accelerograms. Seismic performances were evaluated in terms of base shear values, story accelerations, interstory drifts, and story shears. The results indicate that base isolation is highly effective in controlling seismic responses in both far-fault and near-fault earthquakes, with average base shear values in the base-isolated models reduced by approximately 60%–75% compared with the fixed-base models. Displacements, accelerations, drifts, and story shears were also decreased by more than 50% compared with the fixed-base models. Base isolation demonstrated acceptable performance in the 4-, 7-, and 10-story models, but supplemental damping was necessary for effective structural control of the 13-story model in near-fault earthquakes, as well as the 16-story and 19-story models in both far-fault and near-fault earthquakes. The incorporation of supplemental damping significantly enhances structural control by further mitigating displacements, shears, and accelerations.
1. Introduction
The safety of structures in earthquake-prone areas is crucial [1]. Base isolation is a well-known and effective method for achieving seismic safety. The concept of isolation for aseismic control of structures dates back more than 40 centuries [2]. Aseismic base isolation reduces seismic demand by lowering the fundamental frequency of the structure and providing damping [3, 4]. It also helps in reducing interstory drifts and floor accelerations in buildings [5, 6]. Supplemental damping can further enhance seismic performance [7, 8]. Understanding the necessity for supplemental damping is important for the extended use of aseismic base isolation [9, 10]. Structures equipped with dampers exhibit distinct responses under far-fault and near-fault earthquake conditions. The maximum displacement demand of near-fault earthquakes in low-rise buildings occurs at lower stories, while in high-rise buildings, it occurs at intermediate stories due to increased Tp/T value in the model [11, 12]. It should be noted that the participation and effect of higher modes on structural responses is greater. Therefore, the higher frequency content of near-fault earthquakes is more effective on the higher stories [13]. In most cases, the base shear force is large in near-fault earthquakes. A pilot study conducted by Akhare and Wankhade in 2014 [14] investigated base-isolated buildings using friction pendulum system (FPS) and high-damping rubber bearing (HDRB). The study found that the base isolation method reduced the base shear value by 94% and 70% and increased the period by 72.5% and 42% for the two mentioned systems, resulting in a considerable decrease in stories drift and significant role in decreasing the seismic responses. A base-isolated building performs very well in reducing seismic responses. The results of the study by Palazzo et al. in 2014 [15] indicate that the FPS dampers have met the provisions in FEMA and NTC codes concerning the isolated buildings.
Bahagat and Wijeywichkrema [16] conducted a study comparing base-isolated buildings using the lead rubber bearing (LRB) isolators and fixed-base buildings under near-fault and far-fault earthquakes. The results showed that the reduction of responses in near-fault earthquakes was 54%–67% in terms of drift and 37%–52% in terms of base shear when using isolators. In far-fault earthquakes, the reduction of responses was 74%–76% in terms of drift and 54%–66% in terms of base shear. In addition, the study found that as the number of stories increased in 4-, 8-, and 12-story buildings, the impact of base isolation decreased. The drift of the base-isolated buildings was measured at 0.1, 0.09, and 0.11, and the roof acceleration was 0.19, 0.22, and 0.26, respectively. The results indicated that in far-fault earthquakes, the stories’ drift in the base-isolated buildings was not problematic. However, in near-fault earthquakes and at the maximum credible earthquake (MCER) level, minor damages were observed. In terms of acceleration, both near-fault and far-fault earthquakes showed that an increase in the Q/W ratio (where Q is the characteristic strength of isolation system and W is the total seismic weight of the building) and building height led to maximum acceleration at the higher and lower stories in some cases exceeding 0.3 g.
The study conducted by Bhandari et al. [17] investigated the behavior of base-isolated buildings under the impact of far-fault and near-fault earthquakes. The findings revealed that seismic isolation was not effective in near-fault earthquakes. The research evaluated base-isolated buildings at two peak ground acceleration (PGA) levels (0.2 and 0.4 g), taking into account the directivity and fling step effects of far-fault and near-fault earthquake records. The impact of base isolation on reducing base shear, acceleration, and maximum story drift at both PGA levels for both far-fault and near-fault earthquakes with directivity effect was found to be significant. Conversely, it was observed that in near-fault earthquakes with fling step effect, the decrease in responses was minimal, indicating the negligible effect of base isolation in such earthquakes. The displacement of isolators was found to be dependent on the PGA, with the maximum displacement at 0.4 g being twice that at 0.2 g. Moreover, the maximum displacement of isolators in near-fault earthquakes was higher compared with far-fault earthquakes. In near-fault earthquakes (0.2 and 0.4 g) with the fling slip effect, significant displacements were observed in the isolators. It is anticipated that the superstructure of base-isolated buildings would remain in an elastic state. Plastic hinge formation in base-isolated buildings is rare in far-fault earthquakes with low PGA values, but nonelastic deformations occur at higher PGA values.
It is important to emphasize that in near-fault earthquakes with the directivity effect, the outcomes are similar, whereas in the case of fling slip effect, the nonelastic deformations resemble those of fixed-base buildings. The use of dampers to reduce isolator displacement and mitigate damages caused by severe earthquakes to base-isolated buildings in both near-fault and far-fault earthquakes is an effective method supported by many researchers. Kaptan et al. [18] conducted a study on energy absorption systems and their impact on reducing horizontal forces acting on buildings. The findings indicated that base-isolated buildings increase the structure period from 0.57 to 2.23 s. In addition, the addition of dampers to the base-isolated building (superstructure) results in a decrease in story displacement ratio, base shear, and columns bending moment, while the drift of the second story decreases from 1.2 to 0.21 mm. Erkal and colleagues [19] conducted a study comparing buildings with fixed bases, isolated bases, those equipped with dampers, and a combination of base isolation and dampers. The inclusion of dampers in the base-isolated building (within the superstructure) led to enhanced system performance. The drift values for the second story of buildings with fixed base, dampers, isolated base, and combined isolator and damper systems are 0.0012, 0.0009, 0.000325, and 0.0002 cm, respectively. Moreover, the bending moment of the columns is recorded as 159, 129, 48, and 31 kN m, respectively. Providakis [20] conducted a study on two different types of base-isolated buildings with FPS and LRB isolators during near-fault and far-fault earthquakes and introduced dampers (within the substructure) parallel to the isolators. The addition of dampers to base-isolated systems has proven highly effective in reducing damper displacement during near-fault earthquakes. However, in far-fault earthquakes, it may lead to increased drifts, and if not carefully controlled, exceeding a certain damping threshold could cause structural damage. Dampers effectively reduce story accelerations during near-fault earthquakes in base-isolated systems, while story accelerations tend to increase in far-fault conditions. To minimize damper displacement during far-fault earthquakes, the damping must be precisely controlled (e.g., kept within 20%) to prevent an increase in drifts.
Fathi, Makhdoumi, and Parvizi [9] conducted a similar study on 2D base-isolated frames with varying numbers of stories and different damping ratios. The research focused on the behavior of the frames during far-fault and near-fault earthquakes. The findings suggested that increasing supplemental damping could enhance the performance of base-isolated buildings, particularly under near-fault earthquakes. The study revealed that higher supplemental damping led to reduced base displacement but increased story acceleration. Moreover, the relative displacement of stories decreased in far-fault earthquakes and increased in near-fault earthquakes, especially in high-rise buildings. Base isolation proved to be highly effective in enhancing building performance during seismic events. However, it was noted that in taller buildings, the large velocities and displacements resulting from seismic excitations could push isolators to their critical state, leading to failure under nonelastic deformations. The use of supplemental damping in base-isolated buildings, whether in the substructure or superstructure, could prevent resonance and alter seismic responses such as story displacements and accelerations. By reducing seismic responses in taller buildings through supplemental damping, the application of isolators could be expanded further.
This study seeks to determine the threshold for the necessity of supplemental damping essential for enhancing the performance of base isolation systems. By evaluating various building configurations and seismic scenarios, the research aims to identify specific conditions where supplemental damping significantly improves structural resilience during seismic events.
2. Methods and Analysis
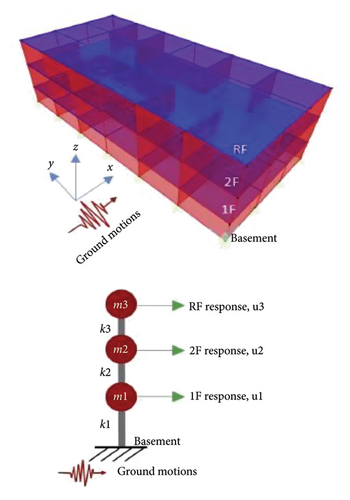
The research conducted by Hur et al. [21] in 2017 involved modeling and analyzing a 3-story structure using a lumped-mass stick model, a commonly used approach in scientific engineering studies on seismic isolation [22–25], as well as a real building in the popular SAP2000 software. The research focused on investigating the seismic performance of nonstructural members within the building. The dynamic characteristics of the 3-story building frame analyzed in the study are presented in Table 1, including the mass and stiffness values of the two-dimensional stick model. Figure 1 illustrates the computer model of the building, showcasing both the three-dimensional finite element model and the two-dimensional stick model.
| Mass (kip-s2/inch) | Stiffness (kip/inch) | ||||
|---|---|---|---|---|---|
| M1 | M2 | M3 | K1 | K2 | K3 |
| 12.71 | 12.71 | 3.66 | 0.827∗106 | 0.288∗106 | 0.292∗106 |
The analyzed framework was simulated using SAP2000 software, and the outcomes were derived from modal analysis and time history analysis during the ELCENTRO earthquake, as depicted in Figure 2. The results from the reference model are used to validate the dynamic simulation results and are detailed in Table 2.
| Reference [21] | Verification (this study) | |
|---|---|---|
| Results obtained based on the modal analysis | ||
| Mode number | Frequency (Hz) | |
| 1 | 17.35 | 17.348 |
| 2 | 46.64 | 46.636 |
| 3 | 54.11 | 54.109 |
| Results obtained based on the time history analysis | ||
| Story level | Displacement (mm) | |
| Roof | 0.576 | 0.545 |
| 2nd floor | 0.499 | 0.468 |
| 1st floor | 0.17 | 0.164 |
| Acceleration (g) | ||
| Roof | 0.626 | 0.628 |
| 2nd floor | 0.576 | 0.55 |
| 1st floor | 0.37 | 0.382 |
The comparison of the data presented in Table 2 indicates that the verification results align closely with those reported in the reference paper. Specifically, the difference between the simulated frequency of the first mode and its reference value is less than 1%. In addition, the estimated maximum displacement at the roof level is approximately 5% lower than the value reported by Hur et al. [21]. Furthermore, the maximum acceleration in this verification study is roughly 1% higher than the corresponding value in the reference paper.
2.1. Structural Design, Computer Modeling, and Seismic Loading
The structures are designed based on the assumption of reinforced concrete moment frames, with consideration of the mass and stiffness values. Each story’s stiffness is determined to have a 5% reduction, while the mass is considered as lumped mass with a fixed value of 50 kN for each story. The lateral stiffness of each story complies with the expected period specified in the IBC Code [26]. Importantly, the stories” drift falls within the standard range outlined in the code. Table 3 presents the utilized stiffnesses in the developed models.
| Story level | Lateral stiffness (MN) | ||||||
|---|---|---|---|---|---|---|---|
| 19-Story | 16-Story | 13-Story | 10-Story | 7-Story | 4-Story | 1-Story | |
| 1 | 120.33 | 103.95 | 89.79 | 77.57 | 67.00 | 57.88 | 50 |
| 2 | 114.60 | 99.00 | 85.52 | 73.87 | 63.81 | 55.13 | |
| 3 | 109.14 | 94.28 | 81.44 | 70.36 | 60.78 | 52.50 | |
| 4 | 103.95 | 89.79 | 77.57 | 67.00 | 57.88 | 50.00 | |
| 5 | 99.00 | 85.52 | 73.87 | 63.81 | 55.13 | ||
| 6 | 94.28 | 81.44 | 70.36 | 60.78 | 52.50 | ||
| 7 | 89.79 | 77.57 | 67.00 | 57.88 | 50.00 | ||
| 8 | 85.52 | 73.87 | 63.81 | 55.13 | |||
| 9 | 81.44 | 70.36 | 60.78 | 52.50 | |||
| 10 | 77.57 | 67.00 | 57.88 | 50.00 | |||
| 11 | 73.87 | 63.81 | 55.13 | ||||
| 12 | 70.36 | 60.78 | 52.50 | ||||
| 13 | 67.00 | 57.88 | 50.00 | ||||
| 14 | 63.81 | 55.13 | |||||
| 15 | 60.78 | 52.50 | |||||
| 16 | 57.88 | 50.00 | |||||
| 17 | 55.13 | ||||||
| 18 | 52.50 | ||||||
| 19 | 50.00 | ||||||
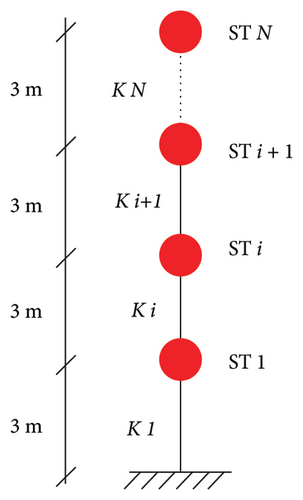
Table 4 presents the calculated damping values for the buildings under study, derived using Rayleigh damping as outlined in the procedure described in [32].
| Story level | Story damping’s (MN.s/m) | ||||||
|---|---|---|---|---|---|---|---|
| 19-Story | 16-Story | 13-Story | 10-Story | 7-Story | 4-Story | 1-Story | |
| 1 | 0.78 | 0.72 | 0.67 | 0.62 | 0.58 | 0.54 | 0.50 |
| 2 | 0.76 | 0.70 | 0.65 | 0.61 | 0.56 | 0.53 | |
| 3 | 0.74 | 0.69 | 0.64 | 0.59 | 0.55 | 0.51 | |
| 4 | 0.72 | 0.67 | 0.62 | 0.58 | 0.54 | 0.50 | |
| 5 | 0.70 | 0.65 | 0.61 | 0.56 | 0.53 | ||
| 6 | 0.69 | 0.64 | 0.59 | 0.55 | 0.51 | ||
| 7 | 0.67 | 0.62 | 0.58 | 0.54 | 0.50 | ||
| 8 | 0.65 | 0.61 | 0.56 | 0.53 | |||
| 9 | 0.64 | 0.59 | 0.55 | 0.51 | |||
| 10 | 0.62 | 0.58 | 0.54 | 0.50 | |||
| 11 | 0.61 | 0.56 | 0.53 | ||||
| 12 | 0.59 | 0.55 | 0.51 | ||||
| 13 | 0.58 | 0.54 | 0.50 | 1 | |||
| 14 | 0.56 | 0.53 | |||||
| 15 | 0.55 | 0.51 | |||||
| 16 | 0.54 | 0.50 | |||||
| 17 | 0.53 | ||||||
| 18 | 0.51 | ||||||
| 19 | 0.50 | ||||||
The buildings being analyzed are located in the California region, with short-term and 1-s spectral response acceleration values of Ss = 1.447 and S1 = 0.532, respectively. This area is characterized by high seismicity and soil type D. The structures are residential in nature, with an importance factor of 1. The structures were modeled based on the assumption of an intermediate moment frame system, incorporating a seismic behavior factor of 5. Specifics about the isolators used are outlined in Table 5.
| The studied structure | Keff (MN/m) | DD (cm) | Ceff (MN.s/m) | TD (s) | Dmin (cm) | Dmax (cm) |
|---|---|---|---|---|---|---|
| 1-Story | 9.73 | 25 | 2.5 | 1.5 | 20 | 30 |
| 4-Story | 15.5 | 35 | 13.4 | 2.5 | 26.5 | 40 |
| 7-Story | 26.5 | 35 | 23 | 2.5 | 26.5 | 40 |
| 10-Story | 30 | 35 | 31.5 | 3 | 29 | 44 |
| 13-Story | 38 | 35 | 37.7 | 3 | 29 | 44 |
| 16-Story | 46.2 | 35 | 50.2 | 3 | 29 | 44 |
| 19-Story | 55.3 | 35 | 59.6 | 3 | 29 | 44 |
Effective stiffness and damping values are integrated into the structural models. Figure 4 illustrates both the fixed-base and base-isolated models, representing the structural analysis using SAP2000 software. To develop a practical model that effectively captures the essential seismic behavior of the structure, we chose to omit advanced structural details, such as those discussed in [33]. This decision aligns with our focus on simplifying the analysis while ensuring the flexibility of the superstructure and the overall performance of the isolation system.
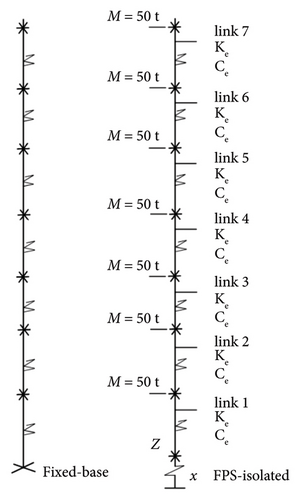
Dampers are incorporated into the base-isolated models within the superstructure to investigate their potential to enhance seismic control through supplementary devices. This innovative approach not only aims to improve structural performance but also offers a practical alternative to the conventional integration of dampers with the isolation system, as highlighted in [34]. The supplemental dampers are positioned to closely replicate the actual structural configuration. These dampers are modeled as braces within the infill frames of a real structure. To achieve this, a support is introduced along an assumed vertical axis, located 3 m from the Z-axis of the main model. Each damper is then diagonally connected to the respective story. The arrangement of the models equipped with dampers [35–40] is shown in Figure 5.
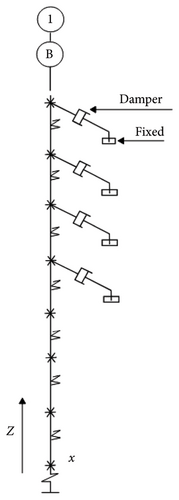
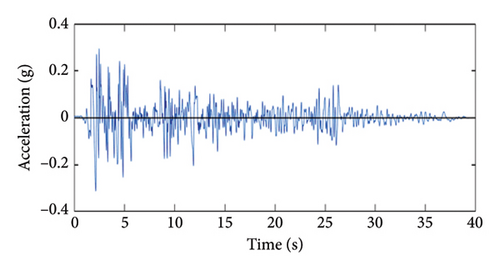
To conduct 2D dynamic time history analysis and to compare the responses of the buildings, a minimum of 3 accelerograms is required as per Section 16.1.3 of ASCE7-22 Code [1]. In this study, a total of 14 accelerograms were utilized, including 7 near-fault accelerograms and 7 far-fault accelerograms, which were previously used in the research conducted by Bahagat and Wijeyewickrema in 2017 [16] and by Fathi, Makhdoumi, and Parvizi in 2014 [9].
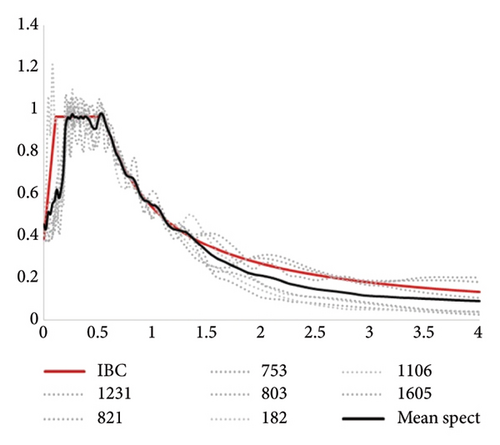
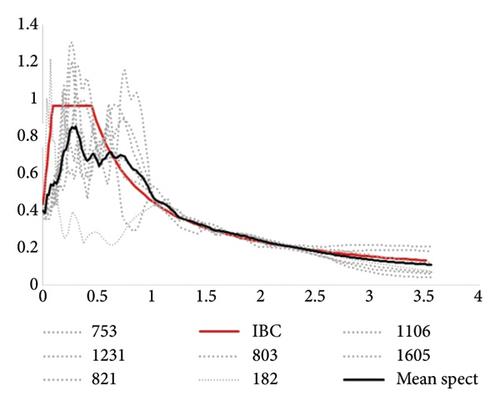
The accelerograms’ spectra must be adjusted to match the spectrum provided in the code. According to Sections 16.1.3.1 and 17.3.2 of ASCE7-22 [31], the accelerograms for fixed-base buildings should be adjusted to fall within the range of 0.2–1.5 T, while for base-isolated buildings they should be adjusted to fall within the range of 0.5 TD–1.5 TM. As a result, the accelerograms are adjusted to meet the specified ranges in the code. Figures 6 and 7 display the acceleration spectra of far-fault earthquakes for the 7-story fixed-base and base-isolated models, which have been adjusted in SeismoMatch software to align with the ASCE 7–22 [31] code spectrum.
2.2. Dynamic Time History Analysis
An examination was carried out to compare the behaviors of fixed-base and base-isolated buildings using dynamic time history analyses on the mass and stiffness models, taking into account the effects of near-fault and far-fault accelerograms. The outcomes were illustrated in terms of base shear, acceleration, displacement, shear, and drift of the stories, enabling the determination of the threshold for the necessity of supplemental damping. Subsequently, the investigation of the effect of supplemental damping was carried out by incorporating dampers into the models and analyzing the responses. To further explore the impact of base isolation, dynamic analysis was performed on the models using SAP2000 software, and the base shear values for both fixed-based and base-isolated models were extracted. The findings were then presented in Figures 8 and 9.
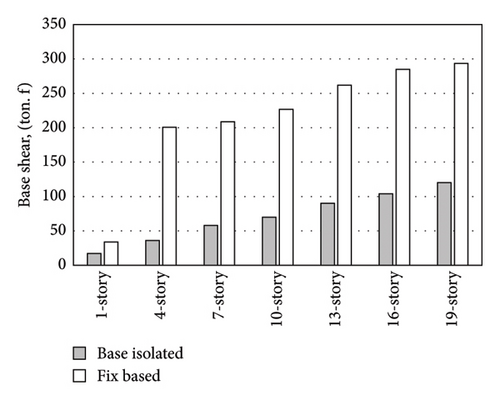
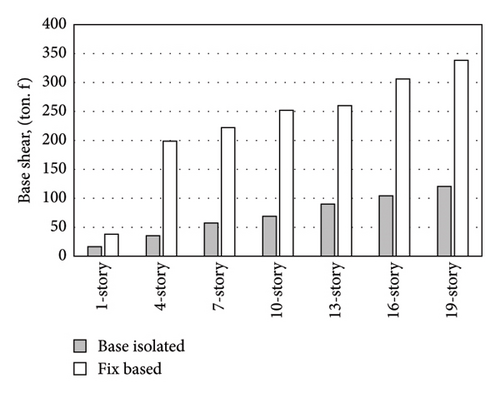
Base shears in the base-isolated buildings subjected to near-fault ground motion records are reduced almost 70%, on average over all the studied buildings. A similar trend is seen in the buildings subjected to far-fault buildings. The findings indicate that base isolation was highly effective in reducing base shear during near-fault earthquakes. Similarly, during far-fault earthquakes, the performance of base-isolated buildings in reducing base shear was clearly evident. The base shear values in the base-isolated models for both types of earthquakes were decreased, with a more noticeable reduction in far-fault earthquakes. To compare building accelerations, the accelerations of all stories in fixed-base and base-isolated models were calculated first, followed by determining the percentage of reduced roof acceleration due to base isolation. Figure 10 illustrates the comparison and examination of responses.
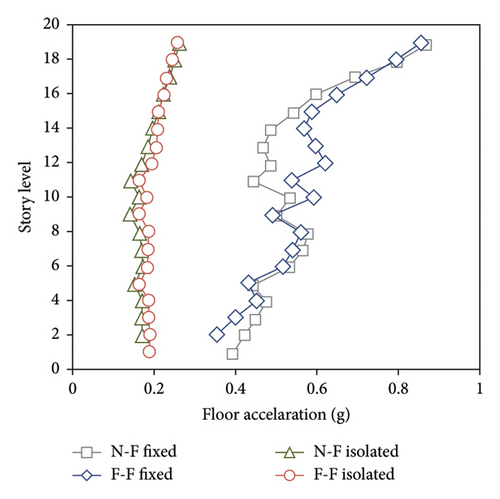
The study also examines the absolute displacement of the stories to compare the behaviors of fixed-base and base-isolated buildings. To support this analysis, displacement diagrams are initially created, with the reduced roof displacement percentages for the 19-story model presented in Figure 11 for a more comprehensive comparison.
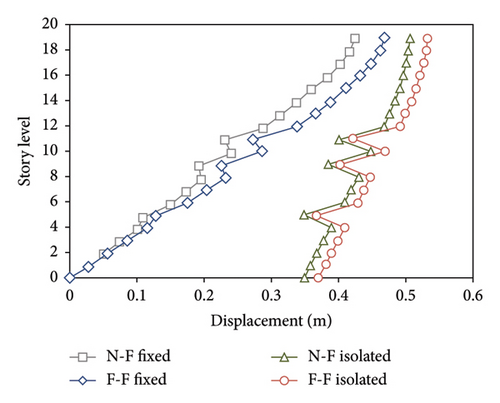
Analysis of the diagrams reveals that the displacement of stories in all base-isolated models is significantly reduced during both far-fault and near-fault earthquakes compared with similar fixed-base models. The displacement of dampers also falls within the range of design displacement, with some instances of increased value under near-fault earthquakes. The decrease in displacements is particularly pronounced in the 1-, 4-, and 7-story models, while the 10- and 13-story models also exhibit considerable reductions in story displacement, albeit to a lesser extent. However, as the number of stories increases in the 16- and 19-story models, the base isolation performance in terms of reduced story displacement becomes less significant. In the 19-story model, the reduction in story displacement is less than 65%, as shown in Figure 12.
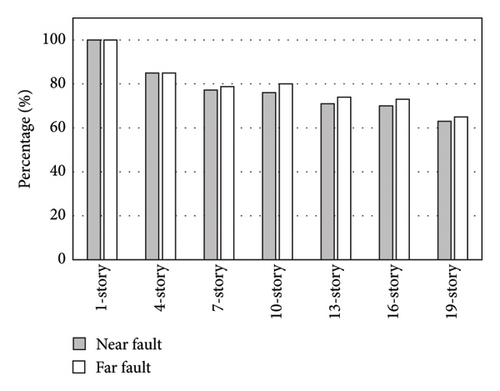
2.3. The Threshold of Supplemental Damping
The analysis of the diagrams clearly demonstrates that base isolation significantly enhances structural safety by effectively reducing various response metrics. The shear base, stories accelerations, stories displacements, drift, and shear of the stories in the base-isolated models have shown significant decreases in both far-fault and near-fault earthquakes when compared with fixed-base models. For instance, the shear base values in the 4- and 7-story models have been reduced by 75%, while in the 10- and 13-story models, this reduction reaches 65%. Moreover, the stories drifts in the 13-, 16-, and 19-story models have decreased by 55%–65%, and in the 4- and 7-story models, they have decreased by 75%–85%. In addition, base isolation has effectively reduced the stories acceleration in the 4- and 7-story models by up to 80% and in the other models by more than 70%. The results reveal that the drifts in the base-isolated models have been reduced by 75%–85% in the 4-, 7-, and 10-story models and by 55%–65% in the other models compared with similar models with fixed bases. The selected modeling method for the buildings, using the mass and stiffness model, aimed to align the fundamental period of the models with code requirements, resulting in stiffer models. Consequently, the story displacements and drifts in the fixed-base models are significantly lower than the code-specified ranges. However, the effectiveness of base isolation diminishes in high-rise buildings, leading to a decrease in base shear under near-fault earthquakes in the 13-story model and in the 16- and 19-story models under both types of earthquakes, reaching less than 65%. In the 10-story building under near-fault earthquakes, the decrease is 67%, and under far-fault earthquakes, it exceeds 72%. The 7-story model experiences a 70% decrease in base shear under near-fault earthquakes, while the 4-story model sees a reduction of over 80% under both types of earthquakes. This reduction in the base isolation effect is evident when comparing the responses. The results suggest that additional damping is required in the 13-story model under near-fault earthquakes and in the 16- and 19-story models under both types of earthquakes to enhance the performance of base isolation.
2.4. Adding Dampers to the Base-Isolated Models in the Superstructure
- 1.
Method one involved the use of 7 dampers at the 7 top stories of the model (referred to as 1 DAM type in the diagrams).
- 2.
Method two also utilized 7 dampers at the 7 middle stories of the model (referred to as 2 DAM type in the diagrams).
- 3.
Method three entailed the use of 7 dampers at the odd stories of the model (referred to as 3 DAM type in the diagrams)

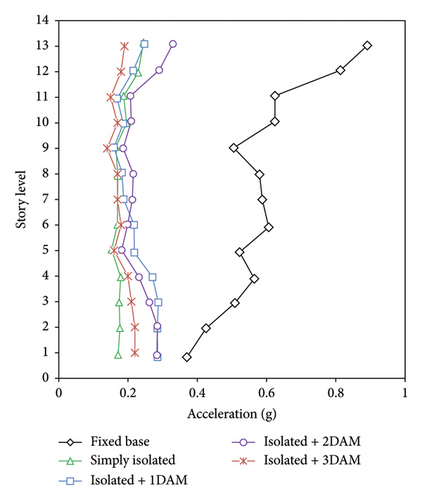
As seen, the seismic performance of the isolated building (which is drastically improved in comparison with that of the fixed-base building) can be affected by utilizing dampers. Utilizing dampers continuously in top stories (Isolated + 1 DAM) can be useful for controlling the response in the middle and top stories but it can make concerns regarding the response control of the lower stories. Utilization of dampers continuously in middle stories (Isolated + 2 DAM) stories is not useful. Seismic performance in the top stories can be further improved by utilizing dampers in odd stories (Isolated + 3 DAM).
3. Conclusions
The current research focused on exploring the threshold for additional damping in the base isolation of multistory buildings. Analysis of the findings indicated that the 4-, 7-, and 10-story structures showed the highest reduction in seismic responses with base isolation. While base isolation performed well in both far-fault and near-fault earthquakes, it was less effective in taller buildings with 13 stories during near-fault earthquakes, and in the 16- and 19-story models in both earthquake scenarios, where the reduction in base shear was below 65%. The displacement, acceleration, shear, and drift of the stories in these models indicated a weakened performance of the base isolation method. Consequently, supplemental damping was introduced to improve the base isolation performance in these buildings.
An evaluation was conducted to determine the optimal threshold for incorporating supplemental damping through dampers. Four different methods were utilized to identify the most effective approach for installing dampers at various stories to achieve maximum reduction in responses. The results indicated that installing dampers at every other story, particularly with lower damping percentage in the initial stories, led to improved performance. By assessing the need for dampers in 13-, 16-, and 19-story base-isolated models, dampers were installed at every other story. The analysis reveals that the base-isolated model with dampers exhibited superior performance in reducing responses compared to the model without dampers, with a significant increase in shear base value reduction from 62% to over 92%. In addition, displacements and drifts of the stories were notably lower when dampers were present. The addition of dampers effectively reduced the displacement of the isolator system by 10–12 cm. Although accelerations in some lower stories were slightly higher than the base-isolated model without dampers, it was not a major concern. By determining the optimal threshold for damper addition, efforts were made to limit accelerations to less than 0.3 g. The findings underscored the effectiveness of supplemental damping in enhancing base isolation performance, particularly when dampers are appropriately placed in superstructure (e.g., in the odd stories in this study).
Conflicts of Interest
The authors declare no conflicts of interest.
Author Contributions
All six authors contributed equally to develop the methodology, were responsible for resources and software, and reviewed and edited the manuscript.
Funding
No funding was received for this research.
Acknowledgments
All six authors would like to acknowledge the College of Technology and Environment at the London South Bank University (LSBU), London, United Kingdom.
Open Research
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.




