Volume 2025, Issue 1 3271534

Research Article

Open Access

Fault Diagnosis of Traction Motor Bearings Based on Shifted Rank-1 Reconstruction

Shubin Zheng

orcid.org/0000-0002-2327-4245

School of Urban Railway Transportation , Shanghai University of Engineering Science , Shanghai , 201620 , China , sues.edu.cn

Higher Vocational and Technical College , Shanghai University of Engineering Science , Shanghai , 200437 , China , sues.edu.cn

Search for more papers by this author

Xieqi Chen,

Corresponding Author

Xieqi Chen

[email protected]

orcid.org/0000-0002-9176-2531

School of Urban Railway Transportation , Shanghai University of Engineering Science , Shanghai , 201620 , China , sues.edu.cn

Search for more papers by this author

Boyu Zou,

Boyu Zou

School of Urban Railway Transportation , Shanghai University of Engineering Science , Shanghai , 201620 , China , sues.edu.cn

Search for more papers by this author

Qianwen Zhong,

Qianwen Zhong

orcid.org/0000-0002-7806-6558

School of Urban Railway Transportation , Shanghai University of Engineering Science , Shanghai , 201620 , China , sues.edu.cn

Search for more papers by this author

Lele Peng,

Lele Peng

orcid.org/0000-0003-2030-0986

School of Urban Railway Transportation , Shanghai University of Engineering Science , Shanghai , 201620 , China , sues.edu.cn

Search for more papers by this author

Liqun Wu,

Liqun Wu

Research Institute of Science and Technology , China Railway Shanghai Group Co., Ltd , Shanghai , 200071 , China

Search for more papers by this author

Shubin Zheng,

Shubin Zheng

orcid.org/0000-0002-2327-4245

School of Urban Railway Transportation , Shanghai University of Engineering Science , Shanghai , 201620 , China , sues.edu.cn

Higher Vocational and Technical College , Shanghai University of Engineering Science , Shanghai , 200437 , China , sues.edu.cn

Search for more papers by this author

Xieqi Chen,

Corresponding Author

Xieqi Chen

[email protected]

orcid.org/0000-0002-9176-2531

School of Urban Railway Transportation , Shanghai University of Engineering Science , Shanghai , 201620 , China , sues.edu.cn

Search for more papers by this author

Boyu Zou,

Boyu Zou

School of Urban Railway Transportation , Shanghai University of Engineering Science , Shanghai , 201620 , China , sues.edu.cn

Search for more papers by this author

Qianwen Zhong,

Qianwen Zhong

orcid.org/0000-0002-7806-6558

School of Urban Railway Transportation , Shanghai University of Engineering Science , Shanghai , 201620 , China , sues.edu.cn

Search for more papers by this author

Lele Peng,

Lele Peng

orcid.org/0000-0003-2030-0986

School of Urban Railway Transportation , Shanghai University of Engineering Science , Shanghai , 201620 , China , sues.edu.cn

Search for more papers by this author

Liqun Wu,

Liqun Wu

Research Institute of Science and Technology , China Railway Shanghai Group Co., Ltd , Shanghai , 200071 , China

Search for more papers by this author

First published: 19 February 2025

https://doi.org/10.1155/vib/3271534

Academic Editor: Gang Tang

Share a link

Email
Wechat
Bluesky

Abstract

Rolling bearings are one of the important components of rotating machinery, and effective bearing fault diagnosis is a necessary condition to ensure the normal operation of mechanical systems. In the rolling bearing operation process, the working conditions are usually harsh, and the sensor for collecting signals is usually placed on the outer surface of the mechanical system, resulting in the signal collected by the sensor eventually containing various interference components, increasing the difficulty of fault identification. Therefore, traditional bearing fault diagnosis methods make it difficult to detect periodic transient features from the signal spectrum. The traditional trajectory matrix with singular value decomposition (SVD) method cannot effectively diagnose the weak fault characteristics of bearings, which means that it is difficult to retain effective singular components. Therefore, a new singular value decomposition method based on shift rank-1 matrix is proposed. To begin, generate the trajectory matrix using an approximation of the traversal segment length. The built approximation matrix is then approximated using a shift vector in order to produce a strict rank-1 matrix, which is achieved by optimizing λ in low-rank matrices. Through the singular values of the shift matrix, the fault impact signal may ultimately be reconstructed. Comparative analysis was conducted between the suggested technique and other approaches via quantitative and qualitative evaluation of the algorithm’s performance on simulated and experimental data. In spite of severe background noise (−20 dB), the findings demonstrate that this approach can still recover fault impact signals without requiring a fixed traversal segment length.

1. Introduction

The comprehensive effect of factors such as load, speed, and temperature borne by rolling bearings during operation directly affects the lifespan and performance of bearings. The majority of mechanical failures are caused by bearing failure, and the pace at which a bearing deteriorates increases as damage occurs [1, 2]. Consequently, early bearing fault identification is essential, which can timely avoid economic losses and personal safety accidents caused by severe bearing failures [3, 4]. However, the early weak fault characteristics of bearings will be submerged by harmonic interference and environmental noise caused by imbalance, un-calibration, and mechanical looseness [5–8], making early faults difficult to detect and diagnose. Rolling components come in a variety of forms, including balls, cylindrical rollers, needle rollers, conical rollers, and spherical rollers. Rolling bearings primarily consist of structures like inner rings, outer rings, rolling bodies, and cages [9]. When local faults occur in rolling bearings (such as cracks, small holes, pits, or missing surface materials), vibration pulse signals are generated when the ball passes through the defect. Pulse signals contain many faults in the information that must be extracted. On the contrary, it is common for vibration pulse signals to be accompanied by harmonic components, background noise, amplitude modulation, and frequency modulation signals. Moreover, bearing vibration pulse signals are often nonlinear and nonstationary, with pulse components that are typically too faint to differentiate. Therefore, detecting pulse signals for fault diagnosis under high noise and strong harmonic interference remains a challenge [10–13].

In recent decades, a wide range of signal processing methods have been created with the dual purpose of reducing noise and extracting bearing failure signal features, including Short Time Fourier transform (STFT) [14], discrete wavelet transform (DWT) [15], empirical mode decomposition (EMD) [16], variational mode decomposition (VMD) [17], spectral kurtosis (SK) [18], minimum entropy deconvolution (MED) [19], Stochastic resonance [20] and singular value decomposition (SVD) [21]. One of the drawbacks of STFT is its fixed time-frequency resolution; DWT requires predetermined wavelet basis functions and decomposition levels, lacking adaptability; EMD has the capability to deconstruct the signal adaptively into a sequence of intrinsic mode functions, which unveil the signal’s fundamental nature, by using its local scale properties. However, EMD has problems such as mode mixing and over envelope; VMD can effectively suppress modal aliasing, but the number of modal decompositions configured influences the signal decomposition performance of the VMD approach. MED processes the signal with the kurtosis maximum as the objective function, which can improve the pulse property of the signal. Ke et al. [22] proposed a bandwidth selection scheme based on the Vold–Kalman filter to ensure the reliability of fault diagnosis for offshore wind turbine operating condition monitoring. Qing et al. [23] established a parallel dual-channel residual learning architecture that can automatically extract bearing fault features to integrate bearing fault features. However, when the fault signal is relatively weak and the bearing fault signal is a periodic pulse, effective extraction is not possible using merely the pulse feature. Consequently, nonadaptive signal processing approaches encounter challenges in attaining appropriate outcomes when analyzing actual information.

Extracting pulse features under background noise and nonstationary conditions has become a challenge [24]. Among them, SVD, as an effective nonlinear filtering method, is widely used in mechanical fault diagnosis. The SVD approach is capable of identifying weak eigenmodes concealed within a signal and attenuating noise with varying distributions without requiring a predefined basis function. Notwithstanding the effective use of SVD in bearing fault identification, several concerns persist that need more attention. Firstly, the performance of SVD mainly depends on the selection of traversal length. However, currently, the embedding dimensions are mostly selected based on experience and have poor adaptability, which affects the application of SVD in bearing diagnosis [12, 25, 26].

Li et al. [27] proposed a correlation SVD (C-SVD) method, used envelope kurtosis as an index, studied the optimal structure of the Hankel matrix (number of rows and number of columns), discussed the number of data points of the analysis signal and gave the constraint range. The problems of low singular value aggregation of the Hankel matrix in the SVD method and a large amount of noise in the reconstructed signal are solved; In order to mitigate the effects of harmonics and noise components, Sun et al. [28] presented a dictionary-based data-driven detection technique that combines K-clustering and SVD (K-SVD) to reliably identify pulse components. Nevertheless, it is simple to produce incomplete vibration morphology during the truncation process, which differs from the vibration waveform’s structure and might make it difficult to precisely identify and successfully extract impact components. The fundamental principle behind the SVD-based background noise reduction approach is to generate a matrix with rank-1 and use SVD to identify the greatest singular value, which may be used to construct a fault impulse signal. On the other hand, the traversal period determines the matrix’s rank throughout the trajectory matrix generation process. Typically, the embedding dimension for the traversal length in these contemporary SVD-based algorithms is determined by the characteristic of the input signal, such as the average period of the fault vibration signal. Subsequently, the trajectory matrix is built [29]. To reduce the influence of traversal segment length on the performance of fault impact signal reconstruction and ensure that the resulting trajectory matrix is a strict rank-1 matrix, this is what was done. A shift rank-1 reconstruction (SR1)-based fault impact extraction technique is put forward. Initially, an approximation of λ is carried out and an iteration is initiated for the reconstructed signal following preprocessing, given an arbitrary or approximate traversal segment length. According to this calculated λ, the phase of the matrix and the offset are updated by the offset vector, and the global optimization is carried out in order to determine the maximal left singular vector as well as the global amplitude. By combining the phase of the offset with the global amplitude, the trajectory matrix of the SVD is created, and all potential offsets are updated through local optimization. The reconstruction of the shift rank matrix, which enables the shift operator to compel the creation of the rank-1 matrix while preserving the length of the pre-calculated traversal segment, is the method’s core. By doing so, the performance and robustness of the approach are enhanced, and the influence of the traversal segment length on the reconstruction of the impact signal is reduced. Through simulation and test bench studies, the efficacy of the shift rank-1 building matrix technique has been validated, and it has been contrasted with other methodologies. Simultaneous quantitative and qualitative analysis is conducted, and the impact of traversal segment length on the efficiency of shock information extraction is examined.

2. Algorithm Model

2.1. Scale Space Preprocessing

Define f(x) as a continuous function on the interval [0, x_max], select

p (x; δ) = (1 / \sqrt{2 π δ}) e^{- x^{2} / (2 δ)}

as the kernel function for calculating the scale space, and the continuous scale space of function f (x) can be represented as

\begin{matrix} ψ (x, δ) = p (x; δ) * f (x) . \end{matrix}

()

In the formula: ∗ represents convolution; δ is the scale parameter.

When processing the signal, it is required to be a discrete signal, so it is necessary to discretize the continuous scale space. The discretization of scale space mainly includes the discretization of scale space kernel functions and the discretization of scale parameters. The discretization of scale space can be expressed as

\begin{matrix} ψ (m, δ) = \sum_{n = - L}^{L} f (m - n) p (n; δ) . \end{matrix}

()

In the formula: m is the discrete point in the scale space; N is the eigenvalues of the kernel function; L is the wide window of the kernel function, usually taken as (3 ≤ a ≤ 6, but to ensure that the approximate error of the Gaussian kernel function during discretization is less than 10⁻⁹, a = 6 is generally set).

Gini index (GI) is a statistical inequality indicator proposed by Corrado Gini in 1921 to measure economic wealth inequality. The vibration signal of a malfunctioning rolling bearing is typically focused at specific points in the signal sequence. The sparsity of the fault signal is similar to the imbalance in income distribution described in economics. Therefore, the rolling bearing defect development trend may be described and the health state of an individual can be evaluated using the Gini coefficient. For a real signal sorted in ascending order, |x₁| ≤ |x₂| ≤ ⋯≤|x_N|. The expression for its Gini coefficient G can be defined as

\begin{matrix} G (x) = 12 - \sum_{k = 1}^{N} \frac{|x_{k}|}{{‖x‖}_{1}} (\frac{N - k - 0.5}{N}) . \end{matrix}

()

In the equation, ‖x‖₁ represents the L1 norm of signal x; N is the length of the signal. The stronger the periodic pulse of the real signal x in the frequency domain, the larger the corresponding indicator value G.

2.2. Shift Rank-1 Matrix

The shift rank-1 matrix provides a new method for solving approximate solution problems. Given a signal

A \in R^{M \times N}

M, N \in N

, use the L shift rank-1 matrix

u^{k} {(v^{k})}^{T}

to find an approximate value for matrix A [30]. Therefore, it can be expressed as

\begin{matrix} \min_{\begin{matrix} λ^{1}, \dots λ^{L} \\ u^{1}, \dots u^{L} \\ v^{1}, \dots v^{L} \end{matrix}} {‖A - \sum_{K = 1}^{L} S_{λ^{k}} ({u^{k} (v^{k})}^{T})‖}_{F} . \end{matrix}

()

Among them,

S_{λ^{k}} ({u^{k} (v^{k})}^{T})

is the shifted rank-1 matrix. When λ¹ = ⋯ = λ^k = :λ, (4) is simplified as

\min {‖A - S_{λ^{k}} (U V^{T})‖}_{F}

, and the approximate solution of the problem can be obtained by SVD, which gives the first L eigenvalues. In addition, when k ≠ j and λ^k ≠ λ^j are used, S_λ is defined, and

I \in C^{(M - 1) \times (M - 1)}

is the Identity matrix.

{\tilde{S}}^{k}

shifts the element of u by k entries, where u is the column vector.

{\tilde{S}}^{k}

is defined as follows:

\begin{matrix} \tilde{S} ≔ (\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}) \in C^{M \times M}, \\ {\tilde{S}}^{k} ≔ \prod_{j = 1}^{k} S . \end{matrix}

()

For k ≤ 0, use the identity

{\tilde{S}}^{k} = {\tilde{S}}^{M + k}

, A = [a¹, …, a^N], where y is the column of matrix A. The shift operator S_λ is defined as

\begin{matrix} S_{λ} (A) ≔ [{\tilde{S}}^{λ_{1}} a^{1}, \dots, {\tilde{S}}^{λ_{N}} a^{N}] . \end{matrix}

()

The shift operator S_λ is linear, and the inverse operator is obtained by $S_{λ}^{- 1} = S_{- λ}$ . This operator maintains the integrity of the norm, ${‖S_{λ} (A)‖}_{F} = {‖A‖}_{F}$ . Given $λ^{'} \in Z^{N}$ , $S_{λ} S_{λ^{'}} = S_{λ + λ^{'}}$ can be obtained. If A = S_λ(uv^∗), $u \in C^{M}$ , $v \in C^{N}$ , $λ \in Z^{N}$ , then $A \in C^{M \times N}$ is called a shift rank-1 matrix [31].

In order to resolve equation (4) for every variable, an iterative technique is implemented. After recovering a single shifted rank-1 matrix in each iteration, the process of generating the difference matrix and shifted rank-1 matrix of A is repeated. Iterating L times allows for the reconstruction of all unknowns, defined as

\begin{matrix} \underset{λ, u, v}{minmize} {‖A - S_{λ^{k}} (u v^{T})‖}_{F} . \end{matrix}

()

Rewriting (8) by using the inverse shift operator and utilizing its linearity:

\begin{matrix} \underset{λ, u, v}{\min mize} {‖S_{- λ} (A) - u v^{T}‖}_{F} . \end{matrix}

()

With knowledge of the shift vector λ, SVD may be used to derive the variables u and v [32]. Determining the ideal λ is therefore essential to the solution. σ₁, …, σ_K is assumed to be the singular value of S_−λ(A).

\begin{matrix} {‖S_{- λ} (A) - u v^{T}‖}_{F}^{2} = \sum_{k = 2}^{K} σ_{k}^{2} = {‖S_{- λ} (A)‖}_{F}^{2} - σ_{1}^{2} \\ = {‖A‖}_{F}^{2} - {‖S_{- λ} (A)‖}_{2}^{2} . \end{matrix}

()

Obtain λ by solving:

\begin{matrix} \underset{λ \in Z^{N}}{\max mize} {‖S_{- λ} (A)‖}_{2}^{2} . \end{matrix}

()

The u^k and v^k values associated with the L unique features are used to represent each cycle of fault impact during the extraction of fault impact information and noise interference reduction. Each layer of u^k and v^k represents the segmented period of the vibration signal subsequent to L’s truncation operation. As previously stated, any shift rank-1 matrix may be conceptualized as the product of two matrices, denoted as S_λ(uv^∗) = UV. In order to generate the convolutional matrix U, vector u is used, whereby row positions λ of V correspond to 1-sparse columns. V is a non-zero element. Multiplying the shifted rank-1 matrix with this factorization enables convolution to be performed in the Fourier domain. The shift operator in the Fourier domain is used to represent and

F (A) = \overset{\land}{A}

represents the Fourier transform of the column direction of A.

\begin{matrix} F (S_{λ} A) = \overset{\land}{A} ⊙ P_{λ}, P_{λ} = {[e^{- (2 π i / M) j λ_{k}}]}_{j, k = 0}^{M - 11, N -}, \end{matrix}

()

where P represents the phase matrix and each element contains absolute values.

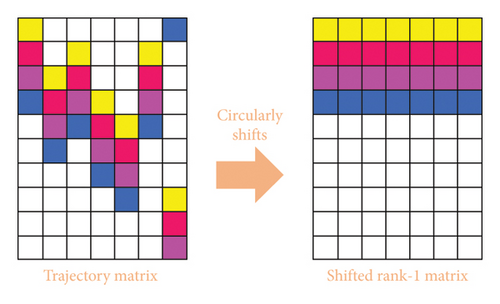
The SR1-SVD technique demonstration indicates that the resultant matrix may be shifted into a strictly rank-1 matrix by using a shift vector. From Figure 1, the discovered original periodic components have been seen to have been moved to various rows. These elements are shifted collectively to create a rigorous rank-1 matrix following the shift rank-1 approximation. Consequently, erroneous components and noise effects may be minimized when reconstructing vibration signals using singular values, in addition to allowing unambiguous fault impact signals to be rebuilt based on singular values.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Trajectory matrix before and after shift rank-1 method.

2.3. Reconfiguration λ

A method for solving optimized λ by rank inequality based on Hadamard product [33]:

\begin{matrix} rank (A) = rank (\overset{\land}{A}) = rank (\overset{\land}{A} ⊙ P_{- λ} ⊙ P_{λ}) \\ \leq rank (\overset{\land}{A} ⊙ P_{- λ}) rank (P_{λ}) \\ = rank (S_{- λ} A) rank (P_{λ}) . \end{matrix}

()

Formula (10) can be computed in Fourier transform (11). Its maximum value can be easily described. Since

{‖A‖}_{2} \geq {‖u^{*} A‖}_{2}

for all ‖u‖₂ = 1 and the equation for the first left singular vector holds, we can rewrite (10) as

\begin{matrix} \max_{{‖u‖}_{2} = 1, λ} {‖u^{*} S_{- λ} (A)‖}_{2}^{2} . \end{matrix}

()

The optimization of the equation above yields the location k of the translation column and the migration coefficient λ_k. A is subsequently modified to reflect the generation of the initial left singular vector u. Continue doing this until the offset coefficient Δλ_k = 0 varies. The Fourier domain allows for the efficient solution of problems (13). There are two terms in the cross-correlation: the cross-correlation at location λ_k for u and k, and the cross-correlation at position 0. The Fourier domain calculation of the cross-correlation yields the value

F^{- 1} (\bar{\overset{\land}{u}} ⊙ {\overset{\land}{a}}^{k})

. We define

\begin{matrix} \bar{\overset{\land}{u}} ⊙ \overset{\land}{A} ≔ [\bar{\overset{\land}{u}} ⊙ {\overset{\land}{a}}^{1}, \dots, \bar{\overset{\land}{u}} ⊙ {\overset{\land}{a}}^{N}] . \end{matrix}

()

As the element-by-element product of each column of a vector and matrix. Define $B = {|F^{- 1} (\bar{\overset{\land}{u}} ⊙ \overset{\land}{A})|}^{2}$ and set b¹ as its first line. Then (13) can be written to find the maximum of B − 1b¹. Repeat this process until you end up with a local maximum. Since there are only a limited number of possible values for λ, this outcome is definitely attained after a limited number of steps.

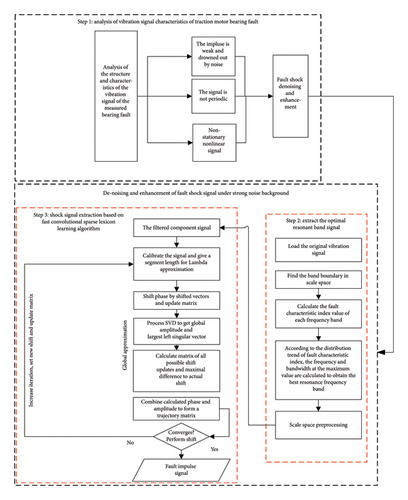
2.4. Application of Shift Rank-1 Algorithm in Extracting Fault Information From Vibration Signals

The bearing fault diagnosis program contains three main steps to diagnose a traction motor bearing fault which can be shown in Figure 2:

•
Step 1: The input vibration signal is analyzed and calculated the fault frequencies based on bearing’s types(diameters and rotating speeds, etc.), then distinguish the vibration impulse whether be drown or disturbed by background noise, and also judge this signal is periodic or not.
•
Step 2: After those processes above, signal enhancements have carried out and preprocess applied by scale-space method to enhance periodic parts of fault signals. The scale-space method contains two substeps, finding the frequency boundary and the maximum characteristics index to locate the best vibration resonance which fully contained the fault information for de-noising.
•
Step 3: According to the output signals in Step 2, the proposed SR1-SVD method is applied. Firstly, in order to find the periodic impulse in signals, a trajectory matrix I produced by using the acquired phase and amplitude information, after which the shift vector is used to calculate the shift phase and updated matrix, as well as the global amplitude and maximum left singular value. Determine whether the matrix is made between the maximum difference between the shift update and the actual shift.
•
Step 4: We compute the best rank-1 approximation if the matrix is convergent. This rank-1 matrix is used to reconstruct the fault shock signal. If not, proceed with a new estimate of λ, choose a different shift, and update the matrix until convergence is achieved by increasing the number of iterations. Finally, the pure fault signal is reconstructed by SVD which only consists of periodic fault information for bearing fault diagnosis.

3. Method Validation

3.1. Simulated Signal Validation

As illustrated in Figure 3, the fault vibration signals received by the sensor end during the actual operation of subway cars may be classified as bearing fault impact signals, harmonic signals, transmission interference signals produced by other component vibrations, and background noise.

In order to validate the efficacy of the SR1-SVD approach that was presented, a bearing outer ring fault model was developed. Given the impact of severe background noise interference that occurs at random on subway trains while they are in service, the random model may be mathematically represented as follows:

\begin{matrix} x_{1} (t) = \sum_{m = 0}^{M - 1} A_{m} e^{- β (t - n T)} \cos [2 π f_{R} (t - \sum_{i = 0}^{m} Δ T_{i})] \times u (t - \sum_{i = 0}^{m} Δ T_{i}) . \end{matrix}

()

\begin{matrix} x_{2} (t) = \sin (2 π f_{R} t), \\ x (t) = x_{1} (t) + x_{2} (t) + n (t), \end{matrix}

()

where x₁(t) is the failure signal of the bearing outer ring, and the failure frequency f_BPFO = 152 Hz; A_m is the fault impact amplitude, A = 1; f_R is the resonant frequency of the system, f_R = 3000; β as attenuation coefficient, β = 1000; T is the impact time interval, T = 1/ f_BPFO; u(t) is the unit step function; x₂(t) represents periodic harmonic interference and n(t) represents Gaussian white noise. The range of values for the signal-to-noise ratio (SNR) setting is −20 dB to 0 dB. Set the signal-to-noise ratio to −10 dB, the sampling frequency f_s to 10 kHz, and the analyzed signal length to 10,000. The mixed-signal and periodic impulse signal are shown in Figure 4, also the pre-processing under scale space has been done and shown in Figure 5. Figure 6(a) shows the time domain signal and Figure 6(b) shows the corresponding envelope spectrum. Despite the visibility of the usual frequency in Figure 6(b), the presence of noise interference hinders the precise identification of issue features. While the characteristic frequency and 2∼4 times frequency are visible, noise interference has resulted in considerable spectral lines surrounding it, making it challenging to discern further fault feature effect information.

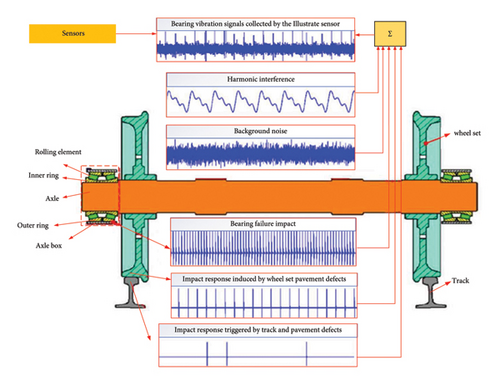
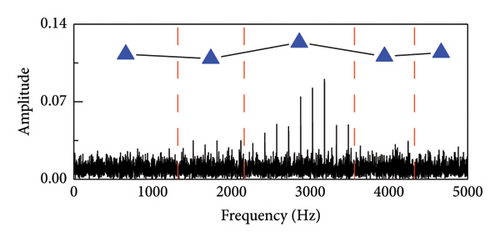
Based on the composition structure and vibration mechanism of the rolling bearings, bearing failures usually occur including the outer ring, inner ring, rolling elements, and cage. Any failures will induce periodic impact excitation, and the frequency of these periodic impacts is the fault characteristic frequency of the bearing, and its determination needs to consider multiple factors such as speed, fault category, and structural parameters of the bearing itself.

The characteristic frequency of outer ring fault f_BPFO:

\begin{matrix} f_{BPFO} = \frac{Z}{2} (1 - \frac{d_{0}}{D} \cos ϕ) f_{r} . \end{matrix}

()

The characteristic frequency of bearing inner ring fault f_BPFI:

\begin{matrix} f_{BPFI} = \frac{Z}{2} (1 + \frac{d_{0}}{D} \cos ϕ) f_{r} . \end{matrix}

()

The fault characteristic frequency of bearing rolling element faults f_BSF:

\begin{matrix} f_{BSF} = \frac{f_{r}}{2} [1 - {(\frac{d_{0}}{D} \cos ϕ)}^{2}] \frac{D}{d_{0}} . \end{matrix}

()

The fault characteristic frequency of the bearing cage f_FTF:

\begin{matrix} f_{FTF} = \frac{f_{r}}{2} (1 - \frac{d_{0}}{D} \cos ϕ), \end{matrix}

()

where f_BPFO, f_BPFI, f_BSF, and f_FTF, respectively, refer to the fault characteristic frequencies of the outer ring, inner ring, rolling elements, and cage of the bearing. Among them, Z is the number of rolling elements, α represents the pressure angle, D is the pitch diameter, d₀ is the rolling element’s diameter, and f_r refers to the rotating speed. According to those fault frequencies equations, the calculated fault frequencies are proportional to rotating speeds.

To impartially evaluate the fault feature information extraction capabilities of various approaches, including SR1-SVD, APSM-SVD, PSM-SVD, Hankel-SVD, MED, SK, VMD, singular spectrum analysis (SSA), and DWT, an envelope spectrum-based signal-to-noise ratio for bearing fault signals is provided. It may be expressed as

\begin{matrix} SNR (f_{p}) = 10 \lg \frac{\sum_{c = 1}^{C} Y^{2} (c f_{p})}{\sum_{f = 0}^{F_{s} / 2} Y^{2} (f) - \sum_{c = 1}^{C} Y^{2} (c f_{p})} . \end{matrix}

()

In the formula, the fault characteristic frequency is represented by f_p, and the amplitude in the signal’s envelope spectrum that corresponds to frequency f is denoted by Y(f). C is the characteristic frequency f_p that is involved in the calculation’s greatest harmonic order. Since the amplitude in the envelope spectrum corresponding to the fault characteristic frequency is negligible beyond the sixth harmonic, C is set to 6. The signal-to-noise ratio comparison range is established as −20 to 0 db.

In order to make a credible comparison among all methods mentioned above, the compared methods like Adaptive Periodic Segment Matrix and SVD (APSM-SVD), PSM and SVD (PSM-SVD), Hankel-SVD, MED, SK, VMD, SSA, and DWT are applied under the suitable parameters for best performance. The core of APSM-SVD, PSM-SVD, and Hankel-SVD methods are forming strict rank-1 matrices for achieving better performance. Similarly, VMD and DWT choose the suitable parameters of K, penalty factor alpha and the base of wavelet functions for best performances. Moreover, the parameters in MED and SK are modified, for example, the Entropy function and kurtosis are the essential factors for best performances. All parameters and ways of optimal implementation for compared methods are shown in Table 1.

Table 1. The parameters used for comparison for different methods.

Method	The way of optimal implementation	Parameters
SR1-SVD	Shift vectors lambda to form a strict rank-1 matrix	Automatically iterated
APSM-SVD	Segment constraints to form a strict rank-1 matrix	Usually 2/3 lengths of signals
PSM-SVD	Signal truncation segments to form a strict rank-1 matrix	Set based on the input signals
Hankel-SVD	The diagonal array in formed matrix	Automatically iterated
MED	Types and lengths of chosen filters, the entropy function	Formed according to the characteristics of input signals
SK	The values of calculated kurtosis	Kurtosis differences between signals
VMD	Centre frequencies, parameters mode K and penalty factor alpha	K set as the number of decomposed signals
SSA	The calculated singular values	Singular values between signals
DWT	Types of wavelet bases	Daubechies wavelet, Meyer wavelet

The SNR of various approaches is shown in Table 2. It is evident that the reconstructed signal’s SNR rises in tandem with the signal’s SNR. As expected from prior study findings, the SR1-SVD approach has the greatest SNR value, followed by ASM-SVD.

Table 2. Analyses of the signal-to-noise ratio using envelope spectrum data (simulated signal).

Method (dB)	SR1-SVD	APSM-SVD	PSM-SVD	Hankel-SVD	MED	SK	VMD	SSA	DWT
SNR = −20	−18.23	−19.87	−29.28	−25.31	−23.45	−22.26	−19.78	−28.09	−21.79
SNR = −15	−10.11	−11.96	−13.14	−22.14	−19.39	−17,39	−18.56	−19.51	−24.07
SNR = −10	−1.24	−2.49	−2.97	−13.41	−13.18	−10.31	−11.23	−20.84	−22.34
SNR = −5	1.25	−0.31	−0.52	−6.78	−2.71	−4,34	−3.64	−1.18	−13.95
SNR = 0	2.68	1.72	0.55	−0.52	−3.24	0.39	−2.59	−2.55	−7.01

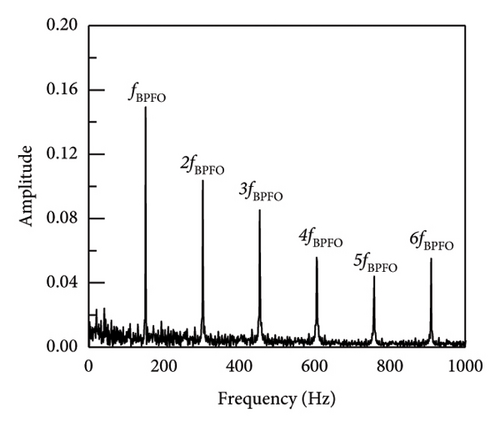
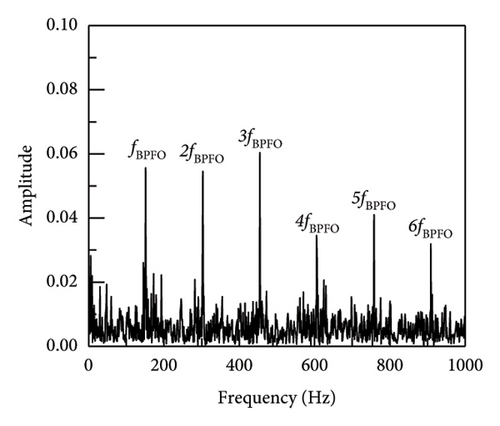
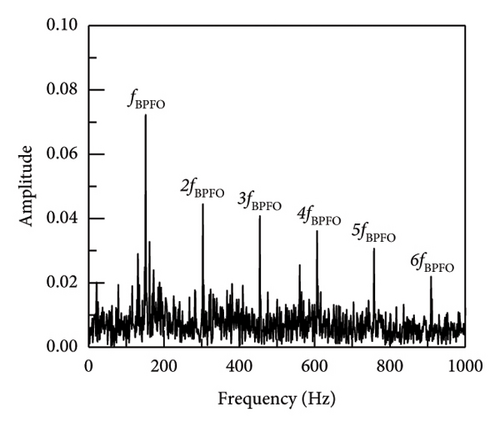
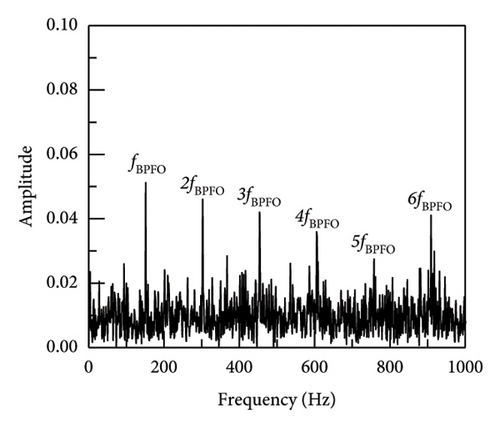
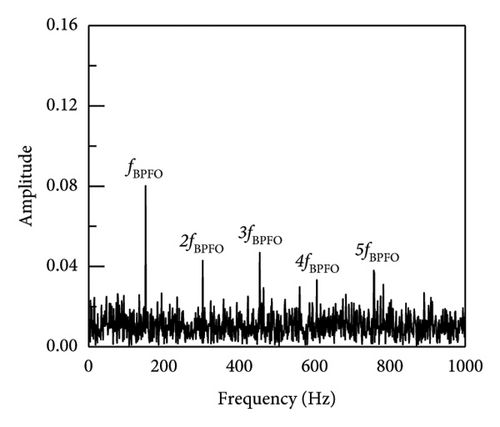
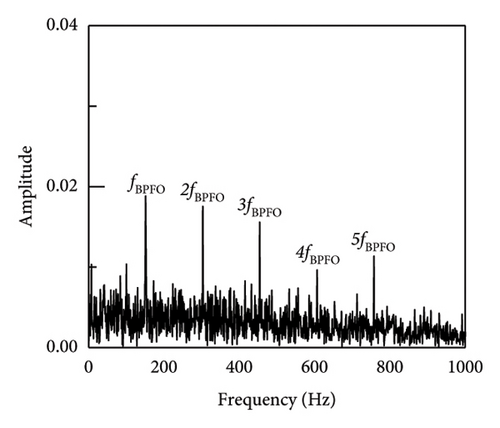
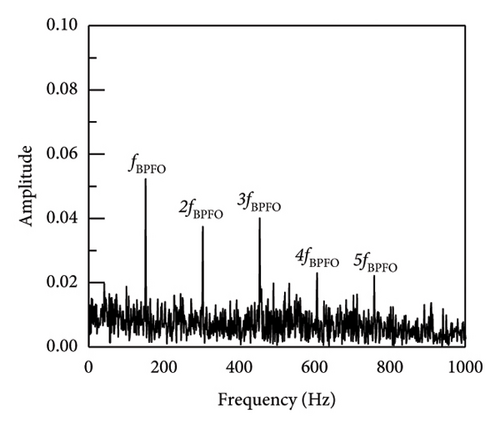
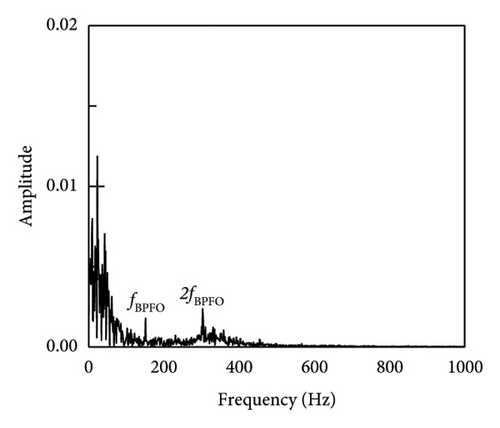
In addition, taking SNR = −10 dB as an example, the envelope spectrum image validation and comparison between SR1-SVD and other methods are shown in Figure 7. The envelope spectrum for the reconstructed impact signal is produced by the implementation of the suggested SR1 approach, as seen in Figure 7(a). The characteristic frequency and multiple frequency components of the outer ring fault can be clearly seen, and there are no other prominent fault characteristic components. The envelope spectrum provides sufficient information to conclude that the bearing is afflicted with an outer ring defect. Simultaneously, methodologies including APSM-SVD, PSM-SVD, Hankel-SVD, MED, SK, VMD, SSA, DWT, and envelope analysis were used to evaluate the outcomes of the proposed SR1-SVD with the deconstructed recovered signal’s time-domain waveform. From the figure, it can be seen that most methods can identify fault impact signals, and find fault characteristic frequencies and their multiples. Firstly, Figures 7(b), 7(c), and 7(d) show the extraction of impact signals using APSM-SVD and PSM-SVD for vibration signals. Additionally, it is evident that 2–6 octaves and the distinctive frequency of the outer ring fault are visible. In contrast to (a), (b), (c), and (d) provide additional information on noise, with interference information located on the left side of the fourth octave in case of (c). The results of MED, SK, VMD, SSA, and DWT indicate that a substantial quantity of noise interference persists in the reconstructed impact signal, and the fault information extraction is insufficient, hence impeding the extraction of the impact components. Consequently, the SR1-SVD suggested in this paper is more effective in removing noise and extracting impact components. When compared to alternative techniques, the reliability of defect detection and diagnosis is improved by the clear and succinct envelope spectral lines of periodic impact signals that have been extracted.

3.2. Experimental Data Analysis

The suggested approach is experimentally verified using the wheel-bearing testing platform depicted in Figure 8. The components of the experimental test bench include a gearbox, collector, rail wheelset, loading apparatus, motor, driving wheels, and analysis laptop. At varying motor speeds and via rubber belts, the motor imparts driving power to the driving wheels, which then transfer traction force to the test wheelset. The experimental double-row tapered roller bearing exhibited an outer ring defect, which was manually positioned and had three piercing wounds on its surface (Figure 8).

All the details of vibration acceleration sensors are shown in Table 3. The experiment uses the 1A110E three-axis acceleration sensor, which is magnetically attached to the drive ends of the motor. The HD2001 16-channels data collector is used to record the bearing vibration signal, with a sampling frequency set to 10 kHz and continuous recording of data for 30 s. The bearing speed is set to 540 r/min. A wheelset rotation frequency of 10.28 Hz. Table 4 displays the characteristics and fault characteristic frequencies of the experimental bearing. For a more comprehensive evaluation of the effectiveness of this method in acquiring early failure information of motor bearings against loud noise environments, harmonic interference, impulse response, and Gaussian white noise with a signal-to-noise ratio of −10 dB are added to the vibration signal.

Table 3. The details of vibration acceleration sensors used in testing platform.

Channel	Sensor	Sensitivity mv/(m ∗ s⁻²)	Installation placement	Precision (g)
X	1A110E	4.998	Longitudinal close to the drive end	100
Y	1A110E	4.998	Horizontal close to the drive end	100
Z	1A110E	4.998	Vertical close to the drive end	100

Table 4. Test bearing specification and fault characteristic frequency.

f_BPFO	f_BSF	Rolling diameter (mm)	Number of rolls	Pitch diameter (mm)	Contact angle
83.23 Hz	33.65 Hz	26.9	19	180	π/20°

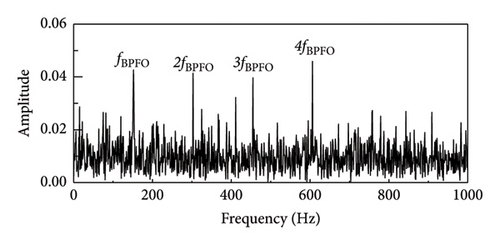
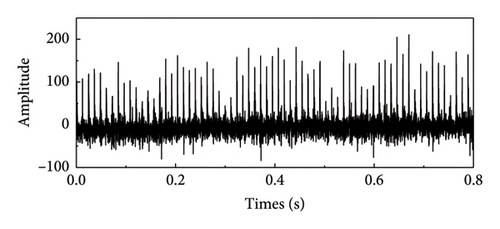
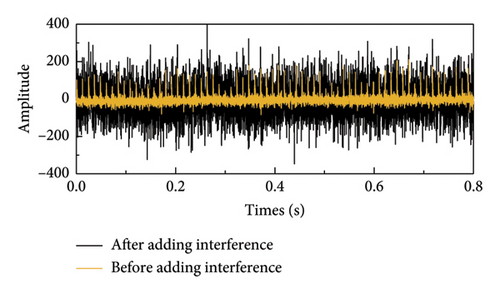
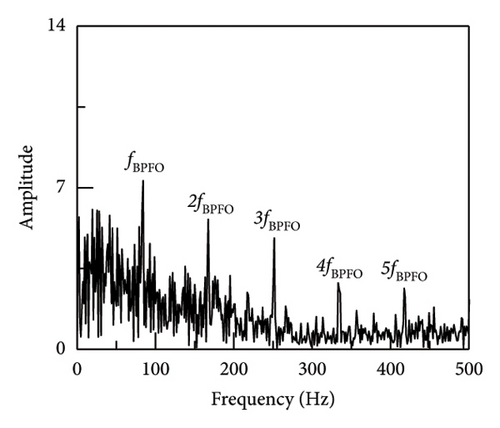
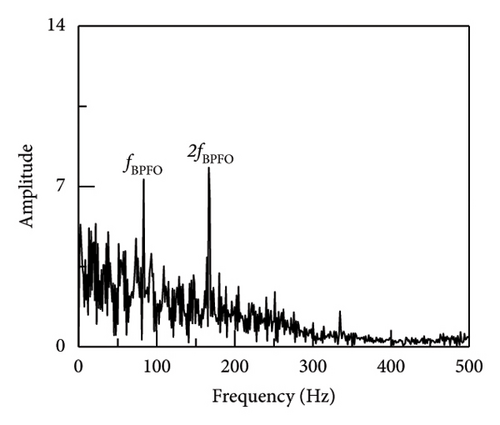
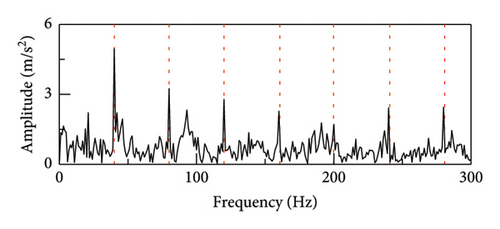
Before interference is introduced, the orange time domain waveform of the interference vibration signal is seen in Figure 9. The impact component is obviously obscured by white Gaussian noise and other information, which complicates the process of determining its regularity and extracting pertinent data. Figures 10 and 11 illustrate the time domain after scale space preprocessing and the denoised fault signal envelope spectrum. Defect feature detection is a complex task due to the difficulty in detecting frequency conversion and other forms of feature doubling. Even when the distinctive frequency is apparent, it is surrounded by considerable noise interference spectral lines.

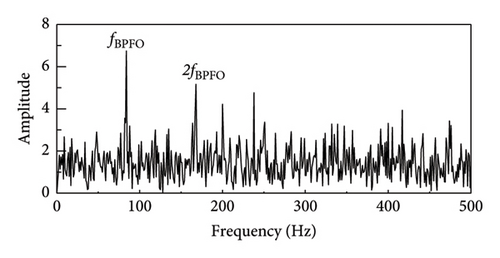
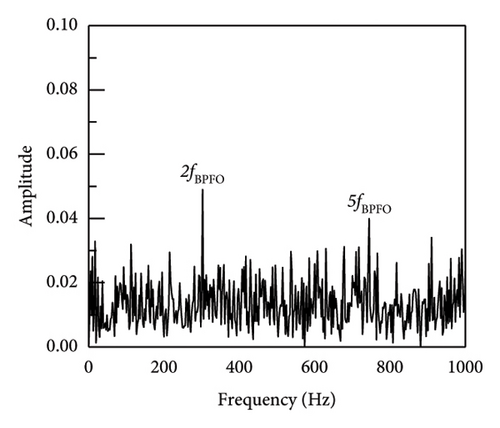
As demonstrated in Figure 12, the study’s proposed SR1-SVD and other techniques discovered the effectiveness of SR1-SVD, APSM-SVD, and PSM-SVD in extracting fault pulse information from vibration signals through reconstructed signals retrieval, as well as generating their envelope spectrum. On the other hand, the PSM-SVD approach has some interference impulse information, while the envelope spectrum of the SR1-SVD method has cleaner fault impulse information. With no additional fault feature components, the approach utilized in this article fully extracts fault information from the signal while avoiding interference signals. Consequently, in situations with high levels of noise, the technique described in this article can be used to obtain early defect information for vehicle motor bearings.

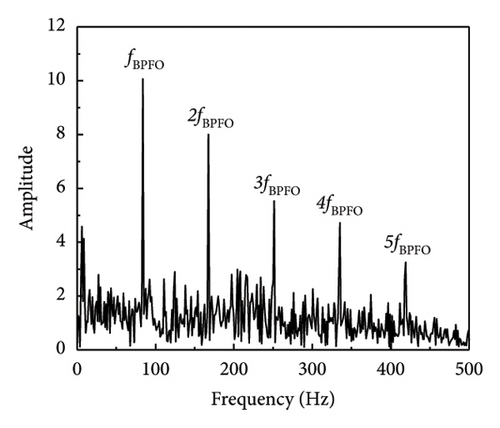
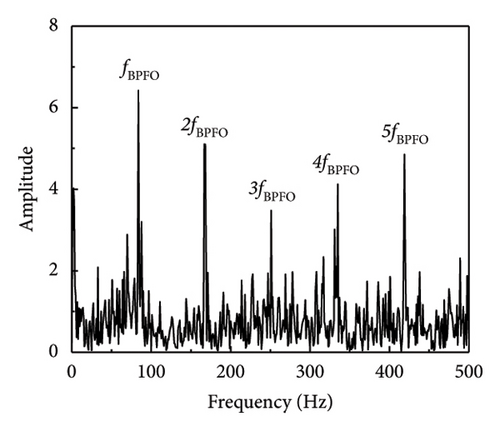
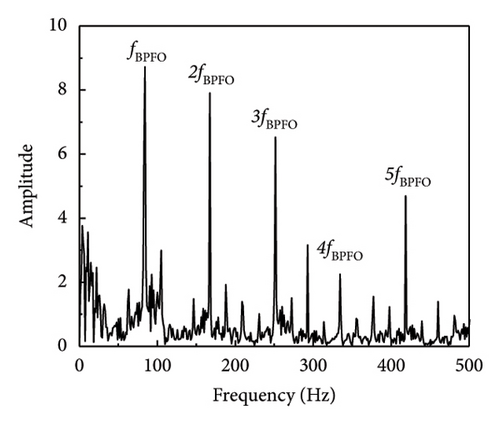
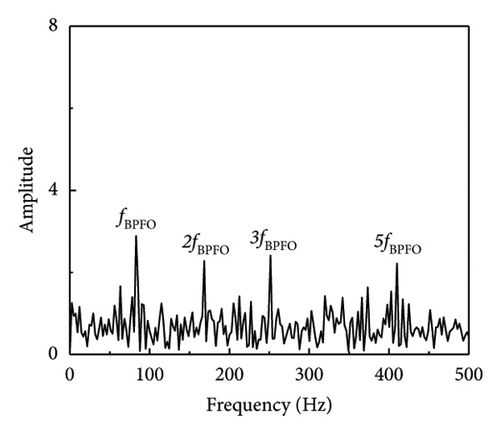
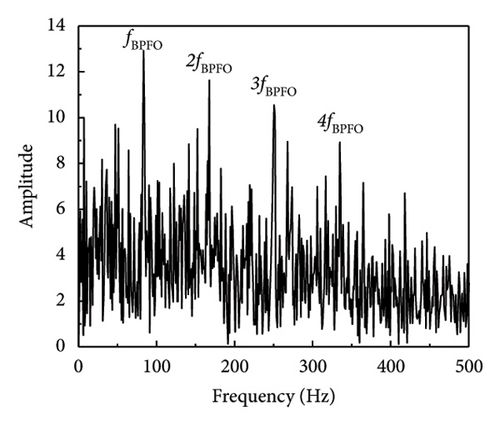
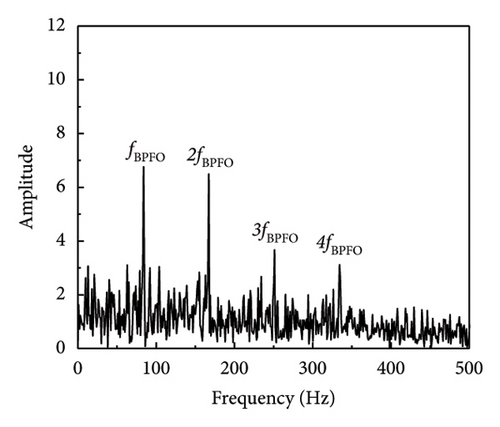
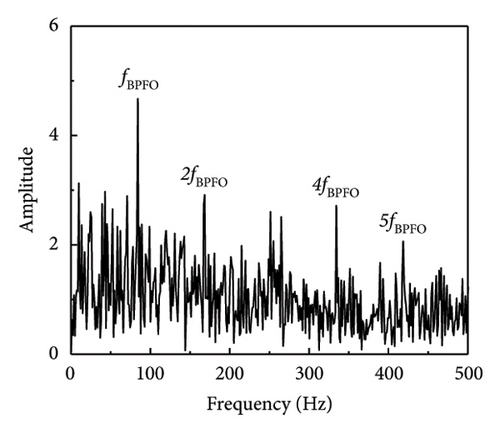
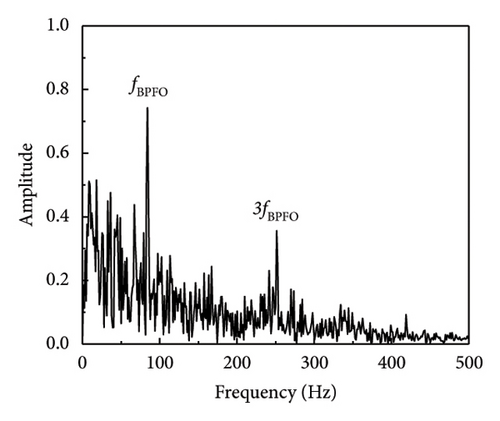
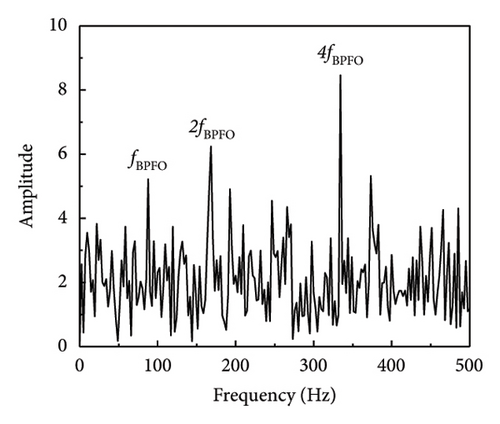
In a similar fashion, the envelope spectrum signal-to-noise ratio of the experimental signal on the test bench is computed using equation (17), which is used to evaluate the efficacy of the defect feature information extraction approach suggested in this article. The SNR derived from the envelope spectrum of the fault characteristic frequency is determined to be −18.79 dB by analysis of the envelope spectrum of the original signal (SNR = −10 dB) (when SNR = −15 dB, the envelope spectrum SNR is −23.95 dB). As shown in Table 5 and Figure 13, the processing results of each approach are calculated using the envelope spectrum-based signal-to-noise ratio, which spans the range of −20 to 0 dB. The table illustrates that the approach suggested in this article effectively distinguishes between fault impact components that are entirely enveloped in noise and the noisy vibration signal.

Table 5. Analyses of the signal-to-noise ratio using envelope spectrum data (experimental signal).

Method (dB)	SR1-SVD	APSM-SVD	PSM-SVD	Hankel-SVD	MED	SK	VMD	SSA	DWT
SNR = −20	−22.31	−24.90	−26.66	−23.57	−24.87	−24.16	−23.91	−25.79	−29.81
SNR = −15	−12.28	−13.64	−15.96	−14.19	−19.75	−19.91	−17.74	−18.16	−22.62
SNR = −10	−3.28	−4.32	−8.13	−13.61	−10.51	−11.89	−11.09	−10.58	−13.42
SNR = −5	−0.78	−0.84	−2.15	−13.56	−4.34	−5.04	−5.13	−4.76	−8.94
SNR = 0	−0.19	−0.69	−0.82	−6.48	−1.70	−1.94	−2.09	−6.51	−5.76

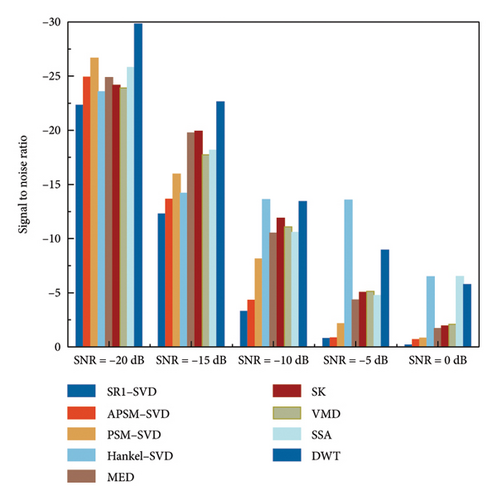
As a result, by using SR1-SVD to analyze fault signals, vibration signals’ noise interference may be greatly reduced, and their evident fault impact components can be distinguished from one another. The signal noise removal method based on SVD performs better than VMD and DWT in fault impulse signal reconstruction. Because the purpose of these methods based on SVD is to construct a strict first-order trajectory matrix to reconstruct the shock signal, rather than decompose the vibration signal. In contrast to other matrices created using SVD, the trajectory matrix created in this research is a pure rank-1 matrix. After using SVD, the rebuilt signal will either produce spurious components or lack fault information. Furthermore, SSA did not minimize noise or provide a rigorous rank-1 trajectory matrix. There would be additional components in the envelope spectrum. VMD requires selecting appropriate K and α values, while DWT requires selecting appropriate wavelet basis functions and adjusting parameters, otherwise accurate fundamental and octave relationships cannot be obtained.

By 20-fold amplification of the noise data acquired from the bogie during a particular line operation and subsequent addition to the vibration signal of the bench test, the efficacy of the model in discerning fault impacts caused by the dynamic response of other components in the measured signals during subway train operation could be more precisely validated. The findings are shown in Figure 14.

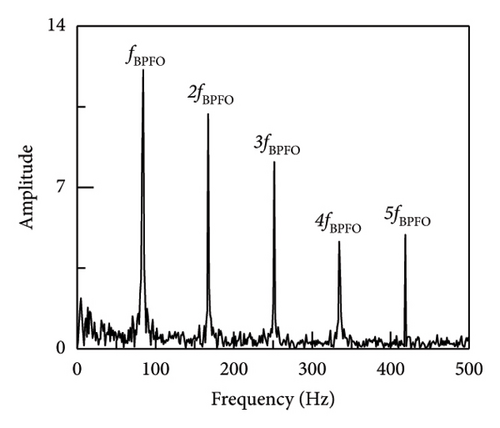
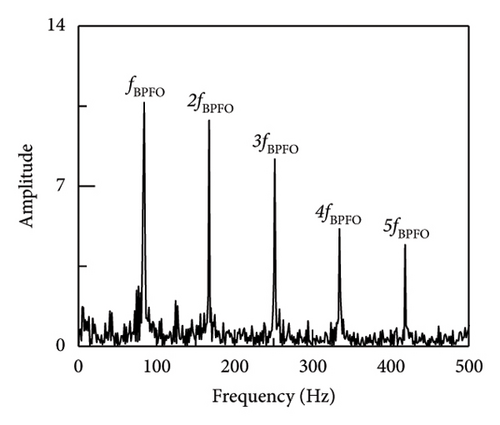
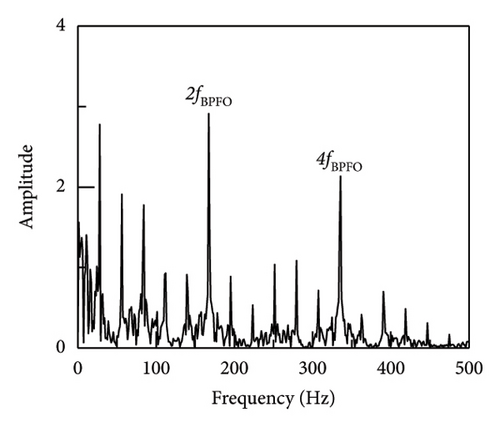
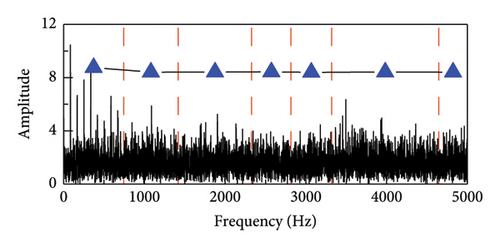
The envelope spectrum fault impulse peak of the SR1-SVD approach is the highest, as shown in the picture; the signal-to-noise ratio of the two envelope spectra is computed using the given equation (17). Among the three methods that can also extract fault impulse, SR1-SVD is more optimal. In addition, amplify the vibration data of the bogie by 40 times and add it to the vibration signal of the bench test. At this time, the noise of the bogie is the main information to verify the denoising ability of SR1-SVD and the ability to extract fault impact information, as shown in Figure 15. The figure reveals that SR1-SVD is capable of extracting the fundamental frequency and a range of 2–5 octaves. In contrast, APSM-SVD and PSM-SVD are only able to detect the fundamental frequency and 2 octaves. As a result, the efficacy of the strategy suggested in this article for extracting fault effects from backgrounds with high levels of noise has been shown.

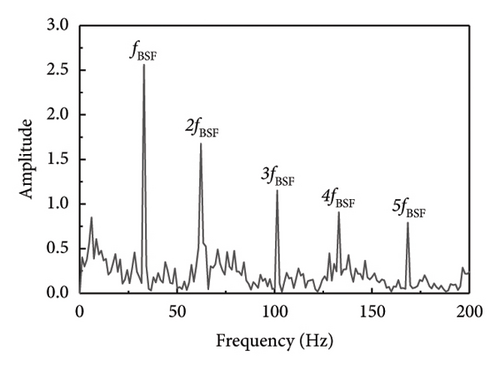
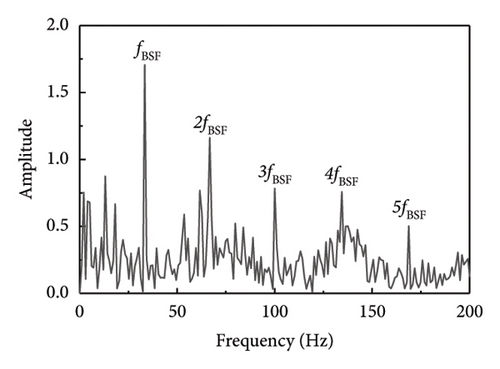
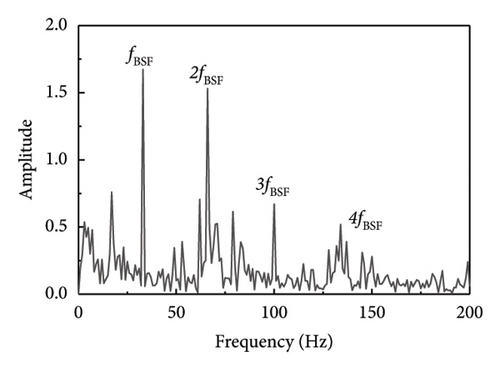
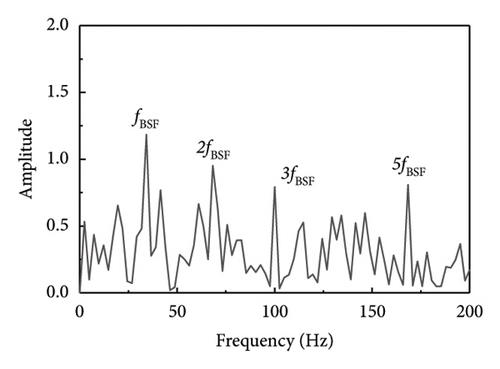
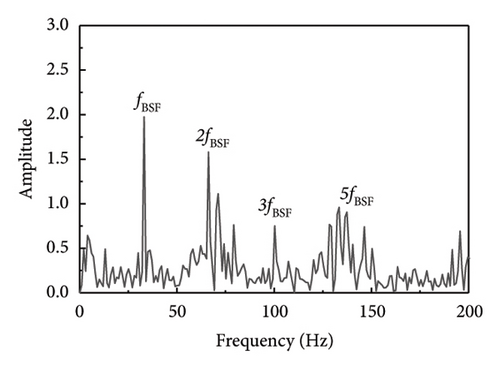
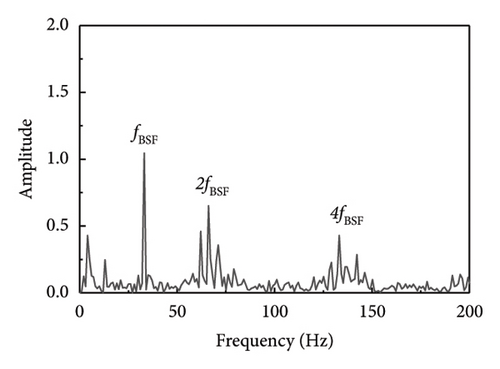
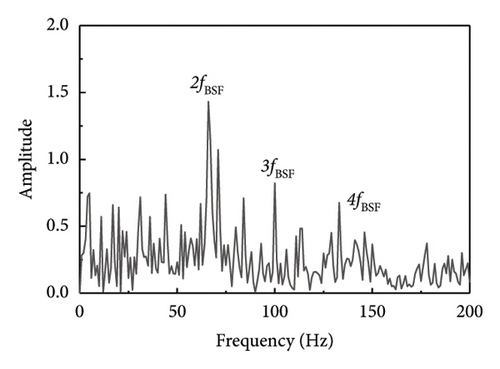
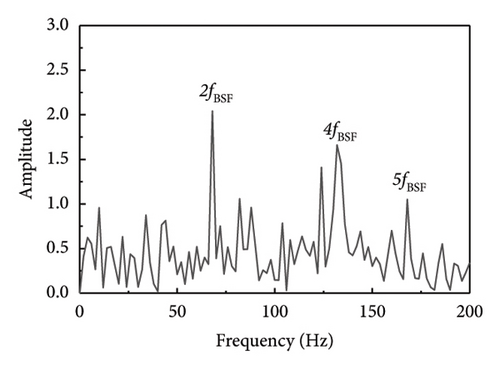
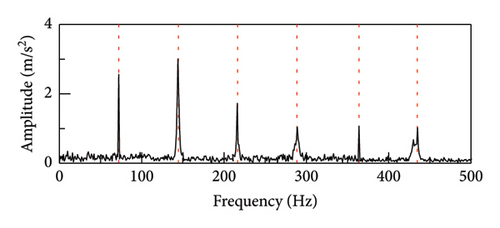
Other types of faulty bearings should also be considered for bearing fault diagnosis, where the main variations among faults are based on their frequency characteristics. As a result, this methodology may also be used to identify defects in the rolling components and inner ring of the bearings. As seen in Figure 16, fault shock data was derived from the rolling element fault vibration signals acquired during the bearing bench test by using several methodologies, including the proposed method SR1-SVD. It is evident from Figure 16 that the fault type can be identified through the fault characteristic frequency and frequency doubling of the rolling element as presented in Table 6.

Table 6. Experimental bearing specifications and the frequency of fault characteristic.

f_BPFI	Rolling diameter (mm)	Number of rolls	Pitch diameter (mm)	Contact angle α/(°)
64 Hz	13.49	14	125	0

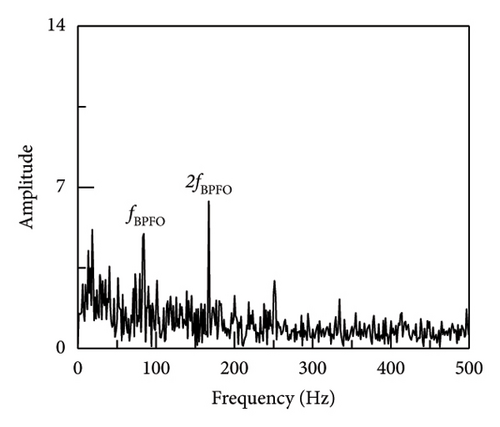
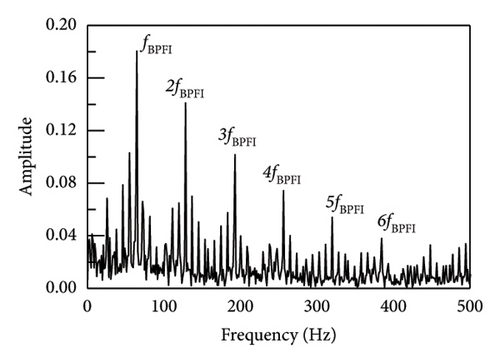
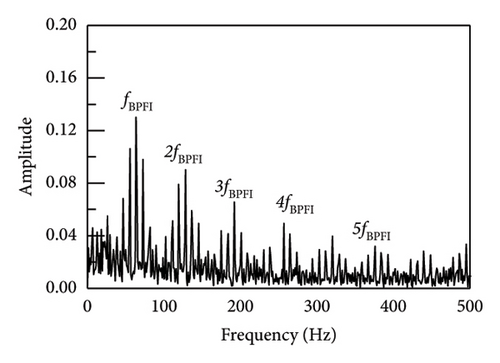
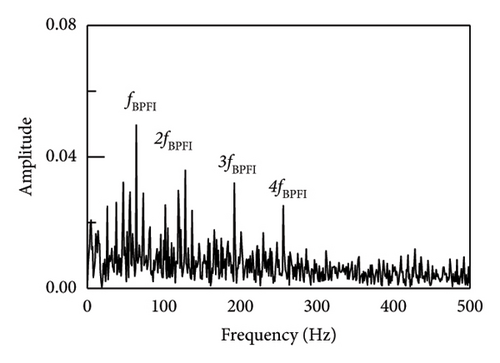
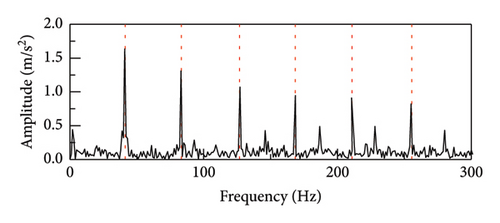
Similarly, in order to assess the precision of the proposed technique for extracting characteristics of faults in the inner rings of bearings, data were collected from inner ring fault bearings on the drive end of the traction motor of a vehicle on a specific test line. The vehicle speed was measured 53 km/h, the sampling frequency was 10 kHz, and the bearing was SKF6016 ball bearing. The parameter data was displayed in Table 4 while the envelope spectrum was depicted in Figure 17. It can be shown that the results of SR1-SVD have better performance and can obtain the fault frequency and its frequency doubling components. Moreover, the average operating speeds of vehicles in metro lines are around 40–80 km/h. According to the fault frequencies equations in equations (17)–(20), the main differences of bearing faults under different speeds are the rotating frequencies which will make the fault characteristics changed. As a result, the identification comparison under different operating speeds has been made by applying SR1-methods. It can be seen from Figure 18, although the fault frequencies changing with operating speeds, the proposed SR1-SVD method still can recognize those fault frequencies and their frequency doubling components. The SR1-SVD method forms a strict rank-1 matrix which represents periodic characteristics of vibration impulses. Once input signals have strong periodic components, the proposed SR1-SVD method can reconstruct these periodic components from others.

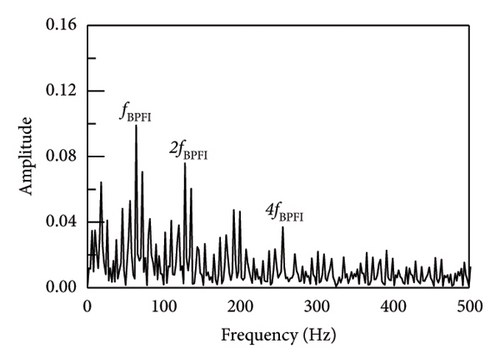
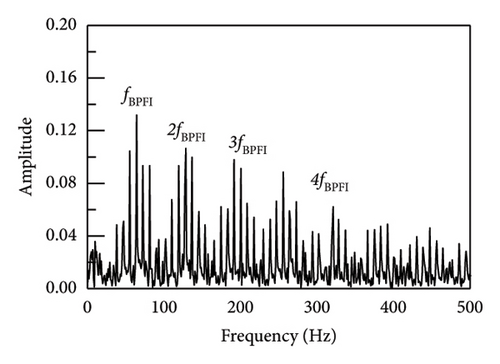
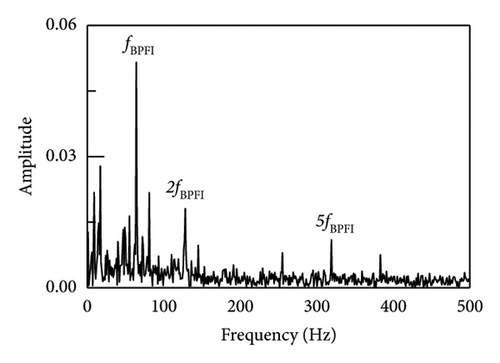
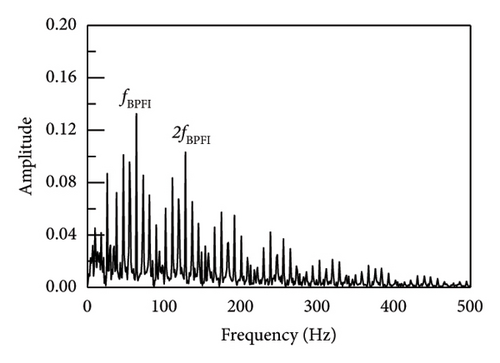
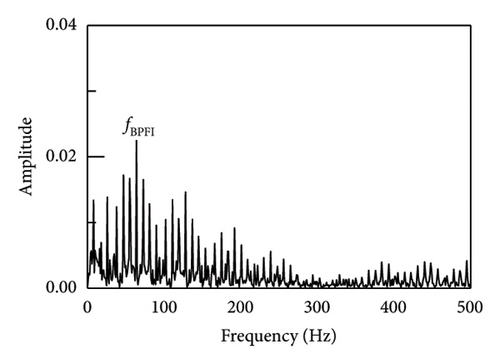
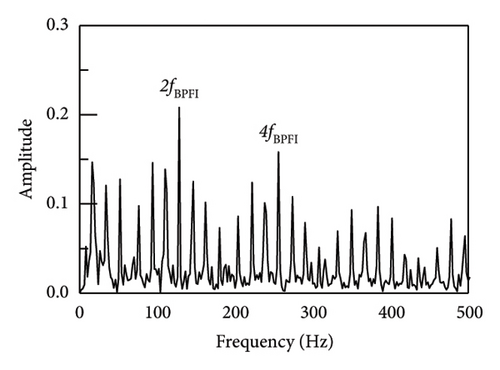
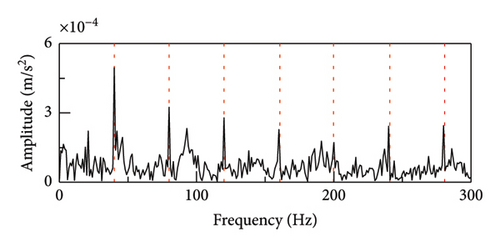
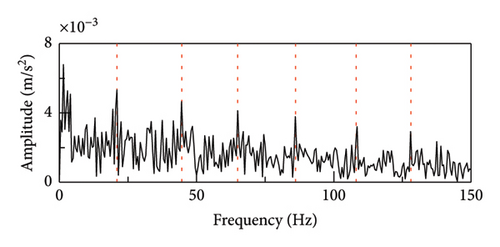
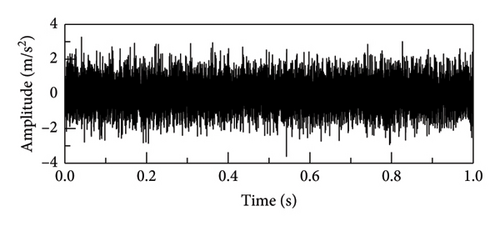
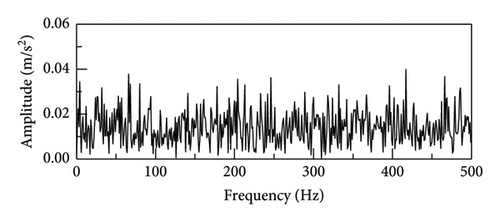
The actual vibration signal is so complex that it cannot be perfectly simulated or emulated. Therefore, in order to verify the true performance of the proposed method, an on-site experiment was carried out and shown in Figure 19. The experiment has been taken on a serviced vehicle consisting of 4 motors and 2 trailers in subway line 3, using a motor model of Siemens 1TB-2010-1GA02. The acceleration vibration signal of motor bearing of the train was collected. The tested vehicle bearing is a deep groove ball bearing, modelled SKF BB1-7361A. The motor speed was set to 720 r/min and the sampling frequency was set to 10 kHz. According to the equation (19), the characteristic frequency of the rolling element fault is 38 Hz.

The time-domain waveform and envelope spectrum analysis of the vibration signal is shown in Figures 20 and 21. Time-domain waveform is interfered by a large amount of noise, and the fault impact signal is almost masked by the noise. Due to the influence of noise, the fault characteristic frequency and its harmonics are almost indistinguishable under the envelope spectrum analysis in the raw signal. After processing the proposed SR1-SVD method, it can be clearly seen that the fault characteristic frequency of the bearing and its harmonics indicated that there is a rolling element fault in the bearing.

4. Discussion

In the previous sections, we conducted quantitative and qualitative comparisons on VMD, SSA, DWT, PSMSVD, APSM-SVD, and SR1-SVD, respectively. The findings indicate that the SVD approach outperforms VMD, SSA, and DWT techniques in noise impact removal during experimental data verification. Furthermore, the SR1 method has the most remarkable performance. Critical to the reconstruction of PSM-SVD and APSM-SVD is the development of an appropriate trajectory matrix in order to precisely represent the fault impact section of the vibration signal. Among them, APSM-SVD is based on the periodic characteristics of the vibration signal, and uses the maximum envelope spectrum to calculate the period constraint to detect the peak of the fault pulse in the noise vibration signal. Then, the trajectory matrix is constructed from periodic constraints and pulse peak positions. PSM-SVD uses the singular value ratio spectrum to calculate the embedding dimension and uses the vibration signal to construct the period truncation matrix, and performs the SVD to reconstruct the signal. The length of the traversal segment dictates the appropriate structure of the trajectory matrix. Various traversal lengths may influence the extraction effect of fault impact components. Better noise removal and shock detection can be achieved by selecting an appropriate traversal segment length. This section examines the effects of traversal length on vibration signal processing as affected by the PSM-SVD, APSM-SVD, and SR1-SVD approaches.

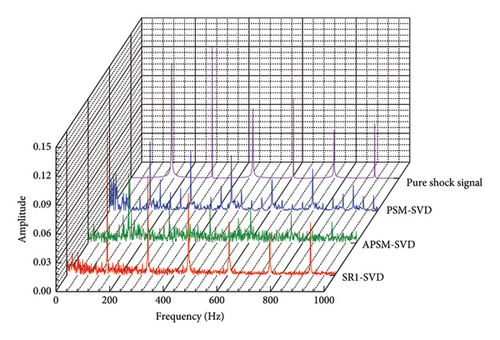
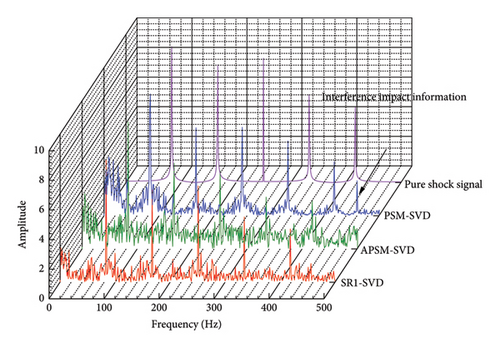
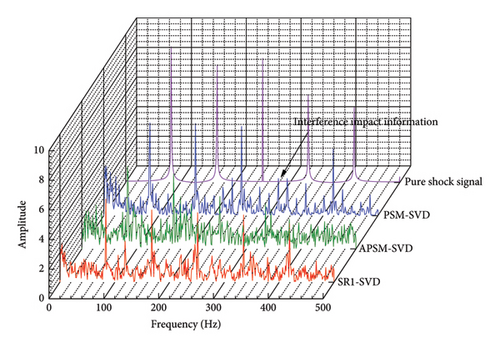
Initially, the sampling frequency and the peak’s position in the envelope spectrum may often be used to compute the traversal length. For simulated signals (SNR = −10 dB), 66 is the ideal traversal segment length. Figure 22 shows how effective methods like APSM-SVD and PSM-SVD are in removing noise and restoring fault impact peaks when the traversal segment is set to 66. However, there is still noise information and impulse interference in the reconstructed signal envelope spectrum of APSM-SVD and PSM-SVD.

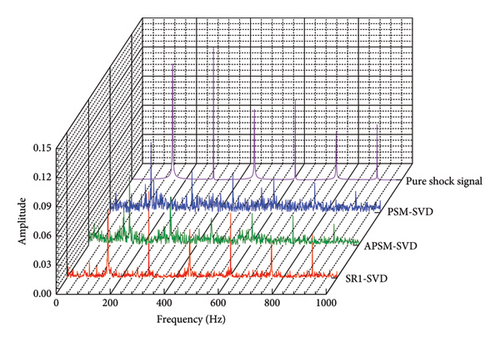
Moreover, the magnitude of fault effect peaks generated using APSM-SVD and PSM-SVD is reduced in comparison to peaks generated using SR1-SVD. Reconstructed impact signal envelope spectrum using APSM-SVD and PSMSVD remains contaminated with impact interference and noise if the traversal segment length is not equal to 66. The suggested SR1-SVD approach is capable of reconstructing fault impact signals irrespective of the suitability of the traversal segment length among these comparative methods. The optimum traversal segment length for the vibration signal of the laboratory single is 120, Figure 23, which is consistent with the simulation signal calculation findings in Figure 18. Both APSM-SVD and PSM-SVD exhibit enhanced capability in reconstructing fault impact signals when the length of the traversal segment approaches 120. Nevertheless, unlike pure vibration signals, the effects of interference persist. In APSM-SVD and PSMSVD, interference prevents the envelope spectrum of the reconstructed impulse signal from differentiating between the 5th and 4th harmonics when the traversal segment length is not equal to 120. However, it has been proposed that alone the SR1 method is capable of extracting purer vibration and shock signals, and from envelope spectrum fault shock peaks.

To evaluate the computational efficiency of the proposed method, experimental data from Section 3.2 was utilized for testing. The experiments were conducted on a laptop equipped with 8 GB RAM and an Intel Core I7-8550U CPU @ 1.80 GHz, running Windows 10 × 64, with all comparative methods from previous sections implemented in MATLAB R2018a. It is important to note that all reported computing times exclusively reflect the operation time of the method itself, excluding data import and collection times. According to the results shown in Table 7, the runtime of the methods increases with the number of samples. Moreover, while SSA and DWT demonstrate faster computing times compared to the SR1-SVD method, their performance in extracting fault impact information is not satisfactory. Additionally, for the length of 50,000, the computing time of SR1-SVD remains around 3 s, showcasing its advantage in both computational efficiency and effectiveness. In order to estimate the processing time for the proposed method in case using in multitask operating systems the Big O notation (Landau’s notation) has been induced and applied on compared methods for calculating their Time and memory complexity [34]. Time and memory complexity is a function that quantitatively describes the running time of an algorithm. It is typically used to represent how the time and memory required for an algorithm will increase as the amount of input data increases. For example, if the time and memory complexity of an algorithm O (n), then when the amount of input data doubles, the time and memory required to execute the algorithm will also roughly double. Here is definition of time and memory O (n):

•
O (1): Constant time and memory, indicating that the time and memory usage of the algorithm does not change with the increase of input data volume. For example, an algorithm that only uses a fixed number of variables.
•
O (n): Linear time and memory, representing that the time and memory usage of the algorithm is proportional to the amount of input data. For example, creating a new array of the same size as the input array.
•
O (n²): Square time and memory, represents that the time and memory usage of the algorithm is proportional to the square of the input data volume. For example, create a new two-dimensional array of the same size as the input two-dimensional array.
•
O (logn): Log time and memory indicating that the execution time and memory of the algorithm is proportional to the logarithm of the input data volume. For example, binary search algorithm.
•
O (nlogn): Linear logarithmic time and memory, indicating that the execution time of the algorithm is proportional to the product of the input data volume and the logarithm of the input data volume. Many efficient sorting algorithms, such as merge sort and quicksort, have this time complexity.

Table 7. The calculation time of different methods is compared.

Signal length	SR1-SVD	APSM-SVD	PSM-SVD	Hankel-SVD	MED	SK	VMD	SSA	DWT
1000	0.16	0.33	1.05	0.57	0.63	7.19	1.93	0.29	0.20
5000	0.26	0.25	2.81	0.93	0.43	9.74	22.19	0.33	0.17
10,000	0.44	0.24	6.33	1.27	0.72	12.01	33.23	0.62	0.30
20,000	0.74	2.40	11.13	4.32	2.88	11.96	58.54	0.61	0.21
50,000	2.84	5.33	58.40	7.91	3.14	12.19	186.56	0.78	4.16

In this case, the time and memory complexity has been calculated in SR1-SVD, APSM-SVD, PSM-SVD, Hankel-SVD, MED, SK, VMD, SSA, and DWT and the results are shown in Figure 24. The main complexity of SVD based methods is induced by the calculation of singular values and formed matrices, PSM, APSM, and Hankel matrices need traversal input data and formed a periodic matrices with fault impulse information. These steps need more time compared with SR1-SVD. However, SR1-SVD method forms a strict rank-1 matrix via shift vector which costs less time and memory compared with other SVD methods. Apart from SVD methods, the MED method has to calculate the minimum entropy and deconvolution and it need more time and memory. Moreover, when applying the DWT, there needs to choose the wavelet base and process the filter programs which makes more time and memory as amounts of input data increase.

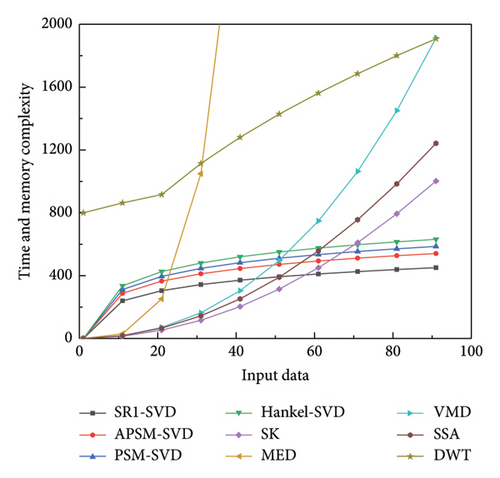
As a result, the proposed SR1-SVD method has the least time and memory complexity among those methods.

5. Conclusions

Qualitative and quantitative comparisons were made with other methods. In accordance with the PSM-SVD concept, the signal is traversed from left to right. Reconstructed signal-to-noise ratios satisfy the necessary criteria only when the traversal segment length is devoid of substantial noise interference. In contrast, the APSM-SVD approach utilizes a distinct trajectory matrix configuration to improve upon the PSM-SVD method. The signal travels from the peak to both ends. If the length of the segment is not appropriate, the reconstructed signal cannot extract fault impact information accurately. In the SR1-SVD approach, λ is utilized to optimize the traversal segment length, resulting in a rank-1 matrix with stringent shift vectors, irrespective of the segment’s length. Consequently, in contrast to other techniques, the SR1-SVD method proposed in this paper performs better in reconstructing impact signals under different traversal segment lengths. The core of the method is the shift rank-1 reconstruction, which shifts the formed trajectory matrix to a strict rank-1 matrix by the shift operator, and forces the formation of the rank-1 matrix without truncating the signal. This reduces the influence of traversal length on the reconstruction of the fault shock signal and improves the robustness and performance of the fault signal removal method. The findings demonstrate that the suggested SR1-SVD approach may improve the reliability of problem detection and diagnosis by extracting clean fault impact signals from vibration signals without the requirement for certain traversal segment lengths. With the progress of intelligence, algorithms, artificial intelligence, and deep learning are being widely used in the industrial field, and the application of deep learning in bearing fault diagnosis is further explored, combining the advantages of big data analysis and neural network models to improve the accuracy and efficiency of fault detection. Secondly, research and development of a more intelligent bearing monitoring system, combined with the Internet of Things technology and cloud computing platform, to achieve real-time monitoring and remote diagnosis of bearing operating status.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

S.Z. did the conceptualization, project administration and funding acquisition, B.Z. did the validation, formal analysis, investigation, data curation, and writing–original draft preparation. X.C. carried out the software, writing–review and editing and visualization, L.P. did the methodology, Q.Z. and L.W. did resources and supervision.

Funding

This work was supported in part by the National Natural Science Foundation of China (Grant Nos. 51975347 and 51907117) and in part by the Shanghai Science and Technology Program (Grant No. 22010501600).

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Che W. C., Zhang G. Q., and Li W. K., Application Analysis of Empirical Mode Decomposition in the Characterization of Nonstary Vibration Signals in Rotating Machinery, Machinery Management Development. (2022) 37, no. 1, 63–66.
Google Scholar
2 Cui J. L., Zhong Q. W., Zheng S. B., Peng L. L., and Wen J., A Lightweight Model for Bearing Fault Diagnosis Based on Gramian Angular Field and Coordinate Attention, Machines. (2022) 10, no. 4, 282–323, https://doi.org/10.3390/machines10040282.
10.3390/machines10040282
Web of Science® Google Scholar
3 Cui L., Sun Y., Wang X., and Wang H., Spectrum-Based, Full Band Preprocessing, and Two-Dimensional Separation of Bearing and Gear Compound Faults Diagnosis, IEEE Transactions on Instrumentation and Measurement. (2021) 70, 1–16, https://doi.org/10.1109/tim.2021.3063189.
10.1109/tim.2021.3063189
PubMed Web of Science® Google Scholar
4 Feng K., Smith W. A., Randall R. B., Wu H., and Peng Z., Vibration-Based Monitoring and Prediction of Surface Profile Change and Pitting Density in a Spur Gear Wear Process, Mechanical Systems and Signal Processing. (2022) 165, https://doi.org/10.1016/j.ymssp.2021.108319.
10.1016/j.ymssp.2021.108319
Web of Science® Google Scholar
5 Peng Z. K., Tse P. W., and Chu F. L., A Comparison Study of Improved Hilbert–Huang Transform and Wavelet Transform: Application to Fault Diagnosis for Rolling Bearing, Mechanical Systems and Signal Processing. (2005) 19, no. 5, 974–988, https://doi.org/10.1016/j.ymssp.2004.01.006, 2-s2.0-18144399334.
10.1016/j.ymssp.2004.01.006
Web of Science® Google Scholar
6 Gu J. and Peng Y. X., An Improved Complementary Ensemble Empirical Mode Decomposition Method and Its Application in Rolling Bearing Fault Diagnosis, Digital Signal Processing. (2021) 113, https://doi.org/10.1016/j.dsp.2021.103050.
10.1016/j.dsp.2021.103050
Web of Science® Google Scholar
7 Xu L., Chatterton S., and Pennacchi P., Rolling Element Bearing Diagnosis Based on Singular Value Decomposition and Composite Squared Envelope Spectrum, Mechanical Systems and Signal Processing. (2021) 148, https://doi.org/10.1016/j.ymssp.2020.107174.
10.1016/j.ymssp.2020.107174
Web of Science® Google Scholar
8 Wei Y., Li Y. Q., Xu M. Q., and Huang W. H., A Review of Early Fault Diagnosis Approaches and Their Applications in Rotating Machinery, Entropy. (2019) 21, no. 4, https://doi.org/10.3390/e21040409, 2-s2.0-85065590043.
10.3390/e21040409
Web of Science® Google Scholar
9 Liang Z., Liu X., and Lu Z., Review of Research on Fault Diagnosis and Analysis Methods for Rolling Bearings, Manufacturing Automation. (2023) 45, no. 05, 172–175.
Google Scholar
10 Chen X. Q., Lin J. H., Jin H., Huang Y., and Liu Z. C., The Psychoacoustics Annoyance Research Based on EEG Rhythms for Passengers in High-Speed Railway, Applied Acoustics. (2021) 171, https://doi.org/10.1016/j.apacoust.2020.107575.
10.1016/j.apacoust.2020.107575
Web of Science® Google Scholar
11 Peng L. L., Zheng S. B., Zhong Q. W., Chai X. D., and Lin J. H., A Novel Bagged Tree Ensemble Regression Method With Multiple Correlation Coefficients to Predict the Train Body Vibrations Using Rail Inspection Data, Mechanical Systems and Signal Processing. (2023) .
10.1016/j.ymssp.2022.109543
PubMed Web of Science® Google Scholar
12 Zheng K., Bai Y., Xiong J. F., Tan F., Yang D., and Zhang Y., Simultaneously Low Rank and Group Sparse Decomposition for Rolling Bearing Fault Diagnosis, Sensors. (2020) 20, no. 19, 5541–6134, https://doi.org/10.3390/s20195541.
10.3390/s20195541
Web of Science® Google Scholar
13 Feng K., Ji J., Ni Q. et al., A Novel Vibration Indicator to Monitor Gear Natural Fatigue Pitting Propagation, Structural Health Monitoring. (2023) 22, no. 5, 3126–3140, https://doi.org/10.1177/14759217221142622.
10.1177/14759217221142622
Web of Science® Google Scholar
14 Prusa Z. and Rajmic P., Toward High-Quality Real-Time Signal Reconstruction From STFT Magnitude, IEEE Signal Processing Letters. (2017) 24, no. 6, 892–896, https://doi.org/10.1109/lsp.2017.2696970, 2-s2.0-85028074148.
10.1109/LSP.2017.2696970
Web of Science® Google Scholar
15 Fan W., Zhou Q., Li J., and Zhu Z., A Wavelet-Based Statistical Approach for Monitoring and Diagnosis of Compound Faults With Application to Rolling Bearings, IEEE Transactions on Automation Science and Engineering. (2018) 15, no. 4, 1563–1572, https://doi.org/10.1109/tase.2017.2720177, 2-s2.0-85028919713.
10.1109/TASE.2017.2720177
Web of Science® Google Scholar
16 Lei Y., Lin J., He Z., and Zuo M. J., A Review on Empirical Mode Decomposition in Fault Diagnosis of Rotating Machinery, Mechanical Systems and Signal Processing. (2013) 35, no. 1-2, 108–126, https://doi.org/10.1016/j.ymssp.2012.09.015, 2-s2.0-84870404381.
10.1016/j.ymssp.2012.09.015
Web of Science® Google Scholar
17 Dragomiretskiy K. and Zosso D., Variational Mode Decomposition, IEEE Transactions on Signal Processing. (2014) 62, no. 3, 531–544, https://doi.org/10.1109/tsp.2013.2288675, 2-s2.0-84893418756.
10.1109/TSP.2013.2288675
Web of Science® Google Scholar
18 Tian J., Morillo C., Azarian M. H., and Pecht M., Motor Bearing Fault Detection Using Spectral Kurtosis-Based Feature Extraction Coupled With K-Nearest Neighbor Distance Analysis, IEEE Transactions on Industrial Electronics. (2016) 63, no. 3, 1793–1803, https://doi.org/10.1109/tie.2015.2509913, 2-s2.0-84962408476.
10.1109/TIE.2015.2509913
Web of Science® Google Scholar
19 Cheng Y., Chen B., and Zhang W., Adaptive Multipoint Optimal Minimum Entropy Deconvolution Adjusted and Application to Fault Diagnosis of Rolling Element Bearings, IEEE Sensors Journal. (2019) 19, no. 24, 12153–12164, https://doi.org/10.1109/jsen.2019.2937140.
10.1109/JSEN.2019.2937140
Web of Science® Google Scholar
20 Zhang G., Chuan J., and Zhang T., A Adaptive Stochastic Resonance Method Based on Two-Dimensional Tristable Controllable System and Its Application in Bearing Fault Diagnosis, IEEE Access. (2020) 8, 173710–173722, https://doi.org/10.1109/access.2020.3022803.
10.1109/ACCESS.2020.3022803
Web of Science® Google Scholar
21 Guo Q., Zhang C., Zhang Y., and Liu H., An Efficient SVD-Based Method for Image Denoising, IEEE Transactions on Circuits and Systems for Video Technology. (2016) 26, no. 5, 868–880, https://doi.org/10.1109/tcsvt.2015.2416631, 2-s2.0-84969800832.
10.1109/TCSVT.2015.2416631
Web of Science® Google Scholar
22 Ke F. J. C. J., Kesheng W., Dongdong W., Chengning Z., and Qing N., A Novel Order Spectrum-Based Vold-Kalman Filter Bandwidth Selection Scheme for Fault Diagnosis of Gearbox in Offshore Wind Turbines, Ocean Engineering. (2022) 266, 1–12.
Google Scholar
23 Ni Q., Nandi A. K., Ji J., Halkon B., and Feng K., Physics-Informed Residual Network (PIResNet) for Rolling Element Bearing Fault Diagnostics, Mechanical Systems and Signal Processing. (2023) 200, https://doi.org/10.1016/j.ymssp.2023.110544.
10.1016/j.ymssp.2023.110544
Web of Science® Google Scholar
24 Liang H., Cao J., and Zhao X. Q., Average Descent Rate Singular Value Decomposition and Two-Dimensional Residual Neural Network for Fault Diagnosis of Rotating Machinery, IEEE Transactions on Instrumentation and Measurement. (2022) 71, 1–16, https://doi.org/10.1109/tim.2022.3170973.
10.1109/tim.2022.3170973
Web of Science® Google Scholar
25 Huang C. G., Lin J. H., and Ding J. M., A New Differential Singular Value Ratio Spectrum and its Application in Wheel Bearing Fault Diagnosis, Vibration and Shock. (2020) 39, no. 04, 17–26, https://doi.org/10.13465/j.cnki.jvs.2020.04.002.
10.13465/j.cnki.jvs.2020.04.002
Google Scholar
26 Li H., Liu T., Wu X., and Chen Q., Research on Bearing Fault Feature Extraction Based on Singular Value Decomposition and Optimized Frequency Band Entropy, Mechanical Systems and Signal Processing. (2019) 118, 477–502, https://doi.org/10.1016/j.ymssp.2018.08.056, 2-s2.0-85053039437.
10.1016/j.ymssp.2018.08.056
Web of Science® Google Scholar
27 Li H., Liu T., Wu X., and Li S., Correlated SVD and Its Application in Bearing Fault Diagnosis, IEEE Transactions on Neural Networks and Learning Systems. (2023) 34, no. 1, 355–365, https://doi.org/10.1109/tnnls.2021.3094799.
10.1109/TNNLS.2021.3094799
PubMed Web of Science® Google Scholar
28 Sun C., Yin H., Li Y., and Chai Y., A Novel Rolling Bearing Vibration Impulsive Signals Detection Approach Based on Dictionary Learning, IEEE/CAA Journal of Automatica Sinica. (2021) 8, no. 6, 1188–1198, https://doi.org/10.1109/jas.2020.1003438.
10.1109/JAS.2020.1003438
Web of Science® Google Scholar
29 Chen X. Q., Lin J. H., Huang C. G., and He L., A Novel Method Based on Adaptive Periodic Segment Matrix and Singular Value Decomposition for Removing EMG Artifact in ECG Signal, Biomedical Signal Processing and Control. (2020) 62, 102060–102122, https://doi.org/10.1016/j.bspc.2020.102060.
10.1016/j.bspc.2020.102060
Web of Science® Google Scholar
30 He L., Yi C., Zhou Q. Y., and Lin J. H., Fast Convolutional Sparse Dictionary Learning Based on LocOMP and Its Application to Bearing Fault Detection, IEEE Transactions on Instrumentation and Measurement. (2022) 71, 1–12, https://doi.org/10.1109/tim.2022.3193962.
10.1109/tim.2022.3193962
CAS Web of Science® Google Scholar
31 Zhou P., He L., Yi C., and Zhou Q. Y., Impulses Recovery Technique Based on High Oscillation Region Detection and Shifted Rank-1 Reconstruction—Its Application to Bearing Fault Detection, IEEE Sensors Journal. (2022) 22, no. 8, 8084–8093, https://doi.org/10.1109/jsen.2022.3159116.
10.1109/JSEN.2022.3159116
CAS Web of Science® Google Scholar
32 Aremu K. O., Izuchukwu C., Abass H. A., and Mewomo O. T., On A Viscosity Iterative Method for Solving Variational Inequality Problems in Hadamard Spaces, Axioms. (2020) 9, no. 4, https://doi.org/10.3390/axioms9040143.
10.3390/axioms9040143
Web of Science® Google Scholar
33 golafshan R. and sanliturk K. Y., SVD and Hankel Matrix Based De-Noising Approach for Ball Bearing Fault Detection and its Assessment Using Artificial Faults, Mechanical Systems and Signal Processing. (2016) 70, 36–50.
10.1016/j.ymssp.2015.08.012
Web of Science® Google Scholar
34 Miller F. P., Vandome A. F., and Mcbrewster J., Big O Notation, Circulation. (2010) 106, no. 3, 195–197.
Google Scholar

All articles

Fault Diagnosis of Traction Motor Bearings Based on Shifted Rank-1 Reconstruction

Abstract

1. Introduction

2. Algorithm Model

2.1. Scale Space Preprocessing

2.2. Shift Rank-1 Matrix

2.3. Reconfiguration λ

2.4. Application of Shift Rank-1 Algorithm in Extracting Fault Information From Vibration Signals

3. Method Validation

3.1. Simulated Signal Validation

3.2. Experimental Data Analysis

4. Discussion

5. Conclusions

Conflicts of Interest

Author Contributions

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Fault Diagnosis of Traction Motor Bearings Based on Shifted Rank-1 Reconstruction

Abstract

1. Introduction

2. Algorithm Model

2.1. Scale Space Preprocessing

2.2. Shift Rank-1 Matrix

2.3. Reconfiguration λ

2.4. Application of Shift Rank-1 Algorithm in Extracting Fault Information From Vibration Signals

3. Method Validation

3.1. Simulated Signal Validation

3.2. Experimental Data Analysis

4. Discussion

5. Conclusions

Conflicts of Interest

Author Contributions

Funding

Open Research

Data Availability Statement

References

Figures

References

Related

Information