Structural Control and Health Monitoring

Volume 2025, Issue 1 8864614

Research Article

Open Access

Domain Knowledge Embedded InSAR-Based 3D Displacement Monitoring of Urban Buildings

Ya-Nan Du

Southeast University , Key Laboratory of Concrete and Prestressed Concrete Structures of the Ministry of Education , Nanjing , 210096 , China , seu.edu.bd

School of Civil Engineering , Southeast University , Nanjing , 211189 , China , seu.edu.bd

Search for more papers by this author

De-Cheng Feng,

Corresponding Author

De-Cheng Feng

[email protected]

orcid.org/0000-0003-3691-6128

Southeast University , Key Laboratory of Concrete and Prestressed Concrete Structures of the Ministry of Education , Nanjing , 210096 , China , seu.edu.bd

School of Civil Engineering , Southeast University , Nanjing , 211189 , China , seu.edu.bd

Search for more papers by this author

Gang Wu,

Gang Wu

Southeast University , Key Laboratory of Concrete and Prestressed Concrete Structures of the Ministry of Education , Nanjing , 210096 , China , seu.edu.bd

School of Civil Engineering , Southeast University , Nanjing , 211189 , China , seu.edu.bd

Search for more papers by this author

Ya-Nan Du,

Ya-Nan Du

Southeast University , Key Laboratory of Concrete and Prestressed Concrete Structures of the Ministry of Education , Nanjing , 210096 , China , seu.edu.bd

School of Civil Engineering , Southeast University , Nanjing , 211189 , China , seu.edu.bd

Search for more papers by this author

De-Cheng Feng,

Corresponding Author

De-Cheng Feng

[email protected]

orcid.org/0000-0003-3691-6128

Southeast University , Key Laboratory of Concrete and Prestressed Concrete Structures of the Ministry of Education , Nanjing , 210096 , China , seu.edu.bd

School of Civil Engineering , Southeast University , Nanjing , 211189 , China , seu.edu.bd

Search for more papers by this author

Gang Wu,

Gang Wu

Southeast University , Key Laboratory of Concrete and Prestressed Concrete Structures of the Ministry of Education , Nanjing , 210096 , China , seu.edu.bd

School of Civil Engineering , Southeast University , Nanjing , 211189 , China , seu.edu.bd

Search for more papers by this author

First published: 17 February 2025

https://doi.org/10.1155/stc/8864614

Citations: 1

Academic Editor: Michael Krommer

Share a link

Email
Wechat
Bluesky

Abstract

Continuous monitoring of building displacement is crucial for urban structural safety. While traditional methods are costly, Interferometric Synthetic Aperture Radar (InSAR) offers a cost-effective alternative, providing long-term displacement data. However, due to the insensitivity of SAR radar to north-south displacement, using InSAR alone can only measure settlement and east-west displacement. To address this limitation, this paper presents a three-dimensional (3D) deformation extraction model. The model embeds domain knowledge to introduce additional constraints, which are then used to establish the relationship between north-south and east-west displacement. This relationship allows for the extraction of 3D displacement of buildings from the line of sight (LOS) displacement measured by InSAR. This model was applied to Tower 2 of Yingli International Financial Center (YIFC) in Chongqing, China, and the 3D displacement of the building between 2018 and 2021 was obtained.

1. Introduction

During long-term use, buildings may be affected by environmental erosion, material deterioration, and the impact of disasters, potentially leading to structural damage [1, 2]. By monitoring the displacement [3–7] of the structure for long-term operation and maintenance of the building, the structural condition of the building can be evaluated, and potential problems can be identified and solved in a timely manner [8]. However, traditional monitoring methods such as sensor networks [2, 9] and global navigation satellite systems [10, 11] are expensive and require installation and daily maintenance of equipment, which consumes significant manpower and resources [12]. Interferometric Synthetic Aperture Radar (InSAR) presents an alternative approach by noninvasively and remotely acquiring deformation information of structures [13, 14]. Although it requires a time gap between two monitoring sessions [15], InSAR demonstrates unique advantages in meeting the long-term and continuous monitoring requirements of daily building operations. InSAR is anticipated to offer long-term, cost-effective, and maintenance-free deformation monitoring, addressing the challenges associated with traditional structural monitoring methods.

InSAR is widely adopted for monitoring surface [16–19] and engineering structure [20–22] deformation due to its inherent advantages, such as high spatiotemporal resolution [23], independence from time and climate conditions [24], and cost-effectiveness in data collection [25]. However, a single InSAR can solely capture deformation along the radar line of sight (LOS) direction [26, 27]. To observe more comprehensive deformation, researchers have developed the two-dimensional (2D) deformation calculation model based on the spatial characteristics of SAR satellite observations [28–31]. This model, when combined with the one-dimensional deformation field along the LOS of both ascending and descending tracks, enables the derivation of high-precision 2D deformation fields in both the vertical and east-west directions.

Nevertheless, simplistic one-dimensional or 2D deformations may not accurately depict the true deformation state of structure. This limitation arises, in part, from the fact that the SAR satellite’s flight direction is typically aligned with the north-south axis, making it difficult to monitor displacements in the north-south direction, which are perpendicular to the LOS direction. To overcome this limitation, many researchers have expanded upon InSAR’s 2D monitoring capabilities by integrating additional radar imagery data [32] or combining InSAR with other measurement techniques, such as Global Positioning System (GPS) [33–36], to increase observational coverage and provide supplementary three-dimensional (3D) deformation data; Alternatively, by combining prior models [37–39] such as the assumption of glacier movement parallel to the surface [34], information on geological structures [39], or the subsidence mechanism of mining areas [38], additional constraints can be added to reconstruct the 3D model.

This paper aims to utilize InSAR for nearly zero-cost long-term monitoring to continuously track the 3D displacement of buildings. However, given that the current application of InSAR for building displacement monitoring primarily focuses on one-dimensional displacement monitoring, such as settlement and specific deformation directions, and the integration of GPS and InSAR still entails equipment installation and maintenance, challenges persist. Additionally, the use of the multitrack InSAR observation method for displacement extraction requires three or more InSAR interferometric pairs with significant geometric differences in radar track imaging. In practice, due to the limited number of SAR radars, it is often difficult to find multiple radar images that simultaneously meet these conditions. Therefore, it is reasonable to employ a method that integrates prior information of buildings to add supplementary constraints for constructing a 3D model.

This paper presents a method of embedding domain knowledge to extract the 3D displacement of buildings from the LOS displacement of InSAR’s ascending and descending tracks. The proposed method is based on the Equivalent Lateral Force Method (ELFM) to obtain the lateral stiffness of each floor of the building, thereby deriving prior information on the displacement ratio of the building’s major and minor axes. Subsequently, the Permanent Scatterer InSAR (PS-InSAR) method is considered to obtain the temporal displacement of the building along the LOS in the ascending and descending tracks, and a displacement calculation model is established. The prior information of the building is then used to add new constraints to the calculation model, enabling the extraction of the cumulative 3D displacement of the building over time series intervals. This work introduces the concept of a 3D displacement extraction model and validates the proposed method by applying it to a practical building, thereby providing a new scientific basis for urban construction and disaster prevention. This study aims to offer safer and more sustainable infrastructure support for urban development, promote the advancement of building monitoring technology, and provide solid assurances for the future development of cities.

2. Methodology

2.1. Introduction of PS-InSAR Technologies

PS-InSAR [40] technology is used to extract and analyze phase information from PS points, such as buildings and facilities. These points are less affected by temporal and spatial decoherence, allowing them to maintain stable phase and amplitude information. Subsequently, atmospheric and noise phases are removed to facilitate the acquisition of precise deformation data from these PS points. Over years of development, PS-InSAR method has reached a high level of maturity, possessing capabilities not only to measure small, individual targets but also to monitor large-scale surface deformations. In contrast to traditional Differential InSAR (D-InSAR) technology, significant enhancements have been made in the accuracy of deformation measurements, which can attain precision at the millimeter level.

The principal processing workflow for PS-InSAR is delineated as follows: initially, N+1 available SAR images, which cover the designated research area over a specified period, are selected from a broader dataset. Following the main image selection rule, one image is chosen as the primary image from the N+1 available, while the remaining N images are deployed as auxiliary images to constitute N pairs of main and auxiliary images. Subsequently, for each image pair, registration and coherence processing are executed to eliminate the topographic phase and flat earth phase, resulting in the generation of N differential interferograms. Thereafter, employing a suitable PS point recognition method, stable PS points within the defined research area are pinpointed. The phase representation for the xth PS point in the ith interferogram extracted is articulated as follows:

()

where θ denotes the radar incidence angle, λ represents the radar wavelength, R signifies the distance from the sensor to the ground, t_i defines the time baseline, B_⊥i is the vertical baseline, v_x is identified as the linear deformation rate of the point PS, h_x represents the elevation error, and

constitutes the residual error term in the ith interferogram, which includes atmospheric errors, nonlinear deformation, and additional noise components. For adjacent PS points, their phase difference is characterized by the following linear relationship:

()

where Δv represents the linear deformation rate increment of PS points, and Δh denotes the elevation error increment. Based on equation (2), the corresponding linear deformation rate and elevation error are determined by maximizing the overall phase coherence coefficient. Subsequently, as evidenced by equation (2), it becomes apparent that the residual error term still contains essential nonlinear deformation information. Consequently, it is necessary to employ filtering techniques to eliminate the atmospheric phase and noise phase, thereby extracting the requisite nonlinear deformation signal. The final deformation outcome for the study area is derived by amalgamating the linear and nonlinear deformation results, as delineated in equation (3):

()

where

is designated as the deformation phase of the xth PS point, while φ_line corresponds to the linear deformation phase of the PS point. Similarly, φ_non−line is identified as the nonlinear deformation phase of the PS point.

2.2. Description of Displacement Calculation Model by InSAR Data

The deformation acquired from the ascending and descending SAR data processed by PS-InSAR represents the deformation of the monitoring point in the LOS. As depicted in Figure 1, the relationship between the LOS deformation and the 3D deformation in the East-North-Up (ENU) coordinate system adheres to equation (4):

()

where D_LOS represents the deformation of the radar LOS, while D_U, D_N, and D_E signify the vertical, north-south, and east-west deformations, respectively. Additionally, ∂ represents the satellite azimuth angle, and the ground range direction indicates the projection direction of the LOS direction on the horizontal plane.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Schematic diagram of displacement calculation model.

Equation (4) represents the decomposition of the LOS deformation of a single orbit in the 3D direction. However, when observation data from multiple orbits are available, it can be expressed in matrix form, as illustrated in equation (5):

()

Due to limitations in the number of satellites and satellite system configurations, there is inadequate geometric diversity in the imaging of radar satellite data [26, 27]. Therefore, we consider using data from both the ascending and descending tracks of the satellite to establish a displacement model. Consequently, equation (5) is simplified to equation (6), representing the displacement calculation model, which serves as the basis for the 3D displacement extraction model.

()

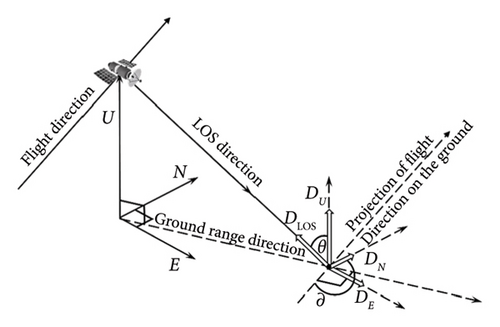
3. Mechanics-Embedded 3D Displacement Decomposition

The objective of this study is to extract the 3D displacement of buildings from the cumulative time series displacement of InSAR. Due to the limited number of radars, only the LOS displacement from the ascending and descending orbits can typically be obtained. As a result, the displacement calculation model is rank-deficient and cannot provide 3D displacement [15, 41, 42]. To mitigate this limitation, the study proposes the introduction of additional constraint conditions by embedding domain knowledge based on existing InSAR displacement calculation model. This proposal aims to enhance the function of the original technology and enable it to analyze the 3D deformation of buildings. Consequently, it offers broader data support for related engineering decisions.

3.1. Domain Knowledge: ELFM

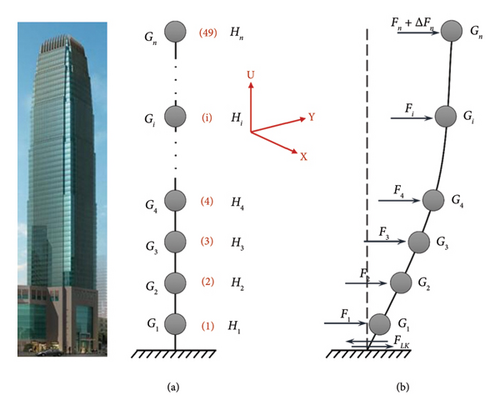
ELFM stands as a widely utilized lateral force analysis and design technique in structural engineering. This method conceptualizes the lateral force exerted on the structure as a solitary lateral force applied to each floor. It streamlines intricate multiparticle systems by simplifying them into an equivalent single particle for consideration, facilitating designers in conducting preliminary lateral calculations.

When employing the ELFM, only one degree of freedom can be considered for each floor (Figure 2(a)). The standard value of horizontal lateral action acting on the structure can be determined using the following formula.

According to the mode decomposition response spectrum method, the maximum horizontal lateral action of particle i in mode j is represented as

()

The total horizontal shear force at the bottom of the i-mode structure is denoted as

()

where ∂₁ denotes the horizontal lateral influence coefficient corresponding to the fundamental period of the structure. G_E signifies the representative value of the total gravity load of the structure, G_i represents the representative value of the gravitational load of the particle and

Furthermore, based on the vibration mode combination principle of the Square Root of the Sum of the Squares (SRSS) method, the standard value of the total horizontal lateral action at the bottom of the structure is defined as

()

where q designates the high mode influence coefficient, expressed as

, and G_eq denotes the representative value of the equivalent total gravity load of the structure.

Moreover, under the assumption that the lateral response of the structure primarily relies on the first mode of vibration, and considering the approximation of the first mode of vibration as a straight line, it is determined that ϕ_1i = ηH_i, the horizontal lateral action of each particle can be approximately regarded as the lateral action corresponding to each particle of the first mode of vibration (as depicted in Figure 2(b)):

()

where η signifies the proportional coefficient, while H_i represents the calculated height of particle i.

Therefore, the following equation can be obtained:

()

where F_Lk denotes the standard value of the total lateral force of the structure, G_k signifies the equivalent total gravity load of the structure. Lastly, F_i represents the horizontal lateral action of particle i.

However, when there are multiple layers in the structure, the horizontal lateral action calculated according to the above formula is smaller than that obtained by the mode decomposition response spectrum method. To correct this, a concentrated force ΔF is added at the top.

()

where δ_n denotes the additional lateral action coefficient at the top of the structure. Consequently, the horizontal lateral action on particle i is

()

3.2. Introduction of Additional Constraints

This study uses ELFM to further derive the deformation rates of supertall structures along the major and minor axes as additional constraints. However, it is worth noting that the application scope of this method is limited by factors such as structural nonlinearity. For buildings with complex geometries or dynamic behaviors, multidegree-of-freedom (MDOF) models can be used for more accurate design, as they allow for a better simulation of the structure’s response. Hence, in practical design scenarios, additional verification measures should be implemented to ensure the accuracy and reliability of the design.

To simplify the calculation, this article assumes that the mass distribution of each floor of the building is uniform. Following the aforementioned assumptions, the lateral horizontal action exerted along the major axis of the building can be delineated by the subsequent equation:

()

The shear force of the frame core tube structure under lateral force is primarily carried by the core tube wall, transverse connecting beams, and column components of that floor [43]. Therefore, this paper consider that the lateral stiffness of structural floors can be briefly divided into the shear stiffness of shear walls and the bending stiffness of beam and column components, as shown in equation (15) [44]:

()

where K_W represents the shear stiffness of the shear wall, K_C denotes the bending stiffness of the column, K_B represents the bending stiffness of the connecting beam, h corresponds to the height of that floor, A_W signifies the effective cross-sectional area in the direction of shear wall calculation, I_C corresponds to the moment of inertia of the column section about the bending axis, and I_B signifies to the moment of inertia of the beam section about the bending axis.

Considering the elastic response exhibited by building structures subjected to lateral force, where the horizontal displacement of each floor is defined as the ratio between the horizontal shear force and the lateral stiffness of that floor. The cumulative displacement at the apex of the building is derived as the summation of the deformations of each floor, as illustrated in equation (16), and the ratio of cumulative displacement between the major and minor axes of the nth layer is shown in equation (17):

()

where Δx and Δy represent the displacement of the major and minor axes at the top of the building, respectively, Δx_i and Δy_i denote the interlayer displacement of the ith layer on the major and minor axes, respectively, k_ix and k_iy represent the stiffness of the ith layer along the major and minor axes, respectively.

3.3. Establishment of a 3D Deformation Extraction Model for Buildings

The ratio of cumulative displacement between the major and minor axes is used as a new constraint to establish the relationship between north-south displacement and east-west displacement, which helps to overcome the limitations of InSAR and derive the 3D deformation relationship characterizing buildings in the settlement direction, as well as along the major and minor axes, as depicted in Figure 3 and equation (18), enabling 3D deformation monitoring of buildings. Figure 4 illustrates the technical approach adopted in this study.

()

where β represents the angle between the major axis of the building and its true eastward direction, and Δz denote the settlement displacement of the building.

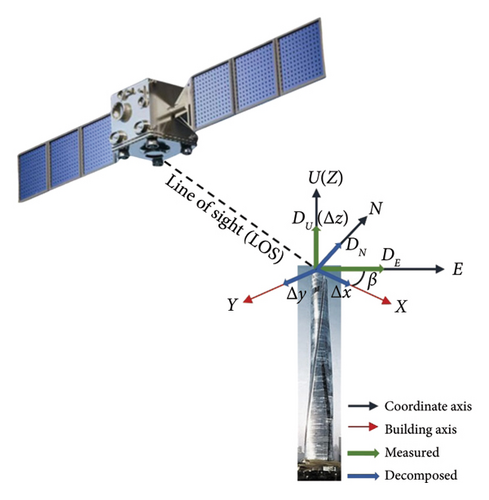
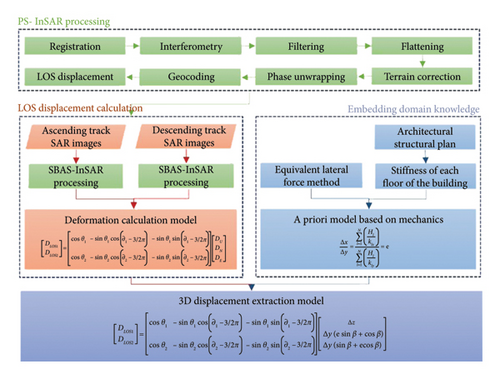
4. Implementation Procedure

The combination of InSAR technology with prior models presents a novel avenue for conducting 3D deformation monitoring of buildings. This chapter offers a comprehensive overview of the specific implementation approach of this method, aiming to facilitate the application of this method in practical applications by relevant researchers. The delineated implementation steps are as follows.

4.1. Preparation of Data

Initially, the location of the building earmarked for monitoring was identified through geographic information system (GIS) analysis, designating it as the research area. Simultaneously, it was verified that the SAR satellite orbiting the area possesses data captured from both ascending and descending trajectories, thereby ensuring the feasibility of subsequent InSAR 3D displacement extraction. Subsequent to this verification, radar satellite images and corresponding observation angles from the study area during the monitoring time were procured, in readiness for subsequent data processing endeavors.

4.2. Determination of the Displacement Ratio Between the Major and Minor Axes of a Building

Transition into discussing how to determine the calculation of displacement ratio along the building axis. This paper introduces a novel approach using design or construction drawings of buildings to determine the deformation ratio between the major and minor axes. By collecting these drawings, detailed information about the building’s layout, structural framework, and support system can be obtained. Substituting the stiffness and other relevant data from each floor’s major and minor axes into formula (18), allows for the computation of the deformation ratio at the building’s top. Additionally, obtaining actual displacement data or using finite element models are also common methods to achieve the deformation ratio.

4.3. Calculation of InSAR LOS Displacement

With the establishment of additional constraints, shift focus to the technical processing of InSAR data. PS-InSAR is used to process the images of Sentinel-1A and obtain the displacement of the building along the LOS on the ascending and descending tracks, respectively. The detailed processing procedure of PS-InSAR technology encompasses several crucial steps: Initially, image registration is essential for ensuring spatial consistency among multitemporal SAR images, which is vital for subsequent analysis. Following this, differential interferograms are produced by calculating the phase differences between adjacent temporal SAR images to estimate minute changes on the earth’s surface. Differential interferograms are typically affected by noise, thus necessitating filtering processes to improve image quality, with common methods including the Goldstein filter and adaptive filters. The final step involves geocoding, which transforms differential interferometry results from the slant range coordinates of the SAR image to the geographic coordinate system of the earth. This step not only provides the geographic location of the displacement information but also facilitates integration with other GIS datasets for further analysis.

4.4. Obtaining 3D Deformation of Buildings

Subsequently, by embedding previously acquired domain knowledge and considering the angle between the building’s major axis and the east-west direction to establish the relationship between the displacements of the building’s major and minor axes and the north-south displacement. Then combining this relationship with the InSAR displacement model to derive the 3D displacement of the building in the direction of settlement and along the major and minor axes.

4.5. Eliminating the Periodicity of Deformation

Finally, eliminate the influence of external factors such as temperature changes on displacement. In the research fields of earth science and geophysics, the investigation of building deformation often encounters various interference factors, with periodic interference, particularly from temperature changes, posing significant challenges to data accuracy and reliability. To mitigate this challenge, Empirical Mode Decomposition (EMD) emerges as a widely employed signal processing technique in this domain, effectively breaking down complex nonlinear and non-stationary signals into a series of Intrinsic Mode Functions (IMFs). Specifically, in the analysis of building deformation, periodic fluctuations induced by temperature variations are prominently reflected in specific IMFs. Through EMD of signals and subsequent analysis of these IMFs, periodic deformation signals can be efficiently identified and eliminated, thereby isolating more realistic trend-oriented deformations from building deformation data.

5. Application to Real Data

5.1. Overview of Engineering Examples

This research was conducted based on Tower 2 of Yingli International Financial Center (YIFC), located in Yuzhong District, Chongqing, China. The building has 49 floors above ground and 4 floors underground, with a roof structure elevation of 231.25m. It adopts a frame core tube structure system, and the architectural effect and the arrangement of shear walls for a certain standard floor are shown in Figure 5.

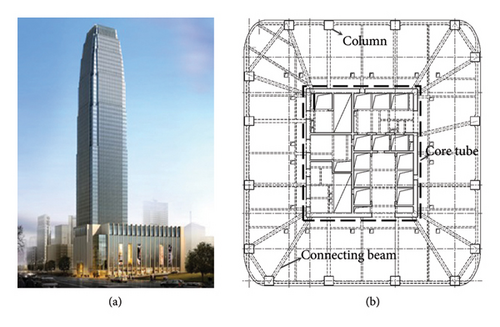
Utilizing the floor plan of the building structure, this study applied equation (15) to compute the stiffness of each floor in both the major and minor axes of the building. The detailed calculation outcomes are compiled in Table 1. Subsequently, employing equation (17), the study derived a deformation ratio of 1.1338 for the major and minor axes at the top of the building, which serves as a basis for further deformation analysis.

Table 1. The lateral stiffness calculation results of each floor of Tower 2 of YIFC.

Layer number	H_i (m)	k_x (×10⁴ kN·m⁻²)	k_y (×10⁴ kN·m⁻²)
1	5.950	6.8891	6.5591
2	11.950	3.4743	3.1443
3	17.350	3.5745	3.2445
4	22.750	3.5745	3.2445
5	28.150	3.5745	3.2445
6	32.650	3.8063	3.4763
7	36.550	3.50953	3.16553
8	40.450	3.50953	3.16553
9	44.350	3.50953	3.16553
10	50.350	2.92605	2.58205
11	54.950	3.03611	2.69211
12	59.550	3.03611	2.69211
13	64.050	3.25808	2.91408
14	68.550	3.25808	2.91408
15	73.050	3.25808	2.91408
16	77.550	3.25808	2.91408
17	82.050	2.93288	2.20382
18	86.550	2.93288	2.20382
19	91.050	2.93288	2.20382
20	95.550	2.93288	2.20382
21	100.050	2.93288	2.20382
22	104.550	2.69057	1.96589
23	109.250	2.61352	1.90023
24	113.950	2.61352	1.90023
25	119.950	2.31568	1.7061
26	124.450	2.69057	1.96589
27	129.150	2.61352	1.90023
28	133.650	2.01269	1.67046
29	138.150	2.01269	1.67046
30	142.650	2.01269	1.67046
31	147.150	2.01269	1.67046
32	151.650	1.49675	1.32245
33	156.150	1.49675	1.32245
34	160.650	1.49675	1.32245
35	165.150	1.49675	1.32245
36	169.650	1.38933	1.34231
37	174.150	1.38933	1.34231
38	178.850	1.36303	1.321
39	183.550	1.36303	1.321
40	189.550	1.28525	1.258
41	194.250	1.36303	1.321
42	198.750	1.36303	1.321
43	203.250	1.36303	1.321
44	207.750	1.36303	1.321
45	212.250	1.20777	1.13839
46	216.750	1.20777	1.13839
47	221.250	1.15089	0.99864
48	226.250	1.15089	0.99864
49	231.250	0.95267	0.93592

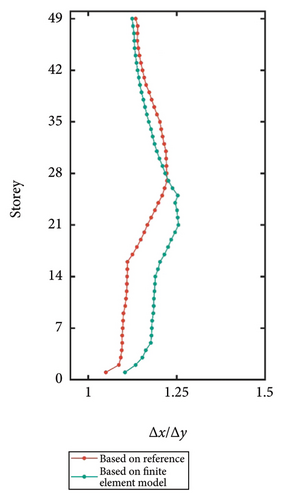
To enhance the reliability of stiffness calculations, this research developed a fiber-based core wall numerical model in the OpenSees software. Beams and columns were simulated using force-based Force Beam Column elements, with material models Concrete02 and Steel02 from OpenSees. Shear walls were modeled using the ShellMITC4 element suitable for simulating plane stress, combined with Concrete02 and Steel02 material models to capture their nonlinear behavior. Using this model, stiffness values for each storey were computed. Subsequently, longitudinal-to-transverse displacement ratios for each storey were calculated using equation (17) and compared against results from equation (15), as shown in Figure 6. The orange line represents axial displacement ratios derived from stiffness calculations based on literature knowledge, while the green line represents axial displacement ratios derived from stiffness calculations using finite element models. The calculation results indicated a 9.53% error between the two, suggesting that the stiffness values calculated based on literature are relatively reliable and can serve as a basis for computing longitudinal-to-transverse displacement ratios.

5.2. Preparation and Preprocessing of Data

The radar dataset used in this study was acquired from the Sentinel-1 constellation, which was designed as a dual-satellite system. Sentinel-1 constellation offers a single satellite revisit period of 12 days [24], which can theoretically be reduced to 6 days with dual satellites functioning concurrently [45]. The radar operates in the C-band, and the image data utilized in this study is acquired in Interferometric Wide Swath (IW) mode, which creates images with a 250 km swath at 5 × 20 m spatial resolution.

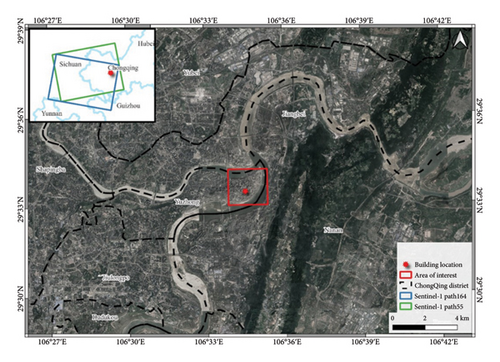
This study focuses on Tower 2 of YIFC, utilizing 283 Sentinel-1A satellite images, comprising 90 ascending 55 track (A-55 Track) images and 93 descending 164 track (D-164 track) images, The temporal coverage of A-55 Track and D-164 Track are 20180509-20210529 and 20180504-20210524, respectively. The parameter information such as the incident angle and azimuth angle of the ascending and descending tracks can be obtained from radar imaging data. Specifically, for the ascending satellite, the flight azimuth angle is 12.68°, while the radar incidence angle is 44.01°. While for the descending satellite, the flight azimuth angle is 167.30°, corresponding to a radar incidence angle of 32.55°. The relationship between the coverage area of the Sentinel-1A image and the location of the research area on ascending and descending tracks is illustrated in Figure 7. The green box indicates the coverage area of path A-55, while the blue box represents the coverage area of path D-164. And the red star denotes the location of the Tower 2 of TIFC.

5.3. Time Series Analysis Using PS-InSAR

This study applied the PS-InSAR [46] to conduct a sequence of data processing on the SAR images of the study region. This study selected multiple radar images that covered the same geographic area and had good temporal distribution. These images were then precisely aligned to ensure geometric consistency among them. Next, permanent scatterers were identified, which are points with stable reflective characteristics over time. Then perform coherent point processing on these scatterers to generate a series of differential interferograms. Adaptive nonlocal InSAR filtering [47] was applied to eliminate certain noisy phases, thereby enhancing the signal-to-noise ratio and improving the clarity of interference fringes. By analyzing these filtered interferograms, this study calculated the relative deformation information of the buildings while removing noise such as atmospheric delays and orbital errors. Phase unwrapping was performed using the Discrete Minimum Cost Flow (DMCF) [48] method.

Following this, the calculation of the differential interferogram after unwrapping was conducted to derive displacement information of the building. Subsequently, geocoding [49] was executed to map the displacement onto the diagram, resulting in the acquisition of the mean displacement rate distribution diagram of the study area along LOS of two tracks, as depicted in Figure 8. The red box indicates the location of Tower 2 of YIFC. This series of meticulous processing steps furnishes reliable data support for research.

5.4. Obtaining 3D Deformation of Buildings From 2018 to 2021

Simultaneously, this research used the structural layout plan (Figure 5(b)) of Tower 2 of YIFC to calculate the lateral stiffness of each floor’s major and minor axes, and determined the displacement rate of the major and minor axes at the top of the building to be 1.1338. Furthermore, based on an actual measurement yielding an angle of β = 11.25°, the 3D displacement extraction model (Figure 3) was applied to obtain 3D displacement information of Tower 2 of YIFC. The 3D displacement map of the top of Tower 2 of YIFC is illustrated in Figures 9(a), 9(b), and 9(c). This comprehensive analysis method not only facilitates a deeper understanding of the displacement behavior of urban infrastructure but also furnishes a reliable scientific basis for disaster risk assessment and urban planning.

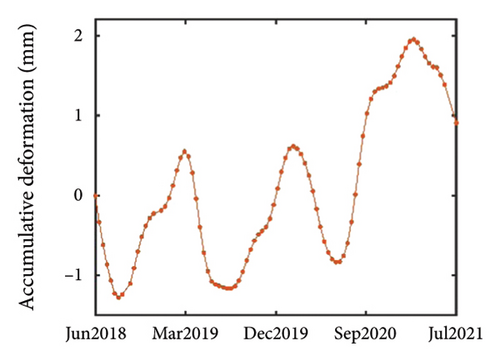
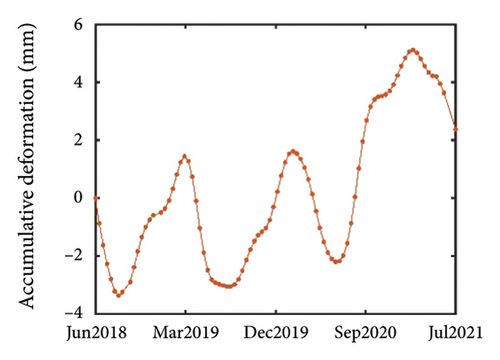
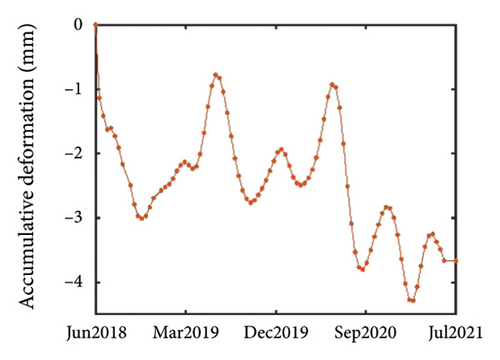
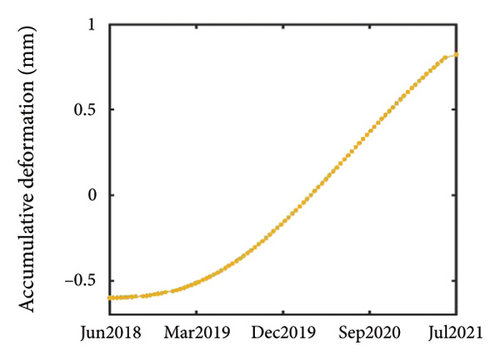
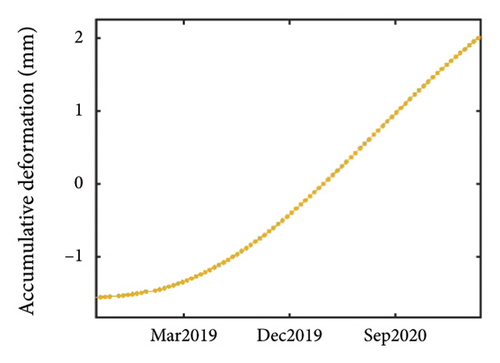
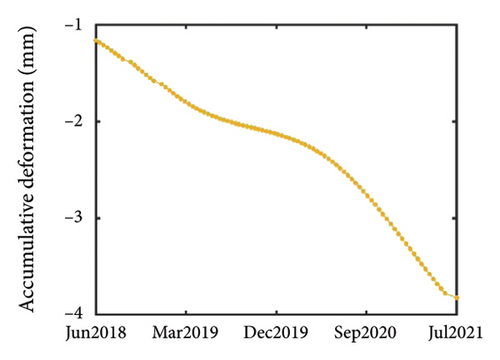
It is evident that the building’s displacement exhibits periodic behavior, consistent with the principles of thermal expansion. Specifically, the building’s displacement changes periodically with the cyclical variations in temperature. Therefore, EMD was used to process the 3D displacement of the top of the building to eliminate periodic displacement caused by temperature effects, thereby generating more reliable trend displacement.

The trend displacement results obtained after EMD processing of the building are depicted in Figures 9(d), 9(e), and 9(f). It is evident that the overall trend of the building is sinking, with continued settlement over time. Moreover, the displacement in both the major and minor axes of the building demonstrates a consistent increasing trend. These trends collectively suggest that the building is continuously tilting in one direction. This observation could stem from inherent design issues within the building [50], resulting in uneven settlement, or from directional deformations induced by environmental factors such as prevailing wind direction in the building’s vicinity [3, 51, 52]. After considering various factors such as periodic displacement and increased settlement, it can be concluded that the trend displacement results obtained through this research method are reasonable and accurately reflect the actual displacement of buildings over the time series intervals.

6. Discussion

The existing monitoring methods for building structures require professional equipment and technical support [12], and a significant amount of human resources and time [53] for installation, measurement, and data processing. They are costly and cannot obtain real-time or continuous displacement data. InSAR can compensate for the shortcomings of traditional methods and provide a low-cost method for long-term continuous monitoring. Additionally, by introducing domain knowledge of architecture and establishing constraints between north-south and east-west displacement of buildings, this study can overcome the technical limitations of InSAR’s insensitivity to north-south displacement monitoring. This enables InSAR to be successfully applied to 3D displacement monitoring of buildings.

It can be noted that several improvement approaches should enhance the 3D displacement extraction model’s ability to monitor more accurate building displacements in the future. Firstly, the low resolution of Sentinel-1A satellite, with a spatial resolution of 5 by 20 m, limits more the precise monitoring of buildings. The displacement of the building obtained in this study is only the trend displacement of the top of the building, and accurate displacement information of various parts of the building cannot be obtained. This limitation arises from the satellite’s resolution, which is insufficient for detecting fine details of building movements. Using higher resolution satellite data will help improve the observation accuracy and detail capture ability of our model for building displacement; Secondly, the insufficient accuracy of the prior model established by embedding domain knowledge has increased the uncertainty of monitoring results. When establishing the prior model, this research employed the ELFM based on certain assumptions, which inevitably affects the accuracy of the results. Additionally, due to limitations in research conditions, only the structural plan of the building to be monitored can be obtained, resulting in limited accuracy in calculating the lateral stiffness. While new constraints are introduced for the model, they still impact the accuracy of the extracted 3D displacement in the horizontal direction. Utilizing the finite element models that can simulate the real load conditions of buildings [54] or actual measured data to obtain more precise main and minor axis displacement relationships can offer more accurate constraint conditions for the 3D displacement extraction model.

This paper successfully decoupled the 3D displacement of the building through the introduction of a prior model. The initial implementation of this method in buildings has allowed us to surmount the technical constraints of InSAR, achieving non-contact, long-term, and cost-effective 3D displacement monitoring. While current accuracy levels have not yet reached their peak, this method introduces a novel approach to monitoring building displacement in three dimensions. Meanwhile, our approach further expands the application potential of InSAR technology, demonstrating its capability to improve the efficiency of building health assessments, offering valuable support for urban safety and sustainability. Furthermore, this methodology holds potential for infrastructure maintenance, enabling the monitoring of urban infrastructure over time.

7. Conclusions

This study introduces a novel approach for monitoring the 3D deformation of super high-rise buildings, which combines InSAR technology and physical prior models. Specifically, the study utilizes PS-InSAR technology to process Sentinel-1 ascending and descending SAR data in the study area, extracting one-dimensional deformation of the building in the LOS direction on different tracks. Based on these deformations, the study calculates 2D deformation of the building in the east-west and vertical directions. Subsequently, leveraging the prior model of the building, the study estimates the ratio of major and minor axis deformation and integrates it with the 2D deformation data obtained from InSAR to derive the 3D deformation of the building. Furthermore, the article provides detailed implementation steps of this method to facilitate researchers in applying it to building monitoring. As an empirical study, a super high-rise building in Chongqing, China, serves as a case study, demonstrating the effectiveness of the proposed method.

Additionally, the study examines the feasibility and limitations of using InSAR technology for monitoring super high-rise buildings, emphasizing the crucial role of physical prior models in compensating for monitoring limitations. While the approach offers a promising avenue for 3D deformation monitoring, the accuracy of the monitoring data in this instance is limited due to factors such as the relatively low resolution of Sentinel-1, which can affect the precision of the observed deformation. To address these challenges, future research directions include the use of higher resolution satellite data to improve observation accuracy and detail capture ability, as well as the development of more accurate prior models. Furthermore, due to the lack of long-term monitoring data for buildings in the current study, we plan to select specific buildings for long-term monitoring in the future to further validate our approach and continue the sustained research and exploration of this methodology. This is expected to provide more reliable data support for the structural health monitoring and safety assessment of urban buildings.

In summary, this study contributes valuable insights into 3D deformation monitoring of super high-rise buildings, offering valuable experience and reference for future research in the field. Despite current technical challenges, ongoing advancements in remote sensing technology are expected to enhance the accuracy and reliability of monitoring results, thereby improving urban safety and sustainability.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

The authors express their sincere gratitude for the financial support received from the Project of National Key Research and Development Program of China (Grant No. 2022YFC3803000), the National Natural Science Foundation of China (Grant No. 52361135806), and the Fundamental Research Funds for the Central Universities.

Acknowledgments

Open Research

Data Availability Statement

The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.

References

1 Sumitro S. and Wang M. L., Sustainable Structural Health Monitoring System, Structural Control and Health Monitoring. (2005) 12, no. 3-4, 445–467, https://doi.org/10.1002/stc.79, 2-s2.0-27144541480.
10.1002/stc.79
Web of Science® Google Scholar
2 Yi T., Li H., and Gu M., Optimal Sensor Placement for Structural Health Monitoring Based on Multiple Optimization Strategies, The Structural Design of Tall and Special Buildings. (2011) 20, no. 7, 881–900, https://doi.org/10.1002/tal.712, 2-s2.0-80755189912.
10.1002/tal.712
Web of Science® Google Scholar
3 Xie Z. N. and Gu M., Across-Wind Dynamic Response of High-Rise Building under Wind Action With Interference Effects From One and Two Tall Buildings, The Structural Design of Tall and Special Buildings. (2009) 18, no. 1, 37–57, https://doi.org/10.1002/tal.393, 2-s2.0-60849088247.
10.1002/tal.393
Web of Science® Google Scholar
4 Park H. S., Hong K., and Seo J. H., Drift Design of Steel-Frame Shear-Wall Systems for Tall Buildings, The Structural Design of Tall Buildings. (2002) 11, no. 1, 35–49, https://doi.org/10.1002/tal.187, 2-s2.0-0036506809.
10.1002/tal.187
Web of Science® Google Scholar
5 Park H. S., Lee H. M., Adeli H., and Lee I., A New Approach for Health Monitoring of Structures: Terrestrial Laser Scanning, Computer-Aided Civil and Infrastructure Engineering. (2007) 22, no. 1, 19–30, https://doi.org/10.1111/j.1467-8667.2006.00466.x, 2-s2.0-33750978713.
10.1111/j.1467-8667.2006.00466.x
Web of Science® Google Scholar
6 Drougkas A., Verstrynge E., Van Balen K. et al., Country-Scale InSAR Monitoring for Settlement and Uplift Damage Calculation in Architectural Heritage Structures, Structural Health Monitoring. (2021) 20, no. 5, 2317–2336, https://doi.org/10.1177/1475921720942120.
10.1177/1475921720942120
Web of Science® Google Scholar
7 Li X., Xie L., Lu W. et al., Structural Health Monitoring of a Historic Building During Uplifting Process: System Design and Data Analysis, Structural Health Monitoring. (2023) 22, no. 5, 3165–3188, https://doi.org/10.1177/14759217221135351.
10.1177/14759217221135351
Web of Science® Google Scholar
8 Brownjohn J. M. W., Pan T. C., and Deng X. Y., Correlating Dynamic Characteristics From Field Measurements and Numerical Analysis of a High-Rise Building, Earthquake Engineering & Structural Dynamics. (2000) 29, no. 4, 523–543.
10.1002/(SICI)1096-9845(200004)29:4<523::AID-EQE920>3.0.CO;2-L
Web of Science® Google Scholar
9 Fukuda Y., Feng M. Q., Narita Y., Kaneko S., and Tanaka T., Vision-Based Displacement Sensor for Monitoring Dynamic Response Using Robust Object Search Algorithm, IEEE Sensors Journal. (2013) 13, no. 12, 4725–4732, https://doi.org/10.1109/JSEN.2013.2273309, 2-s2.0-84885632865.
10.1109/JSEN.2013.2273309
Web of Science® Google Scholar
10 Yi T.-H., Li H.-N., and Gu M., Recent Research and Applications of GPS-Based Monitoring Technology for High-Rise Structures: Recent Research and Applications of Gps-Based Monitoring Technology, Structural Control and Health Monitoring. (2013) 20, no. 5, 649–670, https://doi.org/10.1002/stc.1501, 2-s2.0-84875873750.
10.1002/stc.1501
Web of Science® Google Scholar
11 Im S. B., Hurlebaus S., and Kang Y. J., Summary Review of GPS Technology for Structural Health Monitoring, Journal of Structural Engineering. (2013) 139, no. 10, 1653–1664, https://doi.org/10.1061/(ASCE)ST.1943-541X.0000475, 2-s2.0-84884998084.
10.1061/(ASCE)ST.1943-541X.0000475
Web of Science® Google Scholar
12 Kjærgaard M. B., Blunck H., Godsk T., Toftkjær T., Christensen D. L., and Grønbæk K., P. Floréen, A. Krüger, and M. Spasojevic, Indoor Positioning Using GPS Revisited, 2010, 38–56, https://doi.org/10.1007/978-3-642-12654-3_3, 2-s2.0-77953514814.
10.1007/978-3-642-12654-3_3
Google Scholar
13 Pepe A. and Calò F., A Review of Interferometric Synthetic Aperture RADAR (InSAR) Multi-Track Approaches for the Retrieval of Earth’s Surface Displacements, Applied Sciences. (2017) 7, no. 12, https://doi.org/10.3390/app7121264, 2-s2.0-85037063674.
10.3390/app7121264
Google Scholar
14 Tavakkoliestahbanati A., Milillo P., Kuai H., and Giardina G., Pre-Collapse Spaceborne Deformation Monitoring of the Kakhovka Dam, Ukraine, From 2017 to 2023, Communication Earth Environmental. (2024) 5, 145–149, https://doi.org/10.1038/s43247-024-01284-z.
10.1038/s43247-024-01284-z
Google Scholar
15 Bamler R. and Hartl P., Synthetic Aperture Radar Interferometry, Inverse Problems. (1998) 14, no. 4, R1–R54, https://doi.org/10.1088/0266-5611/14/4/001, 2-s2.0-0032136915.
10.1088/0266-5611/14/4/001
Web of Science® Google Scholar
16 Giardina G., Milillo P., DeJong M. J., Perissin D., and Milillo G., Evaluation of InSAR Monitoring Data for Post-Tunnelling Settlement Damage Assessment, Structural Control and Health Monitoring. (2019) 26, no. 2, https://doi.org/10.1002/stc.2285, 2-s2.0-85052280760.
10.1002/stc.2285
PubMed Web of Science® Google Scholar
17 Macchiarulo V., Milillo P., DeJong M. J., González Martí J., Sánchez J., and Giardina G., Integrated InSAR Monitoring and Structural Assessment of Tunnelling-Induced Building Deformations, Structural Control and Health Monitoring. (2021) 28, no. 9, https://doi.org/10.1002/stc.2781.
10.1002/stc.2781
PubMed Web of Science® Google Scholar
18 Bianchini S., Pratesi F., Nolesini T., and Casagli N., Building Deformation Assessment by Means of Persistent Scatterer Interferometry Analysis on a Landslide-Affected Area: The Volterra (Italy) Case Study, Remote Sensing. (2015) 7, no. 4, 4678–4701, https://doi.org/10.3390/rs70404678, 2-s2.0-84937914093.
10.3390/rs70404678
Web of Science® Google Scholar
19 Rouet-Leduc B., Jolivet R., Dalaison M., Johnson P. A., and Hulbert C., Autonomous Extraction of Millimeter-Scale Deformation in InSAR Time Series Using Deep Learning, Nature Communications. (2021) 12, no. 1, https://doi.org/10.1038/s41467-021-26254-3.
10.1038/s41467-021-26254-3
PubMed Web of Science® Google Scholar
20 Milillo P., Giardina G., Perissin D., Milillo G., Coletta A., and Terranova C., Pre-Collapse Space Geodetic Observations of Critical Infrastructure: The Morandi Bridge, Genoa, Italy, Remote Sensing. (2019) 11, no. 12, https://doi.org/10.3390/rs11121403, 2-s2.0-85068167695.
10.3390/rs11121403
Web of Science® Google Scholar
21 Lazecky M., Hlavacova I., Bakon M., Sousa J. J., Perissin D., and Patricio G., Bridge Displacements Monitoring Using Space-Borne X-Band SAR Interferometry, Ieee Journal of Selected Topics in Applied Earth Observations and Remote Sensing. (2017) 10, no. 1, 205–210, https://doi.org/10.1109/JSTARS.2016.2587778, 2-s2.0-84979870781.
10.1109/JSTARS.2016.2587778
Web of Science® Google Scholar
22 Du Y.-N., Feng D.-C., and Wu G., InSAR-Based Rapid Damage Assessment of Urban Building Portfolios Following the 2023 Turkey Earthquake, International Journal of Disaster Risk Reduction. (2024) 103, https://doi.org/10.1016/j.ijdrr.2024.104317.
10.1016/j.ijdrr.2024.104317
Web of Science® Google Scholar
23 Przyłucka M., Herrera G., Graniczny M., Colombo D., and Béjar-Pizarro M., Combination of Conventional and Advanced DInSAR to Monitor Very Fast Mining Subsidence With TerraSAR-X Data: Bytom City (Poland), Remote Sensing. (2015) 7, no. 5, 5300–5328, https://doi.org/10.3390/rs70505300, 2-s2.0-84930032850.
10.3390/rs70505300
Web of Science® Google Scholar
24 Raspini F., Bianchini S., Ciampalini A. et al., Continuous, Semi-automatic Monitoring of Ground Deformation Using Sentinel-1 Satellites, Scientific Reports. (2018) 8, no. 1, https://doi.org/10.1038/s41598-018-25369-w, 2-s2.0-85046731597.
10.1038/s41598-018-25369-w
PubMed Web of Science® Google Scholar
25 Carlà T., Intrieri E., Raspini F. et al., Perspectives on the Prediction of Catastrophic Slope Failures From Satellite InSAR, Scientific Reports. (2019) 9, no. 1, https://doi.org/10.1038/s41598-019-50792-y, 2-s2.0-85072847801.
10.1038/s41598-019-50792-y
Web of Science® Google Scholar
26 Wright T. J., Parsons B. E., and Lu Z., Toward Mapping Surface Deformation in Three Dimensions Using InSAR, Geophysical Research Letters. (2004) 31, no. 1, https://doi.org/10.1029/2003GL018827, 2-s2.0-2442493121.
10.1029/2003GL018827
Web of Science® Google Scholar
27 Ng A. H.-M., Ge L., Zhang K. et al., Deformation Mapping in Three Dimensions for Underground Mining Using InSAR-Southern Highland Coalfield in New South Wales, Australia, International Journal of Remote Sensing. (2011) 32, no. 22, 7227–7256, https://doi.org/10.1080/01431161.2010.519741, 2-s2.0-82055192131.
10.1080/01431161.2010.519741
Web of Science® Google Scholar
28 Gray L., Using Multiple RADARSAT InSAR Pairs to Estimate a Full Three-Dimensional Solution for Glacial Ice Movement: Multiple Interferograms for 3-D Motion, Geophysical Research Letters. (2011) 38, no. 5, https://doi.org/10.1029/2010GL046484, 2-s2.0-79952380999.
10.1029/2010GL046484
Google Scholar
29 Samsonov S. and d’Oreye N., Multidimensional Time-Series Analysis of Ground Deformation From Multiple InSAR Data Sets Applied to Virunga Volcanic Province, Geophysical Journal International. (2012) 191, 1095–1108, https://doi.org/10.1111/j.1365-246X.2012.05669.x, 2-s2.0-84869097459.
10.1111/j.1365-246X.2012.05669.x
Web of Science® Google Scholar
30 Eriksen H. O., Lauknes T. R., Larsen Y. et al., Visualizing and Interpreting Surface Displacement Patterns on Unstable Slopes Using Multi-Geometry Satellite SAR Interferometry (2D InSAR), Remote Sensing of Environment. (2017) 191, 297–312, https://doi.org/10.1016/j.rse.2016.12.024, 2-s2.0-85012273316.
10.1016/j.rse.2016.12.024
Web of Science® Google Scholar
31 Liu X., Zhao C., Zhang Q., Yang C., and Zhu W., Heifangtai Loess Landslide Type and Failure Mode Analysis With Ascending and Descending Spot-Mode TerraSAR-X Datasets, Landslides. (2020) 17, no. 1, 205–215, https://doi.org/10.1007/s10346-019-01265-w, 2-s2.0-85073954195.
10.1007/s10346-019-01265-w
CAS Web of Science® Google Scholar
32 Hu J., Li Z., Zhu J., Ren X., and Ding X., Inferring Three-Dimensional Surface Displacement Field by Combining SAR Interferometric Phase and Amplitude Information of Ascending and Descending Orbits, Science China Earth Sciences. (2010) 53, no. 4, 550–560, https://doi.org/10.1007/s11430-010-0023-1, 2-s2.0-77952550564.
10.1007/s11430-010-0023-1
CAS Web of Science® Google Scholar
33 Shen Z.-K. and Liu Z., Integration of GPS and InSAR Data for Resolving 3-Dimensional Crustal Deformation, Earth and Space Science. (2020) 7, no. 4, https://doi.org/10.1029/2019EA001036.
10.1029/2019EA001036
Web of Science® Google Scholar
34 Gudmundsson S., Sigmundsson F., and Carstensen J. M., Three-Dimensional Surface Motion Maps Estimated From Combined Interferometric Synthetic Aperture Radar and GPS Data, Journal of Geophysical Research: Solid Earth. (2002) 107, no. B10, https://doi.org/10.1029/2001JB000283.
10.1029/2001JB000283
Web of Science® Google Scholar
35 Samsonov S. V., Tiampo K. F., and Rundle J. B., Application of DInSAR-GPS Optimization for Derivation of Three-Dimensional Surface Motion of the Southern California Region Along the San Andreas Fault, Computers & Geosciences. (2008) 34, no. 5, 503–514, https://doi.org/10.1016/j.cageo.2007.05.013, 2-s2.0-39249085753.
10.1016/j.cageo.2007.05.013
Web of Science® Google Scholar
36 Wang G., A Methodology for Long-Term Offshore Structural Health Monitoring Using Stand-Alone GNSS: Case Study in the Gulf of Mexico, Structural Health Monitoring. (2024) 23, no. 1, 463–478, https://doi.org/10.1177/14759217231169934.
10.1177/14759217231169934
Web of Science® Google Scholar
37 Joughin I. R., Kwok R., and Fahnestock M. A., Interferometric Estimation of Three-Dimensional Ice-Flow Using Ascending and Descending Passes, IEEE Transactions on Geoscience and Remote Sensing. (1998) 36, no. 1, 25–37, https://doi.org/10.1109/36.655315, 2-s2.0-0031675583.
10.1109/36.655315
Web of Science® Google Scholar
38 Zhao R., Viktorovich Z. A., Li J., Chen C., and Zheng M., A New Strategy for Extracting 3D Deformation of Mining Areas From a Single-Geometry Synthetic Aperture Radar Dataset, Remote Sensing. (2023) 15, no. 21, https://doi.org/10.3390/rs15215244.
10.3390/rs15215244
Web of Science® Google Scholar
39 Grandin R., Klein E., Métois M., and Vigny C., Three-Dimensional Displacement Field of the 2015 8.3 Illapel Earthquake (Chile) From Across- and Along-track Sentinel-1 TOPS Interferometry, Geophysical Research Letters. (2016) 43, no. 6, 2552–2561, https://doi.org/10.1002/2016GL067954, 2-s2.0-84978017197.
10.1002/2016GL067954
Web of Science® Google Scholar
40 Frattini P., Crosta G. B., and Allievi J., Damage to Buildings in Large Slope Rock Instabilities Monitored With the PSInSAR™ Technique, Remote Sensing. (2013) 5, no. 10, 4753–4773, https://doi.org/10.3390/rs5104753, 2-s2.0-84887528141.
10.3390/rs5104753
Google Scholar
41 Rosen P. A., Hensley S., Joughin I. R. et al., Synthetic Aperture Radar Interferometry, Proceedings of the IEEE. (2000) 88, no. 3, 333–382, https://doi.org/10.1109/5.838084, 2-s2.0-0034156558.
10.1109/5.838084
Web of Science® Google Scholar
42 Bürgmann R., Rosen P. A., and Fielding E. J., Synthetic Aperture Radar Interferometry to Measure Earth’s Surface Topography and Its Deformation, Annual Review of Earth and Planetary Sciences. (2000) 28, no. 1, 169–209, https://doi.org/10.1146/annurev.earth.28.1.169, 2-s2.0-0033793013.
10.1146/annurev.earth.28.1.169
CAS Web of Science® Google Scholar
43 Paulay T. and Priestley M. J. N., Seismic Design of Reinforced Concrete and Masonry Buildings, 1992, Wiley-Interscience.
10.1002/9780470172841
Web of Science® Google Scholar
44 Smith B. S. and Coull A., Tall Building Structures: Analysis and Design, 1991, John Wiley Sons.
Google Scholar
45 Ghorbani Z., Khosravi A., Maghsoudi Y., Mojtahedi F. F., Javadnia E., and Nazari A., Use of InSAR Data for Measuring Land Subsidence Induced by Groundwater Withdrawal and Climate Change in Ardabil Plain, Iran, Scientific Reports. (2022) 12, no. 1, https://doi.org/10.1038/s41598-022-17438-y.
10.1038/s41598-022-17438-y
Web of Science® Google Scholar
46 Bateson L., Cigna F., Boon D., and Sowter A., The Application of the Intermittent SBAS (ISBAS) InSAR Method to the South Wales Coalfield, UK, International Journal of Applied Earth Observation and Geoinformation. (2015) 34, 249–257, https://doi.org/10.1016/j.jag.2014.08.018, 2-s2.0-84920693680.
10.1016/j.jag.2014.08.018
Web of Science® Google Scholar
47 Gao Y., Zhang S., Li T., Guo L., Chen Q., and Li S., A Novel Two-Step Noise Reduction Approach for Interferometric Phase Images, Optics and Lasers in Engineering. (2019) 121, 1–10, https://doi.org/10.1016/j.optlaseng.2019.03.008, 2-s2.0-85063024448.
10.1016/j.optlaseng.2019.03.008
Web of Science® Google Scholar
48 Chen C. W. and Zebker H. A., Phase Unwrapping for Large SAR Interferograms: Statistical Segmentation and Generalized Network Models, IEEE Transactions on Geoscience and Remote Sensing. (2002) 40, no. 8, 1709–1719, https://doi.org/10.1109/TGRS.2002.802453, 2-s2.0-0036699026.
10.1109/TGRS.2002.802453
Web of Science® Google Scholar
49 Crosetto M., Calibration and Validation of SAR Interferometry for DEM Generation, ISPRS Journal of Photogrammetry and Remote Sensing. (2002) 57, no. 3, 213–227, https://doi.org/10.1016/S0924-2716(02)00107-7, 2-s2.0-0036896279.
10.1016/S0924-2716(02)00107-7
Web of Science® Google Scholar
50 He C.-R., Zhang R., Chen Q., and Han S.-L., Earthquake Characteristics and Building Damage in High-Intensity Areas of Wenchuan Earthquake I: Yingxiu Town, Natural Hazards. (2011) 57, no. 2, 435–451, https://doi.org/10.1007/s11069-010-9624-4, 2-s2.0-79955522250.
10.1007/s11069-010-9624-4
Web of Science® Google Scholar
51 Ogaja C., Wang J., and Rizos C., Detection of Wind-Induced Response by Wavelet Transformed GPS Solutions, Journal of Surveying Engineering. (2003) 129, no. 3, 99–104, https://doi.org/10.1061/(ASCE)0733-9453(2003)129:3(99), 2-s2.0-0346752404.
10.1061/(ASCE)0733-9453(2003)129:3(99)
Web of Science® Google Scholar
52 Kijewski-Correa T. and Pirnia J. D., Dynamic Behavior of Tall Buildings Under Wind: Insights From Full-scale Monitoring, The Structural Design of Tall and Special Buildings. (2007) 16, no. 4, 471–486, https://doi.org/10.1002/tal.415, 2-s2.0-37249088467.
10.1002/tal.415
Web of Science® Google Scholar
53 Yi T., Li H., and Gu M., Full-Scale Measurements of Dynamic Response of Suspension Bridge Subjected to Environmental Loads Using GPS Technology, Science China Technological Sciences. (2010) 53, no. 2, 469–479, https://doi.org/10.1007/s11431-010-0051-2, 2-s2.0-77950807933.
10.1007/s11431-010-0051-2
Web of Science® Google Scholar
54 Bilotta E., Paolillo A., Russo G., and Aversa S., Displacements Induced by Tunnelling Under a Historical Building, Tunnelling and Underground Space Technology. (2017) 61, 221–232, https://doi.org/10.1016/j.tust.2016.10.007, 2-s2.0-84994893822.
10.1016/j.tust.2016.10.007
Web of Science® Google Scholar

Citing Literature

All articles

Domain Knowledge Embedded InSAR-Based 3D Displacement Monitoring of Urban Buildings

Abstract

1. Introduction

2. Methodology

2.1. Introduction of PS-InSAR Technologies

2.2. Description of Displacement Calculation Model by InSAR Data