Structural Control and Health Monitoring
Volume 2025, Issue 1 8548188
Research Article
Open Access

Substructural Damage Identification by Reduced-Order Substructural Boundaries and Improved Particle Filter With Unknown Input for Non-Gaussian Measurement Noises

Ying Lei, 

Corresponding Author

Ying Lei

Department of Civil Engineering , Xiamen University , Xiamen , 361005 , China , xmu.edu.cn

Xiamen Key Laboratory of Integrated Application of Intelligent Technology for Architectural Heritage Protection , Xiamen University , Xiamen , 361005 , China , xmu.edu.cn

Search for more papers by this author
Chang Yin, 

Chang Yin

Department of Civil Engineering , Xiamen University , Xiamen , 361005 , China , xmu.edu.cn

Search for more papers by this author
Junlong Lai, 

Junlong Lai

Department of Civil Engineering , Xiamen University , Xiamen , 361005 , China , xmu.edu.cn

Search for more papers by this author
Shiyu Wang, 

Shiyu Wang

Department of Civil Engineering , Xiamen University , Xiamen , 361005 , China , xmu.edu.cn

Search for more papers by this author
First published: 03 February 2025
https://doi.org/10.1155/stc/8548188
Academic Editor: Ertugrul Taciroglu

Abstract

Substructural identification has shown privileges compared with direct identification of structures. However, unknown substructural interface forces between adjacent substructures are the key but difficult issues in substructural identification. Current substructural identification methods with full-order substructural models still encounter ill-posed identification problems when there are many unknown substructural interaction forces. Thus, it is necessary to study the identification of substructures with reduced-order substructural boundaries. In addition, current substructural identification based on Kalman filtering still assumes that measurement noises are random Gaussian processes. In this paper, a method is proposed for the identification of substructural damage by reduced-order substructural boundaries and an improved particle filter with unknown input for non-Gaussian measurement noises. First, the boundary degrees of freedom of substructural boundaries together with the number of unknown boundary interaction forces are reduced by the characteristic constraint mode approach. Then, based on the reduced-order model of substructure in modal coordinate, an improved particle filter with unknown inputs is proposed, in which the importance density function and particle generation in particle filtering are established by the unscented Kalman filter with unknown inputs. Finally, substructural damage can be identified without the full observations of acceleration responses at the substructure boundaries. The effectiveness of the proposed method is verified through a numerical substructural damage of a planar frame model.

1. Introduction

In the field of structural health monitoring (SHM), structural state assessment is an important issue. Structures are subject to various changes in structural physical parameters and accumulate damage during their service lives. So far, many scholars have studied the identification of structural systems and structural damage using only partial structural response data [1–3].

However, as an inversed problem, structural identification with a large number of degrees of freedom and physical parameters tends to ill condition [4]. Thus, substructural identification methods, which divide a whole structure into several size substructures, have been developed to improve structural system and parameter identification, e.g., Koh, See, and Balendra [5] proposed two methods based on whether the substructure has overlapping degrees of freedom for the identification of substructural stiffness and damping coefficients using the extended Kalman filter (EKF) algorithm. He et al. [6] treated substructural boundary forces as unknown excitation and identified substructural parameters and unknown boundary forces using EKF with the unknown boundary forces estimated by the least-squares method. Tatsis et al. [7] identified the responses and boundary forces of wind tower substructure through the unbiased minimum variance state and input joint estimation by Gillijns and De Moor [8]. However, these methods require the observations of substructural boundary responses. Li et al. [9, 10] investigated damage identification of a target substructure via response transmissibility– and response sensitivity–based methods in time or wavelet domain, respectively. Yuen and Huang [11] modeled shearing frame substructural boundary forces as filtered white noise models and identified structural states and parameters using EKF. The authors also developed some substructural identification methods [12, 13], including parallel substructure identification of linear and nonlinear substructural states, physical parameters, and unknown boundary forces using EKF–UI without direct feedback [14]. However, the above methods are based on the identification of full-order substructural models, yet it is still difficult to identify a target substructure with many unknown substructural interaction forces at structural boundaries.

Therefore, it is necessary to consider the reduced-order model of substructure. Xu et al. [15] adopted the Craig–Bampton method to reduce the internal degrees of freedom of substructures, and then assembled substructures to identify structural damage using the response reconstruction method. Zhu et al. [16, 17] used the Kron substructure method to perform the modal order reduction of each substructure and considered the compensation of higher order modes, and subsequently assembled the reduced-order substructures to update the parameters of the overall structure based on structural response sensitivity. Tian, Weng, and Xia [18] also divided the entire structure into several substructures, reduced the linear substructures using the Kron substructure method, and then updated the physical parameters of the overall structure. Due to the assembling of substructures back into the overall structure, there are still many unknown structural parameters to be identified.

In addition, substructural identification based on Kalman filter or Bayesian filtering still assumes that observed structural response data are contaminated by Gaussian white noises [19–22], including the substructural identification methods by the authors [12–14, 23]. To overcome this limitation, the particle filter (PF) algorithm uses a set of discrete random sampling points to approximate the probability density function of the random system variables, thus there is no need to assume that the system random variables follow Gaussian distributions [24, 25]. Then, some scholars have developed methods of PF with unknown input (PF–UI). Wan et al. [26] proposed a modified PF algorithm to identify structural parameters and unknown inputs. Sen et al. [27] presented an improved interacting particle–Kalman filter for the identification of structural damage and unknown earthquake excitation. Liu et al. [28] developed an extended Kalman PF with the least-square algorithm to identify structural parameters and unknown inputs. However, these algorithms require the measurements of acceleration responses at the locations of unknown inputs/excitations. Later on, the authors [29] proposed a generalized extended Kalman PF–UI (GEKPF–UI) for the identification of structural systems and unknown inputs under non-Gaussian measurement noises. It is applicable when measurement equations do not contain unknown inputs. Furthermore, to solve the problem of particle shortage in the conventional PF algorithm, GEKF–UI is used to estimate the mean and variance of particles, and then the importance density function of PF is established to prepare for particle sampling the importance density function of PF. However, only small-size structures are identified as numerical validation of the proposed GEKPF–UI [29].

In this paper, a method is proposed for identifying substructural state, damage, and substructural interaction forces by reduced-order substructural boundaries and an improved PF–UI for non-Gaussian measurement noises. First, the characteristic constraint mode (CC mode) approach [30] is used to reduce the boundary degrees of freedom of substructures, thereby reducing the number of unknown substructural boundary forces to be identified. The CC mode is a specific constraint mode that is generated by introducing eigenvalue problems associated with the boundary constraints. The solution of this eigenvalue problem can effectively characterize the constraint properties on the boundary, so CC mode is an effective approach to reduce the dimension of the boundary to simplify the model and maintain its dynamic features [30]. Then, based on the reduced-order model of substructure in modal coordinate, an improved PF–UI is proposed to deal with the non-Gaussian measurement noises. The improved PF–UI contributes to the establishment of importance density function in particle filtering by unscented Kalman filter with unknown inputs (UK–UIs) [31, 32] to generate particles carrying the latest observational information in modal space. Superior to the conventional PF algorithm, the particle-carrying observation information generated from the UKF–UI algorithm can effectively drive the prior distribution towards the high likelihood region and improve the accuracy of recognition. Compared to the particle sampling of the importance density function of PF by the GEKF–UI recently developed by the authors, the improved PF–UI uses the merits of UKF–UI to avoid the partial differentiation of the Jacobian matrix in GEKF–UI. This is beneficial for the reduced-order model of substructure in modal coordinates as substructural frequencies and mode shapes are implicit functions of substructural physical parameters and the partial differentiation of the Jacobian matrix is cumbersome. Finally, a set of weighted particles is used to estimate subsystem random variables, and the particle filtering with under unknown input is used to identify the substructural state parameters and the reduced-order unknown modal boundary forces under non-Gaussian measurement noises. Due to the CC mode for the reduced-order model of the structure, which transfers the boundary degrees of freedom to modal coordinates, full observations of acceleration responses at the substructure boundaries are not required to identify the reduced-order unknown modal boundary forces.

2. The Proposed Methodology

The equation of motion of a multidegree-of-freedom linear structure can be represented as
()
where Mg, Cg, Kg represent the mass, damping, and stiffness matrices of the global structure, respectively; represent the acceleration vector, velocity vector, and displacement vector of the overall structure, respectively; fg represents the external force vector acting on the structure; ηg represents the position action matrix of the external forces; and the subscript “g” indicates the “global structure.”
Generally, direct identification of the entire structure is challenging and substructural identification is more efficient. The substructure of interest can be separated from the overall structure, and the equation of motion for a substructure can generally be represented as
()
where Ms, Cs and Ks are the mass matrix, damping matrix, and stiffness matrix of the substructure, respectively. Herein, structural damping is implemented by Rayleigh damping, which is defined as Cs = αMs + βKs; represent the acceleration vector, velocity vector, and displacement vector of the substructure, respectively. gb denotes the boundary force vector in the substructure, where it is assumed that the substructure is only subjected to boundary forces, and ηs represents the influence matrix of the boundary force vector in the substructure. The subscript “s” denotes the “substructure.”
By dividing the substructure into internal degrees of freedom and boundary degrees of freedom, equation (2) can be rewritten as:
()
where the subscript “i” stands for “internal,” representing the internal degrees of freedom of the substructure and the subscript “b” stands for “boundary,” representing the boundary degrees of freedom of the substructure.

2.1. Reduced-Order Substructural Boundary Degrees of Freedom

The substructure may contain many degrees of freedom at substructural boundaries, which causes difficulties in the identification of many unknown substructural boundary forces in the inversed problem of substructural damage detection using only partial substructural responses. Therefore, it is necessary to reduce the degrees of freedom of the substructural boundary.

Characterizing substructure boundaries requires information about adjacent substructures. For example, for the boundary of target Substructure 1 connecting to Substructure 2, the mass matrix and stiffness matrix at the boundary are
()
Then, the characteristic equation for the boundary degrees of freedom is
()
where ϒ is the eigenvalue of the substructure boundary degrees of freedom, is the CC mode of the substructural boundary degrees of freedom, Γd is the principal mode (lower order mode), and Γr is the residual mode (higher order mode).
By rounding off the residual modes, substructural boundary responses in physical coordinates can be transferred to the modal coordinates as
()
where qb is the principal mode coordinate of the boundary degrees of freedom.
Based on equation (6), the substructural coordinates including the internal and boundary degrees of freedom can be reduced as
()
where TROB is the modal transformation matrix of the substructure based on the reduced-order boundary, so the subscript “ROB” denotes the “reduced-order boundary,” and is the coordinate of the substructure.
Equation (7) is put into substructural equations of motion in physical coordinates and left-multiplied of equation (2) by to obtain the modal reduction equations of motion as
()
in which, is the unknown boundary force vector in the reduced-order modal coordinates, and is the action matrix of the modal boundary force.

From equation (8), it is noted that structural boundary degrees of freedom together with the number of boundary forces are reduced by the modal coordinate transformation.

2.2. Reduced-Order Substructural Damage Identification by an Improved PF–UI for Non-Gaussian Measurement Noises

Substructural damage is simulated by reducing the element stiffness of the substructural structure.
()
where is the stiffness matrix of the ith element in the damaged state; is the stiffness matrix of the ith element in the undamaged state; and 0 < θi < 1 is the damage factor of the ith element, which is taken 0 to represent the undamaged state.
Let the substructural state vector be and , the the substructural system state equation can be expressed in state space as
()
By discretizing system equation (10), we get
()
where G(•) represents the state update function, which describes the system state change from time step k to k + 1.
When partial substructural accelerations and displacements are observed, the observation equation is
()
where La is the acceleration observation matrix, Lu is the displacement observation matrix, and vk+1 is the observation noise vector.
Equation (12) can be written as
()
where .

In this paper, an improved PF–UI is proposed to deal with the non-Gaussian measurement noises. In particle filtering, the selection of the importance density function is of great importance as it dictates the quality of the sampled particles. To solve the problem of particle shortage in the conventional PF algorithm, it is proposed to utilize the UKF–UI algorithm to create an effective importance density function that allows particles to encapsulate observational data, steering the prior towards the areas of higher likelihood and enhancing identification accuracy. Especially, compared to the particle sampling of the importance density function of PF by the GEKF–UI recently developed by the authors, the improved PF–UI uses the merits of UKF–UI to avoid the partial differentiation of the Jacobian matrix in GEKF–UI, which is beneficial for the reduced-order model of substructure in modal coordinate.

2.2.1. Construction of the Importance Density Function Based on UKF–UI

By defining a new augmented state vector as , the posterior estimate of the kth step augmented vector is and the corresponding variance matrix is , 2N + 1 Sigma points at step k are constructed based on the posteriori estimate and variance from step k.
()
where N is the number of rows of the state vector; λ = φ2(N + γ) − N; φ = 0.02 is the scale parameter, which is used to adjust the diffusion of sigma points relative to the mean; and γ is the subscale parameter which is usually set to 3 − N [33].
Then, the sigma point of the augmented state vector can be written as
()
where and are the sigma point of the state vector and the sigma point of the unknown force, respectively.
Sigma points are passed through the state equation of equation (11) via the unscented transform as
()
Then, the mean of the predicted values of the state vector is
()
and the prediction variance is
()
where Q is the variance of the system noise and and are the weights of the mean and variance, respectively.
()
where κ = 2 is a parameter that carries information about the prior distribution of the state vector [33].
The estimated function h(Zk+1) in the observation equation (13) is
()
and the corresponding variance matrix is
()
where R is the variance of the observation noise.
Then, the unknown modal boundary forces are estimated from equation (13) as
()
where yk+1 is the observed value vector,
The variance of the unknown modal boundary force is
()
In the observation, the state posterior, state variance, and covariance of the state with the unknown modal boundary force are updated as
()
where
()
and the corresponding variances are
()
()
Then, the augmented state vector and its variance at step k + 1 are
()

In the recursive process from the kth step to the (k + 1)th step, the above UKF–UI provides the mean and variance of the particles at the (k + 1)th step, i.e., the mean in equation (24) and the variance in equation (26) for the reduced substructure.

By using the above mean and variance, a normal distribution can be constructed as a density function of the importance of the particles sampled by
()
where Zk+1 is the particle at step k + 1, Q(Zk+1|Z1:k, y1:k+1) is the importance density function for particle sampling;,and N(∗) represents the multidimensional normal distribution. Therefore, the importance density function for particle sampling is established by equation (29), followed by the particle sampling stage.

2.2.2. Particle Sampling

The proposed particle sampling under generalized unknown excitation based on reduced-order substructure is derived by establishing the importance density function using the UKF–UI method in the framework of PF. Let the number of particles be M, and then M groups of parallel reduced–order substructural UKF–UI algorithms can be executed, followed by generating M groups of mean and variance based on equations (24) and (26) ( is mean and is variance). M groups of mean and variance can be constructed according to equation (29) to construct the M importance density function, which is then sampled for the M particles. k + 1 step of the M particles is the sampling process of
()
where is the importance density function of the jth particle sampling.

The unknown modal boundary forces are identified in the reduced-order substructural UKF–UI, and the particles of the unknown modal boundary forces are , which can be estimated by equation (22).

The particles sampled according to equation (30) may be superior and inferior, so the observation information from the k + 1 step is introduced to correct the particles. The weights of the particles are calculated based on the response of the observation so that the particles move towards their exact values. The weight of the jth particle can be calculated by the following equation (un-normalized weight) [34]:
()
where is the weight of the jth particle in the kth step after normalization and and are the likelihood function and state transfer function of the structure, respectively, whose expressions are generally unknown.
It is worth noting that the expressions of the likelihood function and the state transfer function are related to the probability density of the observation noises and the system noises. However, for the inverse problem of identifying structural parameters with unknown excitation, the probability density functions of the observation noise and system noise are generally unknown. The subgroup optimization fitness function (PSO fitness function) was proposed in the literature [35] to estimate the importance weights. The PSO fitness function is similar to the normal distribution. Therefore, the multidimensional normal distribution function is utilized herein to calculate the importance weights of the particles. Then, the formula for calculating the particle weights can be written as
()
where R is the variance matrix of the observation noise, yk+1 is the observed response vector of dimension d × 1, and is the estimated value of the observed value for the jth particle, which is obtained from the estimated responses with the unknown inputs. Subsequently, the weights are normalized as
()
In order to minimize the effects of particle degradation, resampling of particles is required. The effective number of particles is calculated by using the following equation:
()
When the number of effective particles Neff < NT (NT = 0.8N is a preset threshold [36]), it indicates that the number of effective particles is small and the particle degradation is serious, and the particles need to be resampled. In resampling, particles are sampled according to their weights. Particles with large weights have a higher probability of being extracted, while particles with small weights are easily eliminated. Particles are extracted from the original particle set . The resampling process can be performed by the built-in function randsample (∗) in the MATLAB program, and after resampling, the particles are reset as
()

After resampling, the weight of the particle becomes . The particle weight becomes uniform, and the particle degradation problem is alleviated.

Finally, the (k + 1)-th step state and (k + 1)-th step unknown force vector posteriori are estimated as
()

2.3. Summary of the Proposed Method

In order to facilitate the understanding of the proposed method, the procedures of the proposed method for identifying the reduced-order substructural damage process are summarized as follows (from step k to step k + 1):
  •  

    Step 1: Execute M groups of parallel UKF–UI algorithms in reduced-order substructure to construct the importance density functions (to simplify the presentation, the superscript j of the jth group is omitted, and the following shows the process of one of the groups).

  • (1)

    UKF–UI time prediction of reduced-order substructure: Estimate the sigma point of the predicted value of the state vector according to equation (14), and the predicted value of the state vector according to equation (17). Calculate the variance of the predicted value by equation (18).

  • (2)

    Update the reduced-order substructural model:

    • (2.1)

      Based on the predicted substructural parameters in the state vector , reduce substructural boundary degrees of freedom using the CC mode algorithm by equations (4)–(8).

    • (2.2)

      Identify the reduced unknown modal boundary forces: estimate unknown modal boundary force vector at step k + 1 according to equation (22) and calculate the variance matrix of unknown modal boundary forces according to equation (23).

  • (3)

    Update the estimation of the reduced-order substructural state: Calculate the (k + 1)th step observation update estimate by equation (24), and its variance matrix by equation (26). Also, estimate the variance matrix according to equation (27) and the (k + 1)th step augmented state vector and its variance according to equation (28).

  • (4)

    Construct the importance density based on the UKF–UI for reduced-order substructure by equation (29).

  •  

    Step 2: Particle sampling based on UKF–UI for the reduced-order substructure.

  • (1)

    Particle sampling: The (k + 1)th step state vector mean and variance can be obtained from M sets of the parallel MUKF–UI process, and subsequently M state vector particles are sampled according to equation (30). Particle sampling is based on UKF–UI for the reduced-order substructure and the unknown mode boundary force particles .

  • (2)

    Particle weights of reduced-order substructure: Estimate M particle weights according to equation (31) and the normalized particle weights according to equation (33).

  • (3)

    Posteriori estimation: Estimate the posteriori of the state vector at step k + 1 and the posteriori of the unknown modal boundary forces by equation (36).

  •  

    Step 3: Let k = k + 1 and return to Step 1 until k equals the maximum number of steps.

3. Numerical Validation of the Proposed Method

The model used in the numerical validation is a three-span, four-story planar frame shown in Figure 1. Each column and beam is regarded as one element, so that there are 28 elements. It is assumed that Young’s module of each element is E = 206 GPa, and all columns are of equal length of 1.98 m and all beams are also of equal length of 4.57 m; the cross-sectional area of each beam and column element is 0.012 m2 and 0.024 m2, respectively; and the moment of inertia of the beam and column section is 3.6 × 10−6 m4 and 1.28 × 10−5 m4 and the damping ratio of the first two orders is taken as 0.03. The structure is subjected to a horizontal white noise external load at the top floor, as shown in Figure 1.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Three-span, four-story planar frame model.

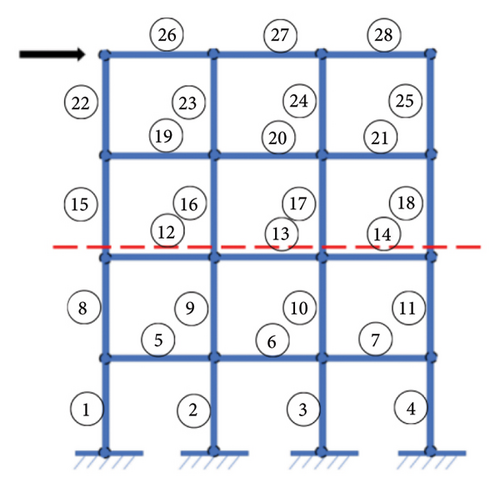
In this example, structural damage of Element 13 is considered, in which its linear stiffness parameter EI/L is discounted by 20%. Subsequently, substructural identification is used to segment the overall planar frame, as shown in Figure 2. In this example, the lower substructure is taken as the target substructure to identify structural damage of the lower substructure.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Sliced upper and lower substructures.

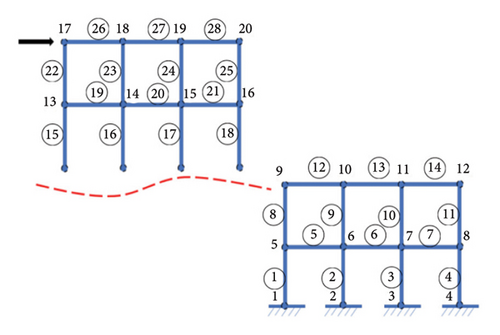
The lower substructure has 14 beam-column elements. Compared to the overall structure, the number of elements and the degrees of freedom of the substructure are significantly reduced. However, there are still 12 unknown boundary forces. Based on the reduced-order of substructural boundary degrees of freedom using the CC mode for the first two orders of modes, the reduced-order substructure model is reduced to two boundary forces in modal coordinates, which greatly reduces the number of unknown boundary forces for the ease of substructural damage identification with unknown boundary forces, as discussed in Sections 2.2 and 2.3.

In this example, observations of the horizontal acceleration of the 2nd story and the angular acceleration of the 5th, 6th, and 7th nodes and the horizontal displacement of the 2nd story and the angular displacement of the 6th and 7th nodes are used. All observed responses are contaminated by 1% non-Gaussian noises, which follows non-Gaussian t-distribution [26].

3.1. Identification Results and Discussion

Figure 3 shows some identification results of velocities in the lower substructure. The horizontal and rotation velocities in the substructure are fitted to their real values, demonstrating that the identification results are accurate.

Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
Identification results of velocity response. (a) 1st story horizontal velocity. (b) 7th node rotational velocity. (c) 2nd story horizontal velocity. (d) 8th node rotational velocity.
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
Identification results of velocity response. (a) 1st story horizontal velocity. (b) 7th node rotational velocity. (c) 2nd story horizontal velocity. (d) 8th node rotational velocity.
Details are in the caption following the image
Figure 3 (c)
Open in figure viewerPowerPoint
Identification results of velocity response. (a) 1st story horizontal velocity. (b) 7th node rotational velocity. (c) 2nd story horizontal velocity. (d) 8th node rotational velocity.
Details are in the caption following the image
Figure 3 (d)
Open in figure viewerPowerPoint
Identification results of velocity response. (a) 1st story horizontal velocity. (b) 7th node rotational velocity. (c) 2nd story horizontal velocity. (d) 8th node rotational velocity.

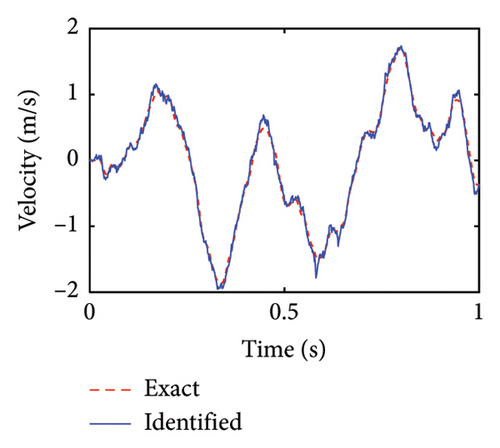
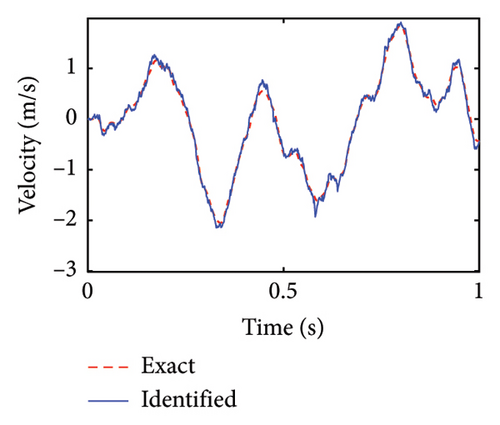
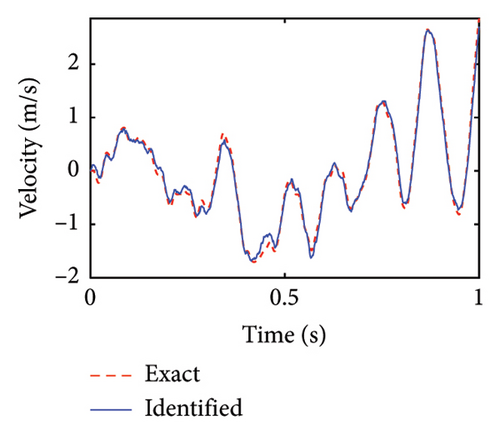
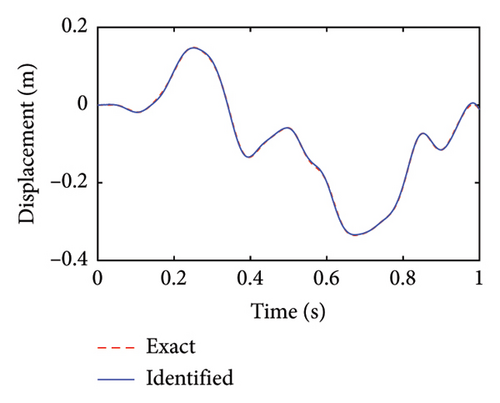
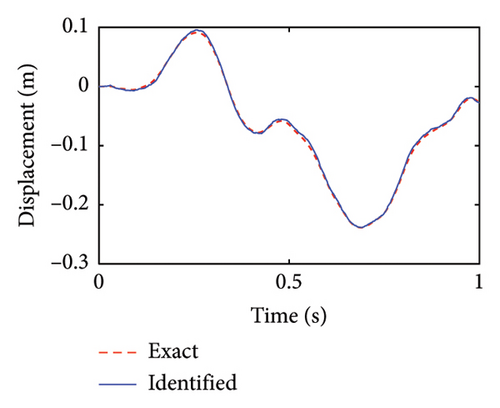
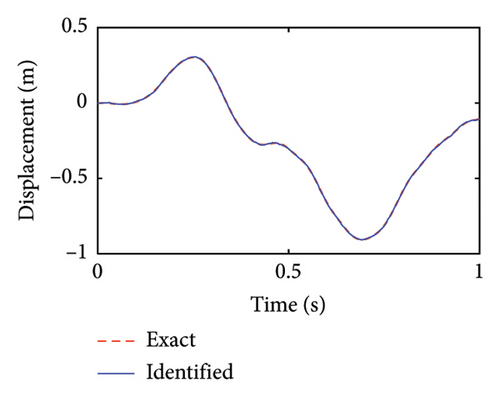
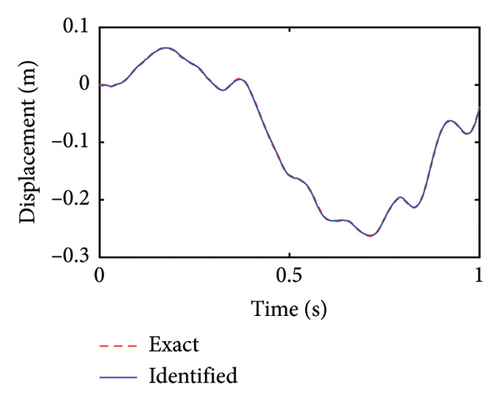
Figure 4 shows the identification results of the unobserved displacement responses of the lower substructure. The identified horizontal and rotational displacements are well overlapped with their real values, showing a good identification effect.

Details are in the caption following the image
Figure 4 (a)
Open in figure viewerPowerPoint
Displacement response identification results. (a) 1st story horizontal displacement. (b) 7th node rotational displacement. (c) 2nd story horizontal displacement. (d) 8th node rotational displacement.
Details are in the caption following the image
Figure 4 (b)
Open in figure viewerPowerPoint
Displacement response identification results. (a) 1st story horizontal displacement. (b) 7th node rotational displacement. (c) 2nd story horizontal displacement. (d) 8th node rotational displacement.
Details are in the caption following the image
Figure 4 (c)
Open in figure viewerPowerPoint
Displacement response identification results. (a) 1st story horizontal displacement. (b) 7th node rotational displacement. (c) 2nd story horizontal displacement. (d) 8th node rotational displacement.
Details are in the caption following the image
Figure 4 (d)
Open in figure viewerPowerPoint
Displacement response identification results. (a) 1st story horizontal displacement. (b) 7th node rotational displacement. (c) 2nd story horizontal displacement. (d) 8th node rotational displacement.

Simultaneously, structural damage factors of the substructure can be identified by the proposed method. The identification results are shown in Figures 5 and 6.

Details are in the caption following the image
Figure 5 (a)
Open in figure viewerPowerPoint
Substructural damage factor identification results. (a) 2nd beam element (undamaged). (b) 8th beam element (undamaged). (c) 10th beam element (undamaged). (d) 13th beam element (damaged).
Details are in the caption following the image
Figure 5 (b)
Open in figure viewerPowerPoint
Substructural damage factor identification results. (a) 2nd beam element (undamaged). (b) 8th beam element (undamaged). (c) 10th beam element (undamaged). (d) 13th beam element (damaged).
Details are in the caption following the image
Figure 5 (c)
Open in figure viewerPowerPoint
Substructural damage factor identification results. (a) 2nd beam element (undamaged). (b) 8th beam element (undamaged). (c) 10th beam element (undamaged). (d) 13th beam element (damaged).
Details are in the caption following the image
Figure 5 (d)
Open in figure viewerPowerPoint
Substructural damage factor identification results. (a) 2nd beam element (undamaged). (b) 8th beam element (undamaged). (c) 10th beam element (undamaged). (d) 13th beam element (damaged).
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Identification results of the substructural damage factor.

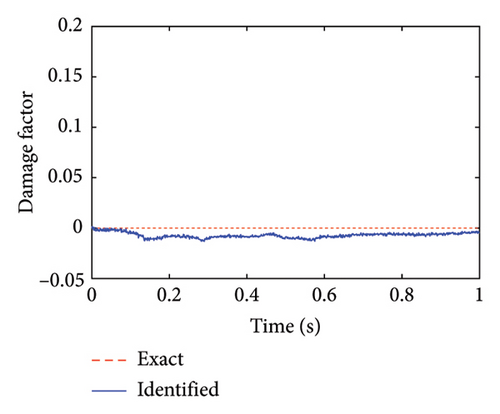
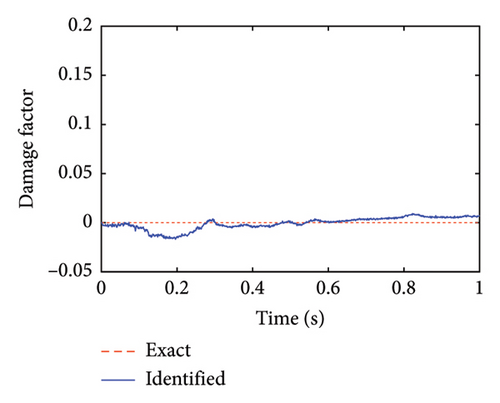
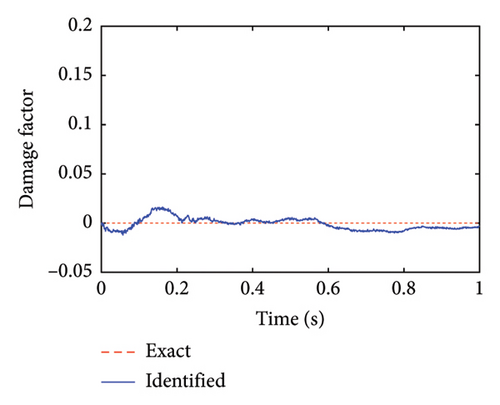
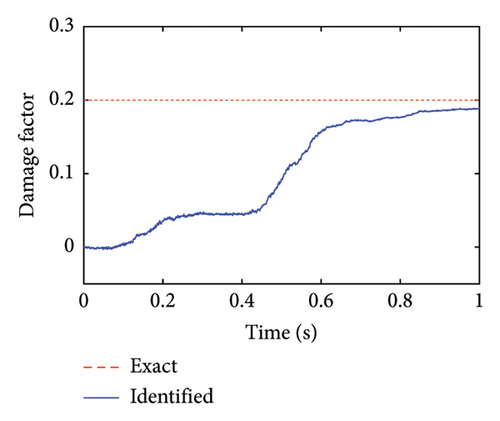
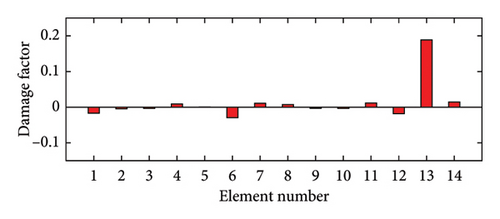
From these figures, it can be found that the identified structural damage occurs in Element 13 with a damage degree of about 20%, which is consistent with the actual damage case. The identification results of the other undamaged elements tend to be 0, which indicates that no damage occurs in these elements. These substructural damage identification results also verify the effectiveness of the proposed method.

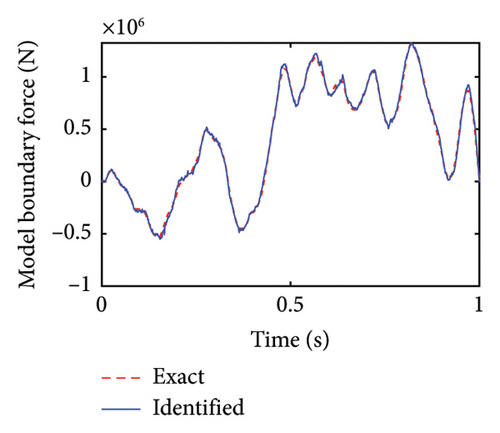
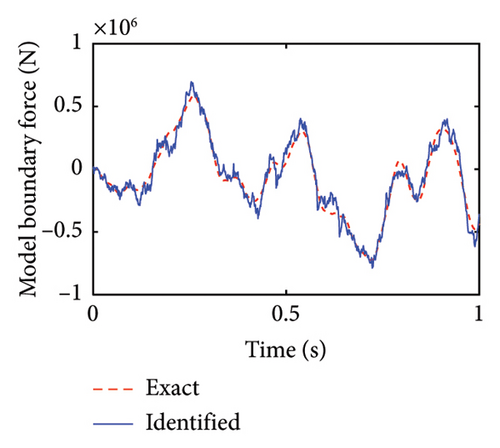
Substructural boundary forces are also identified as unknown inputs to the substructure. The substructural boundary forces in physical coordinates are reduced to two boundary forces using the CC mode algorithm for the reduced-order of substructural boundary degrees of freedom. The results of the identified boundary forces in modal coordinates are given in Figure 7. The identified first modal force is well fitted to its exact values while the identified second modal force is acceptable.

Details are in the caption following the image
Figure 7 (a)
Open in figure viewerPowerPoint
Identification of substructural modal boundary forces. (a) 1st-order modal force. (b) 2nd-order modal force.
Details are in the caption following the image
Figure 7 (b)
Open in figure viewerPowerPoint
Identification of substructural modal boundary forces. (a) 1st-order modal force. (b) 2nd-order modal force.

4. Conclusions

In this paper, a method is proposed for the identification of substructural damage by reduced-order substructural boundaries and an improved PF–UI for non-Gaussian measurement noises. The main contributions of this paper can be summarized as follows.
  • (1)

    Current substructural identification methods use full-order substructural models to encounter the ill-posed identification problem when there are many unknown substructural interaction forces. The proposed method reduces the degrees of freedom of substructural boundaries together with the number of unknown boundary interaction forces in modal space, which reduces the difficulty of substructural identification with unknown boundary interaction forces.

  • (2)

    An improved PF–UI is proposed for substructural damage identification with the reduced-order boundary interaction forces under non-Gaussian measurement noises. Superior to the conventional PF, importance density function and particle generation are established by UKF–UI to effectively drive the prior distribution towards the high likelihood region and improve recognition accuracy.

  • (3)

    Compared with the particle sampling and the importance density function of PF by the GEKF–UI developed recently by the authors, the improved PF–UI uses the merits of UKF–UI to avoid the partial differentiation of the Jacobian matrix in GEKF–UI. This is suitable for the reduced-order model of substructure in modal coordinates.

  • (4)

    A numerical study demonstrates that the proposed method can effectively identify substructural states, damage factors, and modal boundary forces without the observations of acceleration responses at the substructural boundary.

The proposed method needs to be verified with complex structural configurations. Moreover, the reduction method in this paper is based on linear substructures, so the identification of nonlinear substructures remains to be investigated.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This research in this paper was financially supported by the National Natural Science Foundation of China through the Grant No. 52178304 and the 2022 Xiamen Construction Technology Project XJK2022-1-2.

Acknowledgments

This research in this paper was financially supported by the National Natural Science Foundation of China through the Grant No. 52178304 and the 2022 Xiamen Construction Technology Project XJK2022-1-2.

    Data Availability Statement

    All data used in the study are available from the corresponding author upon reasonable request.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.