Structural Control and Health Monitoring

Volume 2025, Issue 1 3576799

Research Article

Open Access

Seismic Performance Analysis of Replaceable Corrugated Steel Plate Composite Shear Walls Based on Interaction Relationships

Qirui Luo,

Qirui Luo

orcid.org/0000-0002-1153-5567

Sichuan Provincial Architectural Design and Research Institute , Chengdu , 610041 , China

School of Civil Engineering , Xi’an University of Architecture and Technology , Xi’an , 710055 , China , xauat.edu.cn

Search for more papers by this author

Wei Wang,

Wei Wang

School of Civil Engineering , Xi’an University of Architecture and Technology , Xi’an , 710055 , China , xauat.edu.cn

Search for more papers by this author

Shixing Zhao,

Corresponding Author

Shixing Zhao

[email protected]

orcid.org/0009-0004-4338-0485

Sichuan Provincial Architectural Design and Research Institute , Chengdu , 610041 , China

Search for more papers by this author

Min Zhang,

Min Zhang

School of Civil Engineering and Geomatics , Southwest Petroleum University , Chengdu , 610500 , China , swpu.edu.cn

Search for more papers by this author

Shuheng Yang,

Shuheng Yang

Sichuan Provincial Architectural Design and Research Institute , Chengdu , 610041 , China

Search for more papers by this author

Qirui Luo,

Qirui Luo

orcid.org/0000-0002-1153-5567

Sichuan Provincial Architectural Design and Research Institute , Chengdu , 610041 , China

School of Civil Engineering , Xi’an University of Architecture and Technology , Xi’an , 710055 , China , xauat.edu.cn

Search for more papers by this author

Wei Wang,

Wei Wang

School of Civil Engineering , Xi’an University of Architecture and Technology , Xi’an , 710055 , China , xauat.edu.cn

Search for more papers by this author

Shixing Zhao,

Corresponding Author

Shixing Zhao

[email protected]

orcid.org/0009-0004-4338-0485

Sichuan Provincial Architectural Design and Research Institute , Chengdu , 610041 , China

Search for more papers by this author

Min Zhang,

Min Zhang

School of Civil Engineering and Geomatics , Southwest Petroleum University , Chengdu , 610500 , China , swpu.edu.cn

Search for more papers by this author

Shuheng Yang,

Shuheng Yang

Sichuan Provincial Architectural Design and Research Institute , Chengdu , 610041 , China

Search for more papers by this author

First published: 25 June 2025

https://doi.org/10.1155/stc/3576799

Academic Editor: Lucia Faravelli

Share a link

Email
Wechat
Bluesky

Abstract

Replaceable systems, including the main structure and components, are the primary means of building a resilient city. However, due to the complex interaction relationships, the energy-dissipation effect of such structural systems is not ideal. Accordingly, this study used a replaceable corrugated steel plate composite shear wall as an example, focusing on the seismic performance and energy-dissipation ratio analyses of each component. We attempted to find a suitable stiffness ratio index to determine the interaction relationship of the replaceable corrugated steel plate shear wall. An energy-dissipation evaluation method is proposed based on the stiffness ratio index, and the bearing-capacity formula of the shear wall was modified. The results show that the revised lateral-bearing-capacity formula based on the energy dissipation evaluation exhibited ideal accuracy and could provide a reference for practical engineering applications.

1. Introduction

Traditional shear wall structures dissipate seismic energy through plastic deformation. However, this approach makes the damaged structural parts diffuse and difficult to repair [1, 2]. Accordingly, scholars have developed shear wall structures with replaceable energy-dissipation components [3, 4]. As opposed to conventional structures, the main structure of the replaceable shear wall should always be in the elastic phase during an earthquake, where damage is concentrated on the damaged components. The structural function can be restored by replacing damaged components after an earthquake.

When an earthquake occurs, a large amount of energy is released into buildings [5–7]. To protect the main body of a structure from damage, it is necessary to effectively control the seismic energy [8–10]. Concentrated-energy-dissipation components are known as damage components and are mostly found in dampers [11–13]. Dampers can be classified into several types: displacement, velocity, and compound dampers. Among them, displacement dampers have been widely used in replaceable structures owing to their clear force, stable performance, and ease of replacement [14]. Researchers have focused on proposing novel dampers and experimentally verifying their performance. Ma et al. proposed a novel rotary amplification friction damper, which was shown to have superior seismic control effectiveness in the experimental analysis [15]. Chen et al. proposed a metallic torsional damper using a gear and rack device, and the configuration and working principle of the proposed damper are introduced [16]. Li et al. proposed the corrugated pipe damper and carried out experiment and finite element analysis. The results showed that the damper exhibited good horizontal deformation and energy dissipation capacities, and excellent seismic fatigue performance [17]. In fact, dampers are generally not used independent of their main structure; their performance efficiency varies with the interaction relationship [18]. Therefore, performance efficiency should be investigated to fully exploit the damper performance; however, research in this area is lacking.

For replaceable shear walls, the following limitations hinder their application in practical engineering: (i) Damage control is the key to a replaceable structure, and the requirements for damaged components are more stringent. The stress transfer mode between the damper and main body of the wall is different, which should ensure that the damper fails before the wall. Currently, the main approach for replaceable shear walls is a parameter sensitivity analysis, and there is a lack of research on damage control methods. (ii) The interaction is the basis for evaluating the structural performance efficiency. The optimal performance state between components cannot be achieved in engineering design for various reasons. However, the evaluation criteria based on these interactions are rare.

In essence, the performance efficiency reflects the synergy between the damper and main body of a structure, and an ideal interaction relationship is a necessary condition for the damper to exert its energy-dissipation capacity. Therefore, this study aimed to explore the seismic performance and interaction relationship of a replaceable shear wall. First, we describe the experiments conducted in this study. Subsequently, the replacement area dimensions and shear wall deformation were analyzed. The seismic performance of the replaceable shear wall was investigated, and the interaction relationships, energy dissipation, and energy-dissipation ratio were analyzed. Finally, an energy-dissipation evaluation method is proposed, and the bearing-capacity formula of the shear wall was modified. The revised formula could serve as a reference for practical engineering applications.

2. Materials and Methods

2.1. Wall Body

A shear wall, which is the main body of a toe-replaceable structure, should have excellent energy-dissipation capacity and sufficient bearing capacity. The application and development of reinforced concrete shear walls in practical engineering are limited by shortcomings such as poor ductility, self-weight, and easy cracking [19, 20]. It is difficult to fully exploit the seismic properties of a steel plate shear wall because of its easy buckling [21–23]. A composite shear wall was developed to address the low ductility of reinforced concrete shear walls and easy buckling of steel plate shear walls [24, 25]. Previous studies have shown that concrete not only directly improves the bearing capacity of the steel plate shear wall but also constrains the steel plate to prevent buckling. This effectively increases the seismic efficiency of the steel plate [26, 27].

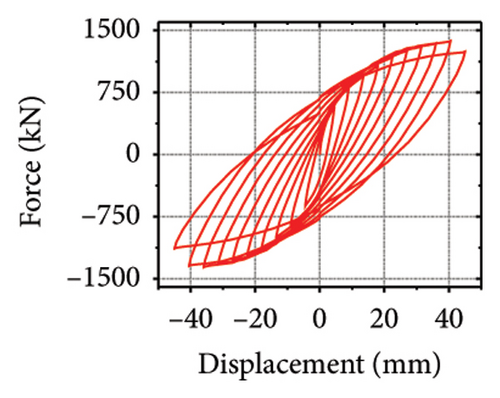
Corrugated plates developed from flat plates are widely used owing to their superior out-of-plane stiffness and lateral bearing capacity [28]. In 2019, our research group applied corrugated steel plates to a shear wall and designed six shear wall specimens [29], as shown in Figure 1. “SPSW” and “SPCSW” represent the steel plate shear wall and steel plate composite shear wall, respectively. “1,” “2,” and “3” represent the flat, vertical corrugated, and horizontal corrugated steel plates. The advantages of the corrugated steel plate shear walls and corrugated steel plate composite shear walls were explored using hysteretic loading. The results showed that the corrugated steel plate was equivalent to “ribbing” outside the flat steel plate, which increased the out-of-plane stiffness and improved its seismic performance. Furthermore, due to the “accordion effect,” the energy-dissipation capacity along the corrugated direction was prominent, while the vertical corrugated direction had higher initial stiffness and bearing capacity.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Failure mode of different shear walls [29]. (a) SPSW-1. (b) SPSW-2. (c) SPSW-3. (d) SPCSW-1. (e) SPCSW-2. (f) SPCSW-3.

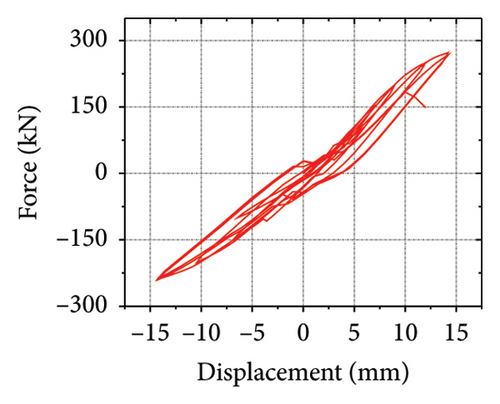
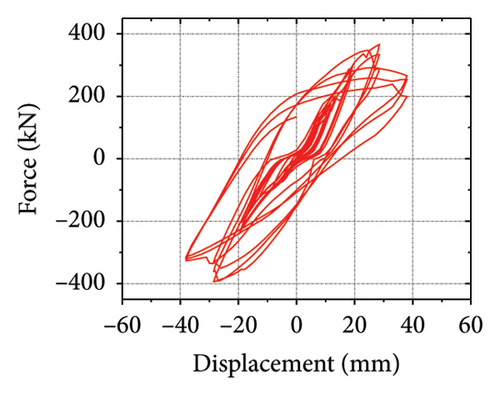
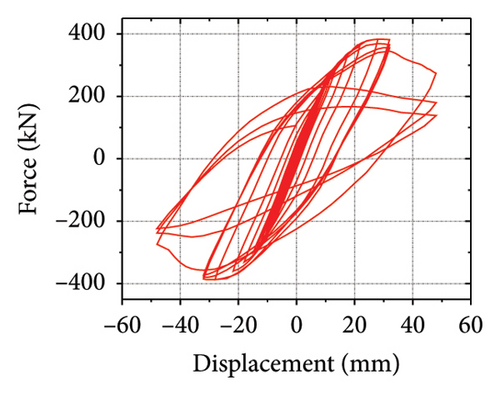
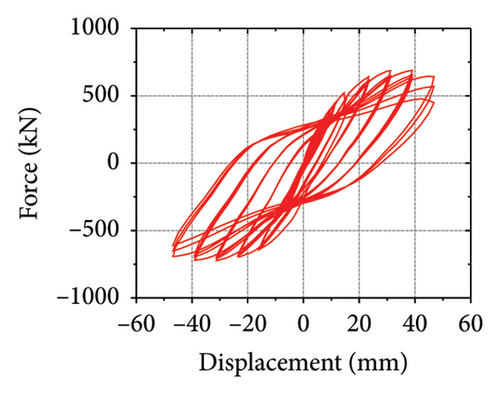
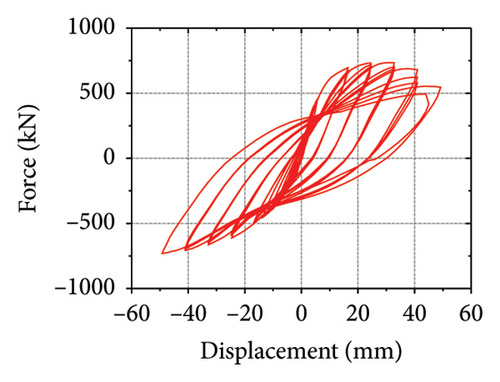
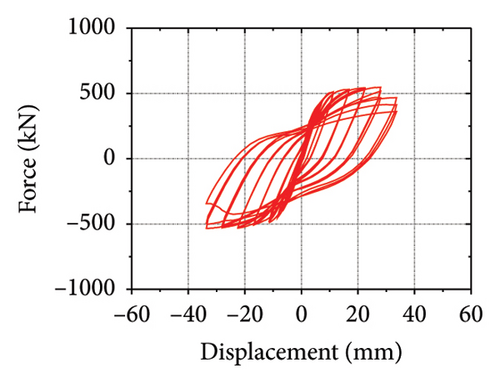
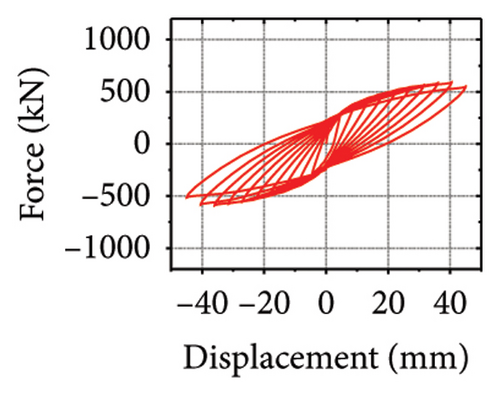
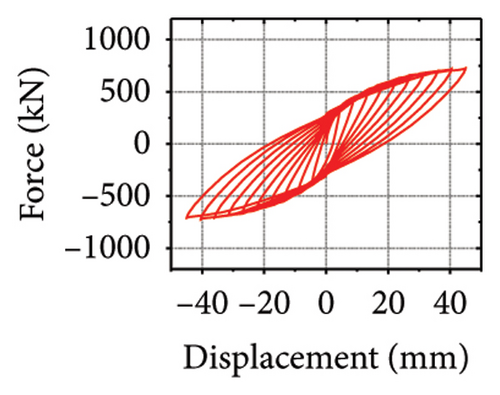
The hysteretic curves are shown in Figure 2. SPCSW-1–3 exhibited a lateral capacity of 688.8, 733.0, and 547.2 kN, respectively. Compared to the SPSW specimens, SPCSW-1–3 exhibited higher bearing capacities, increasing by 252.8%, 200.4%, and 141.8%, respectively. Clearly, the SPCSW specimens exhibited better seismic performance than the SPSW specimens. Compared to SPCSW, SPCSW-3 exhibited the lowest bearing capacity. Combined with the final failure state, it can be inferred that the concrete in SPCSW-3 could not ideally limit the deformation of the horizontal steel plate. Therefore, it was difficult for the horizontally corrugated steel plate to perform the full rule, which resulted in the worst seismic performance. Overall, the corrugated steel plate composite shear walls exhibited excellent seismic performance and could be used as the main components in replaceable structures.

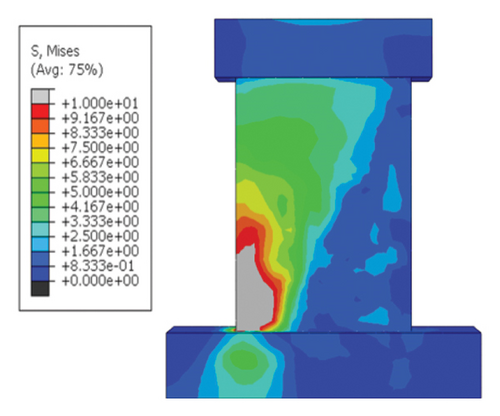
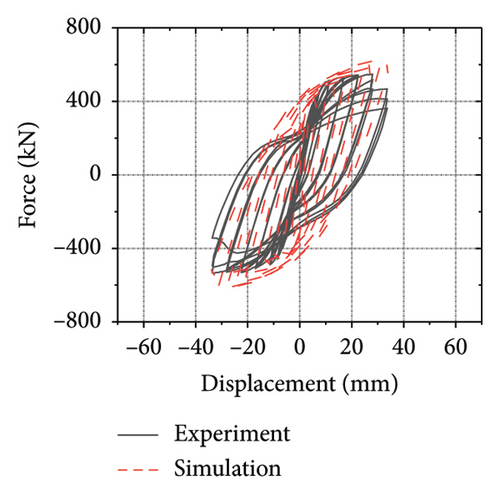
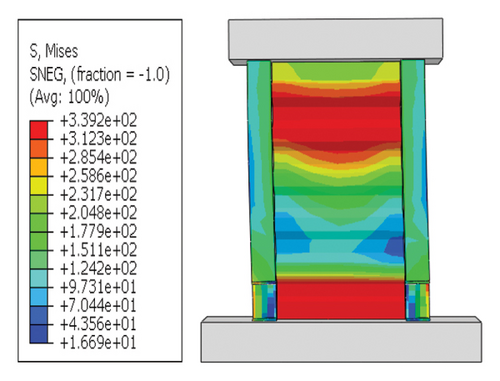
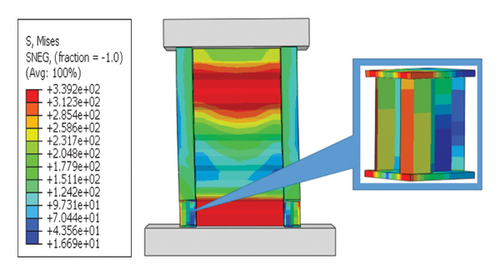
Following the abovementioned results, SPCSW-3 was modeled. Solid element C3D8R was used to simulate the concrete and steel plates, and truss element T3D2 was used to simulate the steel bars. Stud and bond slips were simplified in the model, and the “Embedded” method was used to embed the steel skeleton in the concrete. A more detailed modeling process can be found in [29]. Figure 3 shows the failure modes and hysteresis curves for the modelled and experimental specimens. The ultimate failure in the experiment was concrete spalling at the toe, and the steel skeleton could not continue to bear the load. Although the validation model struggles to reflect the crack failure of the concrete, the stress is still concentrated at the toe of the wall. The hysteresis curves are generally consistent with each other. The differences in the final bearing capacities and corresponding peak displacements were small. In general, the model effectively reproduced the entire experimental failure process.

2.2. Energy-Dissipation Component

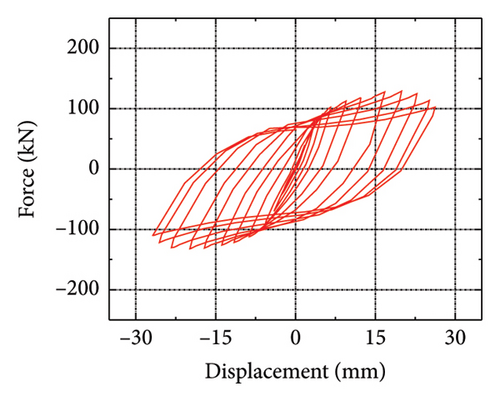
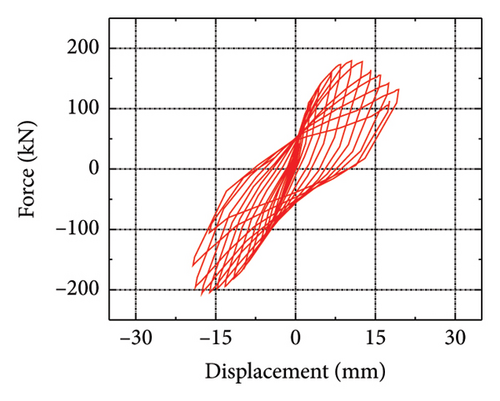
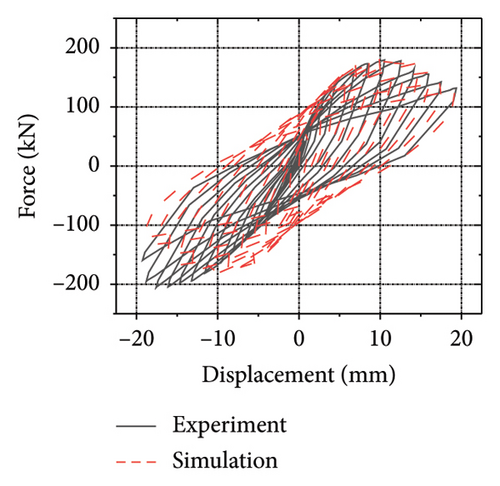
A previous study proposed two new metal dampers with a corrugated web [14, 30], as shown in Figure 4. Additionally, the following steel-type parameters were added: mild steels LYP160 and Q235. The four specimens were named CMSD-H, CSPD-H, CMSD-V, and CSPD-V. CMSD, and CSPD represent steel dampers with mild steels LYP160 and Q235, respectively. H and V represent the horizontal and vertical webs used for the energy-dissipation web, respectively. Figure 5 shows the hysteresis curves of the specimens. The peak loads of CMSD-H, CMSD-V, CSPD-H, and CSPD-V were 129.1, 179.4, 117.7, and 211.5 kN, respectively. Because of the accordion effect, the peak load of the horizontal corrugated web damper was lower than that of the vertical corrugated web damper. Compared with conventional steel dampers, mild steel dampers have a lower initial stiffness. The combination of steel structures and mild steel dampers can achieve the dual goal of damage concentration and energy dissipation improvement. In general, the damper exhibited excellent seismic performance and can be used as an energy-dissipation component in replaceable structures. Subsequently, a model was developed based on the CMSD-V specimen. The energy-dissipation web and the main board were connected via “Tie,” and the energy-dissipation web was simulated by shell element S3R, which was convenient for simulating the buckling deformation of the web. A more detailed modeling process can be found in [18]. A comparison between the simulation and experimental results is shown in Figure 6. Because the simulation was in an ideal state and weld failure was ignored, the hysteresis curve of the numerical model was greater than that of the experiment. The maximum simulated and experimental loads were 182.9 and 179.4 kN, respectively, with a deviation of only 1.9%.

2.3. Replaceable Corrugated Steel Plate Composite Shear Wall

Connecting beams are common replaceable components in shear walls. By weakening the connecting beams, energy dissipation is concentrated to protect the main shear wall structure from damage. However, this replaceable form is only applicable to coupled shear walls and not to single shear walls. In fact, a single shear wall under seismic action exhibits toe failure, as shown in Figure 7. Based on this feature, our research group investigated the seismic performance of a toe-replaceable shear wall [32], as shown in Figure 8. The results indicated that the lateral bearing capacity, initial stiffness, and ductility of the shear wall could be restored by removing the plastic hinge area and setting a metal damper. Toe replacement in a shear wall is an effective means for functionally restoring a single shear wall. However, in that study, we only focused on the change in shear wall performance before and after toe replacement and did not investigate the structural performance interaction relationship in detail. Additionally, the engineering application was limited to a toe-replaceable structure. Therefore, the current study considered a horizontally corrugated steel plate composite shear wall as an example to investigate its hysteretic performance and interaction relationship.

3. Replacement Area and Wall Deformation Analysis

3.1. Replacement Area Analysis

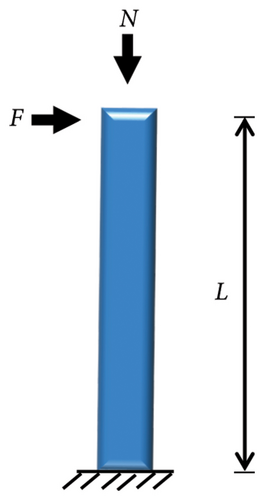
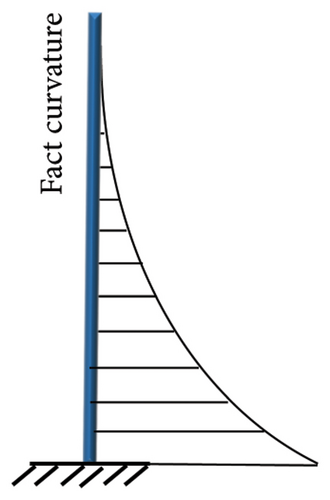
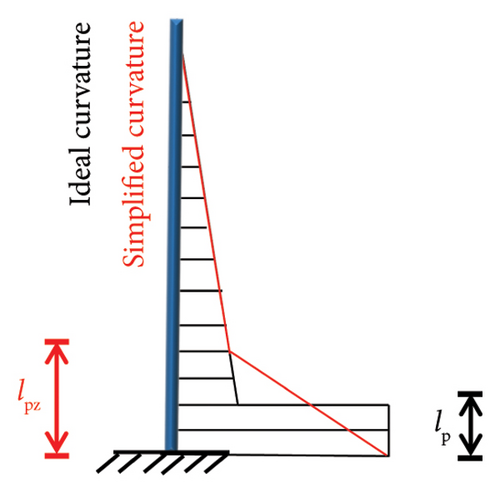
The size of the plastic hinge area of a shear wall determines its seismic performance before and after replacement. Various theoretical calculations have been employed to obtain the plastic-hinge length of shear walls. Among them, the simplified approach of idealizing the wall components as independent rods has been widely adopted [33], as shown in Figure 9. First, it was assumed that (i) the shear wall curvature was linearly distributed along the height before yielding; (ii) after yielding, the shear wall curvature was distributed along the height in a double-fold line; (iii) the plastic hinge length l_pz was equal to the height of the difference between the limit and yield curvatures in the wall height direction; and (iv) the equivalent plastic hinge length l_p was determined according to the principle that the ideal curvature was equal to the theoretical curvature height.

Therefore, the top displacement of the shear wall is equal to the sum of the yield and plastic displacements, as shown in equation (1). The yield displacement was calculated by the quadratic integration of the shear wall curvature distribution, as shown in equation (2). The plastic displacement was calculated by multiplying the cantilever height with the plastic rotation angle of the bottom, as shown in equation (3).

()

where ∆_u, ∆_y, and ∆_p are the ultimate, yield, and plastic displacements of the wall top, respectively; θ is the bottom rotation angle of the shear wall; L is the shear wall height; L_p is the equivalent plastic hinge length; and φ_u and φ_y are the shear wall curvatures at failure and yield, respectively. The bottom of the shear wall reached its ultimate curvature when the edge of the shear wall compression zone reached its ultimate compressive strain [34]. Hence, it was necessary to divide the shear wall according to the types of edge materials. For ordinary reinforced concrete and composite shear walls with embedded steel plates [35], the ultimate curvature is as follows:

()

where ε is the ultimate strain of the edge concrete under compression and c denotes the edge concrete compression zone height. For a reinforced concrete shear wall, the compression zone height is given by equation (5). For a composite shear wall with an embedded steel plate, the compression zone height is given by equation (6):

()

where A_s and

are the cross-sectional area of the longitudinal bars in the tension and compression zones, respectively; A_H and

are the cross-sectional area of the constraint column in the tension and compression zones, respectively; f_y and

are the longitudinal reinforcement yield strength in tensile and compressive zones of the shear wall, respectively; f_H and

are the yield strength of the steel column restrained by the tension and compression zones, respectively; b_w is the shear wall section width; ρ_w and ρ_p are the longitudinal distribution of the steel bar ratio and steel content of the steel plate, respectively; and P is the axial compressive force.

3.2. Wall Deformation Analysis

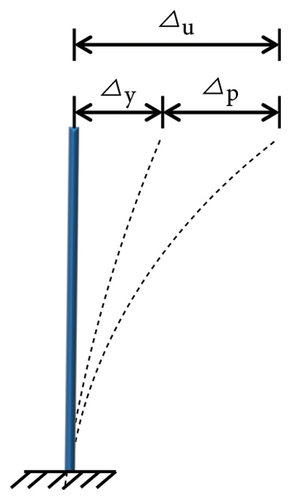
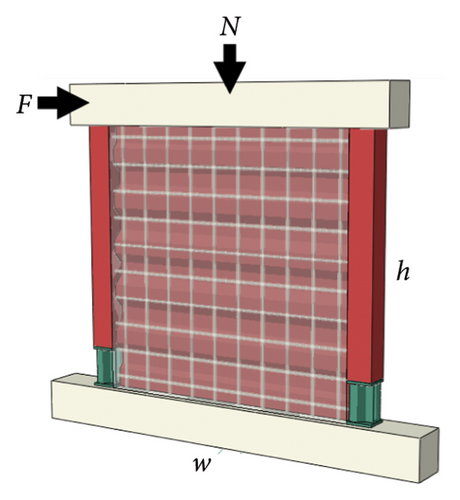
A composite shear wall with a replaceable toe was selected as the research object, as shown in Figure 10. The deformation process of the structure is highly complex and can be divided into shear and bending deformations, as shown in Figures 11(a), 11(b), 11(c). The essence of bending deformation is that under the action of the bending moment, one side of the wall is strained, and the other side is pressurized. Figure 12 shows the bending deformation force diagram. When the wall aspect ratio is large, the wall is prone to bending and deformation, whereas shear deformation occurs in walls with small aspect ratios. However, the damper should also play an energy-dissipating role. The setup principle was to ensure that the damage was concentrated on the damper; meanwhile, the damper should have a good energy-dissipation capacity.

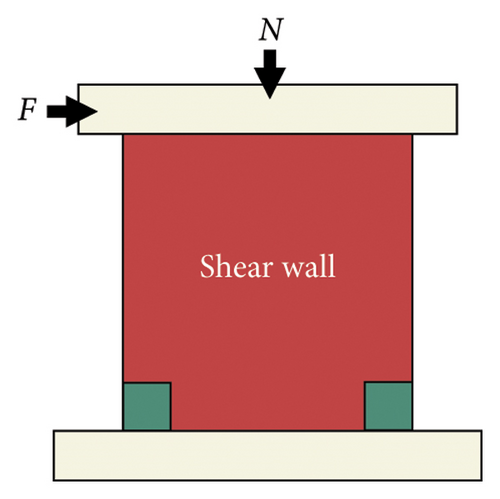
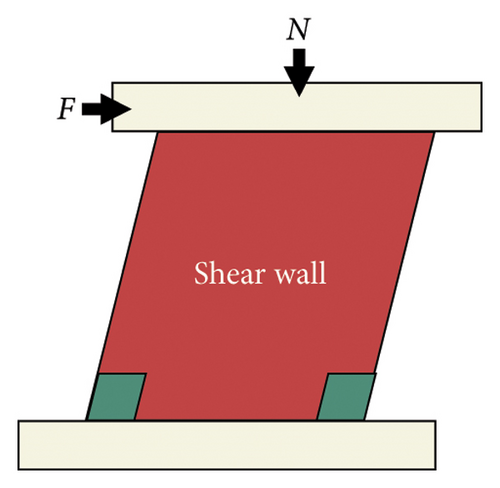
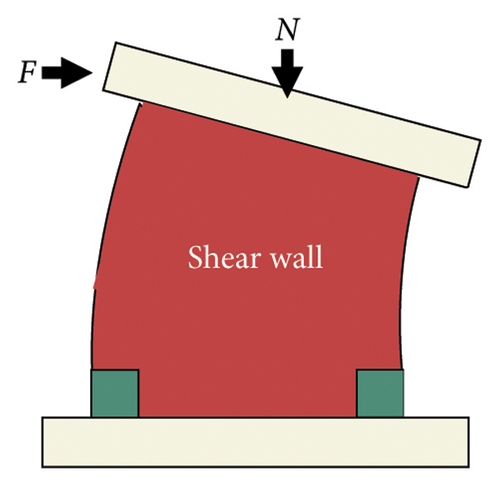
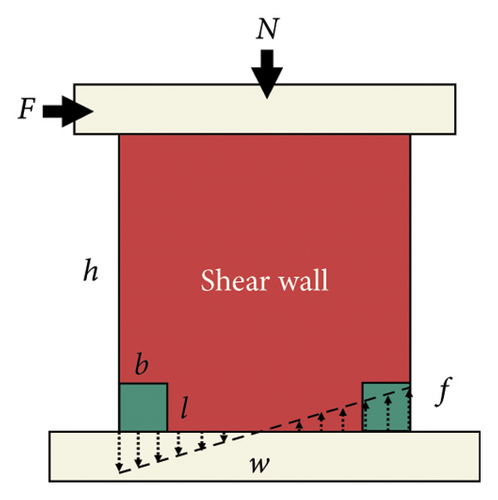
For shear deformation, the lateral deformation of the bottom is much larger than that of the other areas when the damping stiffness is low. When the damper stiffness is high, the deformation of the main structure is large, and the stress is concentrated on the main structure, which is detrimental to the seismic performance of the damper.

To facilitate the quantitative analysis of the relationship between the damper and wall, it was necessary to propose a suitable evaluation index. It should be noted that wall stiffness degradation occurs under loading, and the degradation process is difficult to investigate. Therefore, the stiffness relationships discussed in this paper represent the initial stiffness of the structure. For the bending deformation of the replaceable structure, based on the assumption of a flat cross-section, the damper was in a tension or compression state when the wall was in bending deformation. However, the damper and wall are two different components, and their ideal interaction relationship is such that the stress does not change suddenly, as shown in Figure 12. The moment balance equation is as follows:

()

where F_w is the horizontal load on the wall top; h and w are the wall height and width, respectively; and f is the maximum stress at the wall toe. Then, f can be obtained as follows:

()

The damper force can be obtained by multiplying both sides of equation (8) by the damper width b:

()

When the damper deformation is a unit of displacement, equation (9) can be expressed as the ratio of the axial stiffness of the damper to the lateral stiffness of the wall, as follows:

()

Because the wall did not rotate rigidly, it was necessary to increase the reduction coefficient (β_em) as follows:

()

It can be seen that the right side of equation (11) is the critical value of the ratio between the axial stiffness of the damper and the lateral stiffness of the wall. For convenience, the critical value was defined as r_w. When the ratio is smaller than r_w, the damper is deformed and fully utilized for energy dissipation. The damper deformation is poor when the ratio is greater than r_w. It is difficult to achieve the ideal energy dissipation. The reduction factor should be determined based on a sensitivity analysis and interaction investigation. Therefore, the interaction between the damper and wall can be defined as follows:

()

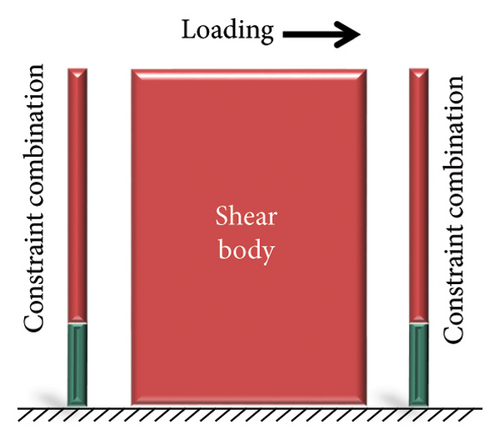
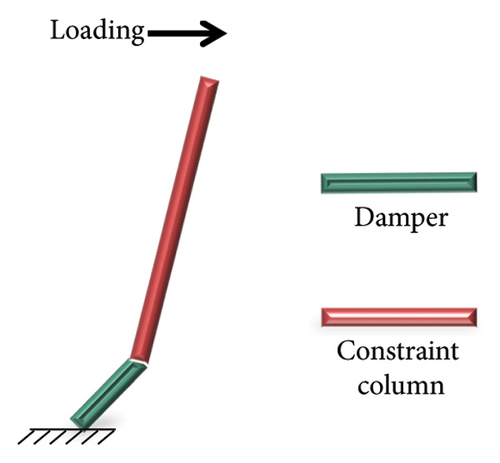
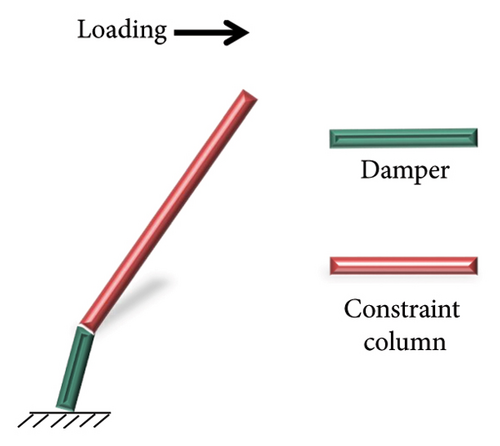
For shear deformation, the damper and constraint column together formed an edge constraint combination, as shown in Figure 13(a). The edge constraint combination consisted of a damper and a constraint column. When the damper stiffness is insufficient, the deformation and stress are primarily concentrated on the damper, which exerts a better energy-dissipation capacity, as shown in Figure 13(b). When the damper stiffness is high, the damper hardly deforms, making it difficult to achieve its energy-dissipation target. Therefore, this situation should be avoided in design, as shown in Figure 13(c).

According to the shear deformation analysis of the shear wall, r_h−cd and r_h−cdw are defined as follows:

()

where K_v−dam and K_h−dam are the compressive and shear stiffness values of the damper, respectively; and K_h−col and K_wal are the initial lateral stiffness values of the constrained columns and walls, respectively.

4. Parameter Analysis

4.1. Coupling Effect of the Wall Aspect Ratio and Damper Web Thickness

Based on the simulation results and calculation for the plastic hinge, the toe replacement size was determined to be 300 × 300 mm². First, the coupling effects of the wall aspect ratio and damper web thickness were analyzed. The specimens were named following the convention “corrugated plate height-width-thickness—damper web thickness—constraint column thickness.” By summarizing the loading process of the specimens, it was found that there were two wall failure modes, as shown in Figure 14. Taking a specimen with an aspect ratio of 1:2 as an example, when the damper stiffness was low, the stress was better concentrated on the damper, and the final failure mode was dominated by the buckling failure of the damper. Conversely, when the damper stiffness was high, the stress did not easily concentrate on the damper.

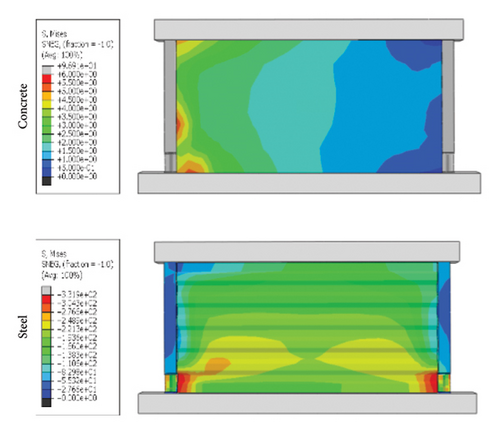
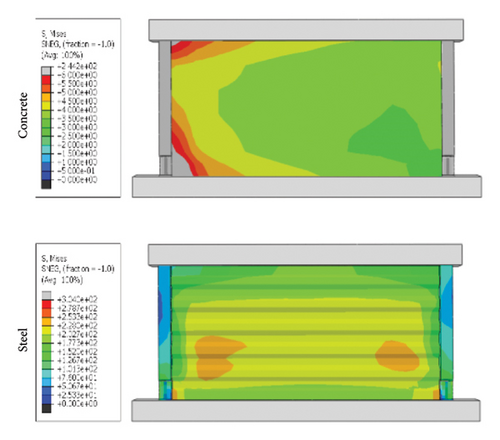
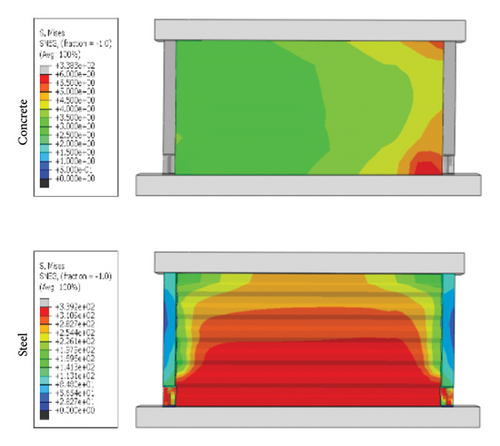
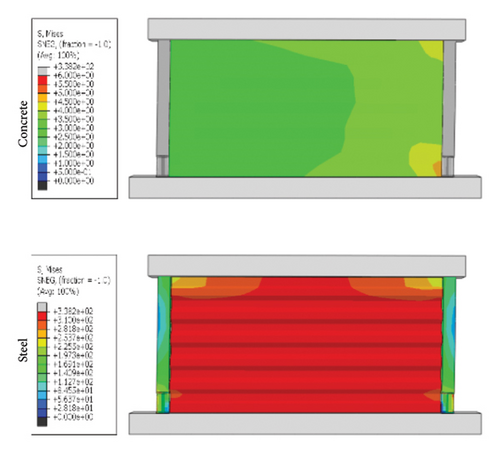
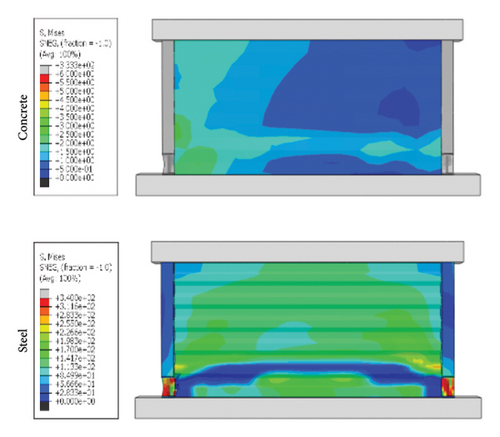
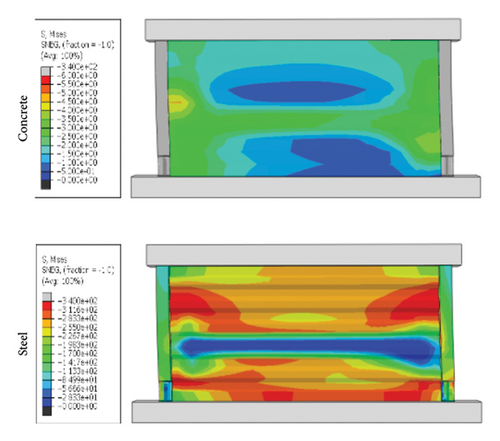
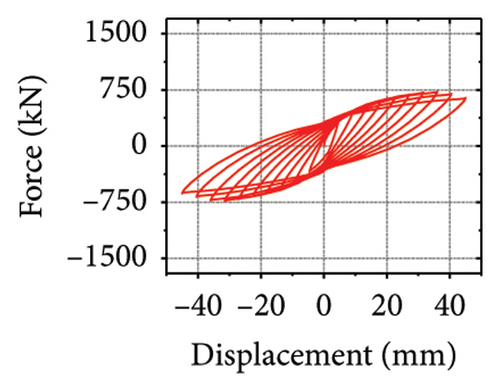
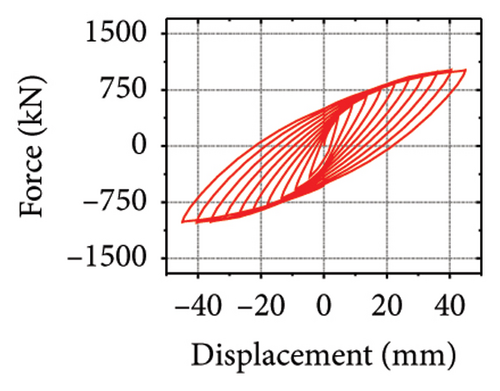
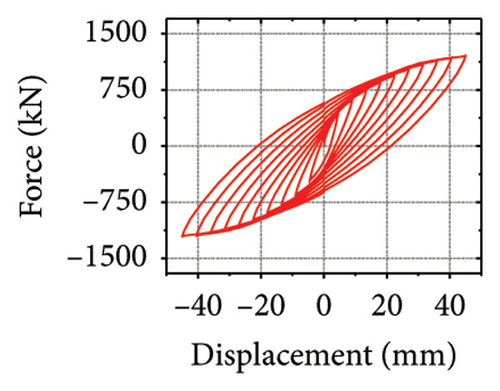
Figure 15 shows the hysteresis curves for all specimens. The aspect ratio was the main factor influencing the ultimate bearing capacity of the replaceable shear wall. However, for the same aspect ratio, the seismic performance of the wall was limited when the damper web thickness was insufficient, making it difficult to provide sufficient restraint to the wall. For example, the ultimate bearing capacities of specimens 3-1-3-dt6-15 and 3-1-3-dt24-15 were 724.0 and 1284.6 kN, respectively, indicating that the damper parameters in the wall toe replaceable structure should be reasonably set to give full play to the seismic performance of the wall. When the restraining ability of the constraint combination on the wall was insufficient, the seismic performance of the shear wall was limited.

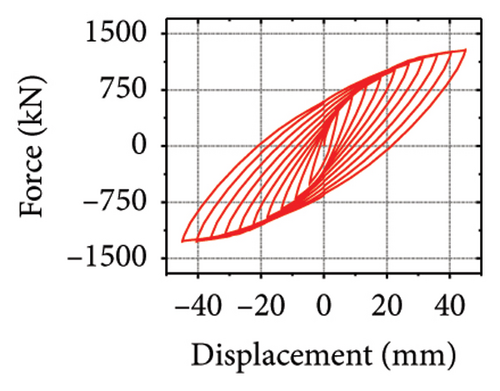
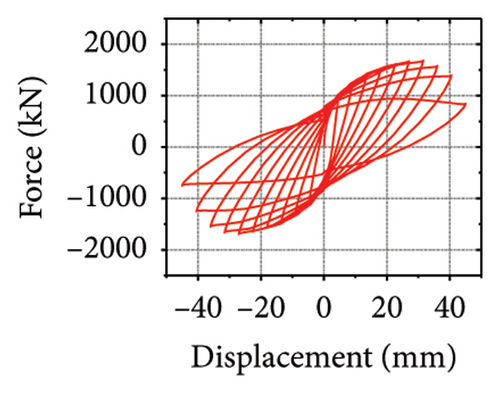
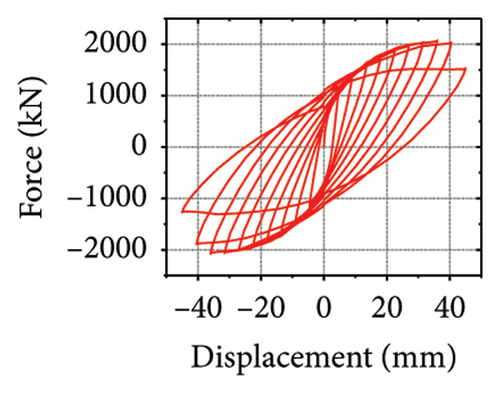
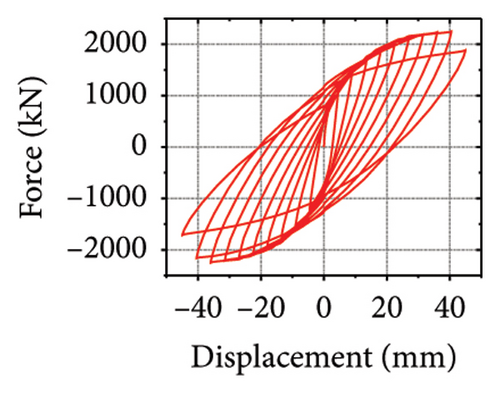
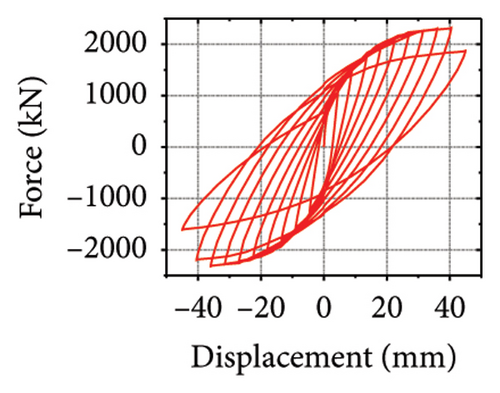
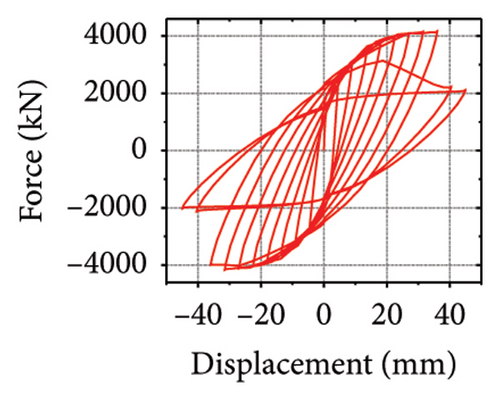
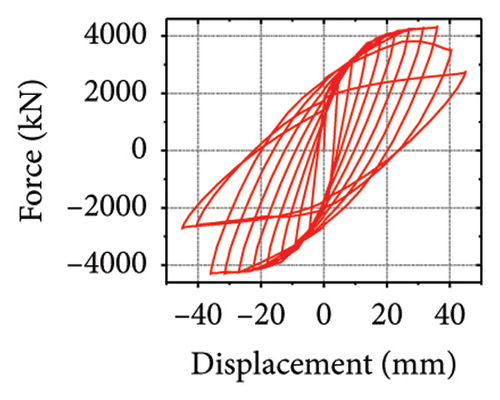
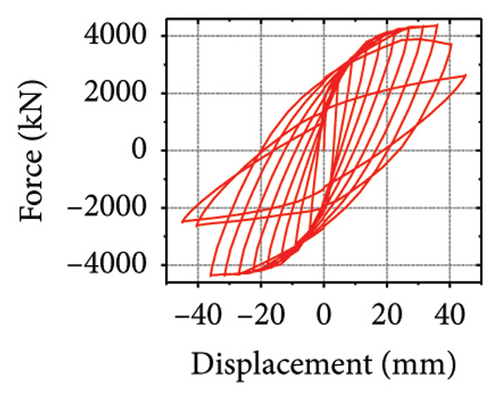
The energy-dissipation and stiffness ratios of each component are listed in Table 1. Different damper and constraint column combinations correspond to different restraint abilities, which reflect the energy-dissipation relationship between the constraint combination and the wall. When r_h−cdw was greater than 2%, the total energy dissipation of the damper and restraint column was larger than that of the wall body. When r_cdw was less than 2%, the total energy dissipation of the wall toe replaceable structure was higher; however, the energy dissipated by the damper was less than that of the corrugated plate. These results indicate that the energy-dissipation capacity of the damper was insufficient. Therefore, the stiffness ratios r_h−cdw and r_v−dw could be important indices for the energy-dissipation relationship of the replaceable shear wall.

Table 1. Stiffness values and simulation results.

Specimen	Stiffness (kN/mm)				Stiffness ratio (%)		Ultimate force (kN)	Energy dissipation (kJ)
Specimen	K_h−dam	K_v−dam	K_h−cd	K_wal	r_h−cdw	r_v−dw	P	E_con	E_dam	E_pla	E_col
2-1-3-dt6-15	48.9	273.9	4.5	487.7	0.9	56.2	724.0	10.0	95.9	48.6	8.2
2-1-3-dt12-15	98.3	546.8	4.7	487.7	1.0	112.1	1019.9	14.2	118.1	68.9	21.2
2-1-3-dt18-15	146.1	811.9	4.7	487.7	1.0	166.5	1206.1	17.4	101.2	95.9	32.2
2-1-3-dt24-15	191.8	1068.8	4.8	487.7	1.0	219.1	1284.6	19.2	84.3	118.0	40.0
1-1-3-dt6-15	48.9	273.9	4.5	1038.2	0.4	26.4	1677.8	35.3	160.6	196.7	10.7
1-1-3-dt12-15	98.3	546.8	4.7	1038.2	0.4	52.7	2069.8	41.7	179.9	281.8	26.4
1-1-3-dt18-15	146.1	811.9	4.7	1038.2	0.5	78.2	2251.7	46.6	125.4	355.7	39.9
1-1-3-dt24-15	191.8	1068.8	4.8	1038.2	0.5	102.9	2323.3	49.4	95.6	393.8	46.8
1-2-3-dt6-15	48.9	273.9	4.5	2110.4	0.2	13.0	3802.5	118.6	188.4	578.1	11.8
1-2-3-dt12-15	98.3	546.8	4.7	2110.4	0.2	25.9	4164.1	129.9	232.1	688.2	24.5
1-2-3-dt18-15	146.1	811.9	4.7	2110.4	0.2	38.5	4317.9	125.2	172.3	817.2	36.5
1-2-3-dt24-15	191.8	1068.8	4.8	2110.4	0.2	50.6	4381.2	133.3	83.0	868.5	47.7

Note: K_h−dam and K_v−dam are the horizontal and vertical stiffnesses, respectively. K_h−cd is the horizontal stiffness of the restraint combination. K_wal is the stiffness of the shear wall. r_h−cdw is the horizontal stiffness ratio of the entire wall. r_v−dw is the stiffness ratio of the damper to the wall. E_con, E_dam, E_pla, and E_col are the energy-dissipation values of the concrete, damper, steel plate, and restraint column, respectively.

4.2. Coupling Effect of the Corrugated Plate Thickness and Damper Web Thickness

The coupling effect of the corrugated plate and damper web thicknesses was investigated for a wall aspect ratio of 2:1. The damper web thicknesses were 6, 12, 18, and 24 mm, while the corrugated web thicknesses were 1, 2, 3, 4, and 5 mm. Under hysteretic loading, two failure modes occurred: damper failure and wall body failure, as shown in Figures 16 and 17, respectively. These two failure modes correspond to the following damper and wall body failure mechanisms:

(i)
Damper failure mechanism: The vertical stiffness and bearing capacity of the corrugated-web damper were insufficient. It was difficult to bear axial deformation at the toe, and the damage was concentrated on the damper. Therefore, the damper was the main factor limiting the seismic performance of the wall toe replaceable structure.
(ii)
Wall body failure mechanism: When the damper had sufficient vertical stiffness and bearing capacity, it hardly deformed. It was difficult for the energy-dissipation capacity of the damper to play a full role, as shown in Figure 17. In addition, this failure mode indicated that the damper failed before the wall; thus, the energy-dissipation relationship between the damper and wall was not ideal.

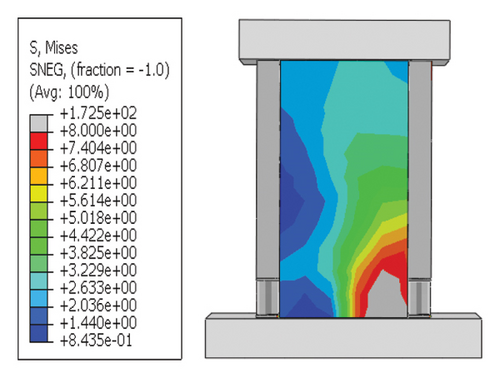
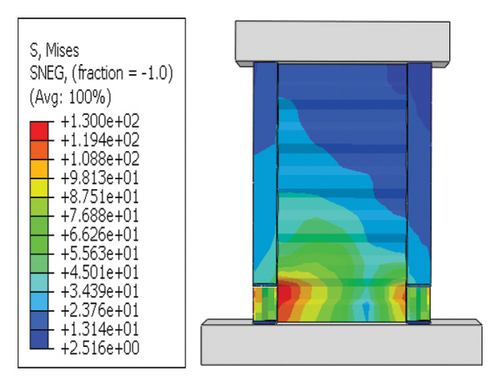
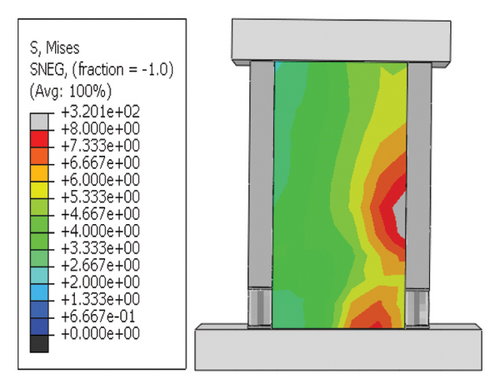
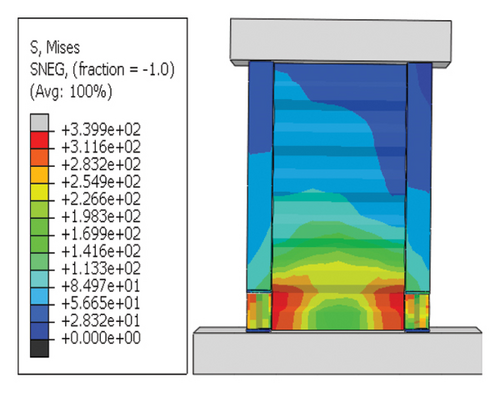
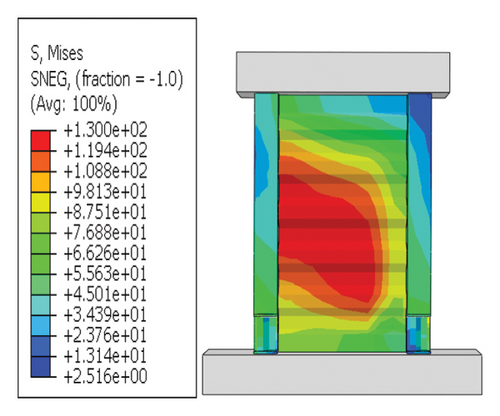
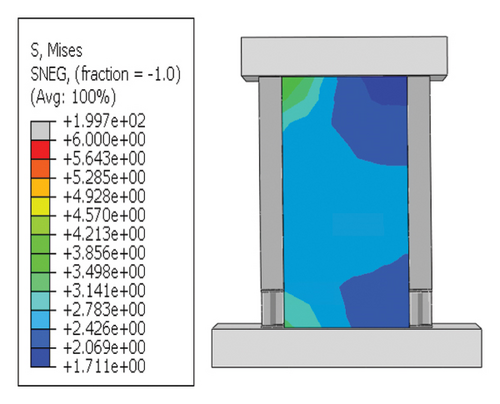
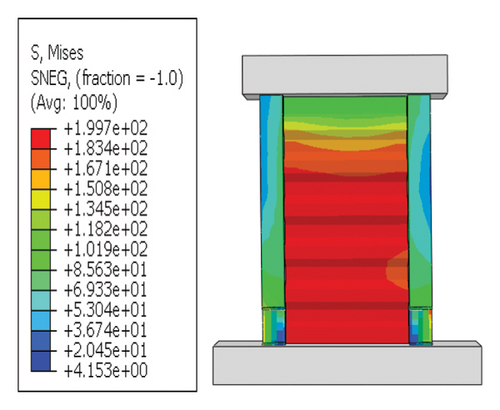
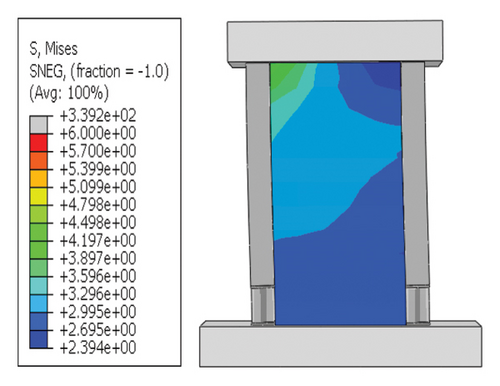
Next, the hysteretic curves of 12 specimens were investigated, as shown in Figure 18. (i) For specimens with a corrugated web thickness of 1 mm, when the damper web thickness increased from 6 to 24 mm, the peak load of the wall increased from 591.0 to 818.9 kN. (ii) For specimens with a damper web thickness of 6 mm, when the corrugated plate thickness increased from 1 to 5 mm, the peak load of the wall increased from 591.0 to 828.5 kN, indicating that the dampers limited the seismic performance of the wall. (iii) For specimens with a damper web thickness of 24 mm, when the corrugated plate thickness increased from 1 to 5 mm, the peak load of the wall increased from 818.9 to 1606.9 kN. Compared with specimen 2-1-DT6-15, the peak load increased by 171.9%. It could be concluded that the seismic performance of the damper was the main factor limiting the seismic performance efficiency of the replaceable shear wall, and that the corrugated plate thickness affected the ultimate seismic performance of the replaceable shear wall.

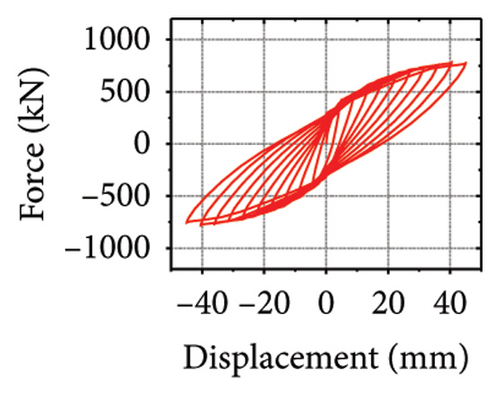
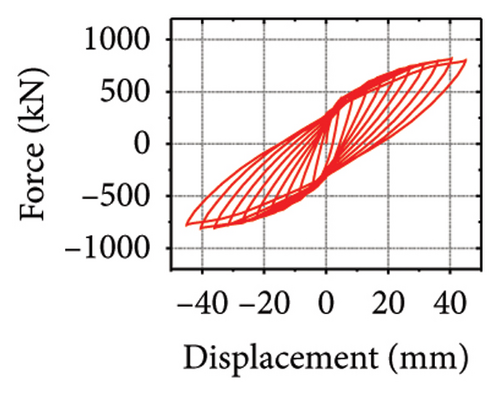
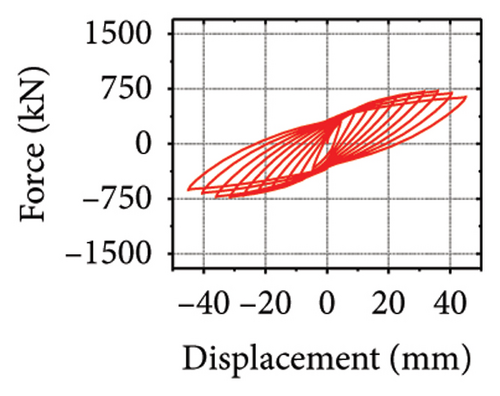
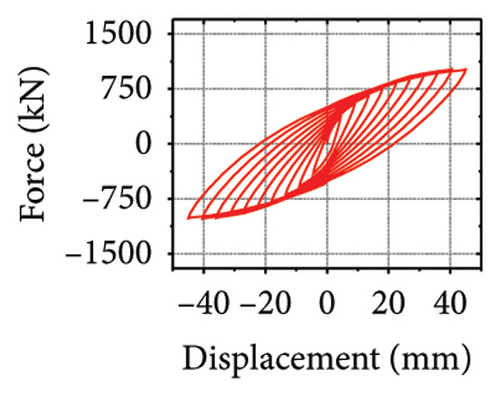
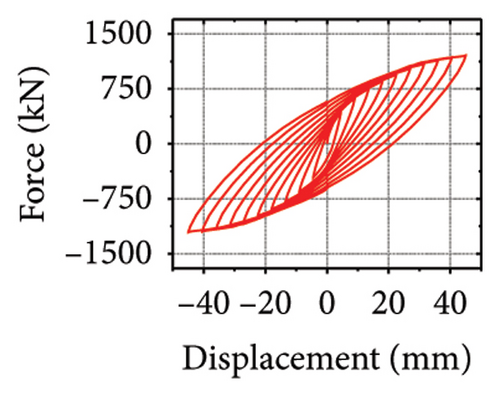
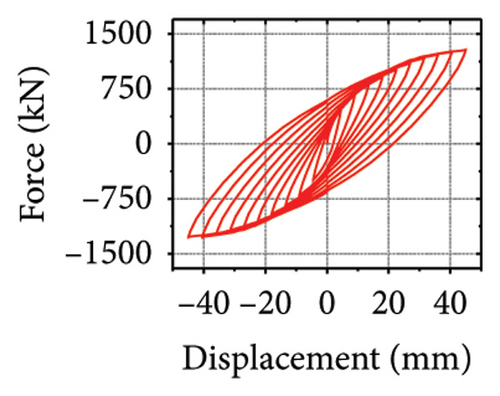
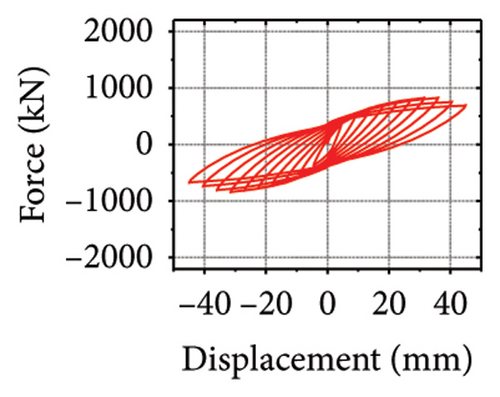
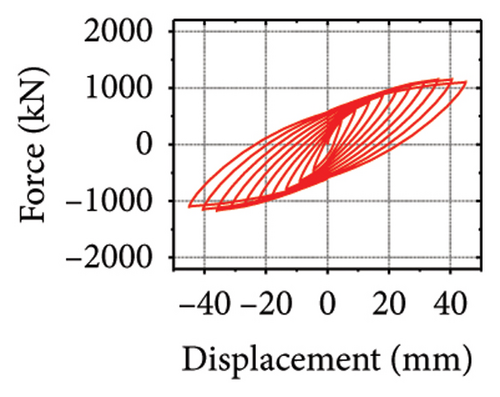
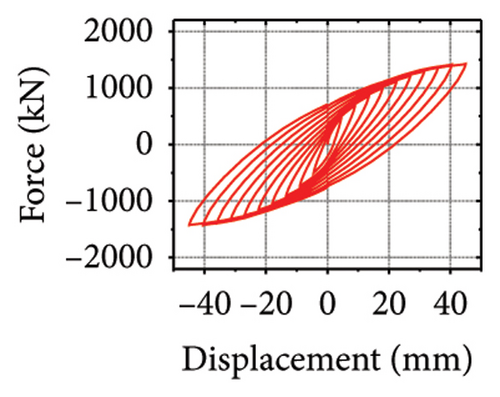
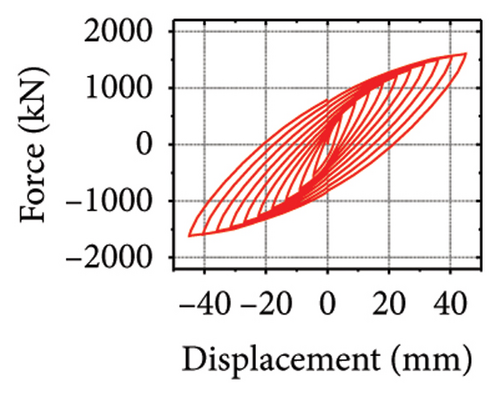
The specimen stiffness values and simulation results are summarized in Table 2. Taking the specimen with a corrugated plate thickness of 1 mm as an example, as the damper web thickness increased from 6 to 24 mm, the energy dissipation of the damper decreased from 59.7 to 39.7 kJ. However, the energy dissipation of the corrugated plate increased from 31.1 to 69.3 kJ. Moreover, the energy dissipation of the concrete increased from 13.8 to 21.7 kJ, indicating that the damper restrained the wall body. As the damper web thickness increased, the restraint was enhanced, which promoted the energy dissipation of the wall. However, the energy-dissipation efficiency of the damper decreased. Nevertheless, it is difficult to effectively protect the main structure from damage.

Table 2. Stiffness values and simulation results.

Specimen	Stiffness (kN/mm)				Stiffness ratio (%)		Ultimate force (kN)	Energy dissipation (kJ)
Specimen	K_h−dam	K_v−dam	K_h−cd	K_wal	r_h−cdw	r_v−dw	P	E_con	E_dam	E_pla	E_col
2-1-1-dt6-15	48.9	273.9	4.5	438.0	1.0	62.5	591.0	13.8	59.7	31.1	9.0
2-1-1-dt12-15	98.3	546.8	4.7	438.0	1.1	124.9	725.7	18.7	53.7	52.1	16.5
2-1-1-dt18-15	146.1	811.9	4.7	438.0	1.1	185.4	781.7	20.7	44.9	63.3	20.9
2-1-1-dt24-15	191.8	1068.8	4.8	438.0	1.1	244.0	818.9	21.7	39.7	69.3	24.1
2-1-3-dt6-15	48.9	273.9	4.5	487.7	0.9	56.2	724.0	10.0	95.9	48.6	8.2
2-1-3-dt12-15	98.3	546.8	4.7	487.7	1.0	112.1	1019.9	14.2	118.1	68.9	21.2
2-1-3-dt18-15	146.1	811.9	4.7	487.7	1.0	166.5	1206.1	17.4	101.2	95.9	32.2
2-1-3-dt24-15	191.8	1068.8	4.8	487.7	1.0	219.2	1284.6	19.2	84.3	118.0	40.0
2-1-5-dt6-15	48.9	273.9	4.5	529.8	0.8	51.7	828.5	9.3	103.0	70.9	9.2
2-1-5-dt12-15	98.3	546.8	4.7	529.8	0.9	103.2	1155.2	12.4	146.8	83.8	23.9
2-1-5-dt18-15	146.1	811.9	4.7	529.8	0.9	153.2	1427.9	14.7	145.0	101.5	40.0
2-1-5-dt24-15	191.8	1068.8	4.8	529.8	0.9	201.7	1606.9	16.4	128.6	120.4	55.3

Note: K_h−dam and K_v−dam are the horizontal and vertical stiffnesses, respectively. K_h−cd is the horizontal stiffness of the restraint combination. K_wal is the stiffness of the shear wall. r_h−cdw is the horizontal stiffness ratio of the entire wall. r_v−dw is the stiffness ratio of the damper to the wall. E_con, E_dam, E_pla, and E_col are the energy-dissipation values of the concrete, damper, steel plate, and restraint column, respectively.

4.3. Coupling Effect of the Constraint Column Thickness and Damper Web Thickness

Twelve specimens were constructed, and the main variation parameters were the damper web thickness and section size of the constraint column. The section thicknesses of the constrained columns were 10, 15, 20, 25, and 30 mm. Under hysteretic force, three failure modes exist, as shown in Figure 19. These failure modes are described next.

(i)
Damper failure mode: When the stiffness of the damper is insufficient, the deformation is mainly concentrated on the damper. However, the damper cannot provide sufficient restraint. The energy dissipation of the structure is not ideal; however, under this failure mode, damage is concentrated on the damper, as shown in Figure 19(a).
(ii)
Comprehensive failure mode: As the damper web thickness increases, the energy dissipation of the damper further improves, and the wall body deformation is limited by the constraint combination. Under this energy-dissipation mechanism, the structure can simultaneously achieve the goals of damage concentration and energy dissipation improvement, as shown in Figure 19(b).
(iii)
Constraint column failure mode: When the shear stiffness of the damper is significantly larger than that of the constraint column, the damper is hardly deformed, as shown in Figure 19(c). This failure mode does not affect the energy-dissipation capacity of the damper, and damage is not concentrated on the damper. This situation should be avoided in the design phase.

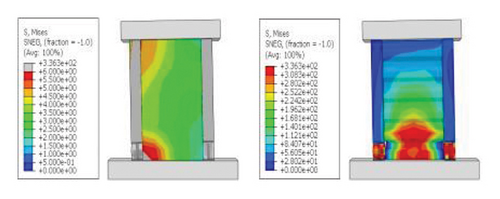
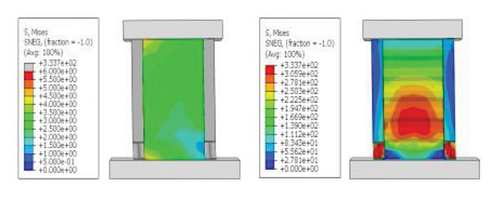
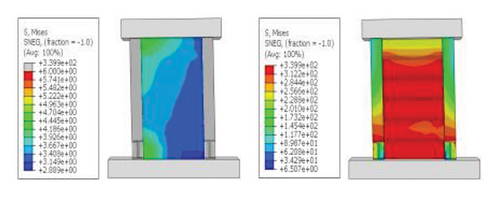
The hysteresis curves of the specimens are shown in Figure 20. For a damper web thickness of 6 mm, the peak load of the replaceable shear wall was not significantly improved by changing the cross-sectional area of the constrained column. For example, the peak loads of specimens 2-1-3-dt6-10 and 2-1-3-dt6-30 were 721.1 and 755.0 kN, respectively, indicating that the seismic performance of the damper was not ideal. Deformation was fully provided by the damper. For damper web thicknesses greater than 12 mm, the peak load changed to a certain extent as the constraint column section size increased, which reflects an improvement in the synergistic effect between the damper and the constraint column. For all specimens, part of the hysteretic curves exhibit a descending phase. The main reason for this could be that the damper experienced severe buckling failure, resulting in a gradual loss of lateral load resistance.

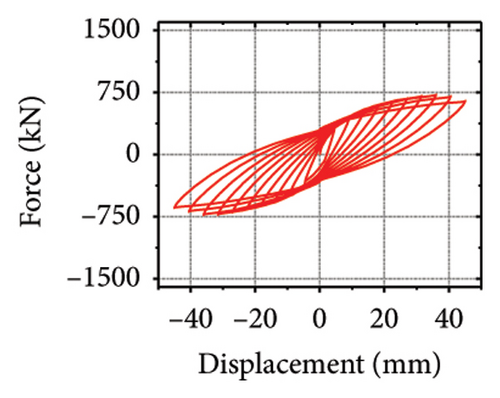
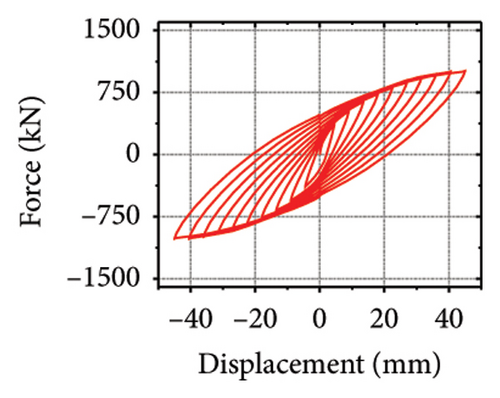
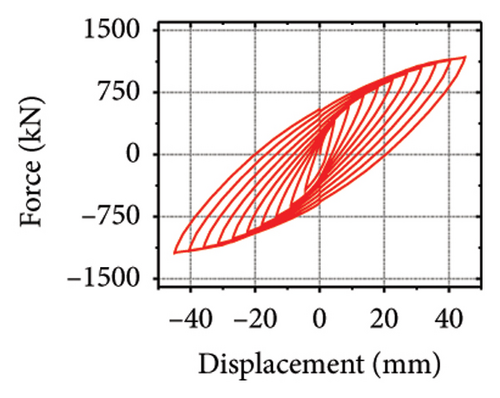
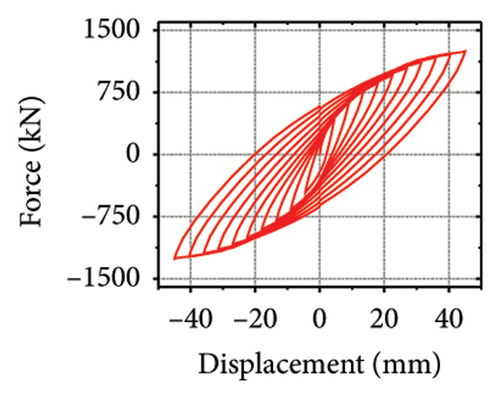
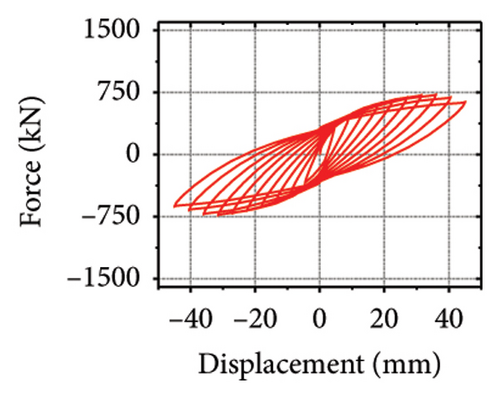
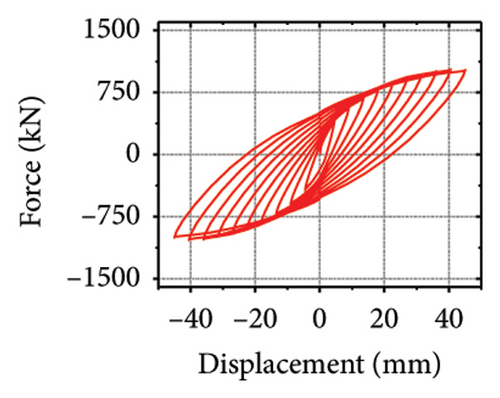
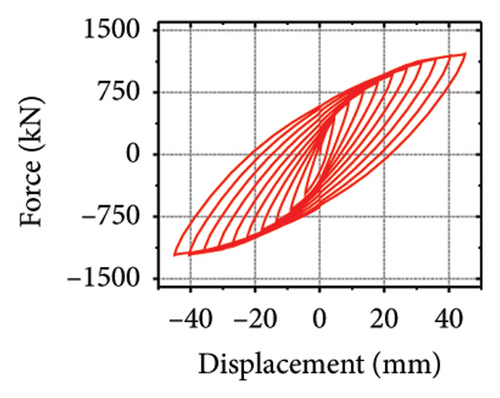
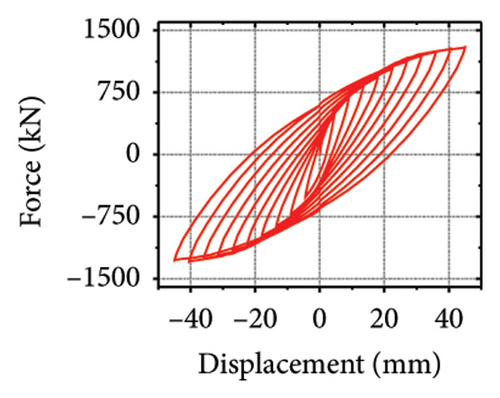
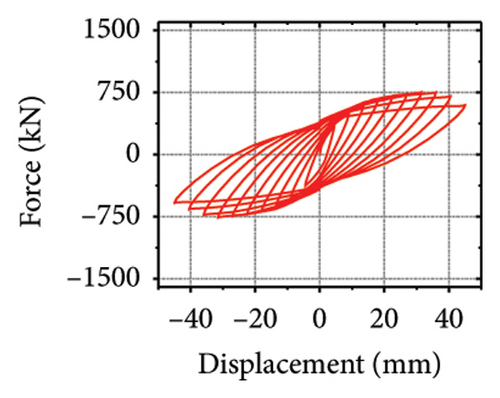
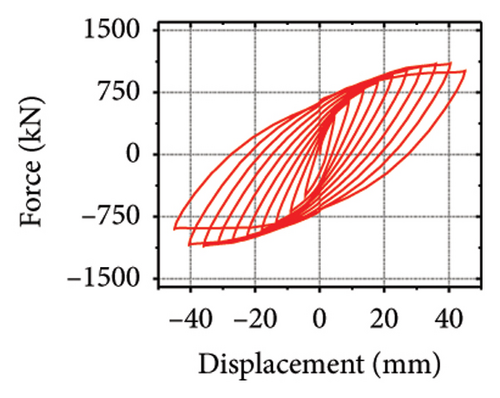
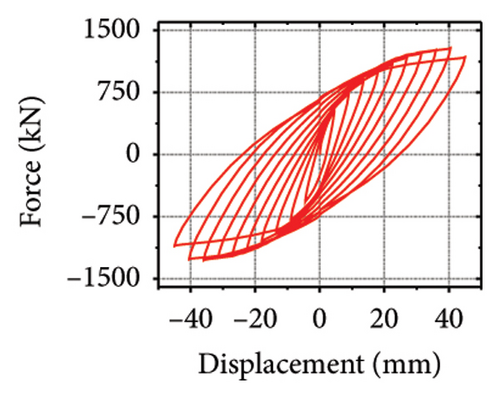
The stiffness ratios and calculated values for all specimens are listed in Table 3. Combined with the failure modes described above, the stiffness relationship between the damper and constraint column can be summarized. The structural features corresponding to different horizontal stiffness ratios are proposed next. Let us define r_h−cd as the lateral stiffness ratio of the constrained column to that of the damper. When r_h−cd is greater than 5%, the constraint column has sufficient constraint capacity and almost no energy dissipation. When r_h−cd is in the range of 2%–5%, the damper and constraint column are both deformed, and the energy dissipation is mainly concentrated on the damper. When r_h−cd is less than 2%, the damper stiffness is high, and the restraint capacity of the column is far from sufficient. The damper is barely deformed, and a pronounced bending deformation occurs in the constraint column.

Table 3. Stiffness values and simulation results.

Specimen	Stiffness (kN/mm)				Stiffness ratio (%)		Ultimate force (kN)	Energy dissipation (kJ)
Specimen	K_h−dam	K_v−col	K_h−cd	K_wal	r_h−cd	r_h−cdw	P	E_con	E_dam	E_pla	E_col
2-1-3-dt6-10	48.9	3.5	3.3	487.7	7.2	0.7	721.1	10.2	89.1	47.0	11.6
2-1-3-dt12-10	98.3	3.5	3.4	487.7	3.6	0.7	1010.0	14.2	102.2	63.7	28.6
2-1-3-dt18-10	146.1	3.5	3.4	487.7	2.4	0.7	1178.4	16.7	84.9	83.6	44.1
2-1-3-dt24-10	191.8	3.5	3.4	487.7	1.8	0.7	1249.6	18.0	70.3	98.9	55.9
2-1-3-dt6-20	48.9	6.1	5.4	487.7	12.5	1.1	725.1	9.8	99.3	49.2	6.3
2-1-3-dt12-20	98.3	6.1	5.7	487.7	6.2	1.2	1025.6	14.2	126.6	71.2	17.6
2-1-3-dt18-20	146.1	6.1	5.9	487.7	4.2	1.2	1217.8	17.6	110.1	101.4	27.4
2-1-3-dt24-20	191.8	6.1	5.9	487.7	3.2	1.2	1298.6	19.6	92.0	126.6	34.3
2-1-3-dt6-30	48.9	8.0	6.9	487.7	16.4	1.4	755.0	10.0	140.5	52.7	3.7
2-1-3-dt12-30	98.3	8.0	7.4	487.7	8.1	1.5	1102.5	15.8	180.2	91.9	14.7
2-1-3-dt18-30	146.1	8.0	7.6	487.7	5.5	1.6	1287.4	20.1	142.0	140.3	25.3
2-1-3-dt24-30	191.8	8.0	7.7	487.7	4.2	1.6	1373.7	23.0	108.1	179.5	32.7

Note: K_h−dam and K_v−col are the horizontal and vertical stiffnesses, respectively. K_h−cd is the horizontal stiffness of the restraint combination. K_wal is the stiffness of the shear wall. r_h−cd is the stiffness ratio of the restraint column to that of the damper. r_h−cdw is the horizontal stiffness ratio of the entire wall. E_con, E_dam, E_pla, and E_col are the energy-dissipation values of the concrete, damper, steel plate, and restraint column, respectively.

5. Interaction Relationship Analysis

5.1. Coupling Effect of the Wall Aspect Ratio and Damper Web Thickness

The damper and shear wall combination formed a double energy-dissipation defense line in which the damper failed before the wall body. The damper and wall body worked together successfully during the elastic stage. After entering the plastic phase, the stress on the replaceable wall is concentrated on the damper, which dissipates energy via plastic deformation to protect the wall body. The functional recoverability of the shear wall with replaceable dampers was significantly improved compared to that of traditional shear wall structures. However, under seismic action, the damper and wall body exhibit two distinct force forms, and the damper mainly relies on tensile and compressive deformations for plastic energy dissipation. When the damper is damaged or fails, the constraint combination loses its ability to restrain. Subsequently, the bearing capacity of the wall body is significantly reduced, and the wall body dissipates energy through bending and shear deformation. It could be concluded that the wall did not fail immediately even if the plastic hinge was generated at the corner of the wall.

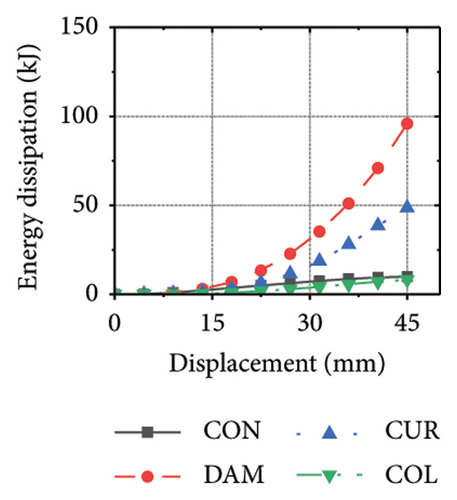
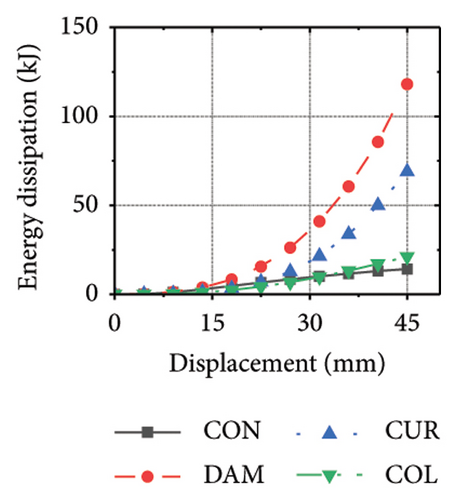
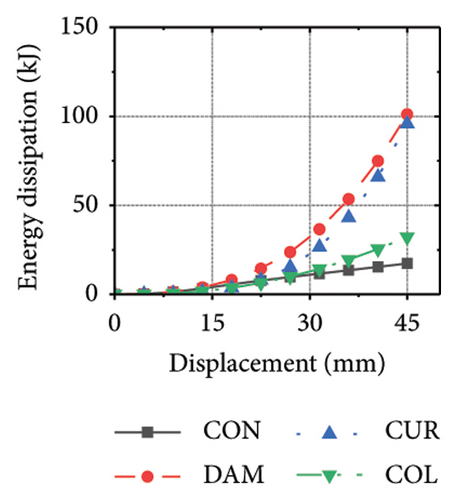
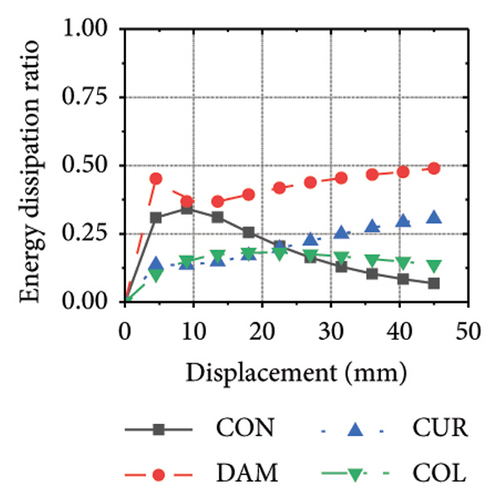
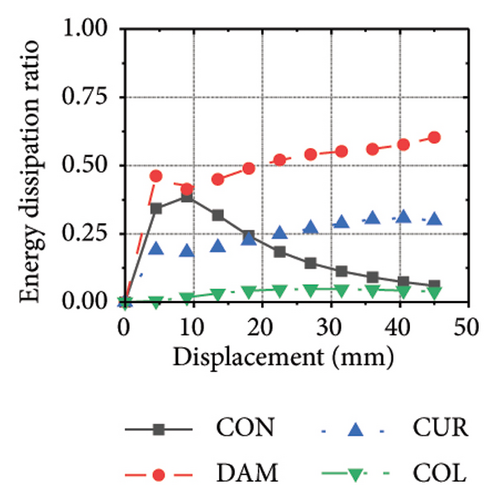
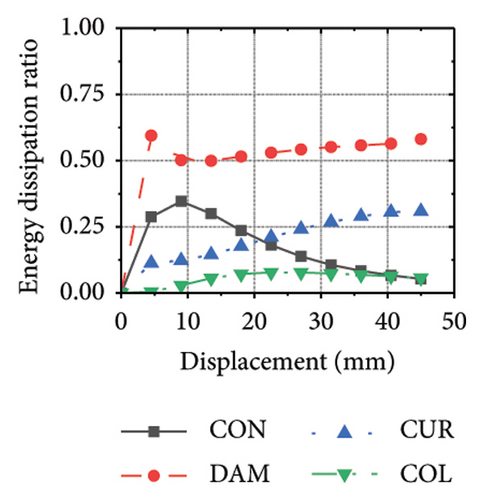
Figure 21 shows the energy-dissipation process of the specimens under different wall aspect ratios and damper web thicknesses. Based on these results, the following conclusions can be drawn. (i) In specimens with the same aspect ratio, the energy dissipation of concrete was almost unaffected by the seismic performance of the damper, whereas the energy dissipation of the corrugated plate changed as the restraint capacity of the damper changed. For example, for an aspect ratio of 1:2, as the damper web thickness increased from 6 to 24 mm, the energy dissipation of the corrugated plate increased from 578.1 to 868.5 kJ. (ii) When the damper web thickness was less than 12 mm, the energy dissipation continued to increase. When the dissipating-plate thickness was greater than 12 mm, the energy dissipation of the damper began to decrease. (iii) For a damper web thickness of 30 mm, the four main components exhibited obvious energy dissipation, where the constraint column exhibited lateral deformation owing to its insufficient restraint ability. (iv) Conversely, the wall aspect ratio had a significant impact on the energy-dissipation ratio between the damper and corrugated plate. When the aspect ratio was low, the energy dissipation of the damper was significantly lower than that of the corrugated plate, indicating that it was difficult for the damper to protect the wall from damage.

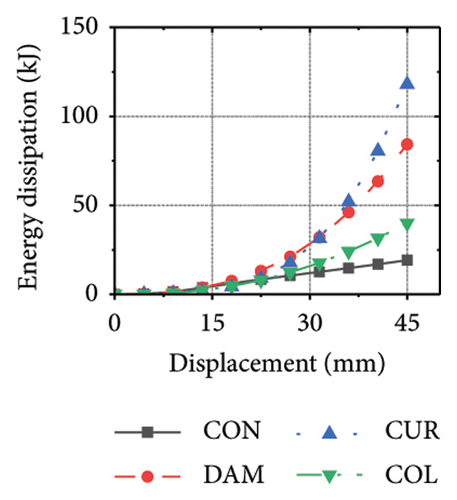
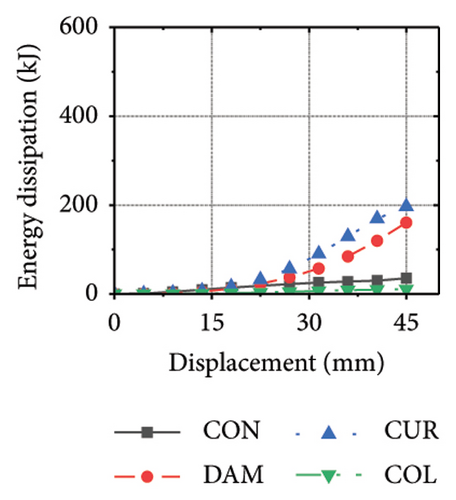
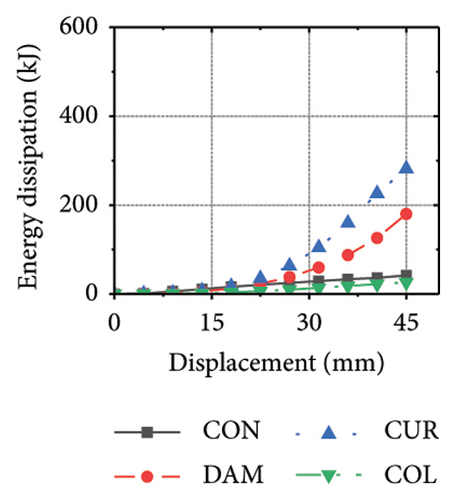
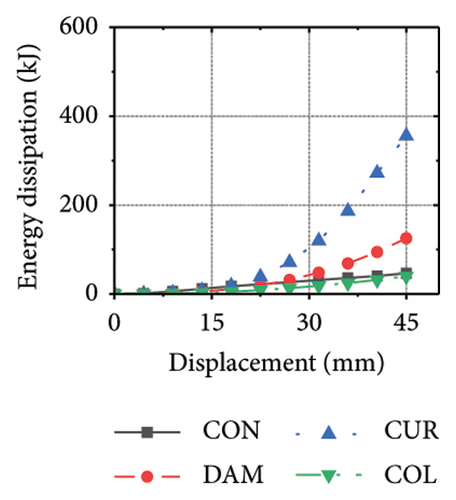
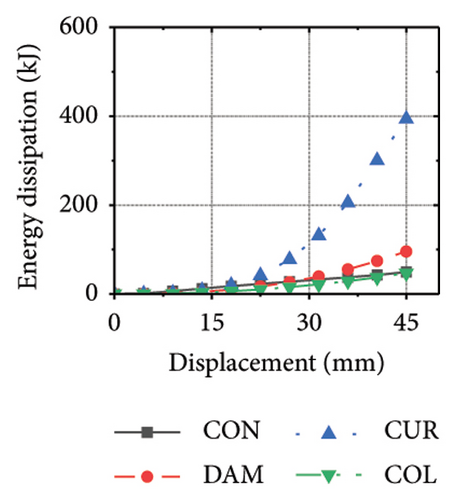
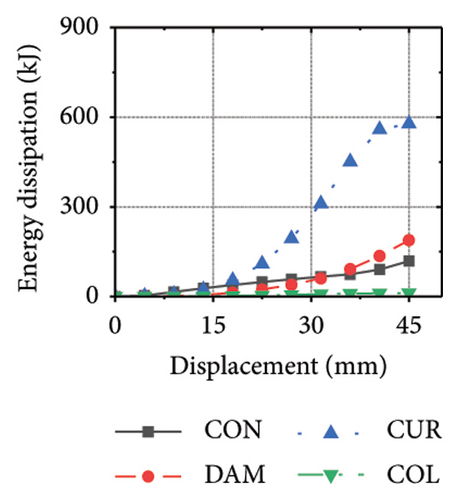
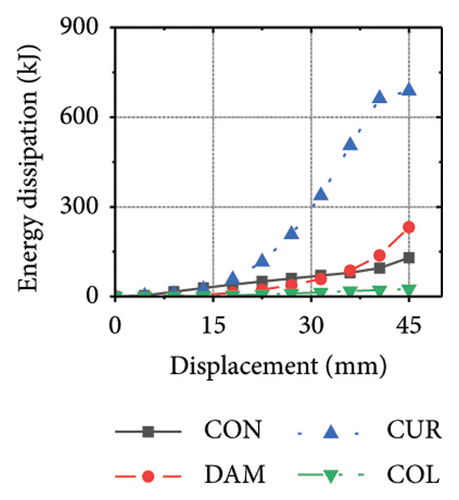
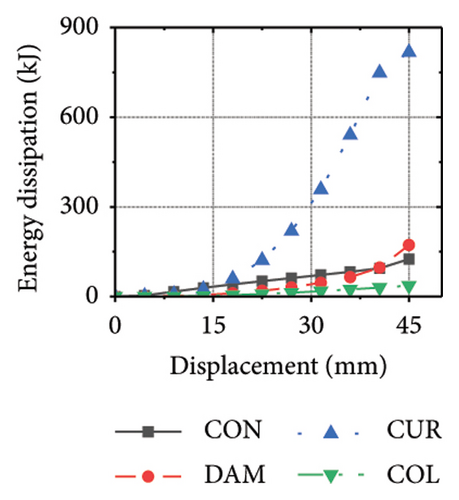
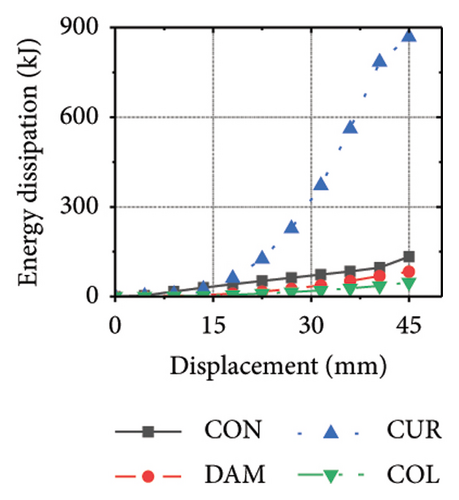
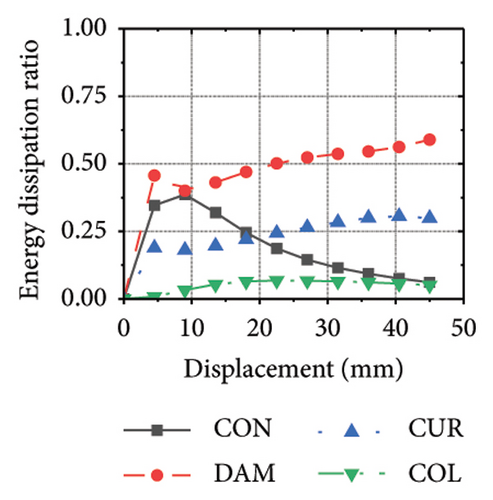
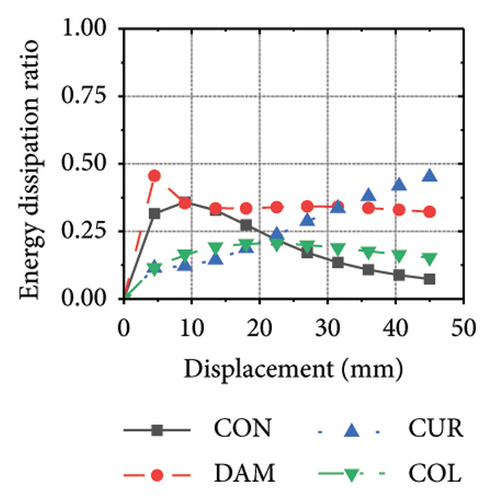
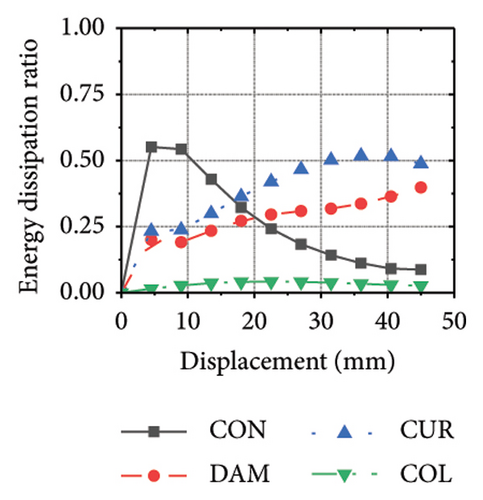
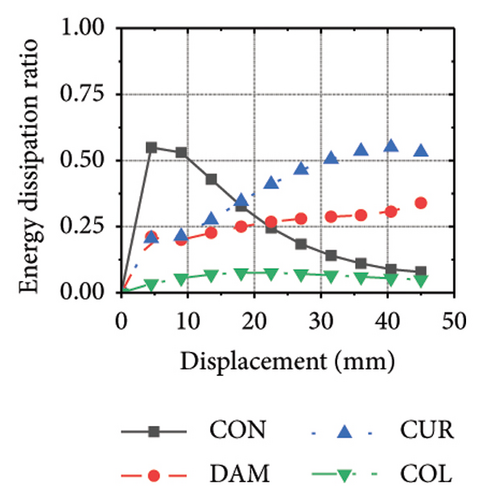
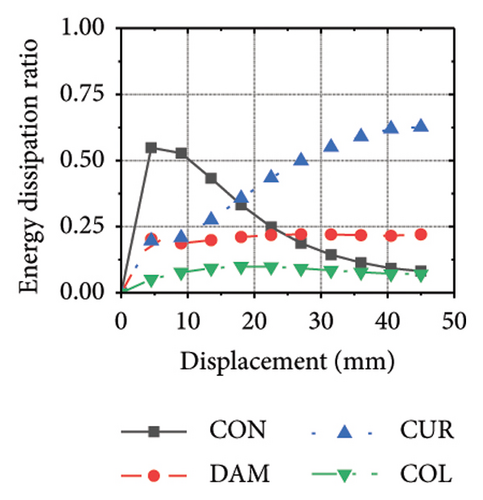
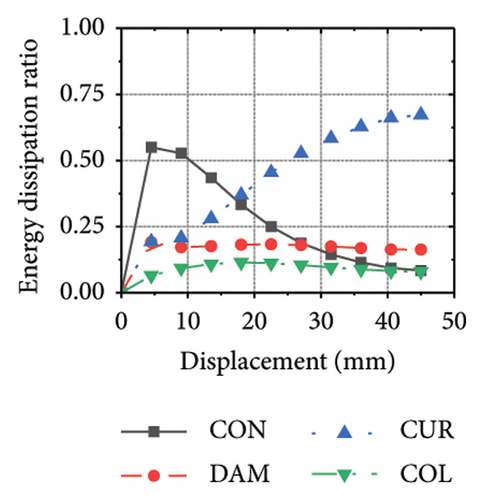
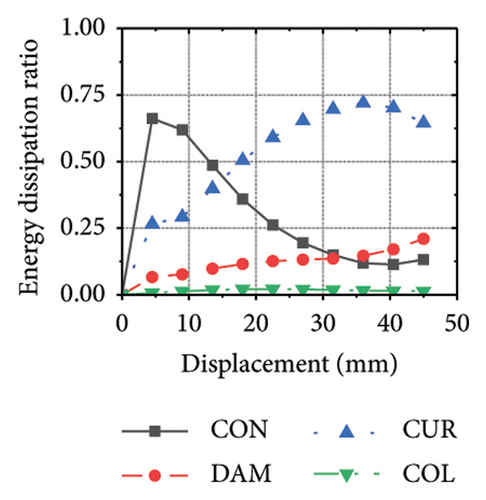
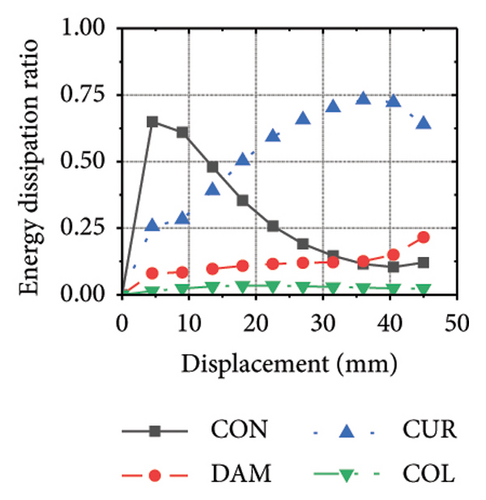
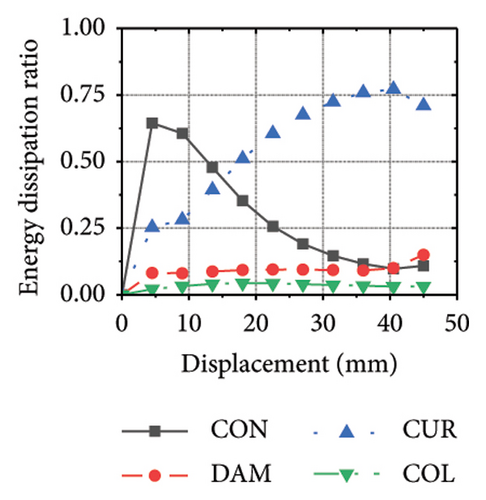
The energy-dissipation process of the specimens was converted into a proportional energy-dissipation process, as shown in Figure 22. As the damper was made of mild steel, it entered the plastic energy-dissipation phase at an early stage in specimens with high aspect ratios. During the early loading stages, the damper and concrete primarily contributed to the energy dissipation of the RSW. When the damper web thickness was small, a large deformation occurred during the energy dissipation of the corrugated plate, leading to a significant reduction in the energy dissipation of the damper. However, for specimens with low wall aspect ratios, the energy-dissipation ratio was unsatisfactory because the toe damper was difficult to deform. The main objective is to increase the energy-dissipation ratio of the damper throughout the loading process. The damper of specimen 1-2-dt24-15 had an energy-dissipation ratio of 8.1%, which was the lowest among all specimens. The embedded corrugated plate exhibited an energy-dissipation ratio of 79.6%. It could be inferred that the damper design parameter was not justified, which made it difficult to achieve the functional restorability of the wall.

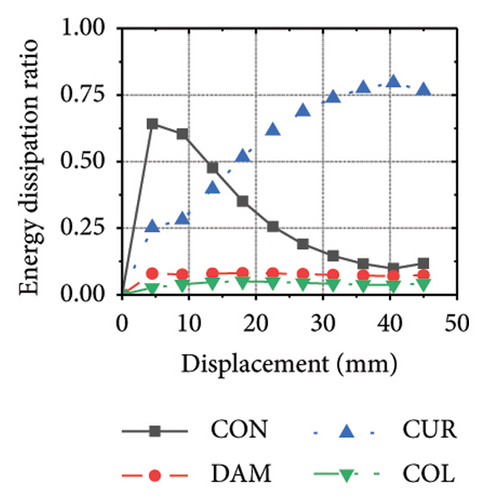
5.2. Coupling Effect of the Corrugated Plate Thickness and Damper Web Thickness

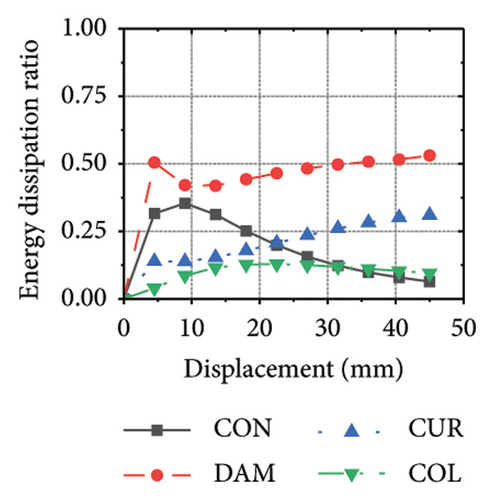
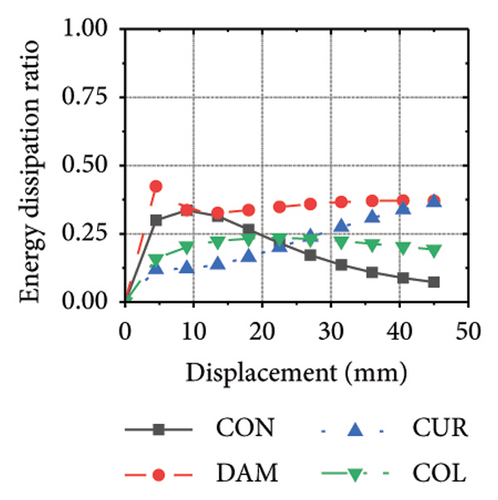
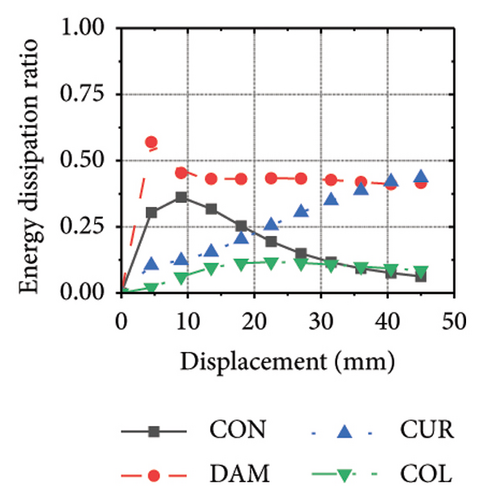
This section focuses on the coupling effect of the corrugated plate and damper web thicknesses on the energy-dissipation process of the replaceable shear wall, as shown in Figure 23. For the specimen with a corrugated plate thickness of 1 mm, when the damper web thickness was 6 mm, the final energy-dissipation values of the corrugated plate and damper were 31.1 and 59.7 kJ, respectively. When the damper web thickness increased to 12 mm, the final energy dissipation of the corrugated plate and damper were 52.1 and 53.7 kJ, respectively. This indicates that the damper provides the necessary restraint for the deformation of the corrugated plate. The 6 mm-thick damper web was insufficient to fully restrain the 1 mm corrugated plate. During the loading process, the damper prematurely underwent a large deformation and lost its ability to restrain, making it difficult for the corrugated plate to fully exploit its energy-dissipation capacity. The main factor limiting the energy-dissipation capacity of this type of the replaceable shear wall is the seismic performance of the damper. As the damper web cross-sectional thickness continued to increase, the energy-dissipation values of the corrugated plate and damper for specimen 2-1-1-dt24-15 were 69.3 and 39.7 kJ, respectively. The energy dissipation of the corrugated plate and damper increased further; however, that of the damper would decrease, indicating that the seismic performance of the damper was not fully developed. It was also difficult to concentrate the stress on the damper; in other words, the energy-dissipation interaction relationship was not ideal.

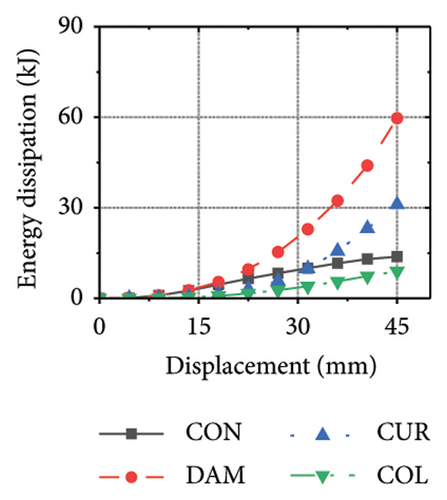
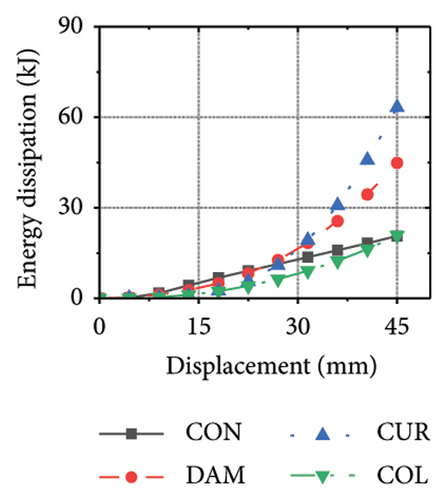
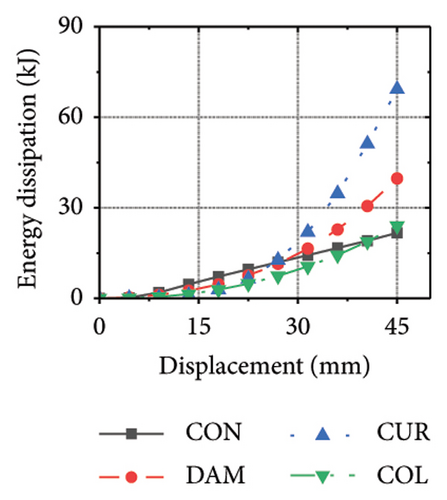
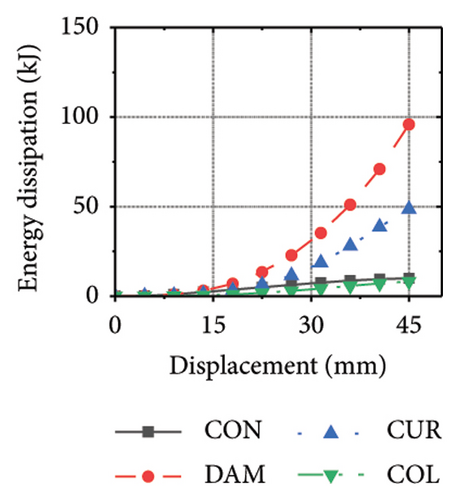
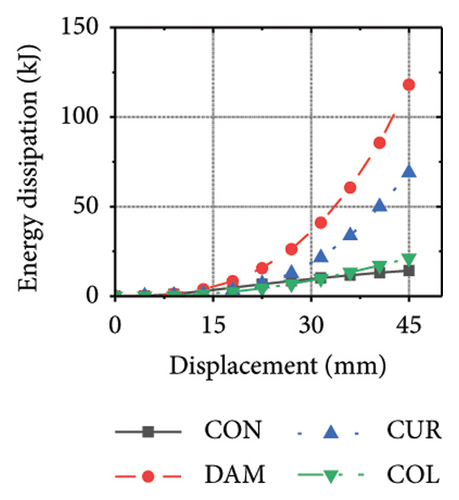
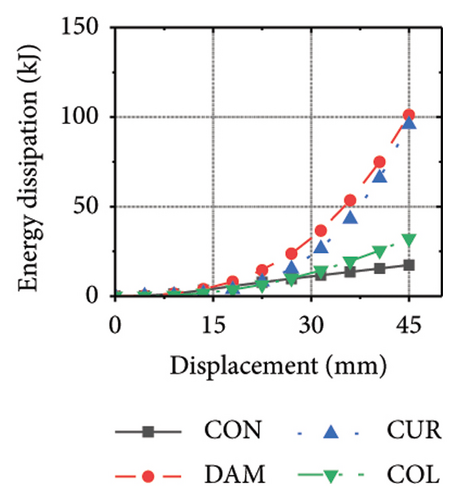
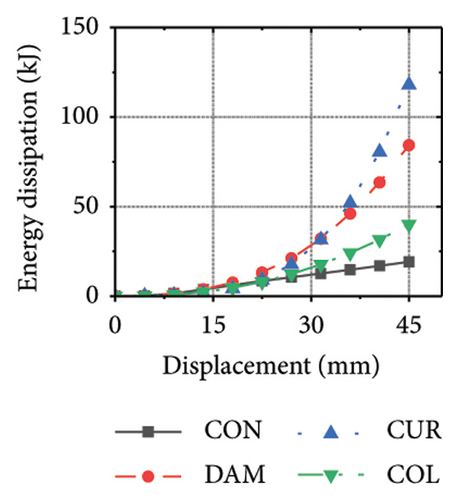
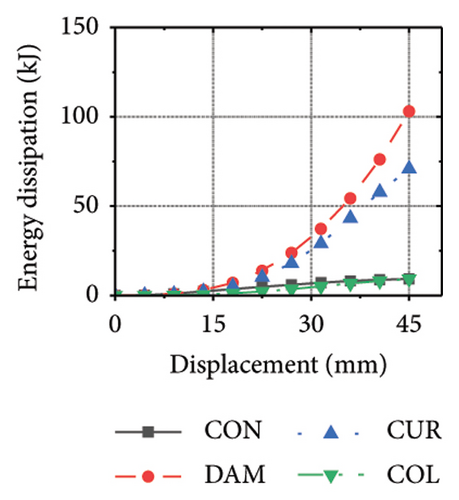
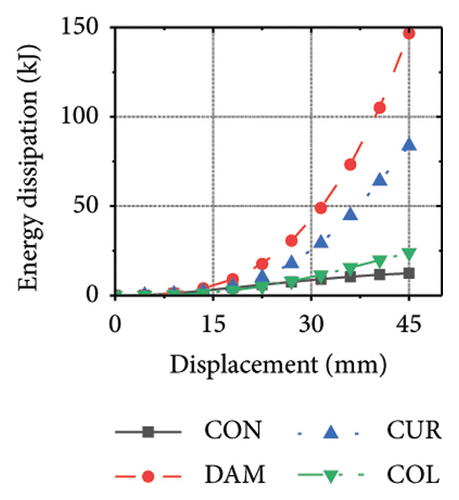
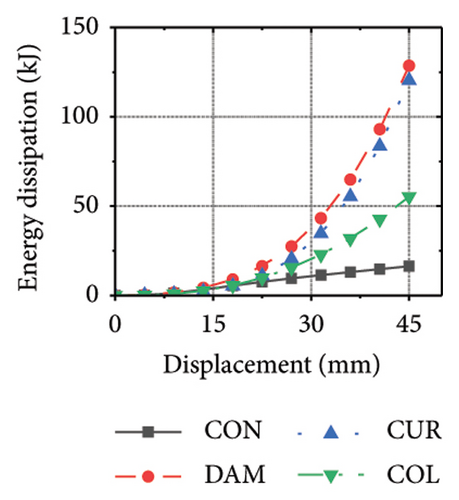
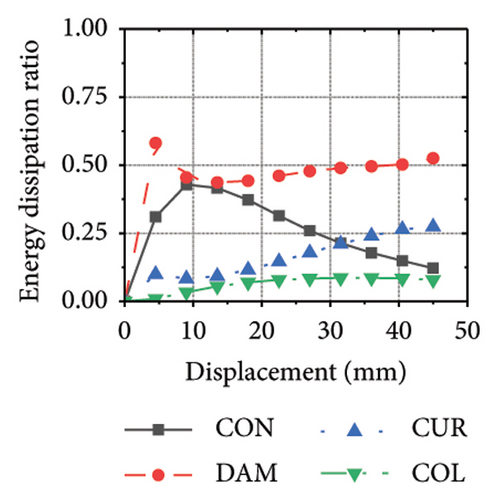
Figure 24 shows the coupling effect of the corrugated plate and damper web thicknesses on the energy-dissipation ratio. For corrugated plates of the same thickness, the energy-dissipation ratio increased with the damper web thickness during the loading process. By contrast, the energy-dissipation ratio of the damper decreased with an improvement in its seismic performance. For example, the final damper energy-dissipation ratio for specimen 2-1-1-dt6-15 was 52.6%, while that for specimen 2-1-1-dt24-15 was 25.7%. We found that damper web thickness changes are positively correlated with the energy-dissipation ratio of the corrugated plate and negatively correlated with that of the damper itself. To fully exploit the energy-dissipation capacity of the wall body, it is necessary to improve the restraint capacity of the damper. However, this makes it difficult for the damper to achieve the ideal energy dissipation.

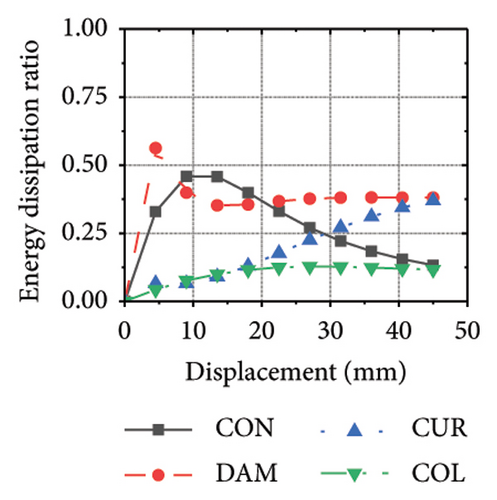
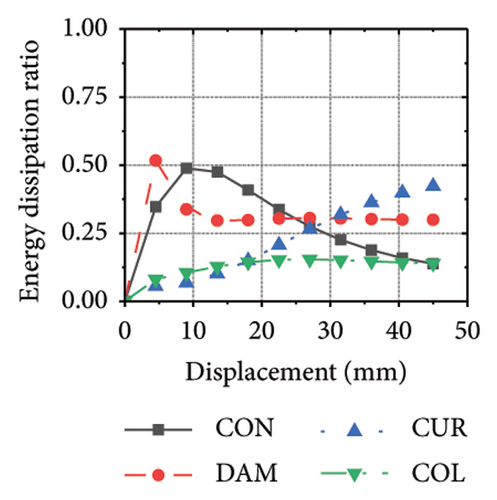
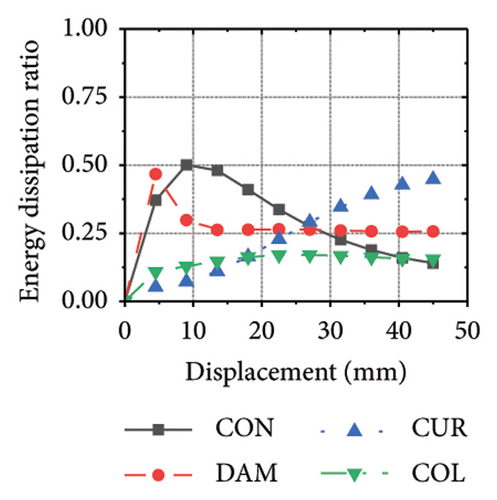
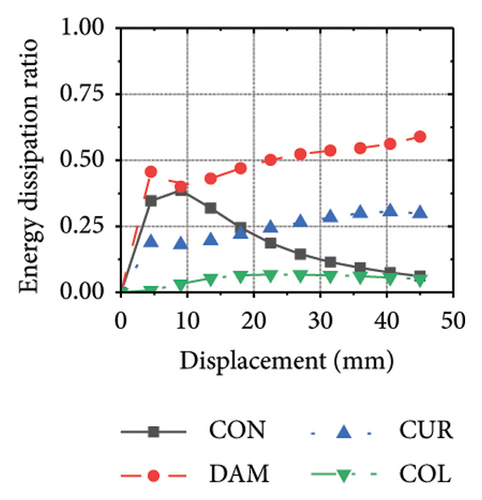
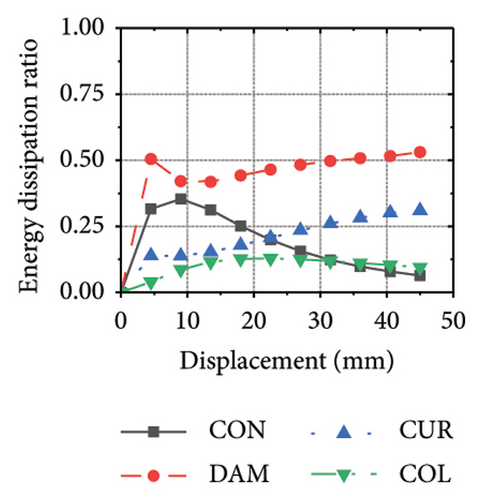
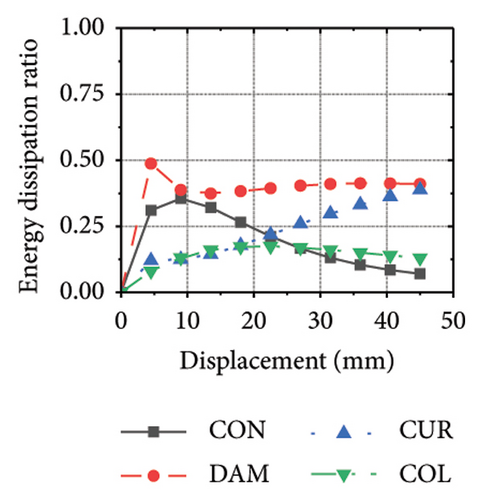
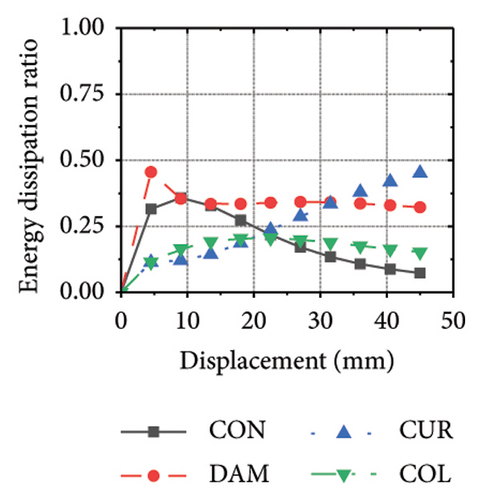
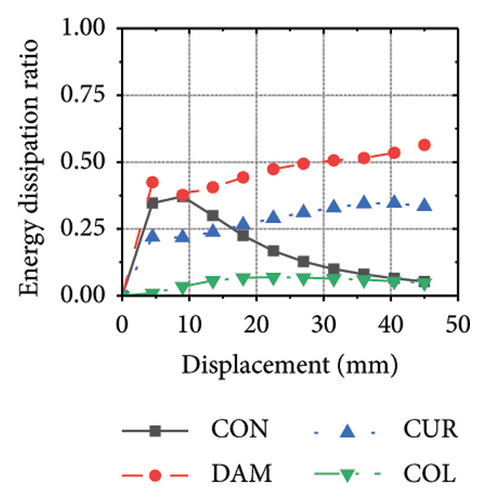
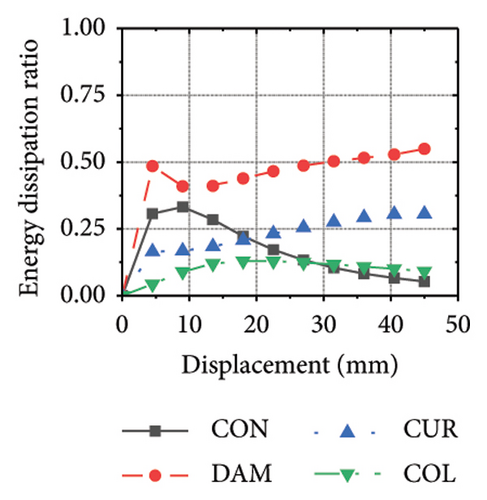
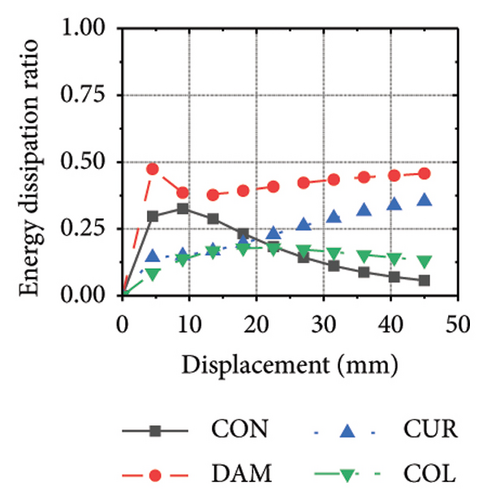
5.3. Coupling Effect of the Constraint Column Thickness and Damper Web Thickness

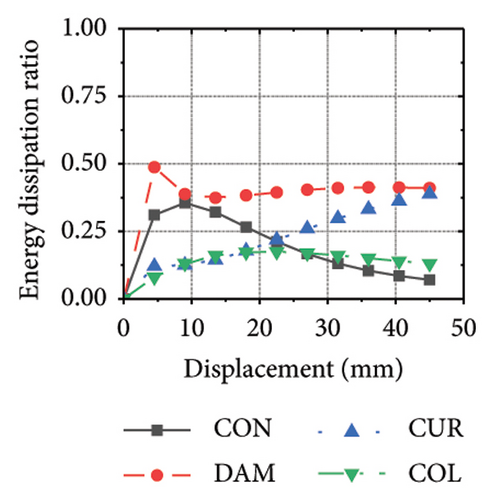
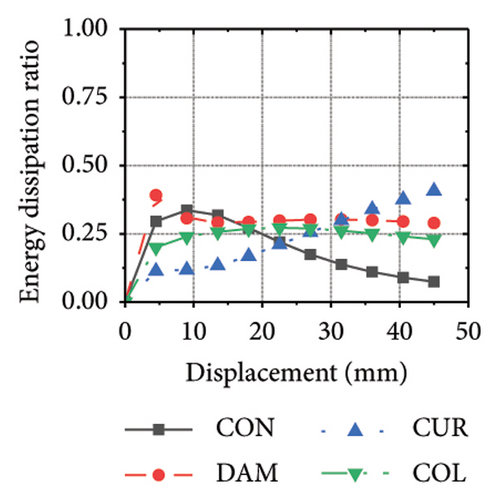
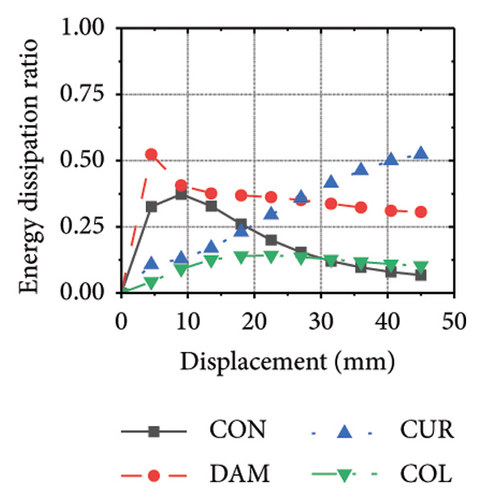
Figure 25 shows the energy-dissipation process curves for each specimen component for different constraint column and damper web thickness combinations. Because the main function of the constraint column in the replaceable shear wall is to facilitate the deformation and energy dissipation of the wall body and damper, it is not necessary to concentrate the damage on the constraint column, and it should have sufficient restraint capability. Based on the energy-dissipation results, the constraint column affected the energy dissipation of the corrugated plate and damper. For example, the energy-dissipation values of the corrugated plate for specimens 2-1-3-dt24-10 and 2-1-3-dt24-30 were 98.9 and 179.5 kJ, respectively, which is only a slight increase. The energy-dissipation values of the damper were 70.3 and 108.1 kJ, respectively, an increase of only 37.8 kJ. It should be noted that the energy dissipation of the corrugated plate increased because the seismic performance of the constraint column was insufficient to restrain the deformation of the damper and corrugated plate. In other words, the constraint column limited the energy dissipation of the replaceable shear wall; therefore, increasing the cross-sectional area of the constraint column could effectively improve the structural energy dissipation. Conversely, for specimens 2-1-3-dt6-10 and 2-1-3-dt6-30, the main factor limiting the energy dissipation of the wall was the damper; therefore, it was difficult to effectively improve the energy dissipation of the main wall by increasing the cross-sectional size of the restraint column (the energy-dissipation values were 47.0 and 52.7 kJ, respectively).

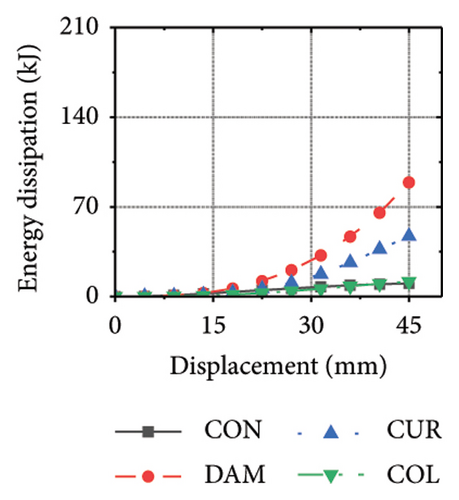
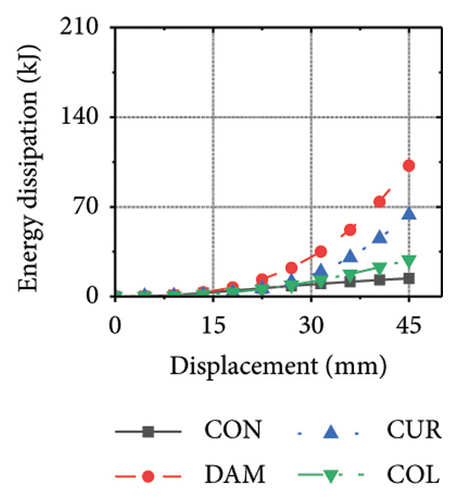
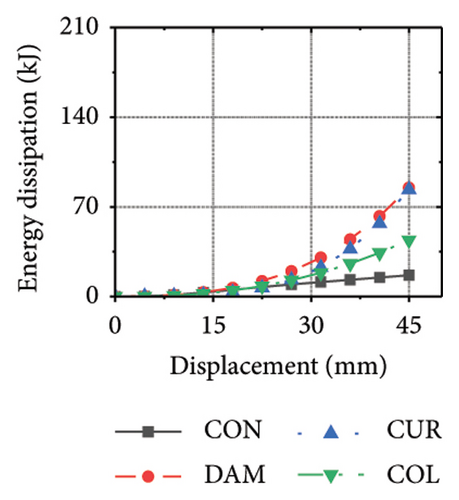
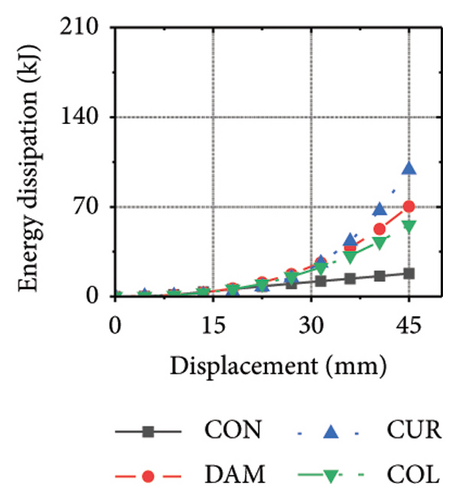
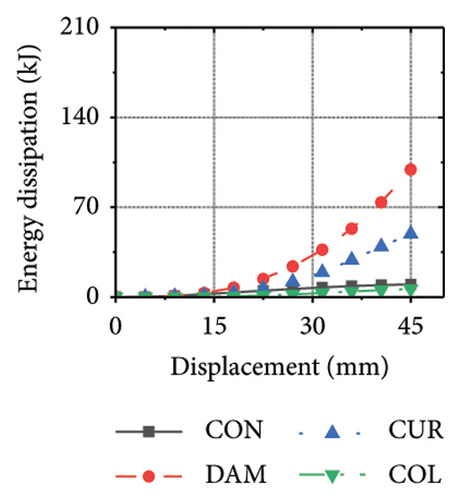
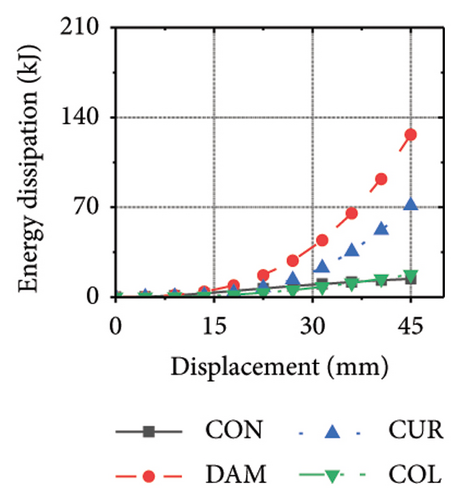
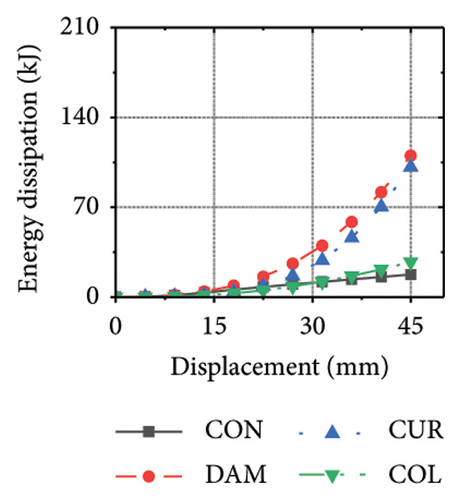
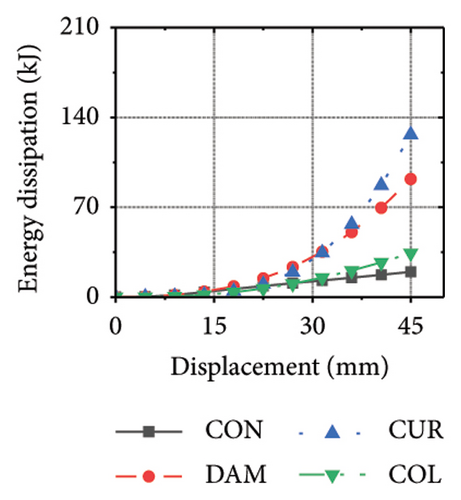
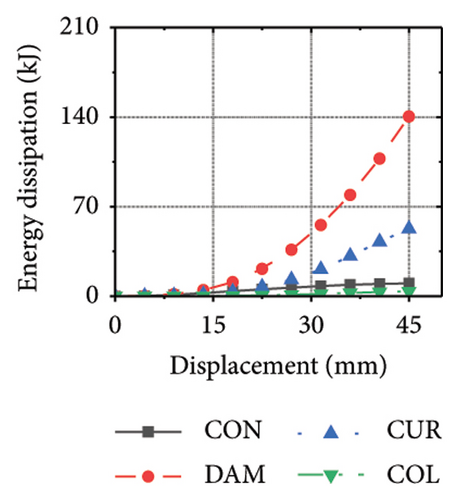
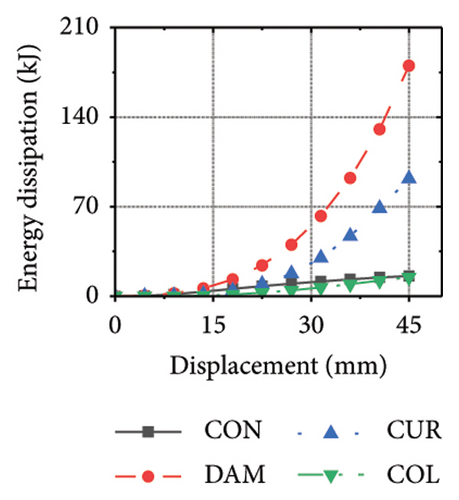
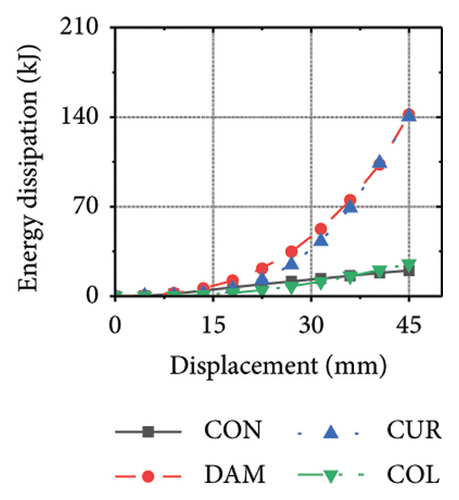
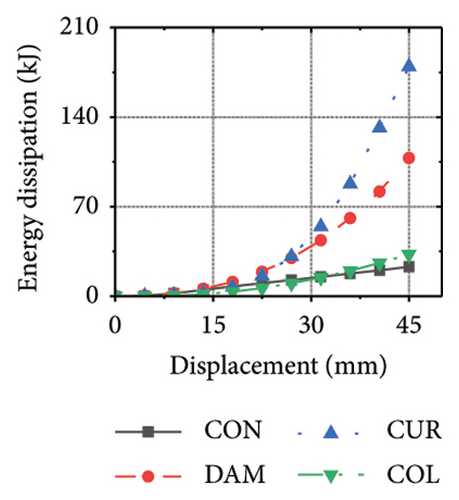
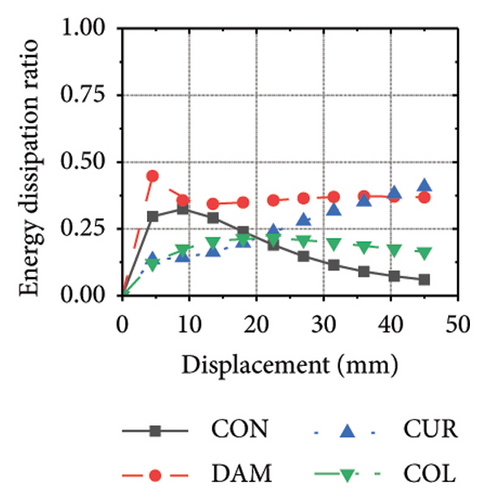
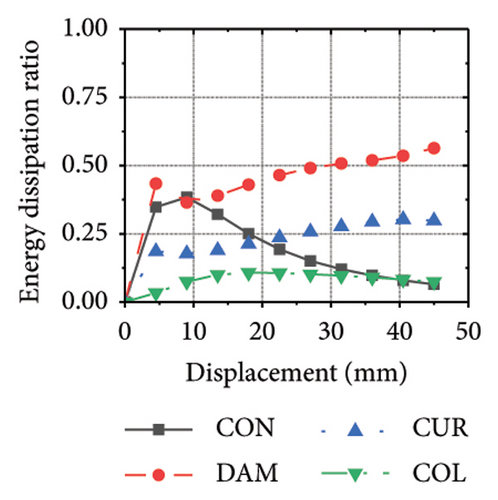
Figure 26 shows the energy-dissipation ratio of each specimen component for different constraint column and damper web thickness combinations. According to previous studies, when the constraint column is constant, the energy-dissipation ratio of the damper does not increase with an increase in damper web thickness. The main reason for this is that the damper stiffness increased while the constraint column remained constant, resulting in a shift in the deformation from the damper to the constraint column. In this situation, it is difficult for a damper to fully utilize its energy-dissipation capacity.

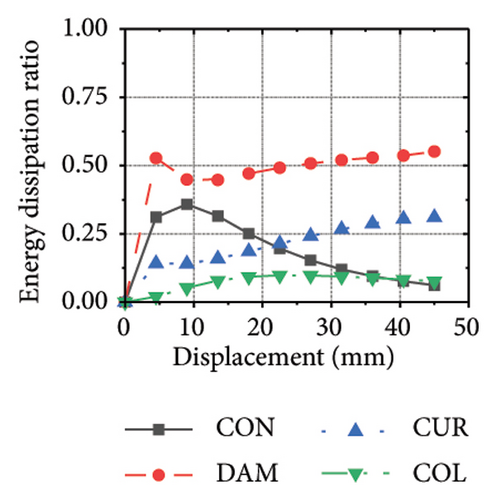
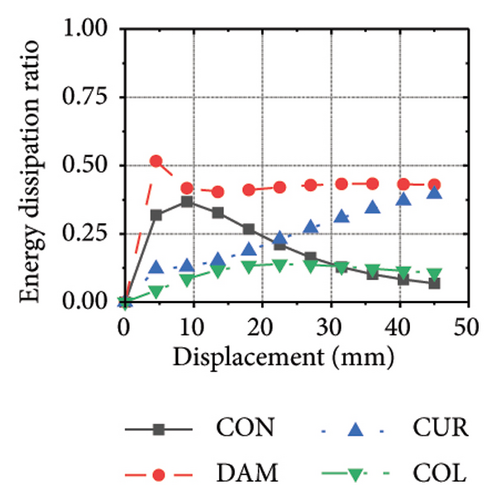
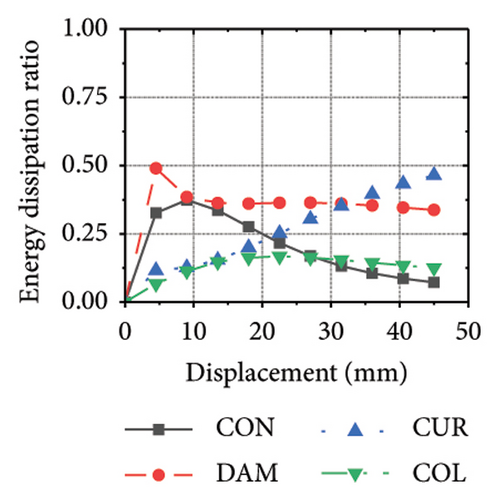
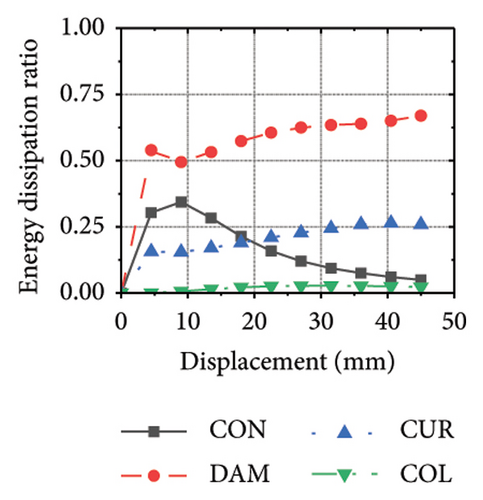
6. Energy Dissipation Evaluation and Lateral Bearing Capacity Calculation

6.1. Energy Dissipation Evaluation

Based on the seismic performance efficiency of the damper and wall body, the damper–energy relationship can be classified by considering the failure mode, hysteresis curve, energy distribution, and energy-dissipation ratio of the structure, as shown in Table 4.

(i)
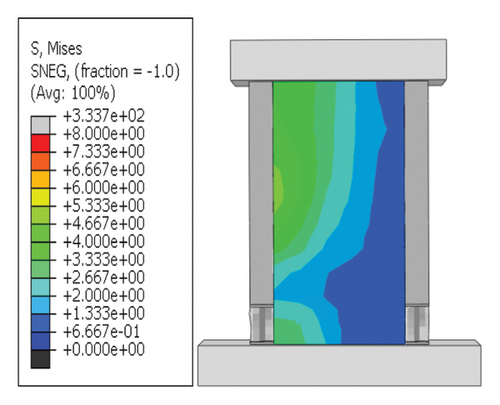
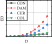
For r_v−dw ≤ r_w and r_h−cd ≥ 5%, the energy dissipation of the damper was larger than that of the wall. The large cross-sectional size of the constraint column provided sufficient confinement to the damper, and the deformation was mainly concentrated on the damper. Therefore, the damper exhibited the highest energy dissipation, and the overall energy dissipation of the structure was weaker than that at the second level. The hysteresis curves are significantly reduced owing to the complete buckling failure of the damper.
(ii)
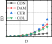
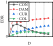
For r_v−dw ≤ r_w and 5%>r_h−cd ≥ 2%, the energy dissipation of the damper was larger than that of the wall. Additionally, the damage could be better concentrated on the damper, and the constraint column could be deformed to dissipate energy; therefore, the entire energy dissipation and damage concentration of the structure were optimal. The hysteresis curves did not decrease significantly because the wall body was not significantly damaged.
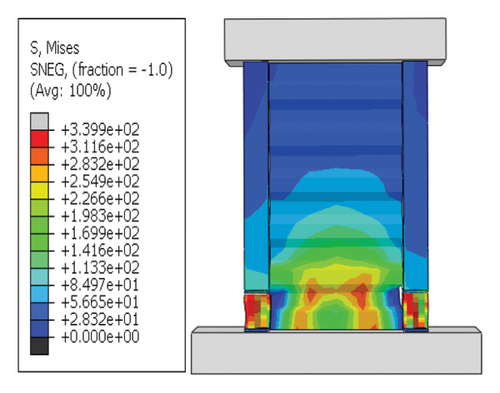
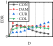
(iii)
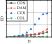
For r_v−dw ≤ r_w and r_h−cd < 2%, the constraint column did not provide the necessary restraint on the damper and deformation occurred mainly on the constraint column. The damper failed to achieve its full energy-dissipation capacity, and the overall energy dissipation of the structure was insufficient. Therefore, the design goal of the damper (i.e., failure of the damper before the wall) under seismic action is difficult to achieve.
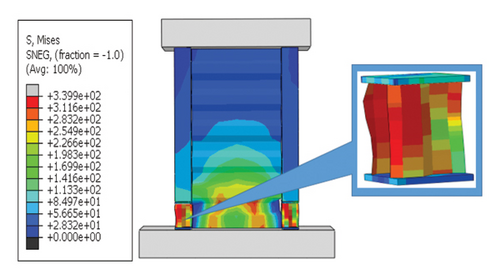
(iv)
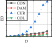
For r_v−dw > r_w and r_h−cd ≥ 2%, the energy dissipation of the damper was less than that of the wall body. When the damper boundary was sufficiently restrained, the damage was concentrated on the damper, and the hysteresis curves decreased. However, the overall energy dissipation of the damper was insufficient, and it was difficult to sufficiently protect the main wall from the damage caused by the earthquake.
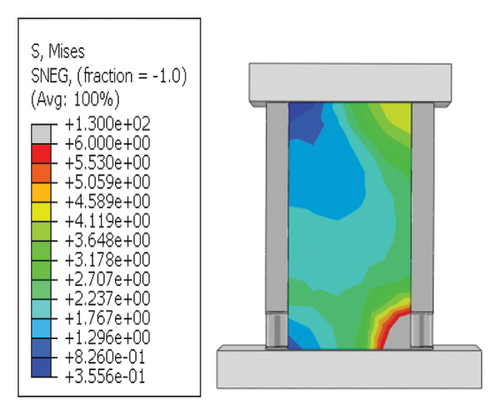
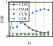
(5)
For r_v−dw > r_w and r_h−cd < 2%, the energy dissipation of the damper was smaller than that of the wall. It was difficult for the constraint column to provide the necessary restraint for the damper, and deformation occurred in the constraint column. The energy-dissipation efficiency of the damper was low, and the damage was concentrated on the main body of the wall. The energy-dissipation relationship was the worst. This situation should be avoided in the design stage.

Table 4. Energy-dissipation evaluation classification.

Level	(I)	(II)	(III)	(IV)	(V)
Range	r_v−dw ≤ r_w			r_v−dw > r_w
Range	r_h−cd ≥ 5%	5%>r_h−cd ≥ 2%	r_h−cd < 2%	r_h−cd ≥ 2%	r_h−cd < 2%
FM
HC
ED
EDR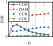

Note: D = displacement, F = force.
Abbreviations: ED = energy dissipation, EDR = energy-dissipation ratio, FM = failure mode; HC = hysteresis curve.

6.2. Lateral Bearing Capacity Calculation

Compared to a composite wall, a damper was added to the replaceable composite shear wall, and its bearing capacity was adjusted based on the change in the seismic performance of the damper. Therefore, the effect of the damper should be considered in the bearing capacity calculation for replacement shear walls. Based on the bearing-capacity calculation formula for a composite wall, as shown in equation (16), the lateral bearing capacity of the replaceable composite shear wall was calculated using the superposition principle. As mentioned in the energy-dissipation evaluation discussion, the damper and restraint columns worked together in proportion to the stiffness. Therefore, the shear-bearing capacity of the damper should be increased according to equation (16). The shear capacity calculation formula for the shear wall replacement is as in equation (17):

()

where α_em−col and α_em−dam denote the shear-performance ratio coefficients of the constraint column and damper, respectively. For r_h−cd ≥ 5%, the constraint column completely restrained the damper, and the shear performance of the edge member was completely provided by the damper. Therefore, α_em−col and α_em−dam were zero and unity, respectively. By contrast, for r_h−cd < 2%, the weak position in the edge member appeared on the constraint column; therefore, α_em−col and α_em−dam were unity and zero, respectively. For 5%>r_h−cd ≥ 2%, linear interpolation was applied to obtain the coefficients.

As the damper should have an ideal energy-dissipation ratio, r_v−dw should be inferior to r_w. The specimens that met this requirements were summarized, and their bearing capacities were calculated, as listed in Table 5. In general, the error between the calculated and simulated values was small, indicating that equation (17) is effective and feasible.

Table 5. Comparison between the calculated and simulated values for wall lateral bearing capacity.

Specimen	F_s (kN)	r_h−cd (%)	r_v−dw (%)	V_c (kN)	V_b (kN)	V_cc (kN)	α_em−col	V_d (kN)	α_em−dam	V_p (kN)	F_t (kN)	E (%)
2-1-1-dt6-15	591.0	10.0	62.5	111.5	42.8	436.2	0.00	182.9	1.00	106.9	444.1	24.9
2-1-2-dt6-15	665.9	10.0	59.0	111.5	42.8	436.2	0.00	182.9	1.00	213.8	551.0	17.3
2-1-3-dt6-15	724.0	10.0	56.2	111.5	42.8	436.2	0.00	182.9	1.00	320.7	657.9	9.1
2-1-3-dt12-15	1019.9	5.0	112.1	121.7	46.0	453.7	0.00	449.4	1.00	362.6	979.7	3.9
2-1-4-dt6-15	776.7	10.0	53.8	111.5	42.8	436.2	0.00	182.9	1.00	427.6	764.8	1.5
2-1-4-dt12-15	1096.3	5.0	107.3	111.5	42.8	436.2	0.00	449.4	1.00	427.6	1031.3	5.9
2-1-5-dt6-15	828.5	10.0	51.7	111.5	42.8	436.2	0.00	182.9	1.00	534.6	871.7	5.2
2-1-5-dt12-15	1155.2	5.0	103.2	111.5	42.8	436.2	0.00	449.4	1.00	534.6	1138.2	1.5
3-1-3-dt6-15	451.8	10.0	94.0	44.6	42.8	290.8	0.00	182.9	1.00	128.3	398.5	11.8
2-1-3-dt6-10	721.1	7.2	56.2	111.5	42.8	290.8	0.00	182.9	1.00	320.7	657.9	8.8
2-1-3-dt12-10	1010	3.6	112.1	121.7	46.0	302.4	0.47	449.4	0.53	362.6	911.1	9.8
2-1-3-dt6-20	725.1	12.5	56.2	111.5	42.8	581.6	0.00	182.9	1.00	320.7	657.9	9.3
2-1-3-dt12-20	1025.6	6.2	112.1	121.7	0.00	604.9	0.88	449.4	1.00	362.6	979.7	4.5
2-1-3-dt6-25	751.7	14.7	56.2	111.5	0.00	727.0	0.00	182.9	1.00	320.7	657.9	12.5
2-1-3-dt12-25	1099.9	7.3	112.1	121.7	0.00	756.1	0.74	449.4	1.00	362.6	979.7	10.9
2-1-3-dt6-30	755	16.4	56.2	111.5	0.00	872.4	0.00	182.9	1.00	320.7	657.9	12.9
2-1-3-dt12-30	1102.5	8.1	112.1	121.7	0.00	907.3	0.62	449.4	1.00	362.6	979.7	11.1

Note: F_s is the bearing capacity used in the simulation. r_h−cd and r_v−dw are the stiffness ratios. V_c, V_b, and V_cc are the shear values of the concrete, steel bars, and restraint columns, respectively. V_d and V_p are the shear values of the damper and steel plate, respectively. F_t is the calculated bearing capacity. E is the error.

7. Conclusions

In this study, a corrugated web damper was installed on a corrugated steel plate composite shear wall to investigate the seismic performance of a replaceable structure. The energy-dissipation relationship between the damper and main wall structure was obtained for different stiffness indices. Finally, based on the different interaction relationships, a method for calculating the lateral bearing capacity of the replaceable corrugated steel plate shear wall was proposed. Based on the results, the main conclusions of this study can be summarized as follows:

(i)
The investigated corrugated steel plate composite shear walls exhibited excellent seismic performance and could be used as the main components in replaceable structures. Mild-steel dampers have an ideal energy-dissipation capacity and can be applied to replaceable structures. For wall toe replaceable shear walls, the interaction relationship between damper and wall body had a significant influence on the seismic performance of the replaceable shear wall.
(ii)
Typically, the region in which the plastic hinge occurs is identified as the replacement region. Research on the plastic-hinge length calculation for shear walls is relatively mature, and the walls are often simplified using independent rod models. This method is convenient and accurate, and can be used to determine the size of the toe-replacement region.
(iii)
By analyzing the shear wall deformation, a stiffness index that can be used to evaluate the energy-dissipation relationship between the damper and wall is proposed. The proposed index can be used to assess the interaction between the damper and wall body.
(iv)
Sensitivity analysis results showed that under the same aspect ratio conditions, the seismic performance of the wall was limited when the damper web thickness was insufficient. In this situation, it is difficult to provide sufficient restraint to walls. This suggests that the damper parameters should be reasonably set to play a full role in the seismic performance of the wall.
(v)
An energy-dissipation evaluation method is proposed. When r_v−dw ≤ r_w and r_h−cd ≥ 5% were used, the energy dissipation was at Level I, indicating that the relationship between the damper and shear wall was optimal. At this level, the damper boundary was sufficiently restrained, and deformation could occur more effectively.
(vi)
According to the analysis results, the interaction relationship influences the bearing capacity and must be considered. The revised lateral bearing capacity formula based on the energy-dissipation evaluation exhibited ideal accuracy and could provide a reference for practical engineering applications.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Qirui Luo: conceptualization, formal analysis, methodology, software, writing – original draft. Wei Wang: funding acquisition, resources, writing – review and editing. Shixing Zhao: data curation, resources. Min Zhang: conceptualization, supervision. Shuheng Yang: methodology.

Funding

This research was supported by Open Fund of the Sichuan Engineering Research Center for Mechanical Properties and Engineering Technology of Unsaturated Soils ∗ SC-FBHT2023-02 ∗ SC-FBHT2024-05 Research Project of the Sichuan Architectural Design and Research Institute ∗ KYYN202313 National Natural Science Foundation of China ∗ 51878548 ∗ 51578449 Science and Technology Department of Sichuan Province ∗ 2024JDRC0101.

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Zhang C. and Tian Y., Simplified Performance-Based Optimal Seismic Design of Reinforced Concrete Frame Buildings, Engineering Structures. (2019) 185, 15–25, https://doi.org/10.1016/j.engstruct.2019.01.108, 2-s2.0-85060754437.
10.1016/j.engstruct.2019.01.108
Web of Science® Google Scholar
2 Tolou Kian M. J. and Cruz-Noguez C., Reinforced Concrete Shear Walls Detailed With Innovative Materials: Seismic Performance, Journal of Composites for Construction. (2018) 22, no. 6, https://doi.org/10.1061/(asce)cc.1943-5614.0000893, 2-s2.0-85053518636.
10.1061/(asce)cc.1943-5614.0000893
Google Scholar
3 Xu D., Xu K. Y., Wang X. T., Wang J.F., Yan J. B., and Wang T., Seismic Behaviour of Connections Between Replaceable Coupling Beam and Double Skin Composite Shear Wall, Structures. (2023) 55, 2389–2402, https://doi.org/10.1016/j.istruc.2023.07.004.
10.1016/j.istruc.2023.07.004
Web of Science® Google Scholar
4 Xiao S., Xu L., and Feng P., Post-Earthquake Performance and Damage Evaluation of Self-Centering Shear Wall With Replaceable Devices, Engineering Structures. (2023) 289, https://doi.org/10.1016/j.engstruct.2023.116248.
10.1016/j.engstruct.2023.116248
Web of Science® Google Scholar
5 Caruso M., Pinho R., Bianchi F., Cavalieri F., and Lemmo M. T., Integrated Economic and Environmental Building Classification and Optimal Seismic Vulnerability/Energy Efficiency Retrofitting, Bulletin of Earthquake Engineering. (2021) 19, no. 9, 3627–3670, https://doi.org/10.1007/s10518-021-01101-4.
10.1007/s10518-021-01101-4
Web of Science® Google Scholar
6 Mieler M. W. and Mitrani-Reiser J., Review of the State of the Art in Assessing Earthquake-Induced Loss of Functionality in Buildings, Journal of Structural Engineering. (2018) 144, no. 3, https://doi.org/10.1061/(asce)st.1943-541x.0001959, 2-s2.0-85038620778.
10.1061/(asce)st.1943-541x.0001959
Web of Science® Google Scholar
7 Bournas D. A., Concurrent Seismic and Energy Retrofitting of RC and Masonry Building Envelopes Using Inorganic Textile-Based Composites Combined With Insulation Materials: A New Concept, Composites Part B: Engineering. (2018) 148, 166–179, https://doi.org/10.1016/j.compositesb.2018.04.002, 2-s2.0-85046701654.
10.1016/j.compositesb.2018.04.002
CAS Web of Science® Google Scholar
8 Ke K. and Yam M. C., A Performance-Based Damage-Control Design Procedure of Hybrid Steel MRFs With EDBs, Journal of Constructional Steel Research. (2018) 143, 46–61, https://doi.org/10.1016/j.jcsr.2017.12.011, 2-s2.0-85039736765.
10.1016/j.jcsr.2017.12.011
Web of Science® Google Scholar
9 Wei B., Xiao B., Hu Z., Jiang L., and Li S., Damage Control Analysis of Components in High-Speed Railway Bridge-Track System Based on Combined Seismic Isolation Design under Earthquake, Structures. (2023) 54, 515–526, https://doi.org/10.1016/j.istruc.2023.05.060.
10.1016/j.istruc.2023.05.060
Web of Science® Google Scholar
10 Chen Y., Wang W., and Chen Y., Full-Scale Shake Table Tests of the Tension-Only Concentrically Braced Steel Beam-Through Frame, Journal of Constructional Steel Research. (2018) 148, 611–626, https://doi.org/10.1016/j.jcsr.2018.06.017, 2-s2.0-85047180036.
10.1016/j.jcsr.2018.06.017
Web of Science® Google Scholar
11 Hu S., Wang W., and Qu B., Self-Centering Companion Spines With Friction Spring Dampers: Validation Test and Direct Displacement-Based Design, Engineering Structures. (2021) 238, https://doi.org/10.1016/j.engstruct.2021.112191.
10.1016/j.engstruct.2021.112191
Web of Science® Google Scholar
12 Akehashi H. and Takewaki I., Comparative Investigation on Optimal Viscous Damper Placement for Elastic-Plastic MDOF Structures: Transfer Function Amplitude or Double Impulse, Soil Dynamics and Earthquake Engineering. (2020) 130, https://doi.org/10.1016/j.soildyn.2019.105987.
10.1016/j.soildyn.2019.105987
Web of Science® Google Scholar
13 Wang Z. and Giaralis A., Enhanced Motion Control Performance of the Tuned Mass Damper Inerter Through Primary Structure Shaping, Structural Control and Health Monitoring. (2021) 28, no. 8, https://doi.org/10.1002/stc.2756.
10.1002/stc.2756
PubMed Web of Science® Google Scholar
14 Wang W., Luo Q., Wang B., Song J., and Quan C., Performance Research and Optimization of Corrugated Mild Steel Damper With Considering Weld Failure, Journal of Earthquake Engineering. (2022) 26, no. 6, 2802–2821, https://doi.org/10.1080/13632469.2020.1772153.
10.1080/13632469.2020.1772153
Web of Science® Google Scholar
15 Ma R., Cheng Z., Zhang X., and Jiang K. Bi & S, Mechanical Behaviors and Seismic Performance of a novel Rotary Amplification Friction Damper (RAFD): Experimental and Analytical Studies, Journal of Constructional Steel Research. (2024) 223.
10.1016/j.jcsr.2024.109051
Web of Science® Google Scholar
16 Chen S., Wang W., Liu G., Zhou C., Chen B., and Chen Z., Mechanical Behavior and Seismic Control Performance of a Metallic Torsional Damper for Flexible Structures, Engineering Structures. (2024) 318, https://doi.org/10.1016/j.engstruct.2024.118674.
10.1016/j.engstruct.2024.118674
Web of Science® Google Scholar
17 Li H., Du Y., Han J., Li F., and Chi P., Experimental and Numerical Study of Low-Yield-Point Steel Corrugated Pipe Dampers, Soil Dynamics and Earthquake Engineering. (2024) 180, https://doi.org/10.1016/j.soildyn.2024.108615.
10.1016/j.soildyn.2024.108615
Web of Science® Google Scholar
18 Wang W., Luo Q., Xu S., Wang B., and Sun Z., Application Research of Corrugated Mild Metal Shear Damper Based on Damage Control and Energy-Dissipation Improvement, Journal of Building Engineering. (2022) 47, https://doi.org/10.1016/j.jobe.2021.103840.
10.1016/j.jobe.2021.103840
Web of Science® Google Scholar
19 Wang W., Li A., and Wang X., Seismic Performance of Precast Concrete Shear Wall Structure With Improved Assembly Horizontal Wall Connections, Bulletin of Earthquake Engineering. (2018) 16, no. 9, 4133–4158, https://doi.org/10.1007/s10518-018-0348-2, 2-s2.0-85044053292.
10.1007/s10518-018-0348-2
Web of Science® Google Scholar
20 Ugalde D. and Lopez-Garcia D., Behavior of Reinforced Concrete Shear Wall Buildings Subjected to Large Earthquakes, Procedia Engineering. (2017) 199, 3582–3587, https://doi.org/10.1016/j.proeng.2017.09.524, 2-s2.0-85029898236.
10.1016/j.proeng.2017.09.524
Google Scholar
21 Dou C., Jiang Z., Guo Y. et al., Elastic Shear Buckling of Sinusoidally Corrugated Steel Plate Shear Wall, Engineering Structures. (2023) 121, 136–146.
10.1016/j.engstruct.2016.04.047
Google Scholar
22 Paslar N., Farzampour A., and Hatami F., Infill Plate Interconnection Effects on the Structural Behavior of Steel Plate Shear Walls, Thin-Walled Structures. (2020) 149, https://doi.org/10.1016/j.tws.2020.106621.
10.1016/j.tws.2020.106621
Web of Science® Google Scholar
23 Sabouri-Ghomi S. and Mamazizi S., Experimental Investigation on Stiffened Steel Plate Shear Walls With Two Rectangular Openings, Thin-Walled Structures. (2015) 86, 56–66, https://doi.org/10.1016/j.tws.2014.10.005, 2-s2.0-84908348978.
10.1016/j.tws.2014.10.005
Web of Science® Google Scholar
24 Epackachi S., Whittaker A. S., and Aref A., Seismic Analysis and Design of Steel-Plate Concrete Composite Shear Wall Piers, Engineering Structures. (2017) 133, 105–123, https://doi.org/10.1016/j.engstruct.2016.12.024, 2-s2.0-85007028378.
10.1016/j.engstruct.2016.12.024
Web of Science® Google Scholar
25 Wang W., Ren Y., Lu Z., Song J., Han B., and Zhou Y., Experimental Study of the Hysteretic Behaviour of Corrugated Steel Plate Shear Walls and Steel Plate Reinforced Concrete Composite Shear Walls, Journal of Constructional Steel Research. (2019) 160, 136–152, https://doi.org/10.1016/j.jcsr.2019.05.019, 2-s2.0-85066236081.
10.1016/j.jcsr.2019.05.019
Web of Science® Google Scholar
26 Guo Z. and Yuan Y., Experimental Study of Steel Plate Composite Shear Wall Units Under Cyclic Load, International Journal of Steel Structures. (2015) 15, no. 3, 515–525, https://doi.org/10.1007/s13296-015-9001-y, 2-s2.0-84944448628.
10.1007/s13296-015-9001-y
Web of Science® Google Scholar
27 Lou G. B., Chen P. X., and Zheng J. H., Seismic Performance of High-Strength Steel Plate-Concrete Composite Shear Walls, Journal of Building Engineering. (2024) 82, https://doi.org/10.1016/j.jobe.2023.108258.
10.1016/j.jobe.2023.108258
Web of Science® Google Scholar
28 Hosseinzadeh L., Kontoni D.-P. N., and Babaei B., Investigation of the Behavior of Steel Plate Shear Walls Considering Double Corrugated Low-Yield-Point Steel Infill Plate, International Journal of Civil Engineering. (2023) 21, no. 10, 1631–1642, https://doi.org/10.1007/s40999-023-00855-z.
10.1007/s40999-023-00855-z
Web of Science® Google Scholar
29 Luo Q., Wang W., Sun Z., Xu S., and Wang B., Seismic Performance Analysis of Corrugated-Steel-Plate Composite Shear Wall Based on Corner Failure, Journal of Constructional Steel Research. (2021) 180, https://doi.org/10.1016/j.jcsr.2021.106606.
10.1016/j.jcsr.2021.106606
Web of Science® Google Scholar
30 Wang W., Song J., Wang W., Ding X., and Lu Z., Experimental Investigation of the Seismic Behavior of Low-Yield-Point Corrugated Steel Plate Dampers, Journal of Structural Engineering. (2021) 147, no. 2, https://doi.org/10.1061/(asce)st.1943-541x.0002924.
10.1061/(asce)st.1943-541x.0002924
Web of Science® Google Scholar
31 Lv X., Chen Y., and Mao W., New Concept of Structural Seismic Design: Earthquake Resilient Structure, Journal of Tongji University: Natural Science. (2011) 39, no. 7, 941–948.
Google Scholar
32 Wang W., Song J., Hou M., Liu G., and Wang W., Experimental Study and Numerical Simulation of Replaceable Corrugated Steel Plate-Concrete Composite Shear Walls, Soil Dynamics and Earthquake Engineering. (2019) 127, https://doi.org/10.1016/j.soildyn.2019.105827, 2-s2.0-85072645390.
10.1016/j.soildyn.2019.105827
Web of Science® Google Scholar
33 Powell G. H., Displacement-Based Seismic Design of Structures, Earthquake Spectra. (2008) 24, no. 2, 555–557, https://doi.org/10.1193/1.2932170.
10.1193/1.2932170
Google Scholar
34 Kazaz İ., Analytical Study on Plastic Hinge Length of Structural Walls, Journal of Structural Engineering. (2013) 139, no. 11, 1938–1950, https://doi.org/10.1061/(asce)st.1943-541x.0000770, 2-s2.0-84886473514.
10.1061/(asce)st.1943-541x.0000770
Web of Science® Google Scholar
35 Wang W., Li Y., Su S., Quan C., Zhen G., and Song H., Equivalent Plastic Hinge Length of Vertical Corrugated Steel Plate Composite Shear Walls, Journal of Building Structures. (2022) 43, no. 07, 219–229.
CAS Google Scholar

All articles

Seismic Performance Analysis of Replaceable Corrugated Steel Plate Composite Shear Walls Based on Interaction Relationships

Abstract

1. Introduction

2. Materials and Methods

2.1. Wall Body

2.2. Energy-Dissipation Component

2.3. Replaceable Corrugated Steel Plate Composite Shear Wall

3. Replacement Area and Wall Deformation Analysis

3.1. Replacement Area Analysis

3.2. Wall Deformation Analysis

4. Parameter Analysis

4.1. Coupling Effect of the Wall Aspect Ratio and Damper Web Thickness

4.2. Coupling Effect of the Corrugated Plate Thickness and Damper Web Thickness

4.3. Coupling Effect of the Constraint Column Thickness and Damper Web Thickness

5. Interaction Relationship Analysis

5.1. Coupling Effect of the Wall Aspect Ratio and Damper Web Thickness

5.2. Coupling Effect of the Corrugated Plate Thickness and Damper Web Thickness

5.3. Coupling Effect of the Constraint Column Thickness and Damper Web Thickness

6. Energy Dissipation Evaluation and Lateral Bearing Capacity Calculation

6.1. Energy Dissipation Evaluation

6.2. Lateral Bearing Capacity Calculation

7. Conclusions

Conflicts of Interest

Author Contributions

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Seismic Performance Analysis of Replaceable Corrugated Steel Plate Composite Shear Walls Based on Interaction Relationships

Abstract

1. Introduction

2. Materials and Methods

2.1. Wall Body

2.2. Energy-Dissipation Component

2.3. Replaceable Corrugated Steel Plate Composite Shear Wall

3. Replacement Area and Wall Deformation Analysis

3.1. Replacement Area Analysis

3.2. Wall Deformation Analysis

4. Parameter Analysis

4.1. Coupling Effect of the Wall Aspect Ratio and Damper Web Thickness

4.2. Coupling Effect of the Corrugated Plate Thickness and Damper Web Thickness

4.3. Coupling Effect of the Constraint Column Thickness and Damper Web Thickness

5. Interaction Relationship Analysis

5.1. Coupling Effect of the Wall Aspect Ratio and Damper Web Thickness

5.2. Coupling Effect of the Corrugated Plate Thickness and Damper Web Thickness

5.3. Coupling Effect of the Constraint Column Thickness and Damper Web Thickness

6. Energy Dissipation Evaluation and Lateral Bearing Capacity Calculation

6.1. Energy Dissipation Evaluation

6.2. Lateral Bearing Capacity Calculation

7. Conclusions

Conflicts of Interest

Author Contributions

Funding

Open Research

Data Availability Statement

References

Figures

References

Related

Information