Identification and Localization of Structural Damage Using the Second-Largest Eigenvalue of the Mutative-Scale Symbolic Matrix as the Damage Indicator
Abstract
Time series–related methods in structural damage detection have gained increasing recognition due to their effectiveness, yet they face limitations in accuracy and efficiency for data processing, particularly in damage localization. In this study, we propose a novel method that utilizes a mutative-scale symbolic matrix, which extracts the second-largest eigenvalue as a damage indicator, to address the difficult problems of damage detection under random excitation. Unlike the conventional symbolized time series method, the mutative-scale symbolic matrix method selects data from the virtual impulse response function series at specific intervals, based on the Pearson correlation coefficient, and uses these data with the intervals to construct the mutative-scale symbolic matrix through joint occurrence entropy. The second-largest eigenvalue of the matrix is identified as an effective damage indicator which significantly magnifies the variations in structural characteristics. Damage localization is achieved by exploring damage occurrence between different reference and measurement points, and the flexibility in selecting these points enables a more precise determination of the damaged area according to the technology process based on dichotomy. A 10-DOF numerical model subjected to random Gaussian white noise is initially employed to validate the accuracy of the damage indicator for damage identification and localization. Subsequently, upon experimental application to a testbed structure, the proposed method exhibited super robustness in data selection under different damage types, with higher computational efficiency than conventional methods.
1. Introduction
Due to the impact of material degradation, initial design flaws, or continuous environmental erosion, various damages manifest in the major parts or components of engineering structures throughout their service life. Consequently, it is crucial to prioritize structural health monitoring (SHM) [1–4], enabling timely identification and remediation of structural damage to prevent substantial economic and life expectancy losses. Recently, vibration-based methods for SHM have seen rapid development. Generally, vibration-based damage detection approaches are categorized into model-driven and data-driven methods [5]. In model-driven methods, high-fidelity structural models are initially established, followed by the application of finite element analysis to identify structural damage [6, 7]. This approach generally necessitates high precision in model details, entailing extensive computational demands, particularly for complex structures. In data-driven methods, various types of signals are collected, processed, analyzed, and evaluated for structural damage detection [8, 9]. Subsequently, damage indicators sensitive to structural impairments are developed by combining other necessary tools and methods [10–13], which can solve the difficult problems of evaluating the occurrence, degree, and location of different types of damage [14, 15]. As artificial intelligence advances, data-driven approaches rely more on machine learning, which is usually divided into supervised learning, semisupervised learning, and unsupervised learning [16], to solve complex problems on time signal processing. Entezami et al. [17, 18] have performed a lot of work on unsupervised learning methods. Among them, clustering is an important method in unsupervised learning [19, 20], which aims to divide time series data samples into partitions that contain data points with similar properties in SHM, thereby heightening the system’s sensitivity to noise pollution and necessitating more sophisticated data processing approaches.
Wavelet analysis has also been employed for damage recognition signal processing in various fields [21, 22]. However, the wavelet transform occasionally fails to meet high-accuracy requirements, as it solely decomposes the signal’s low-frequency band. In contrast, the wavelet packet transform (WPT) not only inherits the wavelet transform’s time-frequency analysis characteristics but also adopts varying resolutions for different frequencies at distinct layers, facilitating further decomposition in the high-frequency band. In damage identification applications, the integration of WPT and the virtual impulse response function (VIRF) markedly diminishes the excitation’s impact on structural models [23–25].
VIRF is commonly defined as the inverse Fourier transform of the frequency-response function, manifesting as a freely decaying real signal in the time domain. It relates solely to the structure’s inherent characteristics and is believed to encompass all the structure’s damage information. Consequently, VIRF also represents damage-sensitive information with high dimensionality, derived from the waveform. In signal processing, the initial step in damage identification involves the dimensionality reduction of VIRF.
Symbolized time series analysis (STSA) [26–29] relies on changes in the statistical behavior of symbol series, effectively capturing the main features of dynamic systems and mitigating the impact of detrimental noise. The symbol space is partitioned using the maximum entropy approach, and the precise number of partitions is determined based on the concept of modified Shannon’s entropy [30]. Shannon’s entropy effectively describes the complexity and uncertainty of dynamic systems. STSA generally preserves crucial information about the underlying time series, simultaneously capturing its main features from a broad perspective. Consequently, the statistical characteristics of the symbol sequences, which describe the system’s dynamic status, serve to reduce the dimensionality of information and its sensitivity to noise. Hu, Qian, and Yan [31] proposed a novel partitioning method, termed space partitioning for symbol-sequence generation, which has proven effective for information extraction and compression, particularly in multifield information processing. However, the robustness and efficiency of this method in damage identification still have difficulty in meeting the computational requirements of large structures, let alone accurately and efficiently capturing the location of damage. Furthermore, SHM necessitates the dissociation of adverse factors and the mitigation of various interferences, a task that requires auxiliary tools such as the VIRF and the Pearson correlation coefficient.
Pearson correlation coefficient, a prevalent measure for detecting linear dependence [32], has been extensively researched in modern statistics. Fisher [33–36] conducted extensive research, including deriving the exact sampling distribution for the coefficient and establishing its convergence to a normal distribution with increasing sample size. These contributions were pivotal in the discovery of variance-stabilizing transformations, sufficiency, and the maximum likelihood estimator. Recently, the application of Pearson correlation coefficients has expanded across various fields to examine associations between two observed variables and to assess the strength of these relationships [37].
Drawing inspiration from the existing achievements of the aforementioned theories, we propose a new method for damage identification and localization. In this study, the key innovation, distinguishing our approach from the conventional STSA method for damage detection, is the selection of the mutative-scale interval. Utilizing the second-largest eigenvalue of the mutative-scale symbolic matrix (MSM) as the damage indicator, this method markedly enhances the accuracy and efficiency of damage identification over other dimension reduction signal processing methods, while also substantially reducing computational requirements. Furthermore, this approach enables damage localization within a minimal range, utilizing various positions of measurement points (MPs) and reference points (RPs). Classical theories underpinning this study are detailed in Section 2, where the rationale behind the innovative MSM method is also thoroughly explained. In Section 3, numerical models validate the effectiveness of the proposed method, and the critical points selected prove the precision of damage localization. In Section 4, experimental data from a laboratory frame are employed to compare other damage indices with their counterparts. Results of damage identification and localization show that under different damage types, the MSM method can accurately identify structural damage like other methods and has better robustness in data selection. The comparison of calculation time verifies the better computational efficiency of the proposed method than conventional methods. Finally, the conclusions of this study are summarized in Section 5, and the limitations and prospects are discussed.
2. Theoretical Derivations
Initially, the theories underpinning the MSM method are comprehensively elaborated. Furthermore, several existing theories, including VIRF, Pearson correlation coefficients, STSA, and Shannon’s entropy, are employed to clarify the theoretical foundation of this study. In the damage identification and localization procedure, VIRF is first utilized to mitigate the effects of random excitation, while the Pearson correlation coefficient is applied to examine the impact of varying intervals of the time series on the system. To effectively capture the main features of the original time series data on a large scale, STSA is frequently referenced, which is known for its ability to significantly reduce the dimensions of the data and decrease their sensitivity to noise contamination. Concurrently, Shannon’s entropy plays a crucial role in STSA by facilitating the rational partitioning of the time series.
Unlike the conventional time series method, the MSM method selects data using the mutative-scale interval τ, as opposed to continuous intervals. Considering the stationary time series X = {x1, x2, …, xN} and Y = {y1, y2, …, yN−τ}, the time series Y is derived from X as Y(yk = xk+τ, k = 1, 2, …, N − τ). Here, N represents the length of the series X, which is substantially greater than τ and sufficiently extensive to ensure the validity of structural damage identification and localization. The interval τ specifically reflects the system’s properties [38]. Since the data are placed in a two-dimensional matrix, the joint occurrence entropy is then proposed as a corresponding two-dimensional entropy to help partition the original data, which makes the features of the signal better extracted. The procedural steps of the proposed methods are depicted in the flowchart presented in Figure 1. The damage localization methods incorporate an additional step beyond damage identification methods, which is elaborated in the subsequent introduction.
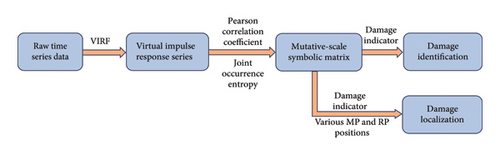
2.1. VIRF
Acquiring and analyzing the VIRF constitute the initial step in the proposed study, ensuring that the collected acceleration signal solely reflects the characteristics of the structure. In damage identification methods, the selection of MP and RP can be arbitrary, but it is advisable to choose points distanced from each other, as this facilitates the belief that damage occurs between the two selected points. However, in damage localization methods, the selection of points becomes significantly more critical, as varying combinations of these points are utilized to ascertain the location of the damage.
2.2. Pearson Correlation Coefficient
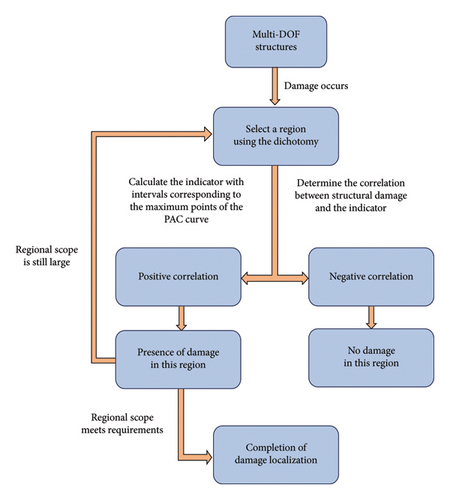
The additional steps for damage localization are also based mainly on the PAC. The simulation and experimental results collectively indicate that if the damage is situated between the MP and the RP, the indicator associated with the τ corresponding to the maximum value of Cτ increases as the damage progresses; when the indicator is tied to the τ corresponding to the minimum value of Cτ, it decreases with increasing damage. Conversely, if the damage is not located between the MP and the RP, the indicator exhibits the opposite behavior. For unfamiliar structures, the MSM method can be employed for progressive damage localization utilizing a dichotomous approach. The approaching points are gradually selected as the MPs and RPs to ascertain if damage occurs between these points until the distance meets the standards. The procedural steps of the damage localization flowchart are presented in Figure 2. This dichotomous method can gradually reduce the range of possible damage at the fastest speed, and the minimum range is the distance between adjacent acceleration sensors. In this study, some critical points are selected to localize the predetermined damage as a validation of the proposed damage localization method.
2.3. STSA
STSA [41–43] represents a feature extraction method rooted in statistical analysis, capable of effectively extracting characteristic information from the original signal through rapid and straightforward computations. The implementation of symbolic time series analysis is depicted in Figure 3.
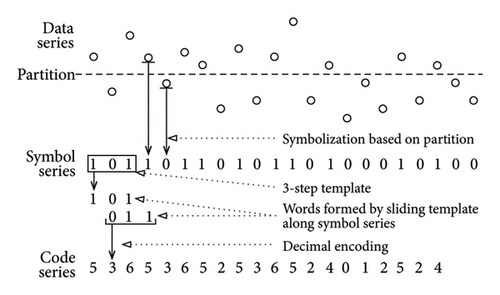
As shown in Figure 3, each generated partition is linked with a unique symbol, and the original time series data are mapped into the symbol space according to the partition they occupy. As a result, the raw time series is characterized by the corresponding series of symbols, and the code series is then computed by the binary algorithm, offering expanded possibilities for further exploration of the dynamical system [43]. The proposed MSM method retains this mode of symbolized data processing based on the new proposed joint occurrence entropy.
2.4. Joint Occurrence Entropy
2.5. MSM
3. Numerical Studies
A simple 10-DOF model is constructed for damage identification and damage localization, which with its schematic is illustrated in Figure 4. The mass M, stiffness K, and damping ratio ζ for each DOF are set to 10 kg, 1200 N/m, and 0.05, respectively. Five damage scenarios are created by reducing the stiffness of the sixth DOF by 0, 10%, 20%, 30%, and 40% relative to its original stiffness. Random Gaussian white noise (20–150 Hz) acting as seismic excitation is applied at M 1. In addition, five independent trials are performed for each damage scenario to validate the simulation’s effectiveness. A total of 50 s of response data is sampled from each DOF at a sampling frequency of fs = 100 Hz.

3.1. Damage Identification
3.1.1. Procedure
- (1)
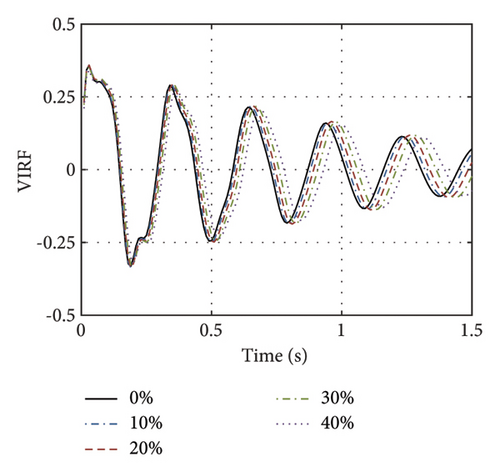
The acceleration response measured at the 1st DOF serves as the virtual input to the structural frequency–response function, while the acceleration at the 10th DOF acts as the output, so the virtual frequency–response function of the structure Fzz(ω, 10, 1) is derived using the 1st and 10th DOF as the RP and MP (RP1 and MP10), respectively. Subsequently, the VIRF F(t) is determined via the inverse Fourier transform, and the mean value of the five trials is depicted in Figure 5(a), highlighting the first 3 s, where the attenuation is notably significant. The Figure 5(a) clearly shows that as the stiffness decreases, the attenuation of VIRF curves progressively slows down, which indicates that VIRF curves can effectively represent the severity of structural damage.
- (2)
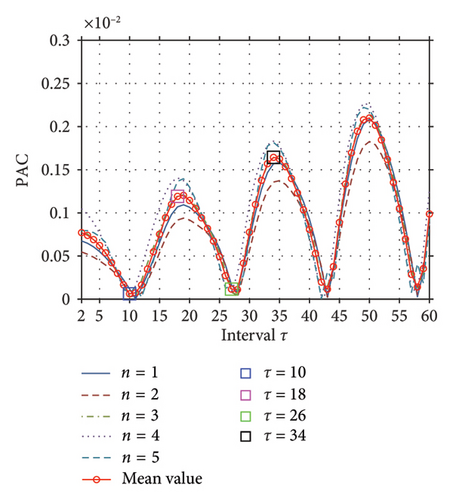
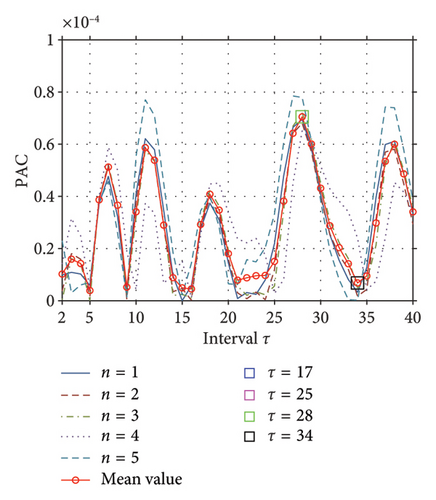
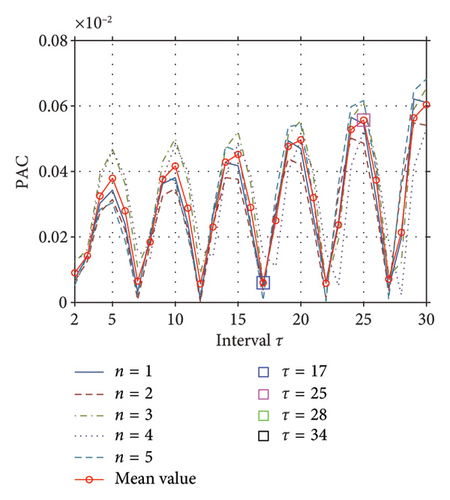
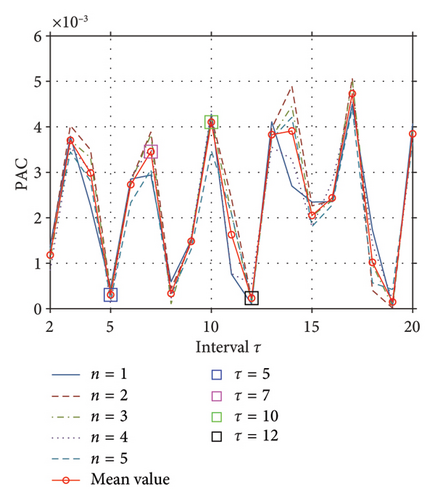
The correlation between PAC Cτ and the interval τ is analyzed and illustrated in Figure 5(b), where five gray curves represent the outcomes of five independent trials, and the average is depicted in red. It is observed that the extreme points on the curves are relatively concentrated at some specific points and alternate regularly, which means the trend of the curve follows a certain periodic law. Starting at the first minimum point, four points are selected to investigate whether the corresponding τ is the suitable interval for reflecting the structural damage condition. Ultimately, Intervals 10 and 26, corresponding to the minimum extreme values, and Intervals 18 and 34, corresponding to the maximum extreme values, are sequentially chosen to validate the method’s effectiveness. In theory, the PAC curves of a structure usually show a cyclical trend, and the choices of extreme values are arbitrary under the principle that N is substantially greater than τ. However, if a structure’s PAC curve does not exhibit a perfect cyclical trend due to factors such as environmental interference, there is still a high probability that the structural characteristic changes can be explored at the relatively concentrated extreme points on this PAC curve.
- (3)
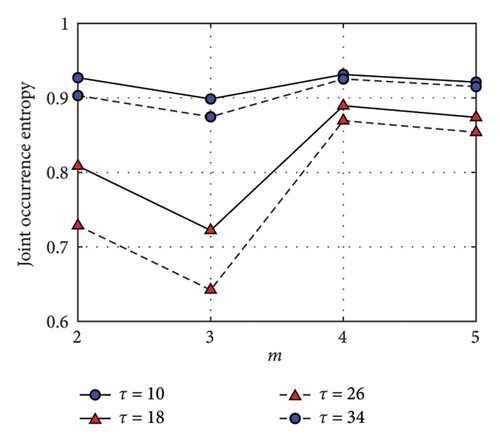
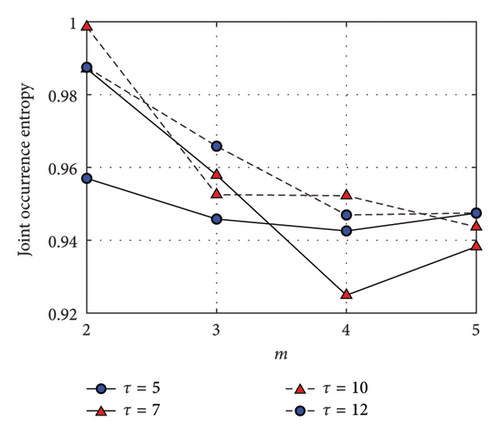
The VIRF F(t) undergoes partitioning and symbolization, guided by the joint occurrence entropy Qm. Intervals 10, 18, 26, and 34 are integrated into Qm curves plotted against m, as illustrated in Figure 6. The entropy curves for these four intervals reach their minimum values when the number of partitions m equals 3, indicating that this is the optimal partition number.
- (4)
Partition number 3 selected above is also the row number and column number of the MSM. Subsequently, a 3 × 3 matrix A(τ) is constructed as
()
The damage indicator D is the second-largest eigenvalue of matrix A, D = |λ2|. The identification of the structural damage can be realized by comparing damage indicators under different damage conditions.
3.1.2. Results
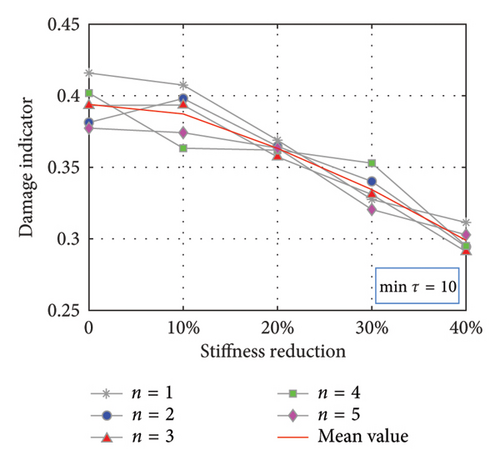
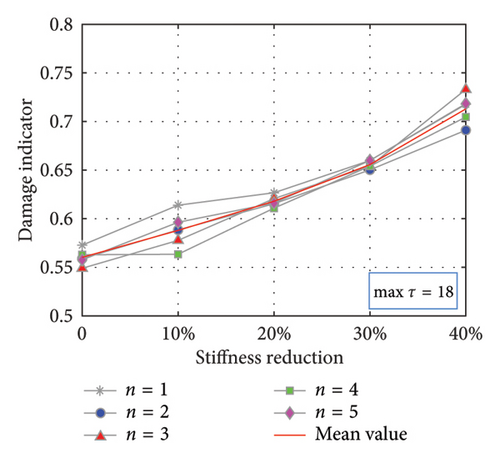
Figure 7 illustrates the correlation between the severity of damage and the damage indicator D, where the five gray curves represent the outcomes of five independent simulations, with their mean value shown in red. Figures 7(b) and 7(d), featuring Intervals of 18 and 34, correspond to the maximum extreme points on the Cτ curves. As the damage severity increases, the curves demonstrate a continuous upward trend. Conversely, Figures 7(a) and 7(c), with Intervals of 10 and 26 corresponding to the minimum extreme points on the Cτ curves, exhibit a downward trend. Therefore, when damage is present between the RP and MP, a positive correlation emerges between the damage indicator and the extent of damage, with intervals corresponding to the maximum extreme points on the Cτ curves. In addition, the damage indicator curves under 5 different excitations display mild fluctuations in some instances, suggesting the robustness of the damage identification method against variations in excitation.
3.2. Damage Localization
The same 10-DOF model, as described in the above section, is utilized for the numerical analysis of damage localization.
3.2.1. Principle
The pivotal step in damage localization is selecting the MP and RP of the structure, where different choices for RP and MP result in contrasting behaviors of the Cτ curves. The fundamental principle of damage localization is that if damage occurs between the RP and MP, and the intervals τ correspond to the maximum extreme points on the Cτ curves, the indicator rises with worsening damage and declines when the intervals correspond to the minimum extreme points. Conversely, if the damage is not present between the RP and MP, and the intervals correspond to the maximum extreme points on the Cτ curves, the damage indicator exhibits a negative correlation with damage severity, whereas a positive correlation is observed when the intervals correspond to the minimum extreme points.
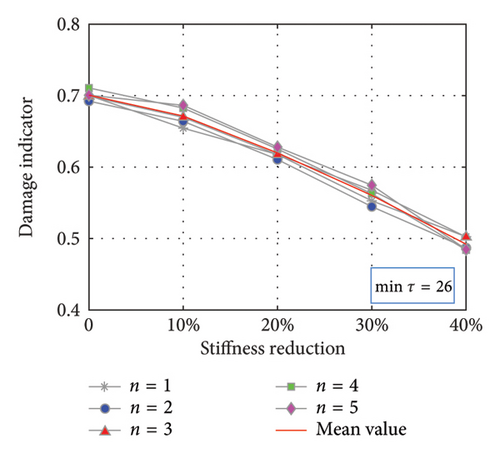
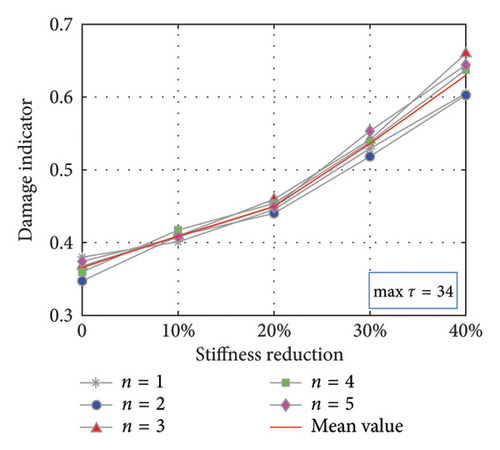
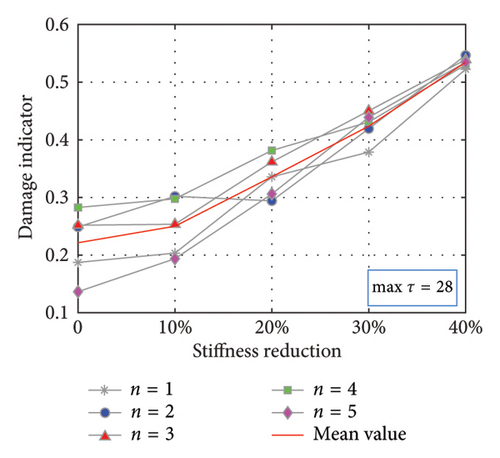
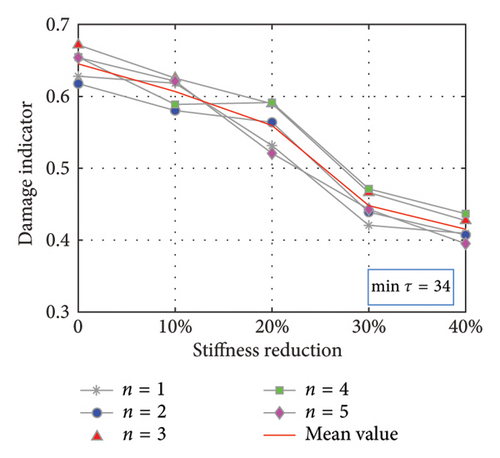
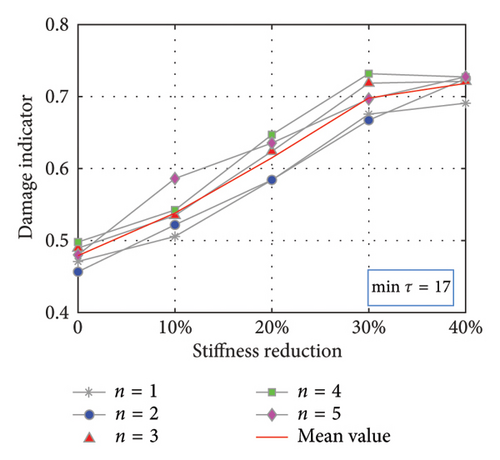
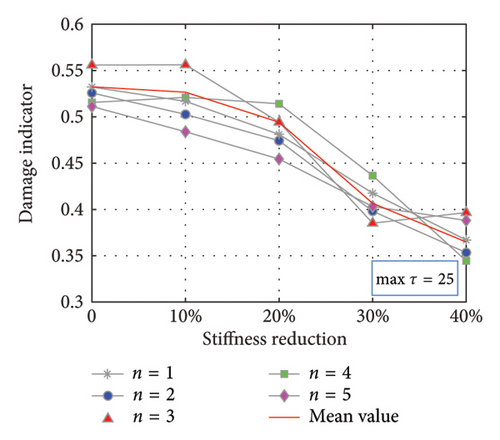
To validate the damage localization method, the critical points DOF5 and DOF7 are, respectively, selected to be the RPs as the control group, and the 10th DOF is always the MP, and the results are compared together. The subsequent steps mirror those outlined in the previous section and the repetition is omitted. The Pearson correlation coefficient Cτ as a function of τ is illustrated in Figure 8. For the condition of RP5 and MP10 in Figure 8(a) that the damage occurs still between the RP and MP, the Maximum point 28 and the Minimum point 35 are arbitrarily chosen; on the contrary for RP7 and MP10 in Figure 8(b), the Maximum point 25 and the Minimum point 17 are selected. It is observed that the trend of the curves still presents a certain periodic law, in which every extreme point theoretically works. The partition number is still 3 and the second-largest eigenvalue D continues to serve as the indicator.
3.2.2. Results
The results are depicted in Figure 9. As observed in Figures 9(a) and 9(b) for RP5 and MP10, when the Cτ curve reaches the maximum extreme points at Interval 28, the damage indicator escalates monotonically with increasing damage severity, in contrast to the behavior at Interval 34 corresponding to the minimum extreme point. Therefore, it is deduced that the damage occurred between the 5th and 10th DOFs. The opposite happens in Figures 9(c) and 9(d) for RP7 and MP10, where Interval 17 represents the minimum point on the Cτ curves, where the damage indicator rises with increasing damage severity. At the interval of 25 corresponding to the maximum point, the trend is reversed, which indicates that there is no damage present between the 7th DOF and 10th DOF. Consequently, combining this with the results of the RP7 and MP10 cases, it can be deduced that the damage is likely near the 6th DOF.
4. Experiment Validation
The experimental model used for damage identification and localization is a testbed structure located at the Los Alamos National Laboratory [48], as illustrated in Figure 10(a). An adjustable bumper mounted on the second floor is enlarged in Figure 10(b). This model is a 4-DOF structure (with the base as the 1st DOF) comprising aluminum columns and plates with bolted joints. Each floor is interconnected by an aluminum plate (30.5 × 30.5 × 2.5 cm), supported by four aluminum columns (17.7 × 2.5 × 0.6 cm). Notably, the structure is designed to slide only in the x-direction, as can be observed in Figure 10(c).


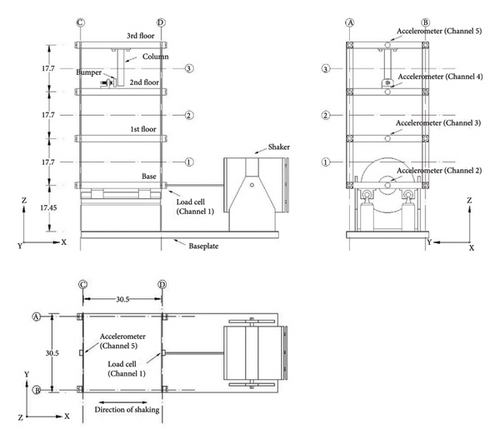
There are 17 structural states in the experiment, eight of which are utilized to validate the proposed method with damage caused by stiffness reduction and nonlinearity, as outlined in Table 1. In addition, band-limited random excitation ranging from 20 to 150 Hz is used to provide lateral excitation to the structure, and four accelerometers are mounted on each DOF to capture the structure’s acceleration responses, and the signal’s sampling frequency is set at 320 Hz, resulting in time histories covering 25.6 s.
| State | Damage condition | Description |
|---|---|---|
| 1 | Undamaged | Baseline |
| 4 | Stiffness reduction 87.5% in column 1BD | 21.8% equivalent stiffness reduction between DOF1 and DOF2 |
| 5 | Stiffness reduction 87.5% in column 1AD and 1BD | 43.7% equivalent stiffness reduction between DOF1 and DOF2 |
| 10 | Gap (0.20 mm) | Nonlinear damage at DOF3 (the lowest level of damage severity) |
| 11 | Gap (0.15 mm) | Nonlinear damage at DOF3 |
| 12 | Gap (0.13 mm) | Nonlinear damage at DOF3 |
| 13 | Gap (0.10 mm) | Nonlinear damage at DOF3 |
| 14 | Gap (0.05 mm) | Nonlinear damage at DOF3 (the highest level of damage severity) |
4.1. Experimental Results of Stiffness Reduction States
The damage caused by stiffness reduction is studied for damage identification with 3 damage cases as described in the Table 1 (State 1, State 4, and State 5). The acceleration responses of the 1st and 4th DOFs are chosen as the virtual excitation and output for damage identification (RP1 and MP4). Approximately 50 sets of independent data are available for each damage case, with 5 randomly selected from five separate trials to ascertain the effectiveness and robustness of the proposed method.
4.1.1. Damage Identification
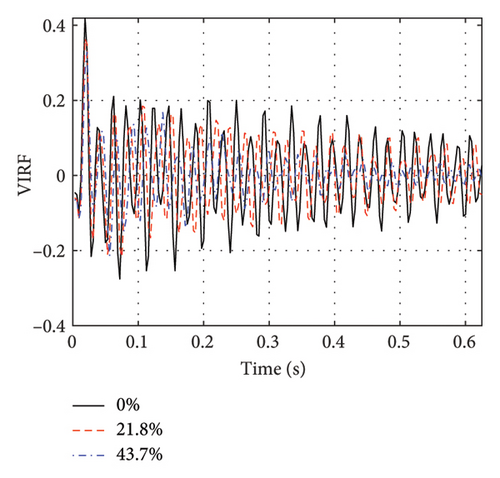
The damage indicator D, identified as the second-largest eigenvalue of the matrix, and its variation with damage severity for different extreme points are depicted in Figure 13. Essentially, the experimental results concerning the variation trend of the damage indicator for both maximum and minimum intervals align with the aforementioned numerical results, thereby corroborating the effectiveness of the proposed method for damage identification.
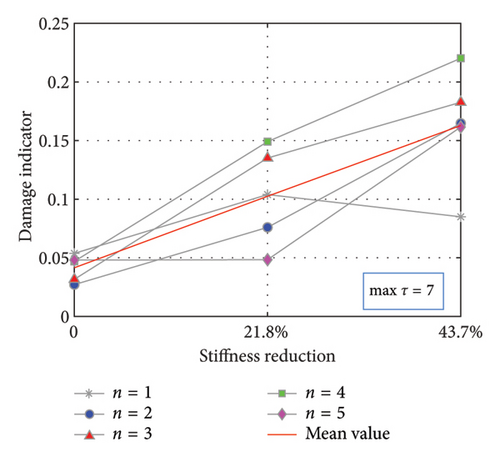
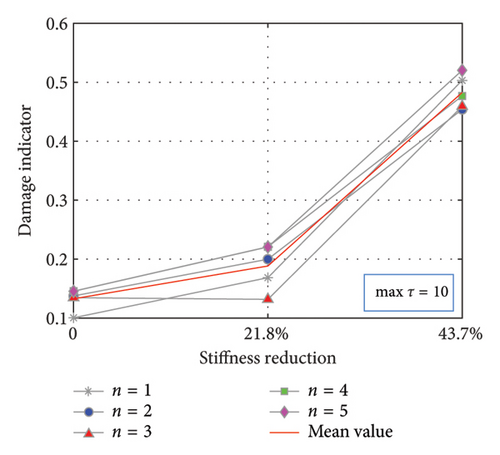
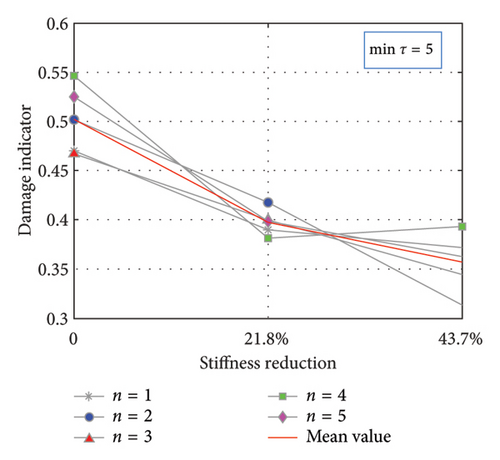
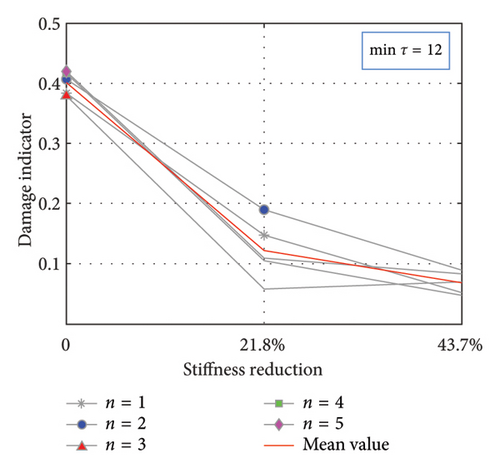
4.1.2. Damage Localization
For damage localization, the 2nd and 4th DOFs are chosen as the RP and MP (RP2 and MP4), respectively, to verify that the damage did not occur between them. In contrast, the choice of RP1 and MP2 was also explored. The operation procedure and parameter selection are the same as the damage identification (RP1 and MP4), and the data of a maximum point of the PAC curve were chosen to compare the results, as shown in Figure 14.
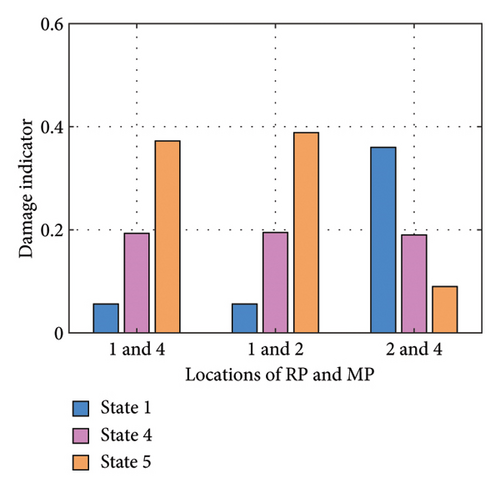
It can be intuitively seen from the bar chart that for RP1 and MP2 and RP2 and MP4, the damage indicators develop opposite with the increase of damage, but there is not much difference between the conditions RP1 and MP2 and RP1 and MP4, which verifies that the damage occurs between DOF1 and DOF2.
In addition, it can be inferred from several other choices of RP and MP that the sensitivity of the damage indicators is heightened when the damage is located between the RP and MP, leading to measured results that are less prone to interference. When the damage is not situated between and is distant from the RP and MP, errors are more likely to occur in the identification and localization of the damage.
4.1.3. Comparison With the WPT Method
Also, as a dimensionality reduction approach in damage identification, the WPT method is employed to facilitate a comparison with the proposed method, and the related conclusions have been drawn by Li and Li [25]. The average values from multiple calculations of the MSM indicator with RP1 and MP2 as well as RP1 and MP4 are displayed together. For a more intuitive comparison, the values from the three damage states collectively subtract the non-damaged state values, and the mean values of the damage indicators are normalized (the value of the non-damaged state is 0 and the value of the max-damaged state is 1), as illustrated in Figure 15(a). Similar procedures are applied to the WPT results, as depicted in Figure 15(b).
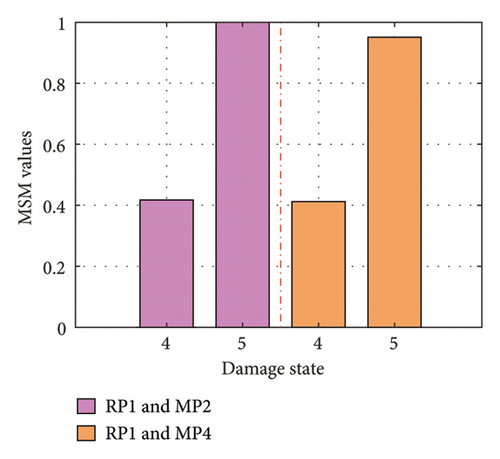
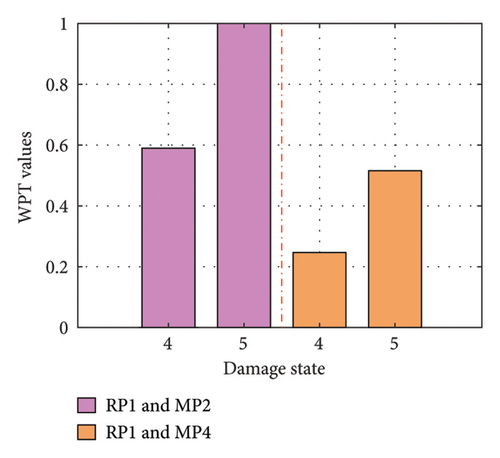
In damage identification, when the RP is RP1 and the MP shifts from MP2 to MP4, the MSM damage indicator remains relatively stable as the MP moves farther from the damage site. In contrast, the damage indicator for the WPT method noticeably decreases, leading to increased errors. Consequently, the proposed method demonstrates greater robustness in the selection of RP and MP locations.
In the context of damage localization, the WPT method relies on comparing the indicator values of different RP and MP; as in the example above, when the RP is fixed, the closer proximity between the damage and MP correlates with a higher damage indicator value. Therefore, the WPT method for damage localization demands extensive calculations, especially for complex structures, and is susceptible to error interference. In contrast, the proposed damage localization method offers better flexibility, as it provides more precise directivity in exploring the damage location.
4.2. Experimental Results of Nonlinear Damage States
The nonlinear damage is caused by the bumper in Figure 10(b). When the column contacts the bumper mounted on the second floor, damage can be simulated by inducing nonlinear behavior. The position of the bumper can be adjusted to vary the extent of impact that occurs at a particular excitation level to form 5 damage states (States 10–14) as outlined in Table 1, where the largest gap (0.20 mm) represents the lowest level of damage severity.
The proposed MSM method is also applicable in the cases of nonlinear damage, and the procedure of damage detection is the same as that of stiffness reduction cases. We select the locations of 4 RPs and MPs that are RP1 and MP4, RP2 and MP4, RP3 and MP4, and RP1 and MP2 as shown in Figure 16(a). The mean values of the indicators are then plotted with the intervals corresponding to the maximum points in the PAC in a bar chart. For the first three conditions, the damage indicators all increase gradually with the damage growth, but for the condition RP1 and MP2, the bar chart shows the opposite trend. Considering the above conditions, the damage may occur between DOF3 and DOF4.
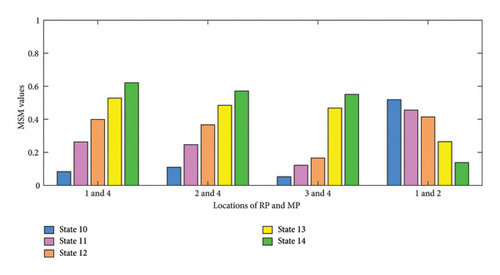
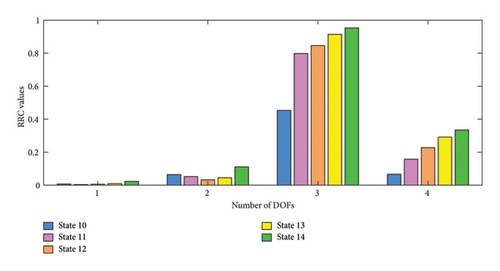
4.2.1. Comparison With the RRC Method
As a damage identification and localization method for damage identification extracting damage-sensitive features from time series models, the damage index residual reliability criterion (RRC) proposed by Entezami [17] was also verified to be reliable with nonlinear damage states in the same laboratory model. This method selected the signal from the accelerator sensors on each DOF for processing and drew a bar graph for all the cases as shown in Figure 16(b). The damage index RRC from DOF3 nearing the damage was significantly larger than other DOFs and increased with the deepening of the damage. However, except for DOF4, the development of damage could not be recognized at other DOFs.
In contrast, no significant attenuation of MSM values is observed with multiple locations of RP and MP which reflects the robustness of the MSM method in damage detection of multifreedom structures. In other words, when applied to a structure that has more degrees of freedom and the possible location of the damage is unknown, the effectiveness of the damage detection method will not deteriorate due to the different choices of signal channels. This allows for faster detection of damage occurrence and progression.
At the same time, MSM values for damage localization are also proven effective. While other methods still rely on comparing data from different locations, the method proposed can lock the scope of damage faster and use dichotomy to reduce this scope; the minimum scope is the distance between adjacent sensors. For example, damage localization on a 5-DOF structure (damage is between DOF4 and DOF5) by their method may need 5 times of calculation to process the signal of each DOF for comparison, while the MSM method only needs, RP1 and MP3 and RP3 and MP4, two steps to lock the location, thereby greatly improving the efficiency of calculation. These two ways can all realize damage localization effectively and will have different application values.
4.3. Computational Efficiency
In addition to the accuracy and robustness of damage detection, this method is also advanced in computational efficiency. Compared to the conventional STSA method [43], it can save more time in calculation because of the application of intermittent points and matrices. We use the stopwatch timer in MATLAB to calculate the time from the start to the indicator calculation of the two algorithms under the three models in Table 2, and the average of the five trials is taken. It can be seen from the Table 2 that for any model, the running time of the proposed method has a certain reduction compared to conventional STSA, which means that in the application of large structures with many DOFs, computing efficiency will be improved significantly.
| Model | Damage type | Computation time (s) | |
|---|---|---|---|
| STSA | MSM | ||
| Simulation | Stiffness reduction | 2.4673 | 1.5013 |
| Experiment | Stiffness reduction | 3.2822 | 1.9408 |
| Experiment | Nonliner damage | 3.7500 | 2.0917 |
5. Conclusions and Discussion
5.1. Conclusions
Time series–based methods for damage identification and localization consistently encounter challenges in the effective and efficient processing of the data in SHM. To address these issues, this study introduces a MSM method, offering an information-rich representation of the overall structural vibration performance for characterizing damage and establishing a reliable damage indicator: the matrix’s second-largest eigenvalue. Along with the corresponding joint occurrence entropy, the proposed MSM efficiently extracts valuable information from complex data with high accuracy.
In the process of MSM, the VIRF is initially employed to mitigate the effects of varying excitations. Subsequently, suitable intervals are selected based on the PAC Cτ, which is derived from the Pearson correlation coefficient, to construct the MSM. Concurrently, joint occurrence entropy, grounded in Shannon’s entropy, is introduced to analyze one-dimensional time series data within a two-dimensional matrix, significantly enhancing the efficiency of the calculations.
In damage localization, the flexibility in selecting MPs and RPs facilitates pinpointing the potential scope of damage and ultimately achieving damage localization by progressively narrowing the scope. In this paper, a detailed flowchart is given for damage location procedures of general structures. Both a 10-DOF numerical model subjected to random Gaussian white noise and a 4-DOF testbed structure under varying excitations have been employed to validate the method. Compared to WPT and RCC values, it is demonstrated that the innovative damage indicator is highly responsive to varying degrees of damage and is not significantly influenced by the choice of MP and RP, affirming that the refined method is more efficient and robust. The MSM method also shows advantages in comparison with the conventional method in computational efficiency.
In conclusion, the proposed method for damage identification and localization offers more precise damage detection outcomes with reduced computational effort. It possesses significant advantages in evaluating the degree of damage and ascertaining its extent, proving to be highly valuable for practical structural applications.
5.2. Limitations and Prospects
Due to the inherent limitation of the theory of VIRF, the research in this paper only considers single-point type random excitation, including the dependent ambient excitation. More validation of the MSM method on in-service structures is currently in progress.
At present, the proposed damage localization method can be applied to the one-dimensional structure that can be simplified into a chain model such as frame structures, long-span bridges, and high-level structures. For more complex spatial structures, some more complicated operations are required which will be shared in subsequent studies.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
This work was supported by the National Natural Science Foundation of China (Grant no. 52078284), the GuangDong Basic and Applied Basic Research Foundation (Grant nos. 2024A1515010090 and STKJ2023067), the Guangdong Provincial University Innovation Team Project (Grant no. 2020KCXTD012), and the Open Projects Foundation (Grant no. BHSKL20-10-KF) of the State Key Laboratory for Health and Safety of Bridge Structures. Their financial support is gratefully acknowledged. In addition, the authors would like to thank Jiezhong Huang for the invaluable guidance and support in managing the funding provided by the National Natural Science Foundation of China (Grant no. 52308318) and Tao Jiang for GuangDong Basic and Applied Basic Research Foundation (Grant no. 2022A1515010812).
Open Research
Data Availability Statement
The data are available from the corresponding author on reasonable request.




