Material Design & Processing Communication

Volume 2025, Issue 1 4664900

Research Article

Open Access

The Effect of Preexisting Fracture Angles on Crack Propagation in Sandstone

Omer Mughieda,

Omer Mughieda

orcid.org/0000-0001-8870-9986

Department of Civil Engineering , Abu Dhabi University , Abu Dhabi , UAE , adu.ac.ae

Search for more papers by this author

Abdoullah Namdar,

Corresponding Author

Abdoullah Namdar

[email protected]

orcid.org/0000-0001-9794-3424

Department of Civil Engineering , Abu Dhabi University , Abu Dhabi , UAE , adu.ac.ae

School of Civil Engineering , Iran University of Science and Technology (IUST) , Tehran , Iran , iust.ac.ir

Structural Department , Engineering Faculty , Afghan International Islamic University , Kabul , Afghanistan

Search for more papers by this author

Marwan Alzaylaie,

Marwan Alzaylaie

orcid.org/0000-0002-3910-7927

Geotechnical Dubai Development , Authority Dubai Studio City Dubai , Dubai , UAE

Search for more papers by this author

Abdul Syukor Abd.Razak,

Abdul Syukor Abd.Razak

orcid.org/0000-0002-8824-6069

Faculty of Civil Engineering Technology , University Malaysia Pahang (UMP) , Kuantan , Malaysia , ump.edu.my

Search for more papers by this author

Omer Mughieda,

Omer Mughieda

orcid.org/0000-0001-8870-9986

Department of Civil Engineering , Abu Dhabi University , Abu Dhabi , UAE , adu.ac.ae

Search for more papers by this author

Abdoullah Namdar,

Corresponding Author

Abdoullah Namdar

[email protected]

orcid.org/0000-0001-9794-3424

Department of Civil Engineering , Abu Dhabi University , Abu Dhabi , UAE , adu.ac.ae

School of Civil Engineering , Iran University of Science and Technology (IUST) , Tehran , Iran , iust.ac.ir

Structural Department , Engineering Faculty , Afghan International Islamic University , Kabul , Afghanistan

Search for more papers by this author

Marwan Alzaylaie,

Marwan Alzaylaie

orcid.org/0000-0002-3910-7927

Geotechnical Dubai Development , Authority Dubai Studio City Dubai , Dubai , UAE

Search for more papers by this author

Abdul Syukor Abd.Razak,

Abdul Syukor Abd.Razak

orcid.org/0000-0002-8824-6069

Faculty of Civil Engineering Technology , University Malaysia Pahang (UMP) , Kuantan , Malaysia , ump.edu.my

Search for more papers by this author

First published: 15 January 2025

https://doi.org/10.1155/mdp2/4664900

Academic Editor: Pavlo Maruschak

Share a link

Email
Wechat
Bluesky

Abstract

The fracture propagation on the rock causes failure and impacts the sustainability time of the structure. As part of the present work, sandstone with the variation of preexisting crack angle was simulated using the extended finite element method (XFEM). The crack propagation on sandstone has a preexisting fracture angle of 30°, 45°, and 60°, with an equivalent crack length. The impact of preexisting fracture angle on the possibility of crack propagation, failure mechanism, and displacement at a critical point of all models was studied. The numerical simulation revealed the crack angle of the model control vibration and its impact on the model’s seismic stability. The XFEM results are validated with reference to those available in the literature. Artificial neural networks (ANNs) are used for prediction by considering the training, testing, and validation process and analyzing prediction errors. The present simulation’s conclusion significantly supports the model’s displacement prediction with no crack propagation occurrence. In addition, by considering the preexisting fracture angle of a model, the load sustainability can be estimated.

Summary

•
The impact of the preexisting fracture angle on crack propagation was studied.
•
To recognize loading and unloading displacement by calling vibration mechanisms.
•
The failure mechanism and displacement were studied.
•
The results of the extended finite element method (XFEM) were validated with reference to the literature.
•
The artificial neural network (ANN) is applied for integrated prediction.

1. Introduction

The displacement and different crack types in bedrock occur due to geostress [1], seismic loading [2], and the application of external forces from the construction process, such as pile nailing [3, 4]. The nonlinear differential displacement on the soil and rock accelerates the crack propagation. Due to the complicated geostress behavior, it is necessary to recognize the seismic stability of the rock stone under seismic loading.

The angle of the preexisting crack appears in different directions and lengths, and it varies in different parts of the bedrock in association with the shape of the rock, which is critical for load transferring [5]. The crack impacts underground structures such as tunnels [6] and the stability of soil-structure interaction [7], and leads to changes in earth structure seismic stability and instability [8]. The impact of the preexisting crack angle on the damage and failure of the sandstone model needs to be investigated. In addition, it is essential to analyze the influence of seismic acceleration on the displacement of critical points of the model.

Propagation of preexisting cracks causes failure of the earth’s structure. With an increase in the number of preexisting cracks in the earth’s structure, the seismic response and nonlinear displacement, strain, stress, vibration mechanism, and failure of the model change and lead to a reduction of the safety of the earth’s structure [9]. Numerous earth structures facing liquefaction cause settlement [10, 11]. Experimental and numerical simulations have been used to study the seismic response of the earth dam, causing liquefaction in the soil foundation and internal cracks on the earth dam due to nonlinear settlement. In the numerical simulation, the crack of the earth’s structure has not been simulated [12]. Appropriate numerical simulation is essential for the cracking of the earth structure model to understand the relationship between the crack and the settlement of the model.

The failure and damage progression in brittle rocks shows that sandstone’s brittle failure is associated with the mechanical properties of rock [13]. The crack initiation and propagation on sandstone are investigated by considering stress and strain development [14]. The fracture toughness of sandstone changes with stress and strain rate mechanism [15]; due to the stress and strain associated with the crack, it is necessary to investigate the strain and strain during the crack propagation.

Fracture damage and mode classification of rock were predicted using uniaxial compression [16, 17]. Several numerical and experimental studies have been conducted to assess crack coalescence [18, 19]. Following this excellent research work, the nondestructive works were proposed through the digital image used for crack analysis in the fracture behavior [20–22], as well as using precursory acoustic emission (AE) time series for forecasting catastrophic rupture in brittle rock and concrete. The damage developments in the samples are identified by the mixing of nondestructive tests of AE and digital image correlation (DIC) with uniaxial compression testing methods in real time [23–25]. Considering previous works, the finite element method is needed to analyze the crack propagation of the rock.

The seismic loading causes sudden failure by raising critical stress on the earth’s structure, concrete [26], and rock [27], with the appearance of single and multidirectional cracks [28]. Therefore, simulation of the damage and failure law for rock containing preexisting cracks under seismic loading is vital for predicting long-term sustainable underground structure construction. In view of engineering design, the impact of the crack angle on damage and failure law must be clearly understood by the geotechnical designer. In addition, the effect of the angle of the preexisting crack on displacement at a selected model point needs to be investigated.

In geotechnical engineering, differential displacement occurs due to factors such as the application of seismic load to the model [29], nonlinear soil structure interaction [30], the shape of the foundation when the model is subjected to the seismic loading [31], heat treatment [32], liquefaction [33], and cyclic high-speed (300 km/h) train loading applying to the soil foundation [34]. Considering these reasons for the development of differential displacement, the crack propagation shape due to the preexisting crack angle must be studied accurately.

Statistical analysis has been reported to predict and classify the geotechnical results obtained from the experimental and numerical simulation outcomes [35–38]. There are several statistical attempts to predict engineering phenomena [39–41]. The ANN supports enhancement prediction through training, testing, and validation of the prediction accuracy.

Using XFEM, the shape of crack propagation due to the initial status of the preexisting crack angle was studied, as well as its impact on the failure mechanism and displacement of the model. Additionally, the displacement associated with the initial status of the preexisting crack angle was predicted using ANNs.

The objectives of the current study are as follows:

•
To evaluate the initial status of the preexisting crack angle in displacement of the model.
•
To predict the displacement of the model by employing ANNs.
•
To study multidirectional displacement at a point, recognizing them from loading and unloading displacement by calling them vibration mechanisms.

2. Method and Materials

Figure 1 demonstrates the entire numerical simulation and application of the statistical analysis process for predicting the displacement. Numerical modeling was conducted to design the clay landfill cover under seismic loading. The fracture’s angle, mechanical properties of the sandstone, and characteristics of seismic acceleration are the main parameters. In addition, the model’s failure mechanism, displacement in its selected critical point, and crack propagation are the model’s primary outcomes. These parameters have been considered according to the crack angle in the numerical simulation of the sandstone, which is subject to seismic loading in a single direction. In order to validate the results of the numerical simulation, the outcome of the simulation has been compared to available data in the literature. Table 1 illustrates the mechanical properties of the sandstone used in the numerical simulation. For all models, a single material type was selected.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The study procedure.

Table 1. Mechanical properties of sandstone [42] and geometrical properties of the model.

Poisson’s ratio, ν	Unit weight, γ (kN/m ³)	Modulus elasticity, E (MPa)	Length (L )/(mm)	Width (W )/(mm)	Thickness (h )/(mm)
0.25	24	35,000	600	600	60

Figure 2 depicts the seismic acceleration of the Florina earthquake, which occurred on January 09, 2022. The earthquake had a magnitude of 5.5 MWW and a depth of 10.0 km. The seismic acceleration in the 0°, 90°, and 360° directions has a dissimilar vibration mechanism.

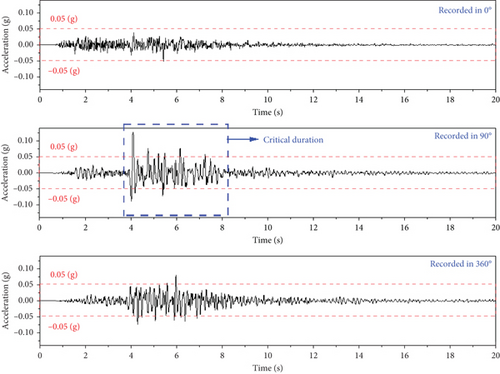
The model has been subjected to multidirectional seismic loading to simulate its boundary conditions accurately [44]. However, in the present work, the seismic acceleration was applied in a single direction for simplification. In addition, the critical duration in the 90° direction has been used in the numerical simulation.

Figure 3 demonstrates the Modified Mercalli Intensity (MMI) for the Florina earthquake with 5.5 MWW. The seismic station was used to estimate the shaking intensity of the earthquake at a specific distance, as shown in Figure 3. This effective shaking intensity of the earthquake impacts structures and objects and causes damage. According to the prediction and observation from data collection in the earthquake station, the seismic acceleration from 19.8 km away from the earthquake station was applied to the model in the numerical simulation.

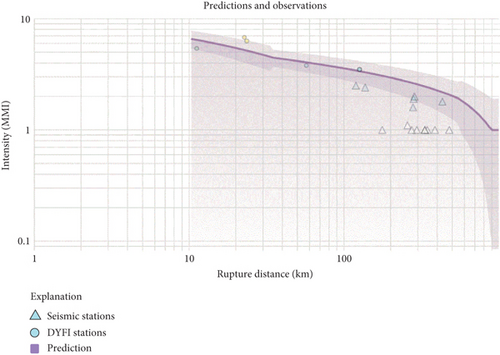
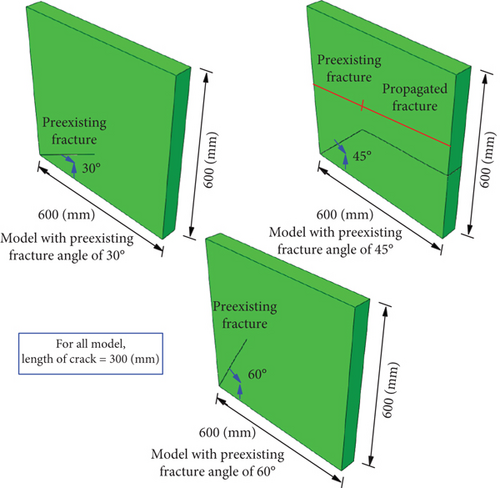
Figure 4 depicts the three models for the numerical simulation. It is assumed that the bottom of the model is rigid, and the seismic acceleration is applied to the model in the vertical direction. According to the boundary condition, the model is subjected to the nonlinear tensile loading in both positive and negative directions. The preexisting fracture’s angle of 30°, 45°, and 60° was simulated in three models. The length for all preexisting fractures is 300 mm. A point of analysis was selected for measuring the nonlinear displacement of the model during the model facing the propagation of the preexisting fracture and leading to the failure of the model.

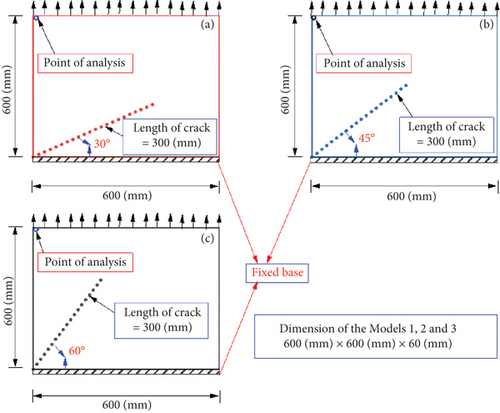
The crack propagation of rock-like material due to seismic loading has been simulated. For simplification, axial nonlinear loading was applied vertically to the model to simulate crack propagation [45]. Figure 5 used the same method of applying seismic loading. The boundary condition used in this study is presented in Figure 4.

The boundary condition of this study was previously verified according to the literature report [45].

During the transfer of seismic waves, the transmission and reflection phenomenon occurs at the interface [46]. However, due to the model’s small size, the reflection and transmission phenomena are usually unrecognizable in the numerical model [45]. As part of a recent 2022-based study, the seismic loading was applied to the specimen with 76 × 152 mm dimensions, and the transmission and reflection phenomenon did not occur [45].

Another experimental study reported appropriate results for crack propagation simulation of the specimen gypsum with 76 × 152 mm dimensions [47]. The numerical approach was carried out for crack propagation of rock-like material with 76 × 152 mm dimensions, and the same numerical simulation results were observed in laboratory experiments [48]. In addition, for the simulation of crack propagation on rock-like material, the experimental investigation has been done by designing a specimen of 635 × 279 × 203 mm dimensions [49]. In the current study, with the transfer of seismic waves, the transmission and reflection phenomenon, and acceptable results from the previous research, the specimen with the size of 600 ×600 ×60 mm dimensions has been designed for the simulation of the crack propagation. The model contains preexisting cracks, and the seismic loading was applied based on the seismic data from the Florina earthquake mentioned previously.

2.1. ANN

ANN establishes a nonlinear connection from the input to the output of a system without acknowledging the statistically simulated model. By using algorithms to train, test, and validate the data, ANN produces appropriate predictions concerning input with acceptable generalization and quality.

The backpropagation (BP) algorithm is the keystone of the neural network training process. The algorithm improves prediction by minimizing error by applying the forward and backward phases. The forward pass provides propagation and transformation of the input at all ANN layers individually, and the backward pass improves the connection of weights and bias [50]. An accurately designed ANN produces a precise input–output. Overfitting data is a potential problem in ANN. Overfitting is an occurrence in ANN that memorizes the training phase data alone. An ANN subjected to overfitting training cannot represent the actual relationship between the inputs and outputs [51, 52]. The training and validation errors are compared to avoid overfitting, and the training error must not be smaller than the validation error. The training phase needs to stop at an appropriate point [53]. BP performs highly in ANN and can develop nonlinear mapping with associated nonlinear relationships between inputs and outputs [54]. It has been seen that ANN presents acceptable precision in the calculation of crack openings [55]. Selecting a single hidden layer for ANN architectural design leads to acceptable results [56]. The present study selects a single hidden layer for ANN architectural design.

Because of the high experimental laboratory requirements budget and to minimize the time in making engineering decisions, ANN is used in many geotechnical engineering [36, 37]. In addition, recent studies show that advanced mathematical methods applied in ANN and statistical methods result in appropriate prediction and also support the integrated results of the experiment with more accuracy compared to the old method [36–41].

The n presented input as x = x₁, x₂, ⋯, x_n. Each input is linked with a weight that is selected randomly. The nodes of the hidden layer output and their values are calculated using Equation (1). And finally, the output of the entire network is calculated by using Equation (2) [57].

()

In Equations (1) and (2), n_in presented the quantity of required input for nodes of the network, n_hid stands for the number of designed hidden nodes, w_ij refers to the weight of joining the i_th input node to the j_th hidden node, b_j refers to the bias of the network for the j_th hidden node, x_i stands for the i_th feature of the input vector, n_in will be the output of the i_th input node, and g presented for the activation function of the hidden nodes. n_out is presented for the number of nodes at the output layer, w_jk refers to the weight linking the j_th hidden node and the k_th output node, b_k stands for the bias of the k_th output node, and f refers to the transfer function of the k_th output node [57].

Each processing element comprises weighted inputs, a transfer function, and one output. Equation (3) indicates the sigmoid function which is a popular activation function. The activation function performs a forceful role in estimating nodes’ output [58]. In the present study, the sigmoid function is used. The sigmoid function is a nonlinear S-shaped function that designs nonlinear planning to make appropriate input and output connections.

()

In this study, the Levenberg–Marquardt algorithms, the training, validation, and test data have been applied by using the Abalone Data Analysis set.

According to the statistical analysis presented in the literature [59], Equations (4) and (5) are used to assess the prediction quality made by ANN.

()

where d is the acquired nonlinear displacement by XFEM, d_p is the predicted nonlinear displacement by ANNs, and

is the mean of nonlinear displacement from XFEM.

The ANN has been used to predict a connection between crack propagation magnitudes and characteristics of the cyclic load [60]. In the lack of crack propagation, the impact of the preexisting crack angle on the displacement mechanism of the model must be investigated using ANN. ANN is a nondestructive testing procedure that supports engineering decision-making, seismic design reliability evaluation, and trustworthiness management performance. Figure 6 shows a flow chart and simplified ANN design.

2.2. XFEM

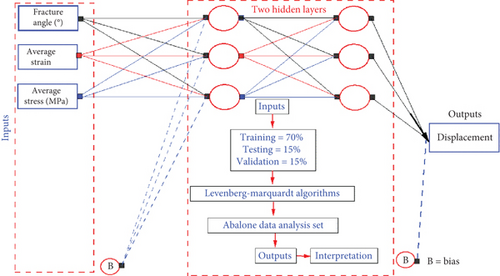
Belytschko and Black proposed the XFEM. Based on this concept, XFEM was applied in the Abaqus, and 3D XFEM was used for crack propagation of the backfill [8, 9] and clayey cover of the landfill [2]. XFEM is usually adopted for geotechnical engineering [2, 8, 9]. Equation (6) is the standard form for crack propagation by performance of XFEM in the advanced numerical simulation [61, 62]. For integration, Belytschko et al. [63] proposed a more accurate Equation (7), entitled the shifted XFEM assessment.

()

Equation (8) is used to obtain the displacement field according to the XFEM [64].

()

where a_i is the unknowns associated with the enrichment, b_i is the degrees of freedom of the enriched nodes, F_α is the crack-tip function, H is the Heaviside function, N_i(x) is the standard finite element shape functions,

is the partition of unity, u_i is the standard finite element unknowns, and Ψ(x) is the global enrichment function

In the present work, the initial preexisting crack is one of the main parameters for using XFEM.

3. Results and Discussion

According to Figure 7, when applying the same magnitude of seismic acceleration and boundary condition, the angle of the preexisting crack is responsible for the propagation crack. The interface strength of the crack was associated with the angle of the propagation crack. The loading and unloading stiffness of the model was changed in association with the crack’s angle on the crack propagation process. According to the numerical simulation results, the model with the preexisting fracture angle of 45° contained the preexisting fracture and propagated fracture sections.

The crack on the model propagates during the changing direction of the seismic loading [45], and the simulated model’s loading and unloading minimize the material’s strength and stiffness and lead to the model’s failure.

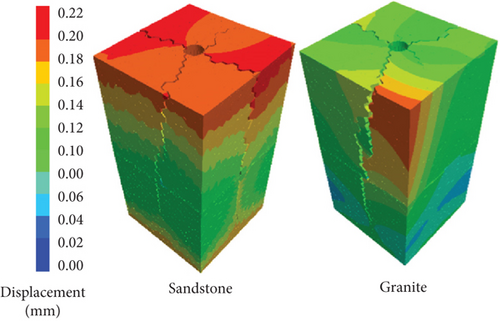
Figure 8 shows the displacement applied to the selected point. Figure 4 highlights the selected point for analyzing the displacement in the vertical direction. Based on the boundary condition, the main applied load on the model is seismic loading in the vertical direction. The vertical displacement is depicted in Figures 8 and 9 for the models with the preexisting fracture angles of 30°, 45°, and 60°. The model with a preexisting fracture angle of 45° has a different displacement mechanism than the model with the preexisting fracture angles of 30° and 60°. The propagation of the crack causes a change in the displacement mechanism.

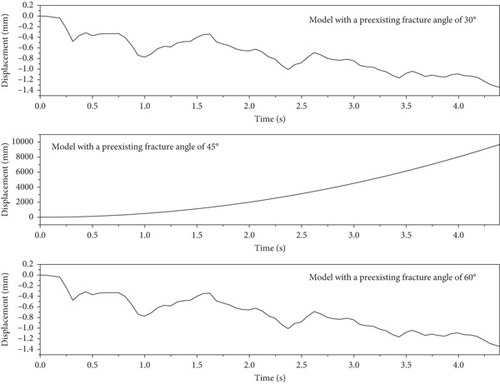
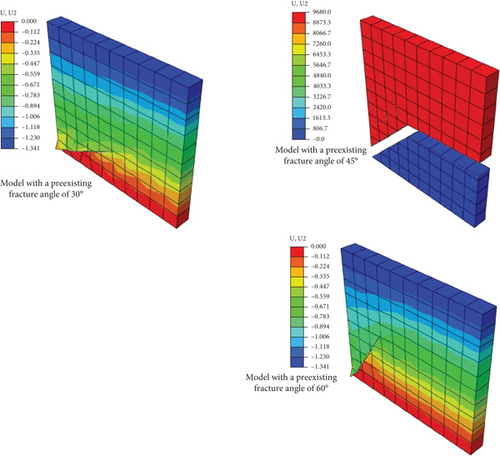
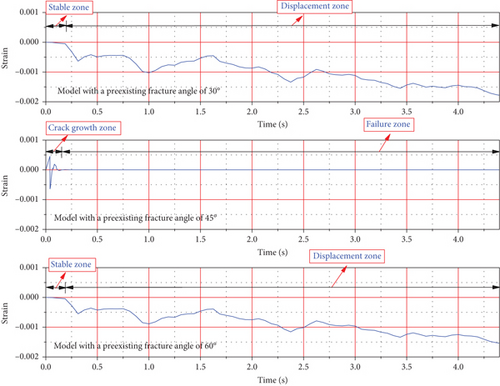
Figure 9 illustrates the displacement and failure mechanisms of the models. The models with the preexisting fracture angles of 30° and 60° are subjected to punching in the lower part of the preexisting fracture. During the final stage of the numerical simulation, two parts of the model, with the preexisting fracture angles of 45°, have been separated, which impacts recording placement. Concerning Figures 10 and 11, by considering stress and strain diagrams, it is observed that the crack propagation of the model with preexisting fracture angles of 45° has been completed in time before 0.14 s. In comparison, the models with the preexisting fracture angles of 30° and 60° have resistance against crack propagation until the applied acceleration loading ends.

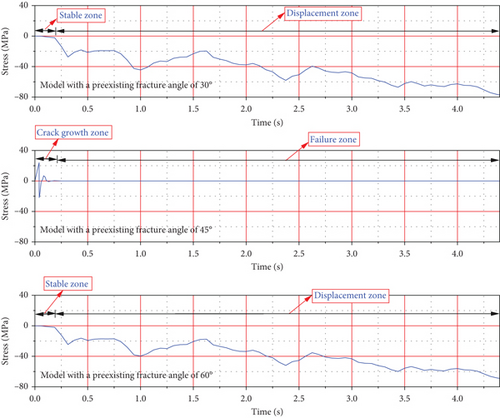
Crack propagation was associated with the stress developing in the model. The model with a preexisting fracture angle of 45° faces a different mechanism of stress fluctuation compared to the model with preexisting fracture angles of 30° and 60°. During crack propagation, the stress exhibits high and low levels. When the model is not subjected to crack propagation, the stress causes displacement in the negative direction. The stress associated with the crack propagation controls the displacement produced in the model.

The seismic loading acts on the rock in multiple directions, developing tension and shear loading. The crack propagation results from seismic loading, rock fracture mechanics, and seismic energy studied [65, 66]. The XFEM outcome was validated using the scale test results [67]. In this study, the XFEM-simulated sandstone fracture agrees well with that available in the literature [45].

Concerning Figures 10 and 11, after applying seismic acceleration to the model, a multidimensional failure configuration model has been depicted. The seismic response process, including the model with preexisting fracture angles of 30° and 60°, exhibits a stable zone and displacement zone, while the model with a preexisting fracture angle of 45° has a crack growth zone and failure zone. Changing preexisting fracture angles leads to modification of the model seismic response. There is a direct relationship between the fracture’s seismic toughness and the shape of the preexisting crack. Preexisting fracture angle morphology changes the seismic response of the model from a developing displacement to crack growth.

Based on the fracture mechanics prediction, it has been observed that the level of fracture seismic toughness and preexisting fracture angle morphology of the model is responsible for the developing, stable zone, displacement zone, crack growth zone, and failure zone of the model. The preexisting crack of the rock model changes the stiffness of the rock through the fracture’s seismic toughness. In addition, the shape of the preexisting fracture angle controls the external nonlinear loading applied to the model.

According to Figure 12, regression analysis for displacement prediction, the regression formula is presented based on the relationship between the target and outcome. Four different regression formulas exist for training, testing validation, and overall. For the relationship between output and target, refer to Figure 12 on the x-axis and y-axis.

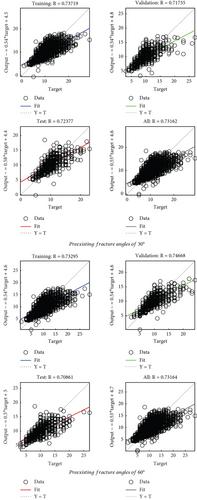
Tables 2 and 3 illustrate the data used in ANN. To integrate the displacement prediction, ANN has been applied to the models with preexisting fracture angles of 30° and 60° that do not face propagation. Table 4 presents the coefficient of determination (R²) and mean squared error (MSE).

Table 2. Data used in ANNs for the model with a preexisting fracture angle of 30°.

No.	Fracture angle (°)	Average strain	Average stress (MPa)	Average displacement (mm)
1	30	−1.46627e − 5	0.60127	0.00524
2	30	−2.17066e − 4	−1.82821	−0.03561
3	30	−4.85433e − 4	−27.26469	−0.44882
4	30	−4.77652e − 4	−19.50649	−0.35018
5	30	−4.43228e − 4	−19.18037	−0.33195
6	30	−5.51786e − 4	−19.86613	−0.35548
7	30	−0.001	−38.1682	−0.68537
8	30	−8.39e − 4	−41.10773	−0.70624
9	30	−7.52002e − 4	−33.06416	−0.5754
10	30	−6.35313e − 4	−28.03959	−0.48665
11	30	−4.67755e − 4	−22.59276	−0.39251
12	30	−6.5899e − 4	−24.26267	−0.41837
13	30	−7.95721e − 4	−32.21675	−0.55821
14	30	−8.68582e − 4	−37.52411	−0.6519
15	30	−9.4283e − 4	−38.05542	−0.65614
16	30	−0.0012	−47.71801	−0.81399
17	30	−0.00121	−55.18875	−0.97479
18	30	−9.69834e − 4	−44.99559	−0.80297
19	30	−0.00105	−43.2751	−0.73785
20	30	−0.0011	−47.76748	−0.828
21	30	−0.00118	−48.82255	−0.83533
22	30	−0.00128	−55.16225	−0.95665
23	30	−0.00142	−60.09551	−1.03435
24	30	−0.00147	−65.74971	−1.16203
25	30	−0.00144	−61.51245	−1.05199
26	30	−0.00149	−64.04928	−1.12105
27	30	−0.00148	−65.02705	−1.15059
28	30	−0.00149	−64.33574	−1.1022
29	30	−0.00158	−67.48391	−1.14975
30	30	−0.00179	−76.67403	−1.29864

Table 3. Data used in ANNs for the model with a preexisting fracture angle of 60°.

No.	Fracture angle (°)	Average strain	Average stress (MPa)	Average displacement (mm)
1	60	−1.2579e − 6	0	0.01045
2	60	−9.94953e − 5	−1.44689	−0.0319
3	60	−4.66846e − 4	−22.03171	−0.4721
4	60	−4.25406e − 4	−16.7743	−0.34048
5	60	−3.81802e − 4	−17.23474	−0.33313
6	60	−4.41857e − 4	−16.98832	−0.34829
7	60	−8.53586e − 4	−32.06744	−0.67297
8	60	−7.58396e − 4	−37.33546	−0.70911
9	60	−6.65477e − 4	−29.43286	−0.57548
10	60	−5.50742e − 4	−25.28501	−0.48562
11	60	−4.19424e − 4	−20.6971	−0.38831
12	60	−5.58429e − 4	−20.37453	−0.43495
13	60	−6.73008e − 4	−28.47592	−0.56483
14	60	−7.5033e − 4	−33.48684	−0.6528
15	60	−7.94566e − 4	−33.59655	−0.66737
16	60	−0.00101	−41.80149	−0.84395
17	60	−0.00105	−50.01415	−0.94668
18	60	−8.52342e − 4	−40.97703	−0.76799
19	60	−8.93517e − 4	−38.22011	−0.76216
20	60	−9.52801e − 4	−42.61824	−0.83185
21	60	−0.00101	−43.15088	−0.86362
22	60	−0.0011	−49.24388	−0.96018
23	60	−0.00122	−53.52478	−1.05297
24	60	−0.00128	−59.17075	−1.12694
25	60	−0.00124	−54.74662	−1.07824
26	60	−0.00129	−57.18973	−1.11867
27	60	−0.00128	−58.2887	−1.12042
28	60	−0.00129	−57.3529	−1.12421
29	60	−0.00137	−60.05804	−1.18921
30	60	−0.00155	−68.30408	−1.34861

Table 4. R² and MSE outcomes of models with preexisting fracture angles of 30° and 60°.

	—	Training	Validation	Test	Number of layers in ANNs
Preexisting fracture angles of 30°	R²	0.7372	0.7174	0.7238	1
Preexisting fracture angles of 30°	RMSE	4.8610	4.9945	4.5595	1
Preexisting fracture angles of 60°	R²	0.7330	0.7467	0.7086	1
Preexisting fracture angles of 60°	RMSE	4.7105	4.8422	5.3731	1

Regarding the literature, the present study designed the ANN with two hidden layers [56]. The input parameters for ANN are average strain and stress in the critical selected point of the model and the preexisting fracture angles of the model. After the data generation by Abalone Data Analysis was applied in the Levenberg–Marquardt algorithms, the training, validation, and test data were 2923, 627, and 627, respectively.

The ANN was designed to treat displacement prediction as a main regression problem. Figure 12 presents regression analysis for displacement prediction in the models with preexisting fracture angles of 30° and 60°. It is essential to observe that the regression analysis is designed for displacement prediction assessment. Multiple variables were considered instead of a single variable.

The target and output are concurrent variables of the prediction model and share correlation information across targets considered for displacement prediction [68]. In the current study, Abalone Data Analysis generated sufficient data to predict displacement without changing the main characteristics of the data.

Figure 13 shows the histograms for displacement prediction in the models with preexisting fracture angles of 30° and 60°. Each input variable directly impacts the output when using a histogram. Based on the displacement prediction by the histograms, the preexisting fracture angles directly impact the model’s vibration mechanism and failure pattern.

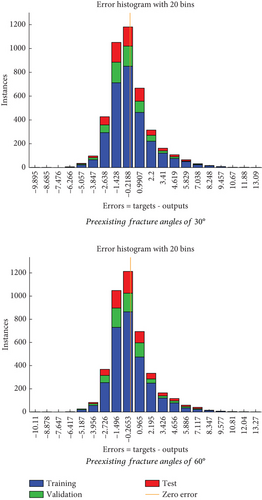
Table 4 illustrates R² and root mean squared error (RMSE) obtained to evaluate prediction accuracy. In ANN related to validation, training, and testing data, the overfitting problem was not observed.

In ANN architectural design, 70% of training data, 15% of testing data, and 15% of validation data were selected. To minimize error in the transformation of the input at all ANN layers, the appropriate ANN architectural design plays a key function. To avoid overfitting data, producing low-quality training data, and pressurizing on validation and test data, ANN architectural design needs to be allocated properly. Due to the huge data in the present study, none of the motioned problems have occurred. Figure 14 shows the cost function variations chart that has been represented for each model concerning the training, validation, and test data. The best validation performance of the prediction accuracy of displacement for models containing preexisting fracture angles of 30° and 60° is illustrated.

3.1. Validation of Simulation and Prediction

Crack propagation initiates if tensile displacement occurs due to the seismic loading applied to the sandstone [45]. In the models with the preexisting fracture angles of 30° and 60°, compressive displacement was observed. Meanwhile, in the model with the preexisting fracture angles of 45°, the tensile displacement has occurred. The effectiveness of the proposed model is validated by comparing it with those reported in the literature.

Figures 15 and 16 describe the wave–crack interactions in the experimental and numerical simulation considering the location of the crack appearance, strain energy magnitude, material’s rock, and displacement mechanism [69]. Based on the crack angle, the crack propagation exhibits differently. The resultant strain energy causes crack propagation or compressive displacement and tensile displacement to the model.

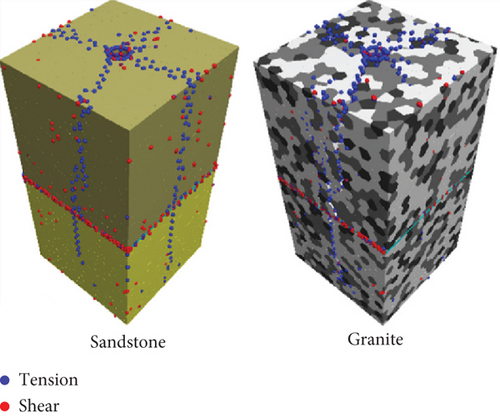
Repeating axial seismic loading causes crack propagation. Due to the change in direction of the seismic loading from axial to lateral, the preexisting fracture angle leads to propagation [45]. When the model contains a preexisting crack with 45°, the seismic loading changes direction, and the fracture seismic toughness model reaches the minimum level. Due to these reasons and based on the boundary conditions of the simulated model, the model with preexisting fracture angles of 30° and 60° has not been subjected to crack propagation.

The model seismic response mode classification is made. To validate the crack simulation mechanism, the seismic response of the model is classified into the stable zone, displacement zone, crack growth zone, and failure zone in association with the preexisting crack angle model.

In the displacement zone, the seismic loading is applied in a single direction, while in the crack growth zone, the seismic loading changes direction from axial to lateral.

4. Conclusion

The current study simulated sandstone with preexisting fracture angles of 30°, 45°, and 60° and equal crack length in all models. The models were then subjected to seismic simulated loading to analyze the shape of crack propagation on the failure mechanism and displacement at a critical point of the model.

-
In equal seismic acceleration, the angle of the preexisting crack is responsible for the propagation of the crack, displacement magnitude, and failure mechanism of the model.
-
A propagation crack occurs when the preexisting crack of the model is 45°. The models with 30 and 60° preexisting cracks exhibit higher interface strength and higher seismic stability.
-
According to the boundary condition of the simulated model, the direction of the applied seismic load was constant, and the preexisting fracture angle is an essential function in the crack propagation.
-
The stiffness and strength of the model are related to preexisting cracks, which have developed in the structure due to previous earthquakes.
-
The direction of the crack growth zone within the simulated specimen has been identified. The seismic response of the model is divided into the model’s stable zone, displacement zone, crack growth zone, and failure zone. There is a direct relationship between the fracture’s seismic toughness and the shape of the preexisting crack. The preexisting crack of the rock changes the stiffness of the rock through the fracture’s seismic toughness. The higher fracture seismic toughness leads to minimized crack propagation of the model. In addition, the tensile displacement is responsible for creating a crack growth zone. The approach of the study lies in the application of the ANN to analyze the multifaceted displacement mechanism performance of the model under seismic acceleration.
-
There are many cracks in the several structures. The paper’s outcome helps to understand which type of crack is more critical for the seismic stability of the structure. Based on the propagation of the crack, the failure of the structure and displacement can be predicted.
-
The present simulation significantly supports the prediction failure mechanism of the model with the changing angle of the preexisting crack.
-
In future research work, the types of cracks, the geometry of the preexisting crack, initial and dynamic boundary conditions, material characteristics, nature of loading, simulation method, and adaptation of the theoretical concept in the numerical simulation could be parameters for investigation.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This study was funded by the Abu Dhabi University, Abu Dhabi, UAE, as a part of an internal project.

Open Research

Data Availability Statement

Data are contained within this manuscript. Enquiries about data availability should be directed to the authors.

References

1 Liu P., Ju Y., Ranjith P. G., Zheng Z., and Chen J., Experimental investigation of the effects of heterogeneity and geostress difference on the 3D growth and distribution of hydrofracturing cracks in unconventional reservoir rocks, Journal of Natural Gas Science and Engineering. (2016) 35, 541–554, https://doi.org/10.1016/j.jngse.2016.08.071, 2-s2.0-84991112443.
10.1016/j.jngse.2016.08.071
CAS Web of Science® Google Scholar
2 Namdar A., Karimpour-Fard M., Mughieda O., Berto F., and Muhammad N., Crack simulation for the cover of the landfill - a seismic design, Frattura ed Integrità Strutturale. (2023) 17, no. 65, 112–134, https://doi.org/10.3221/IGF-ESIS.65.09.
10.3221/IGF-ESIS.65.09
Google Scholar
3 Namdar A., Mughieda O., Liu Y., Deyu Y., Dong Y., and Chen Y., Prediction of the single pile seismic deflection by using FEM and ANN, Geotechnical and Geological Engineering. (2024) 42, no. 3, 2025–2044, https://doi.org/10.1007/s10706-023-02659-3.
10.1007/s10706-023-02659-3
Google Scholar
4 Chen Y., Lu F., Namdar A., and Cai J., Working mechanism of pile group with different pile spacing in dense sand, Advances in Civil Engineering. (2019) 2019, no. 1, https://doi.org/10.1155/2019/5376594, 2-s2.0-85069052208, 5376594.
10.1155/2019/5376594
Web of Science® Google Scholar
5 Gao X., Zhang Y., Hu J., Huang Y., Liu Q., and Zhou J., Site-scale bedrock fracture modeling of a spent fuel reprocessing site based on borehole group in northwest, China, Engineering Geology. (2022) 304, 106682, https://doi.org/10.1016/j.enggeo.2022.106682.
10.1016/j.enggeo.2022.106682
Google Scholar
6 Chen J., Hu T., Hu X., and Jia K., Study on the influence of crack depth on the safety of tunnel lining structure, Tunnelling and Underground Space Technology. (2024) 143, 105470, https://doi.org/10.1016/j.tust.2023.105470.
10.1016/j.tust.2023.105470
Google Scholar
7 Shabani A. and Kioumarsi M., Seismic assessment and strengthening of a historical masonry bridge considering soil-structure interaction, Engineering Structures. (2023) 293, https://doi.org/10.1016/j.engstruct.2023.116589.
10.1016/j.engstruct.2023.116589
Google Scholar
8 Namdar A., Karimpour-Fard M., Berto F., and Muhammad N., Prediction of the displacement mechanism of the cracked soil using NXFEM and artificial neural networks, Procedia Structural Integrity. (2023) 47, 636–645, https://doi.org/10.1016/j.prostr.2023.07.058.
10.1016/j.prostr.2023.07.058
Google Scholar
9 Namdar A., Karimpour-Fard M., and Muhammad N., The seismic resistance simulation for cracked clayey backfill, Engineering Failure Analysis. (2022) 140, 106616, https://doi.org/10.1016/j.engfailanal.2022.106616.
10.1016/j.engfailanal.2022.106616
Google Scholar
10 Namdar A., Liquefaction zone and differential settlement of cohesionless soil subjected to dynamic loading, Electronic Journal of Geotechnical Engineering. (2016) 21, no. 2, 593–605.
Google Scholar
11 Namdar A. and Khodashenas Pelko A., Embankment loading analysis in laboratory conditions, Ingenieria e Investigacion. (2011) 31, no. 2, 48–51, https://doi.org/10.15446/ing.investig.v31n2.23602.
10.15446/ing.investig.v31n2.23602
Web of Science® Google Scholar
12 Cui C. Y., Seismic behavior and reinforcement mechanisms of earth dam and liquefiable foundation system by shaking table tests and numerical simulation, Soil Dynamics and Earthquake Engineering. (2023) 173, 108083, https://doi.org/10.1016/j.soildyn.2023.108083.
10.1016/j.soildyn.2023.108083
Google Scholar
13 Mughieda O., Guo L., Tang Y., Okasha N. M., Azimi S. J., Namdar A., and Azhar F., The displacement mechanism of the cracked rock - a seismic design and prediction study using XFEM and ANNs, Advanced Modeling and Simulation in Engineering Sciences. (2024) 11, no. 1, https://doi.org/10.1186/s40323-024-00261-7.
10.1186/s40323-024-00261-7
Google Scholar
14 Abbas H. A., Mohamed Z., and Abdul Kudus S., Deformation behaviour, crack initiation and crack damage of weathered composite sandstone-shale by using the ultrasonic wave and the acoustic emission under uniaxial compressive stress, International Journal of Rock Mechanics & Mining Sciences. (2023) 170, 105497, https://doi.org/10.1016/j.ijrmms.2023.105497.
10.1016/j.ijrmms.2023.105497
Google Scholar
15 Roy D. G. and Singh T. N., Effect of heat-treatment on the pure-and mixed-mode fracture properties of a homogeneous sandstone, Geomechanics for Energy and the Environment. (2023) 33, 100430.
10.1016/j.gete.2022.100430
Google Scholar
16 Moghaddam R. H. and Golshani A., Fatigue behavior investigation of artificial rock under cyclic loading by using discrete element method, Engineering Failure Analysis. (2024) 160, 108105, https://doi.org/10.1016/j.engfailanal.2024.108105.
10.1016/j.engfailanal.2024.108105
Web of Science® Google Scholar
17 Ray S. K., Sarkar M., and Singh T. N., Effect of cyclic loading and strain rate on the mechanical behaviour of sandstone, International Journal of Rock Mechanics and Mining Sciences. (1999) 36, no. 4, 543–549, https://doi.org/10.1016/S0148-9062(99)00016-9, 2-s2.0-0033150332.
10.1016/S0148-9062(99)00016-9
Web of Science® Google Scholar
18 Pali E., Gravouil A., Tanguy A., Landru D., and Kononchuk O., Three-dimensional X-FEM modeling of crack coalescence phenomena in the Smart CutTMtechnology, Finite Elements in Analysis and Design. (2023) 213, 103839, https://doi.org/10.1016/j.finel.2022.103839.
10.1016/j.finel.2022.103839
Google Scholar
19 Sagong M. and Bobet A., Coalescence of multiple flaws in a rock-model material in uniaxial compression, International Journal of Rock Mechanics & Mining Sciences. (2002) 39, no. 2, 229–241, https://doi.org/10.1016/S1365-1609(02)00027-8, 2-s2.0-0036478775.
10.1016/S1365-1609(02)00027-8
Web of Science® Google Scholar
20 Bhosale A. B., Lakavath C., and Suriya Prakash S., Multi-linear tensile stress-crack width relationships for hybrid fibre reinforced concrete using inverse analysis and digital image correlation, Engineering Structures. (2020) 225, 111275, https://doi.org/10.1016/j.engstruct.2020.111275.
10.1016/j.engstruct.2020.111275
Google Scholar
21 Sharafisafa M., Aliabadian Z., and Shen L., Crack initiation and failure of block-in-matrix rocks under Brazilian test using digital image correlation, Theoretical and Applied Fracture Mechanics. (2020) 109, 102743, https://doi.org/10.1016/j.tafmec.2020.102743.
10.1016/j.tafmec.2020.102743
Web of Science® Google Scholar
22 Khlif I., Pop O., Dupré J. C., Doumalin P., and Huger M., Investigation of microstructure-property relantionships of magnesia hercynite refractory composites by a refined digital image correlation technique, Journal of the European Ceramic Society. (2019) 39, no. 13, 3893–3902, https://doi.org/10.1016/j.jeurceramsoc.2019.05.010, 2-s2.0-85065502689.
10.1016/j.jeurceramsoc.2019.05.010
Google Scholar
23 Lockner D., The role of acoustic emission in the study of rock fracture, International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts.(1993) 30, no. 7, 883–899, https://doi.org/10.1016/0148-9062(93)90041-B, 2-s2.0-0027849372.
10.1016/0148-9062(93)90041-B
Web of Science® Google Scholar
24 Rodríguez P. and Celestino T. B., Application of acoustic emission monitoring and signal analysis to the qualitative and quantitative characterization of the fracturing process in rocks, Engineering Fracture Mechanics. (2019) 210, 54–69, https://doi.org/10.1016/j.engfracmech.2018.06.027, 2-s2.0-85049321270.
10.1016/j.engfracmech.2018.06.027
Web of Science® Google Scholar
25 Aggelis D. G., Classification of cracking mode in concrete by acoustic emission parameters, Mechanics Research Communications. (2011) 38, no. 3, 153–157, https://doi.org/10.1016/j.mechrescom.2011.03.007, 2-s2.0-79955585426.
10.1016/j.mechrescom.2011.03.007
Web of Science® Google Scholar
26 Lak M., Baghbanan A., and Hashemolhosein H., Effect of seismic waves on the hydro-mechanical properties of fractured rock masses, Earthquake Engineering and Engineering Vibration. (2017) 16, no. 3, 525–536, https://doi.org/10.1007/s11803-017-0406-9, 2-s2.0-85021878839.
10.1007/s11803-017-0406-9
Google Scholar
27 Namdar A., Impact of soil crack on embankment seismic resistance, Procedia Structural Integrity. (2022) 39, 47–56, https://doi.org/10.1016/j.prostr.2022.03.071.
10.1016/j.prostr.2022.03.071
Google Scholar
28 Namdar A., Darvishi E., Feng X., Zakaria I., and Yahaya F. M., Effect of flexural crack on plain concrete beam failure mechanism - a numerical simulation, Frattura ed Integrità Strutturale. (2016) 10, no. 36, 168–181, https://doi.org/10.3221/IGF-ESIS.36.17, 2-s2.0-84962481619.
10.3221/IGF-ESIS.36.17
Google Scholar
29 Namdar A. and Dong Y., The embankment-subsoil displacement mechanism, Material Design & Processing Communications (MDPC). (2020) 2, no. 3, https://doi.org/10.1002/mdp2.155.
10.1002/mdp2.155
Google Scholar
30 Namdar A., The multilayered soil-structure seismic interaction and structure vibration mechanism, Frattura ed Integrità Strutturale. (2020) 14, no. 51, 267–274, https://doi.org/10.3221/IGF-ESIS.51.21.
10.3221/IGF-ESIS.51.21
Google Scholar
31 Namdar A., Dong Y., and Deyu Y., The effect of concrete footing shape in differential settlement: a seismic design, Advances in Civil Engineering. (2019) 2019, no. 1, 9747896, https://doi.org/10.1155/2019/9747896, 2-s2.0-85065649172.
10.1155/2019/9747896
Google Scholar
32 Wang S. and Huang Y., Experimental study on the effect of particle breakage on the shear characteristics of large-displacement soil exposed to heat treatment, Engineering Geology. (2023) 323, 107219, https://doi.org/10.1016/j.enggeo.2023.107219.
10.1016/j.enggeo.2023.107219
Google Scholar
33 Maheshwari B. K. and Firoj M., Settlement of combined piled raft foundation of a nuclear power plant in non-liquefiable and liquefiable soils, Nuclear Engineering and Design. (2023) 413, https://doi.org/10.1016/j.nucengdes.2023.112518.
10.1016/j.nucengdes.2023.112518
Google Scholar
34 Luo R., Yang M., and Li W., Normalized settlement of piled raft in homogeneous clay, Computers and Geotechnics. (2018) 103, 165–178, https://doi.org/10.1016/j.compgeo.2018.07.023, 2-s2.0-85050555648.
10.1016/j.compgeo.2018.07.023
Google Scholar
35 Mughieda O. S., Bani-Hani K., and Abu Safeh B. F., Liquefaction assessment by artificial neural networks based on CPT, Journal of Geotechnical and Geoenvironmental Engineering. (2009) 3, no. 2, 289–302, https://doi.org/10.3328/IJGE.2009.03.02.289-302, 2-s2.0-84922791345.
10.3328/IJGE.2009.03.02.289-302
Google Scholar
36 Omar M., Shanableh A., Mughieda O., Arab M., Zeiada W., and Al-Ruzouq R., Advanced mathematical models and their comparison to predict compaction properties of fine-grained soils from various physical properties, Soils Foundations. (2018) 58, no. 6, 1383–1399, https://doi.org/10.1016/j.sandf.2018.08.004, 2-s2.0-85053081292.
10.1016/j.sandf.2018.08.004
Google Scholar
37 Namdar A., Forecasting bearing capacity of the mixed soil using artificial neural networking, Frattura ed Integrita Strutturale. (2020) 14, no. 53, 285–294, https://doi.org/10.3221/IGF-ESIS.23.22.
10.3221/IGF-ESIS.23.22
Google Scholar
38 Namdar A., The application of soil mixture in concrete footing design using linear regression analysis, Material Design & Processing Communications (MDPC). (2021) 3, no. 5, https://doi.org/10.1002/mdp2.179.
10.1002/mdp2.179
Google Scholar
39 Bordonaro G. G., Leardi R., Diviani L., and Berto F., Design of experiment as a powerful tool when applying finite element method: a case study on prediction of hot rolling process parameters, Frattura ed Integrità Strutturale. (2018) 12, no. 44, 1–15, https://doi.org/10.3221/IGF-ESIS.44.01, 2-s2.0-85045751094.
10.3221/IGF-ESIS.44.01
Google Scholar
40 Marsavina L., Iacoviello F., Dan Pirvulescu L., Di Cocco V., and Rusu L., Engineering prediction of fatigue strength for AM50 magnesium alloys, International Journal of Fatigue. (2019) 127, 10–15, https://doi.org/10.1016/j.ijfatigue.2019.05.028, 2-s2.0-85066252811.
10.1016/j.ijfatigue.2019.05.028
CAS Google Scholar
41 Foti P., Berto F., and Filippi S., Fatigue assessment of welded joints by means of the strain energy density method: numerical predictions and comparison with Eurocode 3, Frattura ed Integrità Strutturale. (2019) 13, no. 47, 104–125, https://doi.org/10.3221/IGF-ESIS.47.09, 2-s2.0-85060447533.
10.3221/IGF-ESIS.47.09
Google Scholar
42 Li Y., Cai W., Zhu W., Dong Z., and Zhang Q., Flow analysis of parallel double crack evolution under uniaxial compression, Journal of Central South University. (2019) 50, 3035–3045.
Google Scholar
43 Center for engineering strong motion data (CESMD), https://strongmotioncenter.org/.
Google Scholar
44 Namdar A., The boundary condition simulation quality for embankment seismic response, Engineering Failure Analysis. (2021) 126, 105491, https://doi.org/10.1016/j.engfailanal.2021.105491.
10.1016/j.engfailanal.2021.105491
Google Scholar
45 Zhang X., Zhang Q., Liu Q., and Xiao R., A numerical study of wave propagation and cracking processes in rock-like material under seismic loading based on the bonded-particle model approach, Engineering. (2022) 17, 140–150, https://doi.org/10.1016/j.eng.2021.09.023.
10.1016/j.eng.2021.09.023
Google Scholar
46 Lysmer J. and Kuhlemeyer R. L., Finite dynamic model for infinite media, Journal of the Engineering Mechanics Division. (1969) 95, no. 4, 859–877, https://doi.org/10.1061/JMCEA3.0001144.
10.1061/JMCEA3.0001144
Google Scholar
47 Wong L. and Einstein H. H., Crack coalescence in molded gypsum and Carrara marble: part 2-microscopic observations and interpretation, Rock Mechanics and Rock Engineering. (2009) 42, no. 3, 513–545, https://doi.org/10.1007/s00603-008-0003-3, 2-s2.0-67349160239.
10.1007/s00603-008-0003-3
Web of Science® Google Scholar
48 Zhang X. P., Zhang Q., and Wu S. C., Acoustic emission characteristics of the rock-like material containing a single flaw under different compressive loading rates, Computers and Geotechnics. (2017) 83, 83–97, https://doi.org/10.1016/j.compgeo.2016.11.003, 2-s2.0-84994845448.
10.1016/j.compgeo.2016.11.003
Web of Science® Google Scholar
49 Mughieda O. and Alzo′ubi A. K., Fracture mechanisms of offset rock joints - a laboratory investigation, Geotechnical and Geological Engineering. (2004) 22, no. 4, 545–562, https://doi.org/10.1023/B:GEGE.0000047045.89857.06, 2-s2.0-8144226835.
10.1023/B:GEGE.0000047045.89857.06
Google Scholar
50 Rumelhart D. E., Hinton G. E., and Williams R. J., Learning internal representations by error propagation, parallel distributed processing, explorations in the microstructure of cognition, ed. de rumelhart and j. mcclelland. vol. 1. 1986, Biometrika. (1985) 71, no. 599-607.
Google Scholar
51 Haykin S. S., Neural networks and learning machines, 2009, 3: Pearson Upper Saddle River, NJ, USA.
Google Scholar
52 Shanmuganathan S. and Samarasinghe S., Artificial neural network modelling, 2016, 628, Springer, Cham, Switzerland, https://doi.org/10.1007/978-3-319-28495-8.
10.1007/978-3-319-28495-8
Google Scholar
53 Priddy K. L. and Keller P. E., Artificial Neural Networks: An Introduction, 2005, 68, SPIE press, https://doi.org/10.1117/3.633187.
10.1117/3.633187
Google Scholar
54 Haykin S. S., Neural Networks: A Comprehensive Foundation, 2001, Tsinghua University Press.
Web of Science® Google Scholar
55 Kang J.-Y. and Song J.-H., Neural network applications in determining the fatigue crack opening load, International Journal of Fatigue. (1998) 20, no. 1, 57–69, https://doi.org/10.1016/S0142-1123(97)00119-9, 2-s2.0-0031654502.
10.1016/S0142-1123(97)00119-9
CAS Web of Science® Google Scholar
56 Agatonovic-Kustrin S. and Beresford R., Basic concepts of artificial neural network (ANN) modeling and its application in pharmaceutical research, Journal of Pharmaceutical and Biomedical Analysis. (2000) 22, no. 5, 717–727, https://doi.org/10.1016/S0731-7085(99)00272-1, 2-s2.0-0034213103, 10815714.
10.1016/S0731-7085(99)00272-1
CAS PubMed Google Scholar
57 Isazadeh M., Biazar S., and Ashrafzadeh A., Support vector machines and feed-forward neural networks for spatial modeling of groundwater qualitative parameters, Environmental Earth Sciences. (2017) 76, no. 17, https://doi.org/10.1007/s12665-017-6938-5, 2-s2.0-85028639031.
10.1007/s12665-017-6938-5
PubMed Google Scholar
58 Haghiabi A. H., Nasrolahi A. H., and Parsaie A., Water quality prediction using machine learning methods, Water Quality Research Journal.(2018) 53, no. 1, 3–13, https://doi.org/10.2166/wqrj.2018.025, 2-s2.0-85042769782.
10.2166/wqrj.2018.025
CAS Web of Science® Google Scholar
59 Devore J., Farnum N., and Doi J., Applied statistics for engineers and scientists, 2014, Publisher Richard Stratton.
Google Scholar
60 Pidaparti R. and Palakal M., Neural network approach to fatigue-crack-growth predictions under aircraft spectrum loadings, Journal of Aircraft. (1995) 32, no. 4, 825–831, https://doi.org/10.2514/3.46797, 2-s2.0-0029341357.
10.2514/3.46797
Web of Science® Google Scholar
61 Belytschko T. and Black T., Elastic crack growth in finite elements with minimal remeshing, International Journal for Numerical Methods in Engineering.(1999) 45, no. 5, 601–620, https://doi.org/10.1002/(SICI)1097-0207(19990620)45:5%3C601::AID-NME598%3E3.0.CO;2-S.
10.1002/(SICI)1097-0207(19990620)45:5<601::AID-NME598>3.0.CO;2-S
Web of Science® Google Scholar
62 Moes N., Dolbow J., and Belytschko T., A finite element method for crack growth without remeshing, International Journal for Numerical Methods in Engineering. (1999) 46, no. 1, 131–150, https://doi.org/10.1002/(SICI)1097-0207(19990910)46:1%3C131::AID-NME726%3E3.0.CO;2-J.
10.1002/(SICI)1097-0207(19990910)46:1<131::AID-NME726>3.0.CO;2-J
Web of Science® Google Scholar
63 Belytschko T., Moes N., Usui S., and Parimi C., Arbitrary discontinuities in finite elements, International Journal for Numerical Methods in Engineering. (2001) 50, no. 4, 993–1013, https://doi.org/10.1002/1097-0207(20010210)50:4%3C993::AID-NME164%3E3.0.CO;2-M.
10.1002/1097-0207(20010210)50:4<993::AID-NME164>3.0.CO;2-M
Web of Science® Google Scholar
64 Beizaee S., Xotta G., and Willam K. J., Perforation studies on flat bars for XFEM-based failure analysis, Engineering Fracture Mechanics. (2016) 155, 67–87, https://doi.org/10.1016/j.engfracmech.2015.11.022, 2-s2.0-84955609920.
10.1016/j.engfracmech.2015.11.022
Google Scholar
65 Feng W., Chen Z., Tang Y., Liu F., Yang F., Yang Y., Tayeh B. A., and Namdar A., Fracture characteristics of sustainable crumb rubber concrete under a wide range of loading rates, Construction and Building Materials. (2022) 359, 129474, https://doi.org/10.1016/j.conbuildmat.2022.129474.
10.1016/j.conbuildmat.2022.129474
Google Scholar
66 Lu G., Wang X., and Chen X., Study on tensile-shear failure of fractured rock mass under strong seismic load, Advanced Materials Research. (2011) 243-249, 2607–2612, https://doi.org/10.4028/www.scientific.net/AMR.243-249.2607, 2-s2.0-79958056352.
10.4028/www.scientific.net/AMR.243-249.2607
Google Scholar
67 Liu D. J., Li M., Zuo J. P., Gao Y., Zhong F., Zhang Y., and Chang Y. Q., Experimental and numerical investigation on cracking mechanism of tunnel lining under bias pressure, Thin-Walled Structures. (2021) 163, 107693, https://doi.org/10.1016/j.tws.2021.107693.
10.1016/j.tws.2021.107693
Web of Science® Google Scholar
68 Chen S. Y., Gu C. S., Lin C. N., and Hariri-Ardebili M. A., Prediction of arch dam deformation via correlated multi-target stacking, Applied Mathematical Modelling. (2021) 91, 1175–1193, https://doi.org/10.1016/j.apm.2020.10.028.
10.1016/j.apm.2020.10.028
Web of Science® Google Scholar
69 De Silva V. R. S., Konietzky H., Ranjith P. G., and Manatung U. I., Strain energy dependent numerical simulation of rock fracture initiation and propagation using soundless cracking demolition agents (SCDA): effects of SCDA-filled rock joints, International Journal of Rock Mechanics & Mining Sciences. (2024) 177, 105740, https://doi.org/10.1016/j.ijrmms.2024.105740.
10.1016/j.ijrmms.2024.105740
Google Scholar

All articles

The Effect of Preexisting Fracture Angles on Crack Propagation in Sandstone

Abstract

1. Introduction

2. Method and Materials

2.1. ANN

2.2. XFEM

3. Results and Discussion

3.1. Validation of Simulation and Prediction

4. Conclusion

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

The Effect of Preexisting Fracture Angles on Crack Propagation in Sandstone

Abstract

1. Introduction

2. Method and Materials

2.1. ANN

2.2. XFEM

3. Results and Discussion

3.1. Validation of Simulation and Prediction

4. Conclusion

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Related

Information