Achieving stable and versatile bipedal locomotion remains a major challenge in robotics, with applications in personal assistance, healthcare, and search and rescue. The hybrid zero dynamics (HZD) framework, based on virtual constraints, has shown strong potential for generating provably stable gaits. However, traditional HZD implementations often rely on simple feedback controllers that lack the ability to strictly enforce physical constraints, such as actuator limits and ground contact conditions during real-time execution. This paper presents a full-body, optimization-based walking controller for a bipedal robot that integrates virtual-constraints-based gait planning with online tracking using task-space inverse dynamics (TSID). A gait library is generated offline using two different sets of virtual constraints. It is shown that constraints based on the center of mass (CoM) relative to the feet improve optimization performance, achieving 8% fewer iterations, 12% faster convergence, and an 11.6% better objective value compared to classical constraint sets. The TSID controller, formulated as a weighted quadratic program (WQP), enables simultaneous tracking of multiple task objectives while respecting dynamic consistency and physical constraints. Simulation results on the GR-1 humanoid robot demonstrate stable walking over a range of velocities, smooth transitions between walking speeds, and successful rejection of external disturbances up to 20 N·s, confirming the effectiveness and robustness of the proposed approach.

1. Introduction

Bipedal locomotion remains a challenging and highly researched area in robotics, motivated by potential applications in personal assistance, healthcare, and exploration of hazardous environments. Achieving dynamic and robust walking behaviors requires addressing issues of stability, underactuation, contact interactions, and the complexities of full-body dynamics.

Early approaches focused on maintaining static stability by keeping the center of mass (CoM) within the support area [1], later advancing to dynamic walking methods based on the zero moment point (ZMP) criterion [2]. Although ZMP-based controllers enabled dynamic walking in robots, they relied on simplified models assuming slow motion and constant CoM height [2, 3], resulting in unnatural and conservative gait behaviors compared to biological locomotion.

Hybrid zero dynamics (HZD) [4] addressed these limitations by enforcing virtual constraints through feedback control, creating low-dimensional invariant surfaces within the robot’s full-body dynamics. HZD allows the generation of provably stable walking gaits through offline trajectory optimization, directly minimizing energy consumption while satisfying physical constraints [5–7]. Unlike human motion-capture-based approaches, HZD designs gaits specifically tailored to the robot model, improving feasibility and robustness.

However, the practical implementation of HZD often relies on high-gain PD controllers [8], which can limit compliance and hinder the enforcement of actuator limits and contact conditions during real-world execution. Analytical inverse dynamics methods, such as those proposed in [8], improved control accuracy but still struggled to optimally distribute contact forces or handle multiple inequality constraints.

More recently, control frameworks combining inverse dynamics with control Lyapunov functions (CLFs) within a quadratic programming (QP) structure have been developed [9]. These approaches offer strong theoretical guarantees of exponential stability even in hybrid dynamic systems but require precise modeling, complex Lyapunov function design, and solving larger optimization problems, increasing computational complexity.

In parallel, task-space inverse dynamics (TSID) [10–12] has emerged as a practical alternative for full-body motion and force control. TSID formulates control objectives as a weighted quadratic program (WQP), enabling simultaneous tracking of multiple prioritized tasks while enforcing actuator, torque, and contact constraints. Although TSID does not provide explicit Lyapunov stability guarantees, it offers modularity, computational efficiency, and robustness to modeling errors, making it highly suitable for real-world applications.

Building on these developments, this work proposes an optimization-based walking controller that integrates virtual-constraints-based offline gait planning with real-time online tracking using TSID. Although the controller is designed to be applicable to any humanoid robot, including those exhibiting underactuation, compliance, and multicontact behaviors, it is implemented and evaluated in this study on the GR-1 platform. Our contributions include the generation of a full-body gait library using two different sets of virtual constraints and the validation of the TSID-based tracking controller through extensive simulations on GR-1 [13], demonstrating stable walking across various speeds, effective disturbance rejection, and improved optimization performance. In particular, this work aims to demonstrate that TSID, when combined with virtual-constraints-based reference trajectories, can achieve stable and efficient walking, thereby extending the applicability of virtual constraints to optimization-based real-time control frameworks.

The structure of this paper is as follows: Section 2 describes the proposed methodology, including the HZD approach and the TSID framework. Section 3 details the application of the proposed approach to the humanoid robot GR-1, including the robot model and hybrid walking dynamics. Section 4 presents the simulation results validating the effectiveness of the method. Section 5 provides a discussion of the findings, and Section 6 concludes the paper and outlines directions for future work.

2. Proposed Methodology

Building upon the principles of HZD and the flexibility of TSID, this section details the full-body control framework developed to achieve stable and efficient bipedal walking. The proposed methodology consists of two main components: (i) offline generation of a gait library using optimized virtual constraints and (ii) online tracking of these trajectories through TSID formulated as a WQP. Together, these components allow the robot to perform multiobjective tracking while explicitly enforcing dynamic consistency, actuator torque limits, and contact constraints during locomotion. The general control concept is illustrated in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

An overview over the control framework. A gait library is generated offline using virtual constraints, and a desired velocity command selects and interpolates the appropriate reference trajectory. A Raibert-inspired regulator adjusts foot placement in real time, and the TSID controller tracks the trajectory while enforcing dynamic and physical constraints.

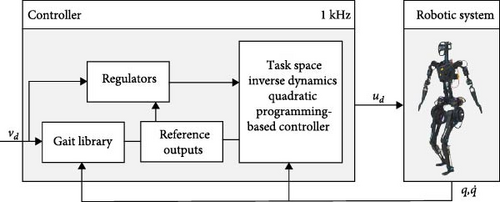
2.1. HZD Framework

The walking dynamics are modeled as a hybrid system, consisting of a sequence of continuous dynamics that represent the robot’s motion between impacts, and discrete (discontinuous) dynamics that capture the instantaneous changes occurring at impact events.

The continuous dynamics can be represented by a floating-base model with holonomic constraints as [8]:

()

with q as the vector of the generalized coordinates, u the vector of motor torque,s and λ the contact wrench. D(q) is the mass–inertia matrix.

contains the velocity and gravitational terms, and B is the motor torque distribution matrix. J is the Jacobian matrix of constraint equations. We can represent the generalized coordinates as:

()

where Ω is the configuration space of the bipedal robot, n is the number of DoF and q_b = (p_x, p_y, p_z, ϕ_r, ϕ_p, ϕ_y) represents the Cartesian coordinates and Euler angles of the floating-base frame

, and q_l represent the joint angles.

Holonomic constraints represent a placement constraint on the robot. They are enforced by prescribing a closure equation, η(q) = const. By differentiating this equation twice, we get constraints on the accelerations:

()

The enforcement of this constraint gives rise to the corresponding force terms, λ, in the equations of motion Equation (1).

The transition from one continuous domain to another, referred to as the guard [8], occurs when the swing foot impacts the ground. The impact is considered to be a fully inelastic instantaneous collision that does not result in any slip or bounce. Therefore, the robot configuration variables are invariant through the impact, and velocities will instantaneously change due to the introduction of new holonomic constraints [8]. The associated reset map, Δ, is given as:

()

Here R is a relabeling matrix that swaps left and right legs after impact, reflecting the symmetry of the walking gait between consecutive steps.q⁻ and q⁺ denote the pre- and postimpact configurations, and

is obtained from the plastic impact equation:

()

After the continuous and impact models are determined, the overall hybrid dynamics model of the robot can be constructed. The double stance domain is treated as instantaneous in this formulation. This treatment requires that the normal reaction force on the nonstance foot cross zero at the impact moment. Therefore, the domain and guard are given by:

()

where

is the vertical ground reaction force of the swing foot and

is the vertical position of the center of the swing foot from the ground.

ensures that the swing foot is moving downward. As a result, the overall model is given as follows:

()

The reset map Δ_R→L represents the discrete impact event in which support transitions from the right foot to the left foot, as defined in Equation (5).

To address the challenges of hybrid systems in bipedal locomotion, one widely adopted strategy is the HZD framework [3]. HZD enforces a set of m virtual constraints using control inputs u^∗(x), defined as

()

where y^a(q) is the actual output, y^d(τ(q), α) is the desired output parameterized by Bézier polynomials, and

denotes the Bézier coefficients of order

. These virtual constraints are designed to drive the output and its derivatives to zero exponentially within each continuous phase. This regulation shapes a low-dimensional invariant manifold, referred to as the zero dynamics surface, embedded within the full-order dynamics.

To ensure formal stability across the hybrid structure, these surfaces must remain invariant not only during continuous evolution but also through discrete transitions. By leveraging trajectory optimization, the HZD framework produces a library of optimized walking trajectories tailored to the robot’s full-body dynamics [14]. This eliminates the need for motion capture data or predefined gait datasets. Instead, virtual constraints are exploited to generate energy-efficient trajectories in both sagittal and lateral planes while enforcing physical limitations such as torque and joint bounds.

The resulting optimized trajectories form a gait library and serve as reference inputs for real-time execution. In this work, these references are tracked using a TSID controller, which ensures accurate trajectory following while maintaining full-body dynamic consistency and enforcing physical constraints, as detailed in the following section.

2.2. TSID Controller

TSID is a control framework that computes joint torques by solving a hierarchy of motion and force tasks, formulated directly in task space [10, 11]. Higher-priority objectives, such as contact consistency and swing foot tracking, are enforced before lower-priority goals like posture regularization. Each task is expressed as an equality or inequality constraint, and the full problem is solved through a sequence of quadratic programs (QPs). The specific set of tasks and their priorities can vary depending on the robot’s structure and the locomotion requirements of the application.

TSID’s task-space formulation enables intuitive control of underactuated, floating-base robots and allows for the explicit enforcement of physical constraints, including torque limits, joint bounds, and friction cones. All resulting motions are dynamically consistent with the robot’s full-body equations of motion. Due to its modularity and flexibility, TSID is particularly well-suited for complex locomotion, compliant behaviors, and multicontact planning. For a detailed mathematical formulation, we refer the reader to [12].

3. Application to a Humanoid Robot

This section describes the application of the proposed gait planning and TSID controller to the GR-1 humanoid robot model. The robot’s dynamics, hybrid walking domain structure, gait interpolation techniques, real-time tracking using TSID, and velocity regulation strategies are presented in detail. The general control concept is illustrated in Figure 1.

3.1. Robotic Model

GR-1 (Figure 2) is a torque-controlled humanoid robot developed by Fourier Intelligence. It stands approximately 1.5 m tall and weighs around 53 kg. The robot features 32° of freedom (DoF): 6 per leg, 7 per arm, 3 for the head, and 3 for the waist.

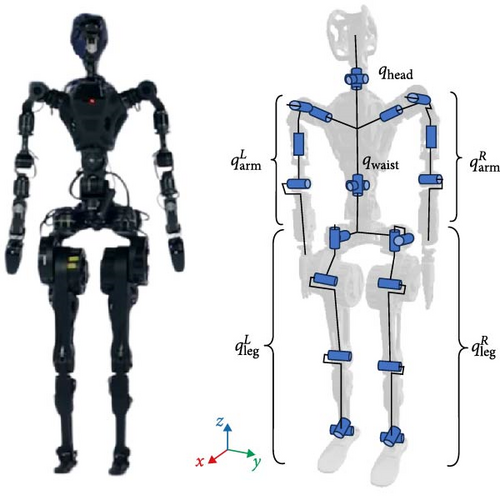
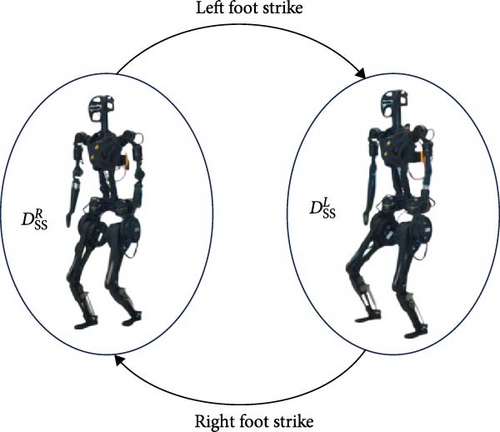
In this study, we assume that walking is symmetric between left and right stance phases when the robot’s average lateral velocity over a step is zero; otherwise, asymmetric walking is allowed. Accordingly, the GR-1 gait is modeled using two single support domains, , as illustrated in Figure 3, along with an instantaneous double support phase. The term “instantaneous” indicates that the new swing leg lifts off immediately after the previous swing leg makes contact with the ground.

For the GR-1 robot, we can represent the generalized coordinates as:

()

where

()

with

A visualization of the prescribed coordinates is shown in Figure 2, and an URDF of the robotic model detailed in this work is provided online [13].

3.2. Gait Library Planning and Optimization

Constructing the gait library requires defining the virtual constraints used in the HZD framework. While various formulations have been proposed in prior work [9, 15, 16], this study focuses on evaluating their influence on optimization performance by comparing two distinct sets. The first set, commonly found in the literature [9, 15], includes constraints on key joint angles of the stance and swing legs (e.g., hip, knee, and ankle joints), as well as the orientation of the nonstance foot, pelvis, torso, and arms. These constraints are intended to regulate the robot’s posture and interlimb coordination during walking and are defined as follows:

()

where st stands for stance and nst for nonstance;

is the ◻ coordinate of the nonstance toe or heel frame;

is the ◻ coordinate of the inside or outside nonstance foot frame. L_a, L_c, and L_t are the height of ankle, the length of calf and thigh of the robot, respectively. The pelvis angles are used to restrict the motion of the pelvis area. The torso angles are used to keep the upper body upright during walking. Figure 4 illustrates the physical meaning of these constraints. More information can be found in [15].

The second set of virtual constraints is rarely used in the literature [16], and to the best of our knowledge, this is the first time it has been applied to generate a complete gait library for a 3D bipedal robot. This formulation focuses on regulating the relative distance between the CoM and the robot’s feet. The torso, arms, and

nonstance foot orientation constraints from the first set are retained, while the remaining constraints are modified as follows:

()

During the optimization process for both groups, the ankle pitch and roll joints were treated as passive, following the approach described in [14]. Our experiments showed that this assumption leads to more stable walking. For both constraint sets, a total of 17 virtual constraints were defined, resulting in an underactuated system during the single stance phase. The head joints and any other joints not explicitly mentioned were considered fixed throughout the study, as they do not significantly influence the robot’s locomotion. Fifth-degree Bézier curves were used to parameterize the desired outputs.

To generate the gait library, a series of nonlinear trajectory optimization problems were formulated and solved using the FROST framework, developed by Hereid and Ames [17]. FROST employs a direct collocation approach to efficiently compute dynamically consistent walking trajectories. This framework has been widely used to generate reference motions for both model-based and model-free control strategies [18–20]. In this work, a dense grid of gaits was constructed, where the average sagittal-plane velocity

ranged in [−0.5, 1.3] m/s with 0.1 m/s increments, and the lateral-plane velocity

ranged in [−0.5, 0.5] m/s. The following cost function was chosen to minimize the power consumed during walking:

()

here τ_i, ω_i denote the i-th joints torque and velocity.

The step duration for all gaits was kept constant to simplify online tracking. Torque, joint angle, and velocity limits were enforced to ensure physical feasibility on the real robot. To maintain movement stability, the waist’s rotational angles were constrained to zero, preventing upper-body inclination. Additionally, the hand joints followed a zero trajectory (rather than being fixed) to prioritize leg movements while allowing future investigation into how hand motions affect stability. Further constraints are listed in Table 1.

Table 1. Constraints used in gait optimization.

Step duration	0.3 s
Torso frame height	>0.8 m
Step width (distance between feet in lateral direction)	(0.15, 0.25) m
Mid-stance foot clearance	0.06 m
Friction cone	0.8
Vertical impact velocity	(−0.5, 0)
Torque for stance foot pitch and roll	0 N·m

3.3. Real-Time Controlling Using TSID

The offline-optimized trajectories from the gait library serve as reference trajectories, sampled at 1 ms intervals to extract the positions and velocities of the CoM and feet. Additional constraints include torque and velocity limits, swing-foot flatness during motion, contact-sequence restrictions, and upright upper-body posture. A posture constraint is also applied to encourage joints to follow their default values. The tasks and their corresponding gains used in the simulation are detailed in Table 2.

Table 2. Set of tasks used in the control scheme.

Task	Priority	Weight	K_p
Torque and velocity bounds	0	1	—

Feet contact	I	1	6 × 500

CoM to feet tracking	I	1	6 × 500

Torso orientation	I	1	3 × 500

Posture regularization	I	10⁻³	Feet	12 × 10
Posture regularization	I	10⁻³	Other	20 × 1000

Note: We denote by n × [.] a vector of n elements. K_d for all tasks is set to be .

In order to find the reference outputs during online walking for a given speed, we use a simple bilinear interpolation method. For instance, given the current robot speed (v_x, v_y), the reference trajectory for any output β is calculated by interpolating along the v_x dimension:

()

Next, we interpolate along the v_y dimension:

()

3.4. Velocity Tracking and Regulation Heuristics

Directly implementing the motion library obtained from FROST on the simulation model results in stable motion but does not accurately track a target walking speed. Therefore, in the same way as in other works [9, 14], a Raibert-like regulator is used to find an offset to the foot strike location [21]:

()

The current step velocity is computed as

, where

is the target step velocity,

is the instantaneous velocity of the robot,

is the average actual walking velocity measured during the previous step, and

is reference speed from the gait library. The term γ is a forgetting factor applied to smooth velocity estimation. Δ_{(x, y)} is added to the nominal cartesian swing foot positions. The tuned values used for our simulation model are as follows:

4. Results

4.1. Generating Gait Libraries Comparison

Each group of virtual constraints was used to generate a gait library. Optimization was performed sequentially using the previous gait as an initial guess for the next speed in the library. Table 3 shows the performance comparisons between the two groups. The comparison indicates that the second group converges with a smaller number of iterations (8% fewer) and spends less time (12% faster). Additionally, calculating the percentage difference in the objective values of the two gait libraries:

Table 3. Performance criteria averages for the optimization process.

Metric	Group 1	Group 2
Avg. number of iterations (iter)	368	338
Avg. time (s)	419	367

shows that group 2 achieves better objective values. Finally, both groups produced similar walking gaits.

4.2. Simulation Results

The PyBullet simulation environment [22] was used to test the control procedure. We first tuned the controllers and then evaluated their performance. The tests included stepping in place, as well as walking forward, laterally, and diagonally. We observed that the two groups of virtual constraints produced similar results in terms of tracking and walking appearance. Therefore, only the results of the second group of constraints will be shown here. The reader is referred to the accompanying submission video for demonstration results.

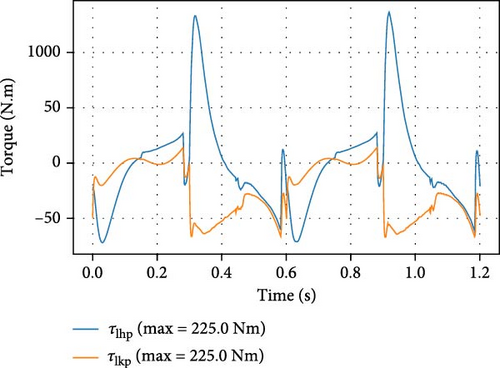
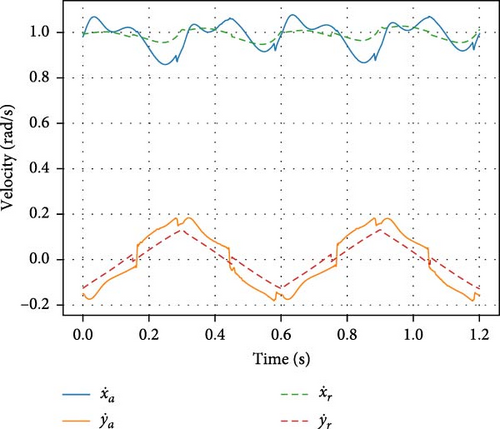
Figure 5 shows time-series motion tiles for the robot in PyBullet environment at a speed of 1 m/s. The output tracking and feed-forward torques for stepping in place are shown in Figures 6 and 7. Figures 8–10 correspond to the forward walking scenario at a target speed of 1 m/s along the sagittal direction.

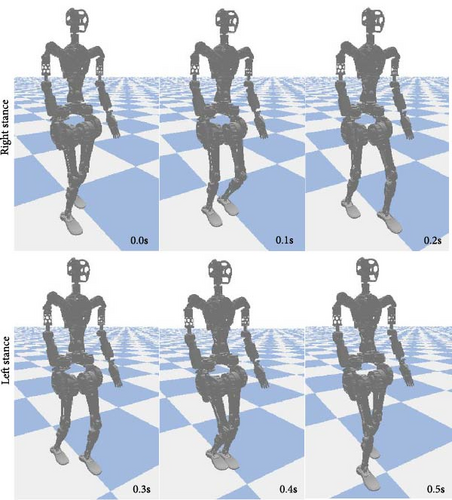
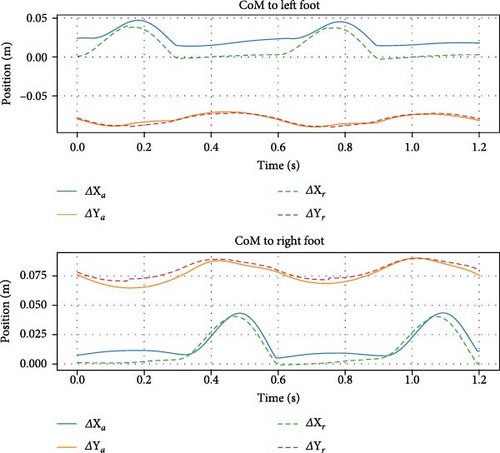
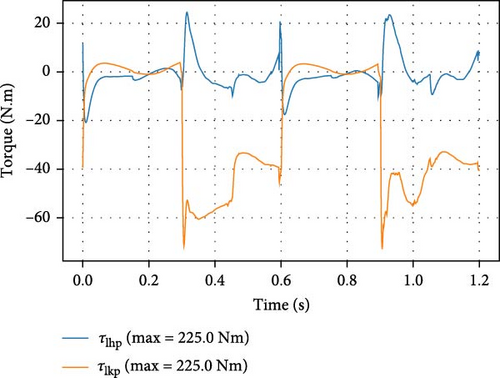
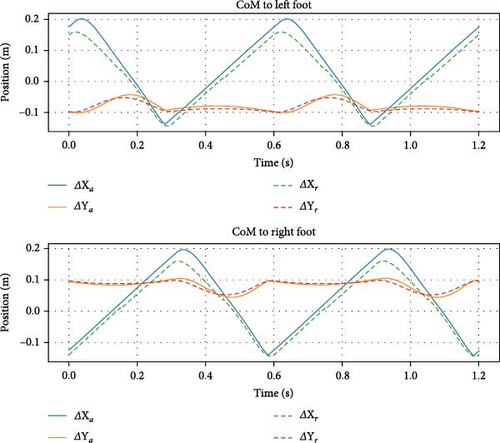
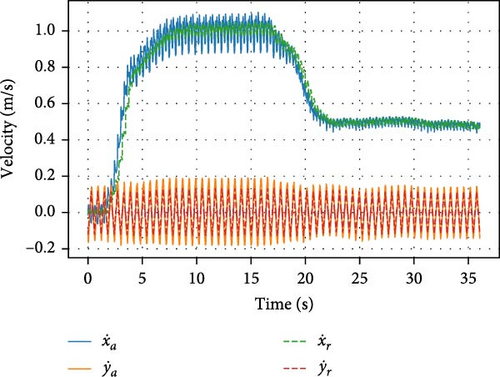
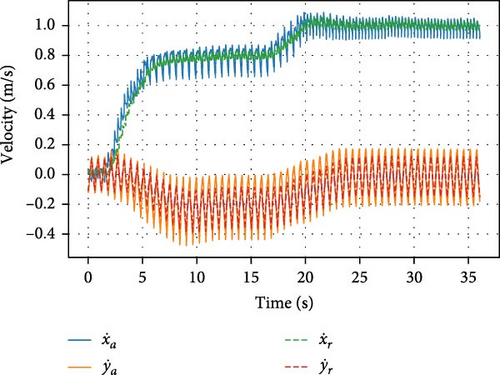
The robot’s ability to transition between several walking speeds is shown in Figures 11–13. Different scenarios are illustrated and described in each figure. This demonstrates the effectiveness of the TSID controller, combined with Raibert-like regulators, in following velocity commands.

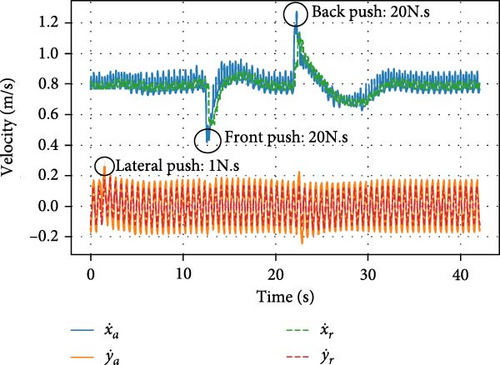
The robot’s ability to overcome external disturbances is also tested. Figure 14 shows the robot’s ability to withstand pushes in the lateral direction and in the sagittal direction during walking. As we can see from the figure, the robot was able to return to stable motion after several steps. We noticed that the robot’s ability to handle lateral pushes is less than its ability to handle sagittal pushes. This is because the motor torques of the roll joints are limited (48 N·m for the hip roll and 15 N·m for the ankle roll).

5. Discussion

Several methods have been used in the literature to track reference trajectories generated by the HZD approach, including PID control [3], analytical inverse dynamics [8], and Lyapunov-based inverse dynamics control (ID-CLF-QP) [9]. While all these methods, including the one employed in this paper, successfully track reference trajectories, each has its own advantages and limitations. This section compares the TSID controller to these methods, highlighting the motivation behind selecting TSID.

PID control offers a simple and computationally inexpensive strategy, often effective for fully actuated or slow systems. However, it does not account for full-body dynamics, has difficulty handling underactuation and contact constraints, and provides no formal stability guarantees beyond local convergence.

The orthogonal decomposition method analytically projects dynamics into the constraint-consistent space and is computationally efficient. Yet, it is limited in its ability to manage multiple simultaneous tasks, lacks a natural way to handle inequality constraints, and offers no formal stability proof.

Lyapunov-based ID-CLF-QP control provides exponential convergence guarantees through Lyapunov constraints even in hybrid systems. However, it demands precise modeling, careful Lyapunov function design, and solving a more complex QP.

In contrast, TSID provides a practical compromise between flexibility, computational efficiency, and robustness. It enables the tracking of multiple prioritized tasks, ensures full-body dynamic consistency, and handles physical inequality constraints. Although TSID does not guarantee Lyapunov stability, its modularity, versatility, and robustness to modeling inaccuracies make it highly practical for real-world applications. A summary comparison between the four methods is presented in Table 4.

Table 4. Comparison between TSID, orthogonal decomposition, Lyapunov-based ID-CLF-QP, and PID control.

Feature	TSID	PID	Orthogonal decomposition	ID-CLF-QP
Main idea	Multitask QP optimization	Simple error feedback	Analytical projection	Lyapunov stability enforced QP
Stability guarantee	No	No (local only)	No	Yes (provable)
Multiple tasks	Yes (prioritized)	No	Limited (only single dominant tracking task)	Limited (only single output focus)
Inequality constraints	Yes	No	No	Yes
Contact switching	Yes (smooth via switching contact constraints)	No (basic)	Requires manual handling	Yes (designed to handle hybrid dynamics)
Computation cost	Medium (solve a moderate size QP)	Very low	Very Low	Medium–high (adds Lyapunov constraints/slack)
Implementation complexity	Medium–high (but modular)	Very low	Low	High (design CLFs carefully)
Robustness	Good	Poor for complex systems	Good for simple tasks	Good for simple tasks
Scalability to complex robots	High (with task prioritization)	Very low	Low (can become messy with many tasks)	Medium (design CLFs for many tasks)
Use of full-body dynamics	Yes	No	Yes	Yes

Overall, TSID provides an effective balance between real-time performance, task flexibility, and robustness, making it highly suitable for controlling complex bipedal robots in dynamic environments.

6. Conclusion and Future Work

In this work, we presented a full-body, optimization-based framework for stable bipedal locomotion, combining offline gait generation with online trajectory tracking. By leveraging virtual constraints and full-body dynamics, we developed an energy-efficient gait library tailored to the GR-1 humanoid robot. Our comparative study revealed that virtual constraints based on CoM-to-feet positions significantly enhanced optimization performance, achieving an 8% reduction in iterations, 12% faster convergence, and an 11.6% improvement in the objective value. These constraints also simplified online tracking by inherently incorporating CoM-based stability strategies. For real-time control, we employed a TSID controller formulated as a WQP. TSID provided a practical balance between computational efficiency, task flexibility, and robustness, critical for complex bipedal locomotion. Extensive simulations demonstrated stable walking across a range of speeds and robust disturbance rejection, withstanding impulsive pushes of up to 20 N·s.

Future work will focus on hardware implementation to experimentally validate the controller’s performance under real-world conditions, including uneven terrain and unmodeled dynamics.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

No funding was received for this research.

Supporting Information

Additional supporting information can be found online in the Supporting Information section.

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Supporting Information

References

1 Lim H.-O. and Takanishi A., Biped Walking Robots Created at Waseda University: WL and WABIAN Family, Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences. (2007) 365, no. 1850, 49–64, https://doi.org/10.1098/rsta.2006.1920, 2-s2.0-33846283103.
10.1098/rsta.2006.1920
PubMed Web of Science® Google Scholar
2 Reher J. and Ames A. D., Dynamic Walking: Toward Agile and Efficient Bipedal Robots, Annual Review of Control, Robotics, and Autonomous Systems. (2021) 4, no. 1, 535–572, https://doi.org/10.1146/annurev-control-071020-045021.
10.1146/annurev-control-071020-045021
Web of Science® Google Scholar
3 Collins S., Ruina A., Tedrake R., and Wisse M., Efficient Bipedal Robots Based on Passive-Dynamic Walkers, Science. (2005) 307, no. 5712, 1082–1085, https://doi.org/10.1126/science.1107799, 2-s2.0-13844306287.
10.1126/science.1107799
CAS PubMed Web of Science® Google Scholar
4 Westervelt E. R., Grizzle J. W., and Koditschek D. E., Hybrid Zero Dynamics of Planar Biped Walkers, IEEE Transactions on Automatic Control. (2003) 48, no. 1, 42–56, https://doi.org/10.1109/TAC.2002.806653, 2-s2.0-0037246813.
10.1109/TAC.2002.806653
Web of Science® Google Scholar
5 Hereid A., Cousineau E. A., Hubicki C. M., and Ames A. D., 3D Dynamic Walking With Underactuated Humanoid Robots: A Direct Collocation Framework for Optimizing Hybrid Zero Dynamics, 2016 IEEE International Conference on Robotics and Automation (ICRA), 2016, IEEE, 1447–1454.
Google Scholar
6 Sreenath K., Park H.-W., and Grizzle J. W., Design and Experimental Implementation of a Compliant Hybrid Zero Dynamics Controller With Active Force Control for Running on MABEL, 2012 IEEE International Conference on Robotics and Automation, 2012, IEEE, 51–56.
Google Scholar
7 Reher J., Cousineau E. A., Hereid A., Hubicki C. M., and Ames A. D., Realizing Dynamic and Efficient Bipedal Locomotion on the Humanoid Robot DURUS, 2016 IEEE International Conference on Robotics and Automation (ICRA), 2016, IEEE, 1794–1801.
Google Scholar
8 Reher J. and Ames A. D., Inverse Dynamics Control of Compliant Hybrid Zero Dynamic Walking, 2021 IEEE International Conference on Robotics and Automation (ICRA), 2021, IEEE, 2040–2047.
Google Scholar
9 Reher J. and Ames A. D., Control Lyapunov Functions for Compliant Hybrid Zero Dynamic Walking, 2021, arXiv preprint arXiv: 2107.04241.
Google Scholar
10 Del Prete A., Mansard N., Ramos O. E., Stasse O., and Nori F., Implementing Torque Control With High-Ratio Gear Boxes and Without Joint-Torque Sensors, International Journal of Humanoid Robotics. (2016) 13, no. 1, https://doi.org/10.1142/S0219843615500449, 2-s2.0-84948408374, 1550044.
10.1142/S0219843615500449
Web of Science® Google Scholar
11 Stack-of-Tasks, Task Space Inverse Dynamics (TSID), 2024, GitHub. Available at: https://github.com/stack-of-tasks/tsid.
Google Scholar
12 Ramuzat N., Boria S., and Stasse O., Passive Inverse Dynamics Control Using a Global Energy Tank for Torque-Controlled Humanoid Robots in Multi-Contact, IEEE Robotics and Automation Letters. (2022) 7, no. 2, 2787–2794, https://doi.org/10.1109/LRA.2022.3144767.
10.1109/LRA.2022.3144767
Web of Science® Google Scholar
13 Gitee, Fourier Intelligence - GRX Models, 2024, Accessed June 27 https://gitee.com/FourierIntelligence/wiki-grx-models.
Google Scholar
14 Gong Y., Hartley R., and Da X., et al. Feedback Control of a Cassie Bipedal Robot: Walking, Standing, and Riding a Segway, 2019 American Control Conference (ACC), 2019, IEEE, 4559–4566.
Google Scholar
15 Yongga A., Dynamic Humanoid Locomotion: Hybrid Zero Dynamics Based Gait Optimization via Direct Collocation Methods, 2016, Georgia Institute of Technology, PhD thesis.
Google Scholar
16 Reher J., Ma W.-L., and Ames A. D., Dynamic Walking With Compliance on a Cassie Bipedal Robot, 2019 18th European Control Conference (ECC), 2019, IEEE, 2589–2595.
Google Scholar
17 Hereid A. and Ames A. D., Frost ^∗: Fast Robot Optimization and Simulation Toolkit, 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), 2017, IEEE, 719–726.
Google Scholar
18 Chaikovskaya E., Minashina I., and Litvinenko V., et al. Benchmarking the Full-Order Model Optimization Based Imitation in the Humanoid Robot Reinforcement Learning Walk, 2023 21st International Conference on Advanced Robotics (ICAR), 2023, IEEE, 206–211.
Google Scholar
19 Galliker M. Y., Csomay-Shanklin N., and Grandia R., et al. Planar Bipedal Locomotion With Nonlinear Model Predictive Control: Online Gait Generation Using Whole-Body Dynamics, 2022 IEEE-RAS 21st International Conference on Humanoid Robots (Humanoids), 2022, IEEE, 622–629.
Google Scholar
20 Li Z., Peng X. B., Abbeel P., Levine S., Berseth G., and Sreenath K., Reinforcement Learning for Versatile, Dynamic, and Robust Bipedal Locomotion Control, 2024, arXiv preprint arXiv: 2401.16889.
Google Scholar
21 Raibert M. H., BrownH. B.Jr., and Chepponis M., Experiments in Balance With a 3D One-Legged Hopping Machine, The International Journal of Robotics Research. (1984) 3, no. 2, 75–92, https://doi.org/10.1177/027836498400300207, 2-s2.0-0021439756.
10.1177/027836498400300207
Web of Science® Google Scholar
22 Coumans E. and Bai Y., Pybullet, A Python Module for Physics Simulation for Games, Robotics and Machine Learning, 2016.
Google Scholar

All articles

Full-Body Optimization-Based Bipedal Walking Control With Task-Space Inverse Dynamics and Virtual Constraints

Abstract

1. Introduction