Effect of Pressure on MHD Flow of Blood-Based Hybrid Nanofluid Through an Inclined Stenotic–Aneurysmal Artery
Abstract
Pressure gradient influence on magnetohydrodynamic (MHD) flow of blood-based hybrid nanofluid containing gold and copper nanoparticles is investigated in the present study. We adopted Caputo’s definition of fractional derivative to transform time-varying terms in governing equations after being appropriately normalized. Partial-analytical solutions of these equations are then numerically sought via the concentrated matrix exponential (CME) method, since complex forms of modified Bessel functions are contained in the normalized equations whose inverse Laplace transforms cannot easily be accomplished using known analytical schemes, which is the overriding novelty of this study. Results for velocity, temperature, and concentration profiles are analyzed graphically. Numerical results for skin friction, Nusselt, and Sherwood numbers are also presented in a table. Our results revealed that the fractional-order derivative increases velocity, temperature, skin friction, and Sherwood’s number, while concentration and Nusselt’s number decrease, accounting for its memory effects in the behavior of the fluid. Additionally, we observed that blood velocity declines with magnetic parameter values, while temperature distribution increases with Eckert’s number values. The study also shows fluctuations in flow motion, temperature, concentration, skin friction, and Nusselt’s number with the stenosis/aneurysmal height. Overall, our findings have significant implications for targeted drug delivery in the arterial system, especially concerning the treatment of atherosclerosis, aneurysms, and other cardiovascular diseases.
1. Introduction
The study of the flow of blood through stenotic–aneurysmal arteries holds great importance in the field of biofluid dynamics due to its close relation with various cardiovascular diseases such as atherosclerosis, hypertension, and aneurysms [1]. Several studies abound to demonstrate that understanding the flow dynamics of blood in such complex geometries is essential for devising novel diagnostic and treatment mechanisms. For instance, [2] conducted an investigation into non-Newtonian fluid models used in the analysis of blood flow within narrowed arteries, emphasizing the importance of understanding its rheological properties in cardiovascular diseases like stenosis and aneurysms. The study revealed that increasing resistive impedance in healthy, anaemic, and diabetic arteries leads to constricted blood flow to organs which potentially causes death. The researchers in [3] also supported this notion after they developed a mathematical model based on the finite difference method, to simulate blood flow within arterial segments with porous walls and stenosis.
The field of biomedical engineering has experienced a rising interest from researchers who are incorporating nanoparticles in their respective studies for biomedical applications. This is due to the exceptional thermal and rheological properties of nanoparticles, which make them well-suited for investigating the flow properties of biological fluids such as blood [4]. Of particular interest is the potential of nanoparticles to enhance drug delivery to diseased arteries and to improve in the manufacturing of artificial devices. In this regard, [5] theoretically modeled blood flow through a constricted artery with a tapering diameter with silver nanoparticles and a catheter using the homotopy perturbation method. Having considered the rheology of blood as a micropolar fluid, they observed that a higher volume fraction of nanoparticles resulted in increased flow velocity and shear stress, which may cause aneurysms. Similarly, [6] also adopted the homotopy perturbation technique to study the hemodynamics of nanofluid flow through stenotic–aneurysmal artery in the presence of a catheter whose surface was coated with nanoparticles. The study also investigated perturbed solutions’ convergence for temperature and concentration, providing an insight into the level of artery deformation. It was observed that delivery of drug to the region of the target was more efficient in the tapered converging artery than in the nontapered diverging artery. The study further revealed that concentration distribution was more pronounced in the region of stenosis, while temperature distribution was more notable in the aneurysmal region. Building on this subject, the researchers in [7] also observed that the resistance to blood flow and impedance are highest at the neck of dilatation’s height but lowest at the neck of stenosis after they also employed the homotopy perturbation method to examine the influences of stenosis and dilatation (aneurysm) on the flow of blood containing suspended nanoparticles. Recent studies such as [8, 9] and [10] have equally made vital contributions to analyzing the impact of hybrid nanofluids on blood flow in diseased arteries, focusing on key aspects like velocity distributions, heat transfer efficiencies, pressure profiles, and the influence of magnetic fields. These studies highlight the enhanced potential of nanoparticle-enriched models to improve diagnostic precision and therapeutic effectiveness in the management of cardiovascular conditions, particularly stenosis, by providing detailed insights into flow dynamics and thermal behavior in stenosed arteries.
Magnetohydrodynamic (MHD) flow, which refers to the interaction between an electrically conducting fluid and an applied magnetic field, has recently wooed the interests of researchers in biomedical engineering as a result of its significant applications in biomedicine. A plethora of these studies have demonstrated that MHD principles influence the flow behavior and characteristics of heat transfer within blood and other biological fluids, making it a crucial factor to consider in the study of cardiovascular diseases [11]. Contributing to this area of research, [12] utilized the perturbation method to analyze the complex rheological behavior of MHD blood flow through stenosed arteries, treating blood as Bingham fluid under peristaltic transport. Particularly focusing on drug transport and blood flow control during surgeries, the study affirmed that the magnetic parameter caused a decrease in velocity and temperature profiles, but slightly improved the magnitude of trapped bolus due to variable viscosity. Other studies such as [13–15] and [16] have equally made vital contributions in analyzing the MHD blood flow’s impact within diseased arteries, with a particular focus on velocity distributions, heat transfer efficiencies, pressure profiles, and the influence of magnetic fields on flow dynamics. These studies have offered valuable insights into the relevance of this field in the diagnosis and management of cardiovascular ailments.
Arterial stenosis, a prevalent cardiovascular disorder that occurs when plaque accumulates in the walls of blood arteries, undoubtedly impairs blood flow by narrowing the arteries. According to [17], this condition generates tangential stress pressure that diminishes arterial pressure, consequently resulting in an aneurysm. In this regard, [18] asserted that pressure gradient plays a vital role in determining blood flow dynamics in arteries, especially in pathological states such as stenosis and aneurysms. Numerous studies have emphasized the necessity of considering pressure gradient effects in accurately modeling hemodynamics of blood flow in diseased arteries. Affirming this assertion, [19] examined unsteady blood flow in a stenosed artery under a uniform magnetic field using the marker and cell method to solve their developed equations and the successive-over-relaxation method to calculate pressure. Their results showed that pressure drop increased when crossing multiple stenoses, while blood flow contours revealed significant changes downstream of stenosis in the presence of a magnetic field. Also, [20] investigated the effects of trihybrid Newtonian nanofluid on blood flow through diseased arteries, considering thermal radiation, thermal conduction, and viscous dissipation. The results showed that the pressure gradient significantly influences the flow behavior in the arteries. In a similar study, [21] examined the collective impact of pressure gradient variation, heat transfer, chemical reaction, and magnetic field influence on nanoblood flow in constricted arteries. The study’s findings revealed that the velocity profile diminished as the magnetic field strength increased at the centerline but increased with greater stenosis height and nanoparticle volume fraction. The study also showed an appreciation in the pressure gradient with an elevation in the height of constriction along the channel’s length.
Researchers in the field of biomedical engineering have also, in recent times, adopted fractional-order derivatives to investigate MHD blood flow characteristics through diseased arteries. These studies have shown that fractional derivatives provide a precise and accurate representation of complex physical phenomena, such as blood flow, compared to integer-order derivatives [22]. In a study by [23] to examine the impact of heat transfer and magnetic field on blood flow within oscillatory arteries using fractional-order derivatives, the researchers firmly postulated that fractional derivative is a very useful tool in controlling both velocity and temperature of blood during the treatment of cardiovascular illnesses. Additionally, [24] reiterated the significance of developing drug delivery systems and biomedicines, after they formulated a fractional second-grade, nonisothermal, hybrid nanofluid model to investigate blood flow characteristics in concentrically catheterized, stenotic–aneurysmal arteries. Similarly, [25] examined the MHD Casson fluid flow through a porous artery with slip velocity effects utilizing the Caputo–Fabrizio fractional-derivative and observed that the fractional parameter, together with the Casson parameter, slip velocity parameter, and Darcy number (Da) resulted in an increase in the fluid’s velocity. Recently, [26] numerically explored the consequences of temperature on the disintegration of magnetic nanoparticles in blood using fractional derivatives and reported that the temperature distribution exhibited a notable reaction to increased fractional parameters, suggesting the existence of a critical threshold.
The present study focuses on the analysis of the effect of pressure on MHD blood flow containing gold (Au) and copper (Cu) hybrid nanoparticles through an inclined stenotic–aneurysmal artery, a topic that has not been adequately explored in existing literature. The study addresses a multifaceted problem taking into consideration other key factors, such as the influence of the Caputo fractional-order derivative, the effect of stenotic–aneurysmal geometry, the use of hybrid nanofluids, and the presence of MHD effects in an inclined stenosed and aneurysmal artery. The study also offers valuable insights that contribute to the development of innovative diagnostic and therapeutic approaches for managing cardiovascular diseases.
2. Formulation of Flow Models
2.1. Flow Problem’s Geometry
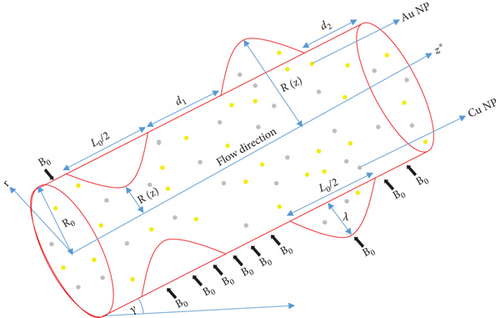
We represented the artery as an oblique, narrowed, and bulging cylinder to illustrate arterial stenosis and aneurysm as depicted in Figure 1.
2.2. Assumptions for Models’ Formulation
- 1.
Blood is considered the base fluid, and Au and Cu are taken to be in thermal equilibrium and randomly dispersed within it.
- 2.
The flow regime is assumed to be laminar, unsteady, fully developed, incompressible, and non-Newtonian.
- 3.
The flow is symmetric about the z∗ (axial) direction.
- 4.
An external magnetic field of intensity B0 is applied uniformly and perpendicularly to the direction of flow.
- 5.
The temperature of the arterial wall is assumed to be equivalent to the body temperature.
- 6.
The electric currents induced within the region of fluid flow are considered insignificant.
- 7.
It is assumed that all incident heat radiation is fully absorbed by the arterial walls.
2.3. Equations That Govern the Flow Problem
The notations L0 and δ represent the arterial length and the greatest height of stenosis or aneurysm, respectively.
3. Solution Process
To solve our flow problem, we initially employed the nondimensionalization technique to transform Equations (1)–(6) into dimensionless forms. For this purpose, we utilized the following dimensionless variables: , z = z∗/R0, r = r∗/R0, R(z) = R∗(z∗)/R0, , , , .
The notations ao, a1, and ω are used to, respectively, denote the amplitude, pulsation, and the frequency of the pressure gradient.
3.1. Models’ Thermophysical Properties
Values of the thermophysical physical properties of blood, Au, and Cu are given in Table 1 [29].
| Physical property | Blood | Gold | Copper |
|---|---|---|---|
| ρ (kgm−3) | 1063 | 19,320 | 8933 |
| k (W/mK) | 0.492 | 314 | 401 |
| cp (J/kgK) | 3594 | 129 | 385 |
| σ (Sm−1) | 6.67 × 10−1 | 4.10 × 107 | 59.6 × 106 |
| β (K−1) | 0.18 × 10−5 | 1.4 × 10−5 | 1.67 × 10−5 |
3.2. Fractional Time Derivatives of Flow Models
3.3. Analytical Procedure for Flow Models
3.3.1. Velocity Profile
3.3.2. Temperature Profile
3.3.3. Concentration Profile
4. Numerical Approach
The notations βk, N and ηk denote the nodes, order, and weights, respectively.
In order to ensure the computational efficacy and numerical precision of the CME approach, the inverted forms of Equations (29)–(31) in the Laplace domain are generated utilizing 33 terms ranging from 0.01 to the greatest time spread equally 100 times [31]. We adopted Python programming language to implement this strategy.
4.1. Important Features of Flow of Blood-Based Hybrid Nanofluid
4.2. Results and Discussion
4.2.1. Validation of Numerical Results
To validate the reliability of our model, we selected parameters that aligned with the conditions used in [33]. Specifically, the values α = 1.0, Pe = 20.0, Re = 2.0, Pr = 19.0, Gr = 0.02, Gc = 0.02, Hartmann (Ha) = 0.4, Ec = 1.0, Schmidt (Sc) = 1.0, Da = 1.0, chemical reaction (Cr) = 0.1, Ra = 0.2, λ = 0.015, Hr = 1.5, γ = π/2, and a0 = 1.5 were chosen based on their close match to [33], allowing us to replicate similar flow conditions. This parameter selection enables a meaningful comparison to validate our model predictions against established data. The observed agreement, as shown in Table 2, provides confidence in the model accuracy, with any minor discrepancies attributable to differences in numerical methods and parameter adjustments. This validation supports the robustness of our model in capturing the key dynamics of axial velocity in stenosed arteries.
| Radius | Tripathi et al. [33] | Present study | MSE |
|---|---|---|---|
| 0.0 | 0.5881 | 0.6013 | 1.63e − 05 |
| 0.1 | 0.5845 | 0.5909 | 3.76e − 06 |
| 0.2 | 0.5725 | 0.5812 | 6.9e − 06 |
| 0.3 | 0.5518 | 0.5689 | 2.7e − 05 |
| 0.4 | 0.5215 | 0.5385 | 2.6e − 05 |
| 0.5 | 0.4802 | 0.4955 | 5.03e − 06 |
| 0.6 | 0.4257 | 0.4313 | 2.11e − 05 |
| 0.7 | 0.3549 | 0.3705 | 2.2e − 05 |
| 0.8 | 0.2637 | 0.2912 | 6.9e − 05 |
| 0.9 | 0.1483 | 0.1810 | 9.73e − 05 |
| 1.0 | 0 | 0 | 0 |
4.2.2. Analysis of Key Findings
In this section, the Python programming language was used to create data intended for the analysis. The velocity profile, along with the temperature profile and concentration profile, is depicted using graphs and subsequently analyzed. The parameters ϕAu, ϕCu, and ω are assigned specific values as follows: ϕAu = 0.025, ϕCu = 0.025, and ω = π/4 [29], while the rest are set as α = 0.6, 0.8, 1.0; Pe = 20.0, 22.0, 24.0; Re = 2.0, 3.0, 4.0; Pr = 19.0, 20.0, 21.0; Gr = 0.01, 0.015, 0.02; Gc = 0.02, 0.04, 0.06; Ha = 0.4, 0.6, 0.8; Ec = 0.5, 0.7, 1.0; Sc = 1.0, 1.2, 1.4; Da = 1.0, 3.0, 5.0; Cr = 0.1, 0.2, 0.3; Ra = 0.2, 0.4, 0.6; λ = 0.0, 0.015, 0.03; Hr = 0.5, 1.0, 1.5; γ = π/9, π/3, π/2; and a0 = 0.5, 1.0, 1.5 [31] and are tuned accordingly to obtain desired results for the analysis.
4.2.2.1. Velocity Profile
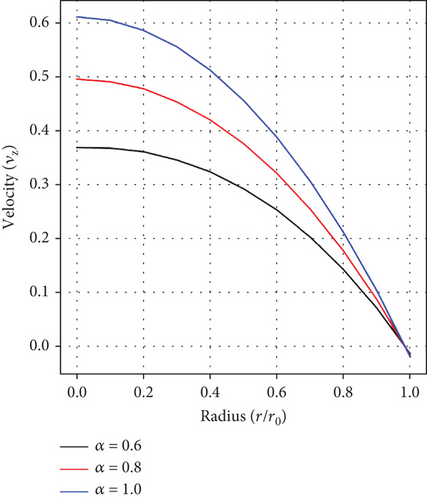
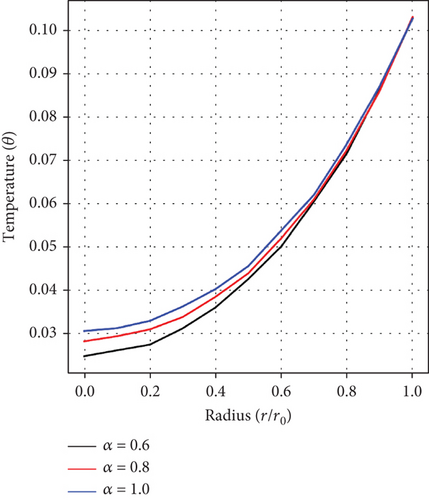
Figure 2(a) depicts the impact of the fractional-order parameter (α) on the velocity distribution. It is observed that the velocity of the fluid increases with increasing values of α.
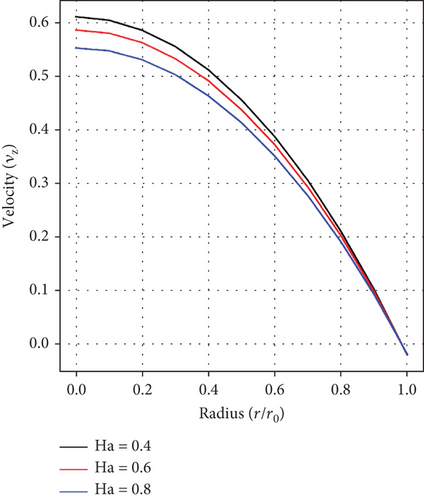
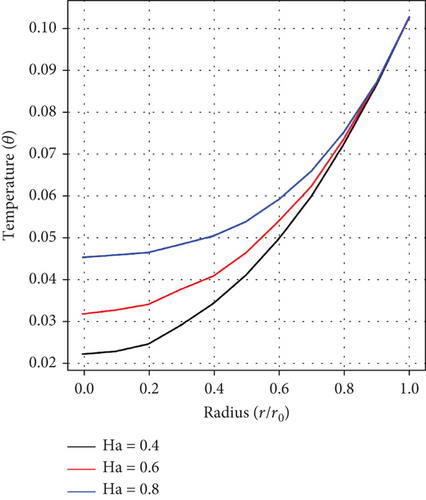
An analysis of the effect of the Ha number on velocity distribution as captured in Figure 2(b) shows that the velocity of blood declines with increasing values of Ha. This is anticipated because of the effects of the Lorentz force created by the applied magnetic field which inherently creates resistance to fluid flow.
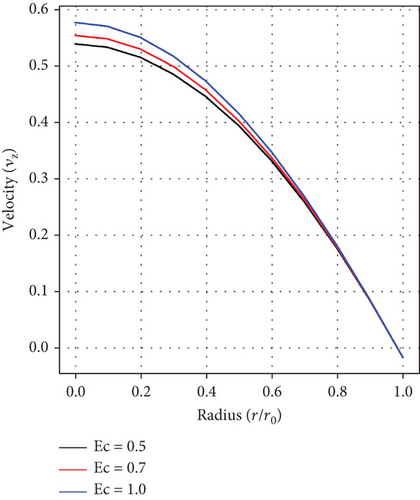
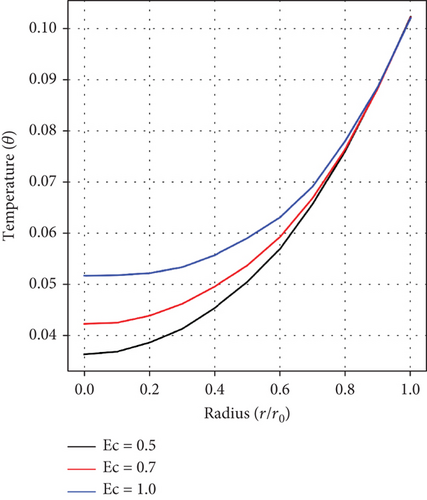
Figure 2(c) illustrates how the Eckert number (Ec) affects fluid velocity. It has been noticed that velocity increases with rising Ec values. This happens because the frictional forces caused by the interaction of the Au and Cu nanoparticles generate heat, which in turn increases the fluid’s velocity. This phenomenon offers a way to optimize medicine delivery to specific parts of the cardiovascular system, particularly for conditions such as atherosclerosis and aneurysm.
Figure 3(a) shows stenosis/aneurysm height’s influence on fluid velocity, with velocity fluctuating with varying values of λ. This correlation between blood velocity and artery narrowing/bulging is crucial for diagnosing and treating cardiac-related issues.
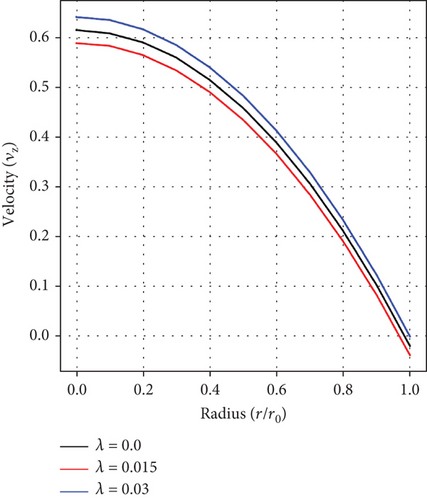
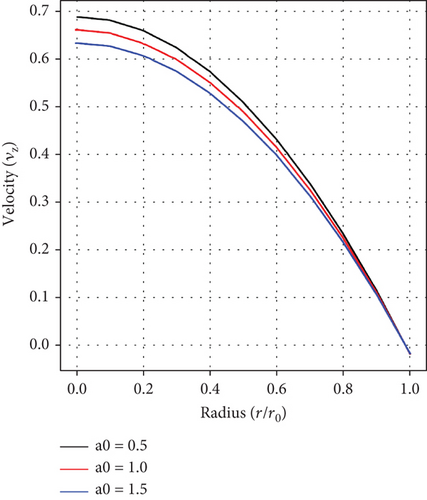
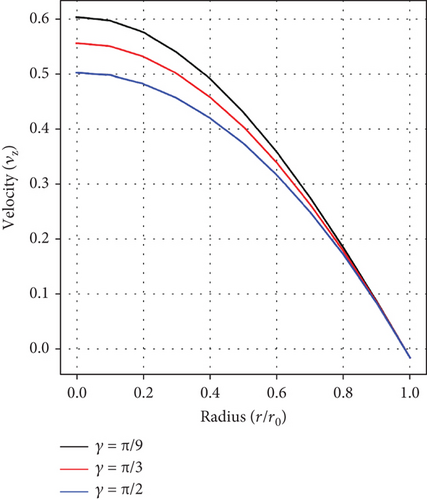
Figure 3(b) shows the effect of the pressure gradient on fluid velocity. It is noticed that the velocity of blood retards with increasing values of a1. Certainly, an increment in the pressure gradient results in an increase in the blood flow within the artery, thereby resulting in a decline in velocity. This inverse relationship between the pressure gradient and blood velocity is crucial for managing cardiovascular-related disorders, such as atherosclerosis and aneurysm.
Figure 3(c) relates the impact of the stenosed/aneurysmal artery’s inclination angle (γ) on the velocity profile. It is clearly observed that velocity decreases with enhancing values of (γ), depicting an inverse relationship. In the context of stenosis, the inclination angle increases resistance to flow, thereby reducing velocity. In aneurysms, the inclination angle changes flow patterns, potentially causing turbulent flow. Knowledge of these phenomena is critical for assessing hemodynamic features, predicting complications, and making treatment decisions.
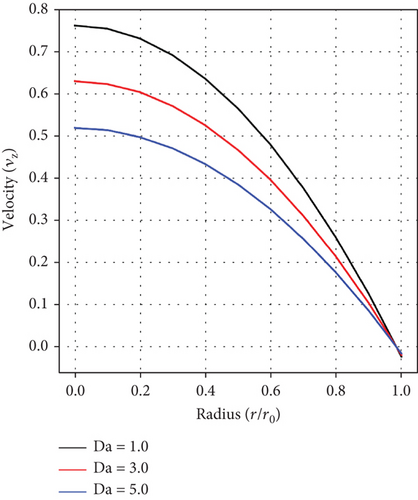
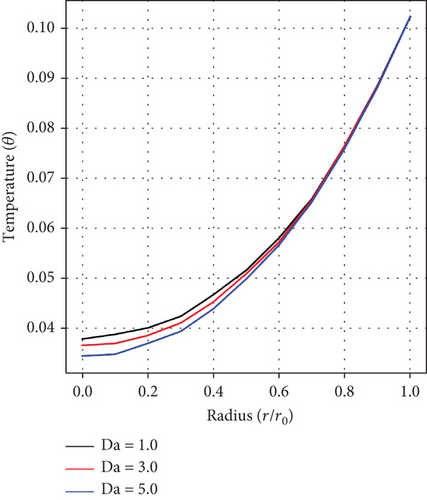
The impact of the permeability/porosity parameter (Da) is captured in Figure 4. Blood velocity is noticed to decline as values of Da ascend. Increasing Da values implies that the artery becomes more resistant to blood flow, which leads to a fall in velocity. In the context of clinical practice, this interplay is crucial in diagnosing, treating, and assessing the severity of diseased arteries, in order to maximize treatment outcomes.
4.2.2.2. Temperature Profiles
It can be observed from Figures 5(a), 5(b), and 5(c), which show the impacts of the fractional-order parameter (α), magnetic parameter (Ha), and Ec on the temperature distribution, that there is a rise in temperature as the values of α, Ha, and Ec increase. This depicts that there is an enhancement in fluid velocity around the stenosed/aneurysmal region which is essential in effectively delivering medications to diseased arteries.
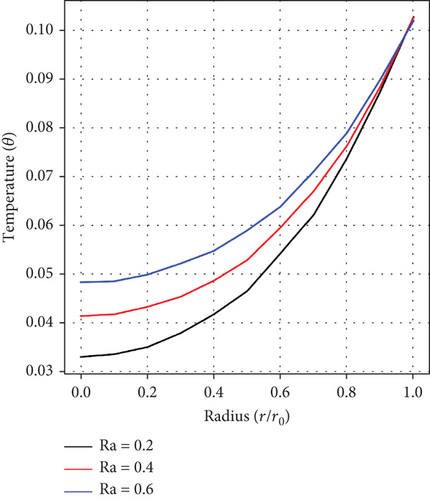
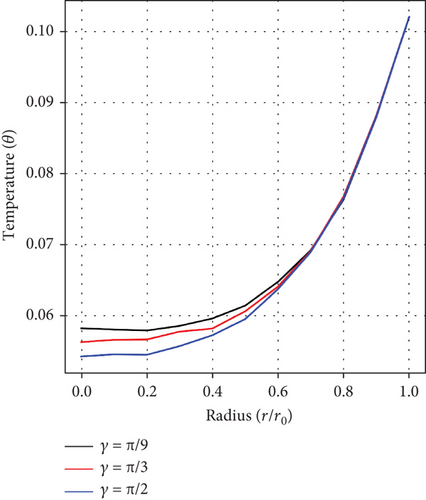
Figures 6(a), 6(b), and 6(c) portray the radiation parameter’s (Ra) impact, as well as influences of the height of stenosis/aneurysm (λ) and the inclination angle (γ) on temperature profile. A rise in temperature is realized as values of Ra ascend but fluctuates and decreases with growing values of (λ) and (γ), respectively. In the context of arterial stenosis and aneurysm, this combined effect is good for controlling the temperature and blood motion within diseased arteries.
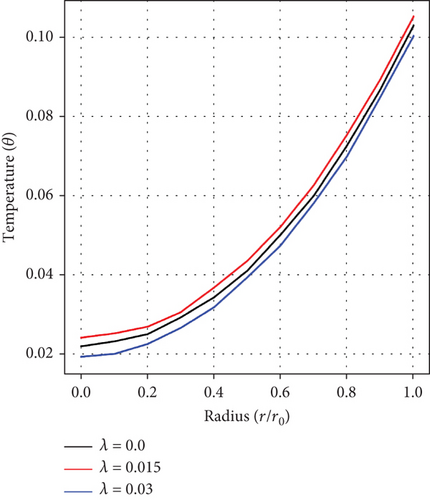
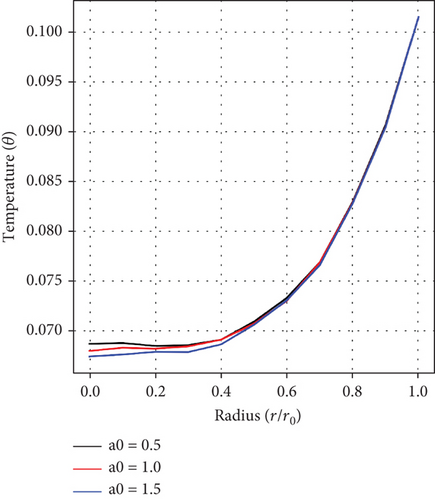
Figures 7(a) and 7(b) record the influences of the pressure gradient (a0), and the Da. It is realized that increase in values of a0 and Da each culminates in a decline in the temperature of blood, indicating an inverse relationship in each case. An increase in pressure gradient leading to a decrease in temperature suggests the existence of an effective heat dissipation or cooling mechanism within the artery. Conversely, a higher value of Da suggests an increase in flow resistance, thereby reducing convective heat transfer and decreasing blood temperature. This interplay is critical in understanding blood physiological structure and the general cardiovascular function, especially in the context of stenosis and aneurysm.
4.2.2.3. Concentration Profiles
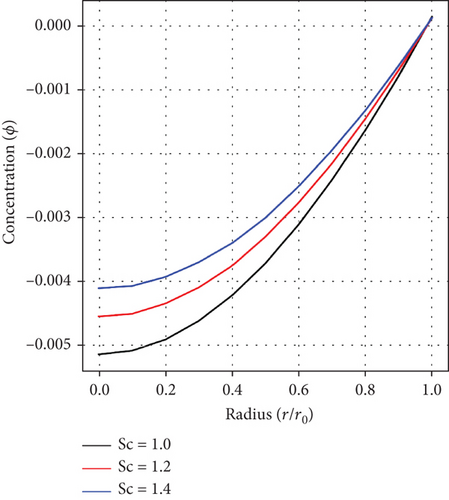
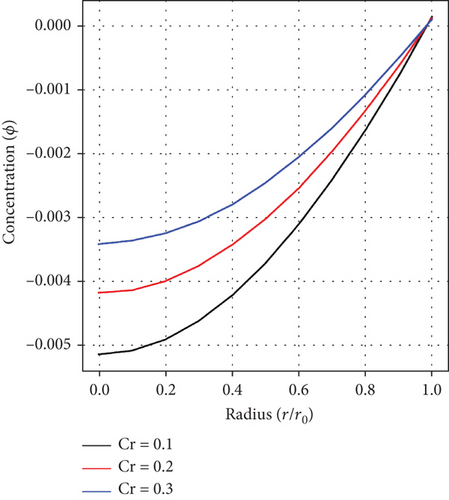
Figures 8(a), 8(b), and 8(c) display the effect of the fractional-order parameter(α), the Sc, and the Cr parameter on the distribution of concentration. Evidently, from graph, fluid’s concentration is noticed to increase with ascending values of α, Sc, and Cr. These principles are essential in an enhanced targeted drug delivery to affected parts within the human body’s arterial structure.

From Figure 9, it is observed that concentration fluctuates as the height of stenosis/aneurysm increases. This relationship provides an important insight into treatment efficacy and long-term outcomes for patients with such cardiovascular disorders.

4.3. Influences of Relevant Parameters on Dimensionless Variables
We analyzed the impacts of the parameters; α = 0.6,0.8,1.0, Ha = 0.4,0.6,0.8, Ec = 0.5,1.0,1.5, Cr = 0.1,0.2.0.3, Ra = 0.2,0.4,0.6, Sc = 1.0,1.2,1.4, λ = 0.0,0.015,0.3, a0 = 0.5,1.0,1.5 [31] and γ = π/9, π/3, π/2 on Cf, Nu, and Sh numbers in this section as shown in Table 3. From the results, it can be seen that Cf coefficient increased with rising values of α, Ec, and Sc but declined with rising values of Ha, Ra, a0, and γ. The Cf coefficient is also observed to increase a bit from 1.486758776 for Cr = 0.1 to 1.487279795 for Cr = 0.2 and remained the same for Cr = 0.3. The Cf is also observed to be fluctuating for varying values of λ.
| α | Ha | Ec | Cr | Ra | Sc | λ | a0 | γ | Cf | Nu | Sh |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.6 | 0.841210745 | −0.16412273 | −0.01666196 | ||||||||
| 0.8 | 1.027224027 | −0.17030172 | −0.016580418 | ||||||||
| 1.0 | 1.221639495 | −0.175265853 | −0.015827579 | ||||||||
| 0.4 | 1.221639495 | −0.16136907 | −0.015827579 | ||||||||
| 0.6 | 1.171957385 | −0.156456754 | −0.015827579 | ||||||||
| 0.8 | 1.106533241 | −0.154298246 | −0.015827579 | ||||||||
| 0.5 | 1.001138929 | −0.138518736 | −0.005035358 | ||||||||
| 1.0 | 1.005158219 | −0.137699991 | −0.005035358 | ||||||||
| 1.5 | 1.014834139 | −0.133159757 | −0.005035358 | ||||||||
| 0.1 | 1.486758776 | −0.160475895 | −0.009317815 | ||||||||
| 0.2 | 1.487279795 | −0.160475895 | −0.007600049 | ||||||||
| 0.3 | 1.487279795 | −0.160475895 | −0.00608929 | ||||||||
| 0.2 | 1.559997555 | −0.15370287 | −0.009317815 | ||||||||
| 0.4 | 1.559662614 | −0.141570792 | −0.009317815 | ||||||||
| 0.6 | 1.558471713 | −0.120358467 | −0.009317815 | ||||||||
| 1.0 | 1.167862862 | −0.143058896 | −0.009317815 | ||||||||
| 1.2 | 1.167937219 | −0.143058896 | −0.008179047 | ||||||||
| 1.4 | 1.16801165 | −0.143058896 | −0.007483755 | ||||||||
| 0.0 | 1.22201167 | −0.140975118 | −0.015827579 | ||||||||
| 0.015 | 1.209209301 | −0.138444528 | −0.015719896 | ||||||||
| 0.03 | 1.235369401 | −0.140081942 | −0.015858036 | ||||||||
| 0.5 | 1.329413038 | −0.10815151 | −0.015827579 | ||||||||
| 1.0 | 1.277535632 | −0.110235587 | −0.015827579 | ||||||||
| 1.5 | 1.227965634 | −0.1106821 | −0.015827579 | ||||||||
| 1.025663344 | −0.16136907 | −0.009317815 | |||||||||
| 1.009028228 | −0.158615187 | −0.009317815 | |||||||||
| 0.98982526 | −0.154000521 | −0.009317815 |
It also observed that the Nu number is enhanced with advancing values of Ha, Ec, Ra, and γ but decreased with augmenting values of α and a0. The Nu number is constant for increasing Cr and Sc values but fluctuates for ascending values of λ.
An increase in Sh number is observed as α, and Cr and Sh values appreciate but remain constant for changing values of Ha, Ec, Ra, a0, and γ. Also, the Sh number is fluctuating as values of λ are varied.
5. Conclusion
- •
Distributions of velocity, temperature, Cf, and Sh number are all augmented, while concentration and Nu number decreased with enhancing fractional-order derivative’s values.
- •
Blood velocity declined with appreciating values of the magnetic parameter (Ha). The reverse phenomenon is, however, observed for temperature distribution.
- •
Velocity, temperature, Cf, and Nu number are enhanced with increments in Ec values.
- •
A fluctuation was observed in the hybrid nanofluids speed, temperature, concentration, Cf, Nu, and Sh numbers as the values of stenosis/aneurysmal height increased.
- •
Both velocity and temperature profiles are depreciated with growing values of pressure gradient, inclination angle, and Da.
- •
The temperature profile exhibited an increase as the radiation parameter’s values grew.
- •
Also, concentration profiles exhibited a rise as values of Cr and Sc are enhanced.
- •
Cf decreases with Ha, pressure gradient, and angle of inclination, while Nu number increases with Ha, thermal radiation, and angle of inclination but decreased with pressure gradient.
Essentially, the outcomes of this research will play a vital role in controlling the body’s temperature and blood flow, as well as administering medications to designated arteries, particularly in the treatment of atherosclerosis, aneurysms, and other cardiovascular disorders.
6. Recommendation
- 1.
Researchers in biomedical engineering should consider incorporating fractional calculus, MHD principles, and Au–Cu nanoparticles, as well as the influence of the pressure gradient and arterial inclination angle, in their studies to thoroughly examine blood flow through diseased arteries.
- 2.
The information observed on Cf, Nu, and Sh numbers could be utilized to
- -
Provide guidance and care for individuals with aberrant body temperatures.
- -
Manage and treat cardiovascular conditions such as atherosclerosis, hypothermia, and thrombus.
- -
7. Research Limitation
The numerical findings of the study have limited clinical validation. Experimental studies and clinical trials are needed to corroborate the results and ensure their applicability in medical practice.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
No funding was received for this manuscript.
Open Research
Data Availability Statement
The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.




