1. Introduction

In several nonlinear scientific fields, like chemical physics, fluid mechanics, nuclear physics, solid-state physics, plasma physics, optical fiber, and geology, there has been a significant focus on the study of nonlinear evolution equations over the past few decades. Using NEEs, numerous academics devised plans to build traveling wave solutions by combining various techniques. Manner of extended Kudryashov [1], manner of modified simple equation [2], new extended (G^′/G) expansion scheme [3, 4], Darboux transformation [5], manner of trial solution [6], Frobenius integrable decomposition [7], manner of exp function [8], manner of multiple simplest equation [9], ansatzes [10], Nofal applied simple equation method for nonlinear partial differential equations [11], and Hirota bilinear [12–14] are some of the well-established procedures that have been well established in recent literature. By using the simplest equation method, many writers have solved a number of models [15–17]. MSE [18] manner to describe explicit solution of Oskolkov and KP equations Gozukızıl and Akcagıl [19] apply the tanh–coth scheme of nonlinear model. Turgut et al. [20] investigated propagation of nonlinear shock waves for the generalized equation. Sviridyuk and Shipilov [21] describe the stability of a model. Akcagil et al. [22] used (G^′/G) expansion to describe exact solution of a nonlinear model. Variational method [23, 24] was applied for modified Camassa–Holm equation.

The analysis of nonlinear evolution equations has made extensive use of fractional derivatives. It can be used to examine how solutions are carried out in different types of nonlinear systems. A more general expression of the nonlinear evolution equation that takes nonlinear effects into account is made possible by the introduction of fractional derivatives. Because fractional derivatives can yield more accurate results than traditional derivatives and can potentially be used to analyze solutions with a wide range of initial conditions, they are advantageous in nonlinear models. Additionally, fractional derivatives can streamline the computational process and eliminate the need for laborious parameter changes. Different kinds of fractional derivatives have been created recently by numerous researchers and applied to a variety of nonlinear systems. M-fractional derivative is used to the paraxial wave model [25], conformable fractional derivative is applied to the Date–Jimbo–Kashiwara–Miwa equation [26], Caputo fractional derivative is applied to the prey–predator model [27], Riemann–Liouville fractional integral is used in the Kudryashov–Sinelshchikov equation [28], fractional beta derivatives is used in the cubic nonlinear Schrödinger equation [29], local fractional derivative [30, 31], application of the variational method [32] in the fractal space, etc.

Ferromagnetism is the basic process by which some materials, like iron, become permanent magnets. Permanent magnets, which are composed of “hard” ferromagnetic materials like alnico and are classified as either ferromagnetic or ferrimagnetic based on the materials that are observably attracted to them, are defined as materials that can be magnetized by an external magnetic field and stay magnetized after the external field is removed. In contemporary technology and industry, ferromagnetism is crucial; it is the foundation of numerous electrical and electromechanical devices, including generators, electric motors, and electromagnets. Ferromagnetic materials can be classified as either hard magnetic (like permanent magnets made from hard ferromagnetic materials like alnico) or soft magnetic (like annealed iron, which does not tend to stay magnetized). The electrons in ferromagnetic materials prefer to have all of their spins point in the same direction, which contributes to their magnetism. Generally speaking, the magnetization decreases as the temperature rises. Lately, the soliton theory and condensed physics matter have shown particular interest in the classical and semiclassical limits to the nonlinear magnetization dynamics of the Heisenberg ferromagnetic material spin chain with various magnetic interactions. High-quality and qualitative studies for numerous phenomena and processes in a variety of fields, including ferromagnetic materials, nonlinear optics, and optical fibers, are characterized by the soliton solutions for the (2 + 1)-dimensional HFSC equation. Additionally, current research on this model has been recorded through [33–35].

In this case, the dependent variable in Equation (1) is q(x, t, y) and the independent variables are x, y and t. The bilinear exchange interaction coefficients along the X and Y axes are represented by J and J₁, respectively, and the parameter σ specifies the lattice parameter. The uniaxial crystal field anisotropy parameter is represented by A and the adjacent interaction on the diagonal by J₂. Numerous nonlinear models have important applications in soliton theory, mathematical physics, and fiber optics.

One well-known method is the truncated M-fractional derivative. The truncated M-fractional derivative is significant because it satisfies the requirements for both fractional and integer-order derivatives. A graphic explanation of the impact of the fractional order derivative on the obtained solutions is also provided. An attractive substitute for the traditional integer-order (2 + 1)-Heisenberg ferromagnetic spin chain equation is with a fractional order term, which gives rise to new optical solutions.

The structure of the article is as follows: Section 2 describes the preliminary section. We spoke about the method’s explanation in Section 3. Section 4 applies the approach to the equation for the nonlinear evaluation. Section 5 delves into the discussion of the graphical depiction and physical explanation of the answers achieved. Section 6 represents comparisons of our solutions with previous published solutions. In Section 7, we have finally reached our conclusions.

2. The Preliminary Section

As a brand-new variation of the M-fractional derivative, Oliveira and Sousa introduced the shortened time M-fractional derivative [38]. The M-truncated fractional derivative provides a more flexible option by doing away with the drawbacks of traditional derivatives.

3. The Advanced exp(−φ(ξ)) Expansion Method

The polynomial of e^(φ(ξ)) can be obtained by injecting Equation (5) with Equation (6) into Equation (4).

Ultimately, we have a system of equations if we fix the coefficient of each term in the obtained polynomial. We solve the set of equations to obtain Ω_i. The necessary solution is achieved by substituting the obtained values of Ω_i and Q.

The differential equation under consideration has the following solution.

4. Implementation of the Advanced exp (−φ(ξ)) Expansion Method

The advanced exp (−φ(ξ)) expansion manner will be utilized in this part to determine the precise traveling wave solutions and solitary wave solutions of Equation (1).

Let us now discuss the following case.

5. Results and Discussion

In this division, we look at the graphical portrayals of the arrangements we have found. The waveforms that are displayed graphically represent these solutions. Involving top to bottom legitimizations and supporting designs, we completely look at the way of behaving and unmistakable elements of the arrangements created from the M-partial (2 + 1)-layered Heisenberg ferromagnetic twist chain conditions.

The singularity of a solution explains some properties of nonlinear media. In nonlinear optics, materials can exhibit a nonlinear response to high-intensity light. This means that the relationship between the electric field of the light and the polarization of the material is not linear. When the intensity of the light becomes very high, it can lead to phenomena like optical self-focusing, where the refractive index of the material depends on the intensity of the light. This can result in the formation of spatial solitons, which are localized, self-sustaining waves of light. The point where such effects become extreme or localized is a singularity in the solution.

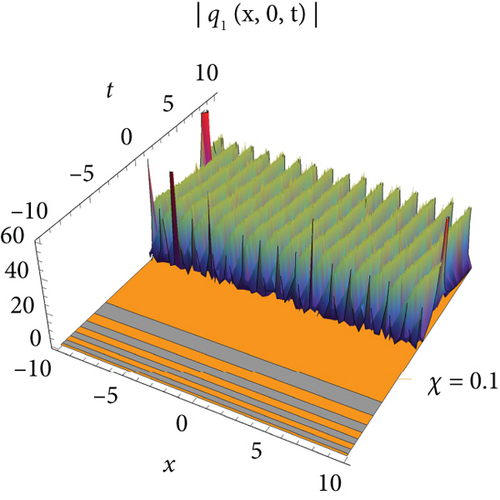
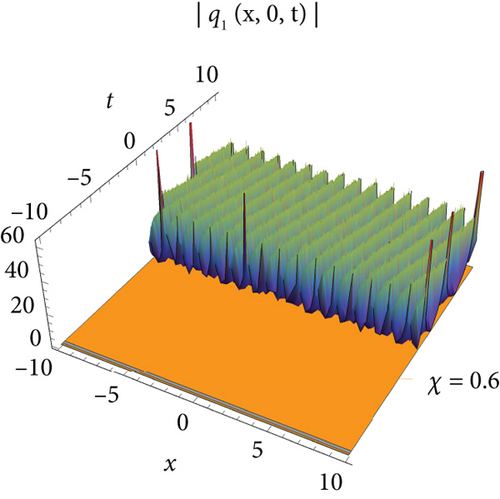
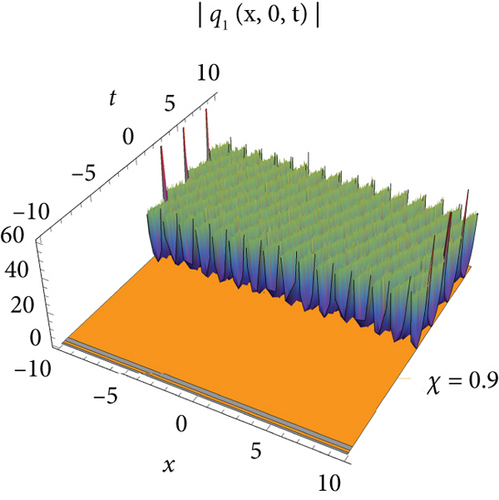
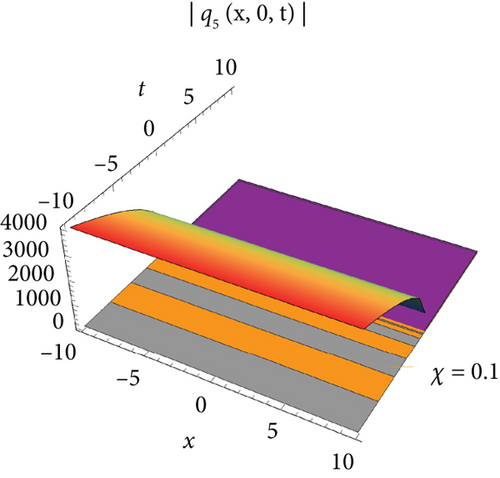
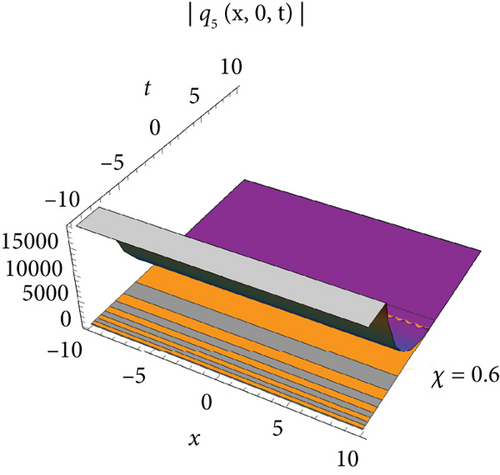
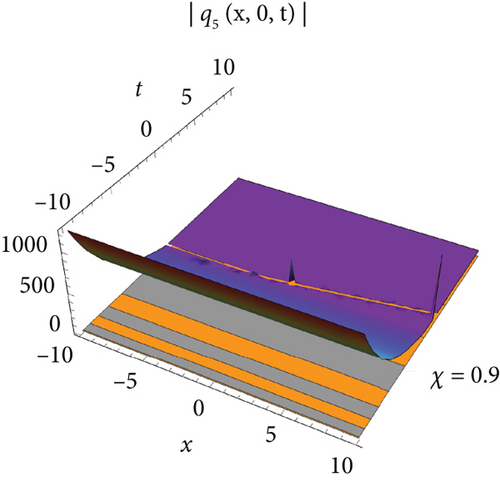
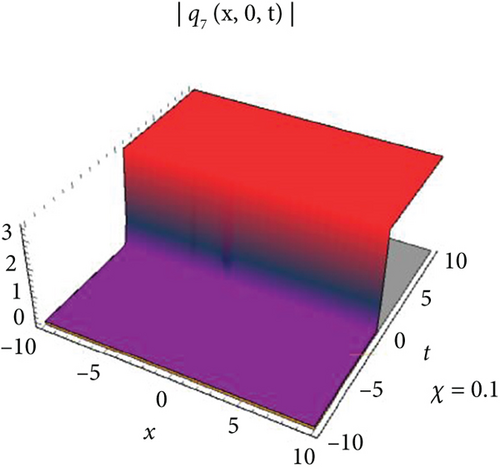
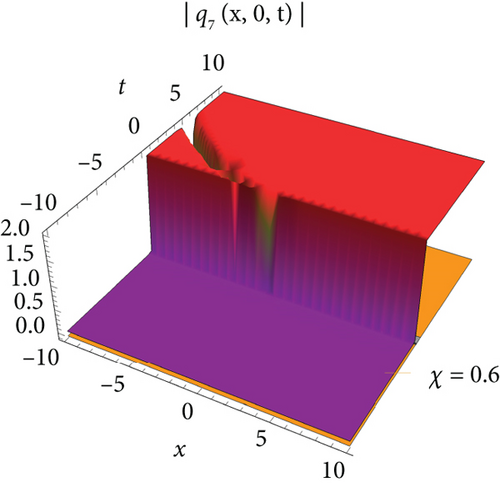
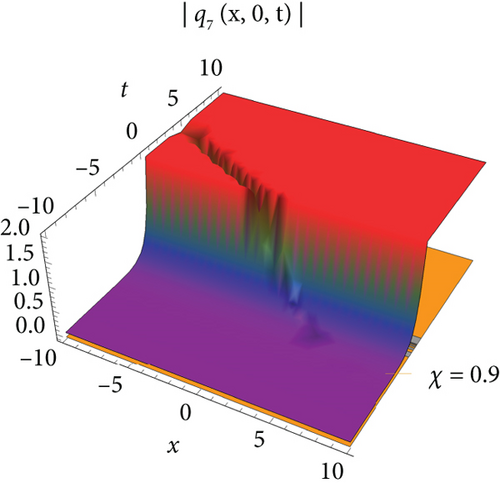
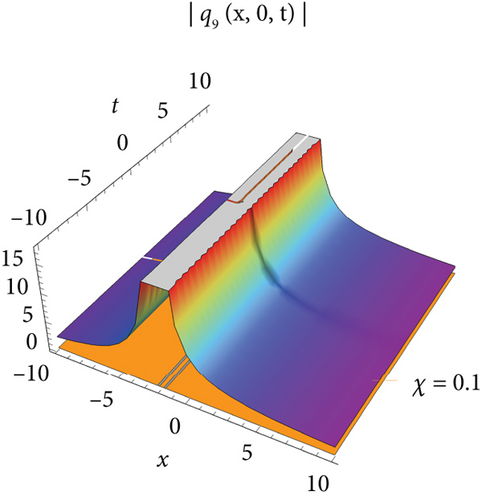
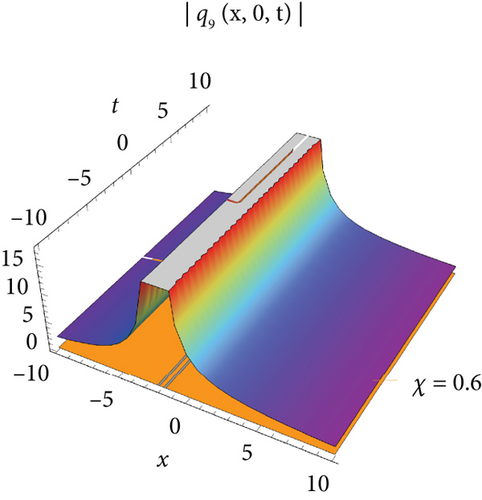
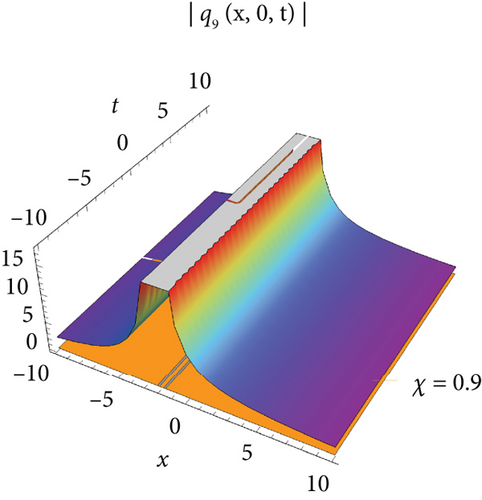
The single waves have importance with regard to the M fragmentary (2 + 1)-layered Heisenberg ferromagnetic spin chain condition that lies in their steadiness and diligence, making them critical for demonstrating nonlinear wave peculiarities in different actual frameworks, for example, shallow water waves and plasma waves. The (2 + 1)-layered Heisenberg ferromagnetic spin chain condition consolidates extra irritation terms that record for certifiable intricacies like higher-request scattering and nonlinear impacts. The single wave arrangements include a harmony among nonlinearity and scattering. Nonlinear impacts will more often than not steepen the wave, while scattering attempts to spread it out. With different condition on the free boundaries, the arrangements are complicated and authentic regarded structure that can be structured as geometrical, exaggerated, and sane capability. Plots of periodic waves, kink waves, antikink wave, kink with interaction, bright bell waves, singular soliton waves, and so on are used to show the numerical form of the obtained solutions in 3D with density. The effect of M-fractional parameters is shown in 3D and density dimensional plots at χ = 0.1, 0.6, 0.9.

Figure 1 visualizes the diagram of singular soliton wave of the solution of q₁ for values J = 1, J₁ = 1, J₂ = 1, σ = 0.6, A = 1, h = 0.2592, E = 3, Π = 2, l = 1, m = 1, Τ = 1. Figure 2 visualizes the diagram of periodic-type wave of the solution of  q₅ for the values of J = −1, J₁ = −5, J₂ = 1, σ = 1, A = 1, h = 2, E = 3, Π = −1, l = 1, m = 0.2, Τ = 1. Figure 3 visualizes the diagram of the solution of q₇ for the values J = 0.021, J₁ = 1, J₂ = 1, σ = 0.009, A = 0.021, h = 2, E = 3, Π = 0, l = 1, m = 1, Τ = 1. Figure 4 visualizes the diagram of the solution of q₉ for the values J = 0.021, J₁ = 1, J₂ = 1, σ = 0.009, A = 0.021, h = 2, E = 3, Π = 0, l = 1, m = 1, Τ = 1.

6. Comparisons

This section will compare the (2 + 1)-layered Heisenberg ferromagnetic spin chain obtained solutions with those of Wang et al. [34], who use two new efficient technologies, the variational method and the subequation method, to study the (2 + 1)-dimensional Heisenberg ferromagnetic spin chain equation.

Using the variational method, Wang et al. [34] investigated the soliton solutions to the classical form of the (2 + 1)-dimensional Heisenberg ferromagnetic spin chain equation and discovered only four solutions (please refer to Reference [34]) and discovered five precise solutions to the (2 + 1)-dimensional Heisenberg ferromagnetic spin chain equation using the subequation method. In contrast, we examine Equation (1) in this article using the sophisticated exp (−φ(ξ)) expansion method. In this study, we employed the (2 + 1)-dimensional Heisenberg ferromagnetic spin chain equation in M-fractional form. Here, we study the dynamical optical solution of the Heisenberg ferromagnetic spin chain equation in (2 + 1) dimensions. For the first time, the advanced exp (−φ(ξ)) expansion method is used to analyze the optical solution of M-fractional form of the (2 + 1)-dimensional Heisenberg ferromagnetic spin chain equation.

7. Conclusion

Specific voyaging wave arrangements of the M-fractional (2 + 1)-layered Heisenberg ferromagnetic spin chain condition have been built effectively using the advanced exp (−φ(ξ)) expansion approach. To locate the arrangements, the voyaging wave change formulas have been employed. The purpose of this research was to distinguish between the new exact solutions, namely, the other soliton arrangements that are periodic waves, kink waves, antikink wave, kink with interaction, bright bell waves, and singular soliton waves. The suggested method is very straightforward and applicable to a wide range of additional nonlinear development scenarios. It truly merits additional examination and has the potential to be highly influential in physical science and design. In the future, we will look into the nonautonomous solitons that different NLEEs might produce if their coefficients were variables and also apply spatiotemporal fractional derivation for these models.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Sakhawat Hossain analyzed and interpreted the data, contributed analysis tools or data, and wrote the paper. Md. Habibul Bashar conceived and designed the analysis, analyzed and interpreted the data, contributed analysis tools or data, and wrote the paper. M.M. Rahman, Shimul Biswas, and Md Mamunur Roshid analyzed and interpreted the data, contributed analysis tools or data, and wrote the paper.

Funding

The authors like to express their gratitude to the Research Grant (Grant No. 1111202309017) of Bangladesh University of Engineering and Technology (BUET).