In graph theory, centrality measures are used to identify the most important or influential nodes within a network. Stress centrality is one such measure, which helps quantify how “stressed” a node is within the overall graph structure based on the number of shortest paths that pass through it. Stress centrality provides a more thorough assessment of a node’s relevance than other centrality metrics since it considers not only the direct connections of a node but also the indirect effects through its neighboring nodes. Furthermore, stress centrality can be applied to biological, technical, and social networks, among other kinds of networks. The idea of stress has been expanded from undirected graphs to directed graphs in our study. The stress on a vertex v in D is half of the number of geodesics passing through the vertex v, denoted by st(v). This definition reduces to the case of stress of undirected graph whenever the digraph is symmetric. We have some findings on the stress on a digraph as well as the stress on a vertex. A few standard digraphs’ stresses are obtained, including the stress on any vertex in the cartesian product of digraphs, and some characterization on stress regular digraphs is made.

1. Introduction

Centrality measures in graph theory are essential tools used to quantify the significance and importance of nodes within a network. Graph theory provides a mathematical framework for studying relationships and connections between entities, represented as nodes, and the links between them, known as arcs. Centrality measures help to identify nodes that play pivotal roles in maintaining the structure and function of the overall network.

Centrality measures find applications in various fields, including social network analysis, biology, transportation networks, and information retrieval. Understanding the centrality of nodes in a graph helps to reveal the structural and functional importance of individual elements within a complex system. Researchers and analysts use these measures to identify key players, vulnerabilities, and potential influencers in different network scenarios.

While centrality measures like betweenness centrality also consider paths between nodes, stress centrality captures the absolute number of the shortest paths passing through a node, not just the proportion of times it lies on the shortest path. This can be particularly important when the actual volume of traffic is relevant rather than just a node’s strategic importance.

Stress centrality measures the importance of a node in terms of how frequently it lies on the shortest paths between other pairs of nodes. Nodes with high stress centrality are critical because many shortest paths pass through them, meaning they are essential in facilitating communication or flow between different parts of the graph.

Stress centrality provides insights into how crucial a particular node is in ensuring efficient information flow and connectivity within the network.

Applications of stress centrality include in transportation or utility networks; stress centrality can help to identify critical nodes whose failure could lead to significant disruptions in the overall system.

Communication networks: in social networks or information networks, stress centrality aids in pinpointing individuals or nodes that play a vital role in maintaining efficient communication channels.

Biological networks: in biological systems, stress centrality can be applied to understand the importance of specific proteins or genes in maintaining the integrity of biological pathways. Readers are referred to [1–6] to know more about applications of centrality measures.

In 1953, Shimbel [7] defined the concept of stress of a vertex in a graph. Stress of a vertex v in a graph G is the number of the shortest paths in G having v as an internal vertex and is denoted by st(v). A graph G is k− stress regular, if all vertices of G have stress k. The total stress of a graph G is defined by Bhargava et al. [8] determined the stress of vertices in some standard graphs. Poojary et al. [9] determined stress of paths, cycles, fans and wheels. They also determined the stress of a cut vertex of a graph G when G has at most two cut vertices. For more on stress of a graph, one can refer to [10–12]. The authors in [13] generalized Freeman’s geodesic centrality measures for betweenness on undirected graphs to the more general directed case in four steps.

Formally, a directed graph is defined by the ordered pair D = ( V, A), where V represents the set of vertices or nodes in the digraph and A represents the set of directed arcs, where each arc is an ordered pair (u, v), indicating that there is a directed arc from vertex u to vertex v. The order and size of D are the number of vertices and edges in D, respectively. A vertex v has an in-degree id(v) and an out-degree od(v), which represent the number of arcs that enter and exit that vertex, respectively. A vertex v in D is called a sink vertex if od(v) = 0 and is called a source vertex if id(v) = 0. A vertex v for which id(v) = od(v) = 0 is called an isolated vertex. In-degree and out-degree are essential metrics in understanding the connectivity and importance of vertices in a directed graph. The diameter of a digraph D, denoted by diam(D), is the maximum distance between any two vertices in D. A vertex v is an out-neighbor of a vertex u, denoted by N⁺(u), if there is a directed arc from u to v. A vertex u is an in-neighbor of a vertex v, denoted by N⁺(v) if there is a directed arc from u to v. The neighbors of a vertex v, denoted by N(v), in a digraph are the union of its in-neighbors and out-neighbors. The removal of a vertex v from D, denoted as V(D)∖v, is obtained by removing all the in-neighbor and out-neighbor of v. Symmetric digraphs are the digraphs in which each pair of adjacent vertices is bidirectional. A digraph with no symmetric pair of arcs is said to be an oriented graph or an orientation of the underlying graph. An orientation of G in which every vertex is a sink vertex or a source vertex is called a sink–source orientation of G. A pair of directed graphs D and H is isomorphic if there exists a bijection ϕ : V(D)⟶V(H) such that μ_D(u, v) = μ_H(ϕ(u), ϕ(v)) for every ordered pair u, v of vertices in D. The mapping ϕ is an isomorphism. A directed path

from vertex u to vertex v is a sequence of vertices (v₁, v₂, …, v_n) such that v₁ = u, v_n = v, and for each consecutive pair (v_i, v_i + 1), there is a directed arc (v_i, v_i + 1) ∈ A(D), where 1 ≤ i ≤ n − 1. A directed cycle

is a closed directed path, where the first and last vertices are the same. In a digraph D, a vertex v is reachable from a vertex u if D has a (u, v)− walk. A digraph is weakly connected if its underlying graph is connected. Strongly connected digraphs have a directed walk from every vertex to every other vertex. A digraph D is complete

if for every pair (u, v) of distinct vertices of D both (u, v) and (v, u) are in A(D). Digraph D is unilateral if for every pair (u, v) of vertices of D, either u is reachable from v or v is reachable from u or both. A geodesic from u to v in D is the shortest uv path in D. The diameter of a strongly connected digraph is defined to be the minimum distance among pairs of vertices. If digraph is not strongly connected, its diameter is taken to be infinity. The distance matrix of a strongly connected digraph D is the real matrix whose ij^th entry is d_D(v_i, v_j). Unfortunately, for a weakly connected digraph, the entry in the distance matrix is infinite. Since it is hard to deal with infinite as an entry, Botafogo defined converted distance matrix C [14] given by

where K is any postitive integer. A subgraph H in a digraph D is a graph that consists of a subset of the vertices and a subset of the directed arcs of the original digraph D. A strongly connected component is a subgraph in which every vertex is reachable from every other vertex. A cut vertex is a vertex whose removal increases the number of strongly connected components in the digraph. A block is a maximal strongly connected component in a digraph. A digraph D = (V, A) is bipartite if the vertex set V is partitioned into X and Y such that there is no arc between any two vertices of X or between any two vertices of Y. Let

be the complete bipartite directed graph in which the vertex set is a disjoint union X ∪ Y with |X| = a and |Y| = b and an arc is directed from each vertex of X to each vertex of Y. A directed bipartite graph D is oriented if for any u, v ∈ V, uv ∈ A implies vu ∉ A. For a directed graph D, the line digraph Q = L(D) has vertex set V(Q) = A(D) and arc set A(Q) = {uv : u, v ∈ V(Q): the head of u coincides with the tail of v}.

An (s, t)-directed star [15] as shown in Figure 1 is a directed graph with s + t + 1 vertices and s + t arcs, s vertices have in-degree zero and out-degree one, t vertices have in-degree one and out-degree zero, and one vertex has in-degree s and out-degree t.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

(3, 4)-directed star.

The directed windmills [16] M₃(r), r ≥ 2 as shown in Figure 2 are the digraph with 2r + 1 vertices together with arcs (1, 2k), (2k + 1, 1), (2k, 2k + 1), for 1 ≤ k ≤ r.

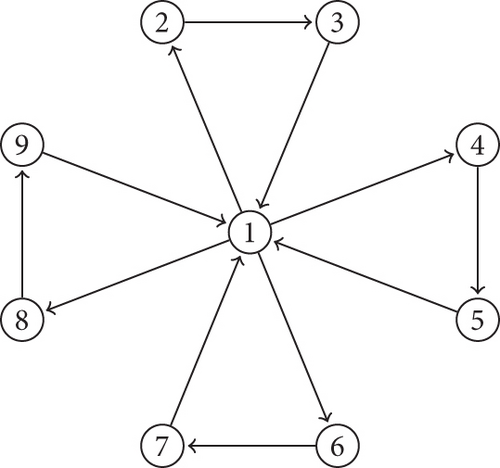
Cartesian product of two digraphs D₁□D₂ [17] as shown in Figure 3 is defined on the Cartesian product V(D₁)□V(D₂) of the vertex set of the factors. The arc set is given by A(D₁□D₂) = {(x, u)(y, v)|xy ∈ A(D₁) and u = v, or x = y and uv ∈ A(D₂)}.

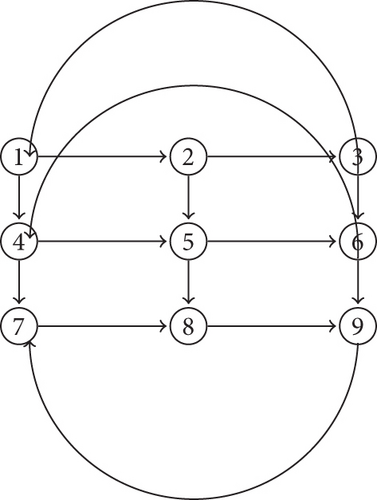
This study extends the notion of stress from symmetric graphs to nonsymmetric graphs. Almost all digraphs considered here are weakly connected. If the digraph is not strongly connected, there exists at least one vertex v ∈ D through which there is no shortest path. In such a case, we set st(v) = 0. Since the digraph is not symmetric always, if we have a uw path that passes through the internal vertex v, then we assign st(v) = 1/2. The notation st_G(v) is substituted with st(v), when the graph being discussed is evident from the context, and the shortest path refers to the shortest directed path throughout the article.

Definition 1. Let D = (V, A) be a digraph. Then, the stress on a vertex v in D is half of the number of geodesics passing through the vertex v, denoted by st(v).

Whenever the digraph is symmetric, it reduces to the case of undirected graphs.

Definition 2. Let D = (V, A) be a digraph. Then, the total stress of D is given by st(D) = ∑_v∈V(D)st(v).

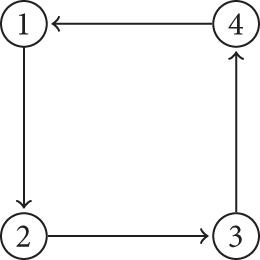
Definition 3. Let D = (V, A) be a digraph. If st(v) = k, for all v ∈ V(D), then D is said to be k−stress regular digraph. Figure 4 illustrates a 3/2-stress regular digraph.

Definition 4. Let D be a connected digraph. Then, the shortest path matrix of D given by

is an n × n matrix in which the ii^th entry is 0 and ij^th entry represents the number of the shortest paths between v_i and v_j.

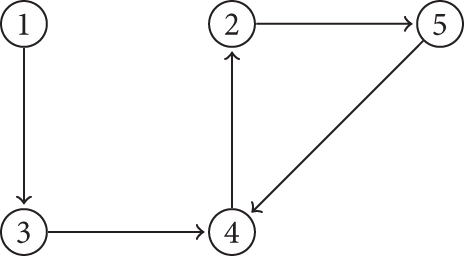
A digraph (in Figure 5) and the calculations of stress on the given digraph are calculated below.

List of the shortest paths: 1⟶3⟶4, 1⟶3⟶4⟶2, 1⟶3⟶4⟶2⟶5, 3⟶4⟶2, 3⟶4⟶2⟶5, 4⟶2⟶5, 2⟶5⟶4.

Stress on the vertices is given by st(1) = 0, st(2) = 3/2, st(3) = 3/2, st(4) = 2, st(5) = 1/2.

Total stress on D is st(D) = 11/2.

2. Results on Stress of a Digraph

Theorem 1. For any strongly connected digraph D with diameter d, we have , where f_i is the number of geodesics of length i in D.

Proof 1. We know the following for any digraph D:

•
The shortest paths of length n have n − 1 internal vertices for any digraph D.
•
Each shortest path contributes 1/2 to the stress on internal vertices.

The result follows because d is the length of the longest geodesic in D.

Theorem 2. Let D = (V, A) be a digraph which is weakly connected and let v ∈ V(D).

Then, st(v) = 0 if and only if

•
Either id(v) = 0 or od(v) = 0 or both,
•
If there is an arc (u, w) in N(v), then uwvu is not a (directed cycle of length 3).

Proof 2. Let D = (V, A) be a digraph which is weakly connected. Let v ∈ V(D) such that id(v) = 0. Then, there is no path passing through the vertex v; it is evident that st(v) = 0. Likewise for od(v) = 0 or both id(v) = od(v) = 0. Suppose id(v) and od(v) both are nonzero. If there is an arc (u, w) in N(v), then uwvu is not a then the shortest path from u to w is the arc (u, w) and hence st(v) = 0.

Conversely, let st(v) = 0. This implies there exists no path passing through vertex v.

Therefore, either id(v) = 0 or od(v) = 0 or both.

Assume id(v) ≠ 0 and od(v) ≠ 0. If there exists arc from vertex u to vertex w in N(v), that forms a cycle uwvu, then st(v) is at least 1/2 because there exists the shortest path from vertex w to vertex u passing through vertex v in D. Hence the theorem.

As a consequence of Theorem 2, we have the following result.

Corollary 1. Let D = (V, A) be a digraph which is weakly connected. Then, st(D) = 0 if and only if, for all v ∈ V(D)

•
Either id(v) = 0 or od(v) = 0 or both
•
If there is an arc (u, w) in N(v), then uwvu is not a

Theorem 3. For digraphs in which any two vertices are reachable with length less than or equal to two, 0 ≤ st(v) ≤ (id(v) · od(v))/2.

Proof 3. Let v ∈ V(D). The case st(v) ≥ 0 is obvious. Also, since D is weakly connected, st(v) = 0 if and only if

•
Either id(v) = 0 or od(v) = 0 or both,
•
If there is an arc (u, w) in N(v), then uwvu is not a .

Let id(v) = i and od(v) = j. If two vertices are reachable within a length of one, it does not contribute anything to the stress of D. If two vertices are reachable within a length of two implies, there exists i number of paths coming into v and j number of paths leaving v. Since every shortest path contributes 1/2 for stress on D, we have st(v) is at most (id(v) · od(v))/2. Therefore, 0 ≤ st(v) ≤ (id(v) · od(v))/2.

Corollary 2. For a digraph D in which any two vertices are reachable with length less than or equal to two, we have 0 ≤ st(D) ≤ (id(v) · od(v))/2, for all v ∈ V(D).

Theorem 4. Let D be a strongly connected digraph of order n and v ∈ V(D) be a cut vertex of D. If B₁, B₂ ⋯ , B_k are the blocks in V(D)∖v, then st_D(v) = (1/2){∑_1≤i≤kb_i + k! ·(n₁ − 1) · (n₂ − 1) ⋯ (n_k − 1)}. Here, b_i is the number of the shortest paths in B_i through vertex v, 1 ≤ i ≤ k ≤ n.

Proof 4. Let D be a strongly connected digraph, and v ∈ V(D) be a cut vertex of D. In V(D)∖v, let B₁, B₂ ⋯ , B_k be the blocks each of order n₁, n₂, ⋯, n_k, respectively, for 1 ≤ i ≤ k. Clearly, v ∈ B_i, for all i = 1, 2, ⋯, k. The total number of the shortest paths passing through the vertex v will be the number of shortest paths through v in B_i and the number of shortest paths from B_i to B_j through vertex v, 1 ≤ i, j ≤ k. Denote b_i as the number of the shortest paths in each B_i, 1 ≤ i ≤ k passing through the vertex v. Since D is strongly connected, there exists (n₁ − 1) · (n₂ − 1) ⋯ (n_k − 1) number of the shortest paths from each B_i to each B_j where i ≠ j and 1 ≤ i, j ≤ k holds. So, the total number of the shortest paths from B_i to B_j is k! ·(n₁ − 1) · (n₂ − 1) ⋯ (n_k − 1). We know that each shortest path contributes 1/2 on stress of vertex v. Hence the theorem.

3. Observations

1.
St(D) ≥ 0.
2.
Let D be a digraph and let D⁻¹ be the reverse of D obtained by reversing the orientation of all arcs of D. Then, St(D) = St(D⁻¹).
3.
Let e = uv be an arc in D. If id(u) = 0 and od(v) = 0, then e is an isolated vertex in L(D).
4.
5.
6.
Let be the sink–source orientation of star graph. Then, st(D) = 0.
7.
Let D be strongly connected graph such that there exists exactly one shortest path of length k between any two vertices. Then, st(D) = ∑_i≠jC_ij − 1, where are the entries of converted distance matrix.
8.
Two isomorphic digraphs have same stress but the converse need not be true.

In Figure 6, digraphs D₁ and D₂ have the same stress, that is, st(D₁) = st(D₂) = 1. But they are not isomorphic.

9.
Only for the orientation of path given in Figures 7, 8, and 9,

10.
Let D^′ and D^″ be strongly connected (unilateral) and weakly connected digraphs, respectively. Then, St(D^″) ≤ St(G) ≤ St(D^′).

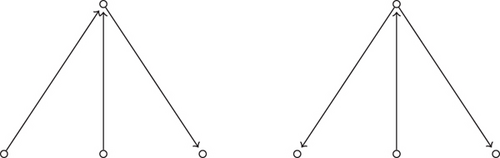
4. Stress of Some Families of Digraphs

Theorem 5. For directed cycles

Proof 5. For directed cycle there will be in total n directed paths from vertex u to vertex v, for all which contribute 1/2, 1, 3/2, 2, ⋯, (n − 2)/2 to the stress of

Therefore, we have

In any orientation of if two vertices are reachable then its length will be at most 2. As a consequence of this, by Theorem 3 we have the following results.

Corollary 3. Let be an orientation of the complete bipartite graph K_m,n. Then,

Corollary 4. Let where m and n are even. If we orient every arc in such that every vertex v in m^th partite set has id(v) = od(v) = n/2, then

Corollary 5. Let where m and n are odd. If we orient every arc in such that every vertex v in m^th partite set has id(v) = m and od(v) = m − 1, then

Theorem 6. Let D be (s, t)-directed star. Then, st(D) = (s · t)/2.

Proof 6. In (s, t)-directed star, let v be the vertex with id(v) = s and od(v) = t. Here, we note that only the nonpendant vertex v possesses stress. We have in total s · t shortest paths from s to t and each shortest path contributes 1/2 to the stress of v. Therefore, st(D) = (s · t)/2.

Theorem 7. For the directed windmills, st(M₃(r)) = (8r² − 5r)/2.

Proof 7. Let D = M₃(r). We have obtained the proof by counting the number of the shortest paths in D.

Note that the diameter of M₃(r) is 4.

The number of the shortest paths of length 1, 2, 3, and 4 is 3r, 2r + r², 2r(r − 1), and r(r − 1), respectively.

By Theorem 1, we have St(D) = 3r(0) + 2r + r∧2((1/2) + 2r(r − 1)(1) + r(r − 1)(3/2) = (2r + r² + 4r(r − 1) + 3r(r − 1))/2 = (8r² − 5r)/2.

5. Stress of a Vertex in Cartesian Product of Digraphs

Theorem 8. If D is a connected digraph with N(D) = σ_ij, then for any vertex v_x ∈ V(D),

Proof 8. The shortest path will pass through a vertex v_x for any two vertices, v_i and v_j, where i ≠ j, if and only if

()

Any shortest path v_iv_j that passes through v_x can be found by connecting the shortest path v_iv_x to the shortest path v_xv_j. Given σ_ix and σ_xj as the number of shortest v_iv_x and v_xv_j paths, let σ_ix · σ_xj denote the number of the shortest paths between v_i and v_j via v_x. Then,

()

Now, according to the definition of stress of v_x, it is given by the sum of the products σ_ix · σ_xj, where the summation is taken over all pair of vertices v_i, v_j, satisfying Equation (1).

Now by Equation (2), we have

()

We are calculating the number of the shortest paths between any two pairs of vertices in the Cartesian product of two digraphs in the following theorem. A similar result was demonstrated by the authors in [18] for the shortest paths between any two pair of vertices in cartesian product of two undirected graphs.

Theorem 9. If u = (g^′, h^′) and v = (g^′′, h^′′) are vertices in D₁□D₂, where (g^′, g^′′) ∈ D₁ and (h^′, h^′′) ∈ D₂, then the number of shortest uv paths in D₁□D₂ is given by

Proof 9. Suppose you have two vertices, u = (g^′, h^′) and v = (g^′′, h^′′), in D₁□D₂. For each u and v in D₁□D₂, let d = d(u, v) represent their distance. Assume that there is only one shortest path between g^′ and g^″ in G and h^′ and h^″ in H. If the sequence of d arcs of the uv path in D₁□D₂ makes a sequence of d_G arcs in G and a sequence of d_H arcs in H, then d = d_G + d_H. The number of the shortest paths between u and v in D₁□D₂ equals the number of ways to select d_G arcs from d arcs, that is, (d/d_G), since d_G and d_H are the same for each shortest uv path. For any pair, there exist (d/d_G) shortest pathways between u and v in D₁□D₂, because there exist σ_G shortest paths between g^′ and g^″ in G and σ_H shortest paths between h^′ and h^″ in H.

Therefore,

Theorem 10. For any connected digraphs D₁ and D₂, the stress of a vertex (g₀, h₀) in D₁□D₂ is given by

where summation runs over all pairs of vertices (g^′, h^′) and (g^′′, h^′′) different from (g₀, h₀) in D₁□D₂ satisfying

and

Proof 10. For any two vertices u and v, u ≠ v, the shortest uv path will pass through a vertex x if and only if

()

So, x = (g₀, h₀) is an internal vertex in the shortest paths between the vertices u = (g^′, h^′) and v = (g^′′, h^′′) if and only if

()

Equation (5) can be written as

()

From d(u, x) + d(x, v) = d(u, v), σ(g^′, g₀) · σ(g₀, g^′′) = σ(g^′, g^′′), the number of shortest uv paths in D₁□D₂ having x as an internal vertex.

From Theorem 9, the number of shortest ux and xv paths in D₁□D₂ is given by

()

respectively. Note that each shortest path contributes 1/2 to the stress on (g₀, h₀).

On substituting Equations (7), (8), and (3), the result follows.

6. Characterization

Theorem 11. Let D be a digraph which is strongly connected. Then, D is 0-stress regular if and only if D is complete.

Proof 11. The in-degree and out-degree of any vertex in the digraph D are nonzero, since it is strongly connected.

Suppose D is 0-stress regular.

In contrast, if D is not complete, then there is at least one shortest path with length of at least two which results in stress on D, a contradiction. Therefore, D is complete.

If D is complete, then every vertex in D is adjacent. Therefore, st(D) = 0.

We know that whenever the digraph D is complete, L(D) is also complete. Therefore, the following result holds from Theorem 11.

Corollary 6. If D is complete, then st(L(D)) = 0.

Theorem 12. Let D be strongly connected and v ∈ V(D). Then, st(v) = 1/2 if and only if there exists only one path through v as an internal vertex.

Proof 12. If there exists only one shortest path P from u to w such that v is an internal vertex, then st(v) = 1/2.

Conversely, let st(v) = 1/2. Assume that there exist two shortest paths P and P^′ passing through vertex v. Both P and P^′ impose a stress of 1/2 on v, a contradiction.

Therefore, st(v) = 1/2 if and only if there exists only one path through v as an internal vertex.

The following result follows from Theorem 12.

Corollary 7. Let D be a weakly connected digraph and let S = {v_iv_jv_k|v_i, v_j, v_j ∈ V(D)}. Then, st(D) = 1/2 if and only if there exists exactly one induced subgraph 〈S〉 that is isomorphic to

Theorem 13. Let D be strongly connected. Then, D is 1/2-stress regular if and only if

Proof 13. If then D is 1/2-stress regular.

Conversely, let st(v) = 1/2, for all v ∈ V(D). From the above theorem, we should have only one shortest path P from vertex u to vertex w passing through v. Since st(w) = 1/2, without loss of generality assume that there exists the shortest path P₁ from vertex v to vertex x passing through the vertex w.

To prove x = u.

If not, there exists the shortest path P^′ = uvwx from u to x. This implies st(w) = 1/2 but P^′ contributes 1/2 to the stress on v. That is, there exist two paths P and P^′ such that st(v) = 1, a contradiction.

Therefore, x = u and hence

The following corollary holds from Definition 1.

Corollary 8. Let H be a subgraph of D and let v ∈ V(H). If all shortest paths in H passing through v are also shortest paths in D, then st_H(v) ≤ st_D(v).

7. Conclusion

Stress centrality is a powerful and versatile metric in graph theory that quantifies the importance of a node based on the number of shortest paths that traverse it. Its application to directed graphs enhances its utility in systems where directionality governs interactions, such as communication networks, supply chains, or biological pathways.

This manuscript defines stress in digraphs and examines some of its properties. An expression for the cut vertex stress in a digraph has been provided. Additionally, the stress of certain digraph families has been calculated. Stress on a vertex in the Cartesian product of two digraphs has also been computed using the matrix approach. Finally, some characterizations on stress regular digraphs are provided.

Stress centrality is an indispensable tool for analyzing directed graphs, offering insights into node importance that are not captured by other metrics. Its ability to identify critical nodes and pathways makes it invaluable for optimizing, securing, and improving the resilience of networks in diverse fields. Future advancements in computational methods and integration with dynamic network analysis will further enhance its applicability and impact.

8. Future Scope

Given that the study of stress in digraphs is very new, there are numerous issues to be resolved. One can try to prove Observation 10. The result st(D^″) ≤ st(G) ≤ st(D^′) was concluded using the following statements.

Let D^′ and D^″ be strongly connected (unilateral) and weakly connected digraphs, respectively.

Let G be the underlying graph obtained from D^′ and D^″. In case of D^′, we know that diam(D^′) ≥ diam(G) and the number of paths in D^′ = n(n − 1) ≥ (n(n − 1))/2 = G, we have st(D^′) ≥ st(G).

In case of D^′′, number of paths in D^′′≤ number of paths in G. Therefore, st(D^″) ≤ st(G).

One may try to observe the results of removing an arc or vertex from the digraph. Characterizing the vertices according to the number of shortest paths that pass through them would be intriguing. One can try to determine which graph in a given graph class has the highest and lowest stress by taking into account various graph families, such as trees, complete bipartite graphs, and unicyclic graphs. Another important avenue for further development is to fix the diameter of the strongly connected graph and attempt to obtain the stress of varying diameters. Also, stress of different digraph products can be studied in the future.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

No funding was received for this research.

Open Research

Data Availability Statement

Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.

References

1 Ashtiani M., Salehzadeh-Yazdi A., Razaghi-Moghadam Z., Hennig H., Wolkenhauer O., Mirzaie M., and Jafari M., A systematic survey of centrality measures for protein-protein interaction networks, BMC Systems Biology. (2018) 12, no. 1, 17–80, https://doi.org/10.1186/s12918-018-0598-2, 2-s2.0-85050768297, 30064421.
10.1186/s12918-018-0598-2
PubMed Web of Science® Google Scholar
2 Bloch F., Jackson M. O., and Tebaldi P., Centrality measures in networks, Social Choice and Welfare. (2023) 61, no. 2, 413–453, https://doi.org/10.1007/s00355-023-01456-4.
10.1007/s00355-023-01456-4
Web of Science® Google Scholar
3 Bringmann L. F., Elmer T., Epskamp S., Krause R. W., Schoch D., Wichers M., Wigman J. T. W., and Snippe E., What do centrality measures measure in psychological networks?, Journal of Abnormal Psychology. (2019) 128, no. 8, 892–903, https://doi.org/10.1037/abn0000446, 2-s2.0-85069646269.
10.1037/abn0000446
PubMed Web of Science® Google Scholar
4 Friedkin N. E., Theoretical foundations for centrality measures, American Journal of Sociology. (1991) 96, no. 6, 1478–1504, https://doi.org/10.1086/229694.
10.1086/229694
Web of Science® Google Scholar
5 Koschützki D. and Schreiber F., Centrality analysis methods for biological networks and their application to gene regulatory networks, Gene Regulation and Systems Biology. (2008) 2, GRSB–S702.
10.4137/GRSB.S702
Google Scholar
6 Landherr A., Friedl B., and Heidemann J., A critical review of centrality measures in social networks, Business & Information Systems Engineering. (2010) 2, no. 6, 371–385, https://doi.org/10.1007/s12599-010-0127-3.
10.1007/s12599-010-0127-3
Web of Science® Google Scholar
7 Shimbel A., Structural parameters of communication networks, Bulletin of Mathematical Biophysics. (1953) 15, no. 4, 501–507, https://doi.org/10.1007/BF02476438, 2-s2.0-51249195602.
10.1007/BF02476438
Google Scholar
8 Bhargava K., Dattatreya N. N., and Rajendra R., On stress of a vertex in a graph, Palestine Journal of Mathematics. (2023) 12, no. 3, 15–25, https://arxiv.org/abs/2208.13493.
Google Scholar
9 Poojary R., Arathi Bhat K., Arumugam S., and Karantha M. P., The stress of a graph, Communications in Combinatorics and Optimization. (2023) 8, no. 1, 53–65, https://doi.org/10.22049/cco.2021.27320.1231.
10.22049/cco.2021.27320.1231
Web of Science® Google Scholar
10 Poojary R., Arathi Bhat K., Arumugam S., and Karantha M. P., Stress of a graph and its computation, AKCE International Journal of Graphs and Combinatorics. (2023) 20, no. 2, 200–208, https://doi.org/10.1080/09728600.2023.2243630.
10.1080/09728600.2023.2243630
Web of Science® Google Scholar
11 Poojary R., Arathi Bhat K., Arumugam S., and Karantha M. P., Stress of wheel related graphs, National Academy Science Letters. (2023) 45, no. 5, 427–431, https://doi.org/10.1007/s40009-022-01149-z.
10.1007/s40009-022-01149-z
Google Scholar
12 Shiny J., Induced stress of some graph operations, Malaya Journal of Matematics. (2021) 9, no. 1, 259–261.
10.26637/MJM0901/0043
Google Scholar
13 White D. R. and Borgatti S. P., Betweenness centrality measures for directed graphs, Social Networks. (1994) 16, no. 4, 335–346, https://doi.org/10.1016/0378-8733(94)90015-9, 2-s2.0-0013034762.
10.1016/0378-8733(94)90015-9
Web of Science® Google Scholar
14 Botafogo R. A., Rivlin E., and Shneiderman B., Structural analysis of hypertexts, ACM Transactions on Information Systems (TOIS). (1992) 10, no. 2, 142–180, https://doi.org/10.1145/146802.146826, 2-s2.0-0026845595.
10.1145/146802.146826
Web of Science® Google Scholar
15 Colbourn C. J., Hoffman D. G., and Rodger C. A., Directed star decompositions of the complete directed graph, Journal of Graph Theory. (1992) 16, no. 5, 517–528, https://doi.org/10.1002/jgt.3190160511, 2-s2.0-84987564393.
10.1002/jgt.3190160511
Web of Science® Google Scholar
16 Gan C. S., On annihilatingly uniqueness of directed windmills, 2003, Mathematics https://api.semanticscholar.org/CorpusID:6355400.
Google Scholar
17 Imrich W. and Peterin I., Cartesian products of directed graphs with loops, Discrete Mathematics. (2018) 341, no. 5, 1336–1343.
10.1016/j.disc.2018.01.021
Web of Science® Google Scholar
18 Kumar S. and Balakrishnan K., Betweenness centrality in Cartesian product of graphs, AKCE International Journal of Graphs and Combinatorics. (2020) 17, no. 1, 571–583, https://doi.org/10.1016/j.akcej.2019.03.012, 2-s2.0-85063255610.
10.1016/j.akcej.2019.03.012
Web of Science® Google Scholar

All articles

Stress in Directed Graphs: A Generalization of Graph Stress

Abstract

1. Introduction

2. Results on Stress of a Digraph

3. Observations

4. Stress of Some Families of Digraphs

5. Stress of a Vertex in Cartesian Product of Digraphs

6. Characterization

7. Conclusion

8. Future Scope

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Stress in Directed Graphs: A Generalization of Graph Stress

Abstract

1. Introduction

2. Results on Stress of a Digraph

3. Observations

4. Stress of Some Families of Digraphs

5. Stress of a Vertex in Cartesian Product of Digraphs

6. Characterization

7. Conclusion

8. Future Scope

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Related

Information