The correlation coefficient (CC) is a statistical measure that is very useful to quantify the strength and direction of the relationship between two variables, processes, or sets. The primary objective of this paper is to propose a novel CC explicitly tailored for spherical fuzzy sets (SFSs), aiming to address the limitations and drawbacks associated with existing CCs. Our approach employs statistical concepts to quantify the correlation between variables and datasets within the context of SFSs. We formulate our proposed CC for SFSs by incorporating variance and covariance as fundamental components. This innovative approach not only accurately quantifies the degree of correlation between two SFSs but also characterizes the nature of their relationship, whether it is positive, neutral, or negative. As a result, our CC yields numerical values within the range of [−1, 1]. In contrast, existing methods focus solely on measuring the degree of association between two SFSs and are unable to differentiate the nature of the relationship, especially in cases of inverse correlation. We conduct a comparison to evaluate the efficiency of our proposed scheme in comparison to existing techniques, using numerical examples to showcase the dominance of our method. The comparative results indicate that our proposed approach effectively addresses the limitations of existing methods and produces more reliable and precise results. Furthermore, we applied our method to address three real-world challenges in pattern recognition, medical diagnosis, and mega-project selection, demonstrating its practicality, advantages, and usefulness.

1. Introduction

In 1965, Zadeh [1] introduced the groundbreaking concept of fuzzy sets (FSs), a framework that has since found widespread use in various fields to deal with uncertainties arising from indeterminacy and the partial membership of elements within a set [2, 3]. FSs use a characteristic function defined within a unit interval [0, 1] to represent the degree of membership (DoM) of an element. The nonmembership value (DNM) , on the other hand, is derived as the complement of the DoM (i.e., ). Over the years, significant efforts have been made to develop more robust extensions to FSs that aim to handle incomplete, vague, and imprecise information with increased accuracy and reliability [4, 5]. In 1986, Atanassov [6] introduced a very useful extension of FS to deal with the vagueness and uncertainty [7], known as intuitionistic fuzzy set (IFS) [8]. He defined both DoM and DNM in an independent manner, but with the caveat that , where both DoM and DNM should be within a unit interval [0, 1].

While IFSs have proven helpful in dealing with vagueness and considering the satisfaction and dissatisfaction levels of elements, they face limitations when handling the situations with more than two independent statements, such as satisfaction, dissatisfaction, neutrality, and rejection [9, 10]. To address this complex scenario, Cuong [11] developed the concept of picture fuzzy sets (PFSs), a powerful extension of IFS characterized by its unique properties. PFSs are characterized by three key attributes: satisfaction degree , dissatisfaction degree , and abstinence degree I(x), given that their sum should be within [0, 1] and . The term is known as the degree of refusal (DoR) of an element to a set.

PFSs have attracted many researchers to work due to their structural proximity to human nature. Therefore, a lot of work has been done to address real-world problems, especially in the scientific and technical fields. However, PFS still has structural limitations due to their limitations [4]. The sum of all three feature functions is greater than 1 in some scenarios. Given the structural limitations associated with PFSs, Mahmood et al. [12] introduced the concept of spherical fuzzy sets (SFSs) as a novel extension of PFSs.

This extension enhances the domain of the characteristic functions and relaxes the constraint to . Due to its less restricted structure and expanded space for characteristic functions, the SFSs provide decision makers with greater flexibility in expressing their judgments and opinions compared to their predecessors and special cases such as FSs, IFSs, pythagorean fuzzy sets (PyFSs), and PFSs.

The correlation coefficient (CC) is an important statistical term used to examine the relationship between two variables. It is widely used in many fields such as natural sciences, life sciences, social sciences, and administrative sciences. It has led many researchers to make their valuable contribution in various fields such as multicriteria decision making (MCDM), medical diagnosis (MD) and pattern recognition (PR) [13].

The application of Spearman-based IF correlation measures in the triage process for effective MD during emergencies is presented in [14]. This method provides a robust tool for handling uncertainty in medical emergencies, potentially improving decision-making in critical situations. The authors in [15] build upon the work of Schweizer–Sklar aggregation operators for handling picture fuzzy information with unknown weights. Gerstenkorn and Manko [16] were the pioneers in proposing CCs to evaluate the relationships between IFSs and introduced the use of dot products of DoM and DNM values in their seminal work in 1991. Over time, advances have been made in FS theory. Numerous researchers [17–28] have formulated their own definitions of CCs tailored to different extensions, spaces, and fuzzy environments. When examining these CCs, it became clear that certain definitions, such as those in [16–21], limit their range of values to the interval [0, 1]. This area only captures positive correlations and overlooks the existence of inverse relationships that may exist between two sets or variables.

In response to this consideration, certain scholars [22–29] have devised CCs that not only gauge positive correlations but also account for negative relationships between variables or sets. These definitions yield numerical values falling within the interval [−1, 1], offering a broader and more comprehensive measure of correlation.

1.1. Motivation and Research Gap Analysis

Mahmood et al. [30] were the first to propose CC for SFSs and to investigate the relationship between two SFSs but their approach confines the values to [0, 1]. This limitation inherently captures only positive correlations, thereby overlooking potential inverse relationships between variables or sets. Although effective in measuring the strength of relationships between SFSs, this method does not address the direction or nature (positive or negative) of these relationships, leaving a significant aspect of correlation unexamined. This study seeks to fill this gap by proposing a novel approach to correlation measurement within SFSs that not only assesses the strength but also captures the direction of relationships. By providing correlation values across the range [−1, 1], our approach offers a more comprehensive tool suited for real-world problems requiring significant insights into both positive and negative associations between variables, processes, and methodologies by enabling a fuller, more nuanced understanding of relationships. The primary contribution of this research study is outlined below:

1.
Formulating the covariance and variance measures for SFSs
2.
Highlighting the limitations of the existing CCs of SFSs
3.
Proposing a novel CC for the SFSs
4.
Outlining advantages of the proposed schemes
5.
Conducting a comparison to show the superiority and novelty of our proposed CC
6.
Utilizing our proposed approach to address real-world challenges in MD, PR, and the selection of mega projects, showcasing its practical effectiveness in tackling complex issues across diverse domains

This paper is structured as follows. In Section 2, we review the fundamental notions and characteristics of IFSs, PyFSs, PFSs, and SFSs. It also discusses some of the existing CCs for SFSs. Section 3 presents our proposed CC for SFSs, which is demonstrated for both weighted and unweighted data. We also prove some propositions and theorems to investigate the characteristics of the proposed method. In Section 4, we perform a comparison of our proposed scheme with several existing definitions of CC for SFSs, using numerical examples to exhibit the advantages and superiority of our method. Section 5 illustrates the application and suitability of our approach in the fields of MD, PR, and mega project selection, using real-world problems in each of these areas. In Section 6, we highlight the limitations of the existing frameworks and outline the advantages of our schemesand we conclude the article with our final annotations.

2. Preliminaries

This section aims to establish a foundation and make easy the progress of this research study. It reviews the several fundamental concepts, operations, and properties that are closely related to SFSs and CCs. Throughout the paper, we denote the membership, nonmembership, abstinence, and refusal degrees as , , , and , respectively. These values are expressed within the unit interval [0, 1].

2.1. Some Extensions of FSs

This section revisits fundamental concepts of relevant FS extensions for this study.

Definition 1 (see [6].)Let E be a universe of discourse (UoD), then an IFS A on E is defined as follows: , with the constraint . is the degree of hesitancy (DH) for an element to be belonging to A.

Definition 2 (see [31].)A PyFS in E is defined as follows: , with the constraint . The DH for to be belonging to can be mathematically articulated as .

Definition 3 (see [10].)Let be a PFS in E. It can be defined mathematically as follows: , with . The DoR for to be in PFS C is denoted as follows: .

Definition 4 (see [32].)For the PFS defined in Definition 3, its standard negation set is .

Definition 5 (see [12].)A SFS in E is defined as follows: , with a constraint . The DoR for to be belonging to can be articulated as follows: .

Definition 6 (see [12].)Let and be two SFSs, then

•
if and only if , for all .
•
if and only if and .

2.2. Existing CCs of SFSs

In this section, we revisit existing CCs tailored for the SFSs environment by various researchers.

Definition 7 (see [30].)Let and be two SFSs in E. The CC between SFSs and is

()

For the SFSs

and

having weights w = {w₁, w₂, …, w_n} for its elements

with F_A(x) = aF_B(x) and

, the authors in [29] introduced the following weighted form of CC:

()

Definition 8 (see [30].)Another form of CC between two SFSs and is

()

In [30], another form of weighted CC for SF weighted information is established as follows:

()

where w = {w₁, w₂, …, w_n} is the weight vector of the SFSs

and

for its elements

with F_A(x) = aF_B(x) and

To overcome the drawbacks related to equations (1) to (4) of CCs, we formulate some novel CCs, which are demonstrated in the following section.

2.3. Limitations of Existing Frameworks

This section highlights the drawbacks of the current structures:

i.
The concept of FSs falls short in modeling nonmembership grade, as it only considers the membership grade when discussing the issues related with them.
ii.
Even though IFSs can tackle issues regarding to both the DoM and DNM, they face failure if there is a situation where we need of considering the degrees of neutrality and refusal.
iii.
Although PFSs can accommodate the degrees of indeterminacy and refusal, they still face limitations in making the decisions due to the tough restriction on their characteristic functions, limiting decision to a specific domain.
iv.
Thus, the constraints present in the frameworks of FSs, IFSs, and PFSs render their CC ineffective in handling information under the framework of SFSs.
v.
The existing CCs for SFSs can investigate the degree of relationship between SFSs or SFI, but they fail to determine the nature (i.e., whether it is positive or negative) of relationship between them. Thus, the existing CCs cannot calculate the correlation between a SFS and its complement SFS and also to its negation sets.

3. Proposed Novel CC for SFSs

In this section, we propose an improved statistical form of CC for both the weighted and unweighted SFSs. We address the weaknesses of existing definitions by introducing our proposed scheme, which is grounded in statistical principles for measuring the correlation between two variables.

To provide greater clarity, we have included a tabular representation of the notations and variables used throughout this paper, as presented in Table 1.

Table 1. Decision variables and notations.

Notation	Description
	Degree of membership to be belonging to
	Degree of indeterminacy
	Degree of nonmembership
	Variance of the SFS
	Covariance between SFSs and
	Correlation coefficient between SFSs and
	Weighted CC between SFSs and
	Spherical characteristic information about patients
	Spherical diagnosis information
J_SN	Standard negation set of SFS J
	CC matrix between the patients and diagnosis
	Set of criteria for evaluation of the alternatives
Q⁺	Ideal alternative
	CC between alternatives and ideal alternative
	Degree of refusal to be belonging to SFS
	Deviation of DoR from its mean

To facilitate a better understanding of our research strategy, we present a visual representation in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Flowchart of the proposed research study.

To establish the basis for our definition, we initially introduce the covariance and variance of the SFSs by considering deviations in their membership components.

Suppose we have two SFSs

and

, on a UoD

. We define the following two new variables in terms of deviations of membership grads:

()

where

()

Here, in the context of a SFS, the deviation of membership values from their mean represents the extent to which individual membership degrees diverge from the average membership degree of the set. Similarly, the deviation of DNM from their overall mean quantifies the variation in nonmembership degrees around their average value. Likewise, the deviation of indeterminacy values from their overall mean measures the spread of uncertainty or hesitation degrees within the set. These deviations provide a comprehensive understanding of the distribution and variability of the membership, nonmembership, and indeterminacy values within the SFS. Moreover, these deviations set a foundation for the calculation of variance and covariance between SFSs, enabling the analysis of relationships and dependencies among FSs. This, in turn, contributes significantly to the formulation of the proposed CC for SFSs, enhancing its effectiveness and applicability in capturing the interconnections between sets.

We then define the covariance and variance of the SFS(s) in the following.

Definition 9. Let us have two SFSs and , defined over E. Then,

a.
The variance of and can be mathematically expressed in terms of new variables as follows:
()

()
b.
The covariance of two SFSs and is defined as follows:
()

Proposition 1. If is the covariance of two SFSs and in E, then it must fulfill the following conditions:

(i)
(ii)
(iii)

Proof 1. We only prove part (iii), as (i) and (ii) are obvious.

(iii) From Cauchy–Schwarz inequality, we know that

()

Hence,

()

Utilizing the previously defined notions of variance and covariance for SFSs, we proceed to introduce our novel definition of the CCs for SFSs in the following.

Definition 10. Let us have two SFSs and , defined over a UoD . Then, the CC between and is defined as

()

where

()

Hence,

()

Theorem 1 can be derived from our proposed CC between two SFSs.

Theorem 1. Let and be two SFSs in , and their CC must satisfy the following criterion:

a.
b.
c.
, if for any constant k > 0. Where means, , , , and
d.
, if , for any constant k < 0

Proof 2.

a.
It is obvious/straightforward.
b.
Using inequality (12) of Proposition 1, we have and so .
By combining the above two inequalities, we have
()
c.
, , , and for any constant k > 0. So
()
Hence,
()
Therefore, for any constant k > 0,
()
d.
As we have for any constant k < 0, hence , , , and . Therefore,
()

()

Therefore, for any constant k < 0,

()

In many of the practical situations, diverse objects are of not equal importance, so we have to consider their weights accordingly. We introduce a weighted CC between two SFSs in the following.

Definition 11. Suppose we have two SFSs and , defined over a UoD with weights T_A(x) = aT_B(x) for its elements having F_A(x) = aF_B(x) and . Then, we can define the weighted CC between and as follows:

()

As , , and .

For all having equal weights (i.e., w = {(1/n), (1/n), …, (1/n)}), there would be a same mathematical expression/definition of CC for both the weighted and unweighted SFSs.

We derive the following proposition from the above definitions of weighted variance and covariance of SFSs.

Proposition 2. If we have two SFSs and in a finite UoD E, then their weighted covariance satisfies the following conditions:

i.
ii.
iii.

Proof 3. Identical to that of Proposition 1.

In the following, Theorem 2 about our proposed weighted CC is being derived using Proposition 2 and the definitions of covariance and variance of SFSs.

Theorem 2. The weighted CC between two SFSs and in a finite UoD E must fulfill the following conditions:

a.
b.
c.
, if for any constant k > 0, where means, , , , and .
d.
, if , for any constant k < 0.

Proof 4. Same as that of Theorem 1.

To facilitate the comparability process in a more intuitive manner, we introduce the concept of the standard negation set for a SFS as follows.

Definition 12. Let be a SFS in E, then its standard negation set can be denoted by and its components can be defined as , , and for all . Thus, the standard negation set of SFS can be mathematically articulated as , with the constraint . Here, is the DoR for an element to be belonging to .

4. Comparison

In this section, we present some intuitive and synthetic numerical examples to conduct a comprehensive performance comparison between our proposed scheme and existing methods, including Mahmood et al. [30]. Our aim is to illustrate the novelty and superiority of our approach. Through these numerical comparisons, we emphasize the limitations of existing methods and showcase the strengths of our proposed scheme in overcoming these drawbacks.

Intuitively, there should be an inverse relationship between a SFS and its negation set, indicating a negative correlation between them. Therefore, the numerical value of their CC should be negative. Our CC is designed to measure and highlight these aspects when dealing with such types of SFSs. Next, we illustrate the aforementioned aspects using intuitive synthetic numerical examples. We apply both our proposed method and existing definitions to showcase the differences and advantages of our approach.

Example 1. Let us consider three SFSs, denoted as, ϒ and L over a UoD . These SFSs are presented as follows:

()

Using our proposed Definition 12, the standard negation set of a SFS J is established as follows: .

By using our proposed CC and the existing methods [29] to the above SFSs, we presented the summary of comparative results in Table 2.

Table 2 clearly indicates that both of the existing methods [30] failed to capture the negative relationship between SFS J and J_SN; instead, they indicated a positive correlation between them, whereas our proposed method precisely depicts this aspect and demonstrates that there exists a strongly negative correlation between SFSs J and its standard negation set J_SN, as indicated by their CC of −0.9879. Furthermore, it is evident that the membership values of SFS K increase while those of SFS L decrease across the elements of the UoD . Similarly, the DNM and indeterminacy values of SFS ϒ decrease as the corresponding values in SFS L increase over the discourse. Intuitively, there should be an inverse relationship between the SFSs ϒ and L. However, Table 2 clearly confirms that the existing methods [30] fail to accurately measure this inverse relationship and erroneously indicate a strongly positive correlation between them, rather than reflecting a strongly negative correlation. In contrast, our proposed definition correctly captures the exact nature of their relationship, revealing a strong negative correlation with a CC of −0.9938. This demonstrates a clear advantage of our scheme over the existing methods for calculating the correlation between SFSs.

Table 2. Correlation coefficient of SFSs.

Correlation coefficient	Existing methods		Our proposed methods
Correlation coefficient	Mahmood et al. [29]	Mahmood et al. [29]	Our proposed methods
M(J, J_SN)	0.3239	0.3197	−0.9879
M(ϒ, L)	0.8852	0.8770	−0.9938

Example 2. In the context of Example 1, consider three SFSs denoted as J, ϒ, and L, defined over a common UoD . These SFSs are associated with different weights represented by a weight vector w = {0.3, 0.5, 0.2}. We present a comparison of performance of our weighted CC and existing methods [30] for measuring correlation between weighted SFSs in Table 3.

It is very clear from Table 3 that the proposed scheme accurately depicts the exact nature of relationship (i.e., negative relationship) between SFS J and its standard negation set J_SN, as their CC is −0.9907. This provides strong evidence that the SFS J and its standard negation set J_SN exhibit a strongly negative correlation. In contrast, the existing schemes [30] depict a positive correlation between SFS J and its standard negation set J_SN, which is intuitively implausible.

Additionally, it is also evident that the characteristic function values (membership grades) of SFSs ϒ and L vary inversely across the elements of the UoD . Intuitively, these two SFSs ϒ and L should exhibit a negative correlation. However, as shown in Table 2, the existing methods [30] fail to accurately measure this inverse relationship and instead indicate a strong positive correlation between them. In contrast, our proposed definition of the weighted CC accurately represents this aspect of the relationship, revealing a strong negative correlation with a CC value of −0.9911. Hence, the aforementioned gray areas and weaknesses reduce the theoretical support and practical reliability of these existing methods. Keeping in view these drawbacks of existing methods and strengths of our proposed scheme, we can say that our method has an upper hand over the existing methods in respect with usefulness, practicality, and accuracy.

Table 3. Comparative analysis of weighted correlation coefficient.

Correlation coefficient	Existing methods		Our proposed methods
Correlation coefficient	Mahmood et al. [29]	Mahmood et al. [29]	Our proposed methods
M_w(J, J_SN)	0.3334	0.3328	−0.9907
M_w(ϒ, L)	0.8947	0.8929	−0.9911

4.1. Advantages of the Proposed Strategies

This section outlines the advantages of the proposed methods in comparison to the existing ones:

i.
Our proposed designs have a very closer alignment with human judgment. It is because these schemes accommodates the four of the human cognition responses, including agreement, disagreement, neutrality, and refusal. Due to its less restricted structure and larger space for characteristic functions, decision makers have more freedom in expressing their judgments and opinions in SFS environment as compared to its previous structural versions and special cases like FSs, IFSs, PyFSs, and PFSs. The proposed CCs not only measures the degree of relationship between SFSs but also highlights whether their correlation is positive, zero, or inverse.
ii.
These methods can easily quantify the correlation of a SFS with its complement SFS and also with its negation SFS in a reliable and accurate way.
iii.
The investigation of the PR, MD, and mega project selection conducted under SF environment in application Section 5 cannot be studied or accomplished by the models of FSs, IFSs, PyFSs, and PFSs.
iv.
The findings presented in comparison Section 4 of this study demonstrated that the proposed CCs are more effective in quantifying the inverse correlation that exists between a SFS and its complement set as well as with its negation SFS. Furthermore, the application in Section 5 also showed that the results of our proposed CCs in MD problem and mega project selection are in complete alignment with the results of the original work from where we had taken the real data.

5. Application in PR, MD, and Mega Project Selection

In this section, we demonstrate the performance and practical applications of our proposed scheme in PR, MD, and mega project selection. Our aim is to showcase the feasibility, effectiveness, and practicality of our method through real-world problems in these fields.

5.1. PR

To demonstrate the usefulness and application of our proposed method in the field of PR, we consider the following two problems of PR in which we have to recognize the belongingness of an unknown pattern to any of the given known patterns using our proposed scheme.

Example 3. Consider a scenario where we have four known synthetic patterns labeled as , , , and along with an unknown sample pattern . These patterns are represented as SFSs over a space of points or a UoD , and each pattern is associated with a weight vector w = {0.26, 0.23, 0.24, 0.27}. Table 4 provides characteristic values for all the aforementioned patterns, forming a SF decision matrix. Using our proposed SFS CC, we calculated the association of with , , , and , determining the unknown pattern’s affinity with each of them. Table 5 displays the results.

Table 5 provides a comprehensive analysis of the correlation between various known patterns and the unknown sample pattern . Notably, among all the known patterns examined, one particular pattern exhibits the highest CC with the unknown sample . This high CC value suggests a significant degree of similarity between the unknown sample and this specific known pattern . Based on the principle that a higher CC indicates a stronger relationship, we can confidently conclude that this known pattern is the most strongly correlated with the unknown sample . Consequently, this strong correlation implies that the unknown sample pattern most likely belongs to or closely resembles this known pattern .

Table 4. Characteristic values of

and

as SFSs.


< 0.12, 0.12, 0.22 >	< 0.22, 0.22, 0.32 >	< 0.33, 0.33, 0.42 >	< 0.42, 0.42, 0.42 >
< 0.22, 0.22, 0.32 >	< 0.33, 0.33, 0.42 >	< 0.42, 0.42, 0.52 >	< 0.53, 0.53, 0.62 >
< 0.12, 0.22, 0.33 >	< 0.22, 0.33, 0.42 >	< 0.33, 0.33, 0.42 >	< 0.32, 0.32, 0.52 >
< 0.12, 0.32, 0.52 >	< 0.12, 0.52, 0.72 >	< 0.12, 0.33, 0.72 >	< 0.12, 0.33, 0.42 >
< 0.12, 0.12, 0.12 >	< 0.12, 0.12, 0.22 >	< 0.33, 0.33, 0.42 >	< 0.42, 0.42, 0.52 >

Table 5. Correlation coefficient of

with

Correlation coefficient
	1.00	0.98	0.96	−0.13

Note: The bold values highlight the highest correlation coefficient observed among all the known patterns with the unknown sample. This signifies that the corresponding pattern exhibits the strongest similarity or association with the unknown sample, making it the most relevant match.

Example 4. Suppose we have another PR problem with set of four known patterns, , and an unknown sample pattern , defined over a UoD , with a weight vector w = {0.31, 0.22, 0.28, 0.19}. SF information about the features of the aforementioned patterns is presented in Table 6. The results of the CCs between and using our proposed scheme are presented in Table 6 to determine the association of the unknown pattern .

Given that exhibits the highest CC with among all the known patterns listed in Table 7, we can confidently conclude that best matches the known pattern .

Table 6. Feature values of

and

as SFSs.


< 0.12, 0.12, 0.22 >	< 0.22, 0.22, 0.32 >	< 0.33, 0.33, 0.42 >	< 0.42, 0.42, 0.42 >
< 0.22, 0.22, 0.32 >	< 0.33, 0.33, 0.42 >	< 0.42, 0.42, 0.52 >	< 0.53, 0.53, 0.62 >
< 0.12, 0.22, 0.33 >	< 0.22, 0.33, 0.42 >	< 0.33, 0.33, 0.42 >	< 0.32, 0.32, 0.52 >
< 0.12, 0.32, 0.52 >	< 0.12, 0.52, 0.72 >	< 0.12, 0.33, 0.72 >	< 0.12, 0.33, 0.42 >
< 0.12, 0.12, 0.12 >	< 0.12, 0.12, 0.22 >	< 0.33, 0.33, 0.42 >	< 0.42, 0.42, 0.52 >

Table 7. Correlation coefficient of

with

Correlation coefficient
	0.98	0.99	0.93	0.86

Note: The bold values indicate the highest CC among all the known patterns and the unknown sample. This demonstrates that the corresponding pattern has the strongest similarity or association with the unknown sample, making it the most significant match.

5.2. Application in MD

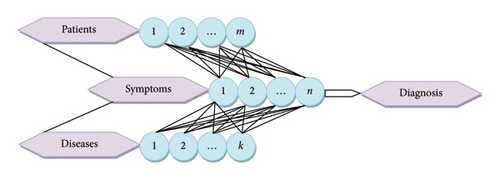
MD is a process of identifying a disease based on a patient’s symptoms and physical signs. To achieve this, the symptoms of various diseases and those of the patient under consideration are carefully examined. Then, the most likely disease affecting the patient is determined using statistical and mathematical measures. In this paper, we used our proposed novel CC for SFSs to address a real-world problem regarding a MD. In order to make a clear understanding, we furnish a generic structure of a MD problem under SF environment in the following.

Thematic settings: Consider a group of patients P, comprising of individuals P_i(i = 1, 2, …, m). Each of these patients may suffer from any of the k diseases in a set D, which includes D_j(j = 1, 2, …, k). In addition to their respective diseases, these patients exhibit a range of symptoms S, encompassing S_l(l = 1, 2, …, n). These symptoms may manifest in different ways depending on the disease that a patient has. Together, the sets P, D, and S form an intricate web of interrelated health data that is critical to understand in order to diagnose and treat patients effectively.

Objective: This framework is designed to determine the underlying disease afflicting a patient. This can be a challenging task, as there may be several diseases that present with similar symptoms. Therefore, a thorough examination of the patient’s symptoms, medical history, and other pertinent factors is necessary to accurately identify the disease and provide effective treatment. By establishing a momentous linkage and investigating the association between diseases and patients in respect with their symptoms using our proposed CC, we aim to provide a comprehensive and accurate diagnosis for each patient, enabling them to receive the appropriate care and support they need.

Criterion for the diagnosis: The diagnostic criterion for identifying a patient’s disease is based on the maximum association between the symptoms of the diseases under consideration and those of the patients. By analyzing the patient’s symptoms and comparing them to those of various diseases, we can determine the most appropriate disease diagnosis. Our methodology is based on the principles of maximum association and correlation using our proposed CC to achieve an accurate and reliable diagnosis. Ultimately, this approach helps to improve patient health by identifying the correct disease and providing appropriate treatment. A diagrammatic representation for the proposed MD scheme is shown in Figure 2.

In the following, we aim to illustrate the practical applicability and effectiveness of our proposed method in the field of MD. To accomplish this, we present a real-world MD problem, sourced from a previous study [12], which serves as an ideal test case for demonstrating the utility of our approach.

Example 5 (see [12].)Let us consider a MD scenario involving four patients , five potential medical diagnoses , and a set of five symptoms to be used to diagnose the patients in connection with the diseases under consideration. These elements are essential for diagnosing the patients in relation to the potential diseases. The spherical diagnosis information related to the aforementioned symptoms is presented in Table 8 as a spherical fuzzy decision matrix (SFDM). Additionally, the spherical characteristic information about the patients concerning the symptoms is displayed as a FSDM in Table 9.

To streamline this MD decision-making process, we applied our proposed CC defined in equation (10) to assess the connection between patients and the set of diagnoses under consideration. This allowed us to establish a CC matrix between them. Adhering to the principle of maximum correlation, we selected the most suitable diagnosis from the options for each patient, based on the highest CC. Following the implementation of our method, we have presented the results in Table 10.

The highest CC between patients and their respective diagnoses indicates the appropriate diagnosis. As observed in the Table 10, patient is diagnosed with . Similarly, patient has the strongest association with , suggesting that is suffering from . Considering the patient , its CC is highest with , making it a candidate for diagnosis with . Furthermore, it is noteworthy that our proposed method’s diagnosis results align with those from [12], the source of this MD problem. This agreement is displayed in tabular form in Table 11.

Hence, we can say that our proposed CC for SFSs is practically reliable, technically sufficient, and effective in dealing with the MD problems.

Table 8. Spherical diagnosis information table with respect to the symptoms.


< 0.4, 0.3, 0.4 >	< 0.7, 0.1, 0.2 >	< 0.4, 0.2, 0.7 >	< 0.0, 0.0, 0.1 >	< 0.7, 0.1, 0.4 >
< 0.5, 0.5, 0.3 >	< 0.0, 0.0, 0.5 >	< 0.2, 0.0, 0.8 >	< 0.34, 0.4, 0.0 >	< 0.0, 0.41, 0.3 >
< 0.6, 0.0, 0.1 >	< 0.5, 0.1, 0.6 >	< 0.5, 0.2, 0.4 >	< 0.9, 0.0, 0.1 >	< 0.5, 0.5, 0.5 >
< 0.4, 0.3, 0.7 >	< 0.4, 0.6, 0.6 >	< 0.1, 0.0, 0.0 >	< 0.1, 0.6, 0.7 >	< 0.76, 0.3, 0.2 >
< 0.3, 0.3, 0.6 >	< 0.1, 0.3, 0.7 >	< 0.1, 0.4, 0.6 >	< 0.7, 0.2, 0.1 >	< 0.2, 0.0, 0.81 >

Table 9. Spherical information table regarding patients and symptoms.


< 0.7, 0.1, 0.4 >	< 0.5, 0.1, 0.8 >	< 0.4, 0.6, 0.5 >	< 0.8, 0.0, 0.4 >	< 0.0, 0.8, 0.5 >
< 0.9, 0.1, 0.0 >	< 0.5, 0.0, 0.2 >	< 0.0, 0.6, 0.8 >	< 0.3, 0.3, 0.3 >	< 0.5, 0.5, 0.7 >
< 0.4, 0.4, 0.4 >	< 0.2, 0.1, 0.2 >	< 0.7, 0.4, 0.2 >	< 0.0, 0.8, 0.4 >	< 0.7, 0.3, 0.3 >
< 0.0, 0.1, 0.6 >	< 0.5, 0.5, 0.5 >	< 0.9, 0.4, 0.1 >	< 0.1, 0.0, 0.0 >	< 0.2, 0.5, 0.7 >

Table 10. Correlation coefficient matrix between the patients and diagnosis.


0.2301	0.6776	0.8949	−0.2388	0.8331
0.5954	0.6863	0.2993	−0.1256	0.2472
0.4165	0.2313	−0.1089	0.8825	−0.1684
0.1398	0.1298	0.3356	0.5242	0.3671

Note: The bold values represent the highest CC between patients and their respective diagnoses, indicating the most appropriate diagnosis for each patient. These values help in identifying the most relevant associations, ensuring clarity and accuracy in the interpretation of the data.

Table 11. Diagnosis results in consensus to [12].

Patients	Diagnosis
Patients	Mahmood et al. [12]	Mahmood et al. [30]	Proposed scheme

5.3. Mega Project Selection

The selection of most feasible and suitable projects plays a pivotal role in accelerating the development process of an area and its population, enduring impact on its economy and the environment. So, in this section, we implement our method to facilitate the process of selecting a best option from the available alternatives of mega projects, which is most beneficial and effective for the development of a region and uplifting the life standard of its community.

Example 7 (see [10].)A country has to invest on a most promising mega project among the designed feasible mega projects, using a fund received from the World Bank as a loan. Suppose there are five projects in the priority list of government as follows.

(1) construction of 1 million houses; (2) construction of dam; (3) orange metro train; (4) investment in industry; and (5) investment in power sector, and they can be presented using set notation as . In order to evaluate these mega project alternatives, a panel of development specialists and strategy experts have designed the following set of criterion: :long-term benefit, :time, :impact, :revenue generation, :cost, :short-term benefits, which can be symbolized as . The relative importance of the criterion has been described with their weights w = (0.12, 0.25, 0.09, 0.16, 0.20, 0.18)^T. Keeping in view the pros and cons of each alternative, the panel of experts have evaluated every mega project and expressed their decisions in the form of SFDM in Table 12.

We apply our proposed weighted CC (12) to identify the best option among the available mega project alternatives. In order to do so, we compute the association between each option and an IA such that we can choose the one, having strongest relationship with ideal choice, keeping in view the principle of highest correlation. The ideal alternative we have is the one, having maximum satisfaction membership value, minimum dissatisfaction value, and minimum indeterminacy value in respect with the entire alternatives for each criterion.

That can be represented in the form of SFS as Q⁺ = {〈0.91, 0.03, 0.02〉, 〈0.89, 0.08, 0.03〉, 〈42, 0.35, 0.05〉, 〈0.73, 0.15, 0.02〉, 〈52, 0.31, 0.05〉, 〈0.91, 0.03, 0.05〉}. After implementing our proposed scheme, we presented the comparative relationship of the available alternatives with ideal choice on the basis of our new scheme in Table 13.

It is very clear from Table 13 that the mega project has the highest correlation with the ideal choice Q⁺. Hence, it can be concluded that the investment in the power sector mega project is the most promising and best option among the available alternatives, to accelerate the development process of the region, revenue generation, and the prosperity of the local communities. Thus, these real-world scenarios and applications can justify the reasonableness and suitableness of our proposed method to handle the problems of mega project selection, MD, and PR processes in a effortless and novel way.

Table 12. Spherical fuzzy decision matrix regarding available mega projects.


< 0.53, 0.33, 0.09 >	< 0.73, 0.12, 0.08 >	< 0.91, 0.03, 0.02 >	< 0.85, 0.09, 0.05 >	< 0.90, 0.05, 0.02 >
< 0.89, 0.08, 0.03 >	< 0.13, 0.64, 0.21 >	< 0.07, 0.09, 0.05 >	< 0.74, 0.16, 0.10 >	< 0.68, 0.08, 0.21 >
< 0.42, 0.35, 0.18 >	< 0.03, 0.82, 0.13 >	< 0.04, 0.85, 0.10 >	< 0.02, 0.89, 0.05 >	< 0.05, 0.87, 0.06 >
< 0.08, 0.89, 0.02 >	< 0.73, 0.15, 0.08 >	< 0.68, 0.26, 0.06 >	< 0.08, 0.84, 0.06 >	< 0.13, 0.75, 0.09 >
< 0.33, 0.51, 0.12 >	< 0.52, 0.31, 0.16 >	< 0.15, 0.76, 0.07 >	< 0.16, 0.71, 0.05 >	< 0.15, 0.73, 0.08 >
< 0.17, 0.53, 0.13 >	< 0.51, 0.24, 0.21 >	< 0.31, 0.39, 0.25 >	< 0.81, 0.15, 0.09 >	< 0.91, 0.03, 0.05 >

Table 13. CCs between Q⁺ and

Correlation coefficient
	−0.0398	−0.0177	0.7525	0.6374	0.7828

Note: The bold values represent the highest CC between the ideal choice and the corresponding Mega Project, highlighting the most appropriate and significant project among all those studied. These values aid in identifying the strongest associations, ensuring clarity and accuracy in data interpretation.

6. Conclusions

The spherical fuzzy framework offers a robust solution for addressing uncertainties and vagueness rooted in human opinions, making it particularly valuable in decision science and various real-world applications where traditional fuzzy systems like FSs, IFSs, PyFSs, and PFSs fall short.

In this study, we introduced an innovative CC specifically designed for SFSs, applicable to both weighted and unweighted cases. This new method draws inspiration from statistical theory to establish clear relationships between variables and datasets, enhancing the framework’s analytical capability. Our contributions begin with the development of new covariance and variance measures for SFSs, which are fundamental to our CC. We thoroughly investigated their properties and proved supporting propositions and theorems. Built upon these measures, our proposed CC not only quantifies the degree of relationship between two SFSs but also determines the nature of the correlation—positive, negative, or neutral—using a range within [−1, 1]. This level of detail addresses a gap in existing CCs, which cannot distinguish between the types of relationships, particularly inverse correlations. To showcase the superiority of our method, we conducted a comparative analysis using numerical examples, confirming that our approach yields more accurate and reliable results while also being simple and computationally efficient. This makes it highly adaptable for various applications. Furthermore, we applied the proposed scheme to develop three mechanisms for addressing real-world problems in PR, MD, and the selection of mega projects, thereby demonstrating its practical relevance and advantages over existing models. Our study also includes an assessment of the limitations in current models compared to the strengths of our approach, underscoring its enhanced performance, novelty, and suitability for complex problem-solving.

It can be challenging to apply our proposed CC to the crisp datasets and complex fuzzy datasets available in repositories and other similar sources. Our future work involves extending our proposed measures in FS theory to the other frameworks of complex structural design and applying them to the problems in various fields, including intelligent systems, robotics, analytics, computational intelligence and cybersecurity, education, HR, and healthcare.

Disclosure

This manuscript was previously submitted as a preprint, as referenced in [33], and is available at the following link: “https://papers.ssrn.com/sol3/papers.cfm?abstract_id=4711978.”

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

The authors received no specific funding for this work.

Acknowledgments

We sincerely thank the anonymous reviewers and editors for their professional input and the dedicated time they invested in reviewing our manuscript.

Open Research

Data Availability Statement

The data used to support the findings of this study are included in the article.

References

1 Zadeh L. A., Fuzzy Sets, Information and Control. (1965) 8, no. 3, 338–353, https://doi.org/10.1016/S0019-9958(65)90241-X, 2-s2.0-34248666540.
10.1016/S0019-9958(65)90241-X
CAS Web of Science® Google Scholar
2 Garg H., Hussain A., Ullah K., and Ashraf A., Assessment of Learning Management Systems Based on Schweizer–Sklar Picture Fuzzy Maclaurin Symmetric Mean Aggregation Operators, Computational and Applied Mathematics. (2024) 43, no. 7, 404–424, https://doi.org/10.1007/s40314-024-02864-7.
10.1007/s40314-024-02864-7
Web of Science® Google Scholar
3 Hussian Z. and Yang M.-S., Distance and Similarity Measures of Pythagorean Fuzzy Sets Based on the Hausdorff Metric with Application to Fuzzy TOPSIS, International Journal of Intelligent Systems. (Oct. 2019) 34, no. 10, 2633–2654, https://doi.org/10.1002/INT.22169, 2-s2.0-85070935249.
10.1002/int.22169
Web of Science® Google Scholar
4 Ullah K., Mahmood T., and Jan N., Similarity Measures for T-Spherical Fuzzy Sets with Applications in Pattern Recognition, Symmetry. (2018) 10, no. 6, https://doi.org/10.3390/sym10060193, 2-s2.0-85048899645.
10.3390/sym10060193
PubMed Web of Science® Google Scholar
5 Yang M. S., Hussain Z., and Ali M., Belief and Plausibility Measures on Intuitionistic Fuzzy Sets with Construction of Belief-Plausibility TOPSIS, Complexity. (2020) 2020, 1–12, https://doi.org/10.1155/2020/7849686.
10.1155/2020/6618245
CAS Web of Science® Google Scholar
6 Atanassov K. T., Intuitionistic Fuzzy Sets, Fuzzy Sets and Systems. (Aug. 1986) 20, no. 1, 87–96, https://doi.org/10.1016/S0165-0114(86)80034-3, 2-s2.0-0002740725.
10.1016/S0165-0114(86)80034-3
Web of Science® Google Scholar
7 Yang M. S. and Hussain Z., Fuzzy Entropy for Pythagorean Fuzzy Sets with Application to Multicriterion Decision Making, Complexity. (2018) 2018, no. 1, https://doi.org/10.1155/2018/2832839, 2-s2.0-85062627235.
10.1155/2018/2832839
PubMed Google Scholar
8 Ashraf A., Ullah K., Božanić D., Hussain A., Wang H., and Puška A., An Approach for the Assessment of Multi-National Companies Using a Multi-Attribute Decision-Making Process Based on Interval Valued Spherical Fuzzy Maclaurin Symmetric Mean Operators, Axioms. (2022) 12, no. 1, https://doi.org/10.3390/axioms12010004.
10.3390/axioms12010004
Google Scholar
9 Ashraf S., Abdullah S., Aslam M., Qiyas M., and Kutbi M. A., Spherical Fuzzy Sets and its Representation of Spherical Fuzzy T-Norms and T-Conorms, Journal of Intelligent and Fuzzy Systems. (2019) 36, no. 6, 6089–6102, https://doi.org/10.3233/JIFS-181941, 2-s2.0-85067264843.
10.3233/JIFS-181941
Web of Science® Google Scholar
10 Khan M. J., Kumam P., Deebani W., Kumam W., and Shah Z., Distance and Similarity Measures for Spherical Fuzzy Sets and Their Applications in Selecting Mega Projects, Mathematics. (2020) 8, no. 4, https://doi.org/10.3390/math8040519.
10.3390/math8040519
Web of Science® Google Scholar
11 Cường B. C., Picture Fuzzy Sets, Journal of Computer Science and Cybernetics. (2015) 30, no. 4, https://doi.org/10.15625/1813-9663/30/4/5032.
10.15625/1813-9663/30/4/5032
Google Scholar
12 Mahmood T., Ullah K., Khan Q., and Jan N., An Approach toward Decision-Making and Medical Diagnosis Problems Using the Concept of Spherical Fuzzy Sets, Neural Computing & Applications. (2019) 31, no. 11, 7041–7053, https://doi.org/10.1007/s00521-018-3521-2, 2-s2.0-85047123393.
10.1007/s00521-018-3521-2
Web of Science® Google Scholar
13 Garg H., Hussain A., and Ullah K., Multi-attribute Group Decision-Making Algorithm Based on Intuitionistic Fuzzy Rough Schweizer-Sklar Aggregation Operators, Soft Computing. (2023) 1–12, https://doi.org/10.1007/s00500-023-09424-x.
10.1007/s00500-023-09424-x
Web of Science® Google Scholar
14 Ejegwa A., Kausar N., Agba J. A., Ugwuh F., Ozbilge E., and Ozbilge E., Determination of Medical Emergency via New Intuitionistic Fuzzy Correlation Measures Based on Spearman’s Correlation Coefficient, AIMS Mathematics. (2024) 9, no. 6, 15639–15670, https://doi.org/10.3934/math.2024755.
10.3934/math.2024755
Web of Science® Google Scholar
15 Khan Q. and Jabeen K., Schweizer-Sklar Aggregation Operators with Unknown Weight for Picture Fuzzy Information, Journal Innovation Research Mathematics Computer Science. (2022) 1, no. 1, 83–106.
Google Scholar
16 Gerstenkorn T. and Mańko J., Correlation of Intuitionistic Fuzzy Sets, Fuzzy Sets and Systems. (1991) 44, no. 1, 39–43, https://doi.org/10.1016/0165-0114(91)90031-K, 2-s2.0-0002303071.
10.1016/0165-0114(91)90031-K
Web of Science® Google Scholar
17 Bustince H. and Burillo P., Correlation of Interval-Valued Intuitionistic Fuzzy Sets, Fuzzy Sets and Systems. (1995) 74, no. 2, 237–244, https://doi.org/10.1016/0165-0114(94)00343-6, 2-s2.0-0000453026.
10.1016/0165-0114(94)00343-6
Web of Science® Google Scholar
18 Hong D. H. and Hwang S. Y., Correlation of Intuitionistic Fuzzy Sets in Probability Spaces, Fuzzy Sets and Systems. (1995) 75, no. 1, 77–81, https://doi.org/10.1016/0165-0114(94)00330-A, 2-s2.0-0040136579.
10.1016/0165-0114(94)00330-A
Web of Science® Google Scholar
19 Hung W. L. and Wu J. W., Correlation of Intuitionistic Fuzzy Sets by Centroid Method, Information Sciences. (2002) 144, no. 1–4, 219–225, https://doi.org/10.1016/S0020-0255(02)00181-0, 2-s2.0-0036645616.
10.1016/S0020-0255(02)00181-0
Web of Science® Google Scholar
20 Mitchell H. B., A Correlation Coefficient for Intuitionistic Fuzzy Sets, International Journal of Intelligent Systems. (2004) 19, no. 5, 483–490, https://doi.org/10.1002/INT.20004, 2-s2.0-2342541067.
10.1002/int.20004
Web of Science® Google Scholar
21 Singh P., Correlation Coefficients for Picture Fuzzy Sets, Journal of Intelligent and Fuzzy Systems. (2015) 28, no. 2, 591–604, https://doi.org/10.3233/IFS-141338, 2-s2.0-84921931747.
10.3233/IFS-141338
Web of Science® Google Scholar
22 Ejegwa A., Ajogwu C. F., and Sarkar A., A Hybridized Correlation Coefficient Technique and its Application in Classification Process under Intuitionistic Fuzzy Setting, Iranian Journal of Fuzzy Systems. (2023) 20, no. 4, 103–120.
Web of Science® Google Scholar
23 Hung W. L., Using Statistical Viewpoint in Developing Correlation of Intuitionistic Fuzzy Sets, International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems. (2001) 09, no. 04, 509–516, https://doi.org/10.1142/S0218488501000910, 2-s2.0-0142017303.
10.1142/S0218488501000910
Google Scholar
24 Liu B., Shen Y., Mu L., Chen X., and Chen L., A New Correlation Measure of the Intuitionistic Fuzzy Sets, Journal of Intelligent and Fuzzy Systems. (2016) 30, no. 2, 1019–1028, https://doi.org/10.3233/IFS-151824, 2-s2.0-84958601080.
10.3233/IFS-151824
Web of Science® Google Scholar
25 Thao N. X., A New Correlation Coefficient of the Intuitionistic Fuzzy Sets and its Application, Journal of Intelligent and Fuzzy Systems. (2018) 35, no. 2, 1959–1968, https://doi.org/10.3233/JIFS-171589, 2-s2.0-85053360897.
10.3233/JIFS-171589
Web of Science® Google Scholar
26 Ganie A. H., Singh S., and Bhatia P. K., Some New Correlation Coefficients of Picture Fuzzy Sets with Applications, Neural Computing & Applications. (2020) 32, no. 16, 12609–12625, https://doi.org/10.1007/S00521-020-04715-Y.
10.1007/s00521-020-04715-y
Web of Science® Google Scholar
27 Ejegwa P. A., Wen S., Feng Y., Zhang W., and Liu J., A Three-Way Pythagorean Fuzzy Correlation Coefficient Approach and its Applications in Deciding Some Real-Life Problems, Applied Intelligence. (2023) 53, no. 1, 226–237, https://doi.org/10.1007/s10489-022-03415-5.
10.1007/s10489-022-03415-5
Web of Science® Google Scholar
28 Ejegwa P. A. and Onyeke I. C., Medical diagnostic analysis on some selected patients based on modified Thao et al.’s correlation coefficient of intuitionistic fuzzy sets via an algorithmic approach, Journal of Fuzzy Extension and Applications. (2020) 1, no. 2, 122–132.
Google Scholar
29 Thao N. X., A New Correlation Coefficient of the Pythagorean Fuzzy Sets and its Applications, Soft Computing. (2020) 24, no. 13, 9467–9478, https://doi.org/10.1007/S00500-019-04457-7.
10.1007/s00500-019-04457-7
Web of Science® Google Scholar
30 Mahmood T., Ilyas M., Ali Z., and Gumaei A., Spherical Fuzzy Sets-Based Cosine Similarity and Information Measures for Pattern Recognition and Medical Diagnosis, IEEE Access. (2021) 9, 25835–25842, https://doi.org/10.1109/ACCESS.2021.3056427.
10.1109/ACCESS.2021.3056427
Web of Science® Google Scholar
31 Yager R. R., Pythagorean Fuzzy Subsets, 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS). (2013) 57–61, https://doi.org/10.1109/IFSA-NAFIPS.2013.6608375, 2-s2.0-84886504961.
10.1109/IFSA-NAFIPS.2013.6608375
Google Scholar
32 Cuong B. C., Kreinovitch V., and Ngan R. T., A Classification of Representable T-Norm Operators for Picture Fuzzy Sets, 2016 Eighth International Conference on Knowledge and Systems Engineering (KSE). (2016) 19–24, https://doi.org/10.1109/KSE.2016.7758023, 2-s2.0-85006976888.
10.1109/KSE.2016.7758023
Google Scholar
33 Ali M., Ali W., Hussain I., and Shah R., A Novel Correlation Coefficient for Spherical Fuzzy Sets and its Application in Pattern Recognition, Medical Diagnosis and Mega Project Selection.
Google Scholar

All articles

A Novel Correlation Coefficient for Spherical Fuzzy Sets and Its Application in Pattern Recognition, Medical Diagnosis, and Mega Project Selection

Abstract

1. Introduction

1.1. Motivation and Research Gap Analysis