International Journal of Intelligent Systems

Volume 2025, Issue 1 3183819

Research Article

Open Access

Blind Recognition Algorithm of Convolutional Code via Convolutional Neural Network

Pan Deng,

Corresponding Author

Pan Deng

[email protected]

orcid.org/0000-0002-9242-2934

School of Communications and Information Engineering , Chongqing University of Posts and Telecommunications , Chongqing , 400065 , China , cqupt.edu.cn

Faculty of Intelligence Manufacturing , Yibin University , Yibin , 644000 , China , yibinu.cn

Search for more papers by this author

Tianqi Zhang,

Tianqi Zhang

School of Communications and Information Engineering , Chongqing University of Posts and Telecommunications , Chongqing , 400065 , China , cqupt.edu.cn

Search for more papers by this author

Lianghua Wen,

Lianghua Wen

Faculty of Intelligence Manufacturing , Yibin University , Yibin , 644000 , China , yibinu.cn

Search for more papers by this author

Baoze Ma,

Baoze Ma

School of Communications and Information Engineering , Chongqing University of Posts and Telecommunications , Chongqing , 400065 , China , cqupt.edu.cn

Search for more papers by this author

Ying Wei,

Ying Wei

School of Communications and Information Engineering , Chongqing University of Posts and Telecommunications , Chongqing , 400065 , China , cqupt.edu.cn

Search for more papers by this author

Linhao Cui,

Linhao Cui

School of Communications and Information Engineering , Chongqing University of Posts and Telecommunications , Chongqing , 400065 , China , cqupt.edu.cn

Search for more papers by this author

Pan Deng,

Corresponding Author

Pan Deng

[email protected]

orcid.org/0000-0002-9242-2934

School of Communications and Information Engineering , Chongqing University of Posts and Telecommunications , Chongqing , 400065 , China , cqupt.edu.cn

Faculty of Intelligence Manufacturing , Yibin University , Yibin , 644000 , China , yibinu.cn

Search for more papers by this author

Tianqi Zhang,

Tianqi Zhang

School of Communications and Information Engineering , Chongqing University of Posts and Telecommunications , Chongqing , 400065 , China , cqupt.edu.cn

Search for more papers by this author

Lianghua Wen,

Lianghua Wen

Faculty of Intelligence Manufacturing , Yibin University , Yibin , 644000 , China , yibinu.cn

Search for more papers by this author

Baoze Ma,

Baoze Ma

School of Communications and Information Engineering , Chongqing University of Posts and Telecommunications , Chongqing , 400065 , China , cqupt.edu.cn

Search for more papers by this author

Ying Wei,

Ying Wei

School of Communications and Information Engineering , Chongqing University of Posts and Telecommunications , Chongqing , 400065 , China , cqupt.edu.cn

Search for more papers by this author

Linhao Cui,

Linhao Cui

School of Communications and Information Engineering , Chongqing University of Posts and Telecommunications , Chongqing , 400065 , China , cqupt.edu.cn

Search for more papers by this author

First published: 22 July 2025

https://doi.org/10.1155/int/3183819

Academic Editor: Weiwei Jiang

Share a link

Email
Wechat
Bluesky

Abstract

Pointing at the vexed question of blind recognition in the convolutional code class, this paper proposes a convolutional code blind identification method via convolutional neural networks (CNNs). First, this algorithm uses the traditional method to generate different convolutional codes, and the feature extraction algorithm adopts the theorem of Euclid’s algorithm. Then, the input signal is loaded to the CNN; next, the feature is extracted by convolutional kernel. Finally, the Softmax activation function is applied to full-connection layer network. After the input signals pass through the above layers, the system classifies the signals. The research results indicate that the presented algorithm has improved the recognition performance of code length and rate. For different convolutional codes with parameters of (5, 7), (15, 17), (23, 35), (53, 75), and (133, 171) and similar convolutional codes with parameters of (3, 1, 6), (3, 1, 7), (2, 1, 7), (2, 1, 6), and (2, 1, 5), the recognition rate of parameter classification can reach 100% at signal-to-noise ratio (SNR) of 3 dB.

1. Introduction

To ensure that the channel coding performance is close to approximate the Shannon limit, in 1955, P. Elas [1] proposed a promising encoding method, which is named the convolutional code. Compared with linear block codes, convolutional codes have the advantage that it can obtain higher coding gain than linear block codes in the same complexity. Convolutional codes are a kind of error correction coding with better performance and lower complexity of encoding and decoding. At present, as one of the supreme significance coding methods, convolutional code’s blind recognition has strong application prospects in satellite correspondence [2], unmanned aerial vehicle (UAV) measurement and control [3], deep space communication [4], mobile communication [5], underwater acoustic communication [6], and other digital communication systems and is even adopted into some wireless communication standards [7]. Blind distinction of convolutional codes is a key technology in intelligent communication and information countermeasures. It can be foreseen a growing number of digital communication systems utilizing convolutional codes will advent down the line. In terms of noncooperative correspondence realms, convolutional code parameter recognition is a problem we should solve immediately.

Therefore, in the realm of noncooperative correspondence, the blind distinction of convolutional coding has been a crucial problem in recent years. From the published literature, there are many literatures on parameter distinction of linear block codes, cyclic codes, BCH codes, and Turbo codes and low-density Parity-Check (LDPC) codes; so far, there are few research studies on blind identification of convolutional code parameters in the world. In view of the poor fault tolerance of the current blind identification methods of linear block code arguments, literature [8] proposed a blind recognition method for linear block code arguments on account of the iterative column elimination method, which uses the dual code word for elementary line transformation recognition check matrix. The proposed method has good fault tolerance performance, but it is complex to calculate and has poor recognition effect for high rate linear block code parameters. Literature [9] proposed an algorithm for parameter identification based on the verification relation of cyclic codes under soft decision. For cyclic codes with different polynomials generated under different code lengths, the algorithm can correctly identify their code lengths, synchronization starting points and generated polynomials under certain signal-to-noise ratio (SNR) and certain amount of code word interception, but the recognition rate is poor when the SNR is poor. Literature [10] proposed a shortened BCH code recognition method under soft decision conditions, which can both recognize shortened BCH codes and apply to the original BCH codes. A complete method is proposed for the distinction of code size, original multinomial, and generating multinomial; however, computational complexity of this algorithm is high.

For random interleaver of Turbo code, literature [11] proposed an algorithm for estimation by taking advantage of accepted soft-decision series and realizes the estimation of interleaver position. However, if the RSC parameter is unknown or the estimation is wrong, the algorithm is invalid. Literature [12] proposed a moment-multiplication-rank reduction algorithm, which restores the code length and starting point of LDPC code in the case of low probability of error. To achieve the same recognition effect, the proposed algorithm can save at least 20% of the data. However, its computational complication is comparatively high. Literature [13] proposed a unified expression method for solving the generating matrix of master and extended convolutional codes. The corresponding relation model between the algorithm and the polynomial coefficient of the extended encoder is constructed. Fast calculation of the extended convolutional code generation matrix can be realized by the theorem, and provide convenience for traversing and rebuilding the deleted convolutional code of deletion pattern and master code generation matrix. However, its computational complexity is relatively high. Literature [14] proposed a fast blind recognition method of (2, 1, m) convolutional codes with better fault tolerance, aiming at the problems of existing convolutional code recognition methods with low fault tolerance, known coding parameters and large amount of computation. In the case of unknown coding parameters, the coding parameters can be quickly identified according to the detection result of the estimated value of the check sequence. But its recognition accuracy needs to be further improved. Literature [15] proposed a new approach via the improved Walsh–Hadamard conversion, analyzes the shortcomings of the existing approach via Walsh–Hadamard conversion to directly solve the equations, and obtains the polynomial matrix generated by (n, 1, m) convolutional code. But other types of convolutional codes are not recognized. From the above analysis, it can be seen that there are few algorithms for convolutional code parameter recognition alone, while convolutional codes are more and more widely used in practical engineering. Literature [16] proposes a channel code recognition algorithm based on two types of neural networks, including bidirectional long and short term memory (BiLSTM) and convolutional neural network (CNN). The received signals are first preprocessed into BiLSTM and then processed by CNN. It inherits the advantages of BiLSTM and CNN, respectively. It can effectively recognize convolutional codes, LDPC codes, and polarization codes, but the extracted features are not obvious, and the recognition accuracy is not high under low and high SNR. Literature [17] proposes a channel code recognition algorithm based on deep learning to automatically extract features to avoid complex calculations. Three convolutional codes are considered candidate code words. It can recognize convolutional codes effectively. But the discernible convolutional codes have a single category and a small number. The recognition accuracy is not high at low SNR. Literature [18] presents a recognition method based on multitask deep convolutional neural network (MT-DCNN). The method can automatically identify baseband in-phase ECC type and quadrature phase (IQ) data without relying on any traditional demodulator. Experimental results show that the architecture can identify the target accurately. It can recognize 4 channel codes, but the recognition accuracy is not high at low SNR. For noncooperative communication, convolutional code parameter recognition is a hard challenge to be settled imminently.

Accordingly, this paper proposes a convolutional code parameter blind identification method via CNN. This algorithm first generates convolutional codes with different parameters through traditional coding methods, and feature extraction algorithm adopts the theorem of Euclid’s algorithm. Second, CNN is introduced to isolate characteristic of convolutional codes with different parameters and send them into the CNN for training, thus realizing the classification and recognition of different parameters of the same type of convolutional codes. The results of these experiments demonstrate that the proposed method is available and has good fault tolerance. Simulation results show that the suggested method achieved strong performance, indicating its high efficiency and strong fault tolerance.

2. Method Introduction of the Blind Identification System of Convolutional Code

The convolutional code blind recognition system model is shown in Figure 1. The algorithm first generates convolutional codes with different parameters through traditional coding. This paper focuses on convolutional codes whose parameters are (5, 7), (15, 17), (23, 35), (53, 75), and (133, 171) and similar convolutional codes with parameters of (3, 1, 6), (3, 1, 7), (2, 1, 7), (2, 1, 6), and (2, 1, 5). Second, CNN is introduced, which extracts features of the convolutional codes encoded with different parameters and sends them to CNN for drilling. After passing through each layer of CNN, the classification of convolutional codes is realized. Finally, the classification and parameter recognition of convolutional codes with different parameters are realized. The effect of various SNR and various NN about the classification and recognition accuracy of convolutional codes is contrasted. The effect of various code word numbers, various code word lengths, and various code rates on the algorithm is also analyzed.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Blind recognition model of the convolutional code.

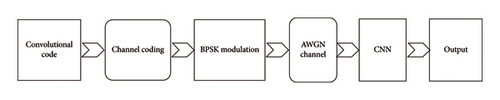
3. Coding Process of Convolutional Codes

Half of construction of convolutional code encoder is expressed in Figure 2.

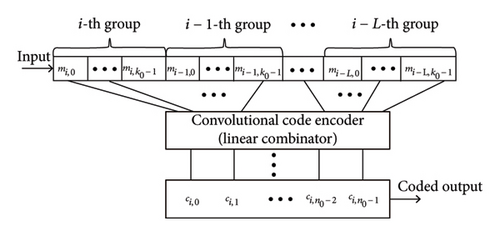
k is the number of information bits and L + 1 is the constraint length. It shows each symbol is the outcome of linear combination of k ∗ (L + 1) data. Similarly, the encoded course of convolutional code is represented in the form of matrix product.

The generated matrix G can be expressed as a function form of D, which is called the generated polynomial matrix G(D).

()

Its element g(D) represents relation of how ith input influences the jth output. Coding process may be represented by:

()

The feature extraction algorithm adopts the theorem of Euclid’s algorithm. For any two integers a, b. When b ≠ 0, it must exist certain integers q and r such that a = b q + r. This theorem is a commonly used division algorithm, where the integer q is the quotient in division and r is the remainder of a divided by b. For any two integers a and b, define (a, b) as the greatest common divisor of a and b. The algorithm explains the way to find (a, b) by first finding the remainder r₁ of a divided by b and then finding the remainder r₂ of b divided by r₁. Find r_j + 1 and the remainder of r_j − 1 and r_j by analogy until the remainder is 0. Specific steps are as follows:

1.
Parameter initialization:
()

()
2.
For i, define q_i(x), r_i(x), which satisfies
()
3.
Recursive algorithm:
()

()
4.
Conditions precedent:
()

Assuming i = n, we can obtain

()

4. Generation of the Dataset

The dataset utilized in this paper is produced by the traditional coding method, and the theorem of Euclid’s algorithm is used to extract important features. Simulation dataset is produced in Matlab2020a, and white Gaussian noise is added. The dataset consists of 2048 samples, 100,000 data points, and 10 convolutional code-encoded signals.

5. CNN

CNNs can be self-coded and combined with preformed and fine-tuned neural networks. The construction diagram of CNN is displayed in Figure 3. This paper puts forward an algorithm on account of CNN, which consists of 7 NN layers. This paper is upon five existed NN methods, called deep neural networks (DNNs) [19], long short-term memory (LSTM) [20], ResNet [21], Attention [22], and recurrent neural network (RNN) [23].

Figure 3 shows the CNN architecture we used. The ReLU activation function is expressed as follows:

()

The composition of CNN is shown in Figure 4. A hybrid neural network with multiple inputs is used, and it can be expressed as follows:

()

The pooling layer is called the subsampling layer, and the ith output vector may be expressed as follows:

()

The output vector can be expressed as follows:

()

, where W represents the delegate weight matrix and b represents the deviation. Output is

, and the variable

is defined as follows:

()

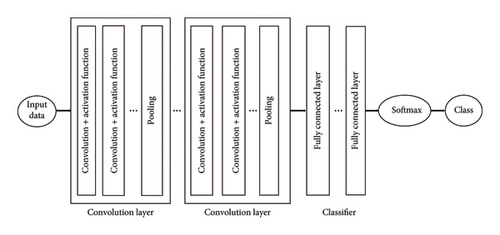
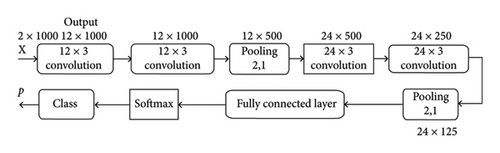
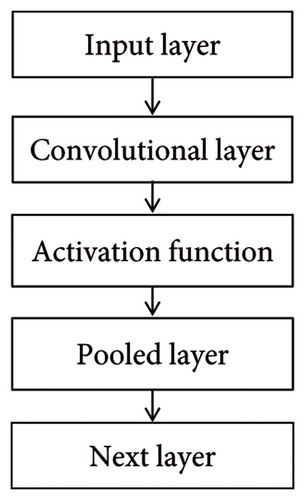
A complete convolutional layer operation is shown in Figures 5. In the first part, multiple convolutions are computed in parallel to produce a set of linear activation responses. Each linear activation response in Part 2 will be augmented by a nonlinear activation function. In the third part, we take advantage of the pooling function to further tune output of this layer.

The pooling layer is frequently used after convolution layer to simplify information output from pooling layer, reduce the overfitting phenomenon of the model, and maintain the invariance of rotation, translation, and scaling. The average pooling layer adopted in this paper is taken as the output, that is,

()

The output layer neurons will display the classification results and classify them in a way encoded in the form of one-dimensional hot tags, and the full connection layer connects each neuron of the maximum mixed layer to each output neuron separately. In the case of input x, the probability of c₁ is P(c₁|x), and its expression is

()

Let

()

Then, the formula described above may be arranged as

()

When x is a continuous variable, assuming that the input pairs of the two types of conditions obey the Gaussian distribution with the same variance, probability density function of Gaussian distribution is

()

So, we can write down the probability of any situation.

()

Then, the above formula can be obtained after indexation as follows:

()

This gives the Softmax function as follows:

()

It is very natural to define Softmax in the exponential form, and the log in logarithmic likelihood can cancel out the exp in Softmax. That is,

()

z_j is logarithmic likelihood and z_j approximates the original input after maximizing, then log ∑_i exp(z_i) ≈ z_j; at this time, the cost function is approximately 0. More types of features of the data are learned by introducing higher-order terms, that is,

()

The expression for weight regularization is as follows:

()

when α is the penalty factor, it indicates that there is no regularization and when α is 0, the greater the α, the greater the regularization penalty. w represents all weights that should be affected by the norm penalty.

A sufficient condition to ensure convergence of stochastic gradient descent is

()

Also, it satisfies

()

η_k is learning rate of step k iteration. General learning rate will linearly decay to the τ iteration.

()

where α = k/τ. After the τ iteration, η remains constant.

The flowchart of the algorithm in this paper is shown in Figure 6.

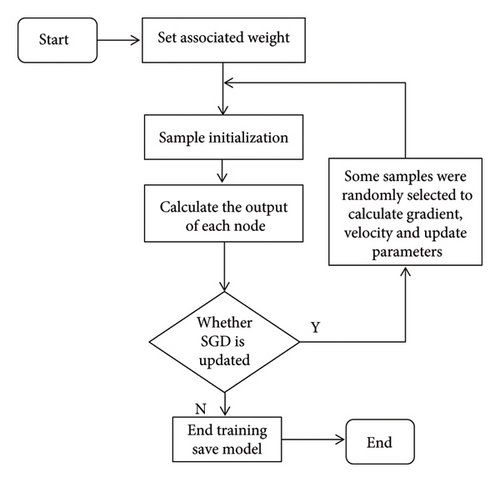
Presuppose: the learning rate is η_k, the initial parameter is θ, the momentum parameter is α, and the initial velocity is v.
Process: SGD update in the Kth training iteration.
While not meet training stop requirement, do
Sample a small batch of samples including m specimen {x⁽¹⁾, x⁽²⁾, …, x^(m)} ochastically from the training set, where the target output corresponding to xⁱ is yⁱ;
Temporary renewal:
Calculate the gradient of small batch data:
()
Calculate speed update:
()
Update parameter:
()
End while

As shown in Tables 1 and 2, labels are applied to the obtained 5 types of channel coding datasets, such as 5 common convolutional codes and 5 similar convolutional codes, which is advantageous to proper estimation of identification results. The input data of the neural network are noisy information fragments, and the CNN training samples in the paper are convolutional codes, accounting for 60%, test samples for 20%, and verification sets for 20%. The composition of the entire training dataset has been thoroughly verified, as shown in Table 3.

Table 1. Form of annotation.

Convolutional code	The label
Convolutional code (5, 7)	10000
Convolutional code (15, 17)	01000
Convolutional code (23, 35)	00100
Convolutional code (53, 75)	00010
Convolutional code (133, 171)	00001

Table 2. Form of annotation.

Convolutional code	The label
Convolutional code (3, 1, 6)	10000
Convolutional code (3, 1, 7)	01000
Convolutional code (2, 1, 7)	00100
Convolutional code (2, 1, 6)	00010
Convolutional code (2, 1, 5)	00001

Table 3. The composition of the entire training dataset.

Training data set	Training set	Validation set	Test set
1	60%	20%	20%
100,000	60,000	20,000	20,000

6. Simulation Result

6.1. Performance Comparison of Network Models

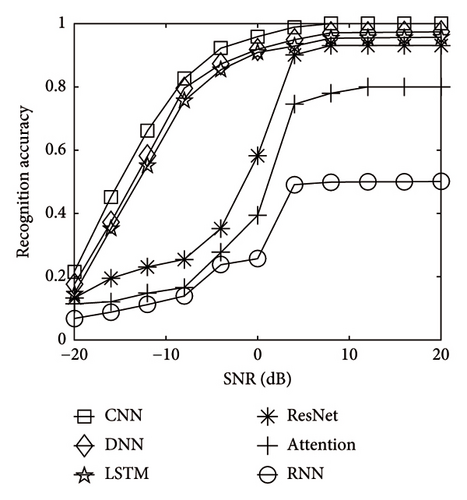
First, the proposed model was compared with alter neural networks DNN, LSTM, ResNet, Attention, and RNN. The model used datasets of 100,000 samples for training, and the SNR ranged from −20 to 20 dB. Exactly as Figure 7, this way was superior than other NNs in the side between maximum precision and fault-tolerant capacity. CNN can reach 100%, but DNN, LSTM, ResNet, Attention, and RNN networks only had identification precision of 92%, 90%, 88%, 78%, and 52%, respectively. The identification precision of CNN was optimal than that of the rest of methods, and the identification precision can attain 100% when SNR was higher than 3 dB.

6.2. The Influence of Code Word Number, Code Length, and Code Rate on Algorithm

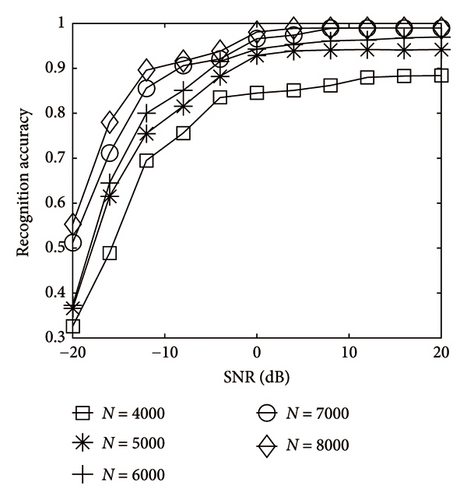
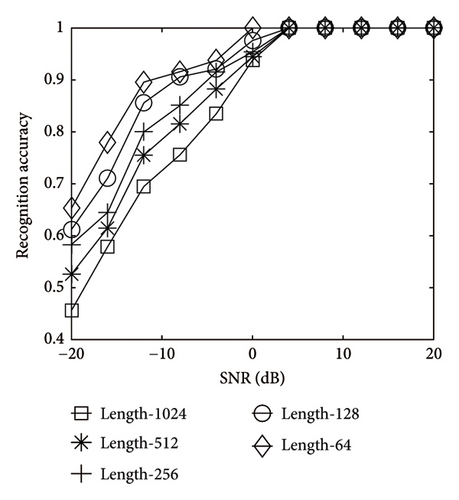
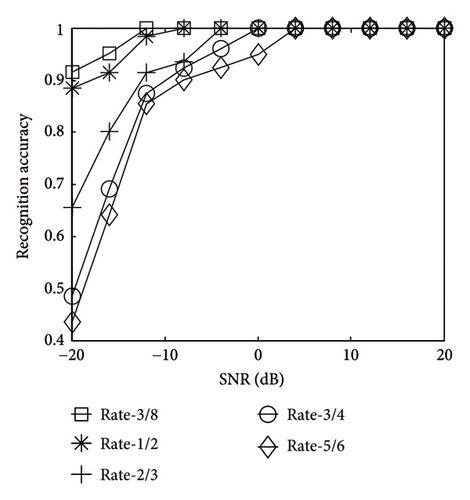
As shown in Figure 8, the accuracy increased as the number of code words increased, and for each curve, the accuracy reached its maximum at SNR. As number of code words aggrandized, the less it grew. It indicated that the number of code words had limited influence on the recognition accuracy. In Figure 9, with the continuous increase of SNR, the recognition result of code length 64 was optimal, attaining 100% first. In Figure 10, with the growth of SNR, the recognition result of bit rate 3/8 was the best, reaching 100% the earliest.

6.3. The Effect of the Loss Function

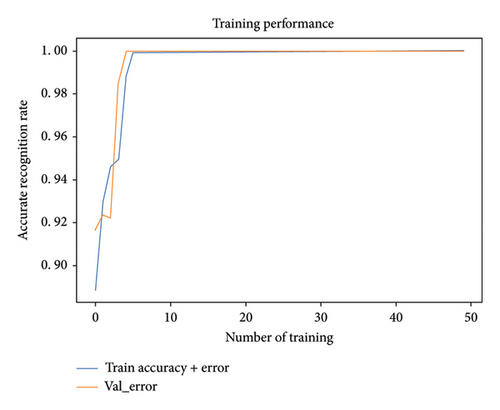
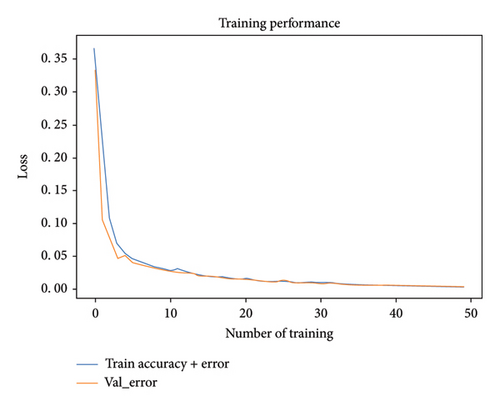
In Figures 11 and 12, converging bight of loss function when SNR was 3 dB can be quickly stabilized when a deterministic number of frequency of drilling were arrived.

6.4. Accuracy of Code Categorization

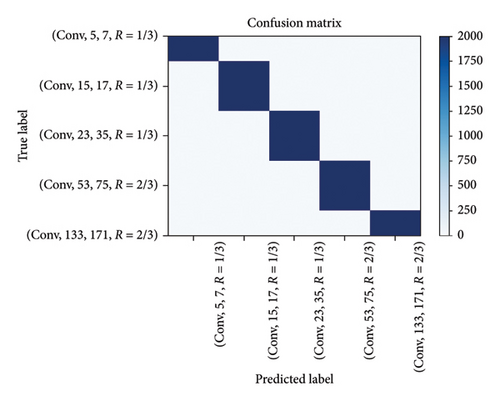
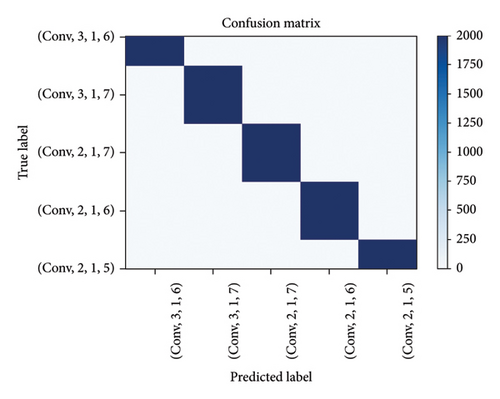
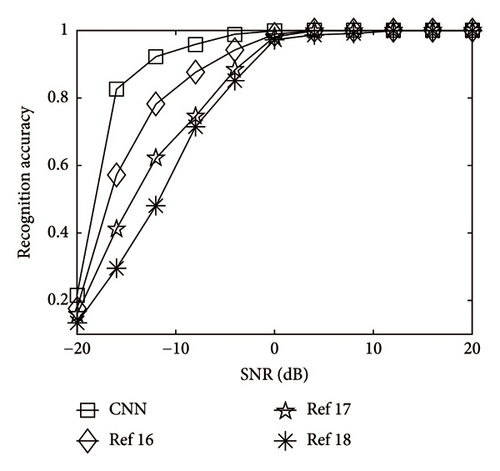
Figure 13 presents the standardized confusion matrix of 5 kinds of encoding in 3 dB. The standardized confusion matrix showed that 5 kinds of convolutional codes may be discriminated in most cases. The CNN model presented in this paper can discriminate 5 different convolutional codes. Figure 14 presents the standardized confusion matrix of five kinds of encoding in 3 dB. The CNN model presented in this paper may also discriminate five similar convolutional codes and has certain accuracy. Figure 15 shows that the algorithm proposed in this paper had better recognition performance under low SNR, indicating that extracting features through the Euclidean algorithm combined with the improved CNN is more conductive to the recognition of various convolutional codes, especially under low SNR.

6.5. Operation Time Contrastion

Table 4 shows the operation time contrastion between CNN and the rest of 5 ways. The performance of the proposed CNN was the best.

Table 4. Average operation time.

Ways	Operation time (ms)
CNN	4.732
DNN	6.395
LSTM	12.576
ResNet	16.814
Attention	18.828
RNN	10.124

7. Conclusion

In this paper, five sorts of convolutional codes with various rates were produced by traditional coding ways. So as to achieve categorization and identification of convolutional codes with various rates in circumstances of low SNR, the feature coefficient of 5 kinds of convolutional codes with different rates was integrated into CNN so as to quickly identify the coding parameters of convolutional codes under low SNR. Experimental results showed that the suggested algorithm had strong results, indicating its efficiency and strong fault tolerance when the SNR was relatively small, in addition to good application prospects in noncooperative communication.

Disclosure

Intellectual property protection measures have been thoroughly discussed, and there are no impediments to its dissemination, including publication timing. Accordingly, we confrm our adherence to our institutions’ guidelines on intellectual property.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

All authors have reviewed and approved the manuscript, and no supplementary contributors who meet authorship criteria have been excluded. The sequence of authors has been agreed upon mutually.

Funding

This work was supported by National Natural Science Foundation of China (no. 61671095, no. 61371164, no. 61975171, and no. 62201113), the Project of Key Laboratory of Signal and Information Processing of Chongqing (no. CSTC2009CA2003), the Natural Science Foundation of Chongqing (no. cstc2021jcyj-msxmX0836), the Research Project of Chongqing Educational Commission (nos. KJ1600427 and KJ1600429), Yibin University of College- Level Research and Cultivation Program (2019PY35), the Open Project Fund of Intelligent Terminal Key Laboratory of Sichuan Province of China under Grant SCITLAB-0020, the China Postdoctoral Science Foundation (no. 2023MD744168), and the Science and Technology Research Program of Chongqing Municipal Education Commission (no. KJQN202300625).

Acknowledgment

The authors extend their appreciation to the Image and Communication Signal Processing Innovation Team, School of Communications and Information Engineering, Chongqing University of Posts and Telecommunications for funding this work through National Natural Science Foundation of China (no. 62201113).

Open Research

Data Availability Statement

The data used to support the findings of this study are available on reasonable request from the corresponding author.

References

1 Elias P., Predictive Coding–I, IEEE Transactions on Information Theory. (1955) 1, no. 1, 16–24, https://doi.org/10.1109/tit.1955.1055126, 2-s2.0-84937999311.
10.1109/tit.1955.1055126
Google Scholar
2 Sun P., A Kind of Punctured Convolutional Code Suitable for Satellite Communication, Proceedings of the National Graduate Communication Academic Conference, 1987, Shanghai, China, 306–311.
Google Scholar
3 Yu G., Wang Z., and Li Y., Application Research of Channel Coding in UAV Data Link, Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition). (2014) 26, no. 6, 845–849.
Google Scholar
4 Xie Z., Liu B., and Zhang B., Channel Coding Technology in Deep Space Communication, Digital Communications World. (2010) 69, no. 9, 78–82.
Google Scholar
5 Xiao J., Liu Q., and Xu Z., Design of Convolutional Code Encoder in Mobile Communication Based on FPGA, Modern Electronics Technique. (2012) 35, no. 5, 65–67.
Google Scholar
6 Chen K., Zhao A., and Chen Y., Application of RS Code and Convolutional Code in PDS Underwater Acoustic Communication System, Journal of Jilin University (Engineering and Technology Edition). (2010) 28, no. 2, 119–123.
Google Scholar
7 Pang L., Research on the Application of Convolutional Code and RS Code in Wireless Communication, 2015, Southwest University of Science and Technology.
Google Scholar
8 Wang J., Zhang T., and Qiang X., Blind Recognition of Linear Block Code Parameters Based on Iterative Column Elimination Algorithm, Telecommunications Engineering. (2017) 57, no. 2, 197–202.
CAS Google Scholar
9 Zhang T., Wang X., and Fang Z., Blind Recognition of Cyclic Code Parameter Based on Check Relation Under Soft Decision, Journal of Signal Processing. (2023) 1–14.
Google Scholar
10 Liu J., Zhang L., and Peng H., A New Method for Binary Shortened BCH Code Recognition, Journal of Xidian University. (2017) 44, no. 6, 92–98.
Google Scholar
11 Liu J., Li J., and Peng H., Interleaver Estimation of Turbo Code Based on Average Coincidence of Check Equations, Acta Electronica Sinica. (2016) 44, no. 5, 1213–1218.
Google Scholar
12 Liu Q., Zhang H., and Song Y., Estimation Method of LDPC Parameter Based on Matrix Multiplication and Rank Analysis Under Small Sample Conditions, Acta Electronica Sinica. (2022) 50, no. 5, 1075–1082.
CAS Google Scholar
13 Bao X. and You L., A Unified Description of Generator Matrix of Expansion Convolutional Codes, Telecommunication Engineering. (2016) 56, no. 3, 267–272.
Google Scholar
14 Han S., Zhang M., and Li X., Fast Blind Recognition Method With High Fault Tolerance (2, 1, m) Convolutional Codes, Xi’an Jiaotong University. (2017) 51, no. 12, 28–34.
Google Scholar
15 Zhang L., Liu J., and Zhong Z., Blind Recognition of (N, 1, M) Convolutional Codes Based on Improved Walsh-Hadamard Transform, Journal of Electronics and Information Technology. (2018) 40, no. 4, 839–845.
Google Scholar
16 Huang X. R., Sun S. J., and Yang X., Recognition of Channel Codes Based on BiLSTM-CNN, 2022 31st Wireless and Optical Communications Conference, 2022, 1–4.
Google Scholar
17 Qing X. F., Peng S. L., and Yang X., Deep Learning Based Channel Codes Recognition Using Textcnn, 2019 IEEE International Symposium on Dynamic Spectrum Access Networks, 2019, 1–5.
Google Scholar
18 Wang J., Huang H., Liu J. X., and Li J., Joint Demodulation and Error Correcting Codes Recognition Using Convolutional Neural Network, IEEE Access. (2022) 10, 104844–104851, https://doi.org/10.1109/access.2022.3201354.
10.1109/access.2022.3201354
Web of Science® Google Scholar
19 Chen M., Pan J., and Zhao Q., Multi-Task Learning in Deep Neural Networks for Mandarin-English Code-Mixing Speech Recognitio, IEICE—Transactions on Info and Systems. (2016) 99, no. 9, 2554–2557.
10.1587/transinf.2016SLL0004
Google Scholar
20 Shi X., Chen Z., and Wang H., Convolutional LSTM Network: A Machine Learning Approach for Precipitation Nowcasting, 2015, MIT Press.
Google Scholar
21 He K., Identity Mappings in Deep Residual Networks, European Conference on Computer Vision, 2016, Springer, 630–645.
Google Scholar
22 Knyazev B., Understanding Attention and Generalization in Graph Neural Networks, 33rd Conference on Neural Information Processing Systems, 2019, Vancouver, Canada, 310–325.
Google Scholar
23 Fan M., Chen H., and Lei Y., Blind Recognition of Forward Error Correction Codes Based on Recurrent Neural Network, Sensors. (2021) 13, no. 6, 3884–3896.
Google Scholar

All articles

Blind Recognition Algorithm of Convolutional Code via Convolutional Neural Network

Abstract

1. Introduction

2. Method Introduction of the Blind Identification System of Convolutional Code

3. Coding Process of Convolutional Codes

4. Generation of the Dataset

5. CNN

6. Simulation Result

6.1. Performance Comparison of Network Models