The channel estimation technique is crucial for the development of wireless communication systems. By accurately estimating the channel state, transmission parameters such as power allocation, modulation schemes, and encoding strategies can be optimized to maximize system capacity and transmission rate. In this paper, we propose a hybrid deep learning model for channel estimation in multiple-input multiple-output (MIMO) wireless communication system. By combining the advantages of convolutions and gated recurrent units (GRUs), the generalization capability of deep learning models across various wireless communication scenarios can be fully utilized. Furthermore, a series of regularization techniques such as data augmentation and structural complexity constraints have been introduced to avoid overfitting problems. The stochastic gradient descent (SGD) based on error backpropagation is used to iteratively train the model to convergence. During the simulation process, we have validated the effectiveness of the hybrid deep learning model on two wireless channel conditions, including quasi-static block fading and time-varying fading condition. All the samples are generated offline with SNRs from 10 to 40 dB with a step size of 5 dB. The comparison results with a series of conventional methods and deep learning models have proven the effectiveness of the proposed method.

1. Introduction

Compared to traditional wireless communication where only one antenna exists for signal transmission and reception, the multiple-input multiple-output (MIMO) communication [1] is a technology that utilizes multiple antennas for signal transmission and reception. MIMO technology is able to effectively increase the capacity, throughput, and reliability of wireless communication systems by using multiple antennas at the transmitter and receiver ends to send multiple independent data streams over different transmission paths at the same moment. With MIMO technology, multiple transmission paths in a multipath channel environment can be utilized to increase channel capacity and improve the spectral efficiency of the system [2]. Together with spatial diversity and spatial multiplexing, MIMO technology can further improve the whole system’s interference immunity and transmission quality. At present, MIMO technology has been widely used in wireless communications to improve data transmission performance and network capacity, such as wireless fidelity (Wi-Fi), long-term evolution (LTE), and fifth-generation (5G) communication systems [3].

Channel estimation [4, 5] in MIMO communication systems refers to the estimation of channel state information (CSI) between multiple antennas, that is, the estimation of channel gain and phase information between each antenna, which plays an important role in MIMO systems. Accurate channel estimation helps to reduce distortion and interference in signal transmission, thereby improving system’s transmission performance and reliability [6]. Specifically, MIMO systems with the estimated CSI can dynamically adjust transmission parameters and modulation schemes to improve communication performance and capacity. By utilizing CSI, the MIMO communication systems are also able to perform precoding and postprocessing operations to maximize transmission efficiency, reduce multipath signal interference, and improve anti-interference capabilities [7]. In addition, accurate channel estimation can be used to optimize the power allocation strategy, helping the wireless communication system allocate power reasonably to maximize energy efficiency [8].

In MIMO systems, signal estimation still faces a series of factors, such as multipath channels [9], spatiotemporal correlation [10], channel fading [11], pilot design [12], antenna selection and configuration [13], and hardware conditions [14]. There are multiple transmission paths in MIMO systems, where the signal arrival time and amplitude on each path may be different. This leads to signals being mixed together at the receiving end, making it difficult to accurately estimate the independent CSI between each antenna [15]. The channels between antennas are often spatiotemporal correlated, meaning that the channel states between adjacent antennas are relatively similar. Therefore, it is necessary to consider the impact of spatial correlation on estimation accuracy. In practical communication scenarios, the time-varying nature of wireless channels results in their states changing over time, which requires channel estimators to track changes such as channel fading in a timely manner. Moreover, channel estimation typically requires sending some known pilot symbols for the receiver to estimate, but pilot design needs to consider issues such as the selection, positioning, and insertion of pilot sequences to ensure the effectiveness and accuracy of pilots. In addition, channel estimation usually requires high-speed sampling and processing, which has certain hardware performance requirements [16]. In real communication systems, achieving efficient channel estimation under limited hardware resources is also a challenge. The reasonable setting of antenna quantity, position, and directionality is also a key factor in achieving well channel estimation performance [17].

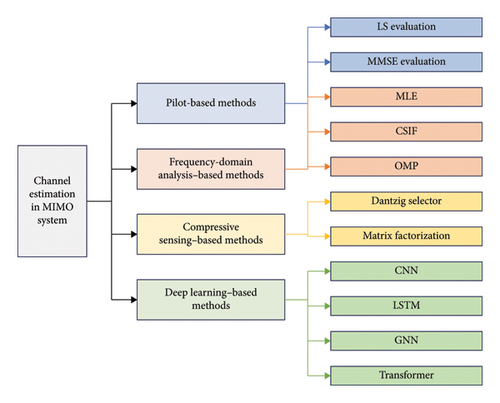
At present, channel estimation methods in MIMO systems can be divided into four categories: pilot-based methods, frequency-domain analysis–based methods, compressive sensing–based methods, and deep learning (DL)–based methods. The relevant research directions are summarized in Figure 1. The pilot-based method estimates the channel response matrix by sending a known pilot sequence and then receiving the transmitted signal. By comparing the difference between the received signal and the known pilot sequence, the channel characteristics can be inferred. The evaluation method using the least square (LS) [18] is applicable to single-input single-output (SISO) systems. The minimum mean square error (MMSE) method [19] incorporates noise and signal correlation on the basis of LS, making it more suitable for MIMO systems. The time-domain pilot interpolation method [20] interpolates the pilot signal in the time domain, reducing the impact of interpolation errors on channel estimation. The method based on frequency domain analysis first converts the received signal to the frequency domain and then compares the frequency-domain similarity between the received signal and the pilot sequence to obtain an accurate estimation of the channel response matrix. The commonly used similarity measurement methods include maximum likelihood estimation (MLE) [21], channel state information feedback (CSIF) [22], and orthogonal matching pursuit (OMP) [23]. Compressive sensing utilizes the sparsity of the channel response matrix for channel estimation. Based on the sparse representation of the received signal, the sparse signal recovery algorithm is introduced to reconstruct the channel response matrix. For example, Dantzig selector [24] transforms the channel estimation problem into the sparse optimization problem, using a convex combination of L1-norm and L∞-norm as a penalty function to find the optimal sparse solution. Low rank matrix factorization [25] decomposes the channel matrix into a weighted sum of low rank matrices and then solves an optimization problem to estimate the channel response matrix. DL methods utilize deep neural network models to complete the channel estimation. By conducting end-to-end channel feature learning on a large amount of training data, the deep network models can directly recover CSI from the received signal. Common DL models include convolutional neural networks (CNNs) [26, 27], long short-term memory (LSTM) [28, 29], graph neural networks (GNNs) [30, 31], and Transformers [32, 33].

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Relevant research directions and related work of channel estimation in MIMO systems.

In recent years, the DL method has achieved remarkable achievements in multiple fields and has gradually been developed for wireless communication and signal processing, such as modulation classification [34–36], parameter estimation [37], spectrum sensing [38, 39], the design of intelligent hypersurfaces [40], and long-term prediction [41, 42]. DL models with adaptive learning capabilities can learn complex nonlinear mapping relationships of channels from a large amount of training data, thus adapting to various communication scenarios and channel environments. The end to end DL can automatically extract effective features from original data without the need for manually designed features or preprocessing, simplifying the system designing process. A large number of studies have been developed for DL enabled channel estimation in MIMO systems. For example, Balevi, Doshi, and Andrews [43] proposed a channel estimation method based on DL for large-scale MIMO systems with limited multicell interference. The channel estimator adopts a specially designed deep neural network based on depth image priors, which first denoises the received signal and then performs traditional LS estimation. Kang, Chun, and Kim [44] designed a deep autoencoder via CNN for joint channel estimation and pilot signal design in the quasi-static block fading scenario. In the time-varying fading communication scenario, a new channel estimation method was then developed by connecting recurrent neural network (RNN) to CNN. Gao et al. [45] introduced an attention assisted DL channel estimation framework for traditional large-scale MIMO communication systems and designed an embedding method to effectively integrate attention mechanisms into the fully connected neural network. Zhang et al. [46] constructed a tensor trained deep neural network (TT-DNN) to address the challenge of time-varying channel estimation in MIMO communication systems. Belgiovine et al. [47] suggested building a multilayer perceptron (MLP) structure to enable the channel estimation task on large-scale parallel architectures, such as field-programmable gate array (FPGA). By utilizing the angular domain compressibility of massive MIMO channels, Ma and Gao [48] designed a DL structure consisting of a dimensionality reduction network for simulating pilots and a reconstruction network for estimating channels, to efficiently reconstruct high-dimensional channels from insufficient measurements. Liu and Huang [49] pointed out that networks based on multilayer CNN can extract the inherent sparse features of mmWave massive MIMO channels through training and learn sparse channel support. However, DL often requires a large amount of data to train the model and condense expert knowledge, which is difficult and expensive in practical communication systems. Due to the involvement of large-scale parameter deployment and complex computing processes, DL models require high-performance hardware devices and a large amount of computing resources to support model training and inference. It is challenging to deploy channel estimators on resource-limited devices and systems [50]. In addition, the structural complexity of deep neural network and the opacity of high-dimensional optimization process lack interpretability, making it difficult to understand the internal operating mechanism of the model and make targeted improvements [51].

In fact, the use of DL for channel estimation still faces a series of problems, among which the most crucial is to choose an appropriate model structure to handle wireless signals. Wireless signals with temporal representation are subject to interference from various factors, which poses a challenging requirement for the model’s feature extraction capability. In this paper, we propose a hybrid DL model for channel estimation in MIMO wireless communication system. By combining the advantages of conventional convolution and gated recurrent unit (GRU), the generalization capability of DL models across various wireless communication scenarios can be fully utilized. Furthermore, a series of regularization techniques such as data augmentation and structural complexity constraints have been introduced to avoid overfitting problems. The stochastic gradient descent (SGD) based on error backpropagation is used to iteratively train the model to convergence. During the simulation process, we have validated the effectiveness of the hybrid DL model on two wireless channel conditions, including quasi-static block fading and time-varying fading condition. The comparison results with a series of conventional methods and DL models have proven the effectiveness of the proposed method.

The remainder of this paper is organized as follows. Section 2 first introduces the MIMO communication system model. Section 3 presents the hybrid DL model for channel estimation. In Section 4, we introduce the adopted regularization technique for improving the generalization capability of the DL model. Simulation results and analysis are shown in Section 5. Finally, we conclude our work in Section 6.

2. MIMO System Model

The MIMO communication system utilizes multiple antennas for wireless communication, typically configured with multiple antennas at both the transmitting and receiving ends. By utilizing spatial multiplexing and diversity techniques, the MIMO communication system is able to significantly improve channel capacity, transmission rate, and spectrum utilization. In addition, the MIMO system utilizes the multipath propagation effect in wireless channels to transform the originally harmful multipath reflections into favorable factors for improving system performance. At present, the MIMO communication technique has been widely used in 5G communication systems. If the intelligent reflective surface (IRS) is introduced, the propagation path of wireless channels can be dynamically adjusted to make wireless channel characteristics more controllable. The IRS improves signal coverage and transmission quality, enhancing the accuracy of channel estimation.

As shown in Figure 2, a wireless communication system consisting of N_T and N_R antennas is considered, in which the MIMO channel modeled by the 5G communication channel profile is constructed. At the transmitter side, the raw data are first converted into binary codewords suitable for transmission. The encoded data are mapped to a symbol set to generate the symbol sequence, where space-time coding technology is commonly used to process the symbol sequence to enhance the system’s anti-interference and fault tolerance capabilities. The channel encoded data are mapped onto the baseband to generate an analog signal. Next, the analog signal is further converted into a high-frequency signal, and the baseband signal is mapped onto the carrier through a modulation module. Consider the system transmits data in T time slots and the symbols at time slot t are combined to a vector as

()

where N denotes the total number of modulation symbols. Then the encoded data are separated into N_T vectors corresponding to N_T transmitting antennas, as given by

()

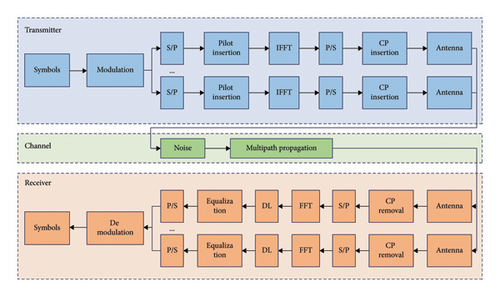
The data of each antenna are converted from serial to parallel (S/P), and then the known pilot signal is inserted into each layer along with the data. Then the inverse fast Fourier transform (IFFT) is applied to x, transforming it back into the time domain. Finally, a cyclic prefix (CP) with a length of N_G is inserted as a guard interval to alleviate inter-symbol interference by using CP insertion blocks.

During the transmission process, the received signal r can be expressed as

()

where h represents the MIMO channel matrix from the transmitter to the receiver at the kth symbol, and its elements are corresponding channel coefficients. s is the pilot symbol matrix. q is the matrix of channel noises.

At the receiver side, the received signal is first separated to process the signals received by different antennas separately, such as space-time equalization and space-time demodulation. Then the signals received by multiple antennas that have undergone signal processing are combined into a single overall signal stream, which is converted from parallel to serial (P/S). By utilizing the proposed DL model, the 5G channel can be estimated based on the received signal and known information to obtain the CSI. The merged signal is demodulated to convert it into a baseband signal. Finally, the demodulated signal is decoded and mapped to restore the data information sent by the transmitter.

3. Hybrid DL Model

3.1. Channel Estimation

In the case of negligible receiver mobility, i.e., under quasi-static block fading conditions, the channel coherence time is much longer than the duration of the codeword. Due to the relative stillness between the receiver and transmitter, Doppler frequency shift and time-varying characteristics can be ignored. Although the receiver does not move, there may still be multipath effects caused by fixed reflection, diffraction, and scattering objects. In addition, the signal may still experience instantaneous and spatial shadow fading. MIMO channels remain constant over continuous symbol time, and these channels independently change from one block to another. Therefore, we need to focus on the estimation of specific h (k). In the communication scenario of quasi-static block fading, our goal is to develop the accurate channel estimator and design appropriate pilot signals in the sense of minimizing the mean square error (MSE). Specifically, the channel estimation task can be expressed as

()

where

()

where F represents the DL model, θ represents the learnable parameters, and

is the estimation result of DL model F.

In the wireless communication scenarios where the receiver is moving with high speed, the channel coherence time is shorter than the duration of the codeword. At this point, the time-varying fading characteristics need to be considered, in which the channel h (k) varies dependently within each block. In mobile scenarios, observation signals are also limited by time and frequency resources, which leads to sampling rate limitations and a limited number of sample data. Usually, it is necessary to optimize observation resources and consider how to obtain accurate channel estimates in limited samples. In the time-varying fading scenario, we use feedback information from the (k − T + 1)th symbol time to the kth symbol time to estimate h (k). In addition, considering the correlation of channel variations, we further utilize MIMO channel estimation from the (k − T)th symbol time to the (k − 1)th symbol time for channel estimation of h (k). In this case, our goal is to develop the channel estimator that minimizes MSE, as defined by

()

Therefore, the key to the channel estimation task lies in developing a reliable DL model structure that can accurately capture the channel characteristics under various wireless communication conditions.

3.2. Model Structure

In this section, we introduce the proposed hybrid DL model structure for channel estimation. The specific structure is shown in Figure 3. The hybrid DL model can obtain more comprehensive feature representations by integrating different types of structures. A single CNN performs well in processing context, while the LSTM has an advantage in processing temporal data. By combining convolution and GRU, hybrid DL models can possess better feature extraction and modeling capabilities than single model, thus possessing good generalization ability across various types of communication scenarios. The channel estimation task in MIMO systems involves the spatiotemporal correlation between multiple antennas. The hybrid DL model can fully utilize the modeling ability of each module for spatial and temporal relationships. For example, CNN can capture spatial correlations in antenna arrays, while LSTM can capture long-term dependencies in temporal data. By integrating the feature extraction capabilities of multiple modules, hybrid models can reduce the risk of overfitting and improve performance on unseen data. This is very important for the practical application of MIMO channel estimation tasks, as communication channel conditions will change with time and location.

At the beginning, the received wireless signals without preprocessing are fed into the model. In the proposed hybrid DL model, three convolutional layers accompanied by batch normalization (BN) [52] and parametric rectified linear unit (PReLU) activation function [53] are used to extract and analyze expert knowledge from input signals. A total of 32, 64, and 64 convolutional kernels with the step sizes of 1 × 3, 1 × 5, and 1 × 5 are sequentially used for three convolutional layers. During the training process of the hybrid DL model, the input distribution of different layers may change, leading to the slower convergence speed of the network. Therefore, the BN layer is adopted to solve the problem of internal covariate shift and accelerate the convergence of the model’s objective function. The BN operation can be calculated according to

()

where

()

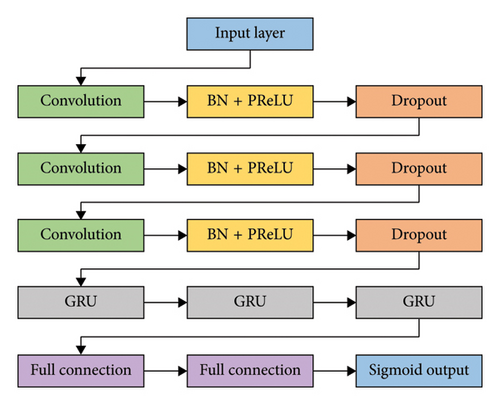
In the equations, the superscript i represents the ith dimension of the variable, indicating that BN operates independently across various dimensions of a mini-batch set. x and y represent input and output, respectively. M denotes the batch size. μ and σ denote mean and standard deviation, respectively. γ and β represent translation and scaling parameters, respectively. ε is a small constant to ensure the numerical stability. To a certain extent, BN has the effect of regularization. By normalizing each mini-batch set of training samples, BN introduces a certain amount of distribution noise, which helps to suppress the overfitting problem faced by DL models.

The output of BN layer is transformed nonlinearly through the PReLU activation function, as defined by

()

where a is a learnable parameter used to solve the issue of neuronal necrosis in the original ReLU activation function. The learnable parameters can be adaptively adjusted according to the distribution and characteristics of the data, which enables PReLU activation function to have stronger expressive power, adapt to different data distributions and complexities, and better fit the data. In addition, the negative slope part of PReLU can be updated through gradient backpropagation, which helps to alleviate the problem of gradient vanishing and promotes better gradient propagation and network convergence.

After each PReLU activation function, dropout [54] is introduced to randomly remove some neurons with a certain probability. Dropout can improve the generalization capability of DL models by sparsifying the output dimensions of each layer to constrain the structural complexity of the model.

As for GRU, it is part of a recursive neural network. GRU reduces the number of gating units by simplifying the structure of LSTM, thereby improving computational efficiency. GRU consists of update gate, reset gate, candidate hidden state, and final hidden state, in which the update gate is merged with forget gate and input gate while the output gate is omitted. The update gate generates a weight between 0 and 1 based on the current input and the previous hidden state, controlling the degree of information update. Then, the sigmoid activation function is used to determine whether to update the content of the memory unit since the output range can be limited between 0 and 1, as calculated by

()

where

()

In the equations, h_t represents the hidden state and can be computed by

()

where

()

The tanh function is adopted because its nonlinear transformation can ensure that the mean is 0, which helps accelerate the convergence speed of the optimization algorithm. The reset gate also uses the sigmoid activation function to generate a weight vector to determine whether to discard the previous hidden state

()

Then the output of the GRU can be obtained by

()

GRU controls the flow and forgetting of information by providing mechanisms for update gates and reset gates, thereby better handling the dependency relationships of long sequences and capturing important time-related information.

Finally, the channel estimation results are obtained through two fully connected layers with a sigmoid function.

3.3. Model Training

The hybrid DL model can be trained using SGD algorithm [55] based on error backpropagation, i.e., Adam. All learnable parameters are initialized according to Gaussian distribution and gradually updated to optimize the objective function as much as possible. The objective function adopts the MSE function to evaluate the channel estimation performance of the model. Then all the learnable parameters can be updated by

()

where

()

In the above equations, m and v are biased first and second moment estimates, respectively. and are bias-corrected first and second moment estimates, respectively. ∇_t represents gradient at the tth training iteration. The DL model undergoes iterative training until the objective function converges. Then the converged model can be used for channel estimation of new received signals.

4. Regularization of Channel Estimator

DL models often have a large number of parameters, which gives them high fitting ability on training data but also easily leads to overfitting. In other words, the DL model performs well on training data but performs poorly on unseen test data. By introducing regularization technique, the DL model is able to suppress the overfitting problem, improve its generalization capability, and maintain the stable channel estimation performance under different channel conditions.

4.1. Data Augmentation

In practical applications, collecting large-scale real channel data may face difficulties due to high costs. Data augmentation technique effectively expands the dataset by transforming and perturbing existing data to generate more training data. Data augmentation generates more diverse data samples, allowing DL models to be exposed to more wireless channel conditions during training, thereby improving its generalization ability. In this case, the DL model will focus more on the essential characteristics of the wireless channel rather than remembering specific data samples, which helps the model maintain well performance in the face of unseen channel environments.

During the process of applying DL model to channel estimation, we can increase the diversity of training data, thereby reducing the risk of overfitting and improving the generalization ability of DL models on unseen signals. In practical applications, appropriate data augmentation methods can be selected and adjusted according to the specific requirements of MIMO systems and channel estimation tasks. During the simulation process, we first perform the random rotation operation on the antenna vectors of the received signal through randomly selecting the rotation angle and performing corresponding mathematical transformations on the antenna vector. The rotation operation can simulate the position and direction changes between antennas, thereby increasing the model’s adaptability to different channel states. The amplitude of each antenna receiving the signal was also randomly scaled. Scaling operations can simulate different signal propagation distances, enabling DL models to adapt to different channel fading situations. Moreover, the addition of random noises in the received signals can simulate noise interference in real communication environments. We introduce the random noise that follows the specific distribution in the amplitude or phase of each antenna receiving the signals. By increasing the range and amplitude of noise changes, the DL model can better learn its resistance to noises. Furthermore, flipping and translating in the temporal dimension can simulate changes in signal delay, while mirroring in the spatial dimension can simulate changes in antenna position or direction.

4.2. Constraints on Structural Complexity

One critical challenge faced by DL is a well trade-off between optimization and generalization. Fewer parameters make it difficult to extract robust features, while more parameters can easily make the model overfitting. The constraint of the structural complexity in DL models is an important aspect, as overly complex models may lead to overfitting and wastage of computational resources. We empirically set up a hybrid DL model structure. We initially designed a relatively simple model architecture to limit the complexity of the model. Compared to typical deep neural network structures used for processing images or temporal signals, our proposed model structure has fewer convolutional kernels. For example, considering the number and length of signals, fewer layers and fewer neurons were used in the hybrid DL model, with 32/64/64 convolutional kernels in the first three convolutional layers. The L2 regularization term is also introduced into the objective function of the model, which plays a role in constraining the complexity of the model structure by limiting the magnitude of weights during the training process. In addition, L2 regularization shares weights with highly correlated features, thereby alleviating the impact of collinearity. The early stopping technology has also been introduced into the training process of the model. By monitoring the performance changes of the model on the training set, training can be stopped before the model begins overfitting. This can prevent the model from becoming too complex, thereby improving the accuracy of the model.

5. Simulation Results and Analysis

5.1. Simulation Settings

During the simulation process, many settings followed the widely adopted situations in many standards. For example, the number of transmitting and receiving antennas used is {2, 4, 8} in 4G LTE and {16, 32, 64, 128} in 5G and beyond 5G. The layout of transmitting and receiving antennas is determined based on actual communication system requirements and available resources. It is also common to use pilot signals of appropriate length like 8, 16, 32, and 64 in these standards. The length of the signal is set as 1024. The 128-QAM modulation scheme is adopted, and the Rician channel models with quasi-static block fading and time-varying fading are designed. The elements of channel noises are independently drawn from the additive Gaussian distributions. A total of 120,000, 30,000, and 30,000 training, validation, and testing samples are used for training and evaluation of the hybrid DL model.

As for the training process of the proposed hybrid DL model, the samples are generated offline with SNRs from 10 to 40 dB with a step size of 5 dB. During the whole training process, hyperparameters including the learning rate, batch size, training epoch, L2-regularization intensity, and dropout rate are set to 0.01, 64, 30, 0.0005, and 0.4, respectively. The above hyperparameters are empirically set, taking into account the complexity of the channel estimation task and the difficulty of optimization. All the training and testing are conducted with PyTorch using the workstation consisting of Intel i7-13700K, NVIDIA GeForce RTX 4080 GPU, and 32 × 2 GB DDR5 RAM.

5.2. Performance Analysis

In order to observe the effectiveness of the proposed method, a series of experiments have been conducted and analyzed. As shown in Figure 4, we first observe the channel estimation performance of the proposed hybrid DL model under the different number of transmission antennas, including {2, 4, 8, 16, 32, 64, 128}. The wireless channel estimation performance of the hybrid DL model is consistent under two channel conditions. According to the results, it can be seen that as the number of transmitting antennas increases, the error of channel estimation gradually increases. As the number of transmitting antennas increases, the correlation between antennas, that is, the degree of mutual influence between signals from different antennas, will increase. When the correlation increases, the channel estimation algorithm may be affected by interference. As the number of transmitting antennas increases, the system will allocate total power to more antennas, resulting in a corresponding decrease in signal power on each transmitting antenna. Lower signal power may cause the signal to be more affected by noise, leading to an increase in channel estimation error. In addition, multipath interference between multiple transmitting and receiving antennas may lead to increased channel estimation errors. In addition, as the SNR increases, the channel estimation error gradually decreases from 0.001 to 1 × 10⁻⁵, which can be negligible in the practical applications.

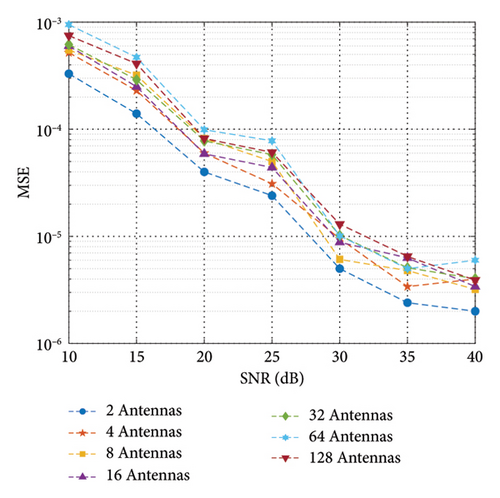
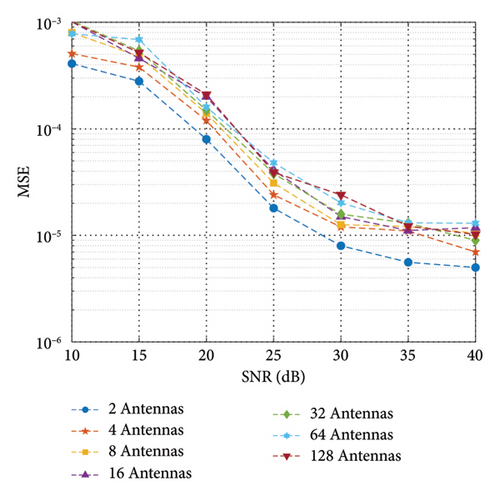
On the other hand, the overall performance of channel estimation gradually improves with the increase of SNR. Under high SNR conditions, the signal power is relatively high, while the noise power is relatively low. Under low SNR conditions, the noise power may approach or even exceed the signal power, which increases the degree of mixing between the signal and noise and reduces the accuracy of channel estimation. A higher SNR can provide a larger dynamic range of signals, i.e., a larger range of differences between the received signal strength and amplitude. The channel estimation method needs to accurately estimate the amplitude and phase of the signal, and a higher SNR makes it easier for channel estimation methods to identify and extract the dynamic range of the received signal, thereby improving the accuracy of channel estimation.

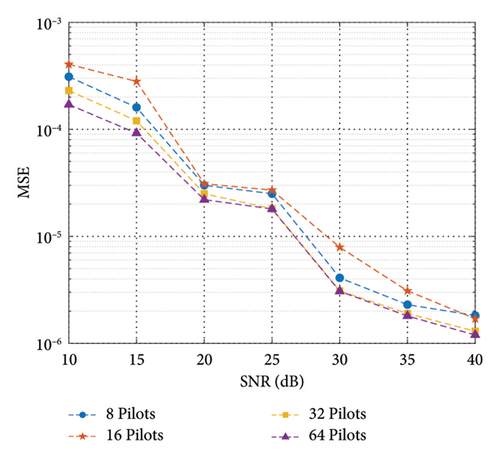
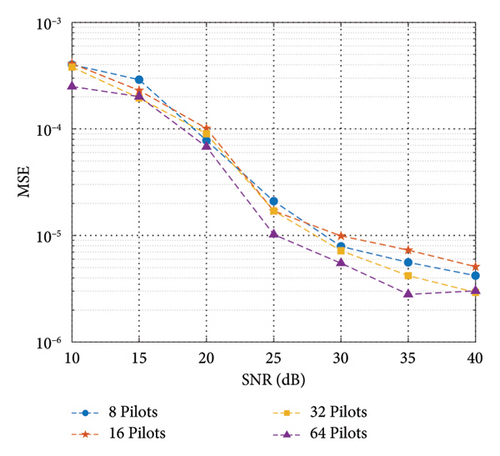
Then we report the channel estimation performance of the proposed hybrid DL model under different number of pilots, such as 8, 16, 32, and 64, as shown in Figure 5. An increase in the number of pilot signals helps improve channel estimation performance. A larger number of pilot signals mean that there are more known channel samples available for utilization, providing more information and enabling channel estimation algorithms to more accurately capture the characteristics of the channel. In MIMO systems, the channel is a complex multidimensional matrix due to the presence of multiple transmitting and receiving antennas. Increasing the number of pilot signals is able to improve the degree of freedom of channel estimation, i.e., increasing the number of observations on each element of channel matrix, which can better constrain the channel estimation problem and make the estimation more accurate. Moreover, more observation data can help DL models better remove noise and interference and improve model stability and robustness.

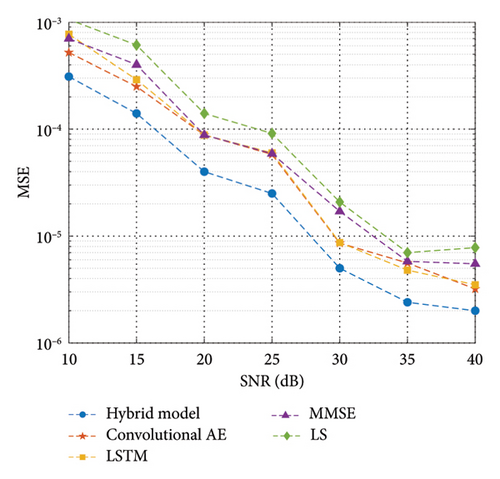
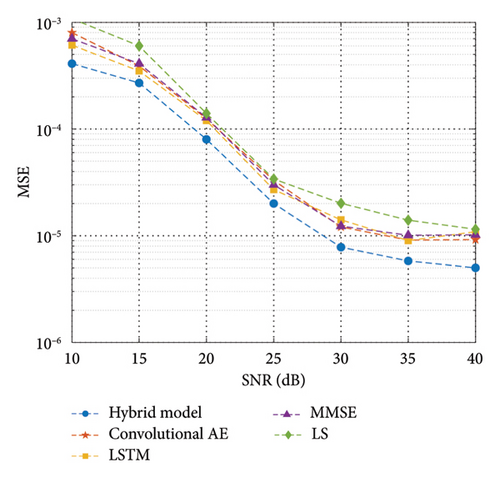
In order to verify the superiority of the proposed method, we compared different channel estimation algorithms and different DL models, including traditional methods (i.e., MMSE and LS) and DL models (i.e., convolutional AE and LSTM). As shown in Figure 6, the proposed hybrid DL method achieves the best channel estimation results on both quasi-static block fading and time-varying fading conditions. It is worth noting that DL models have shown better channel estimation performance than traditional methods. The channel estimation problem of MIMO systems often involves complex nonlinear mapping relationships, and traditional linear and LS estimation methods often cannot fully capture and model this complexity. DL models have stronger model fitting capabilities and can learn more complex channel mapping relationships through multilayer neural networks, thereby improving the accuracy of channel estimation. Compared to multistage processing in traditional methods, end-to-end learning can improve the integrated performance of the entire channel estimation system, reduce the need for signal processing and feature extraction, and reduce system complexity. Compared to single CNN or LSTM models, the hybrid model possesses stronger channel feature learning capability. The hybrid DL model combines the spatial analysis capability of CNN with the temporal processing capability of LSTM, making it better able to handle complex channel conditions.

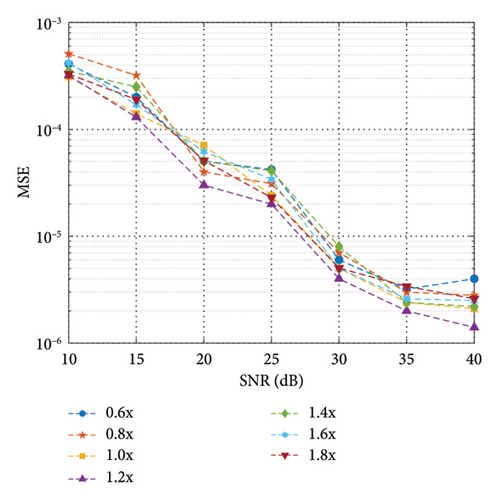
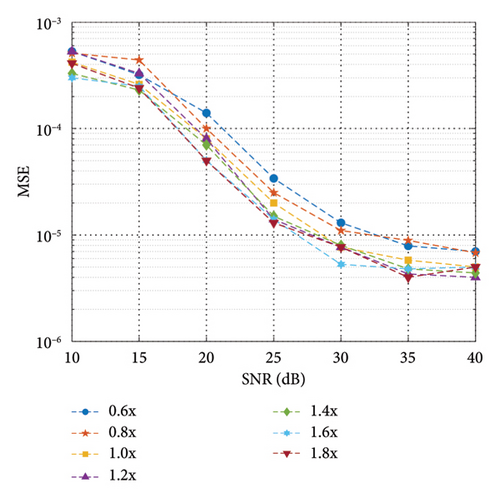
In order to observe the robustness of channel estimation performance to the model structure, we further observe the channel estimation results of DL at different sizes, as shown in Figure 7. The increase in the scale of DL models will increase the number of model parameters, thereby enhancing the fitting ability of the model. When the model size is too large, it is easy for the model to overfit the training data, resulting in overfitting of noisy and variable channel conditions and losing the generalization ability to unknown data. Large-scale DL models typically require more training data for parameter tuning and optimization. If the training data are insufficient, especially in cases where the diversity of channel conditions is not high, large-scale models may overfit the training data and fail to generalize well to unknown channel conditions. Considering the deployment difficulties and limited computing resources encountered in practical wireless communication applications, we further observe the inference speeds and corresponding channel estimation results of hybrid DL models of different sizes. According to the results in Table 1 where 0.6x represent a reduction of 0.6 times in the number of model parameters compared to before, an appropriate model size like 0.8x can achieve a well trade-off between inference speed and channel estimation accuracy.

Table 1. Inference speed and channel estimation error of hybrid deep learning model with different sizes.

Model size	0.6x	0.8x	1x	1.2x	1.4x	1.6x	1.8x
Speed (ms)	6.8	9.3	11.2	13.1	15.5	17.6	18.7
MSE (quasi-static)	3.06 × 10⁻³	2.44 × 10⁻³	2.21 × 10⁻³	2.17 × 10⁻³	2.14 × 10⁻³	2.12 × 10⁻³	2.15 × 10⁻³
MSE (time-varying)	3.22 × 10⁻³	2.78 × 10⁻³	2.46 × 10⁻³	2.40 × 10⁻³	2.39 × 10⁻³	2.37 × 10⁻³	2.39 × 10⁻³

6. Conclusions

In this paper, we propose a hybrid DL model for channel estimation in MIMO wireless communication system. By combining the advantages of convolution and GRU, the generalization ability of DL models across various communication scenarios can be fully utilized. Furthermore, a series of regularization techniques such as data augmentation and structural complexity constraints have been introduced to avoid overfitting problems. The SGD based on error backpropagation is used to iteratively train the model to convergence. During the simulation process, the comparison results with a series of methods (e.g., conventional CNN, LSTM, MMSE, and LS) have proven the effectiveness of the proposed method on both quasi-static block fading and time-varying fading conditions. Moreover, the performance of the proposed hybrid DL model at different scales in dealing with wireless channel estimation has also been observed. Experimental results demonstrate that the hybrid DL model is able to achieve a well trade-off between the channel estimation accuracy and the structural complexity.

Although DL has shown potential in addressing channel estimation task, they still face a series of challenges. The wireless communication environment is usually dynamically changing, and channel characteristics change rapidly. DL models may struggle to quickly adapt to these changes without retraining. Although online learning and incremental learning methods can partially alleviate this problem, they also bring additional complexity and computational overhead. DL models are considered as “black boxes,” since it is difficult to explain their internal workings and decision-making processes. In the field of wireless communications, understanding the decision-making process of models is critical, especially when key decisions and subsequent optimizations need to be made. Besides, DL models are sensitive to noise and attacks on input data, while channel data may be subject to various interferences and malicious attacks. Therefore, improving the security and robustness of the model is also an important research direction.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This research was supported by Shandong Provincial Natural Science Foundation (Grant no. ZR2023QF125) and Programme for Young Innovative Research Team in Higher Education of Shandong Province (Grant no. 2024KJH005).

Acknowledgments

Open Research

Data Availability Statement

The experimental data used to support the findings of this study are included within the article.

References

1 Lu L., Li G. Y., Swindlehurst A. L., Ashikhmin A., and Zhang R., An Overview of Massive MIMO: Benefits and Challenges, IEEE Journal of Selected Topics in Signal Processing. (2014) 8, no. 5, 742–758, https://doi.org/10.1109/jstsp.2014.2317671, 2-s2.0-84907196728.
10.1109/JSTSP.2014.2317671
Web of Science® Google Scholar
2 Elhoushy S., Ibrahim M., and Hamouda W., Cell-free Massive MIMO: A Survey, IEEE Communications Surveys & Tutorials. (2022) 24, no. 1, 492–523, https://doi.org/10.1109/comst.2021.3123267.
10.1109/COMST.2021.3123267
Web of Science® Google Scholar
3 Wang Z., Zhang J., Du H. et al., A Tutorial on Extremely Large-Scale MIMO for 6G: Fundamentals, Signal Processing, and Applications, IEEE Communications Surveys & Tutorials. (2024) 26, no. 3, 1560–1605, https://doi.org/10.1109/comst.2023.3349276.
10.1109/COMST.2023.3349276
Web of Science® Google Scholar
4 Han Y., Jin S., Wen C. K., and Ma X., Channel Estimation for Extremely Large-Scale Massive MIMO Systems, IEEE Wireless Communications Letters. (2020) 9, no. 5, 633–637, https://doi.org/10.1109/lwc.2019.2963877.
10.1109/LWC.2019.2963877
Web of Science® Google Scholar
5 de Araujo G. T., de Almeida A. L. F., and Boyer R., Channel Estimation for Intelligent Reflecting Surface Assisted MIMO Systems: A Tensor Modeling Approach, IEEE Journal of Selected Topics in Signal Processing. (2021) 15, no. 3, 789–802, https://doi.org/10.1109/jstsp.2021.3061274.
10.1109/JSTSP.2021.3061274
Web of Science® Google Scholar
6 Arvinte M. and Tamir J., MIMO Channel Estimation Using Score-Based Generative Models, IEEE Transactions on Wireless Communications. (2023) 22, no. 6, 3698–3713, https://doi.org/10.1109/twc.2022.3220784.
10.1109/TWC.2022.3220784
Web of Science® Google Scholar
7 Zhang W., Kim T., and Leung S. H., A Sequential Subspace Method for Millimeter Wave MIMO Channel Estimation, IEEE Transactions on Vehicular Technology. (2020) 69, no. 5, 5355–5368, https://doi.org/10.1109/tvt.2020.2983963.
10.1109/TVT.2020.2983963
Web of Science® Google Scholar
8 Demir O. T., Bjornson E., and Sanguinetti L., Channel Modeling and Channel Estimation for Holographic Massive MIMO With Planar Arrays, IEEE Wireless Communications Letters. (2022) 11, no. 5, 997–1001, https://doi.org/10.1109/lwc.2022.3152600.
10.1109/LWC.2022.3152600
Web of Science® Google Scholar
9 Dai J., Zhou L., Chang C., and Xu W., Robust Bayesian Learning Approach for Massive MIMO Channel Estimation, Signal Processing. (2020) 168, https://doi.org/10.1016/j.sigpro.2019.107345.
10.1016/j.sigpro.2019.107345
Web of Science® Google Scholar
10 Zheng Q., Zhao P., Li Y., Wang H., and Yang Y., Spectrum Interference-Based Two-Level Data Augmentation Method in Deep Learning for Automatic Modulation Classification, Neural Computing & Applications. (2021) 33, no. 13, 7723–7745, https://doi.org/10.1007/s00521-020-05514-1.
10.1007/s00521-020-05514-1
Web of Science® Google Scholar
11 Mohades Z. and Tabataba Vakili V., Deep Neural Network for Compressive Sensing and Application to Massive MIMO Channel Estimation, Circuits, Systems, and Signal Processing. (2021) 40, no. 9, 4474–4489, https://doi.org/10.1007/s00034-021-01675-z.
10.1007/s00034-021-01675-z
Web of Science® Google Scholar
12 Ke M., Gao Z., Wu Y., Gao X., and Schober R., Compressive Sensing-Based Adaptive Active User Detection and Channel Estimation: Massive Access Meets Massive MIMO, IEEE Transactions on Signal Processing. (2020) 68, 764–779, https://doi.org/10.1109/tsp.2020.2967175.
10.1109/TSP.2020.2967175
Web of Science® Google Scholar
13 Wei X. and Dai L., Channel Estimation for Extremely Large-Scale Massive MIMO: Far-Field, Near-Field, or Hybrid-Field?, IEEE Communications Letters. (2022) 26, no. 1, 177–181, https://doi.org/10.1109/lcomm.2021.3124927.
10.1109/LCOMM.2021.3124927
Google Scholar
14 Ghazanfari A., Van Chien T., Björnson E., and Larsson E. G., Model-Based and Data-Driven Approaches for Downlink Massive MIMO Channel Estimation, IEEE Transactions on Communications. (2021) 70, no. 3, 2085–2101.
10.1109/TCOMM.2021.3133939
Google Scholar
15 Wei X., Hu C., and Dai L., Deep Learning for Beamspace Channel Estimation in Millimeter-Wave Massive MIMO Systems, IEEE Transactions on Communications. (2021) 69, no. 1, 182–193, https://doi.org/10.1109/tcomm.2020.3027027.
10.1109/TCOMM.2020.3027027
Web of Science® Google Scholar
16 Dovelos K., Matthaiou M., Ngo H. Q., and Bellalta B., Channel Estimation and Hybrid Combining for Wideband Terahertz Massive MIMO Systems, IEEE Journal on Selected Areas in Communications. (2021) 39, no. 6, 1604–1620, https://doi.org/10.1109/jsac.2021.3071851.
10.1109/JSAC.2021.3071851
Web of Science® Google Scholar
17 Hussein H. S., Hussein S., and Mohamed E. M., Efficient Channel Estimation Techniques for MIMO Systems With 1-Bit ADC, China Communications. (2020) 17, no. 5, 50–64, https://doi.org/10.23919/jcc.2020.05.006.
10.23919/JCC.2020.05.006
Web of Science® Google Scholar
18 Marzetta T. L., Noncooperative Cellular Wireless With Unlimited Numbers of Base Station Antennas, IEEE Transactions on Wireless Communications. (2010) 9, no. 11, 3590–3600, https://doi.org/10.1109/twc.2010.092810.091092, 2-s2.0-78449301600.
10.1109/TWC.2010.092810.091092
Web of Science® Google Scholar
19 Li Y. G., Winters J. H., and Sollenberger N. R., MIMO-OFDM for Wireless Communications: Signal Detection With Enhanced Channel Estimation, IEEE Transactions on Communications. (2002) 50, no. 9, 1471–1477, https://doi.org/10.1109/tcomm.2002.802566, 2-s2.0-0036748244.
10.1109/TCOMM.2002.802566
Web of Science® Google Scholar
20 Tsai P. Y. and Chiueh T. D., Frequency-Domain Interpolation-Based Channel Estimation in Pilot-Aided OFDM Systems, IEEE 59th Vehicular Technology Conference (VTC 2004-Spring). (2004) 1, 420–424.
10.1109/VETECS.2004.1387987
Google Scholar
21 Rousseaux O., Leus G., Stoica P., and Moonen M., Gaussian Maximum-Likelihood Channel Estimation With Short Training Sequences, IEEE Transactions on Wireless Communications. (2005) 4, no. 6, 2945–2955, https://doi.org/10.1109/twc.2005.858353, 2-s2.0-29144442078.
10.1109/TWC.2005.858353
Web of Science® Google Scholar
22 Kim W., Ahn Y., Kim J., and Shim B., Towards Deep Learning-Aided Wireless Channel Estimation and Channel State Information Feedback for 6G, Journal of Communications and Networks. (2023) 25, no. 1, 61–75, https://doi.org/10.23919/jcn.2022.000037.
10.23919/JCN.2022.000037
Web of Science® Google Scholar
23 Lee J., Gil G. T., and Lee Y. H., Channel Estimation Via Orthogonal Matching Pursuit for Hybrid MIMO Systems in Millimeter Wave Communications, IEEE Transactions on Communications. (2016) 64, no. 6, 2370–2386, https://doi.org/10.1109/tcomm.2016.2557791, 2-s2.0-84976471182.
10.1109/TCOMM.2016.2557791
Web of Science® Google Scholar
24 Albataineh Z., Hayajneh K., Bany Salameh H., Dang C., and Dagmseh A., Robust Massive MIMO Channel Estimation for 5G Networks Using Compressive Sensing Technique, AEU-International Journal of Electronics and Communications. (2020) 120, https://doi.org/10.1016/j.aeue.2020.153197.
10.1016/j.aeue.2020.153197
PubMed Web of Science® Google Scholar
25 Hu C., Wang X., Dai L., and Ma J., Partially Coherent Compressive Phase Retrieval for Millimeter-Wave Massive MIMO Channel Estimation, IEEE Transactions on Signal Processing. (2020) 68, 1673–1687, https://doi.org/10.1109/tsp.2020.2975914.
10.1109/TSP.2020.2975914
Web of Science® Google Scholar
26 Zheng Q., Yang M., Tian X., Jiang N., and Wang D., A Full Stage Data Augmentation Method in Deep Convolutional Neural Network for Natural Image Classification, Discrete Dynamics in Nature and Society. (2020) .
Web of Science® Google Scholar
27 Zheng Q., Tian X., Yang M., and Su H., CLMIP: Cross-Layer Manifold Invariance Based Pruning Method of Deep Convolutional Neural Network for Real-Time Road Type Recognition, Multidimensional Systems and Signal Processing. (2021) 32, no. 1, 239–262, https://doi.org/10.1007/s11045-020-00736-x.
10.1007/s11045-020-00736-x
Web of Science® Google Scholar
28 Zheng Q., Wang R., Tian X. et al., A Real-Time Transformer Discharge Pattern Recognition Method Based on CNN-LSTM Driven by Few-Shot Learning, Electric Power Systems Research. (2023) 219, https://doi.org/10.1016/j.epsr.2023.109241.
10.1016/j.epsr.2023.109241
Web of Science® Google Scholar
29 Peng T., Zhang R., Cheng X., and Yang L., LSTM-Based Channel Prediction for Secure Massive MIMO Communications Under Imperfect CSI, IEEE International Conference on Communications (ICC). (2020) 1–6, https://doi.org/10.1109/icc40277.2020.9148836.
10.1109/icc40277.2020.9148836
Google Scholar
30 Yang Y., Zhang S., Gao F., Ma J., and Dobre O. A., Graph Neural Network-Based Channel Tracking for Massive MIMO Networks, IEEE Communications Letters. (2020) 24, no. 8, 1747–1751, https://doi.org/10.1109/lcomm.2020.2990487.
10.1109/LCOMM.2020.2990487
Web of Science® Google Scholar
31 Tzirakis P., Kumar A., and Donley J., Multi-Channel Speech Enhancement Using Graph Neural Networks, IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), 2021, 3415–3419, https://doi.org/10.1109/icassp39728.2021.9413955.
10.1109/icassp39728.2021.9413955
Google Scholar
32 Zheng Q., Saponara S., Tian X., Yu Z., Elhanashi A., and Yu R., A Real-Time Constellation Image Classification Method of Wireless Communication Signals Based on the Lightweight Network MobileViT, Cognitive Neurodynamics. (2023) 18, no. 2, 659–671, https://doi.org/10.1007/s11571-023-10015-7.
10.1007/s11571-023-10015-7
PubMed Web of Science® Google Scholar
33 Jiang H., Cui M., Ng D. W. K., and Dai L., Accurate Channel Prediction Based on Transformer: Making Mobility Negligible, IEEE Journal on Selected Areas in Communications. (2022) 40, no. 9, 2717–2732, https://doi.org/10.1109/jsac.2022.3191334.
10.1109/JSAC.2022.3191334
Web of Science® Google Scholar
34 Zheng Q., Zhao P., Wang H., Elhanashi A., and Saponara S., Fine-Grained Modulation Classification Using Multi-Scale Radio Transformer With Dual-Channel Representation, IEEE Communications Letters. (2022) 26, no. 6, 1298–1302, https://doi.org/10.1109/lcomm.2022.3145647.
10.1109/LCOMM.2022.3145647
Web of Science® Google Scholar
35 Zheng Q., Tian X., Yu Z. et al., MobileRaT: A Lightweight Radio Transformer Method for Automatic Modulation Classification in Drone Communication Systems, Drones. (2023) 7, no. 10, https://doi.org/10.3390/drones7100596.
10.3390/drones7100596
Web of Science® Google Scholar
36 Zheng Q., Tian X., Yu Z., Wang H., Elhanashi A., and Saponara S., DL-PR: Generalized Automatic Modulation Classification Method Based on Deep Learning With Priori Regularization, Engineering Applications of Artificial Intelligence. (2023) 122, https://doi.org/10.1016/j.engappai.2023.106082.
10.1016/j.engappai.2023.106082
Web of Science® Google Scholar
37 Kwon H. Y., Yoon H. G., Lee C. et al., Magnetic Hamiltonian Parameter Estimation Using Deep Learning Techniques, Science Advances. (2020) 6, no. 39, https://doi.org/10.1126/sciadv.abb0872.
10.1126/sciadv.abb0872
Web of Science® Google Scholar
38 Zheng Q., Zhao P., Zhang D., and Wang H., MR-DCAE: Manifold Regularization-Based Deep Convolutional Autoencoder for Unauthorized Broadcasting Identification, International Journal of Intelligent Systems. (2021) 36, no. 12, 7204–7238, https://doi.org/10.1002/int.22586.
10.1002/int.22586
Web of Science® Google Scholar
39 Gao J., Yi X., Zhong C., Chen X., and Zhang Z., Deep Learning for Spectrum Sensing, IEEE Wireless Communications Letters. (2019) 8, no. 6, 1727–1730, https://doi.org/10.1109/lwc.2019.2939314.
10.1109/LWC.2019.2939314
Web of Science® Google Scholar
40 Liu C., Zhang H., Li L., and Cui T. J., Towards Intelligent Electromagnetic Inverse Scattering Using Deep Learning Techniques and Information Metasurfaces, IEEE Journal of Microwaves. (2023) 3, no. 1, 509–522, https://doi.org/10.1109/jmw.2022.3225999.
10.1109/JMW.2022.3225999
Web of Science® Google Scholar
41 Zheng Q., Tian X., Yu Z. et al., Application of Complete Ensemble Empirical Mode Decomposition Based Multi-Stream Informer (CEEMD-MsI) in PM2. 5 Concentration Long-Term Prediction, Expert Systems With Applications. (2024) 245, https://doi.org/10.1016/j.eswa.2023.123008.
10.1016/j.eswa.2023.123008
Web of Science® Google Scholar
42 Zheng Q., Tian X., Yu Z. et al., Application of Wavelet-Packet Transform Driven Deep Learning Method in PM2. 5 Concentration Prediction: A Case Study of Qingdao, China, Sustainable Cities and Society. (2023) 92, https://doi.org/10.1016/j.scs.2023.104486.
10.1016/j.scs.2023.104486
PubMed Web of Science® Google Scholar
43 Balevi E., Doshi A., and Andrews J. G., Massive MIMO Channel Estimation With an Untrained Deep Neural Network, IEEE Transactions on Wireless Communications. (2020) 19, no. 3, 2079–2090, https://doi.org/10.1109/twc.2019.2962474.
10.1109/TWC.2019.2962474
Web of Science® Google Scholar
44 Kang J. M., Chun C. J., and Kim I. M., Deep Learning Based Channel Estimation for MIMO Systems With Received SNR Feedback, IEEE Access. (2020) 8, 121162–121181, https://doi.org/10.1109/access.2020.3006518.
10.1109/ACCESS.2020.3006518
Web of Science® Google Scholar
45 Gao J., Hu M., Zhong C., Li G. Y., and Zhang Z., An Attention-Aided Deep Learning Framework for Massive MIMO Channel Estimation, IEEE Transactions on Wireless Communications. (2022) 21, no. 3, 1823–1835, https://doi.org/10.1109/twc.2021.3107452.
10.1109/TWC.2021.3107452
CAS Web of Science® Google Scholar
46 Zhang J., Ma X., Qi J., and Jin S., Designing Tensor-Train Deep Neural Networks for Time-Varying MIMO Channel Estimation, IEEE Journal of Selected Topics in Signal Processing. (2021) 15, no. 3, 759–773, https://doi.org/10.1109/jstsp.2021.3051490.
10.1109/JSTSP.2021.3051490
Web of Science® Google Scholar
47 Belgiovine M., Sankhe K., Bocanegra C., Roy D., and Chowdhury K. R., Deep Learning at the Edge for Channel Estimation in Beyond-5G Massive MIMO, IEEE Wireless Communications. (2021) 28, no. 2, 19–25, https://doi.org/10.1109/mwc.001.2000322.
10.1109/MWC.001.2000322
Web of Science® Google Scholar
48 Ma X. and Gao Z., Data-driven Deep Learning to Design Pilot and Channel Estimator for Massive MIMO, IEEE Transactions on Vehicular Technology. (2020) 69, no. 5, 5677–5682, https://doi.org/10.1109/tvt.2020.2980905.
10.1109/TVT.2020.2980905
Web of Science® Google Scholar
49 Liu S. and Huang X., Sparsity-Aware Channel Estimation for Wave Massive MIMO: A Deep CNN-Based Approach, China Communications. (2021) 18, no. 6, 162–171, https://doi.org/10.23919/jcc.2021.06.013.
10.23919/JCC.2021.06.013
Google Scholar
50 Zheng Q., Tian X., Yang M., Wu Y., and Su H., PAC-Bayesian Framework Based Drop-Path Method for 2D Discriminative Convolutional Network Pruning, Multidimensional Systems and Signal Processing. (2020) 31, no. 3, 793–827, https://doi.org/10.1007/s11045-019-00686-z.
10.1007/s11045-019-00686-z
Web of Science® Google Scholar
51 Li X., Xiong H., Li X. et al., Interpretable Deep Learning: Interpretation, Interpretability, Trustworthiness, and Beyond, Knowledge and Information Systems. (2022) 64, no. 12, 3197–3234, https://doi.org/10.1007/s10115-022-01756-8.
10.1007/s10115-022-01756-8
Web of Science® Google Scholar
52 Bjorck N., Carla P., Gomes B. S., and Kilian Q. W., Understanding Batch Normalization, Advances in Neural Information Processing Systems. (2018) 31.
Google Scholar
53 Thakur R. S., Yadav R. N., and Gupta L., PReLU and Edge-Aware Filter-Based Image Denoiser Using Convolutional Neural Network, IET Image Processing. (2020) 14, no. 15, 3869–3879, https://doi.org/10.1049/iet-ipr.2020.0717.
10.1049/iet-ipr.2020.0717
Web of Science® Google Scholar
54 Srivastava N., Hinton G., Krizhevsky A., Sutskever I., and Salakhutdinov R., Dropout: A Simple Way to Prevent Neural Networks From Overfitting, Journal of Machine Learning Research. (2014) 15, no. 1, 1929–1958.
Web of Science® Google Scholar
55 Zheng Q., Tian X., Jiang N., and Yang M., Layer-Wise Learning Based Stochastic Gradient Descent Method for the Optimization of Deep Convolutional Neural Network, Journal of Intelligent and Fuzzy Systems. (2019) 37, no. 4, 5641–5654, https://doi.org/10.3233/jifs-190861.
10.3233/JIFS-190861
Web of Science® Google Scholar

Citing Literature

All articles

A Massive MIMO Channel Estimation Method Based on Hybrid Deep Learning Model With Regularization Techniques

Abstract

1. Introduction

2. MIMO System Model