Modelling Near-Field Aerosol Exposure for Respiratory Infection Risk Assessment
Abstract
Quantitative microbiological risk assessment (QMRA) is a method to estimate the risk of infectious disease transmission from human exposure to pathogens. QMRA is a helpful tool to inform health policies to control the impact of infectious disease transmission from human-to-human transmissible infectious respiratory diseases. QMRA combines an estimate of pathogen exposure with information on the probability of infection given the dose. The infection risk of respiratory diseases is generally assumed to depend on the interpersonal distance between the infectious person (index) and the exposed recipient. To account for close-proximity exposure in QMRA, specific generic models are required. To be helpful in policy information, these models should be sufficiently accurate in describing elevated air concentrations of pathogens near the index. On the other hand, they should be sufficiently generic and flexible to be applied in generalized situations without requiring very specific and detailed situational information. In this work, we identified different models to account for near-field exposure in the literature: multizone, diffusion, and jet models. These methods were tested with respect to their applicability in QMRA. We evaluated them on the criteria of ease of use, the availability of parameter values for generic application, and their ability to describe air concentrations in realistic situations as replicated in experiments. It was found that only diffusion modelling appeared to be both flexible enough to describe experimental data and to be supported by sufficient information to allow for parametrization in a wide variety of situations. The multizone models were found to be easy to use but difficult to parametrize given the arbitrariness of aspects of the modelling method. The jet models were found to be more complex to implement and adapt to specific exposure scenarios.
1. Introduction
In the control and mitigation of infectious respiratory diseases, quantitative microbiological risk assessment (QMRA) is a valuable tool to inform health policies. QMRA estimates the risk of infection by combining two aspects: an assessment of exposure to the microbial agent (e.g., virus or bacteria) and information on the likelihood of infection as a function of the exposure dose, the dose–response relation [1].
Human-to-human transmission of respiratory infectious diseases follows after expulsion of aerosol particles containing pathogens by an infectious person (or “index”) with respiratory activities such as breathing, speaking, coughing, or sneezing. Subsequent exposure of a susceptible individual may occur via different exposure pathways such as contact with contaminated surfaces, inhalation of pathogens via respirable aerosol particles, or close contact exposure via large, ballistic droplets that impact mucosal tissue directly. The relative importance of transmission pathways is still debated and generally depends on the pathogen considered [2–4]. In this work, we focus on the inhalation of pathogens with the smaller, respiratory aerosol particles. These are small droplets and droplet cores that remain after the evaporation of fluid components from respiratory aerosol droplets. These particles, in contrast to the larger ballistic droplets, remain suspended in air for prolonged durations and have a potential to travel over significant distances. Their transport is mostly determined by air movement and less by particle kinetics, such as sedimentation. The distinction between aerosol particles and ballistic droplets is often pragmatically but arbitrarily set at a diameter of 5 μm. In fact, the distinction is not clear-cut. Or, as it is put in [5]: “IRPs [i.e., infectious respiratory particles] exist on a continuous spectrum of sizes, and no single cut off points should be applied to distinguish smaller from larger particles, this allows to move away from the dichotomy of previous terms known as ‘aerosols’ (generally smaller particles) and ‘droplets’ (generally larger particles).” In particular, particles with diameters up to 20–30 μm may remain airborne for durations long enough to disperse over significant distances [6]. In this work, we will consider transmission via particles with diameters up to 20 μm.
To inform policy, fast, generic tools for exposure assessment are needed. For a tool to be fit for this purpose, it does not need to be able to accurately analyze exposure in very specific situations. Rather, it needs to project reasonable estimates of exposure across a wide range of scenarios and to rapidly evaluate the potential impact of different policy options. Generic exposure modelling is the most suitable approach and is commonly employed. Examples are models that explicitly consider aerosol particle transport and fate [7–10] and models based on a Wells–Riley [11] approach in its simplest formulation [12, 13]. These models typically assume instantaneous mixing of the aerosol particles after emission in the room air (the so-called “well-mixed” approach). After which, removal by, for example, ventilation, sedimentation, and inactivation, are commonly described as linear processes.
These well-mixed approaches are limited in an important way in that they do not distinguish between air concentrations close to the infectious index (“near-field”) and those further away (“far-field”) within a room. As pathogen concentrations will be higher close to the index, well-mixed models may underestimate infection risk in scenarios in which a susceptible person spends time in close proximity to the infectious index.
The contribution of exposure in the index’s near-field to infection risks, compared with exposure in the far-field, is not evident and may be situational. Specific studies on exposure and transmission risk in a proximity of 1–1.5 m from an infectious index for SARS-CoV-2 have been conducted. Collectively, these studies indicate that infection risk may be by one to two orders of magnitude larger close to the index than at a larger distance. Additionally, these studies suggest that aerosol particles do play a significant role in this near-field transmission [14–18].
To help alleviate the limitations of the well-mixed modelling approaches, we took a closer look into available exposure modelling methods to describe air concentrations of aerosol particles in close proximity to the index. We evaluated three modelling methods that were identified in literature sources. We selected modelling methods that accurately describe aerosol concentrations near the source of emission but are still sufficiently generic for wide application in QMRA, without the need for specific location and scenario details. The models were implemented and tested in simulation scenarios, where their results were compared with those of a well-mixed model. Additionally, we tested the near-field models with independent measurement data on the dispersion of aerosol particles in a test room and in an aircraft during flight.
The motivation of this work was to improve the risk assessment for SARS-CoV-2, and our focus is on discussing the near-field models in that context. But the methods should be applicable in general risk assessment of airborne pathogens. This work results in an evaluation of the near-field exposure modelling methods, considering the ease of implementation and the parametrization of the model, the comparison with the well-mixed models, and the accuracy with which measurement data can be simulated. Aspects of actual infection risk modelling, such as dose–response modelling or modelling of pathogen emission from an infectious person, were not considered in this work. We exclusively focused on the transport of pathogen-laden particles. Ultimately, the decision on whether more refined near-field exposure models are needed depends on whether projected close proximity risks are significantly different from those predicted with the well-mixed models. This will vary from one case to the next, as it depends on the considered pathogen as well as on the exposure scenarios considered.
2. Methods
2.1. Identification of Modelling Methods
We queried exposure and risk assessment studies published in the literature for near-field exposure modelling methods. This was done using a nonsystematic search of the literature on exposure and risk assessment studies. An iterative, explorative search in Scopus and PubMed on keywords including, but not limited to, “near field,” “exposure,” “indoor air,” and “modelling,” let to the identification of a number of modelling papers for both chemical and infectious disease studies, in residential, occupational, and public settings. The search was expanded further by snowballing both cited references and citing references. Full text reading was done on a subselection of studies to identify modelling methods that (1) specifically describe air concentrations near an emitter or source; (2) are sufficiently generic, that is, are applicable to general scenarios and do not require very specific input on the indoor environment; and (3) allow for model parametrization on general considerations, that is, without the need for detailed situational information or case specific measurement.
Three modelling methods were identified and selected for further evaluation: multizone models [19–21], turbulent (or eddy) diffusion models [22–24], and jet or puff models [25–27].
2.2. Model Comparison
The three near-field models were evaluated based on their utility in generalized QMRA and their quantitative results. To assess the utility of a model, we considered the complexity of the implementation of the model and the ease with which the model can be parametrized in any particular scenario. To evaluate the quantitative results, we implemented the near-field models in Mathematica (Version 13.2, Wolfram, Champaign, IL, United States). Then, we (1) compared the model results to those of a well-mixed model in several emission scenarios and (2) tested the models against experimental data sets obtained from controlled aerosol release experiments in realistic settings.
2.3. Exposure Models
In this section, we briefly provide the formulations of the well-mixed, multizone, diffusion, and jet models. The near-field modelling methods discussed here assume that the transport of pathogen-laden aerosol particles is with air movement (convective transport). The movement of particles with respect to the surrounding air, which is an important aspect in the movement of ballistic droplets, is not considered. This limits the validity of the analysis to the aerosol particles of smaller diameters (up to 20 μm, or so).
2.3.1. Well-Mixed Model
In the well-mixed modelling approach, it is assumed that the aerosol particles are emitted by a source of strength S(t) for a duration of te. The source is a rate of mass/time and may vary with time t. After emission, the emitted mass immediately disperses in an indoor environment with volume V. Subsequently, aerosol particles are removed by ventilation q.
Here, c is the aerosol particle mass concentration in the air (mass per cubic meter), te is the duration of emission (time), S is the strength emission source (mass/time), V is the indoor environment volume (cubic meters), and q is the ventilation rate (air changes/time).
The Heaviside step function θ(t) equals 1 if t > 0 and 0 otherwise. The term with θ describes a source that emits for a duration of te and is then switched off.
2.3.2. Multizone Models
In multizone models [19–21], the inhomogeneity of indoor concentrations is modelled by subdividing the indoor air into different zones. In the different zones, the air concentration is assumed to be well mixed. Movement of air and virus-laden aerosol particles is described as an exchange of air between adjacent zones. Here (see Figure 1), we consider a two-zone model as an example, but the method is easily extended to a larger number of zones. In the two-zone model, the indoor environment is modelled as a near-field zone around the index (volume VNF) and a far-field zone (volume VFF) that represents the rest of the indoor environment volume. Aerosol particles are emitted in the near-field at a volume rate S(t) that may depend on time t. Near-field and far-field exchange air with exchange rate β (volume/time).
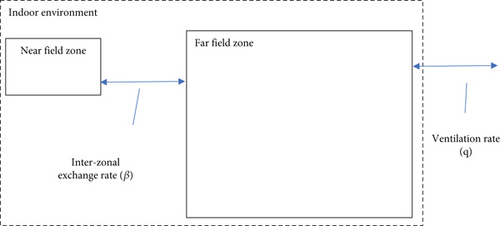
To parametrize this model, assumptions need to be made for the near-field volume VNF and the interzonal air exchange rate β. These do not follow straightforwardly from specifications of an indoor environment. Values for VNF and β were suggested by Keil and Zhao [28]. These were derived from the fitting of the model to measurement data for a range of indoor settings. Next to this, a method to estimate the near-field volume and β is suggested [20]. The method is to assume the near-field to be a sphere of some representative diameter (e.g., 1.0–1.5 m). Then, β is estimated from the flux over the zone’s surface area, assuming air transport with a representative indoor air speed. For the latter, the authors suggest 0.1 m/s.
In the model simulations with the two-zone model, we included two sets of parameter values for VNF and β representing lower and higher bounds of a plausible range (see Section 2.4). Model simulations with the two sets of values may be interpreted as the range of uncertainty in this aspect of the model parametrization.
2.3.3. Diffusion Models
The infinite sums in (8) tend to converge quite rapidly, usually about 10 terms suffice for typical simulation durations. The time integral in (7) has only a trivial analytical solution for a single, pulse-like release. In a more general case, it has to be solved numerically.where c is the aerosol particle concentration in air (mass/volume), q is the ventilation rate (volume/time), D is the turbulent coefficient of diffusion (area/time), S is the source strength emission (mass/time), L is the length indoor environment (meters), W is the width indoor environment (meters), and H is the height indoor environment (meters).
| K | Von Karmann’s constant, assumed 0.1 in [29] |
| H | Representative length, that is, room height |
| D | Diffusion coefficient [m2/s] |
| g | Gravitational constant |
| ΔT | Temperature gradient between floor and ceiling of the room [K] |
| T | Temperature of the room [K] |
| a | Ventilation rate [1/s] |
| uo | Air velocity at inlet [m/s] |
The predictions of D by this model tend to be in the same range as values given in Cheng et al.’s [22] study for typical indoor conditions.
Based on the methods and data on D given here, in this work, we consider a range 0.002–0.01 m2/s for D to represent values that will typically occur in realistic conditions. This range is used in the model simulations below to represent variability in indoor conditions.
2.3.4. Jet Models
Jet (also referred to as “puff”) models describe the emission and dispersion of particles with convective air flow from human expulsion, such as those occurring during coughing or breathing. The models describe air movement after emission from the mouth. Jet models are aerodynamic models that approximately solve the Navier–Stokes model equations of aerodynamics. A variety of jet models for the exposure estimation of respiratory infectants has been proposed. In this work, we considered the formulation proposed by Balachandar et al. [25] and Cravero and Marsano [26]. Other examples are given by Cortellessa et al. [15] and Li et al. [27]. The jet model approximation neglects specific boundary conditions defining the indoor space, essentially assuming that puff emission occurs in an infinite empty space of still air. Typically, two phases are identified: a first phase (here referred to as “ejection phase”) in which the ejected puff of air is slowed down due to resistance from surrounding still air and a second phase (here referred to as “dispersion phase”) in which the puff expands because of turbulent air movement (analogous to the diffusion modelling).
As the model formulation is complex, we chose not to reproduce it here, but refer to Balachandar et al. [25] and Cravero and Marsano [26].
To run the jet model for the ejection phase, parameter input on the size of the mouth and the velocity of the emitted air is required. The latter varies with activity (i.e., breathing, speaking, singing, and coughing). Generally, information for these parameters is available. For the dispersion phase, the model needs as input values for two coefficients in particular: the turbulent dissipation c′ε (m2/s3) and the so-called “entrainment parameter” α (dimensionless). These two determine the speed at which the puff cloud expands due to turbulent air movement. Typical indoor air values have been suggest as c′ε = 1.5 × 10−5 (m2/s3) and α = 0.1 [25]. It is not clear how these model parameters may be extrapolated to specific indoor settings that deviate from the settings assumed in the original paper. In the model simulations in this work, we kept parameter values fixed at the recommended values. This may not adequately reflect variability in indoor environments.
Also, the model does not provide a clear instruction on how to include the effects of ventilation. In view of this latter point, the jet model described here only describes short-term exposure and is limited to the near-field only. In the model simulations, the durations of the scenario were therefore limited to 20 min, as longer durations are expected to be outside the validity domain of the model.
2.4. Scenario-Based Comparison
To compare the outcomes and performance of the three near-field models with the well-mixed model, two different emission scenarios were considered: one of a single pulse-like emission, simulating, for example, a human cough, and one of continuous emission, simulating human emission during speech or breathing. In the scenarios, air concentrations after emission were simulated for three near-field models and the well-mixed air model. The simulated indoor space was a room with dimensions (width (x) × depth (y) × height (z)) of 6 × 6 × 3 = 108 m3. The mouth of the index was assumed to be located in the middle of the room, at 3, 3, and 1.5 m, facing the positive x-direction, in all scenarios. Scenario settings are given in Table 2. As jet models only project short-term near-field air concentrations and the model is not expected to be valid for long-term scenarios, the duration of the continuous emission scenario for this model was limited to 20 min.
| Single emission | Continuous emission | |||
|---|---|---|---|---|
| Mass release | 1 | mg | 1 mg/sec | |
| Simulation duration | 150 | Seconds | 4 hours | |
| Ventilation | 1 | Air changes/hour | 1 air change/hour | |
| Model parameters | ||||
| Two-zone model | ||||
| Low | High | Unit | Monte Carlo simulation | |
| β | 0.1 | 0.24 | 1/s | Uniform (0.1, 0.24) |
| Volume near field | 4 | 14 | m3 | Uniform (4, 14) |
| Volume far field | 68 | 58 | m3 | |
| Diffusion model | ||||
| Low | High | |||
| D | 0.002 | 0.01 | m2/s | Uniform (4, 14) |
| Jet model | ||||
| Diameter mouth | 0.024 | m | ||
| Air emission speed | 1.0 | m/s | ||
| Entrainment parameter α | 0.1 | Uniform (0.05, 0.2) | ||
| Turbulent dissipation c′ε | 1.5 × 10−5 | m2/s3 | Uniform (0.75 × 10−5, 3.0 × 10−5) | |
In the formulation of the near-field models given above, we identified a set of critical model parameters for which it is difficult to provide specific input values as these parameters are either uncertain or highly variable between environments. For these model parameters, we selected plausible high and low values as scenario inputs and conducted simulations for both extremes. In addition, a Monte Carlo simulation was conducted. For the critical model parameters, we described the plausible domain of values by uniform probability distributions between the plausible high and low bounds. From these distributions, a 1000 samples were randomly drawn. For each parameter sample, the scenario was evaluated, leading to a sample of air concentrations at either a set of time points (two-zone model) or a set of locations (diffusion and jet models). The Monte Carlo simulation provided more insight in the distribution of potential scenario outcomes between the extremes. This procedure was followed, in particular for the near-field zone volume VNF and near-field–far-field air exchange rate β of the two-zone model and the diffusion coefficient D of the turbulent diffusion model.
For the jet model, model inputs that should be provided are the mouth diameter and emission speed, the turbulent dissipation c′ε, and the entrainment parameter α. For these parameters, only best estimate nominal values were available. The Monte Carlo simulation was conducted for variations in α and c′ε by assuming that their values may range from half to twice their nominal values. This range does not represent a realistic indication of their plausible values, but at least allows us to evaluate model sensitivity with respect to these parameters. To approximate a single pulse using the jet model, a short duration emission of 1 s was used.
2.5. Evaluation of the Near-Field Modelling Approaches With Experimental Data
After the comparison of the near-field models with the well-mixed model, we tested the near-field models with an experimental data set of two aerosol dispersion experiments: one experiment on the dispersion of aerosol particles in an unventilated room and one data set obtained from an aerosol dispersion experiment in an aircraft.
2.5.1. Experiment 1: Measured Concentrations of Artificial Aerosol Released in an Unventilated Room
An artificial aerosol with particles simulating human aerosol expulsion was dispersed in a small room using a spraying device [31]. Air concentrations of the aerosol particles with a diameter 1 μm were recorded directly next to the emission source. A full description of the experimental procedure is given by Niese et al. [31]. In short, a Medspray aerosol generating device (MAGD) was used to spray aerosols into the air. These aerosols are created by manually pressing artificial saliva into the MAGD using a lever drive that provided controlled liquid pressure. The artificial saliva is a combination of 2% w/w NaCl with 1% glycerol. Over a period of 2 min, 700 μL of liquid was dispersed, equivalent to an estimated number of 7 × 109 particles. The point of aerosol release was at a height of 1.5 m. Using an aerodynamic particle sizer (APS) (APS 3321, TSI Inc., United Kingdom), the particle size of the aerosols was measured about 50 cm from the emission point at a height of 1.25 m. Ventilation was minimized during the experiment (doors and windows closed). The dimensions of the room were 6 × 4 × 3 = 72 m3. Here, we used the results from a pilot run from that work.
To simulate the experimental data, parameter values given in Table 3 were used. The diffusion coefficient in the turbulent diffusion model was adjusted to visually fit the data. As experimental data were specified in aerosol volume/volume air, we converted particle mass concentration to volume concentration using an aerosol particle density of 1.3 g/cm3.
| Parameter | Scenario value | Unit |
|---|---|---|
| General | ||
| Emitted aerosol particle volume | 700 | μL |
| Emission duration | 120 | s |
| Distance sample point from source | 0.36 | m |
| Simulation duration | 15 | Minutes |
| Air exchange | 0 | Air changes/hour |
| Fraction with diameter 1 μm | 0.08 | |
| Total number aerosol particles released | 7 × 109 | |
| Two-zone model | ||
| β | 0.24 | 1/s |
| Volume near-field | 14 | m3 |
| Volume far-field | 58 | m3 |
| Diffusion model | ||
| D | 0.04 | m2/s |
| Jet model | ||
| Speed emitted air | 2.65 | m/s |
| Diameter source emitter | 0.004 | m |
2.5.2. Experiment 2: Dispersion of Artificial Aerosol in Aircraft
A combined measurement and CFD modelling study determined the dispersion of artificially generated aerosol particles in an aircraft cabin under a variety of indoor environmental conditions [32]. The aerosol was emitted at a middle seat in the middle row of a seven-row test section. A total of 700 μL artificial saliva (water with 1% w/w glycerol and 2% w/w NaCl) was dispersed over a period of 3–6 min. Evaporation of the water component was expected to be fast. After evaporation, the total released aerosol particle volume, Vemission, was about 25 μL. At each seat in the seven-row test section, the time-averaged air concentration (pL/cm3) of the volume of respirable aerosol particles (particles with diameter less than 10 μm) was measured.
Model testing was performed by simulating Experimental Run #2 (a single aisle aircraft during cruise conditions) from Schijven et al. [32]. Simulated particle volume air concentrations were compared to the measured ones. The plane was simulated as a closed volume that exchanged air with the outdoor air as dictated by the aircraft’s overall ventilation. The aircraft’s air exchange rate varied between 7.3 and 22.5 air changes per hour during flight. The depth of the simulated plane volume was limited to 20 m. Transfer of aerosol was assumed not to take place beyond that distance. The height was restricted by the presence of luggage bins and was estimated as 1.6 m. The width of the aircraft was given in the experiment description as 3.5 m. The presence of furniture and manikins in all chairs of the seven-row compartment was ignored. This may lead to a (potentially significant) underestimation of the air-concentration but reflects the practical use of generic models in risk or exposure estimation settings.
Parameter input values were manually adjusted within their plausible domain to fit the observed data as well as possible (see Table 4). No attempt at a formal parameter optimization was made. The results should be interpreted as an illustration of the capabilities of the near-field modelling approach to capture realistic exposures, not as a test to accurately project aerosol particle concentrations a priori.
| Parameter | Value | Unit |
|---|---|---|
| General | ||
| Emitted aerosol particle volume | 25 | μL |
| Emission duration | 356 | s |
| Simulation duration | 6 | Minutes |
| Air exchange | 7.5 | Air changes/hour |
| Room volume (depth × width × height) | 20 m × 3.5 m × 1.6 m = 112 | m3 |
| Two-zone model | ||
| β | 0.24 | 1/s |
| Volume near-field | 14 | m3 |
| Volume far-field | 98 | m3 |
| Diffusion model | ||
| D | 0.002 | m2/s |
| Jet model | ||
| Speed emitted air | 2.65 | m/s |
| Diameter source emitter | 0.004 | m |
3. Results
3.1. Scenario-Based Evaluation
3.1.1. Multizone Model
The results of the two-zone model simulations are shown in Figure 2 for the two different sets of model parameters. In the single pulse scenario, the near-field concentration has a clear maximum in the initial stage of emission. The height of the maximum depends on the parameters: a smaller near-field volume results in a higher peak air concentration.
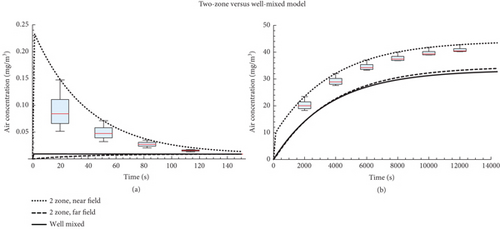
In the continuous emission scenario, the concentration approaches a steady state. The ratio between the near- and far-field depends on the near-field volume, near-field–far-field exchange rate, and room air exchange rate, but differences are modest. Both near-field and far-field air concentration levels in the steady state are (slightly) higher than for the well-mixed scenario.
3.1.2. Diffusion Model
A comparison of the well-mixed and diffusion models in the continuous emission scenario is shown in Figure 3. The diffusion model is plotted for two values of the turbulent diffusion coefficient, namely, D = 0.002 and 0.01 m2/s. For the diffusion model, the steady-state air concentrations after 4 h of simulation are plotted along the x-direction (with the distance from the index on the x-axis). The air concentration as predicted by the diffusion model is isotropic, that is, is the same in all directions. The source is positioned at x = 3.0 m. For comparison, the well-mixed model is plotted as a time course (its projection does not depend on the x position or the direction from the source, as it provides a spatially uniform concentration). It is observed that there is a large difference in concentration profile between the low and high diffusion coefficient scenarios. The low diffusion scenario predicts near-field concentrations that are up to three times higher than the steady-state well-mixed air concentration. The higher diffusion coefficient scenario, on the other hand, predicts a more or less homogeneous air concentration and does not deviate much from the well-mixed model. The well-mixed model approaches a steady-state concentration after about 2 h. This level is significantly lower than the low-diffusion near-field concentration (< 1 m from the source) but is comparable (slightly higher in fact) to the far-field concentration as predicted by the diffusion model.
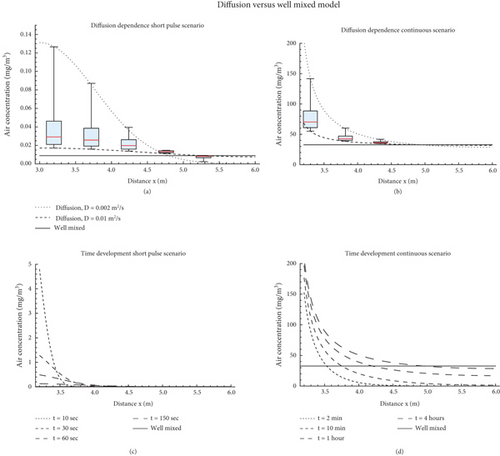
The concentrations are plotted at the end of the simulation duration (t = 150 s and t = 4 h, respectively). The near-field simulations give the boundaries of a range of reasonable model parametrizations. Box and whiskers summarize the results of the Monte Carlo simulation, representing median (line) 25th–75th percentiles (box) and minimum and maximum (whiskers).
3.1.3. Jet Model
For the jet model, it was assumed that emission was in the positive x-direction with an initial speed of 1.0 m/s, representing breathing. Simulated air concentrations featured a steep maximum at a small distance away from the index mouth (within 0.5 m) (see Figure 4). The location of this maximum depends on the air speed at emission and will be further away when coughing or sneezing.
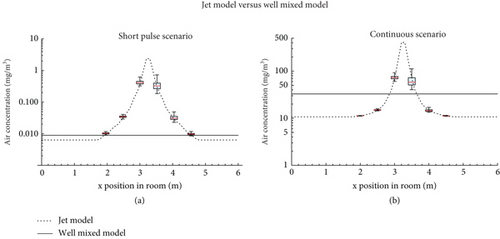
The peak air concentration in the puff model is more than 10 times higher than predicted by the well-mixed model, both in the short pulse and the continuous emission scenario.
3.2. Comparison With Experimental Data
3.2.1. Dispersion of Aerosol in an Unventilated Room
Results of simulations are presented in Figure 5, together with the measured air concentrations. Standard parameters for the two-zone and puff models were used, because no method for adjusting model parameters to specific environmental conditions was available. The diffusion coefficient used in the diffusion model was set to 0.04 m2/s to visually fit the data. This value is somewhat higher than the maximum value of 0.01 m2/s in the range we previously adopted but is still consistent with literature sources [29], where values up to 0.15 m2/s were reported.

Both two-zone and diffusion models represent the measured data reasonably well, with concentration levels close to observed levels. The exact timing of the peak concentration is off in both models. The jet model severely overestimates peak concentrations around the index. This may be an indication that the transport velocity, dictated by the turbulent dissipation c′ε, in the jet model is in reality much higher than assumed.
3.2.2. Aerosol Particle Exposure in Aircraft During Flight
Results of the simulations with different near-field models are shown in Figure 6, together with the measured data.

3.2.2.1. Two-Zone Model
For the two-zone model, the difference between the modelled near-field and far-field (more distant seats) was limited to less than a factor of 3. Comparison with the measured data showed that near-field concentrations were underestimated by a factor of up to 40. Also, the modelled far-field concentrations did not capture the measured concentrations very well. At these more distant seats, concentrations were up to about 30 times overpredicted.
3.2.2.2. Diffusion Model
For the diffusion model, to best describe the measured data, a low ventilation value and a low diffusion coefficient were selected. Under these assumptions, the diffusion model captures the measured data reasonably well, with per-seat deviations mostly within a factor of 4. The diffusion model (being isotropic in its formulation) did not capture the backward/forward asymmetry apparent in the data. Also, despite the assumption of low ventilation and limited diffusion, the modelled concentration systematically remained below the measured concentration.
3.2.2.3. Jet Model
The jet model with the standard parameters did not fit the measured data very well. The near-field concentrations were underestimated by a factor of 10 or more. This has likely to do with the fact that the turbulent expansion of the puff in the standard parametrization underestimates the expansion that occurred in the experiment. The far-field concentrations were significantly overpredicted. This may stem from the fact that the jet model does not account for ventilation.
3.2.3. Model Evaluation
Based on our experience with model implementation and testing, we evaluated the near-field exposure models based on a number of criteria that jointly determine the utility of the models in a policy-informing QMRA context. These criteria include ease of implementation of the model, the availability of a method to parametrize the model, and the performance of the model in the test simulations. The results of this evaluation are summarized in Table 5.
| Criterium | Two-zone model | Diffusion model | Jet model |
|---|---|---|---|
| Ease of implementation | Easy | Easy | Moderately complex |
| Parametrization of the model | No mechanistic method to underpin parametrization. Experimentally based parametrizations difficult to extrapolate to other conditions. | A fairly good data set is available from experiments. Mechanistic methods to estimate the diffusion coefficient are available. However, large variations with indoor settings is possible. | Parametrization of a standard situation is available from literature. But, there is no method given for extrapolation to different settings. |
| Comparison with well-mixed model |
|
For low turbulence conditions, the near-field concentration of the diffusion model is substantially higher than that of the well-mixed model. Predicted air concentrations decrease strongly with increasing distance from the index. For high turbulence conditions, diffusion model predictions are similar to well-mixed model predictions. | The jet model in the standard parametrization provides much higher near-field air concentrations than the well-mixed model. For the far-field, for short emission scenarios, the jet model tends to provide much lower predictions. The jet model is not well suited for longer duration emissions as it does not properly describe the effects of ventilation, which become more prominent in long duration scenarios. |
| Accuracy in predicting measurement data | The two-zone model was not able to capture the different experimental situations very well. Especially the larger volume, high ventilation situation of emission in an aircraft was not adequately described. | The model could be adjusted to describe the experimental settings of the different experiments considered. This was done by the optimization of the diffusion coefficient. In practice, a priori selection of a representative parametrization will be challenging. | Given the default parametrization, the jet model did not describe experimental data very well in the scenarios considered. |
4. Discussion
In this work, we evaluated generic exposure models for QMRA. Such models have the important merit that they are flexible, parsimonious, and may be quickly employed in the evaluation of alternative scenarios to inform policy. They may be contrasted with the more specific CFD modelling that is often used to evaluate exposure in very specific situations. CFD models are typically more accurate in that they account for the distribution of aerosol particles resulting from air movement in complex situations. CFD models, however, require a significant amount of resources to set up, run, and postprocess. This includes both modelling and measurement to define, for example, geometry and meshes, heat sources, boundary and initial flow fields, modelling turbulence and boundary layers, and the interaction of particles with surfaces. Then, CFD simulations themselves usually require a significant time to run, depending on modelling assumptions, available hardware, and scenario duration, but will typically take hours to days. Lastly, CFD models require a lot of expertise to properly set up, run, and interpret. All these factors limit the application of CFD modelling to very specific studies and render them unsuitable for profiling ranges of alternative scenarios.
In recent years, generic near-field models such as discussed in this text have been applied in the transmission risk assessment of SARS-CoV-2 in particular. Fierce et al. [33] used a turbulent diffusion model to evaluate the effects of masking and distancing in a large ensemble of simulations, using Monte Carlo simulation. The QMRA tool “CAiMIRA” [34] combines a jet model with a multizone model to cover both short distances and longer range exposures in one model. They applied the tool to study SARS-CoV-2 transmission in different occupational settings. Variability in infection risk as a function of different factors such as mask efficiency, viral load, and infectious dose was assessed by means of Monte Carlo simulation. As a final example, the CEAT tool [35] was developed for SARS-CoV-2 QMRA, in which a simplified version of the turbulent diffusion model is used to project near-field exposures. CEAT allows for a quick calculation of varied scenarios addressing variations in numbers of people gathering, proportion of infected, mask compliance in the group, surveillance testing, and transmission effectiveness of different variants. These applications demonstrate how generic NF models can be used to analyze trends and dependencies across a large set of scenarios, allowing one to generalize findings, something that would be impossible to do with dedicated measurements or CFD simulations.
The different models to describe near-field aerosol particle concentrations indoors differ both qualitatively and quantitatively when evaluated against the well-mixed modelling method. Near-field was loosely defined as within a distance of 1.5 m of the index.
The two-zone model features a pronounced difference between near- and far-field when considering short time scales (up to a few minutes). For longer time scales (up to hours), the near-field concentrations tend to deviate only very little from the well-mixed model projections in all scenarios considered.
The turbulent diffusion model shows significant differences between near- and far-field for short scenarios. The projected near-field concentrations are substantially higher than those predicted in the far-field. For continuous emissions, model behavior depends strongly on the strength of turbulence (as quantified by the diffusion coefficient). For moderate to low turbulence, a significantly elevated near-field concentration was observed, while the predicted far-field concentrations are equal to the predictions of the well-mixed model. For the high diffusivity situation, there is no clear difference between the predictions of the near- and far-field. Apparently, air turbulence in these situations suffices to bring about homogeneous mixing of indoor air. This seems to suggest that a consideration of near-field exposure to aerosol particles vis-à-vis that at a more remote distance need only be considered in situations of relatively still air. That is, with low ventilation, little influence of thermal heat sources, and not much person movement. Such situations may be assumed in conservative scenarios to evaluate the probability of infection in high-risk situations.
For the jet, both the single pulse and the continuous emission scenario showed a marked difference with the well-mixed model simulations. The near-field concentrations were more than 10 times higher than those predicted by the well-mixed model. The projected far-field concentrations, in contrast, were negligible compared with the well-mixed model predictions. The zone of elevated concentrations was limited to a distance of about 0.5 m.
When comparing the modelling methods to experimental data, it was found that the turbulent diffusion model was flexible enough to describe the data sets and scenarios considered. The jet model severely overpredicted experimental air concentrations. The two-zone model showed mixed results, describing the room data satisfactorily but failing to provide a reasonable reproduction of air concentrations in the aircraft study. The difference between these findings may partly be explained by the limitations in model parametrization of the different models. To describe experimental data, the model parameters were manually adjusted within the established domain of plausibility. For the jet model in particular, little background information on its parametrization was available, severely limiting its parametrization to a very narrow applicability domain.
Considering the results of evaluation in this work, the turbulent diffusion model seems the most promising candidate to use to describe near-field aerosol particle exposure. The model is easy to implement and use in generic scenarios. It has a clear physical interpretation, in contrast to the multizone models with the hypothetical distinction between different well-mixed zones. The domain of applicability of the model’s principle input parameter, the diffusion coefficient is reasonably well-established in contrast to the jet model. Lastly, the model was able to describe different experimental data sets successfully, as opposed to the jet and two-zone models that proved to be more limited. This observation is based on a limited number of cases. It may be that in particular instances, multizone or jet models are more suitable. For example, when modelling of occupational exposures to particulate matter [36], more standardized model parametrizations may be available, which alleviates the problems of finding appropriate model parameters. As another example, the diffusion model is not suited to explicitly describe expulsion of larger particles (sometimes referred to as “ballistic droplets”) during sneezing or coughing. In such circumstances, a jet-based model may be required.
To simplify things, we assume a single emission by coughing. According to Schijven et al. [10], the estimates of Nvirus from a single cough range over almost five orders of magnitude. For this example, we take 106 as a somewhat high estimate. We further assume vinh of 0.4 m3/h (mean of data from Schijven et al. [10]). Next, using the scenario assumptions given in Section 2.4, we find an 〈cair〉 of 0.066 1/m3 and a dose of 1096 RNA copies for the near-field in the two-zone model (with a 1-m zone radius). For the well-mixed model, 〈cair〉 is 0.0091 m−3, leading to a dose of 151 RNA copies.
Using the dose–response model for risk of illness with a dose–response parameter fr of 0.0007 as proposed by Schijven et al. [10], we find for the near-field a risk of illness of 0.5. By contrast, the well-mixed model would in this scenario estimate a risk of 0.1. Both seem substantial, but the near-field risk is considerably higher. In this case, it seems reasonable to consider the close-proximity risks separately, using a dedicated near-field exposure model. However, in a different setting, the predicted difference in risk may be much less.
When using the diffusion model in the routine risk assessment of respiratory infection diseases, an important issue of selection of appropriate values for the diffusion coefficient remains. As risk assessment of this sort is never targeted at specific (individual) situations, measurement of a scenario-representative value is not an option. As a rule, near-field concentrations are expected to be more elevated above the background (and thus more important to properly evaluate) when the indoor space volume decreases and air movement increases (i.e., with higher ventilation, stronger thermal gradients, and more movement of people). To account for variability in indoor environments, the turbulent diffusion coefficient may be varied in the simulation. For example, in smaller, low ventilation spaces where air flow is obstructed, the diffusion coefficient should be set to lower values; for higher ventilation circumstances and larger spaces such as offices, conference rooms, and public spaces, a more high-end value for the diffusion coefficient should be more appropriate. The reader is referred to the works of Foat et al. [29], Karlsson et al. [30], and Shao et al. [37] that provide indications of how the diffusion coefficient changes with natural ventilation, mechanical ventilation, number of air ducts, and room size.
For scoping assessments, a conservative low value (e.g., D = 0.002 m2/s) could be proposed. This value represents realistic low-turbulence situations, in which near-index exposures are expected to be the most significant. For more realistic assessments, however, the range of variability should be accounted for by, for example, Monte Carlo simulation. The assessor could, for example, consider a uniform distribution of diffusion coefficients in a range from 0.002 to 0.01 m2/s.
Overall, explicitly considering the distance between index and susceptible individuals in QMRA seems mostly relevant for intermittent, short-duration exposure situations, typically lasting a few minutes. Also, in this work, we found that the distance to an index over which notable elevated concentrations might arise was limited to 0.5–1.5 m. However, these specific observations may be situational and cannot be generalized without careful consideration.
5. Conclusions
Different models to describe near-field air concentrations of airborne infectious pathogens are available. In this work, multizone, diffusion, and jet models were evaluated for feasibility in policy informing QMRA. Evaluation criteria were ease of use, the availability of parameter values for generic application, and their ability to describe aerosol particle concentrations in realistic situations as mimicked in experiments. It was found that only the diffusion model was flexible enough to describe experimental data and was supported by sufficient information to allow for parametrization in a wide variety of situations. The multizone models were found easy to use but difficult to parametrize given that they lack mechanistic underpinning. The jet models are more complex and difficult to implement and use. Also, information that could be used to extrapolate between exposure scenarios was unavailable for this model. This limits the capability of this type of model to accurately simulate experimental data. The jet model may be more useful in practical risk assessment if more insight or information becomes available on how to extrapolate model parametrizations between scenarios. This would require additional research. The diffusion modelling approach seems particularly well-suited for use in QMRA. However, the pivotal parameter in this model, the diffusion coefficient, is difficult to quantify a priori for any particular scenario. In practical applications of the diffusion model, it is advised to consider a range of parameter values of the diffusion coefficient as an uncertainty margin, for example, in a probabilistic evaluation.
Whether elevated near-field concentrations will actually lead to increased infection risks depends on various additional aspects, for example, the presence of other exposure pathways such as fomites of ballistic droplets and the pathogen’s infectivity. Generic, simple to use near-field exposure models such as described in this work will be helpful to quickly identify situations in which a detailed consideration of close proximity infection risks from airborne pathogens is warranted.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
This study was funded by the Dutch Ministry of Health, Welfare and Sport through the Pandemic Preparedness Program (Grant Number V/170026/24/AT).
Acknowledgments
We acknowledge Frank Verhoeven, Medspray, Enschede, the Netherlands, for kindly providing the measurement data of the aerosol dispersion in a closed room that was used in this work to evaluate model performance. We would furthermore like to thank Floor Biemans, Alvin Bartels, and Matthijs de Winter for reading and reviewing the manuscript.
Open Research
Data Availability Statement
Data is available on request from the authors.




