Considerations for Computational Fluid Dynamics Studies of Cleanrooms Exceeding Classical Indoor Air Simulations: A Systematic Review
Abstract
We provide a systematic review of the literature on computational fluid dynamics (CFD) in the cleanroom sector. The objective is to provide simulation engineers with an overview of studies in the field of cleanroom simulation, as well as to identify the most commonly used simulation parameters. Our findings indicate a persistent preference for the k − ε model for turbulent flow situations, although recent studies suggest a shift toward more sophisticated models, such as the RNG k − ε and SST k − ω. This reflects advancements in the available computational power made in the past years. Our analysis of particle tracking models indicates a clear preference for the Euler–Lagrange method over the Euler–Euler method. Moreover, the analysis of inlet models used indicates that geometrically resolved diffusers are preferred over simplified models. As every simulation study requires proper validation, full-scale experiments are clearly preferred in the reviewed studies. A best practice guide is distilled out of previous studies to provide a meaningful starting point for future CFD studies in the cleanroom sector.
1. Introduction
Cleanrooms represent a significant aspect of production environments across numerous industrial sectors. A key aspect of a cleanroom is the contamination of the air with particles: The DIN EN ISO 14644 [1] is the most important regulation in the field, and it is also the basis for other guidelines, for example, the EU Guidelines for Good Manufacturing Practice (EU-GMP) for Medicinal Products for Human and Veterinary Use [2]. In order to comply with the relevant standards, cleanrooms are equipped with heating, ventilation, and air conditioning (HVAC) systems to tightly control airflow and consequently airborne contamination. Next to the HVAC system, airflow within a cleanroom is influenced by a number of factors, including the movement of personnel and internals, thermal effects, and other sources of interference, for example, equipment with fans or rotating internals. This, together with the fact that air flow control in cleanrooms is of extreme importance, is the reason why the airflow within cleanrooms and cleanroom design has been the subject of numerous studies.
System modeling plays a significant role in the planning and optimization of contemporary HVAC systems and the corresponding ventilation strategy. Here, we focus on modeling the airflow in these systems, for which various methodologies exist. A highly specialized application of HVAC systems is in the domain of cleanrooms: The primary objective of cleanrooms is to maintain extremely low levels of particulate and microbial contamination in order to ensure product quality and safety. Similarly, in (bio)safety laboratories, particulate contamination has to be controlled with the main objective of safety for staff members, and these laboratories can hence also be seen as some kind of cleanroom. In some applications, for example, semiconductor manufacturing, molecular contamination (i.e., gasses or vapor) has to be tightly controlled due to process and safety reasons.
Cleanrooms play a pivotal role in numerous industries, including pharmaceuticals, biotechnology, semiconductor manufacturing, aerospace, and research. Cleanrooms are increasingly used in other manufacturing disciplines, for example, components for cars, or battery manufacturing [3, 4]. The latter production processes require cleanrooms because of two factors: (i) Product contamination must be avoided (batteries consist of thin layers of particles, and contaminants may cause defects), and (ii) personnel must be protected due to the composition of the involved particles. In addition to the particle control mechanisms present in cleanrooms, these facilities differ in several ways from classical HVAC systems. For instance, the air change rate (ACR) of cleanrooms is typically higher, with rates varying from 10 to 160 for nonunidirectional cleanrooms [5]. The direction of airflow in a cleanroom can be unidirectional, meaning that a parallel stream of air flows through the entire cross-section of the room, or nonunidirectional. In order to achieve this kind of flow, unidirectional cleanrooms are typically equipped with perforated floors. We will come back later to specific components in cleanrooms and continue with a review of modeling studies of HVAC systems.
In order to simulate the airflow of HVAC systems, a variety of models and approaches are typically used. In 2009, Chen [6] provided an overview of the methodologies used to predict the ventilation performance of buildings. The review revealed that 70% of the literature reviewed employed computational fluid dynamics (CFD) models, with large- and full-scale models representing the next most common approaches. Although large- and full-scale models were primarily used for the validation of CFD models [6], Aflaki et al. conducted a comparative analysis of various methodologies employed for building airflow simulations, including analytical, empirical, zonal, and CFD models. The authors recommend the use of CFD over zonal and empirical models, yet acknowledge the necessity for further research on the selection of turbulence models [7]. In a more recent study from 2023, Nugrahanti et al. also compared different building simulation models for indoor airflow: the multizone, the zonal model, and CFD. It is demonstrated that CFD models yield the most comprehensive results for indoor airflow, although they require the most computational resources and are the most intricate to utilize [8]. In a previous review on CFD for room air in 2015, Nielsen demonstrated the relevance and necessity of CFD in indoor air applications. He postulates that with the advance of increasingly powerful computational resources, more intricate indoor airflow issues can be addressed, including those related to airborne particles and energy-efficient ventilation strategies [9]. Although cleanrooms are not explicitly addressed, they are included within the scope of the complex problems identified by Nielsen. These studies demonstrate that CFD is the optimal methodology for modeling HVAC systems in general. However, as it is the most complex tool to use, it has been the subject of numerous reviews and studies.
In their 2012 study, Ramponi and Blocken examined the influence of various computational parameters on the efficacy of natural cross-ventilation strategies for buildings. The parameters under investigation include the mesh element size and the turbulence model. As the indoor air flow is significantly influenced by the external air flow, a comparison to cleanrooms is not possible [10]. Liu et al. conducted a comprehensive review of studies examining the use of CFD models for the analysis of personalized ventilation systems in indoor built environments. A particular focus is placed on the accuracy of computational thermal manikins [11]. Personalized ventilation systems deviate significantly from classical room ventilation systems. Consequently, a straightforward extrapolation of the outcomes to other indoor air simulations or even cleanrooms without further verification is suboptimal. In their comparison of different simulation models, Nugrahanti et al. also provide a brief overview of studies in the field of indoor air simulation, though no studies of cleanrooms are included [8]. Marashian et al. conducted a review of CFD methods for indoor environmental simulations, analyzing 25 articles on turbulence models, geometry, and meshing [12]. The specific requirements for cleanroom ventilation systems are not addressed in this analysis. Unfortunately, important work on turbulence models (e.g. Zhang et al. [13]) has also not been taken into consideration. Tsang et al. provide a summary of the most commonly used turbulence models in CFD studies in their review of studies on airborne transmission in hospitals [14]. The focus is set on hospitals and therefore not specifically for cleanrooms. There was no review found that specifically deals with the special case of CFD of cleanrooms including heat transfer (e.g., effects of mixed convection) and airborne particle transport.
- •
determine whether the flow is expected to be laminar, low turbulent, or fully developed turbulent.
- •
determine which turbulence model should be selected.
- •
ascertain whether the flow is expected to be unsteady or steady.
- •
ascertain whether the flow is expected to have one, two, or several solutions.
- •
determine whether the flow can be considered two-dimensional (2D) or symmetrical, and if this effect can be used?
In a previous publication, Sørensen and Nielsen also provide recommendations for the quality control of CFD studies [15]. Subsequently, each study should incorporate a mesh independency study, a wall layer with an appropriate y-plus value, a sufficiently converged solution, and double precision numerical calculation. Moreover, for scientific publications, it is recommended that the aforementioned quality parameters are thoroughly documented. Also, the overall simulation setup should be described in sufficient detail to enable the simulation to be reproduced. Finally, it is recommended that the simulation be validated against experimental data or similar cases [15].
The publication most relevant for our current contribution is Bhattacharya et al. [16]: In their review, they identified that approximately one quarter of publications on cleanrooms are within the field of CFD. The use of CFD simulation allows for the cost-effective evaluation of alternative cleanroom designs, which is of course crucial for the success of a new cleanroom project. Early simulations tailored specifically for cleanrooms were conducted in the late 1980s and early 1990s (e.g., [17, 18]). Even with relatively coarse meshes, good agreement between simulation and experiment was found in these studies. This initial application illustrates the significance and precision of CFD in cleanroom applications.
Also, Nielsen provides overall guidelines [9] and quality control [15] for CFD of indoor air; The special needs of cleanrooms are not considered. This also accounts for the aforementioned studies that deal with different kinds of indoor airflow [8, 10–12, 14] but not the case of cleanroom airflow. The airflow in cleanrooms differs strongly from other indoor environments. Dependent on the type of cleanrooms, the airflow can be (i) nearly laminar, with a constant velocity in the horizontal cross-section of the room, with a flow direction from the ceiling to the floor (unidirectional air flow) or (ii) turbulent, with mixing of room air with supply air and an overall flow direction (e.g., ceiling to floor or side to side) but with local changes in the flow directions through the cross-section of the flow (nonunidirectional air flow). This special airflow in cleanrooms is crucial to its function and therefore sensitive to disturbances through personnel or moving machinery inside the room or through heat sources that yield convective air flows. To achieve the airflow in cleanrooms, special room and HVAC design is needed. Compared to normal indoor air environments, cleanrooms have more supply air inlets and exhaust air outlets (depending on the type of cleanroom the whole ceiling or just part of it is equipped with inlets) and, for unidirectional cleanrooms, the need for a perforated floor. Both are not considered in typical indoor environment CFD studies. Additionally, the flow velocity and ACRs are significantly higher than in normal rooms. Though Bhattacharya et al. [16] review studies dealing with CFD of cleanrooms, they do not go into detail on how the simulations were conducted, for example, which boundary conditions, turbulence model, or particle transport methods were used. The study focuses on giving an overview of conducted studies in the field of cleanroom ventilation and understanding ventilation systems and their correlation with particle contamination and energy efficiency. It is shown that the trend in recent cleanroom studies shifts toward energy efficiency through system optimization at constant cleanliness. It further concludes that simulations are crucial for future cleanroom designs. Unfortunately, no guidelines or further insight on CFD for cleanrooms are given. In summary, no comprehensive guidance is offered on the methodology for conducting a CFD study in the field of cleanrooms.
To date, no review has specifically addressed the unique requirements of CFD models for cleanrooms compared to classical HVAC systems. Therefore, the primary objective of this paper is to enhance the accessibility of CFD for cleanrooms for engineers and scientists via a set of guidelines: These guidelines should (i) enhance the utilization of CFD for cleanroom applications, for example, for design and troubleshooting purposes, (ii) and allow a science-based optimization of cleanrooms, for example, with respect to their energy efficiency. A secondary objective is to highlight research needs that are key for the further development of CFD tools for cleanroom applications: On the one hand, the availability of a comprehensive guideline will help nonexperts in the field to judge the feasibility of CFD studies for a specific cleanroom application. On the other hand, CFD experts without a background in cleanroom application will benefit from the guideline by pointing them to commonly used turbulence or particle transport models. Consequently, for those engaged in the development of a cleanroom flow simulation, our current review also offers an overview of the current state of the art. We think that both aspects will further enhance the accessibility of CFD for cleanrooms, which is certainly crucial for industry sectors in which cleanrooms are new (e.g., battery manufacturing).
After describing the methods of the literature review in Section 2, we structured this paper chronologically through the typical steps of a CFD simulation. Section 3 describes the setup of the simulation. First, it provides an (Section 3.1) overview of the reviewed studies and continues with the (Section 3.2) mesh requirements, (Section 3.3) turbulence modeling, (Section 3.4) porous walls, (Section 3.5) particle transport, and (Section 3.6) inlet models. The following Section 4 deals with postprocessing the simulation results. Section 5 focuses on the (Section 5.1) verification and (Section 5.2) validation process as well as the (Section 5.3) calibration of model parameters. The key findings and a best practice guideline are summed up in the conclusion of this review. Additional insight can be found in the Supporting Information section. Supporting Information 1 is the literature matrix containing all reviewed studies, Supporting Information 2 gives further insight on porous walls by providing an analytical solution for the flow in channels behind a porous wall and optimal porosity distribution, and Supporting Information 3 shows the flow below a raised floor in a video animation.
2. Methods
A comprehensive literature search was conducted, combining both unsystematic and systematic approaches. A preliminary search was conducted on Google Scholar to identify any existing literature on the subject. Furthermore, all pertinent publications concerning the CFD of cleanrooms, as identified through the recent literature review of Bhattacharya et al. [16], were considered. This initial examination of the literature yielded 33 relevant studies, which provided a basis for formulating constructive search strings for a systematic literature search.
The initial search string encompasses all studies that include the keywords “(CFD or fluid dynamics) and cleanroom,” as well as the various forms of punctuation used to denote this phrase, including “clean room”. The second string was employed to encompass studies in which the term CFD was not utilized. Consequently, the string was modified to read “(simulation or modeling or numerical) and cleanroom and airflow”. The additional keyword “airflow” was necessary to narrow the results to a more manageable set. A comprehensive literature search was conducted using three different databases: Science Direct, Scopus, and Web of Science. Table 1 provides an overview of the search strings, databases, and results utilized. The list is presented in chronological order. This is the reason for the considerable number of duplicates in the later searches. In total, 103 studies out of 514 hits were found to be relevant for our current review. The 514 hits included 207 duplicates or studies that were found in at least two databases. A total of 83 studies found could not be considered for this review either because (i) they were hidden behind a paywall or (ii) no full text was available (e.g., conference contributions). The pertinent data from the studies, including simulation parameters, were compiled into a matrix, which is included in Supporting Information 1. For a more comprehensive examination of various CFD closures (e.g., turbulence or particle and vapor transport), not only cleanroom studies are considered. In addition to the specific case of cleanrooms, studies of indoor air and enclosed environments are also considered. An overview of the goals of the reviewed studies, the type of cleanroom flows, and the industry the cleanroom is used for is given in the next chapter followed by an investigation of the used simulation parameters.
| Database | Search string | Date mm/dd/yyyy | Results | Doubles | Relevant |
|---|---|---|---|---|---|
| — | Unsystematic search | 01/10/2024 | 27 | 0 | 27 |
| Science Direct | Title, abstract, keywords: (CFD OR “fluid dynamics”) AND (cleanroom OR “clean room”) | 12/04/2024 | 30 | 10 | 12 |
| Web of Science | TS = (((CFD) OR (fluid dynamics)) AND ((cleanroom) OR (“clean room”))) | 12/04/2024 | 74 | 18 | 22 |
| Scopus | TITLE-ABS-KEY ((CFD OR “fluid dynamics”) AND (cleanroom OR “clean room”)) | 12/04/2024 | 191 | 58 | 23 |
| Scopus | TITLE-ABS-KEY ((simulation OR modeling OR numerical) AND (cleanroom OR “clean room”) AND (airflow)) | 12/04/2024 | 141 | 66 | 24 |
| Web of Science | TS = (((simulation) OR (modeling) OR (numerical)) AND ((cleanroom) OR (“clean room”)) AND (airflow)) | 12/04/2024 | 66 | 57 | 0 |
| Science Direct | Title, abstract, keywords: (simulation OR modeling OR numerical) AND (cleanroom OR “clean room”) AND (airflow) | 12/04/2024 | 37 | 30 | 0 |
3. Flow Simulation
3.1. Overview
The objective of the studies reviewed varies in detail, however, can be grouped into the following four categories: (i) airflow, (ii) design study, (iii) particle distribution, and (iv) thermal influences (compare Figure 1a). The category (i) “airflow” refers to the study’s exclusive focus on the movement of air in a cleanroom, without incorporating additional models such as those pertaining to particle transport or thermal effects. These publications date back to the 1980s and have an average age of 15 years. Moreover, the aforementioned studies do not include any design or operational variations within the cleanroom. The objectives of the studies include the movement of objects, a comparison of different models and a detailed examination of flow characteristics [13, 17–54].
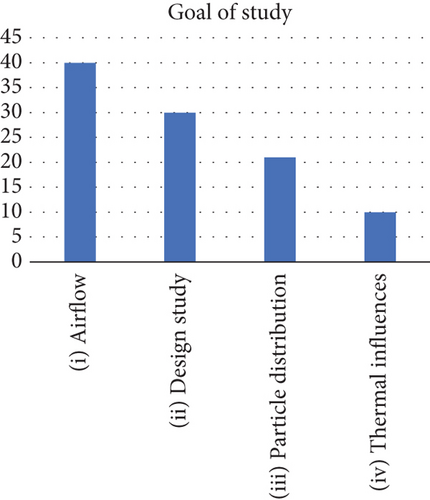
In the context of category (ii) “design study,” the implementation of various cleanroom configurations (i.e., the shape of internals or equipment) has been in the focus. The authors of such studies (average age 11 years, earliest 1992) have then observed how these design changes influence the flow within the cleanroom. The objective of this study was to optimize existing rooms or validate different inlet and outlet configurations [55–85].
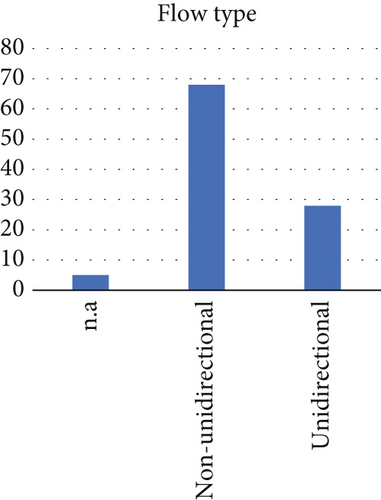
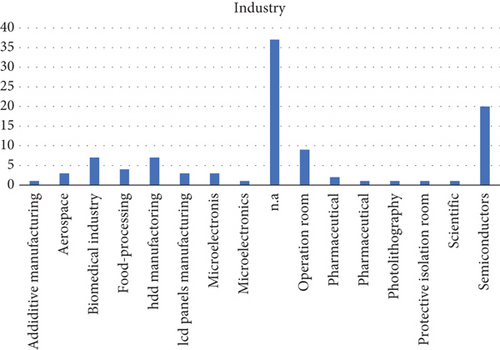
Furthermore, more complex (but fewer) studies incorporated particle distribution analysis [86–105] (Category iii; average age 12 years, earliest 1992) and thermal effects (Category iv; average age 15 years, earliest 1979) [106–115]. Approximately two-thirds of the clean rooms under consideration had nonunidirectional air flow (compare Figure 1b). With regard to the application of the cleanroom, the majority of studies focused on industrial cleanrooms used in the manufacture of semiconductors, hard disk drives, and other electrical products (compare Figure 1c). The second most represented category was biological cleanrooms, which include operating rooms and rooms dedicated to the biomedical industry. Approximately one-third of the studies did not clearly define the purpose of the room.
In the following section, the studies are examined with respect to specific simulation parameters and models. This is done in order to distill all relevant parameters utilized in such simulations. The findings will be employed to formulate recommendations for future simulation studies in terms of meshing, turbulence modeling, particle transport modeling, and boundary conditions.
3.2. Mesh Requirements
A proper mesh is essential to obtain meaningful simulation results. Consequently, a mesh study is a critical component of any simulation project to verify the independence of the solution from the mesh. This approach allows for the identification of an optimal balance between simulation accuracy and calculation time. Although the increase in computational power allows the generation of finer meshes with more elements, there is no apparent trend in the data (Figure 2). Also, our linear regression analysis indicates only a slight decrease in the element size and an increase in element number. The majority of meshes comprise fewer than four million elements, with an average element size of approximately 100 mm. It is assumed that the majority of meshes have refinements in critical regions, and thus, the element size within the room is considerably larger than 100 mm. Unfortunately, there is often a lack of information about the mesh other than the number of elements. Only in some cases, information about the mesh metrics and the y-plus value is provided.
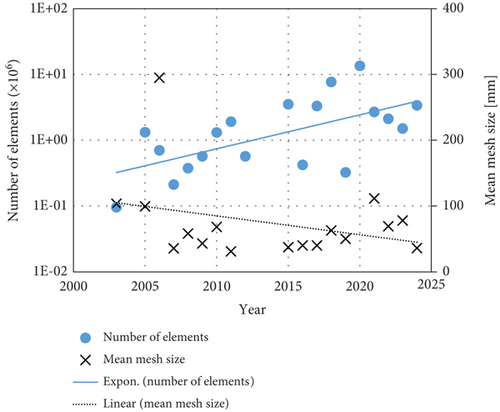
A mesh dependency study was documented in approximately half of the studies. In the majority of cases, no further information was provided beyond the number of elements for the considered meshes. The permitted error in the mesh varies from 0.3% to 10%, with an average of 3.1% and a median of 2%. However, only 11 studies provided such detailed information regarding the mesh dependency of the results. Even fewer provided metrics for the mesh, such as skewness ory-plus values, which precludes any significant conclusions on suitable values. One study, however, did investigate the y-plus value in particular: In his review of turbulence models for CFD in built environments, Serra also paid particular attention to the y-plus value when using the k − ε − v2 − f turbulence model without special wall treatment [116]. He concluded that a y-plus value below 1 does not guarantee grid independence or reliable results. In the case of displacement ventilation, a y-plus of less than 1.15 × 10−2 was found to be necessary [116]. As displacement ventilation is typically buoyancy-driven and exhibits low velocities, a direct transfer of these y-plus values to cleanrooms is not feasible. However, his work underscores the necessity for a comprehensive mesh independence study, since potentially low y-plus values are needed.
3.3. Turbulence Modeling
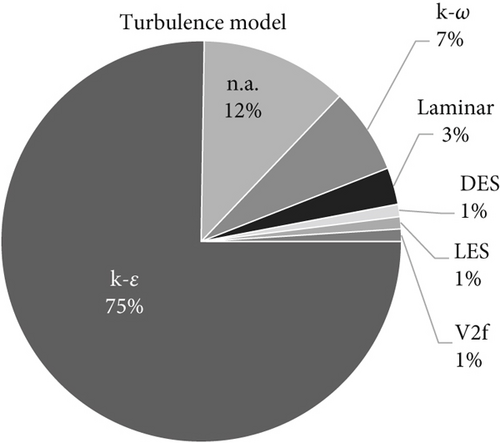
In the context of RANS simulations, there are a number of turbulence models available, each with their own specific advantages and disadvantages. Two models that are widely used in the field of CFD are the SST k − ω model [117] and the k − ε model [118] with its variants the RNG k − ε model [119] and the realizable k − ε model [120]. The k − ε model was developed by Launder and Sharma 1972 [118] and is one of the earliest and most widely applied turbulence models in RANS simulations. The model solves for the turbulent kinetic energy (k) and its dissipation rate (ε), thereby providing a means to quantify the turbulent viscosity of the flow field. The model’s primary development focused on fully developed turbulent shear flows, and its numerical robustness and computational efficiency have been demonstrated in such contexts. However, the formulation of this model is predicated on the assumption of isotropic turbulence and relies on empirical constants and wall functions, which limits its accuracy in flows exhibiting adverse pressure gradients, rotation, or separation. The width of applicability of the k − ε model was demonstrated by Launder and Spalding [121]. The RNG (Renormalization Group) k-ε model was developed to extend the applicability of the standard formulation to more complex flows. The implementation of statistical methods (i.e., the renormalization group theory) has led to the enhancement of improved expressions for turbulent transport [119]. The RNG model modifies the ε-equation to account for effects of mean strain rate and introduces an analytical formula for the turbulent viscosity, which varies with local turbulence properties. This allows it to better represent flows characterized by strong streamline curvature, rapid strain, and swirl conditions. The realizable k − ε model, as proposed by Shih et al. [120], offers an alternative formulation that satisfies certain mathematical and physical constraints, known as realizability conditions. These conditions are not guaranteed in the standard k-ε model; however, enabling the realizable model ensures that the modeled Reynolds stresses do not result in nonphysical behavior, such as negative normal stresses or excessive shear. The model modifies the ε-equation and introduces a variable model coefficient Cμ, calculated from the local flow field rather than being a fixed empirical value. This enhancement in model adaptability to flow conditions is particularly beneficial in predicting flows involving rotation, separation, and recirculation. The k − ω SST model, developed by Menter [117], employs a hybrid approach that integrates the k − ω model near walls and the k − ε model in the free stream. The motivation behind this approach was to exploit the superior near-wall resolution of the k − ω formulation (developed in 1988 by Wilcox [122]) while avoiding its sensitivity to inlet conditions in the outer region. The blending is accomplished through a switching function and includes a shear stress limiter. This limiter prevents overprediction of turbulent transport in regions characterized by adverse pressure gradients. The incorporation of this limiter significantly enhances the model’s capacity to predict flow separation and heat transfer. The SST k − ω model does not rely on wall functions, which makes it particularly useful in simulations where resolving the viscous sublayer is feasible.
In 1989, Murakami and Kato were one of the first to successfully simulate a cleanroom with nonunidirectional airflow using the k − ε model [17]. But since then, there are new possibilities in CPU power, and new turbulence models have evolved. The selection of a turbulence model has a significant impact on the performance and results of a CFD study. Consequently, selecting an appropriate turbulence model is not a simple process, and it has been the subject of numerous studies in various fields of engineering. For the interested reader, the turbulence models are briefly explained in different literatures (e.g., [13, 123]) and in CFD code documentations. The following section presents a review of studies that have compared different turbulence models in cleanrooms. Additionally, studies pertaining to analogous cases, such as convective or turbulent flow in closed rooms, are reviewed.
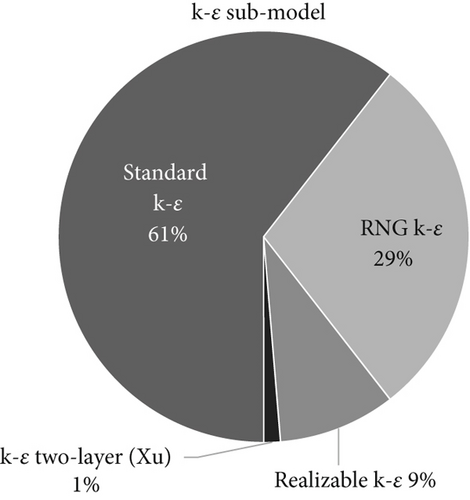
In a study utilizing a simulation of a cleanroom for food processing, Rouaud and Havet compared the standard and the RNG k − ε turbulence models and the influence of the turbulence intensity on the flow field. The ISO Class 7 cleanroom with two ISO Class 5 work areas was considered to be in a steady state. Although the RNG model required a greater number of iterations (due to the lower Courant number employed), more accurate results were attained. A clear recommendation is given for the RNG k − ε model with the remark that the quality of the numerical prediction depends on the turbulence intensity [24]. In their study regarding the airflow of different air supply inlets in cleanrooms, Whyte et al. also noted that there is currently no established best turbulent model. The researchers compared the standard, realizable, and RNG k − ε models with the k − ω model for a four-way diffuser and a filter-fan unit (FFU) as an air supply inlet. It was concluded that the k − ω model did not provide reliable results. With regard to the four-way diffuser, the three k − ε models yielded nearly identical results, with the results obtained with the RNG differing for the FFU. The realizable and standard k − ε models yielded nearly identical results in both cases. For their subsequent simulation, they proceeded with the standard k − ε model [64]. In addition to simulating the recovery period of an ISO 5 cleanroom, Pourfarzaneh et al. also evaluated the differences between large eddy simulation (LES), detached eddy simulation (DES), and SST k − ω turbulence models. The DES method yielded the most accurate results. In comparison to the results of a previous study, the SST k − ω method demonstrated a notable improvement in accuracy relative to the RNG k − ε method [101]. In her doctoral thesis, Hofer compared various turbulence models for use in unidirectional cleanrooms with heat sources through convection. To capture the convection effects, a y-plus value smaller than 1 together with an inflation layer was used in the meshing process, though no further details on the wall treatment of the turbulence models were given. She concluded that the k − ω models overrate the effects of buoyancy. The realizable k − ε model yielded the most favorable outcomes when compared to the standard k − ε, standard k − ω, and SST k − ω models [114]. In a recently published study, Permana and Wang conducted a comparative analysis between the standard k − ε model and the RNG k − ε model. The RNG k − ε model yielded a smaller error in the simulated air temperature compared with the standard k − ε model. It is therefore recommended that the RNG k − ε model is used for CFD simulations of cleanrooms [80]. Table 2 gives an overview of the recommended turbulence model of the different studies. The RNG k − ε model is the only model recommended by more than one study but was only compared to the standard k − ε model in both cases. However, as only one study recommends a model not from the k − ε group (namely, the SST k − ω model), there is a trend toward k − ε models, which is visible.
| Case | Models used | Recommendation | Study |
|---|---|---|---|
| Nonunidirectional cleanroom |
|
RNG k − ε | Rouaud and Havet [24] |
| Nonunidirectional cleanroom |
|
Standard k − ε | Whyte et al. [64] |
| Unidirectional cleanroom |
|
SST k − ω | Pourfarzaneh et al. [101] |
| Unidirectional cleanroom |
|
Realizable k − ε | Hofer [114] |
| Nonunidirectional cleanroom |
|
RNG k − ε | Permana and Wang [80] |
As mentioned before, studies not specifically dealing with cleanrooms but with analog cases are also reviewed: In 1995, Chen compared various k − ε models for use in indoor air simulations, including the standard k − ε, the low-Reynolds-number k − ε, the two-layer k − ε, the two-scale k − ε, and the RNG k − ε model. He considered cases involving natural, forced, and mixed convection, as well as impinging jet. The RNG k − ε model is recommended as the most stable and most accurate model [124]. To determine the effectiveness of different turbulence models for turbulent flow in enclosed environments, Arun and Tulapurkara performed a simulation of flow in a small rectangular box (0.4 m × 0.4 m × 0.6 m). In their study, the SST k − ω model showed better quantitative agreement with the experimental data compared to the RNG k − ε and Reynolds stress models. It is recommended that the SST k − ω model be used for simulation of isothermal turbulent flow through enclosures [29]. In the second part of a two-part series, Zhang et al. conducted a comparative analysis of turbulence models for closed air volumes. While the focus was not on clean rooms per se, the results can be applied to such environments. A variety of cases were considered, but those most relevant for the simulation of cleanrooms are forced and mixed convection. In this case, the V2f-dav model demonstrated superior performance compared to the RNG k − ε model. Nevertheless, the V2f-dav model necessitates a twofold increase in calculation time [13]. More details on the investigated turbulence models by Zhang et al. and their performance is given in Table 3. Teodosiu et al. compared different turbulence models in a room with a single supply air inlet in the ceiling and a single air exhaust on the bottom of a wall. In comparison to the data obtained from the measurements, the k − ω models demonstrated superior performance in relation to the k − ε models. It is recommended that the transition SST k − ω model should be employed [125]. Mičko et al. compared the RNG k − ε model with the k − ω model in their analysis of flow in an operating room. The authors validated their simulation with particle image velocimetry measurements and found that the k − ω model provided more accurate results [74]. In 2023, Serra compared various turbulence models for typical mixing and displacement ventilation strategies. A laboratory-scale office room was constructed and equipped with a heat source. The optimal results were achieved with the k − ε RNG VisEff and k − e − v2 − f(LKM) turbulence models [116]. Table 4 gives an overview of the conducted and recommended turbulence models for each study. Each study recommends a different turbulence model with a slight shift toward the k − ω model group.
| Case | Compared items | RNG k − ε |
SST k − ω |
V2f- dav |
DES | LES |
|---|---|---|---|---|---|---|
| Forced convection | Mean velocity | A | C | A | C | A |
| Turbulence | B | C | B | C | B | |
| Mixed convection | Mean temperature | A | A | A | B | A |
| Mean velocity | B | B | A | B | B | |
| Turbulence | A | D | A | B | B | |
- Note: A = good, B = acceptable, C = marginal, D = poor.
| Case | Models used | Recommendation | Study |
|---|---|---|---|
| Indoor airflow with convection and impinging jet |
|
RNG k − ε | Chen [124] |
| Flow in rectangular box |
|
SST k − ω | Arun and Tulapurkara [29] |
| Convection in closed air volume |
|
V2f-dav | Zhang et al. [13] |
| Indoor airflow |
|
Transition SST k − ω | Teodosiu et al. [125] |
| Operating room |
|
k − ω | Mičko et al. [74] |
| 1:30 lab-scale room with heat source |
|
|
Serra [116] |
The comparisons of turbulence models show that there is no single turbulence model recommended by several studies. The choice differs with each special case. This underlines the necessity to use and compare different turbulence models when conducting a CFD study for cleanrooms. Adding studies that conducted cleanroom CFD without a comparison of turbulence models, a clearer trend is visible: the k − ε model is the most commonly used group of turbulence models, followed by the k − ω model (compare Figure 3). Among the k − ε models, the standard model was employed with greater frequency than the RNG and realizable versions. This leads to the question of why different turbulence models have been employed. The majority of studies did not address this question. If a source for the selection of the turbulence model was provided in a previous study, the results differed significantly across studies. In total, 17 distinct sources were referenced for the selection of the turbulence model. The two most frequently referenced studies were those conducted by Launder and Spalding [121] and Chen [124].
3.4. Porous Walls
Porous walls or baffles are essential for cleanrooms, since the air distribution in a room and among multiple inlets/outlets is often decisive of the success of a flow design. These walls are modeled as permeable membrane (patch) in a CFD simulation that features a pressure drop depending on the local flow velocity. Of specific interest to the cleanroom community are (i) so-called “raised floors” (i.e., perforated floors that enable a vertical extraction from a room via a porous wall) and (ii) large porous baffles to distribute the flow at the inlet (and similarly at the outlet in analogy to a raised floor). Modeling of porous regions (i.e., the pressure drop in a volume) in CFD simulations of cleanrooms can be done similar to what is done for porous walls. An example would be models for heat exchangers. However, such models are of significantly lower importance due to the rare need to account for them in a cleanroom or cleanroom system. Next, we briefly summarize the analytical description of pressure drop at a porous wall using the example of a raised floor. Further details related to the derivation of these equations are provided in Supporting Information 2.
A small pressure drop at porous walls (in this case, a raised floor) typically leads to low energy consumption, but a poor (i.e., inhomogeneous) flow distribution. In contrast, a large pressure drop requires more energy but yields a more homogeneous flow distribution. For a simple one-dimensional raised floor problem, an optimum porosity distribution can be derived that yields low pressure drop and a (theoretically perfect) homogenous vertical velocity distribution [126]. Unfortunately, due to the fact that standard floor systems are often used, this optimal porosity distribution can be realized only approximately in most cases. Zielke [126] provides the derivation of the optimal porosity distribution, which suggest the pressure loss coefficient ζ to vary quadratically with the lateral position in the channel (see Supporting Information 2 and Section 14.2 of Zielke [126] for details).
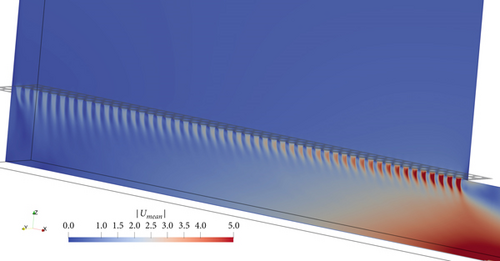
Interestingly, the size and shape of the openings in the porous walls do not play a role in these correlations. Supporting Information 2 provides comprehensive details regarding the comparison of two simulation approaches applied to a porous wall (in this case, a raised floor system): (i) a LES case and (ii) a Reynolds-averaged Navier–Stokes (RANS) case. The analysis focuses on the ability of each method to capture the dynamics of airflow and pressure distributions in the context of cleanroom environments.
A highlight of this analysis is shown in Figure 4: Here, we show the results of a highly resolved LES-type simulation. The raised floor (i.e., a porous wall) has been resolved in these simulations, that is, the holes in the raised floor are represented geometrically correct. As can be seen, there is significant turbulence beneath the raised floor, which is driven by tiny air jets extending from each hole. Interestingly, these jets penetrate deeper at the left corner of the channel, that is, at small x values, compared to the relatively small penetration near the outlet of the channel. As is shown in Supporting Information 2, these LES predictions are in surprisingly good agreement with RANS-based simulations with an unresolved porous wall model (i.e., the pressure loss coefficient model presented above).

3.5. Particle Transport
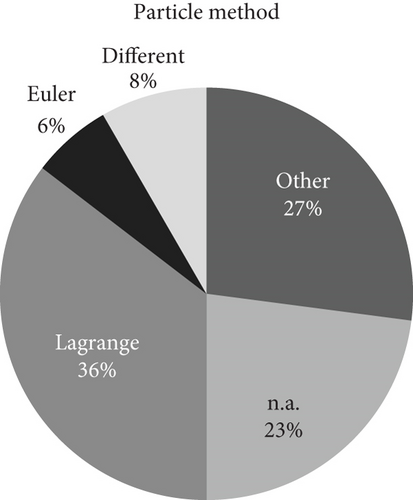
As with the turbulence models presented in Section 3.3, there are various methods for incorporating particle transport into the airflow. Two primary approaches exist for particle tracking in room airflows: the Eulerian method and the Lagrangian method. These two methods have been extensively studied for their applicability in indoor air CFD. The two models differ strongly in their basic approach: As the Lagrangian method considers each single particle for its calculation, the Eulerian method treats the particle phase as a continuum. A comprehensive overview of the two models is provided by Zhang and Chen [89]. As with the turbulence models before, not only cleanroom studies are considered but also studies with transferable flow characteristics.
Already in 1992, Kuehn et al. conducted a study on particle transport in a microelectronics cleanroom. In their 2D simulation, they observed no significant difference between the Eulerian and Lagrangian modeling approaches [18]. In 2002, Loomans and Lemaire conducted a comparative analysis of the two models in a nonunidirectional cleanroom. The authors concluded that the Eulerian model is a useful alternative to the Lagrangian model, but that it also has drawbacks in terms of precision. Though there is no further information on the settings except the particle sizes used (0, 10, and 50 μm) [127], Zhang and Chen compared the two models with regard to their suitability for use in enclosed spaces, specifically a nonunidirectional cleanroom, a room with displacement ventilation, and an aircraft passenger cabin. For the cleanroom case, they investigated monodisperse particles with a size of 0.31 μm. Both the Eulerian and Lagrangian methods were in reasonable agreement with experimental data. The use of a different number of particles showed that the Lagrangian method needs at least 100,000 particles for a statistically stable solution in this case. Though higher particle counts can yield more reliable results for the Lagrangian approach, it comes with a higher CPU cost. Summarizing all three cases, the Eulerian method required less computational time. In contrast, it presents a challenge in handling the unsteady case due to small time steps required. Given that the Lagrangian approach demonstrated superior performance in unsteady simulations, it is recommended for future applications [89]. Saidi et al. conducted a comparative analysis of the Lagrangian and Eulerian approaches for aerosols, examining three case studies: free diffusion, 2D parallel flow, and 3D expanding flow. The authors of the study concluded that the Eulerian approach is not suitable for problems with low concentrations of particles and short time scale problems. For the 3D expanding flow case, both approaches yielded reliable results when the number of released particles was high enough (i.e., 20,000 in this case). In the other two cases, a minimum particle count of 100,000 was necessary for the Lagrangian approach to have similar results as the Euler method [128]. In 2016, Eslami et al. conducted a comparative analysis of the Eulerian and the Lagrangian methods in a cleanroom with varying inlet and outlet positions. For the Lagrangian method, 60,000 particles with a diameter of 10 μm are considered. The researchers were unable to identify any significant discrepancies in the outcomes of the two models when simulating a steady state. Consequently, no recommendation was provided regarding the optimal model to employ [67]. The most recent comparison was conducted by Pourfarzaneh et al. In their study, they tested the Eulerian and Lagrangian approaches with different turbulence models. By stepwise increasing the number of particles for the Lagrangian approach, the numerical error was minimized analogously to a typical mesh independency study. This resulted in 364,715 particles. The study concluded that the Eulerian model yielded superior overall results, with the exception of LES and DES simulations. Conversely, the Lagrangian approach demonstrated superior accuracy in predicting particle concentration [101]. As hinted by the results of Pourfarzaneh et al. [101], the results of particle simulations also depend on the choice of turbulence model. In the case of an enclosed room with single-sided opening, Muto et al. investigated that when conducting the Laplacian approach, their LES simulation had better agreement with theoretical data than the employed RANS Low-Re k − ε model [129]. While half of the studies did not examine a difference in both approaches, the other half favored the Lagrange method (compare Table 5). An overview of the advantages and drawbacks of different approaches, together with recommendations, is given in Table 6.
| Preferred method | Case | Source |
|---|---|---|
| No difference | 2D simulation of cleanroom | Kueh et al. [18] |
| Lagrange | Nonunidirectional cleanroom | Loomans and Lemaire [127] |
| Lagrange | Nonunidirectional cleanroom | Zhang and Chen [89] |
| Lagrange | Parallel 2D-flow, expanding 3D-flow, free diffusion | Saidi et al. [128] |
| No difference | Nonunidirectional cleanroom | Eslami et al. [67] |
| Case dependent | Nonunidirectional cleanroom | Pourfarzaneh et al. [101] |
| Approach | Euler | Lagrangian |
|---|---|---|
| Basic principle | Particles are modeled as a continuous phase governed by a conservation equation similar to that for fluids. | Particles are regarded as a discrete phase, with each individual particle’s trajectory recorded. |
| Advantages |
|
|
| Drawbacks | ||
| Recommended for |
|
|
| Not recommended for | - Scenarios with very high particle loads due to excessive computational cost | |
Extracting data from all reviewed studies that simulated particle transport, it was found that 47% of the studies included particle tracking. Unfortunately, 23% did not provide information regarding the model used or the manner in which particle tracking was included in these studies (compare Figure 5). The Lagrange method was employed significantly more frequently than the Euler method. A mere 7% of the studies reviewed compared different approaches for particle tracking. An alternative approach, the use of a second fluid as a tracer gas, was employed by 29% of the studies.
The number of particles used in Lagrangian simulations ranged between 125 [39] and 106 [63] overall particles with a mean of 0.5 particles per grid cell. Only 21% used particle trajectories in the postprocessing, though calculating these trajectories for each is key to the Lagrange method [128]. Local particle concentrations were evaluated from contour plots in 36% of the studies. For contour plots of particle concentration, the Euler method has smoother contours than the Lagrange method, which looks more like a rag rug. Nonetheless, the results are qualitatively similar. This can be observed in two studies [67, 89].
3.6. Inlet Models
In the majority of cases, the simulation of airflow in cleanrooms includes the supply air inlet, the exhaust air outlets and the cleanroom wall as boundary conditions. In certain instances, the entire HVAC system including the fans and the ceiling plenary is used (e.g., in [27, 30, 36, 57, 60, 94, 110, 115]). When using supply and exhaust air boundary conditions, the critical boundary condition in the context of cleanroom CFD is the inlet. This is particularly relevant for nonunidirectional airflow cleanrooms that use air supply diffusers. These diffusers can be simplified or meshed in detail. While the latter approach may yield more accurate results, it requires additional computational time. In his review of indoor air simulation, Nielsen predicts that diffusers will be included in more detail in the coming years [9]. When the entire HVAC system is simulated additionally the fan must also be taken into account. This may be either a central fan or several fans in filter fan units. Simulating the fan requires additional modeling either in full detail or simplified with the fan’s momentum source.
There are various methods for modeling the supply air inlet, which have been employed in numerous studies. The most advanced approach is likely the direct modeling of diffusers. This method involves meshing the diffuser geometry in detail within the computational domain, enabling direct simulation of the airflow. While this approach offers the most accurate representation of air distribution, it also requires the highest computational cost. To reduce calculation time, a simplified boundary condition can be applied. In this simplified boundary condition method, assumptions are made about the boundary conditions at the air inlets, such as uniform velocity profiles or fixed flow rates, which are used for inlet modeling and geometry simplifications. There are three common approaches that do not require the diffusers’ geometry. The prescribed velocity method directly prescribes the velocity distribution at the inlet boundary based on either measured data or theoretical assumptions [130]. The box method models the supply air inlet as a box of specified dimensions. The box is defined as a volume within the computational domain through which air is introduced [131]. The momentum method calculates the momentum flux of the supply air and introduces it into the simulation domain accordingly. It focuses on the momentum characteristics of the air rather than its volume [132]. These models have been used and evaluated in several studies.
Srebric and Chen evaluated the box method and the momentum methods for eight different diffusers: nozzle, valve, displacement, grille, slot, square ceiling, round ceiling, and vortex. They concluded that the box method performed well for all diffusers except the displacement diffuser. However, due to its simpler handling, the momentum method should be used whenever applicable [133]. It is unfortunate that none of the diffusers can be compared to the typical swirl diffusers in nonunidirectional cleanrooms. Zhao et al. developed a simplified model for supply air diffusers in 2003 and validated it for displacement diffusers, grille diffusers, and square ceiling diffusers. It was developed as a combination of the momentum method and the air supply opening model (ASOM) specifically for a zero-equation turbulence model with the goal of simulating airflow quickly. The model demonstrates a high degree of agreement with measured data and has a lower computational cost than conventional CFD methods [134]. However, it is not compatible with any commercial CFD code other than the one used in the study. In his paper on the quality level of CFD for room air movement, Nielsen also discusses the description of supply openings. He evaluated the simplified boundary condition, the box method, and the prescribed velocity method. All methods necessitate the generation of several predictions and descriptions of the flow resulting from them, yet they can yield high-quality results. With the availability of greater computational power, a direct simulation of the diffuser is possible [135]. In 2009, Zhang et al. published their findings for a simplified approach to describe diffusers for CFD simulations. The model was specifically developed for displacement ventilation diffusers and demonstrated a high degree of agreement with corresponding measurement data. The examined ACRs yielded values ranging from 4.09 to 8.62 [136]. Given that cleanrooms have much higher ACRs, the applicability of this model for cleanrooms is limited. For a four-way diffuser, Whyte et al. concluded that direct modeling was not sufficient in their study from 2010 due to the computational requirements. The inlet opening was divided into four equal triangles with a velocity direction set at 90° to each other and 20° to the ceiling. If no diffuser was used, the velocity was defined vertically [64]. In the same year, Lambert et al. compared different geometry simplifications of the inlet with a direct modeling approach. They observed significant discrepancies in the flow field between the models and subsequently concluded that direct modeling is the most accurate approach [91]. Li and Nielsen provide a comprehensive review of the various methods for defining boundary conditions for diffusers. They discuss the simplified method, the box method, the prescribed velocity method, and the momentum method as potential alternatives to direct modeling. Although the direct method is becoming increasingly feasible with the progression of computational power, it can present challenges in the treatment of multiple length scales [137]. Sajadi et al. successfully simulated the airflow of a swirl diffuser with a detailed mesh for the purpose of diffuser design optimization [65]. They did not derive any simplifications, but their study underlines that direct modeling is a growing possibility. Li et al. developed a simplified method for a four-way diffuser by replacing the actual diffuser geometry with 68 squares, each with its own inlet velocity defined in the x, y, and z directions. They achieved an average deviation in the temperature field compared to the measurement results of 3.0%. Additionally, they noted that direct modeling of the diffuser yields the most accurate flow field and temperature distribution [138]. In summary, the studies agree that direct modeling is the most accurate approach and should be used whenever possible, though they also show that various simplifications of inlets can still yield reliable results. Table 7 gives an overview of the studies and recommended approaches.
| Case | Inlet models compared | Inlet model recommended | Study |
|---|---|---|---|
| Eight different diffusers |
|
Momentum method | Srebric and Chen [133] |
| Smith and Hutton problem [139] |
|
No recommendation, reliable results with all models | Nielsen [135] |
| Experimental room |
|
Direct modeling | Lambert et al. [91] |
| Review from literature data |
|
Direct modeling | Li and Nielsen [137] |
| Experimental room |
|
Direct modeling | Li et al. [138] |
As the inlet geometry is not a determining factor in the absence of a diffuser (e.g., unidirectional cleanrooms), the turbulence intensity is a necessary consideration for both inlet types. Angiolett et al. conducted experimental investigations of various diffusers. In the absence of a diffuser and direct flow through the filter face, the turbulence intensity reached a maximum of 4.5% with no reported average value [140]. In a separate experimental analysis, Whyte et al. observed an average turbulence intensity of 3% with a maximum of 8% at the face of a filter. They proceeded to simulate the phenomenon with a turbulence intensity of 6%. Despite the fact that higher values, such as 20% or above, yielded results that were closer to experimental data, the authors concluded that the turbulence intensity of 6% was a reasonable approximation [64]. A summary of all studies including air supply through a filter without a diffuser indicates that the inlet turbulence varies from 0.6% to 15% with a mean of 5% and a median of 3.5%. In contrast, when a diffuser is used for the air supply inlet, only two studies mention the turbulence intensity of 4% and 6%, respectively.
4. Postprocessing and Learning From Data
The primary goal of CFD in cleanroom applications is to enable accurate predictions, particularly in areas such as building energy prediction or HVAC system performance. Since accurate simulations often come with long calculation times, another goal is to make predictions and therefore simulations faster [141]. By using CFD, engineers can generate extensive datasets and simulate extreme conditions without costly and time-intensive experimental setups. This enables the development of advanced control strategies independent of the plant size. A core concept in CFD-based cleanroom applications is the establishment of predictive models that link target variables (e.g., particle concentration or temperature to evaluate thermal comfort) to features that can be easily measured [142] (e.g., temperature, time, relative humidity and outdoor parameters). However, identifying all relevant features and ensuring that the dataset spans a sufficiently large parameter space remains challenging. For example, Kim and Park [143] demonstrated the use of artificial intelligence (AI) to analyze CFD data in a simplified test room. The approach did not account for geometric changes in the environment. Zhou and Ooka also underline the need for effective data preprocessing to achieve meaningful insights [144]. Particularly important in cleanroom applications is the particle concentration. Kek et al. [145] addressed this while using different ACRs to predict the air velocity and particle concentration using a deep neural network (DNN) approach. However, their approach was limited to fixed geometrical arrangements, such as specific room layouts and particle emitter positions. While this methodology is well-suited for troubleshooting plants with fixed setups—eliminating the need for CFD expertise during evaluation—it primarily serves as a tool for data compression rather than a generalized solution.
Several comprehensive reviews have explored the application of advanced computational and machine learning (ML) techniques for CFD. Calzolari and Liu [141] provide a detailed analysis of how artificial neural networks (ANNs) can enhance turbulence modeling. One application involves fine-tuning model constants, allowing high-Re turbulence closures to be adapted for the relatively slow indoor flows characteristic of many indoor air problems. Another approach discussed by Calzolari and Liu is the complete replacement of traditional turbulence models with ANNs or even tensor-based neural networks. In addition to turbulence modeling, they highlight advanced flow analysis methods such as super-resolution techniques. These techniques leverage (i) the combination of high- and low-resolution CFD data or (ii) physics-informed convolutional neural networks (CNNs) trained on low-resolution CFD data. Quang et al. [146] offer a more critical perspective on the limitations of ML in CFD applications. Three major challenges are identified: (i) the lack of high-quality experimental data for model training and validation, (ii) the inherent complexity of CFD simulations that limits the applicability of ML models, and (iii) the interpretability issues associated with ML, often regarded as “black box” systems that provide little insight into their decision-making processes. Despite these limitations, Quang highlights specific applications of ML, including thermal comfort prediction and indoor air quality modeling. However, these applications face significant hurdles due to the vast and complex feature space, which includes factors such as room geometry, ventilation conditions, outdoor environmental parameters, pollutant type and location, and the necessary simplifications of geometric details. The review also documents broader, less specific applications, such as the use of ML for turbulence model improvements, particularly for low-Reynolds-number flows. While these approaches demonstrate potential, the overall findings are presented in a relatively general and nonspecific manner.
Physics-informed neural networks (PINNs) have recently gained attention as a promising tool for solving fluid dynamics problems by incorporating physical laws into the training of neural networks. Cuomo et al. [147] provide a comprehensive review of PINNs, outlining their fundamental concepts and diverse applications within CFD. The basic framework of PINNs was introduced by Raissi et al. [148], who demonstrated their application to the Navier–Stokes equations. In their study, they simulated a Kármán vortex street and achieved qualitatively accurate predictions of the pressure field, illustrating the potential of PINNs in resolving unsteady flow structures. Jin et al. [149] further advanced this approach by successfully solving the incompressible Navier–Stokes equations for both laminar and turbulent flow regimes. Their model was trained using data from direct numerical simulations (DNS) and did not require labeled data beyond initial and boundary conditions, along with the known fluid properties. In addition, Cai et al. [150] extended the application of PINNs by coupling the Navier–Stokes equations with the energy equation to model forced and mixed convection problems. Their findings suggest that PINNs can bridge the gap between experimental and computational heat transfer studies and even solve problems that are difficult or impossible to approach with conventional numerical methods—such as those involving unknown thermal boundary conditions. Recent research continues to enhance the accuracy and applicability of PINNs, particularly for complex flow scenarios. For instance, Zhang et al. [151] incorporated RANS equations and a turbulence model (i.e., the k–ε model) into the PINN framework. This advancement is aimed at improving the performance of PINNs in simulating realistic turbulent flows with intricate geometries and boundary conditions. Son et al. [152] applied a PINN approach to estimate ACRs in an office setting, using long-term CO₂ concentration data alongside time-varying meteorological and operational conditions. Their study integrated Shapley additive explanations (SHAP) to assess feature importance, revealing that wind direction and window states were dominant influences on ventilation rates. Gao et al. [153] introduced operator learning architectures—DeepONet and Fourier neural operators (FNO)—for reconstructing 2D indoor airflow fields using minimal training data. Their approach, which divides the domain into subregions and reassembles predictions, achieved high accuracy with errors below 2% and inference times under 0.01 s. Zhang et al. [154] proposed a CNN-based surrogate model specifically designed to improve local prediction accuracy in indoor environments. Compared with ANNs and graph neural networks, the CNN-based model achieved an average accuracy improvement of over 45%, while reducing computational time to 0.05% of conventional CFD simulations. A key contribution was the introduction of a spatial geometry encoding technique, enabling the model to handle complex room configurations effectively. Li et al. [155] conducted a comprehensive comparison of regression-based ML models—including backpropagation neural networks (BPNN), XGBoost, random forests, and support vector regression (SVR)—for reconstructing indoor airflow fields. Their findings showed that XGBoost consistently outperformed other models in both accuracy and speed, with speeds up to 250 times faster than traditional neural networks. The model’s interpretability also supports its use in practical design optimization tasks. Quang et al. [156] combined CFD and DNNs to predict airflow and temperature distributions in naturally ventilated multistory residential buildings. The DNN surrogate achieved an 80% reduction in computational time while maintaining high prediction accuracy.
Together, these studies underscore the rapid progress in ML-based surrogate modeling for airflow prediction. Whether through physics-constrained methods like PINNs or purely data-driven approaches, ML is emerging as a critical tool in advancing the efficiency, adaptability, and interpretability of indoor airflow simulations. These approaches hold particular promise for cleanroom environments, though no single cleanroom-related study was found in the literature by us.
5. Verification, Validation, and Calibration
5.1. Verification
Verification in CFD refers to the process of ensuring that the numerical model accurately solves the mathematical equations that govern fluid dynamics. It answers the fundamental question: “Are we solving the equations correctly?” This step is essential to establish the reliability of the computational framework and ensure that any errors introduced by the numerical methods or coding are minimized. Verification is distinct from validation, which checks whether the CFD results accurately represent physical reality. While validation compares results against experimental or real-world data, verification focuses purely on the numerical accuracy and mathematical fidelity of the CFD implementation. One of the most common approaches to verification is comparing CFD results with analytical solutions. Analytical solutions are exact solutions to the governing equations, often derived for simplified cases where the equations can be solved explicitly. These solutions serve as benchmarks for evaluating the numerical solver.
5.2. Validation
Validation represents a pivotal stage in the conduct of a simulation study. The goal of the validation is to ensure that the used models predict real world phenomena. It is important to note that a simulation is a numerical approximation and a simplified model. Given that the adage “all models are wrong but some are useful” [157] is true, it is imperative that a validation be conducted. Chen and Srebric provide a manual on validation of indoor environment CFD [158]. They define validation as estimation how accurately real-world physics are simulated. They describe an ideal scenario, where all important physics like heat transfer and airflow could be obtained from measurements. However, this ideal scenario is not always feasible. In such cases, the validation should be restricted to the most important subsystems for the simulated case. For cleanrooms, this could add particle transport phenomena to the before mentioned physics. Due to the high complexity of indoor air flows and especially in cleanrooms, it is recommended to employ a multifaceted validation approach. Starting with lower complexity physics to higher complexity a validation can be done for (i) the isothermal flow to understand and validate the basic flow pattern (ii) adding heat transfer effects (possible stepwise for convection, radiation and conduction) followed by (iii) particle transport phenomena. The simulated data is compared against measurement data where meaningful criteria have to be chosen. In the event that the validation case is found to be less complex than the simulation, or if it employs only a subsystem, it is recommended that the criteria employed be more stringent than those applied when a complete system is used for validation. Hajdukiewicz et al. describe a method for an iterative validation and calibration method based on on-site measurements [159]. For validation they conduct on-site measurements of air velocity on four evenly spaced positions each 0.3 m above the floor and temperature on different heights at the same position. Their proposed method for the iterative calibration will be discussed in the following chapter [158].
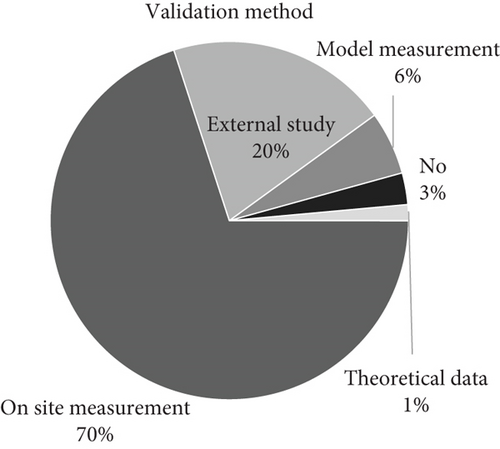
In the studies reviewed, 49% validated their simulation through full-scale experiments or on-site measurements (compare Figure 6). This is also the preferred method by the studies specifically dedicated to validation [158, 159]. An additional method for validating CFD results is through the utilization of data from an external or previous study, as employed by 15% of the studies reviewed. A lack of information on the validation process was evident in 30% of the studies, though it is expected that some kind of validation has been done. The remaining studies employed either model-scale experiments or theoretical data. One study explicitly stated that it did not require validation.
5.3. Calibration of Model Parameters
After validation of a CFD model, it is possible to enhance the predictive accuracy by calibrating certain parameters. Beyond traditional turbulence model adjustments, calibration can extend to other influential parameters like boundary conditions. This is demonstrated by Hajdukiewicz et al. who focused on naturally ventilated rooms. Their methodology employed response surface techniques, linking key response variables (air temperature and velocity within the room) to a set of eight features. These features included air density (to account for average indoor temperature), inlet velocity, heat sources, and heat transfer coefficients. The study simplified the problem by modeling adiabatic walls and excluding explicit wall-flow interaction. The final calibrated model achieved an absolute temperature difference of 2.17 K and a velocity discrepancy of 0.1 m/s. Their iterative approach for validation and calibration can be generalized as follows: (i) Build an initial model based on technical documentation and measurements. (ii) Apply a mesh independence study. (iii) Validate important physics like temperature and air velocity with meaningful criteria (e.g., measurement uncertainties or regulations). (iv) If the criteria are not met, the iterative calibration starts. Based on a parametric analysis (e.g., response surface methodology), the boundary conditions with the highest influence on the results should be determined. (v) Adjust relevant parameters and repeat until criteria for validation are met. (vi) Repeat mesh independency study with the new parameters. In their review on naturally ventilated buildings, Sakiyama et al. [160] acknowledge the general significance of calibration for models, though their focus was not specific to CFD. Instead, they centered their discussion on tools like “EnergyPlus,” a whole-building energy simulation program. The review identified Hajdukiewicz et al. [159] as the only study combining CFD with calibration processes, highlighting a gap in the literature. A more recent review by Peng et al. [161] briefly reiterated the necessity of calibration for “physics-based” models, particularly in the context of model predictive control (MPC). These studies collectively highlight both the potential and the underexplored nature of calibration in CFD, particularly for complex indoor airflows and thermal comfort modeling.
6. Conclusion
The focus of the present literature review was to extract guidelines for higher accessibility of CFD simulations for cleanrooms and to highlight research needs to further enhance cleanroom CFD studies. Also, a guideline for CFD simulations of airflow in cleanrooms is derived from our discussion.
In regard to the utilized simulation grids, it is notable that the majority of cases only provide the number of elements as the only information of the mesh. Although a mesh independence study is typically a mandatory component of a numerical study, it is not always mentioned in the literature and often lacks sufficient detail regarding the allowed error. To facilitate comparison of meshes, it is recommended that additional mesh metrics, such as characteristic y-plus values, should be provided in simulation studies. The ongoing growth in computational power enables the use of finer meshes. This has a direct impact on the specification of boundary conditions: For example, the complex geometry of different kinds of diffusers can be included directly in a CFD simulation and in full detail.
As is well established, there is no single turbulence model that is universally applicable. In studies that compared different turbulence models, the RNG k − ε model was found to be the most accurate [24, 80, 124], followed by the SST k − ω model [29, 101]. However, the evaluation of turbulence models was not conducted with sufficient depth to ascertain the reasons behind the observed variations in performance under specific flow conditions. In future studies, an in-depth analysis of this kind should be given greater attention, as it would allow for the selection of a turbulence model depending on the specific case (e.g., nonunidirectional flow with swirl diffusers vs. direct filter fan unit inlet). The fact that the 11 studies which compared different turbulence models recommended eight different models underlines that there is no single best model. Upon consideration of all reviewed studies, it can be concluded that the standard k − ε model was the most frequently utilized model, followed by the RNG k − ε model. This reaffirms that the choice of turbulence model depends on the case and should be based on an investigation of the most suitable turbulence model. Consequently, to obtain simulations with meaningful outcomes, it is imperative to conduct a comparative analysis of distinct turbulence models in each simulation study. Literature on deep learning-based calibration [141] even suggests a “tuning” of parameters in the turbulence model to account for specifics in cleanrooms (i.e., relatively low Reynolds numbers and transitional flow). Even more extreme, the complete replacement of the turbulence model with a machine learned substitute is thinkable, simply because of the great challenge of predicting turbulence in cleanrooms. Also, our case study on flow through raised floors highlights the importance of more research on turbulence in cleanrooms, simply because such flow details can be critical. An example would be the release or resuspension of particles from floors in cleanrooms which might contaminate the product or even result in a health risk in (bio)safety laboratories. The reviewed studies also show that current advances in turbulence modeling are yet to be investigated for use in cleanroom CFD. This also hints at a gap in the reviewed studies: The conducted and tested turbulence models are the traditional RANS models based on early cleanroom CFD research. Modern alternative approaches like (i) LES, (ii) detached-eddy simulation (DES), (iii) unsteady Reynolds-averaged Navier–Stokes (URANS) or Hybrid RANS/LES strategies, and even newer (iv) ML approaches have not been considered in cleanroom CFD studies yet. Detailed information on these approaches can be found in Argyropoulos and Markatos [162]. Another approach, the lattice Boltzmann method (LBM) was successfully used for simulating airflow patterns surrounding a manikin recently [163]. Compared to LES, the accuracy was similar; however, only one-sixth of the calculation time was needed for the LBM.
Our analysis of ML in the context of CFD in cleanrooms reveals that such ML models are only relevant if the feature space can be limited as much as possible. This might be, for example, realized by considering a single geometry or pollutant strength/location. Thus, ML might be relevant for troubleshooting an existing cleanroom, but less important for geometrical optimization or the conceptual design of cleanrooms. A current overview for the use of ML for indoor airflows is given by Olivas and Yee [164], though future studies should address cleanroom specifics like inlet design, buoyant flow, and particle transport within three-dimensional environments.
With respect to particle tracking, studies that compare the Eulerian and Lagrangian approaches tend to recommend the latter approach [67, 89, 128]. However, in two studies [18, 67], both approaches yielded to reliable results. This trend is also evident in the studies without comparison of both approaches. The Lagrangian approach was the most frequently utilized method. As a preliminary approach, the Lagrangian method can, therefore, be recommended for future cleanroom CFD studies. The current literature shows that detailed diffuser modeling is capable of yielding the most accurate results and offers the greatest flexibility for airflow studies (e.g., the positioning of an inlet in a room, or a comparison of the effects of different diffusers on the airflow). However, this approach is not without its drawbacks. The increased complexity of the detailed modeling process leads to a more time-consuming meshing process and naturally results in higher number of mesh elements (and therefore longer computation times). This results in higher costs, both personnel and computational. This prompts the following question: under what circumstances does the enhanced accuracy and adaptability of the detailed inlet modeling outweigh the increased expense? Though Li et al. [138] introduced a methodology for simplifying diffuser inlets to multiple face inlets with different velocity boundary conditions based on a detailed diffuser simulation, they did not compare the computational cost. It has been demonstrated that the developed methodology utilizes surface-boundaries exclusively (instead of complex 3D diffuser geometries), thereby enabling a substantial reduction in the number of elements while preserving model accuracy. This approach resulted in an average deviation of -3.0% in the velocity field. Considering the definition of model complexity established by Liu et al. [165] in their meshing strategy for indoor airflow (i.e., model complexity defined as the ratio of the overall geometry surface area compared to the surface area of a cube with equivalent volume), it is evident that future studies may be able to more directly define the cost-benefit problem with regard to model complexity. Specifically, this may be achieved by identifying the appropriate range for the model complexity, as outlined in the following categories defined by Liu et al. [165]: (i) simple geometries: ratio ≤ 1.3, (ii) medium geometries: ratio < 2, (iii) complex geometries: ratio ≥ 2.
It was found that the majority of studies (i.e., 49%) used on-site measurements for validation purposes as is also recommended by studies specifically dedicated to verification, validation, and calibration [158, 159]. If on-site measurements are not possible, it is advisable to either build a model based on existing data or use lab-scale measurements. Either way, validation is a crucial step in CFD studies and should be treated with the special rigor and attention to ensure reliable and meaningful results. While calibration has proven effective in enhancing CFD model accuracy ([159]), its application remains relatively scarce in the context of cleanroom CFD. The limited number of studies integrating CFD with systematic calibration, as also noted by Sakiyama et al. [160], underscores this gap in the literature. Further research is needed to develop standardized calibration frameworks, explore their applicability across diverse cleanroom types, and quantify their impact on the model’s predictive capabilities.
The reviewed literature revealed that not all simulations are adequately described as recommended by Sørensen and Nielsen [15]. They propose that the simulation parameters should be documented in such detail that the simulation can be reproduced by the reader.
7. Best Practice Guideline
- •
For the meshing process, a mesh independency study and a reasonably chosen y-plus of 1 for heat transfer problems are mandatory. The overall mesh size depends on the geometric size of the cleanroom. As a starting point for the mesh independency study, five million elements with the mean cell size not exceeding 100 mm should not be a problem with modern CPU power.
- •
It is recommended that the supply air inlet be modeled in its entirety in order to achieve the highest possible degree of accuracy. In the event that a reduction in complexity is required, one should be clear about the inlet condition (turbulence intensity, main flow direction, and swirl)
- •
Interestingly, a turbulence intensity of 5% was considered adequate in the majority of studies, irrespective of the type of supply air inlet.
- •
It is imperative that every CFD study undergoes validation against experimental data, preferably on-site measurements but at least for benchmark cases from literature. In case no data on a full-scale experiment is available, a comparison with literature data or model-scale experiments is an acceptable alternative.
- •
To ensure reliable results, the validation process should be coupled with verification and parameter calibration in the following order: (i) verification against analytical solutions, (ii) optional calibration of parameters in the simulation model by using a training data set, and (iii) validation against validation data. Important is, of course, that the training data set and the validation data set are different.
- •
In a preliminary assessment of the flow in a cleanroom, the RNG k − ε turbulence model should be used as the most promising candidate. As it was the second most utilized model in all studies and one of the most preferred models in case different turbulence models were compared, it reflects the current state of research. However, as with the meshing process, it is essential to conduct a comparative analysis of a plurality of turbulence models, ideally also using an LES-type of simulation as a benchmark.
- •
If particle tracking is of interest, it is recommended to employ a Lagrangian method. To ensure that enough particles are tracked to gather enough statistics on local particle concentrations, an independency study with a starting point of 0.5 particles per grid cell is recommended.
- •
In publishing a cleanroom CFD study, it is essential to provide a detailed description of the simulation, following the recommendations of Sørensen and Nielsen [15]. Additionally, of special interest for CFD studies of cleanrooms are (i) the boundary conditions with parameters (velocity and turbulence intensity) and, for diffusers, the modeling of the inlet, (ii) modeling of porous walls (e.g., raised floor systems), (iii) employed particle transport approach with particle description (size, number, and density), (iv) the choice and justification of the turbulent model, and (v) type and purpose of the cleanroom.
- •
To ensure the most detailed documentation, use of an open source CFD software package (e.g., OpenFOAM) with export of all used scripts and settings is strongly recommended. This allows full reproduction of CFD studies.
Certainly, the CFD simulation of a cleanroom was and always will be an iterative process consisting of a (geometrically) simplified model and this subsequent improvement.
Future research might explicitly address challenge by providing data on how geometrical simplifications affect CFD predictions or identify key geometrical features that are most important to be captured by a CFD analysis of a cleanroom. Also, looking at the effect of wall treatment in the case of buoyancy-driven flows might be interesting, since current literature did not investigate this detail in its full beauty. Expanding the body of research on calibration methods tailored to CFD simulations remains a key area for future work, especially in applications requiring high accuracy and integration with control systems.
Disclosure
The research was performed as part of the authors’ employment at Rosenheim Technical University of Applied Sciences and Graz University of Technology.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
The research did not receive specific funding.
Acknowledgments
S.R. acknowledges the support of NAWI Graz by providing access to the “dcluster” supercomputing infrastructure. We thank Dr. Gerhard Lindner (Fluentum GmbH, Graz, Austria) and Dr. Bernhard Streibl (DrS3 - Strömungsberechnung und Simulation e.U., Vienna, Austria) for valuable hints with respect to an early version of Supporting Information 2 (Application Case “Raised Floor”).
Supporting Information
Additional supporting information can be found online in the Supporting Information section.
Open Research
Data Availability Statement
The data that supports the findings of this study are available in the Supporting Information section. Supporting Information 3 is openly available in TU Graz Repository at 10.3217/8qzf0-2sx40, Reference [166].




