The restricted detour distance between two vertices is the length of longest path P such that the induced subgraph for a vertex set of P is identical P. The number of restricted detour distance of a vertex v of a connected graph Ǥ is a summation of restricted detour distances from v to all vertices of Ǥ. In this paper, we give a new definitions called restricted detour median graph (RDM-graph) and restricted detour self-median graph (RDSM-graph) and then we find many results related with them.

1. Introduction

There are many types of distance in a simple connected graph Ǥ in graph theory [1, 2], some of them depend on distance between two vertices from the set vertex of Ǥ, V(Ǥ), such as ordinary distance [3], detour distance and restricted detour distance [4, 5], and Steiner distance [6], while others depend on two subsets of V(Ǥ), such as maximum (or average or minimum) distance between two subsets of V(Ǥ) [7], sometimes depends on one vertex and a subset of V(Ǥ) such as min −k−distance and max −k−distance, where k does not exceed the number of vertices of the graph [8], in addition to the presence of a invariant number that depends on degrees [9] only or depends on the ordinary distance and degrees [10, 11]. The reason for the diversity of finding definitions of distance in graph theory is because of its very great importance of applications, such as geometric communications [12], computer science [13], and chemistry science [14]. For any two vertices, u and v, the shortest path is the ordinary distance, denoted by d(u, v). The longest path between two distinct vertices, u and v, is the detour distance, d_D(u, v), but the restricted detour distance is the longest path P that connected two vertices u and v such that <V(P) > = P, where <V(P)> reference to a subgraph of Ǥ that is induced by V(P) where V(P) is its vertex set; furthermore, if an edge of Ǥ connects two vertices of V(P), then it is an edge of <V(P)> [15]. The topics of detour distance and restricted detour distance have been the subject of numerous recent studies; you can see them in references [16–18]. Therefore, our aim in this paper is to present a new concept related with restricted detour number.

Definition 1. For any connected graph Ǥ, the restricted detour distance [4] of the vertex v ∈ V(Ǥ) is

(1)

Definition 2. The restricted detour median graph (RDM-graph) for all connected graph Ǥ is a subgraph M^∗(Ǥ) of a graph Ǥ that is induced from those vertices which have minimum number of restricted detour distance.

The importance of RDM-graph is that we can obtain a new chemical compound from a given chemical compound that is more stable and clearer in terms of some of the chemical properties of the chemical compounds, for example, boiling point or melting point.

It is unknown whether for every a connected graph Ǥ, there exists a graph H such that M^∗(H) = Ǥ. For any connected graph Ǥ and every vertex u that does not belong to the set of vertex of Ǥ, we note that , ∀ v ∈ V(Ǥ), where Ǥ^′ is got from Ǥ by joining u to at last one vertex of Ǥ. To illustrate this, we provide the next example.

Example 1. Consider a graph Ǥ that appears in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Graphs Ǥ and Ǥ^′.

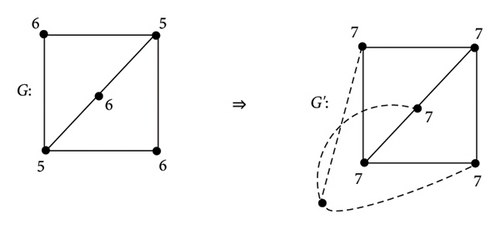
Definition 3. For any connected graph Ǥ, if M^∗(Ǥ) = Ǥ, then Ǥ is called a restricted detour self-median graph (RDSM-graph).

Example 2. The graphs C_p, K_ᶆ,ᶆ, and K_p are RDSM-graphs, p, ᶆ ≥ 3.

It is very difficult to find graph H such that M^∗(H) = H⊃Ǥ.

Definition 4. The graph which has p of vertices and without edges is called an empty graph, which is denoted as E_p [2].

Definition 5. Let Ǥ be a simple connected graph of order p which has the vertex set V(Ǥ) = {u₁, u₂, …, u_p} and T = {t₁, t₂, …, t_p} be an n-tuple of nonnegative integers. The thorn graph is a graph generated by joining t_i vertices of degree one to the vertex u_i ∈ V(Ǥ), i = 1, 2, …, p [19].

2. RDM-Graph Containing Some Special Graphs

In this section, we find RDM-graph for some special graphs, such as complete bipartite, path, and cycle graphs.

2.1. Complete Bipartite Graph

If Ǥ ≡ K_ᶆ,ᶇ, ᶆ, ᶇ ≥ 2 and ᶆ ≠ ᶇ, say ᶆ > ᶇ, then there is graph H ≡ K_ᶆ,ᶆ, which is a RDM-graph containing induced subgraph K_ᶆ,ᶇ, that is, M^∗(K_ᶆ,ᶆ)⊃K_ᶆ,ᶇ, see Figure 2.

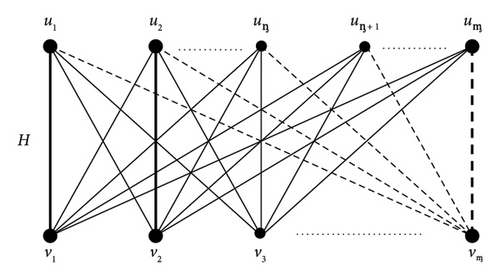
Moreover, for , |ᶇ_i| = ᶇ, i = 1, 2, …, t, we have , for each v in V(K_ᶇ(t)); thus, K_ᶇ(t) isa RDM-graph for itself. Consider K_ᶆ,ᶇ,t, with ᶆ, ᶇ, t not equal integers without loss of generality, and we assume ᶆ > ᶇ ≥ t. One may check that K_ᶆ,ᶇ,t is an induced subgraph of K_ᶆ,ᶆ,ᶆ, which is a restricted detour median itself. Thus, in general, is an induced subgraph of self-RDM-graph K_ᶇ(t), where ᶇ = max{ᶇ₁, ᶇ₂, ᶇ₃, …, ᶇ_t}.

Proposition 1. If the empty graph Ǥ of order ᶇ has a vertex set {u₁, u₂, …, u_ᶇ}, ᶇ > 1, then Ǥ is a RDM-graph of a graph K_ᶆ,ᶇ, for ᶆ > ᶇ.

Proof 1. In K_ᶆ,ᶇ, we have

(2)

2.2. Path Graph

We shall give some examples for special path graphs P_p such that there exits a graph H, with a path P_p as an induced subgraph of H, and M^∗(H) = P_p for some p.

If Ǥ = P₁, (Ǥ is a trivial graph), then H₁ is a hand fan graph, where

, for i = 1, 2, …, p − 1, see Figure 3.

(3)

1.
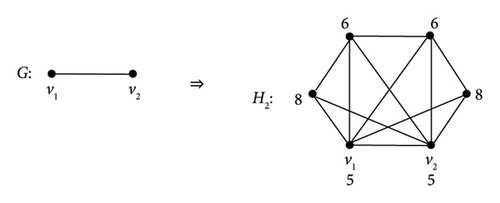
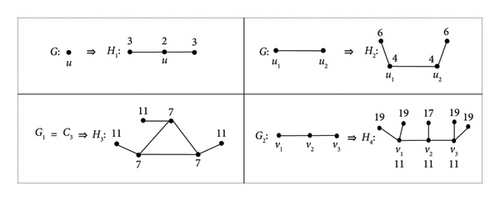
If Ǥ = P₂, then H₂ is a graph as illustrated in Figure 4.
(4)
2.
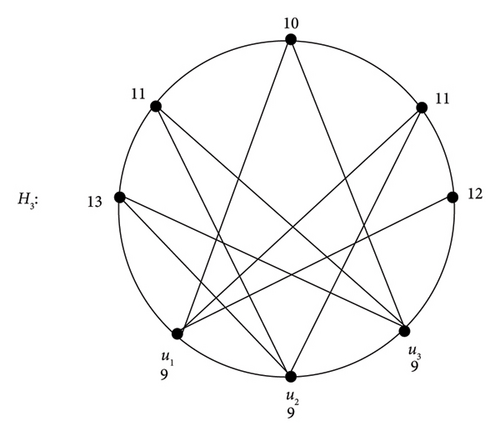
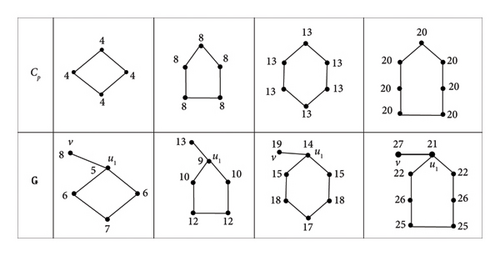
If Ǥ = P₃ : u₁, u₂, u₃, one may easily check that restricted detour distance for each vertex of H₃ in Figure 5 shown in the following.
Thus, M^∗(H₃) = P₃.
3.
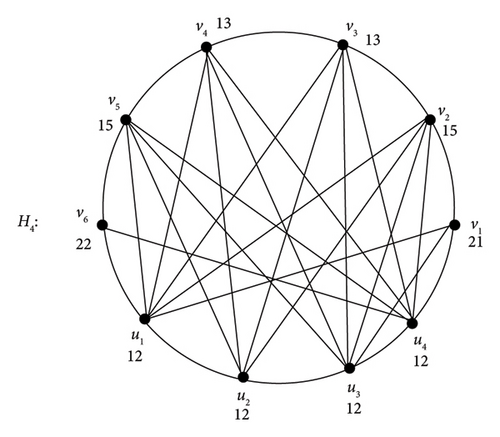
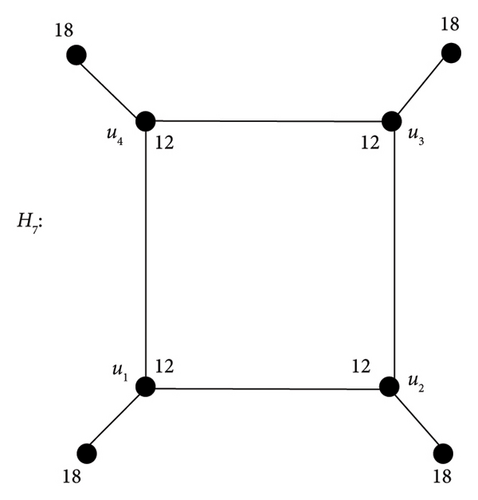
If Ǥ = P₄ : u₁, u₂, u₃, u₄, then H₄ is shown in Figure 6, and the depicted graph satisfies M^∗(H₄) = P₄.
4.
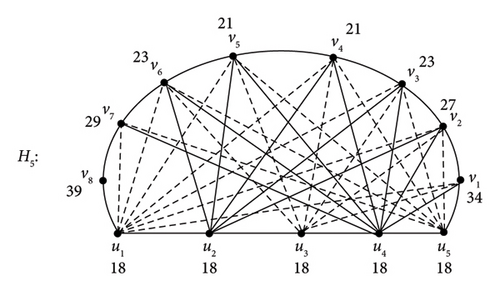
If Ǥ = P₅ : u₁, u₂, u₃, u₄, u₅, then M^∗(H₅) = P₅, where H₅ is illustrated in Figure 7.

Finally, we think that, there exists a graph H for every path P_p, p ≥ 6, containing P_p as induced subgraph such that M^∗(H) = P_p.

Problem 1. How to describe the construction of such H?

2.3. Cycle Graph

In this subsection, we got some results through which we were able to obtain thorn cycle graph

at t = 1 from Ǥ that resulted from adding vertices and creating edges between the added vertices and the vertices of Ǥ such that M^∗(H) = C_p, p ≥ 4.

1.
If Ǥ = C₃ : u₁, u₂, u₃, u₁, then H₆ in Figure 8 satisfies M^∗(H₆) = C₃.
2.
If Ǥ = C₄ : u₁, u₂, u₃, u₄, u₁, then H₇ in Figure 9 satisfies M^∗(H₇) = C₄.

Theorem 1. For any cycle C_p:u₁, u₂, u₃, …,u_p, u₁, p ≥ 4, there exists a graph H in which C_p is an induced subgraph of H and M^∗(H) = C_p.

Proof 2 (see Figure 10.)The following cases is clear for i = 1, 2, 3, …, p.

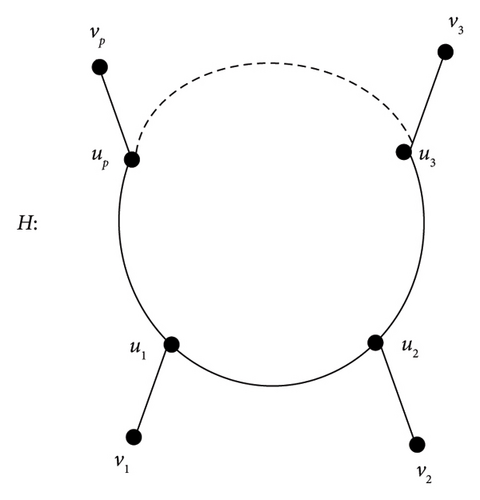
Case 1. If p is even, then

(5)

Also,

(6)

Hence, M^∗(H) = C_p = <{u₁, u₂, u₃, …,u_p}>.

Case 2. If p is odd, then

(7)

Also,

(8)

Hence, M^∗(H) = C_p = <{u₁, u₂, u₃, …,u_p}>.

From (5) (or (7)) and (6) (or (8)), we note that .

Proposition 2. For all connected graph Ǥ of order p, p ≤ 3, there exists a graph H_i in which M^∗(H_i) = Ǥ and Ǥ is an induced subgraph of H_i, where i = 1, 2, 3, 4.

Proof 3. For p = 1, we have H₁ = P₃.

For p = 2, we have H₂ = P₄.

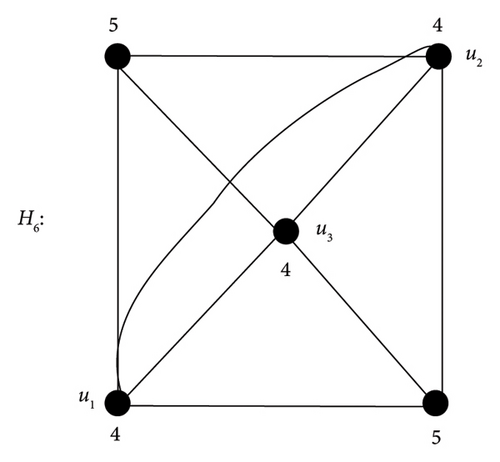
For p = 3, we have H₃ and H₄ as shown in Figure 11.

Hence, the proof is complete.

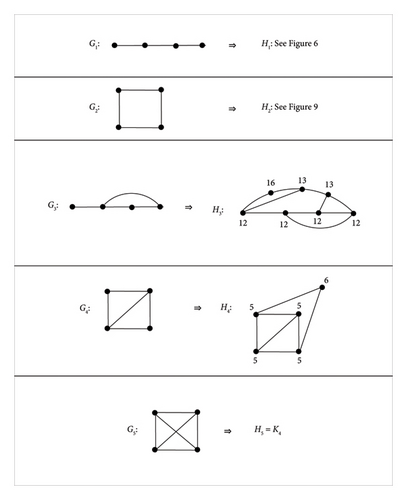
Proposition 3. For any connected graph Ǥ_i which has the order p = 4, Ǥ_i ≠ S₄ (star graph of order 4), there exists a graph H_i such that Ǥ_i is an induced subgraph of H_i and M^∗(H_i) = H_i, where i = 1, 2, 3, 4, 5.

Proof 4. For p = 4, the corresponding H_i such that M^∗(H_i) = Ǥ_i, i = 1, 2, 3, 4, 5 is shown in Figure 12.

Hence, the proof is complete.

3. RDSM-Graph Containing Some Special Graphs

Proposition 4. Suppose that Ǥ is a RDSM-graph with |V(Ǥ)| = p and V(Ǥ) = {u₁, u₂, …, u_p} Then, there exists a graph H of order 2p constructed from Ǥ by adding vertices v₁, v₂, …, v_p with edges {v_iu_i:i = 1, 2, …, p}, and Ǥ is the induced subgraph of H and M^∗(H) = Ǥ.

Proof 5. From Figure 13(a), one may easily notice that for all i = 1, 2, …, p, and , in which .

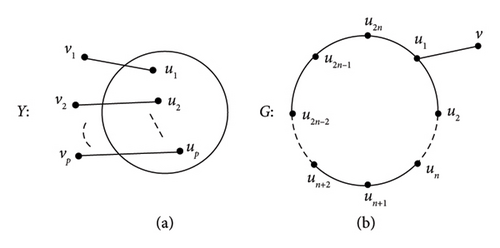
Thus, Ǥ is the detour median of H, and Ǥ is the induced subgraph of H.

The special graphs K_p, K_ᶆ,ᶆ, and C_p are the graphs satisfying the property mentioned in Proposition 4, M^∗(H) = Ǥ.

Proposition 5. If Ǥ is an RDSM-graph of order p, p ≥ 3, then Ǥ contains no end-vertex.

Proof 6. If v is a vertex has degree one, and u is the unique vertex adjacent to v, then

(9)

Thus, v ∉ M^∗(Ǥ) contradicting M^∗(Ǥ) = Ǥ.

Proposition 6. Suppose that Ǥ is a connected RDSM-graph where |V(Ǥ)| = p, p > 4, and v is an end-vertex of G, then v ∉ M^∗(Ǥ).

Proof 7. By contradiction (see Figure 13).

Let u be the vertex adjacent to v in Ǥ, and let Ǥ^′ = Ǥ − v.

(10)

Thus, .

Therefore, .

By the definition of the median vertex, v ∉ M^∗(Ǥ).

Corollary 1. If u is a median vertex in Ǥ, then u is the only median vertex in Y.

Proof 8. Let w ∈ V(Ǥ^′), then from Figure 13, we obtain

(11)

If u ∈ M^∗(Ǥ^′), then .

From (10), we have .

From (11), we have .

Hence, if w ≠ u, then , which implies that u is the only median vertex in Y.

To explain the previous propositions, we take the following examples:

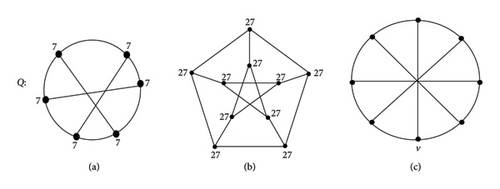
Example 3. Let C_2ᶇ : u₁, u₂, … , u_2ᶇ−1, u_2ᶇ, u₁, ᶇ ∈ N − {1} and v is an isolated vertex, then the graph Ǥ is constructed from C_2ᶇ with edge vu₁.

It is easy to calculate

(12)

Since C_2ᶇ is a RDSM-graph, then

, for i = 1, 2, …, 2ᶇ, is of the value, say N; therefore,

(13)

Example 4. Let C_2ᶇ+1 : u₁, u₂, … , u_2ᶇ−1, u_2ᶇ, u_2ᶇ+1, u₁, ᶇ ∈ N − {1}, and v is an isolated vertex, then the graph Ǥ constructed from C_2ᶇ+1 with edge vu₁.

As in the previous example, we calculate

(14)

Hence, , j > 1.

Since C_2ᶇ+1 is a RDSM-graph, then there is a value N such that

(15)

To illustrate the above two examples in Figure 14, we take the cycle graph C_p of different orders.

Example 5.

1.
For S₄, we have a RDSM-graph Q in Figure 15(a), containing S₄ as induced subgraph, but S₄ ⊂ M^∗(Q), S₄ ≠ M^∗(Q).
2.
The Peterson graph, shown in the following is restricted detour self-median, with the number of restricted detour distance of each vertex is 27, see Figure 15(b).

Moreover, the cubic graph of order 8 has for each vertex v, see Figure 15(c), d^∗(v) = 3 + 4 + 4 + 3 + 3 = 17. We notice that not every cubic graph is a RDSM-graph.

3.
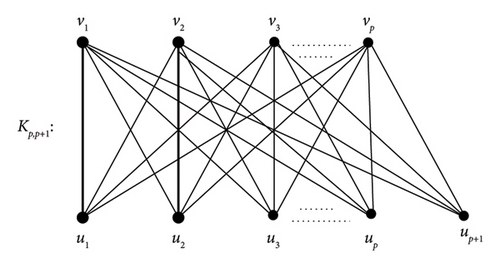
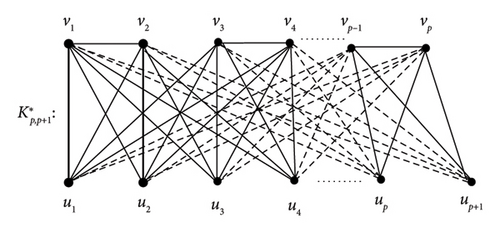
For empty graph E_p of order p, we have K_p,p+1

It is obvious that

(16)

Therefore, M^∗(K_p,p+1) = E_p, see Figure 16.

4.
For the graph even order p with exactly p/2 nonadjacent edge v₁v₂, v₃v₄, …, v_p−1v_p, p ≥ 4. We have graph which is illustrated in Figure 17.

From Figure 17, we note that

(17)

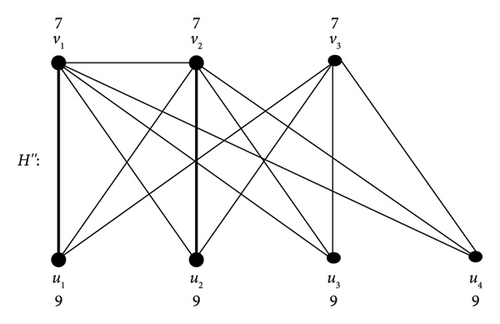
Remark 1. For disconnected graph Ǥ^″ of order 3 and an edge v₁v₂, we have a graph H^″ as shown in Figure 18; it is clear that Ǥ^″ is an induced subgraph of H^″ and M^∗(H^″) = Ǥ^″ because d^∗(v_i) = 7, d^∗(u₁) = 9 for i = 1, 2, 3 and d^∗(u₄) = 8

Now, consider a disconnected graph Ǥ of ᶇ nonadjacent edges and ᶆ isolated vertices. Let p = ᶆ + 2ᶇ. Take H^∗ as

with ᶇ nonadjacent edges v₁v₂, v₃v₄, …, v_2ᶇ−1v_2ᶇ, and ᶆ as removed edges v_2ᶇ+1u_2ᶇ+2, v_2ᶇ+2u_2ᶇ+3, …, v_2ᶇ+ᶆu_2ᶇ+ᶆ+1, which is shown in Figure 19.

(18)

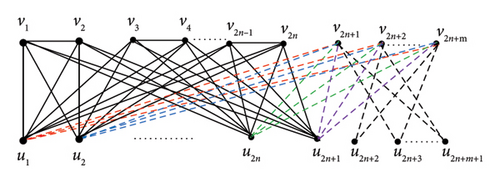
Therefore, Ǥ is an induced subgraph of H and M^∗(H^∗) = Ǥ.

4. Conclusions

In this article, a new definition “RDM-graph” was presented, which through it is possible to obtain new graphs that is more relevant and consistent, which allows us to find new properties that can be described as an application for some chemical compounds that need bonding between their atoms in order to be more stable.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

All the authors have equally contributed to the final manuscript.

Funding

No funding was received for this paper.

Acknowledgments

This paper was conducted at the College of Computer Science and Mathematics, University of Mosul, Iraq, and the General Directorate of Education in Nineveh, Iraqi Ministry of Education-Mosul, Iraq.

Open Research

Data Availability Statement

The information and data used in this research are theoretical and not derived from any other research or institution.

References

1 Buckley F. and Harary F., Distance in Graphs, 1990, Addison-Wesley.
Google Scholar
2 Chartrand G. and Lesniak L., Graphs and Digraphs, 2016, 6th edition, Wadsworth and Brooks/Cole.
Google Scholar
3 Wayne G. and Ortrud R. O., Distance in Graphs, Structual Analysis of Complex Networks. (2010) 49–72, https://doi.org/10.1007/978-0-8176-4789-6_3, 2-s2.0-84874967008.
10.1007/978-0-8176-4789-6_3
Google Scholar
4 Chartrand G., Johns G. L., and Tian S., Detour Distance in Graphs, Annals of Discrete Mathematics. (1993) no. 55, 127–136, https://doi.org/10.1016/S0167-5060(08)70381-9, 2-s2.0-77957071580.
10.1016/S0167-5060(08)70381-9
Google Scholar
5 Herish O. A. and Ivan D. A., The Restricted Detour Polynomial of the Theta Graph, Al-Rafidain Journal of Computer Sciences and Mathematics. (2020) 14, no. No.1, 13–20, https://doi.org/10.33899/CSMJ.2020.164664.
10.33899/CSMJ.2020.164664
Google Scholar
6 Dankelmann P., Goddard W., Henning M. A., and Swart H. C., Generalized Eccentricity, Radius, and Diameter in Graphs, Networks. (1999) 34, no. 4, 312–319, https://doi.org/10.1002/(SICI)1097-0037(199912)34:4%253C312::AID-NET11%253E3.0.CO;2-V.
10.1002/(SICI)1097-0037(199912)34:4<312::AID-NET11>3.0.CO;2-V
Web of Science® Google Scholar
7 Caceres J., Marquez A., and Puertas M. l., Steiner Distance and Convexity in Graphs, European Journal of Combinatorics. (2008) 29, no. 3, 726–736, https://doi.org/10.1016/j.ejc.2007.03.007, 2-s2.0-39749171158.
10.1016/j.ejc.2007.03.007
Web of Science® Google Scholar
8 Mustafa R., Ali A. M., and Khidhir A. M., M_n–Polynomials of Some Special Graphs, Iraqi Journal of Science. (2021) 62, no. 6, 1986–1993, https://doi.org/10.24996/ijs.2021.62.6.24.
10.24996/ijs.2021.62.6.24
Google Scholar
9 Rasool K. B., Rashed P. A., and Ali A. M., Relations Between Vertex–Edge Degree Based Topological Indices and Mve-Polynomial of r−Regular Simple Graph, European Journal of Pure and Applied Mathematics. (2023) 16, no. 2, 773–783, https://doi.org/10.29020/nybg.ejpam.v16i2.4698.
10.29020/nybg.ejpam.v16i2.4698
Web of Science® Google Scholar
10 Najm E. A. and Ali A. M., Some Properties of Generalized Schultz and Generalized Modified Schultz Distances, Palestine Journal of Mathematics. (2024) 13, no. 4, 921–933.
Google Scholar
11 Najm E. A. and Ali A. M., Generalized Schultz and Modified Schultz Polynomials for Some Special Graphs, Iraqi Journal of Science. (2024) 65, no. 1, 271–279, https://doi.org/10.24996/ijs.2024.65.1.23.
10.24996/ijs.2024.65.1.23
Google Scholar
12 Khidhir A. M., Ali A. M., and Aziz S. M., Application of Width Distance on Semi–Star Link Satellite Constellation, Journal of Discrete Mathematical Sciences and Cryptography. (2021) 24, no. 3, 797–807, https://doi.org/10.1080/09720529.2020.1843265.
10.1080/09720529.2020.1843265
Web of Science® Google Scholar
13 Elumalai A., Graph Theory Applications in Computer Science and Engineering, Malaya Journal of Matematik. (2020) no. 2, 4025–4027, https://doi.org/10.26637/MJM0S20/1043.
10.26637/MJM0S20/1043
Google Scholar
14 Haithm N. M., Hanadi D. S., and Ahmed M. A., Zagreb Indices for Chains of Identically Hexagonal Cycles, Palestine Journal of Mathematics. (2023) 12, no. 1, 147–157.
Google Scholar
15 Chen Z., Dehmer M., and Shi Y., A Note on Distance-Based Graph Entropies, Entropy. (2014) 16, no. 10, 5416–5427, https://doi.org/10.3390/e16105416, 2-s2.0-84908439470.
10.3390/e16105416
Web of Science® Google Scholar
16 Herish O. A., Ivan D. A., and Rashad R. H., Average Distance and Average Restricted Detour Distance of a Straight Chain of K-Wheels Graph, Palestine Journal of Mathematics. (2023) 12, no. 4, 399–409.
Google Scholar
17 Ahmed M. A., Haveen J. A., and Gashaw A. M., Detour Polynomials of Generalized Vertex Identified of Graphs, Baghdad Science Journal. (2023) 20, no. 2, 705–712, https://doi.org/10.21123/bsj.2022.6350.
10.21123/bsj.2022.6350
Web of Science® Google Scholar
18 Abdullah H. and Ali I., Restricted Detour Polynomial of a Straight Chain of Wheel Graphs, Al-Rafidain Journal of Computer Sciences and Mathematics (RJCM). (2023) 17, no. 1, 99–106, https://doi.org/10.33899/csmj.2023.179505.
10.33899/csmj.2023.179505
Google Scholar
19 Azari M., On the Gutman Index of Thorn Graphs, Kragujevac Journal of Science. (2018) no. 40, 33–48, https://doi.org/10.5937/KgJSci1840033A.
10.5937/KgJSci1840033A
Google Scholar

All articles

On Restricted Detour Median of Special Graphs

Abstract

1. Introduction