Predicting origin-destination (OD) flow presents a significant challenge in intelligent transportation due to the intricate dynamic correlations between starting points and destinations. Although existing OD prediction methodologies leveraging graph neural networks have demonstrated commendable performance, they often struggle to address the complexities inherent in two-sided correlations. To address this gap, this paper introduces a novel approach, the 2D spatiotemporal hypergraph convolution network (2D-HGCN), designed specifically for forecasting OD traffic flow. Our proposed model employs a two-stage architecture. Initially, temporal characteristics of traffic flow between OD pairs are captured using a 1D convolution neural network (1D-CNNs). Subsequently, a 2D hypergraph convolutional network is introduced to uncover spatial correlations in OD flow patterns. The unique aspect of our 2D-HGCN lies in its dynamic hypergraph, which evolves over time, enabling the model to adaptively learn changing spatial dependencies. Experimental evaluation conducted on real-world datasets highlights the efficiency of our suggested model for predicting OD flows. Our results demonstrate a promising predictive performance, showcasing the ability of the 2D-HGCN to effectively capture the intricate dynamics of OD traffic flow.

1. Introduction

Applications for ride-hailing, such as DiDi, UCAR, and Uber, are now broadly embraced for daily travel necessities. These platforms aim to offer convenient ride services to passengers and enhance public transportation efficiency. For example, in Beijing alone, DiDi logs millions of requests for taxis each day. To offer unparalleled services and secure financial success, platforms for ride-hailing require immediate understanding of customer needs. They must efficiently assign orders to service vehicles ahead of time to meet passenger mobility patterns and maximize profits by identifying popular and profitable routes from historical passenger demand data, thus minimizing empty rides. Therefore, rather than just predicting passenger demand quantities within a region, understanding passenger demands in terms of trip origins and destinations is crucial. This information not only reflects passenger demand strength but also serves as a foundation for mining valuable mobility patterns. Origin-destination (OD) flow prediction is very important for understanding passenger travel demand at both local region and global city network.

Effectively predicting traffic flow within urban areas has become a fundamental task in the domain of intelligent transportation systems. Urban traffic flow encompasses inflow and outflow, indicating the passenger count traveling to or from the target regions, and OD flow, indicating passenger travel between stations. Figure 1 clearly shows the OD traffic flow between different parts of the city, while observing the figure, we can find that some interregional traffic flows show similar patterns. These similar patterns may reflect similar travel habits or travel demand. Despite the emphasis on predicting inflow or outflow, there has been inadequate attention directed toward OD flow prediction. In addition, we can see that there are complex higher order correlations between the origin and the destination. These correlations can include multihop flows and interdependencies between multiple O-D pairs, which are influenced by temporal dynamics, spatial proximity, and contextual factors such as public events or traffic conditions. There are also complex correlations between origins and origins and between destinations and destinations. These higher order dependencies reflect the interconnected nature of urban mobility flows and highlight the need for models capable of capturing these complex patterns.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

OD traffic flow between multiple areas.

Conventional methods for predicting OD traffic flow often fail to grasp the complex spatial and temporal interconnections that are fundamental to OD dynamics. Recently, researchers have attempted to predict OD matrices using various deep neural network architectures. They have employed graph convolutional networks (GCNs) and their variants to capture spatial interdependencies within transportation systems. Recurrent neural networks (RNNs) are used to model temporal dependencies in traffic prediction. Although these methods have achieved good performance in traffic prediction, they still have many limitations:

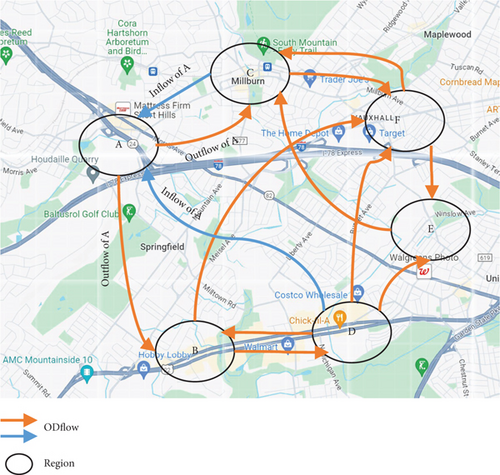
1.
Firstly, they struggle to handle complex two-sided correlations. For the OD flow problem, there exist correlations among both starting points and destinations. Existing approaches only consider correlations among origins and disregard those among destinations.
2.
Additionally, these methods tend to utilize the predefined graph to capture spatial relationships. For instance, a deep learning method based on GCNs for ride-hailing networks establishes connections between regions considering distance and traffic volumes. But spatial correlations designed manually may not accurately represent the changes in spatial interdependencies caused by diverse factors, potentially resulting in bad prediction outcomes.

The real spatial correlation in the road network is hidden in the data, and this implicit spatial correlation cannot be expressed simply by connectivity or distance. Two spatially distant nodes may be strongly correlated. Recently, there has been a focus on research involving graph convolution operations that employ adjustable adjacency matrices. However, the adaptive matrix cannot model the spatial association between nodes well. Meanwhile, the complex spatial associations between nodes cannot be represented by a simple graph. To tackle these issues, we present a hypergraph approach for modeling the complex interrelations described previously. We developed a 2D hypergraph convolution technique to analyze the attributes of both the origin and destination. The dynamic hypergraph with hyperedges is designed to represent nonpairwise relationships between vertices, capturing evolving correlations among regions as the starting point and destination. Finally, we utilize a 1D convolution neural networks (1D-CNNs) to learn temporal dynamics from these historical high-level representations.

•
To better to model complex two-sided correlations between the starting point and destination, dynamic hypergraphs is introduced in our method for OD traffic flow prediction.
•
2D spatiotemporal hypergraph convolution is designed for OD traffic flow prediction. It leverages hypergraph-based spectral convolution and temporal convolution layers to achieve accurate predictions.
•
Experimental outcomes from tests on two public OD datasets confirm our model’s efficacy.

2. Related Works

2.1. Traffic Demand Forecasting

Over the course of several decades, the realm of OD flow prediction has been extensively explored, yielding a plethora of proposed models to grapple with this multifaceted issue. A prominent strategy for addressing the complexities of static OD prediction problems centers on the application of the gravity model. Nonetheless, the model’s efficacy is fundamentally constrained by the dynamic and nonlinear attributes characterizing transportation flows, which transcend the capacities of its underlying mathematical framework. Consequently, to address these challenges, statistical models like generalized least squares (GLS), maximum likelihood (ML) estimation, and Bayesian methodologies have emerged as standard tools for navigating the intricacies of OD estimation and prediction. For example, GLS is designed to reduce the discrepancy between predicted and actual flows [1, 2], whereas ML estimators aim to enhance the probability of observed flows by considering the estimated OD flows [3]. Within the Bayesian framework, the posterior probability is calculated through the amalgamation of prior probability expressions derived from OD flows and the likelihood of link flows, conditioned on estimated OD flows. The Bayesian approach [4, 5] diligently endeavors to unveil OD flows that maximize this posterior probability.

In recent years, the advent of deep neural networks has demonstrated their effectiveness in approximating nonlinear features across a diverse array of applications, encompassing classification, regression, and control problems [6, 7]. Simultaneously, supervised learning has firmly established its pivotal position within the domain of deep learning. Convolutional neural networks (CNNs) excel in discerning spatial patterns, while RNNs have proven to be adept at capturing temporal patterns [8, 9]. Considering that transportation systems often take the shape of nodes and links, the prominence of graph-structured information is notably evident in this field. Notably, graph neural networks (GNNs) have garnered recognition for their effectiveness in handling such data [10]. Particularly, GCNs leverage the adjacency matrix to represent node connections, [11], a strategy that expedites convergence and bolsters predictive performance by incorporating network topology.

While a substantial body of literature has addressed zone-based demand prediction, there has been comparatively limited attention directed toward OD-based demand prediction. In a seminal work by Liu et al. [12], they unveiled a contextual spatial-temporal framework for forecasting OD taxi demand across New York. This innovative approach involved dividing the city into grid segments and using a three-dimensional matrix, where two dimensions correspond to the city’s geographical breadth and length, and the third dimension represented the total number of squares. This matrix proficiently encoded OD information, facilitating the ability of various CNN architectures to effectively capture spatial dependencies among square-shaped regions. Furthermore, in a notable study by Wang et al. [13], the calculation of the OD matrix was achieved using multitask learning based on grid embedding. This module played a vital role in acquiring preweighted features, involving the modeling of passengers’ spatial mobility patterns. Following this, the features were incorporated into the multitask learning framework to forecast upcoming OD demand. Moreover, Xiong et al. [14] introduced an innovative method that seamlessly integrated line GCN and Kalman filter techniques, the technique aimed at predicting OD demand across the entirety of the traffic network.

Deep learning–based OD prediction methods have achieved good performance. However, the complex and high-order correlations between origins and destinations are not well utilized, which limits the improvement of prediction performance. Furthermore, these models tend to rely on predefined static graph structures to capture spatial relationships among stations.

2.2. Hypergraph Learning

The need for addressing certain limitations inherent in graph representations, particularly their inability to adequately capture multiple associations, has led to the development of hypergraph learning theory. Hypergraph, initially a mathematical concept, encompasses the conventional graph as a specific case with a fixed order of two. Hypergraph learning was first introduced to the field of computer science by Zhou et al. [15]. Their pioneering work extended from the normalized graph cut and random walk theory to derive a normalized hypergraph cut and express the hypergraph Laplacian. Furthermore, they introduced a methodology for spectral clustering based on hypergraphs and put forth algorithms for transductive classification in their research article.

Building on the foundation laid by Zhou’s work, hypergraph learning methods have found gradual adoption in addressing clustering and classification challenges. Notable instances include the application of geometric hypergraph learning by Arya et al. [16] for social information classification and inhomogeneous hypergraph clustering by Li et al. [17] for network motif clustering. In addition, Li et al. [18, 19] introduced hypergraphs into the object counting domain to alleviate the problems of uneven object distribution and feature alignment. Leordeanu and colleagues [20] improved image matching by employing a semisupervised hypergraph learning approach, which increased resilience to changes in scale, distortions, and anomalies. In different domains, Su et al. [21] utilized vertex-weighted hypergraphs for classifying multiview 3D objects, integrating algorithms for hypergraph partitioning. Within a similar framework, Guo et al. [22] expanded the hypergraph partitioning to design algorithms for person reidentification. Their work introduced innovative hypergraph fusion methods, offering new perspectives on feature fusion.

It is noteworthy that hypergraph learning methods are progressively merging with GNN techniques, leading to the development of novel approaches. Gao et al. [23] and Liao et al. [24] have introduced methods for training GNNs on hypergraphs. These approaches, when applied to citation classification using the CORA dataset, have demonstrated improved accuracy. Wang et al. [25] extend hypergraph convolution to multitask learning for traffic prediction.

Hypergraph representation learning has been proven to be effective in addressing clustering and certain classification challenges, showcasing its capacity to capture high-order associations and its potential in the realm of hypergraph learning.

3. Methodology

In Figure 2, the fundamental concept of the proposed method revolves around the utilization of hypergraph representation to address the OD flow prediction challenge. This involves deriving hypergraph spectral convolution techniques based on the principles of hypergraph learning theory. Subsequently, a 2D hypergraph neural network framework is meticulously designed, incorporating dynamic mechanisms, to effectively accomplish the prediction of the OD matrix.

3.1. Overview

The prediction of OD demand represents a segmented aspect within the broader context of traffic flow forecasting. The task at hand pertains to addressing a distinct time series challenge, with the objective of predicting the OD matrix at a future time point based on data gathered from specific observation sites during preceding time intervals. The schematic diagram of OD traffic flow prediction is shown in Figure 2. Therefore, with a fundamental graph framework and a collection of past records, OD_t ∈ R^N×F denotes the input matrix of historical OD flow data with size of time t, and N represents the magnitude of stations, while F denotes the feature channel size; we predict the OD flow matrix at a future time. As a result, our ultimate objective is to forecast using the historical data and the structure of the graph, with T representing the temporal sequence length.

(1)

where p denotes time length of the future OD flow and H denotes the incidence matrix.

In the OD matrix, both regional and worldwide spatial interrelationships intertwine and exist on both ends of the source and destination. These OD flows are dynamic over time and encompass inherent spatial interconnection. We utilize the hypergraph representation of higher order connections to capture such spatial interdependence. Additionally, there exist correlations between origins and destinations that necessitate simultaneous modeling; thus, we leverage 2D-HGCN to capture both.

Furthermore, the travel patterns exhibited by individuals create a dynamic system. For example, individuals engage in commuting between their place of work and residence on weekdays, resulting in a cyclic travel pattern. This correlation undergoes dynamic fluctuations over time.

Figure 3 presents the model’s architecture. The input data consists of OD flow data and the graph structure. Initially, we construct dynamic hypergraphs based on the input data. Following this, both hypergraph Laplacian matrices and OD flow data are introduced into the 2D-HGCN. This network incorporates spatiotemporal blocks that integrate hypergraph convolution layers and temporal convolution layers. These combined layers effectively capture both spectral and temporal features associated with each vertex in the hypergraphs. Ultimately, the model proposed in this study produces predictions at the node level.

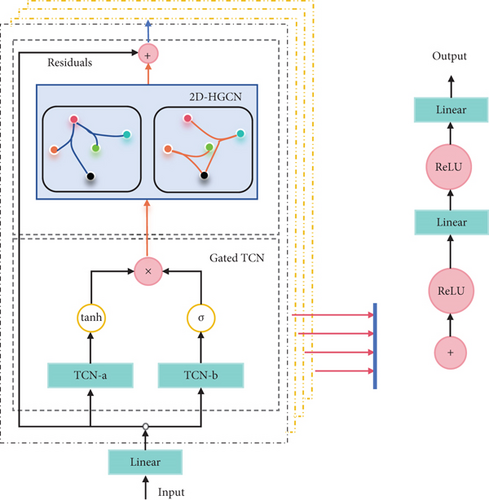
3.2. Dynamic Hypergraph Construction

Graphs denoted as G = (V; E) are commonly utilized topological structures consisting of abstract entities known as vertices. These vertices are linked in pairs through edges. Conversely, the original concept of a hypergraph G^h = (V; E^h) involves an extension of a graph where any subset of vertices can be covered by a hyperedge. This is a departure from traditional graphs, where the connections are limited to two-element subsets. To elaborate, the primary definition of a hypergraph involves a generalization of a traditional graph, which is specified by a vertex set V, hyperedge set E^h, and a weight matrix W, symbolized as

; hypergraph is considered regular if every vertex has the same degree. Typically, a standard graph is a 2-regular hypergraph, establishing an equivalence in certain definitions between graphs and hypergraphs. When constructing hyperedges, the number of nodes within each hyperedge is dynamically determined by the dataset’s characteristics. For instance, denser urban datasets with more interconnected locations tend to produce larger hyperedges, whereas sparse regions may result in smaller hyperedges. This adaptive construction enables the hypergraph model to better capture the spatial and temporal variability across different datasets, thereby improving prediction accuracy in diverse scenarios. In graph theory, the incidence matrix illustrates the connections among vertices and edges. In the case of an undirected hypergraph that lacks isolated vertices, it is represented as ∪_i∈Ie_i = V; the incidence matrix H ∈ R^N×I of N vertices and I hyperedges is defined as follows:

(2)

where the degree of a vertex v in a hypergraph is determined by the summation of weights w (e) of the hyperedges attached to the vertex:

(3)

where the symbol e denotes an individual hyperedge comprising a collection of vertices, while E represents the entire collection of hyperedges. The degree of a hyperedge is precisely determined by the count of vertices it connects:

(4)

In our method, hypergraph construction involves two main procedures: the construction of the primary hypergraph and the dynamic hypergraph . Algorithm 1 shows the process of hypergraph construction.

The primary hypergraph serves as the foundational representation of the network structure, while the dynamic hypergraph provides additional spatial insights into OD patterns for forecasting purposes. The acronym “OD” standing for origin-destination is a standard terminology in transit studies, used to analyze travel patterns in a specific area over temporal dimensions. As passenger travel patterns undergo dynamic changes, corresponding variations manifest in their OD relationships. To address this dynamism, we propose a novel approach utilizing diverse hypergraphs to capture a broader spectrum of temporal features.

To begin, we compute the average traffic tensor for identical hours across different days, resulting in a 24-h OD tensor denoted as X^(h), symbolizing traffic from the i-th origin to the j-th destination in the k-th time slot. Cosine similarity is then employed to quantify the correlation between two origins, producing values within the range of 0–1. A higher cosine value signifies a stronger correlation between the two origins. Hence, the correlation between the i1-th and i2-th origins is expressed as follows:

(5)

where COS denotes cosine similarity and Corr_t(O_i1, O_i2) indicates the calculated similarity coefficient between i1 and i2.

An analogous computation can be applied to ascertain the correlation between two destinations. The filtering parameters of the hypergraph convolutional network (HGCN) are shared across diverse time points, concurrently employing distinct hypergraphs for different time slots and employing separate hypergraphs for both origins and destinations.

Algorithm 1: Dynamic hypergraph construction.

Algorithm 1 Dynamic Hypergraph Construction
Input: Traffic tensor X^(h), Hypergraph incidence matrix H, Hyperedge set E^h, Vertices set V
Output: Dynamic hypergraph
Procedure: Construction of Dynamic Hypergraph
Initialize empty hyperedge set
for each time slot t do
Compute 24-hour OD tensor X^(h)(⋅, ⋅, t)
for each origin i₁ and i₂ do
Compute cosine similarity
if then Adjust threshold as needed
Add hyperedge to
for each destination j₁ and j₂ do
Compute cosine similarity
if then
Add hyperedge to
end if
end for
end if
end for
end for
return

3.3. 2D Hypergraph Convolution

In our methodology for OD flow prediction, we leverage a graph-based neural network. Nonetheless, applying graph convolution directly to hypergraphs presents challenges. Spectral hypergraph convolution is derived by integrating principles from hypergraph neural networks and traditional spectral graph theory.

Hypergraph partitioning based on spectral methods has become an important part of hypergraph research. Aiming at the research problem of partitioning on hypergraphs, the introduction of the hypergraph Laplacian matrix establishes the connection between hypergraph neural networks and traditional hypergraph research. The optimization process of hypergraph partitioning can be expressed as the following formula:

(6)

where u and v denote different vertices and ω(e) signifies the weight of a hyperedge e. δ(e) and d(v) represent the degree of the hyperedge e and vertice v, respectively. The formulation above could be expressed as 2f^TΔf. In this context, Δ is positive semidefinite and possesses exclusively real eigenvalues. The minimum eigenvalue of Δ is 0. These inherent characteristics lead to Δ being designated as the hypergraph Laplacian, represented as follows:

(7)

where H, D_V, and D_E denote, respectively, the incidence matrix, degree matrix of vertices, and hyperedges.

Therefore, for a hypergraph with N vertices, the dimensions of its Laplacian matrix Δ are N × N. Based on the eigendecomposition operation on the Laplacian matrix, we obtain the eigenvalue matrix Λ = diag(λ₁, ⋯, λ_n) and the orthonormal eigenvector Φ = diag (φ₁, ⋯, φ_n). Then, the calculation processes of Fourier transform and inverse Fourier transform are

and

, respectively. The hypergraph convolution process based on spectral graph theory is defined as follows:

(8)

where ⊙ represents the Hadamard product. Φ^Tg is considered a trainable hypergraph filter, which can be denoted as g_θ(Λ), serving as the representation for Fourier coefficients. The time complexity of the above equation is O(n²), and the eigendecomposition process in GNNs is very time-consuming. We use a streamlined yet efficient computational approach akin to the one proposed by [23] in 1stChebNet. Chebyshev polynomials are used to optimize the filtering process of hypergraph convolution.

(9)

Compared to conventional OD prediction methods, 2D-OD prediction effectively captures spatiotemporal correlations by introducing dynamic hypergraph CNNs. Emphasizing particularly the intricate spatial correlations at the origin and destination levels, this approach proves more potent in addressing bilateral correlations and dynamic spatial dependencies. As a result, it enhances the accuracy and robustness of OD flow prediction. We apply HGCN to both origins and destinations, extending it to a 2D-HGCN for processing a 2D signal on graphs. In particular, the computation during the 2D-HGCN process is as follows:

(10)

where the activation function σ(·) is introduced for nonlinearity. ×₁, ×₂, and ×₃ symbolize the fusion at the origin level, destination level, and feature level, respectively. The Laplace matrix L is obtained through Equation (6), L₁ represents the hypergraph Laplace matrix at the origin level, L₂ represents the destination level of the hypergraph Laplace matrix, and T(·) represents the Chebyshev polynomials.

represents the trainable parameter matrix, H(l) is the feature representation of the l-th layer. Timing dependencies captured by the temporal modeling part are propagated through multiple layers, enabling information traversal across more hops and introducing additional nonlinearity to enhance the model representation. After multiple layers of 2D-HGCN, a linear regression layer is employed to obtain the predicted traffic matrix. In other words, the feature dimension is aggregated into 1, resulting in X = H_L×₃W^(L), where X ∈ R^N×N.

3.4. Dynamic Spatiotemporal Hypergraph Neural Networks

Following the introduction of spectral hypergraph convolution, our focus transitions to exploring temporal convolution for capturing temporal flow features. Subsequently, we formulate spatiotemporal convolution blocks, which constitute the central component of our comprehensive framework.

Our temporal convolution layer (temporal convolutional network [TCN]) employs dilated causal convolution to capture the temporal trends of a node. Dilated causal convolution networks enhance the receptive field exponentially by increasing layer depth. In contrast to RNN-based methods, dilated causal convolution networks effectively handle long sequences in a nonrecursive manner, facilitating parallel computation and mitigating the gradient explosion issue. By commencing with the preservation of temporal causal order through zero-padding inputs, the dilated causal convolution ensures that predictions at the current time step depend solely on historical information. As illustrated in Figure 4, serving as a specific instance of standard 1D convolution, the dilated causal convolution operation traverses inputs by skipping values with a specified step. Mathematically, considering a 1D sequence input X ∈ R^T and a filter f ∈ R^k, the dilated causal convolution operation of x with f at step t is expressed as follows:

(11)

where d represents the dilation factor, governing the skipping distance. Through the stacking of dilated causal convolution layers with progressively increasing dilation factors, the model’s receptive field experiences an exponential expansion. This characteristic empowers dilated causal convolution networks to effectively capture longer sequences with a reduced number of layers, thereby conserving computational resources. For gated TCN, the gating mechanisms assume a pivotal role in RNNs, as they effectively regulate information flow through layers. They hold equal significance in temporal convolution networks. A fundamental gated TCN incorporates solely an output gate. Represented by the input X ∈ R^N×D×S, it can be represented as follows:

(12)

where Θ₁, Θ₂, b, and c symbolize model parameters, ⊙ denotes the element-wise product, g(·) serves as the activation function for the outputs, and σ(·) represents the sigmoid function, determining the ratio of information passed to the next layer. The integration of the gated TCN into our model facilitates the capture of intricate temporal dependencies.

Algorithm 2: 2D hypergraph convolution.

Algorithm 2 2D Spatio-Temporal Hypergraph Neural Networks for OD Flow Prediction
Input: Historical OD flow data matrix, OD_data (size: time t), Hypergraph representation parameters: V, E, ω, Temporal sequence length, n
Output: Predicted OD flow matrix at future time
Procedure: Construction of Dynamic Hypergraph
1. Construct the primary hypergraph H0 using V, E, and ω.
2. Construct the dynamic hypergraph 𝐻𝑑 to capture additional spatial information.
3. Apply spectral hypergraph convolution Hd with a trainable filter g.
4. Implement efficient computation using Chebyshev polynomial approximation.
5. Construct a 2D Hypergraph Convolutional Network (2DHGCN) for processing a 2D signal on graphs:
a. Apply hypergraph convolution (HGCN) to both origins and destinations.
b. Use dilated causal convolution as the temporal convolution layer (TCN).
c. Stack dilated causal convolution layers with increasing dilation factors.
d. Integrate a Gated TCN to capture intricate temporal dependencies.
6.Propagate temporal features through multiple layers of 2DHGCN.
7. Use a linear regression layer to aggregate feature dimensions for predicted traffic matrix.
end procedure
for each origin i₁ and i₂ do
Compute cosine similarity
if then Adjust threshold as needed
Add hyperedge to
for each destination j₁ and j₂ do
Compute cosine similarity
if then
Add hyperedge to
end if
end for
end if
end for
return

3.5. Loss Function

In the context of the 2D spatiotemporal hypergraph neural networks proposed in this work, the choice of a suitable loss function is crucial for measuring the model’s performance and guiding the optimization process during training. We opt for the mean absolute error (MAE) as our loss function. MAE is a commonly used loss function for regression problems, calculated as the average of the absolute differences between predicted and actual values. For our OD flow prediction model, the MAE loss can be defined as follows:

(13)

where N denotes the number of samples, y_i represents the actual OD flow value, and

is the model’s predicted OD flow value.

The selection of MAE offers several advantages. Firstly, it is robust to outliers due to its use of absolute differences, which is particularly important in traffic flow prediction where abnormal events such as accidents or construction may influence traffic conditions. Secondly, MAE provides an intuitive measure of the average discrepancy between model predictions and actual observations, enhancing interpretability. Lastly, MAE is a convex function, contributing to the stability of the optimization process.

In summary, choosing MAE as the loss function for our model ensures that reduces the average absolute difference between predicted and actual OD flow values, consequently enhancing its predictive efficacy.

3.6. Overall Algorithm

As shown in Algorithm 2, this paper introduces a dynamic spatiotemporal hypergraph neural network algorithm for predicting OD demand. The algorithm begins by establishing the primary hypergraph structure to capture fundamental network topology. Subsequently, spectral hypergraph convolution is applied for spatial feature learning, coupled with a dynamic hypergraph construction method to reveal additional spatiotemporal information behind passenger OD patterns. The integration of 2D hypergraph convolution effectively processes two-dimensional signals, capturing crucial spatiotemporal features. Temporally, dilated causal convolution captures node-specific temporal trends, and a gated TCN regulates information flow. Finally, multiple layers of 2D hypergraph convolution propagate the extracted spatiotemporal features, culminating in linear regression for predicting traffic matrices. This algorithm combines spatiotemporal hypergraph learning and CNNs, providing an effective solution for traffic flow prediction.

4. Experiments and Analysis

4.1. Datasets

Validating the proposed model involves utilizing two real OD flow datasets, specifically JAP(47) and NYC_TAXI, which are the historical OD flow data of Japan and New York, respectively.

The JAP refers to the Japan OD flow dataset collected in 2021, comprising a significant volume of human GPS trajectory data encompassing 5 million individuals across Japan’s 47 prefectures. The data attributes include anonymous IDs, timestamps, longitudes, latitudes, accuracy, and operating system types. The raw data file for a single month comprises approximately 1 TB in CSV format, with around 180 GPS records per user per day. After undergoing data cleaning and trip segmentation processes, each ID is associated with an average of 10 GPS records, corresponding to either origin or destination locations. The time period selected for analysis is from January 1, 2020, to February 28, 2021 (425 days) as the target time frame.

The NYC_TAXI dataset consists of 22,349,490 taxi trip records from NYC in 2015 (NYC 2017b), spanning from January 1, 2015, to March 1, 2015. We partitioned the entire city into 10 × 20 regions, with each region roughly measuring 1 km×1 km. Each time interval is set to 30 min in length.

4.2. Evaluating Indicator

Following the previous works, to evaluate the performance of all methods, we employ the MAE and root mean square error (RMSE) as the metrics. They are defined as follows:

(14)

(15)

where z represents the total number of testing samples, Xˆ_t denotes the predicted taxi demand, and X_t represents the corresponding ground truth in time interval t.

4.3. Experimental Settings

To achieve a more manageable distribution, we logarithmically transform the original OD tensor using the natural logarithm. The data is partitioned into training, validation, and test datasets with a ratio of 6.4:1.6:2, respectively. For the training process, the optimizer selected is Adam, with a batch size of 16 and a learning rate of 0.0001. The training algorithm is designed to terminate early if the validation error converges within 20 epochs or stop after 200 epochs. Both the observation step (α) and prediction step (β) are set to 7, indicating the utilization of the past 1 week of observations.

4.4. Baselines

The baselines contain seven methods, which include the following:

3.
ST-ResNet [26]: ST-ResNet is a deep learning–based approach, effectively addresses the challenging task of forecasting urban crowd flow by integrating spatiotemporal and external factors
4.
PCRN [27]: Built on ConvGRU, PCRN learn recent prediction data and periodic modes.
5.
ST-GCN [28]: A novel deep learning framework designed for time series prediction in the traffic domain. By formulating the problem on graphs and employing complete convolutional structures, ST-GCN efficiently captures spatiotemporal dependencies in traffic flow.
6.
DCRNN [29]: DCRNN is a typical traffic prediction method that use diffusion graph and gated recurrent unit to learn the spatial-temporal features.
7.
Graph WaveNet [30]: Graph WaveNet is an adaptive spatial-temporal prediction architecture for graph constructing, addressing limitations of predefined graph structures by accurately capturing hidden spatial dependencies and demonstrating superior performance on transportation network datasets.
8.
MPGCN [31]: MPGCN is a novel approach for OD flow prediction in intelligent transportation, adeptly addresses dynamic correlations and complex spatial dependencies by combining LSTM [32] for temporal feature extraction and a two-dimensional GCN.
9.
ODCRN [33]: It is composed of two learning modules: a predefined static graph learning module (e.g., adjacency matrix) as auxiliary input and a dynamic graph constructor (DGC) that obtain OD graph pairs dynamically based.

4.5. Forecast Results and Analysis

Tables 1 and 2, respectively, present the performance evaluation results of our proposed dynamic hypergraph OD passenger flow prediction model compared to other models. The results in two tables denote that 2D-HGCN outperforms baselines in various evaluation metrics, especially showing significant performance improvements on the NYC_TAXI dataset with a large number of nodes.

Table 1. Comparison of the overall performance between baselines and JAP datasets.

Model	MAE	RMSE
ST-ResNet	0.2822	0.4060
PCRN	0.2864	0.4044
ST-GCN	0.2910	0.4070
DCRNN	0.2954	0.4102
Graph WaveNet	0.2887	0.4040
MPGCN	0.2859	0.4011
ODCRN	0.2802	0.3947
2D-HGCN	0.2731	0.3854

Table 2. Performance of different methods on the whole NYC-TOD testing set.

Model	MAE	RMSE
ST-ResNet	1.7567	2.6609
PCRN	1.7072	2.6414
ST-GCN	1.3679	2.6528
DCRNN	1.3260	2.5211
Graph WaveNet	1.3360	2.5548
MPGCN	1.3876	2.6752
ODCRN	1.3854	2.6604
2D-HGCN	1.1749	2.4630

Specifically, the performance on the JAP dataset is as follows: ST-ResNet model and PCRN model use CNN to model spatial correlations, but their performance is limited due to the challenges of capturing non-Euclidean spatial correlations by CNN. ST-GCN model and DCRNN model include spatiotemporal modules, but their spatial modeling is restricted to predefined origin-level spatial modeling, overlooking comprehensive spatial relationships. Graph WaveNet uses adaptive matrices to further model spatial relationships. MPGCN model attempts to model spatial correlations and temporal correlations of OD data separately using graph convolution and LSTM, but graph convolution performs poorly in handling complex spatial correlations, and LSTM fails to capture the temporal dependencies of OD passenger flows effectively. In contrast, the ODCRN model employs two adaptive matrices to model spatial correlations at both origin and destination levels, resulting in improved predictive performance. However, the DHGCN (dynamic hypergraph) model achieves the best performance, further demonstrating the superior ability of hypergraphs to capture high-order spatial correlations.

It is worth noting that both the MPGCN and ODCRN models perform poorly on the NYC_TAXI dataset, which has a large number of nodes. The MPGCN model struggles to effectively model spatial correlations in the large-scale data using graph convolution, while the adaptive matrices used in the ODCRN model do not adequately capture the spatial relationships in data with numerous nodes, indicating limitations in the design of the adaptive matrices for modeling spatial correlations in large-scale data. Nevertheless, the dynamic hypergraph model continues to achieve the best results, further highlighting its exceptional capability in capturing high-order correlations.

4.6. Limitations

In a comprehensive analysis of the OD traffic prediction model, we have identified several notable advantages and, simultaneously, confronted significant challenges arising from its innovative use of hypergraph structures. The model endeavors to capture spatiotemporal dependencies more effectively, particularly in addressing the complexities associated with bidirectional correlations in OD traffic flow, by introducing hypergraph structures, specifically 2D hypergraph convolution. However, through a thorough examination, several key issues have surfaced, demanding more detailed investigation.

The model necessitates careful consideration in balancing complexity and efficiency. The introduction of intricate hypergraph structures may result in a decline in training and inference efficiency, a concern not to be overlooked in practical applications. For instance, the complexity of hypergraphs could potentially extend training times on large-scale datasets, thereby limiting the model’s practical utility. Therefore, a meticulous adjustment of model complexity is imperative to ensure enhanced performance without compromising efficiency. The initial attempt at employing hypergraph structures highlights an affirmative exploration of handling complex structures in OD traffic flow. Nevertheless, this signifies a need for additional efforts to optimize the construction of hypergraph structures in practical applications. For instance, while the model indicates advantages in complex scenarios, defining the specific attributes of “complexity” requires clarification through empirical research. Considering the diversity of urban landscapes, disparities in traffic flow structures across different regions necessitate specific scenario analyses to validate the model’s superiority in complex situations.

Regarding the applicability of hypergraph structures, the model underscores their advantages in dealing with intricate structures and asymmetric relationships. For example, in addressing scenarios with numerous one-way streets or traffic congestion in urban settings, the modeling capability of hypergraphs to capture asymmetric relationships may lead to more accurate predictions. Nevertheless, further insight is required to understand the specific scenarios where hypergraphs outperform traditional methods in practical applications. Moreover, the impact of model complexity on efficiency demands particular attention. The introduction of hypergraph structures may lead to a decrease in training and inference efficiency, especially in large-scale real-time applications. For example, during peak hours, exploring methodologies to maintain prediction accuracy while enhancing model real-time capabilities becomes a crucial avenue for in-depth investigation. Fine-tuning model complexity through detailed parameter adjustments and algorithm optimizations holds promise in alleviating efficiency concerns.

In conclusion, to unleash the full potential of the model, a deeper empirical investigation into its performance across various scenarios is imperative. Furthermore, detailed adjustments to hypergraph structures and parameter optimization are essential for enhancing the model’s robustness and practicality. Through concrete case studies and analyses of real-world scenarios, a more profound understanding of the model’s application potential in OD traffic prediction can be achieved, providing robust support for future research and practical implementation.

5. Conclusions

In this paper, we tackle the challenge of OD flow prediction by employing a dynamic hypergraph learning method and a 2D spatiotemporal hypergraph CNN. Our model capitalizes on the spatial correlation of travel OD to improve the precision of OD prediction. Through comprehensive experiments, we have demonstrated that 2D-HGCN surpasses the SOTA methods. Moving forward, we aim to refine the structure and parameters of our proposed approach and delve deeper into the theory of hypergraphs, exploring their potential applications in intelligent transportation systems.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work was supported by the Changsha City Education Science “14th Five-Year Plan” Research Project (Grant No. CJK2024079), titled “Research on Generative Artificial Intelligence Empowering Learning Support Services and Implementation Pathways for Full-Time Vocational College Farmer Students.” The funder provided financial support for the design, data collection, and analysis of this study.

Open Research

Data Availability Statement

Data can be obtained by contacting the authors.

References

1 Yu Nie H. M. and Zhang W. W. R., Inferring Origin–Destination Trip Matrices With a Decoupled GLS Path Flow Estimator, Transportation Research Part B: Methodological. (2005) 39, no. 6, 497–518, https://doi.org/10.1016/j.trb.2004.07.002, 2-s2.0-11244330349.
10.1016/j.trb.2004.07.002
Google Scholar
2 Cao P., Miwa T., Yamamoto T., and Morikawa T., Bilevel Generalized Least Squares Estimation of Dynamic Origin–Destination Matrix for Urban Network With Probe Vehicle Data, Transportation Research Record. (2013) 2333, no. 1, 66–73, https://doi.org/10.3141/2333-08, 2-s2.0-84883259990.
10.3141/2333-08
Google Scholar
3 Hazelton M. L., Estimation of Origin–Destination Matrices From Link Flows on Uncongested Networks, Transportation Research Part B: Methodological. (2000) 34, no. 7, 549–566, https://doi.org/10.1016/S0191-2615(99)00037-5, 2-s2.0-0033915027.
10.1016/S0191-2615(99)00037-5
Web of Science® Google Scholar
4 Carvalho L., A Bayesian Statistical Approach for Inference on Static Origin–Destination Matrices in Transportation Studies, Technometrics. (2014) 56, no. 2, 225–237, https://doi.org/10.1080/00401706.2013.826144, 2-s2.0-84900848731.
10.1080/00401706.2013.826144
Web of Science® Google Scholar
5 Hazelton M. L., Statistical Inference for Time Varying Origin–Destination Matrices, Transportation Research Part B: Methodological. (2008) 42, no. 6, 542–552, https://doi.org/10.1016/j.trb.2007.11.003, 2-s2.0-44149093609.
10.1016/j.trb.2007.11.003
Web of Science® Google Scholar
6 Wang S., Zhang Y., Yongli H., and Yin B., Knowledge Fusion Enhanced Graph Neural Network for Traffic Flow Prediction, Physica A: Statistical Mechanics and its Applications. (2023) 623, 128842, https://doi.org/10.1016/j.physa.2023.128842.
10.1016/j.physa.2023.128842
Web of Science® Google Scholar
7 Wang S., Lv Y., Peng Y., Piao X., and Zhang Y., Metro Traffic Flow Prediction via Knowledge Graph and Spatiotemporal Graph Neural Network, Journal of Advanced Transportation. (2022) 2022, no. 1, https://doi.org/10.1155/2022/2348375, 2348375.
10.1155/2022/2348375
Web of Science® Google Scholar
8 Lai G., Chang W.-C., Yang Y., and Liu H., Modeling Long-and Short-Term Temporal Patterns With Deep Neural Networks, Proceeding of the 41st International ACM SIGIR Conference on Research & Development in Information Retrieval, 2018, Association for Computing Machinery, 95–104, https://doi.org/10.1145/3209978.3210006, 2-s2.0-85051553862.
10.1145/3209978.3210006
Google Scholar
9 Wang Y., Long M., Wang J., Gao Z., and Yu P. S., Regularized Modal Regression With Applications in Cognitive Impairment Prediction, Advances in Neural Information Processing Systems. (2017) 30, 1448–1458, 29657513.
CAS PubMed Google Scholar
10 Jin M., Koh H. Y., Wen Q., Zambon D., Alippi C., Webb G. I., King I., and Pan S., A Survey on Graph Neural Networks for Time Series: Forecasting, Classification, Imputation, and Anomaly Detection, 2023, https://arxiv.org/abs/2307.03759.
Google Scholar
11 Yang F., Zhang H., and Tao S., Hybrid Deep Graph Convolutional Networks, International Journal of Machine Learning and Cybernetics. (2022) 13, no. 8, 2239–2255, https://doi.org/10.1007/s13042-022-01520-y.
10.1007/s13042-022-01520-y
Web of Science® Google Scholar
12 Liu L., Qiu Z., Li G., Wang Q., Ouyang W., and Lin L., Contextualized Spatial–Temporal Network for Taxi Origin-Destination Demand Prediction, IEEE Transactions on Intelligent Transportation Systems. (2019) 20, no. 10, 3875–3887, https://doi.org/10.1109/TITS.2019.2915525.
10.1109/TITS.2019.2915525
Web of Science® Google Scholar
13 Wang Y., Yin H., Chen H., Wo T., Xu J., and Zheng K., Origin-Destination Matrix Prediction via Graph Convolution: A New Perspective of Passenger Demand Modeling, Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, 2019, Association for Computing Machinery, 1227–1235.
10.1145/3292500.3330877
Google Scholar
14 Xiong X., Ozbay K., Jin L., and Feng C., Dynamic Origin–Destination Matrix Prediction With Line Graph Neural Networks and Kalman Filter, Transportation Research Record. (2020) 2674, no. 8, 491–503, https://doi.org/10.1177/0361198120919399.
10.1177/0361198120919399
Web of Science® Google Scholar
15 Zhou D., Huang J., and Schölkopf B., Learning With Hypergraphs: Clustering, Classification, and Embedding, Advances in Neural Information Processing Systems. (2007) 19, https://doi.org/10.7551/mitpress/7503.003.0205.
10.7551/mitpress/7503.003.0205
Google Scholar
16 Arya D. and Worring M., Exploiting Relational Information in Social Networks Using Geometric Deep Learning on Hypergraphs, Proceedings of the 2018 ACM on International Conference on Multimedia Retrieval, 2018, Association for Computing Machinery, 117–125.
10.1145/3206025.3206062
Google Scholar
17 Li P. and Milenkovic O., Inhomogeneous Hypergraph Clustering With Applications, Advances in Neural Information Processing Systems. (2017) 30, https://doi.org/10.1007/978-3-319-70139-4.
10.1007/978-3-319-70139-4
PubMed Google Scholar
18 Li B., Zhang Y., Zhang C., Piao X., and Yin B., Hypergraph Association Weakly Supervised Crowd Counting, ACM Transactions on Multimedia Computing, Communications and Applications. (2023) 19, no. 6, 1–20, https://doi.org/10.1145/3594670.
10.1145/3594670
CAS Web of Science® Google Scholar
19 Li B., Zhang Y., Zhang C., Piao X., Yongli H., and Yin B., Multi-Scale Hypergraph-Based Feature Alignment Network for Cell Localization, Pattern Recognition. (2024) 149, 110260, https://doi.org/10.1016/j.patcog.2024.110260.
10.1016/j.patcog.2024.110260
Web of Science® Google Scholar
20 Leordeanu M. and Sminchisescu C., Efficient Hypergraph Clustering, Artificial Intelligence and Statistics, 2012, PMLR, 676–684.
Google Scholar
21 Lifan S., Gao Y., Zhao X., Wan H., Ming G., and Sun J., Vertex-Weighted Hypergraph Learning for Multi-View Object Classification, Proceedings of the Twenty-Sixth International Joint Conference on Artificial Intelligence (IJCAI-17), 2017, AAAI Press, 2779–2785.
Google Scholar
22 Guo C., Zhao X., and Zou Q., Relation Network Based on Multi-Granular Hypergraphs for Person Re-Identification, Applied Intelligence. (2022) 52, no. 10, 11394–11406, https://doi.org/10.1007/s10489-021-02992-1.
10.1007/s10489-021-02992-1
Web of Science® Google Scholar
23 Gao Y., Feng Y., Ji S., and Ji R., HGNN+: General Hypergraph Neural Networks, IEEE Transactions on Pattern Analysis and Machine Intelligence. (2023) 45, no. 3, 3181–3199, https://doi.org/10.1109/TPAMI.2022.3182052.
10.1109/TPAMI.2022.3182052
PubMed Web of Science® Google Scholar
24 Liao X., Xu Y., and Ling H., Hypergraph Neural Networks for Hypergraph Matching, Proceedings of the IEEE/CVF International Conference on Computer Vision, 2021, IEEE, 1266–1275.
10.1109/ICCV48922.2021.00130
Google Scholar
25 Wang J., Zhang Y., Wang L., Yongli H., Piao X., and Yin B., Multitask Hypergraph Convolutional Networks: A Heterogeneous Traffic Prediction Framework, IEEE Transactions on Intelligent Transportation Systems. (2022) 23, no. 10, 18557–18567, https://doi.org/10.1109/TITS.2022.3168879.
10.1109/TITS.2022.3168879
Web of Science® Google Scholar
26 Zhang J., Yu Z., and Qi D., Deep Spatio-Temporal Residual Networks for Citywide Crowd Flows Prediction, Proceedings of the AAAI Conference on Artificial Intelligence. (2017) 31, no. 1, https://doi.org/10.1609/aaai.v31i1.10735.
10.1609/aaai.v31i1.10735
Google Scholar
27 Yu B., Yin H., and Zhu Z., Spatio-Temporal Graph Convolutional Networks: A Deep Learning Framework for Traffic Forecasting, 2018, https://arxiv.org/abs/1709.04875.
Google Scholar
28 Li Y., Yu R., Shahabi C., and Liu Y., Diffusion Convolutional Recurrent Neural Network: Data-Driven Traffic Forecasting, 2018, https://arxiv.org/abs/1707.01926.
Google Scholar
29 Wu Z., Pan S., Long G., Jiang J., and Zhang C., Graph WaveNet for Deep Spatial-Temporal Graph Modeling, 2019, 1907–1913, https://arxiv.org/abs/1906.00121.
Google Scholar
30 Kong X., Wang K., Hou M., Xia F., Karmakar G., and Li J., Exploring Human Mobility for Multi-Pattern Passenger Prediction: A Graph Learning Framework, IEEE Transactions on Intelligent Transportation Systems. (2022) 23, no. 9, 16148–16160, https://doi.org/10.1109/TITS.2022.3148116.
10.1109/TITS.2022.3148116
Web of Science® Google Scholar
31 Shi H., Yao Q., Guo Q., Li Y., Zhang L., Ye J., Li Y., and Liu Y., Predicting Origin-Destination Flow via Multi-Perspective Graph Convolutional Network, Proceedings of the 2020 IEEE 36th International Conference on Data Engineering (ICDE), 2020, IEEE, 1818–1821.
10.1109/ICDE48307.2020.00178
Google Scholar
32 Lin X., Liang Y., Zhang Y., Yongli H., and Yin B., IE-GAN: A Data-Driven Crowd Simulation Method via Generative Adversarial Networks, Multimedia Tools and Applications. (2024) 83, no. 15, 45207–45240, https://doi.org/10.1007/s11042-023-17346-x.
10.1007/s11042-023-17346-x
Web of Science® Google Scholar
33 Jiang R., Wang Z., Cai Z., Yang C., Fan Z., Xia T., Matsubara G., Mizuseki H., Song X., and Shibasaki R., Countrywide Origin-Destination Matrix Prediction and Its Application for COVID-19, Machine Learning and Knowledge Discovery in Databases. Applied Data Science Track: European Conference, ECML PKDD 2021, Bilbao, Spain, September 13–17, 2021, Proceedings, Part IV 21, 2021, Springer International Publishing, https://doi.org/10.1007/978-3-030-86514-6_20.
10.1007/978-3-030-86514-6_20
Google Scholar

All articles

2D Spatiotemporal Hypergraph Convolution Network for Dynamic OD Traffic Flow Prediction

Abstract

1. Introduction

2. Related Works

2.1. Traffic Demand Forecasting

2.2. Hypergraph Learning

3. Methodology

3.1. Overview

3.2. Dynamic Hypergraph Construction

3.3. 2D Hypergraph Convolution

3.4. Dynamic Spatiotemporal Hypergraph Neural Networks

3.5. Loss Function

3.6. Overall Algorithm

4. Experiments and Analysis

4.1. Datasets

4.2. Evaluating Indicator

4.3. Experimental Settings

4.4. Baselines

4.5. Forecast Results and Analysis

4.6. Limitations

5. Conclusions

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley