International Journal of Differential Equations

Volume 2025, Issue 1 4138176

Research Article

Open Access

Solar Energy Utilization of Radiative Implication of Trihybrid Xue-Modeled Nanofluid Flow for Oblique Stagnation Point Flows

Yasir Mehmood,

Yasir Mehmood

Department of Mathematics and Statistics , The University of Lahore , Sargodha , 40100 , Pakistan , uol.edu.pk

Search for more papers by this author

Areej Asif,

Areej Asif

Department of Mathematics and Statistics , The University of Lahore , Sargodha , 40100 , Pakistan , uol.edu.pk

Search for more papers by this author

Ikram Syed,

Ikram Syed

Department of Information and Communication Engineering , Hankuk University of Foreign Studies , Yongin , 17035 , Republic of Korea , hufs.ac.kr

Search for more papers by this author

Waseem Abbasi,

Corresponding Author

Waseem Abbasi

[email protected]

orcid.org/0000-0003-4114-7773

Department of Computer Science , The University of Lahore , Sargodha , 40100 , Pakistan , uol.edu.pk

Search for more papers by this author

Syed Sajid Ullah,

Syed Sajid Ullah

orcid.org/0000-0002-5406-0389

Department of Information and Communication Technology , University of Agder (UiA) , Grimstad , N-4898 , Norway , uia.no

Search for more papers by this author

Muhammad Shahid Anwar,

Muhammad Shahid Anwar

orcid.org/0000-0001-8093-6690

Department of AI and Software , Gachon University , Seongnam-si , 13120 , Republic of Korea , gachon.ac.kr

Search for more papers by this author

Yasir Mehmood,

Yasir Mehmood

Department of Mathematics and Statistics , The University of Lahore , Sargodha , 40100 , Pakistan , uol.edu.pk

Search for more papers by this author

Areej Asif,

Areej Asif

Department of Mathematics and Statistics , The University of Lahore , Sargodha , 40100 , Pakistan , uol.edu.pk

Search for more papers by this author

Ikram Syed,

Ikram Syed

Department of Information and Communication Engineering , Hankuk University of Foreign Studies , Yongin , 17035 , Republic of Korea , hufs.ac.kr

Search for more papers by this author

Waseem Abbasi,

Corresponding Author

Waseem Abbasi

[email protected]

orcid.org/0000-0003-4114-7773

Department of Computer Science , The University of Lahore , Sargodha , 40100 , Pakistan , uol.edu.pk

Search for more papers by this author

Syed Sajid Ullah,

Syed Sajid Ullah

orcid.org/0000-0002-5406-0389

Department of Information and Communication Technology , University of Agder (UiA) , Grimstad , N-4898 , Norway , uia.no

Search for more papers by this author

Muhammad Shahid Anwar,

Muhammad Shahid Anwar

orcid.org/0000-0001-8093-6690

Department of AI and Software , Gachon University , Seongnam-si , 13120 , Republic of Korea , gachon.ac.kr

Search for more papers by this author

First published: 19 March 2025

https://doi.org/10.1155/ijde/4138176

Academic Editor: Md. Kamrujjaman

Share a link

Email
Wechat
Bluesky

Abstract

This study uses the Xue model to explore how well a nanofluid transfers heat in a steady oblique stagnation-point flow. It examines the impact of nonlinear thermal radiation on a mixture of three different nanoparticles as the fluid moves along a stretching surface. This intended comparison model is unique and still scarce in the literature. Trihybrid nanofluids or composites have, therefore, been created to enhance heat transfer efficiency. Three different types of nanoparticles (Fe₃O₄, Cu, and TiO₂) are exploring circumstances where ethylene glycol is the base medium. A mathematical framework is developed. Using the appropriate transformations, the system of partial differential equations (PDEs) is transformed into an ordinary differential system of three equations (ODEs), which is evaluated numerically using the bvp4c method. This integrated technique facilitates the convergence process effectively. A detailed analysis is conducted of the graphical representation and the physical behavior of important factors. On temperature and velocity profiles, the impacts of several variables, including a thermal radiation, surface heating parameter, stretching ratio, and particle volume fraction, are investigated thoroughly. The results show that the (Fe₃O₄ + Cu + TiO₂)/ethylene glycol nanofluid outperforms with a high particle volume fraction of TiO₂. It has been demonstrated that (Fe₃O₄ + Cu + TiO₂)/ethylene glycol nanofluid with a high particle volume fraction of TiO₂ has considerably greater thermal radiation than other nanoparticles.The inclusion of nanofluids significantly improves heat transfer compared with conventional fluids due to their higher thermal conductivity, which is crucial for enhancing heat dissipation at stagnation points in solar systems.

1. Introduction

Technology is advancing quickly in all aspects of life; as a result, there is currently a huge increase in demand for renewable energy technology on a global scale, particularly solar thermal aspects. Solar thermal energy is created by gathering the energy of the sun and converting it into thermal energy, which can then be utilized for a range of tasks such as manually producing electricity. Because heat transfer processes are now a cause of variety of losses in solar thermal energy systems, several nanoliquids have been used to improve the functionality of solar panels by absorbing direct sunlight. The word “nano” is defined as 1 billionth of a meter, or 10⁻⁹ m, and could be formed by minuscule particles of the size of nano of various solid materials such as alumina and titanium oxide that have comparatively good thermal conductivity. Viscosity and thermal conductivity of nanofluids are considerably impacted by the size of the nanoparticles [1]. When the temperature and nanoparticle concentration rise, the thermal conductivity of nanofluids gradually rises. According to Xuan and Li [2], the addition of nanoparticles to a base fluid can improve heat transfer by up to 50%.

In general, it is acknowledged that solid particles conduct thermal energy more efficiently than liquids. Thus, adding nanoparticles to conventional fluids greatly enhanced their ability to conduct heat. Nanoparticles are the name given to these solid particles. Due to their excellent thermal conductivity and numerous engineering and industrial uses, as described by Choi and Eastman [3], nanofluid analysis was beginning to catch the interest of researchers. The typical convection of a two-dimensional cavity has been filled with nanofluids. Hoghoughi et al. [4] examined a variety of issues that are in opposition to the physical characteristics of nanofluids. The discovery of nano liquids has useful uses in manufacturing, heat exchangers, electronic device cooling, transportation, coatings, and biomedicine. Yu, Xu, and Liao [5] investigated whether nanofluids may be used to solve modern engineering issues concerning the effectiveness of polymerase chain reactions, radiators, solar collectors, and electronic cooling systems. The buoyancy-driven flows enclosed by an enclosure studied by Purusothaman, Murugesan, and Chamkha [6] were a crucial source of thermal properties and natural convection fluid flow.

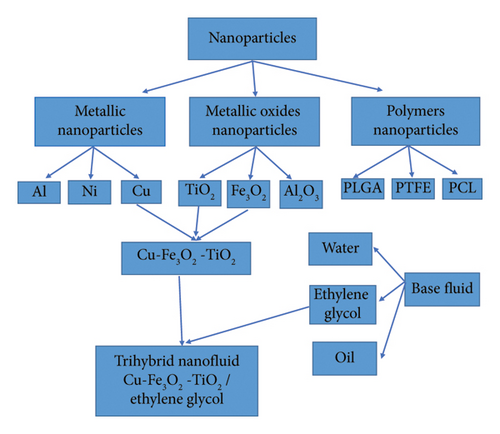
Nowadays, the objective of scientists and researchers is seeking hybrid nanofluids. It is made up of two or more irregular particles that are less than 100 nm in size. Due to their widespread use in the manufacturing of pharmaceuticals, automobiles, IT equipment (TVs, computers, and laptops), food packaging, buildings, home goods, cosmetics, fabrics, and textiles, we have chosen to utilize polystyrene and titanium oxide as our examples of nanoparticles in this article. Nanofluid characteristics are made available by Waini and Ishak [7] to analyze the heat transport of a hybrid nanofluid under shear flow. They examined the stability of a solution and came to the conclusion that one of the dual solutions is stable. Tassaddiq et al. [8] investigated the effects of CNT—Fe₃O₄/H₂O hybrid nanofluid on an infinite spinning disc. They found that compared with Fe₃O₄/H₂O, the heat transmission of the CNT—Fe₃O₄/H₂O hybrid nanofluid is higher. The characteristics of a hybrid nanofluid with Cu and Al₂O₃ nanoparticles that is surrounded by elliptical cylinders and has natural convection were examined by Tayebi, Öztop, and Chamkha [9]. They looked into whether entropy generation increases with increasing the Rayleigh number. Zahid, Akbar, and Abbasi [10] performed entropy generation in peristaltic flow of a hybrid nanofluid. For numerical solutions, the shooting method is used. It has been noted that an enlarged hall parameter causes the rate of heat transmission and entropy creation to decline. In order to examine whether the rate of entropy formation increases with radiation parameter, Yusuf et al. [11] examined a stretched sheet with nonlinear radiations on a hybrid nanofluid. Wanatasanapan, Abdullah, and Gunnasegaran [12] used a fixed volume percent of TiO₂ and Al₂O₃ particles and a temperature range of 30°C–70°C. They came to the conclusion that a 50:50 hybrid nanofluid at 70°C had the highest thermal conductivity. Said et al. [13] utilized MATLAB to analyze hybrid nanofluid at various doses. Entropy formation increases with increased nanoparticle volume concentration. At 60°C, there was a noticeable increase in thermal conductivity of 19.14. In a rotating cylinder, a hybrid nanofluid with slip and sloping MHD was taken into consideration by Abbas et al. [14]. Arani and Aberoumand [15] discussed the effects of the silver-CuO/H₂O nanofluid with stretched sheet and stagnation point. Along with the shooting technique, they employed the RK approach. They get to the conclusion that for hybrid nanofluid with injection/suction parameter, the heat transfer rate increases by 100%. Li, Wang, and Luo [16] investigated the improvement of heat transmission in a radiator of a car using hybrid nanofluid. They discovered that thermal conductivity increases by 32.01% at 0.4% volume fraction. In addition, squeezed flow across a porous sensor surface was investigated. Results indicated that for λ ≤ −1, a solution was obtained. They also come to the conclusion that only the first option is stable.

Naganthran, Nazar, and Pop [17] showed how a viscoelastic fluid passes over a shrinking sheet that has an oblique stagnation point. By converting the equations into Lagrangian coordinates, Moshkin, Pukhnachev, and Bozhkov [18] constructed the theory of the unstable Maxwell fluid. Weidman [19] indicated the impact of the Hiemenz stagnation point on the rotating plate. Hybrid nanofluids have attracted a lot of attention because of their excellent improvement in thermal performance. In order to evaluate the effects of hybrid nanoparticles on the thermal performance of working fluids, researchers have suggested models for effective thermal characteristics in terms of hybrid nanoparticles. For instance, Chamkha, Dogonchi, and Ganji [20] investigated the impact of hybrid nanoparticles on the working fluid’s thermal performance. Afridi, Qasim, and Saleem [21] examined the impact of hybrid nanostructures on working fluid thermal performance improvements during temperature fluctuations. By precisely solving the Navier–Stokes equations, Hiemenz [22] was the first to study the stagnation point flow. Steady or unsteady, viscid or inviscous, oblique or normal, two or more dimensions, and onward or opposing are all characteristics of stagnation point flows. Similar flow typically condenses when fluid is traveling toward the zone of stagnation of a hard surface that has been kept in motion, as stated by Khan et al. [23]. In addition to the heat transmission characteristic, stagnation point flows are also quite evident in the manufacturing of paper, rotating melt spinning processes, filaments, continuous molding, and crystal puffing. Numerous industrial applications for non-Newtonian fluids exist, including in high molecular weight systems, the majority of multiphase mixes, foods, and solutions. Isolated gas bubbles are sorted in the fluids provided by Zhan et al. [24] when air is used in processes including mixing, agitation, kneading, and dispersion. Biological fluids, natural products, lavas and magmas, food products, dairy wastes, building materials, agricultural wastes, polymer melts and solutions, multiphase mixtures, soap solutions, and personal care items such as toiletries and cosmetics are just a few examples of materials that exhibit non-Newtonian flow characteristics, given by Ijaz, Zeeshan, and Bhatti [25]. Non-Newtonian fluids have a significant role in engineering sciences, the medical community, and business. Non-Newtonian fluids are finding more and more uses in the polymer extrusion, petroleum-drilling industries, steel making, and glass blasting. According to Hussain et al. [26], just a few polymers are used in agriculture, communication equipment, and medicine. Chen et al. [27] found that Cu–EGW, Al₂O₃–EGW and Fe₃O₄–EGW had equilibrium temperature values that were greater than the base fluid under the same heating conditions. Cu–EGW nanofluid had the greatest equilibrium temperature and the quickest heating time to reach that temperature. Compared with Al₂O₃–EGW and Fe₃O₄–EGW nanofluids, Cu–EGW nanofluid demonstrated superior heat transfer performance. This results from the existence of nanoparticles, which raises the heat conductivity of the nanofluid. The conclusion is that heating times and heat transfer capabilities of nanofluids are superior to those of basic fluids. According to Sahin and Namli [28], the thermal characteristics of Al₂O₃-oil nanofluids were superior to those of TiO₂-oil nanofluids. Al₂O₃/water nanofluids were employed by Nguyen et al. [29] in the cooling systems of electrical devices, and they saw significant improvements in coefficients of heat transport for a low level of nanoparticle volume percentage.

The main purpose of the previously described investigation is to scrutinize the thermal performance of the nonorthogonal stagnation flow of ethylene-based nanofluids containing Fe₃O₄, Cu, and TiO₂ trihybrids nanoparticles striking on a stretching surface. The most effective solar nanoliquid system needs to be identified through research and characterization. Therefore, the thermal conductivity model, i.e., the Xue model [30], is used in this study to generate and evaluate nanoliquids. The prevailing results are analyzed graphically and numerically. This study aims in order to respond to the following queries:

1.
What is the effect of trihybrid nanoparticles on thermal performance?
2.
What effects do velocity ratio parameters with trihybrid nanoparticles have on temperature and velocity profiles?
3.
Does stretching work well to raise temperatures in systems of solar thermal?
4.
How heat transmission of trihybrid nanoparticles (Fe₃O₄, Cu, and O₂) will be impacted by nonlinear thermal radiation? Which nanoparticle will operate in solar thermal systems most effectively?
5.
In ethylene glycol fluid containing Fe₃O₄, Cu, and TiO₂ nanoparticles, how is the temperature profile affected by the temperature ratio parameter? Which nanoparticle will be responsible for the increased fluid heating in solar thermal systems?
6.
Which kind of nanoparticle performs the best in a solar energy system?

2. Mathematical Model

Take into consideration a steady, two-dimensional, and incompressible flow of trihybrid nanofluids at a stagnation point (the nanoparticles may improve heat transmission and thermal conductivity at this point) formed by suspending Fe₃O₄, Cu, and TiO₂ in base fluid, that is, ethylene glycol impinging on a surface that is stretching. In solar collectors like flat-plate or parabolic trough systems, the heat transfer rate can be greatly increased by using trihybrid nanofluids. As shown in Figure 1, in order to expand the surface while preserving its origin, two equal forces that opposite in direction are applied along the x-axis with velocity u = ex and y-axis is in the normal direction. Furthermore, the plate is assumed to have a temperature T_w (ambient temperature) and liquid having temperature T_∞ that is distant from the surface, where T_w > T_∞. Moreover, a higher temperature than the fluid is crucial for better heat transfer in solar thermal systems. Provided that there is no slide between the liquid and trihybrid nanoparticles, they are included in thermal balance. The thermophysical properties of nanoparticles (Fe₃O₄, Cu, and TiO₂) and base fluid (C₂H₆O₂) are shown in Table 1, and the flowchart of the formation of trihybrid nanofluid is also shown in Figure 2.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Geometry of a model.

Table 1. Thermophysical characteristics of trihybrid nanofluids (Fe₃O₄, Cu, and TiO₂) and basefluid (C₂H₆O₂) [31, 32].

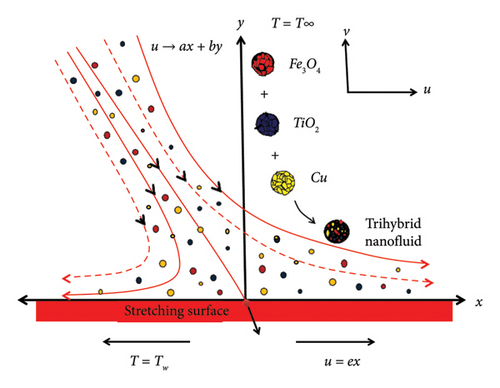
Base fluid/nanoparticles	Ethylene glycol	Fe₃O₄	Cu	TiO₂
ρ(kg/m³)	1114	5200	8933	4250
C_p(J/kgK)	2415	670	385	686.2
k (W/mK)	0.252	9.7	401	8.9538

3. Problem Statement

Based on above assumptions, the governing equations take the following form [32–35].

()

The corresponding boundary conditions are described as

()

Consider the following relations of stream equation:

()

Putting of stream equation (6) into equations (1)–(4) and using p_yx = p_xy to obliterate the following pressure term:

()

Suitable boundary conditions are

()

Now, shear stream is provided by γ = b/e, and v and u are components of velocity in the y direction and x direction, respectively. We obtain the solution of equations (7)–(9) in the form of

()

We derive the following ordinary differential equations by inserting equation (10) into equations (7)–(9) after simplification by the relevant boundary conditions and comparing the x-powers, we reached out the following results:

()

with boundary conditions

()

Using the limit y approaches to ∞ in equations (11) and (12) and using boundary condition f^′(∞) = a/e and g^″(∞) = γ, and we get B₁ = a²/e² and B₂ = −Aγ, respectively. As a result of these substitutions, equations (11) and (12) become

()

Introducing

()

Using equation (18) in equation (17), we have

()

with boundary conditions

()

From the aforementioned equations, the dimensionless parameters are

()

After substitution of equation (22) in equations (15), (16) and (19), we have

()

whereas

()

As a result equations (22)–(24), assume the following form with same boundary conditions given in equations (14) and (20):

()

3.1. Thermophysical Characteristics of Trihybrid Nanofluids

There are many mathematical formulas are given in the following for the thermophysical characteristics of trihybridity nanofluid (Sunder et al. [36], Ghadikolaei et al. [37], and Hayat and Nadeem [38]).

•
Viscosity:
Depending on the system’s geometry and flow conditions, viscosity may affect how heat is transferred. It is determinable by using the following equation:
()
•
Effective heat capacity:
The effective heat capacity has an impact on heat transfer characteristics. It measures how much heat is needed to change the temperature of a substance by one degree. It can be calculated as follows:
()
•
Density:
The density has an effect on heat transfer. With the following theoretical model equation, it may be estimated:
()
•
Thermal conductivity:
The heat transfer rate is greatly influenced by thermal conductivity. With the following theoretical model equation, it may be estimated:
()
•
Physical quantities
The dimensional form of N_u and C_f are given in equations (34) and (35).
()

()

Equation (36) mentions the dimensionless expression of the aforementioned quantities.

()

Here, Re = ex²/ν_f is the local Reynold number.

4. Numerical Solutions

The ordinary differential equations (22)–(24) are a nonlinear system subject to the condition equations (14) and (20) that have been numerically examined using the shooting method for different parameter values. Furthermore, it is important that limited values η_∞ should be determined. For numerical computations, the boundary conditions on η_∞ are limited, i.e., η = 4 and 7 for the given case, which is necessary to explain the behavior of the desired equation. The highest value of has been regarded as η = 7 because for η > 7, the solutions are discovered settled asymptotically. Using MATLAB’s built-in bvp4c function helps to enhance the results even more. For the first order differential equations, we can obtain the following equations in addition to the initial conditions and representing y₁ to f, y₄ to h, and y₆ to θ have the following equations:

()

Newton’s method is used to insert the values of s, t, and u until the following requirements are met, where ϵ > 0.

()

All mathematical solutions are done with ϵ = 10⁻⁶. Equation (39) provides transformed boundary conditions.

()

We built in MATLAB function bvp4c to achieve nearly identical numerical results for various quantities of interest, and we validated our MATLAB code with a limiting case comparison to increase reliability, as mentioned in Table 2.

Table 2. Comparing the numerical values of h^′(0) and f^″(0) with Nadeem, Mehmood, and Akbar [33] and Labropulu, Li, and Pop [39], when ϕ_thnf = 0.

Values of a/e	f^″(0)			h^′(0)
Values of a/e	Present	Labropulu, Li, and Pop [39]	Nadeem, Mehmood, and Akbar [40]	Present	Labropulu, Li, and Pop [39]	Nadeem, Mehmood, and Akbar [40]
1.0	0.0	0.0	0.0	1.0	1.0	1.0
0.8	0.29935	−0.29938	−0.29938	0.93471	0.93430	0.93473
0.3	0.84938	−0.84942	−0.84942	0.60629	0.60573	0.60631
0.1	−0.96930	−0.96938	−0.96938	0.26339	0.26278	0.26341

4.1. Comparison of Numerical Results

Furthermore, a comparison of the recently calculated findings and the literature is made in limited circumstances to confirm the accuracy of the recently calculated results compared with previously published data. Using comparisons between Nadeem, Mehmood, and Akbar [33] and Labropulu, Li, and Pop [39], Table 2 is constructed to assess the accuracy of the mathematical model presented.

To enhance the clarity of the comparison, Table 3 presents the temperature profile that has been computed for multiple values of y. This table clearly shows that the temperature profile of TiO₂/C₂H₆O₂ nanofluid is higher than the temperature profile of the Fe₃O₂/C₂H₆O₂ and Cu/C₂H₆O₂ nanofluids.

Table 3. Numerical values of −θ^′(y) for P_r = 6.5 and A = 0.5.

ϕ₁	ϕ₂	ϕ₃	a/e	N_r	θ_w	−θ^′(y)
0.01	0.02	0.03	0.6	0.5	0.5	1.376281658610982
0.02						1.328168016600648
0.03						1.283154155398341
	0.01					1.418693955226068
	0.02					1.376281658610982
	0.03					1.336198160102594
		0.01				1.563327148936855
		0.02				1.462967315952215
		0.03				1.376281658610982
			0.1			1.280511945570944
			0.2			1.300873990245872
			0.3			1.324372119314320
				0.1		1.390899484193149
				0.2		1.394557696856367
				0.3		1.397855720092215
					0.1	1.424509961399272
					0.2	1.428401761547879
					0.3	1.427955263670749

5. Analysis and Discussion of Results

The aforementioned problems are solved using MATLAB software’s bvp4c function. For the situation under consideration, the tolerance is kept at 10⁻⁶, and Δη = 0.08 is assumed to be the step size. This section’s primary objective is to evaluate the variations of various graphically displayed parameters. Various parameters utilized in analysis are given specified values that include a/e = 0.6, A = 0.5, = 22, and N_r = θ_w = 0.5. Each graphs show trihybrid nanoparticles suspension in an ethylene glycol as a base fluid.

5.1. Analysis of Results

The nature of tangential velocity, normal velocity, and temperature profile are examined in this section with the effects of different factors. Figures 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, and 13 are depicted in this study. Figure 3 explained the normal velocity f^′(y) profile for different values of stretching ratio (a/e), i.e., a/e = 0.3, 0.5, 0.7, 1.3, 1.5, and 1.7. Here, we observed that velocity increase when value of stretching ratio (a/e) is considered as large. We see the variation in the term stretching ratio (a/e). When a/e< 1, the thickness of the boundary layer in a/e is increased. In this figure, the variations in normal velocity for different values of volume fractions ϕ₁, ϕ₂, and ϕ₃ of nanoparticles Cu, Al₂O₃, and TiO₂, respectively, are also examined. Physically, the rise in volume fraction indicates the addition of numerous particles.

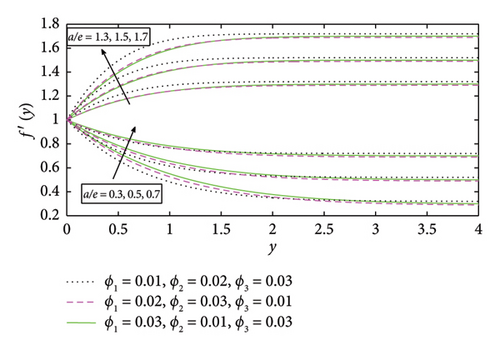
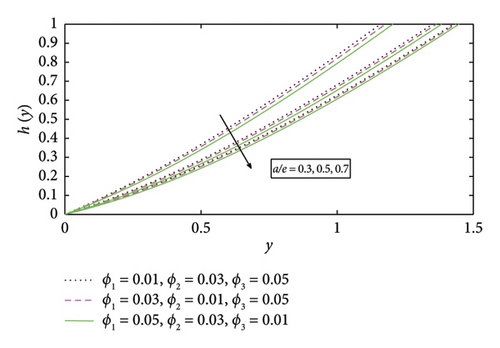
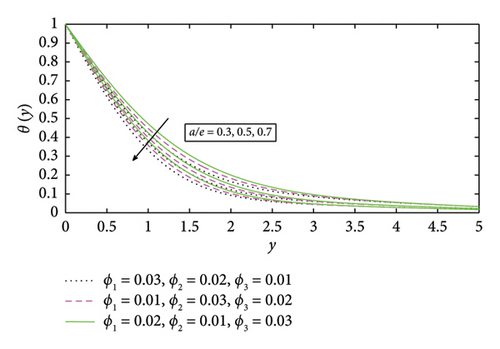
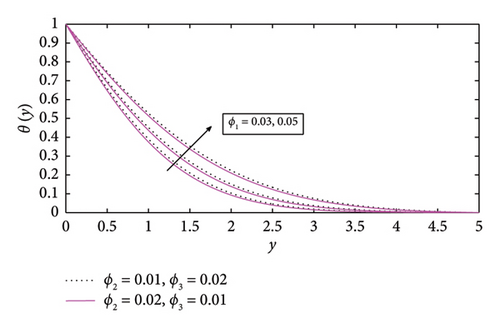
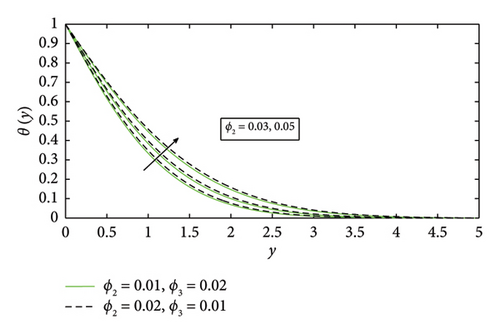
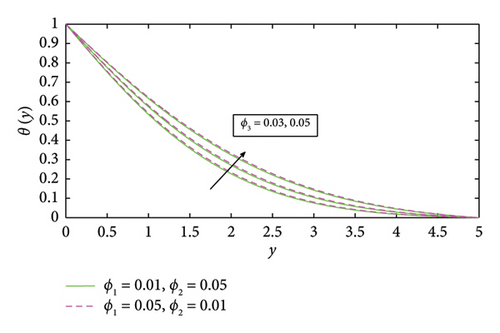
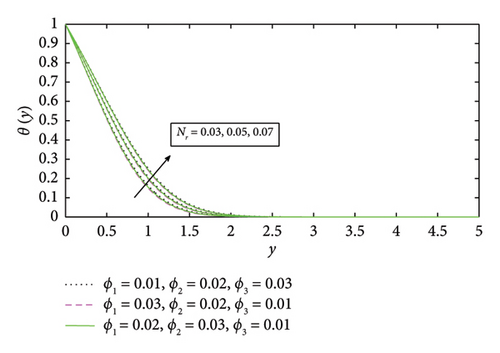
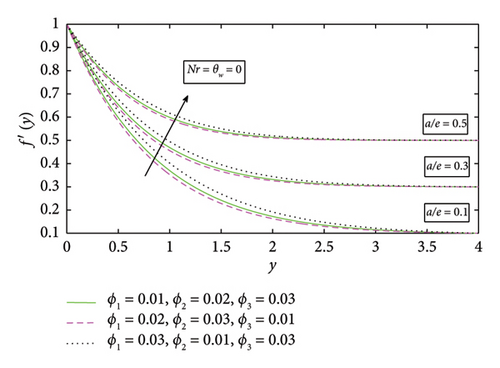
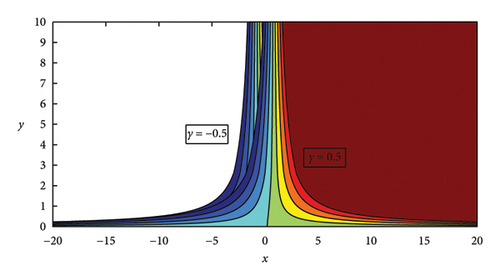
Figure 4 demonstrates the tangential velocity h(y) profile for different values of stretching ratio (a/e), i.e, a/e = 0.3, 0.5, and 0.7. The values on the y-axis show high values with increasing values of the volume fraction (a/e). It is observed that tangential velocity is found to decrease with enhancement in values of partial fraction a/e. The variation in volume fractions ϕ₁, ϕ₂, and ϕ₃ of nanoparticles on tangential velocity is also observed. So, the stretching causes a smaller thermal boundary layer by increasing the fluid velocity gradient close to the surface. This makes heat transfer from the surface of the solar energy system more effective.

On other hand, temperature in Figure 5 decreases by increasing the stretching ratio parameter a/e. According to the Stefan–Boltzmann law, radiative heat loss decreases as temperature drops. Because more energy may be stored for later use, this could have a good impact on solar thermal systems.

Figures 6, 7, and 8 are drawn for diverse values of ϕ₁, ϕ₂, and ϕ₃, respectively. In these figures, the temperature profile for different values of ϕ₁, ϕ₂, and ϕ₃ is observed. The temperature profile rises for increasing values of ϕ₁ = 0.3, 0.5, 0.7, ϕ₂ = 0.3, 0.5, 0.7, and ϕ₃ = 0.3, 0.5, 0.7. The thermal conductivity and heat transfer rate of nanofluids used in solar collectors may be improved by a rising temperature profile, hence boosting their efficiency. However, extremely high temperatures may cause suspensions of nanofluids to lose stability.

The effect of different values of radiation parameter N_r = 0.3, 0.5, 0.7 on temperature profile is seen in Figure 9. By increasing the radiation parameter, the temperature profile increases. In Figure 10, the influence of surface heating parameter θ_w with different values of ϕ₁, ϕ₂, and ϕ₃ on fluid temperature is observed. With increasing temperature, the surface heating parameter θ_w increases, i.e., θ_w = 0.5, 1.0, and 1.5. The earth’s surface absorbs more heat when the surface heating parameter is raised. Solar thermal systems that use solar heat energy may become more efficient as a result.

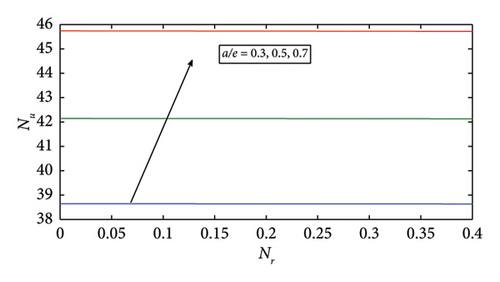
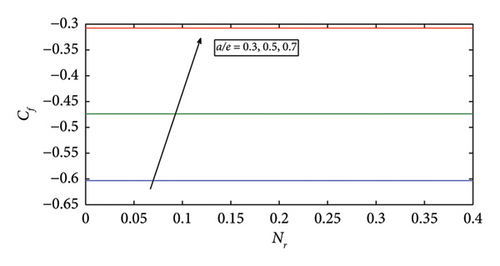
Figure 11 shows the numerical plots of velocity profile for different values of stretching ratio parameter a/e without thermal radiation and surface heating parameter. The velocity increases by increasing values of stretching ratio parameter a/e, i.e., a/e = 0.1, 0.3, and 0.5. Increased fluid velocity can enhance heat dissipation in solar thermal collectors, improving heat transfer efficiency and preventing overheating. Figures 14 and 15 depict the Nusselt number and skin friction is enhancing for both N_r and a/e.

5.2. Discussion of Results

The controlling parameter results on thermal profiles and velocities presented in above part will all be verified in this part. Fraction of free stream velocity and stretching velocity is the definition of the stretching ratio parameter. Therefore, for a fixed value of a/e related to the stretched surface in use, the increase in a/e suggests an improvement in the straining action close to the stagnation area, which could lead to an acceleration of the external stream. This is the reason of increasing the normal velocity in Figure 3. Hence, the rate of convective heat transfer is increased when the normal velocity rises. This is due to the fact that increased velocity results in a thinner thermal boundary layer, which improves energy exchange between the collector surface and the nanofluid.

Since in Figure 4, the tangential profile is parallel to the x-axis, it exhibits the opposite tendency and stretching is equal to e, which is below the fraction of the stretching ratio parameter a/e, and the tangential velocity decreases as the stretching ratio increases. Furthermore, it is determined that the tangential velocity further decreases with a high volume fraction of ϕ₁(Cu) as compared with increasing the volume fraction of ϕ₂(Fe₃O₂) and ϕ₃(TiO₂) in basefluid. The fluid may stay in touch with the heated surface longer when the tangential velocity is slower, which improves the fluid’s ability to absorb heat from the solar collector.

The temperature profile likewise drops further when raising the stretching ratio parameter a/e in Figure 5. The ϕ₃(TiO₂) nanoparticle will be more suitable for future solar thermal systems due to its significantly high temperature profile. Temperature profile of ϕ₁(Cu) shows a more marked propensity to drops. The effect of volume fraction of ϕ₁(Cu) on temperature profile is shown in Figure 6, in which temperature profile enhances by mounting values of volume fraction of ϕ₁(Cu). Furthermore, it is also observed that temperature increases with high volume fraction of ϕ₃(TiO₂) as compareed with other nanoparticles in the base fluid. This helps in better absorption and transfer of solar energy, making it efficient. The temperature profile increases by increasing in the values of volume fraction of ϕ₂(Fe₃O₂) and ϕ₃(TiO₂) as shown in Figures 7 and 8, respectively. It can be concluded that the temperature profile enhances by increasing the volume fraction of nanoparticles. Physically, as the volume fraction of nanoparticles rises, viscous forces within the nanofluid begin to develop. The resistance that the fluid particles create with one another causes the temperature profile to increase and the fluid particles ‘s velocity to decrease. The increase of viscous forces inside the nanofluid is caused physically by increasing the volume fraction. In Figure 7, the temperature profile increases with increasing values of ϕ₂(Fe₃O₂) when ϕ₃(TiO₂) is high in basefluid. The temperature profile in Figure 8 improves with increasing values of ϕ₃(TiO₂) when ϕ₁(Cu) is high in basefluid. Further research has shown that by increasing the values of trihybrid particle volume fraction for ϕ₁(Cu), ϕ₂(Fe₃O₂), and ϕ₃(TiO₂) nanoparticles, the temperature profile rises but the ϕ₃(TiO₂) nanofluid has higher temperature than ϕ₁(Cu) and ϕ₂(Fe₃O₂) nanofluids, which is advantageous for thermal performance in solar systems. The temperature curve in Figure 9 grows as N_r values increase. This is due to the fact that rising N_r values tend to enhance the thermal boundary layer and the conduction effect. At every distance from the surface, this element causes the temperature to rise. In other words, heat transmission can be managed by increasing nonlinear radiation on the surface. The surface heating parameter θ_w values grow together with the temperature profile seen in Figure 10. It was discovered that the temperature profile increases with a high value of surface parameter with different volume fraction parameters in basefluid, and it is also observed that a high value of ϕ₁(Cu) nanoparticle with an extreme value of θ_w expanding the trend of fluid temperature was more prominent than extreme values of ϕ₂(Fe₃O₂) and ϕ₃(TiO₂) nanoparticles, indicating that ϕ₁(Cu) with surface heating parameter will be more suitable for raising the fluid’s temperature in solar thermal systems. Figure 11 shows the numerical graphs of velocity profiles with the literature that is available for various values of the stretching ratio parameter a/e. Figures 12 and 13 show the streamline parameter for oblique flow of γ = 0, 3.5, 0.5 and −0.5. In Figure 14, the Nusselt number is increasing with increasing the stretching ratio. A higher Nusselt number ensures that the working fluid absorbs and removes heat more effectively in systems such as solar air heaters, photovoltaic/thermal (PV/T) systems, and solar water heaters. This can extend the life of the system and stop components from overheating. Figure 15 shows that the increment in skin friction corresponds to a/e and N_r. As the skin fiction rises, the fluid maintains improved thermal contact with the collection surface for extended periods of time. Higher temperature gains in the fluid and more efficient energy transmission are thus guaranteed.

6. Concluding Remarks

We have studied the heat transfer flow analysis of (Cu + Fe₃O₂ + O₂/(C₂H₆O₂) trihybrid nanofluid along a stretched surface at a steady and oblique stagnation point. Using the similarity approach, the controlling nonlinear partial differential equations were converted into ordinary differential equations, which is evaluated numerically using the bvp4c method. Investigations are conducted on the impact of relevant parameters on normal and tangential velocity, temperature, thermal radiation, and surface heating parameter. The thermal conductivity by the Xue model is employed in evaluation of the heat transfer analysis of nanofluids. The following is a summary of the conclusions that were reached after the analysis:

•
After adding hybrid nanofluid, the thermal properties of ethylene glycol are greatly enhanced.
•
The utilization of diverse hybrid nanoparticles enhances the heat transmission capabilities of nanofluids.
•
The stretching ratio parameter for the normal velocity has risen but decreased for temperature profile and tangential profiles. Stretching results decrease in the profile of temperature, proving that stretching the surface of thermal solar systems will not increase efficiency.
•
Trihybrid nanofluid with a high value of ϕ₃(TiO₂) nanoparticle exhibits significantly higher thermal radiation N_r than increasing the volume of other nanoparticles in terms of temperature profile. Lower absorptivity of ϕ₃(TiO₂) nanofluid’s decreased absorptivity suggests that raising the fluid’s temperature will be more effective in solar thermal systems, which makes sense.
•
When the surface heating parameter θ_w is raised, the temperature profile gets better. ϕ₃(TiO₂) nanofluid exhibits this characteristic more clearly than other nanoparticles. When employed to provide heating in solar thermal systems, ϕ₃(TiO₂) nanofluid performs better than other nanoparticles.
•
The temperature of the hybrid nanofluid increases as the heat source parameter increases.
•
The proposed model suggests that, as compared with the suspension of ϕ₁ and ϕ₂ nanoparticles, the addition of ϕ₃(TiO₂) nanoparticles can lead to enhanced efficiency in a solar energy system. This is due to inconsistently outstanding thermal performance in ϕ₃(TiO₂)/ethylene glycole nanofluid as compared with thermal performance in ϕ₂(Fe₃O₂)/ethylene glycole and ϕ₃(Cu) nanofluid.
•
At stagnation points, temperature distribution and heat transfer efficiency are impacted by nonorthogonal flow circumstances, in which the fluid interacts with surfaces at an angle. Compared with pure fluids, nanofluid flow demonstrated a better heat transfer efficiency in these circumstances.
•
The stretching ratio (a/e) enhances the skin friction and Nusselt number.
•
Effective heat transfer is crucial in solar energy systems, particularly in concentrating solar power systems where high temperatures are frequently attained. By increasing the thermal conductivity of the fluid used to transfer heat from the solar surface, research on thermal radiation on nanofluids may help develop solar collectors or heat exchangers.

Nomenclature

a/e: Stretching ratio
α_f: Fluid thermal diffusivity
α_nf: Nanofluid thermal diffusivity
B₁, B₂: Integration constants
C_f: Surface drag force
f(y): Dimensionless normal velocity
g(y): Dimensionless velocity
γ: Shear in stream
h(y): Dimensionless tangential velocity
k₁: Thermal conductivity of Cu
k₂: Thermal conductivity of Fe₃O₂
k₃: Thermal conductivity of TiO₂
k_f: Thermal conductivity of fluid
k_nf: Nanofluid thermal conductivity
k_thnf: Tribybrid nanofluid thermal conductivity
k^∗: Mean absorption coefficient
N_r: Nonthermal radiation parameter
ν: Kinematic viscosity
μ: Dynamic viscosity
ν_thnf: Kinematic viscosity of trihybrid nanofluid
q_w: Heat flux
q_r: Radiative heat flux
Re_X: Local reynold number
ρ₁: Density of Cu
ρ₂: Density of Fe₃O₂
ρ₃: Density of TiO₂
ρ_f: Density of fluid
ρ_nf: Density of nanofluid
σ^∗: Stefan–Boltzmann constant
T: Temperature (K)
T_∞: Ambient temperature
τ_w: Wall shear stress
v, u: Velocity component along y and x direction
θ_w: Surface heating parameter
: Fluid heat capacity
: Nanofluid heat capacity
: Particle heat capacity
ψ: Stream function
P_r: Prandtl number
θ(y): Dimensionless temperature
ϕ: Particle volume fraction
x, y: Coordinates axis

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

To the writing of this paper, each author made an equal contribution.

Funding

No funding was received for this research.

Acknowledgments

The University of Lahore provided the research project plate form necessary for the completion of this study activity, for which the authors are grateful.

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Jabbari F., Rajabpour A., and Saedodin S., Thermal Conductivity and Viscosity of Nanofluids: A Review of Recent Molecular Dynamics Studies, Chemical Engineering Science. (2017) 174, 67–81, https://doi.org/10.1016/j.ces.2017.08.034, 2-s2.0-85028986940.
10.1016/j.ces.2017.08.034
CAS Web of Science® Google Scholar
2 Xuan Y. and Roetzel W., Conceptions for Heat Transfer Correlation of Nanofluids, International Journal of Heat and Mass Transfer. (2000) 43, no. 19, 3701–3707, https://doi.org/10.1016/s0017-9310(99)00369-5, 2-s2.0-0343192359.
10.1016/S0017-9310(99)00369-5
CAS Web of Science® Google Scholar
3 Choi S. U. S. and Eastman J. A., Enhancing Thermal Conductivity of Fluids With Nanoparticles, 1995, Argonne National Lab.(ANL), Argonne, IL.
Google Scholar
4 Hoghoughi G., Izadi M., Oztop H. F., and Abu-Hamdeh N., Effect of Geometrical Parameters on Natural Convection in a Porous Undulant-Wall Enclosure Saturated by a Nanofluid Using Buongiorno’s Model, Journal of Molecular Liquids. (2018) 255, 148–159, https://doi.org/10.1016/j.molliq.2018.01.145, 2-s2.0-85041468479.
10.1016/j.molliq.2018.01.145
CAS Web of Science® Google Scholar
5 Yu Q., Xu H., and Liao S., Analysis of Mixed Convection Flow in an Inclined Lid-Driven Enclosure With Buongiorno’s Nanofluid Model, International Journal of Heat and Mass Transfer. (2018) 126, 221–236, https://doi.org/10.1016/j.ijheatmasstransfer.2018.05.109, 2-s2.0-85048566274.
10.1016/j.ijheatmasstransfer.2018.05.109
CAS Web of Science® Google Scholar
6 Purusothaman A., Murugesan K., and Chamkha A. J., 3D Modeling of Natural Convective Heat Transfer From a Varying Rectangular Heat Generating Source, Journal of Thermal Analysis and Calorimetry. (2019) 138, no. 1, 597–608, https://doi.org/10.1007/s10973-019-08259-9, 2-s2.0-85065032041.
10.1007/s10973-019-08259-9
CAS Web of Science® Google Scholar
7 Waini I., Ishak A., and Pop I., Squeezed Hybrid Nanofluid Flow Over a Permeable Sensor Surface, Mathematics. (2020) 8, no. 6, https://doi.org/10.3390/math8060898.
10.3390/math8060898
Web of Science® Google Scholar
8 Tassaddiq A., Khan S., Bilal M. et al., Heat and Mass Transfer Together With Hybrid Nanofluid Flow Over a Rotating Disk, AIP Advances. (2020) 10, no. 5, https://doi.org/10.1063/5.0010181.
10.1063/5.0010181
Web of Science® Google Scholar
9 Tayebi T., Öztop H. F., and Chamkha A. J., Natural Convection and Entropy Production in Hybrid Nanofluid Filled-Annular Elliptical Cavity With Internal Heat Generation or Absorption, Thermal Science and Engineering Progress. (2020) 19, https://doi.org/10.1016/j.tsep.2020.100605.
10.1016/j.tsep.2020.100605
Web of Science® Google Scholar
10 Zahid U. M., Akbar Y., and Abbasi F. M., Entropy Generation Analysis for Peristaltically Driven Flow of Hybrid Nanofluid, Chinese Journal of Physics. (2020) 67, 330–348, https://doi.org/10.1016/j.cjph.2020.07.009.
10.1016/j.cjph.2020.07.009
CAS Web of Science® Google Scholar
11 Yusuf T. A., Mabood F., Khan W. A., and Gbadeyan J. A., Irreversibility Analysis of Cu-TiO2-H2Ohybrid-Nanofluid Impinging on a 3D Stretching Sheet in a Porous Medium With Nonlinear Radiation: Darcy-Forchhiemer’s Model, Alexandria Engineering Journal. (2020) 59, no. 6, 5247–5261, https://doi.org/10.1016/j.aej.2020.09.053.
10.1016/j.aej.2020.09.053
Web of Science® Google Scholar
12 Wanatasanapan V., Abdullah M. Z., and Gunnasegaran P., Effect of TiO2-Al2O3nanoparticle Mixing Ratio on the Thermal Conductivity, Rheological Properties, and Dynamic Viscosity of Water-Based Hybrid Nanofluid, Journal of Materials Research and Technology. (2020) 9, no. 6, 13781–13792, https://doi.org/10.1016/j.jmrt.2020.09.127.
10.1016/j.jmrt.2020.09.127
CAS Web of Science® Google Scholar
13 Said Z., Ghodbane M., Sundar L. S., Tiwari A. K., Sheikholeslami M., and Boumeddane B., Heat Transfer, Entropy Generation, Economic and Environmental Analyses of Linear Fresnel Reflector Using Novel rGO-Co3O4 Hybrid Nanofluids, Renewable Energy. (2021) 165, 420–437, https://doi.org/10.1016/j.renene.2020.11.054.
10.1016/j.renene.2020.11.054
CAS Web of Science® Google Scholar
14 Abbas N., Nadeem S., Saleem A., Malik M., Issakhov A., and Alharbi F. M., Models Base Study of Inclined MHD of Hybrid Nanofluid Flow over Nonlinear Stretching Cylinder, Chinese Journal of Physics. (2021) 69, 109–117, https://doi.org/10.1016/j.cjph.2020.11.019.
10.1016/j.cjph.2020.11.019
CAS Web of Science® Google Scholar
15 Abbasian Arani A. A. and Aberoumand H., Stagnation-Point Flow of Ag-CuO/water Hybrid Nanofluids Over a Permeable Stretching/Shrinking Sheet With Temporal Stability Analysis, Powder Technology. (2021) 380, 152–163, https://doi.org/10.1016/j.powtec.2020.11.043.
10.1016/j.powtec.2020.11.043
CAS Google Scholar
16 Li X., Wang H., and Luo B., The Thermophysical Properties and Enhanced Heat Transfer Performance of SiC-MWCNTs Hybrid Nanofluids for Car Radiator System, Colloids and Surfaces A: Physicochemical and Engineering Aspects. (2021) 612, https://doi.org/10.1016/j.colsurfa.2020.125968.
10.1016/j.colsurfa.2020.125968
Web of Science® Google Scholar
17 Naganthran K., Nazar R., and Pop I., Stability Analysis of Impinging Oblique Stagnation-Point Flow Over a Permeable Shrinking Surface in a Viscoelastic Fluid, International Journal of Mechanical Sciences. (2017) 131-132, 663–671, https://doi.org/10.1016/j.ijmecsci.2017.07.029, 2-s2.0-85027501388.
10.1016/j.ijmecsci.2017.07.029
Web of Science® Google Scholar
18 Moshkin N. P., Pukhnachev V. V., and Bozhkov Y. D., On the Unsteady, Stagnation Point Flow of a Maxwell Fluid in 2D, International Journal of Non-Linear Mechanics. (2019) 116, 32–38, https://doi.org/10.1016/j.ijnonlinmec.2019.05.005, 2-s2.0-85066414503.
10.1016/j.ijnonlinmec.2019.05.005
Web of Science® Google Scholar
19 Weidman P., Hiemenz Stagnation-Point Flow Impinging on a Uniformly Rotating Plate, European Journal of Mechanics-B: Fluids. (2019) 78, 169–173, https://doi.org/10.1016/j.euromechflu.2019.06.008, 2-s2.0-85068514578.
10.1016/j.euromechflu.2019.06.008
Web of Science® Google Scholar
20 Chamkha A. J., Dogonchi A. S., and Ganji D. D., Magneto-Hydrodynamic Flow and Heat Transfer of a Hybrid Nanofluid in a Rotating System Among Two Surfaces in the Presence of Thermal Radiation and Joule Heating, AIP Advances. (2019) 9, no. 2, https://doi.org/10.1063/1.5086247, 2-s2.0-85061345134.
10.1063/1.5086247
Web of Science® Google Scholar
21 Afridi M. I., Qasim M., and Saleem S., Second Law Analysis of Three Dimensional Dissipative Flow of Hybrid Nanofluid, Journal of Nanofluids. (2018) 7, no. 6, 1272–1280, https://doi.org/10.1166/jon.2018.1532, 2-s2.0-85047875223.
10.1166/jon.2018.1532
Google Scholar
22 Hiemenz K., Die Grenzschicht an Einem in den Gleichformigen Flussigkeitsstrom Eingetauchten Geraden Kreiszylinder, Dinglers Polytechnisches Journal. (1911) 326, 321–324.
Google Scholar
23 Khan A. U., Saleem S., Nadeem S., and Alderremy A. A., Analysis of Unsteady Non-Axisymmetric Homann Stagnation Point Flow of Nanofluid and Possible Existence of Multiple Solutions, Physica A: Statistical Mechanics and Its Applications. (2020) 554, https://doi.org/10.1016/j.physa.2019.123920.
10.1016/j.physa.2019.123920
Web of Science® Google Scholar
24 Zhan X., He Yu, Shen B., Sun Z., Shi T., and Li X., Removal of Gas Bubbles From Highly Viscous Non-Newtonian Fluids Using Controlled Vibration, Chemical Engineering Science. (2018) 185, 76–83, https://doi.org/10.1016/j.ces.2018.04.012, 2-s2.0-85045560116.
10.1016/j.ces.2018.04.012
CAS Web of Science® Google Scholar
25 Ijaz N., Zeeshan A., and Bhatti M. M., Peristaltic Propulsion of Particulate Non-Newtonian Ree-Eyring Fluid in a Duct Through Constant Magnetic Field, Alexandria Engineering Journal. (2018) 57, no. 2, 1055–1060, https://doi.org/10.1016/j.aej.2017.02.009, 2-s2.0-85014870128.
10.1016/j.aej.2017.02.009
Web of Science® Google Scholar
26 Hussain A., Akbar S., Sarwar L., Nadeem S., and Iqbal Z., Effect of Time Dependent Viscosity and Radiation Efficacy on a Non-Newtonian Fluid Flow, Heliyon. (2019) 5, no. 2, https://doi.org/10.1016/j.heliyon.2019.e01203, 2-s2.0-85060920384.
10.1016/j.heliyon.2019.e01203
Web of Science® Google Scholar
27 Zheng D., Wang J., Chen Z., Baleta J., and Sundén B., Performance Analysis of a Plate Heat Exchanger Using Various Nanofluids, International Journal of Heat and Mass Transfer. (2020) 158, https://doi.org/10.1016/j.ijheatmasstransfer.2020.119993.
10.1016/j.ijheatmasstransfer.2020.119993
Web of Science® Google Scholar
28 Sahin F. and Namli L., Thermal Performances and Stabilities of Nanofluids in an Electrical Oil Heater, Journal of Thermal Analysis and Calorimetry. (2021) 145, no. 6, 3195–3206, https://doi.org/10.1007/s10973-020-09826-1.
10.1007/s10973-020-09826-1
CAS Web of Science® Google Scholar
29 Nguyen C. T., Roy G., Gauthier C., and Galanis N., Heat Transfer Enhancement Using Al2O3–Water Nanofluid for an Electronic Liquid Cooling System, Applied Thermal Engineering. (2007) 27, no. 8-9, 1501–1506, https://doi.org/10.1016/j.applthermaleng.2006.09.028, 2-s2.0-33846598376.
10.1016/j.applthermaleng.2006.09.028
CAS Web of Science® Google Scholar
30 Xue Q. Z., Model for Effective Thermal Conductivity of Nanofluids, Physics Letters A. (2003) 307, no. 5-6, 313–317, https://doi.org/10.1016/s0375-9601(02)01728-0, 2-s2.0-0037429012.
10.1016/S0375-9601(02)01728-0
CAS Web of Science® Google Scholar
31 Dinarvand S., Rostami M. N., and Pop I., A Novel Hybridity Model for TiO2-CuO/Water Hybrid Nanofluid Flow Over a Static/Moving Wedge or Corner, Scientific Reports. (2019) 9, no. 1, https://doi.org/10.1038/s41598-019-52720-6.
10.1038/s41598-019-52720-6
Web of Science® Google Scholar
32 Unyong B., Vadivel R., Govindaraju M., Anbuvithya R., and Gunasekaran N., Entropy Analysis for Ethylene Glycol Hybrid Nanofluid Flow With Elastic Deformation, Radiation, Non-Uniform Heat Generation/Absorption, and Inclined Lorentz Force Effects, Case Studies in Thermal Engineering. (2022) 30, https://doi.org/10.1016/j.csite.2021.101639.
10.1016/j.csite.2021.101639
Web of Science® Google Scholar
33 Nadeem S., Mehmood R., and Akbar N. S., Oblique Stagnation Point Flow of Carbon Nano Tube Based Fluid Over a Convective Surface, Journal of Computational and Theoretical Nanoscience. (2015) 12, no. 4, 605–612, https://doi.org/10.1166/jctn.2015.3774, 2-s2.0-84929311237.
10.1166/jctn.2015.3774
CAS Web of Science® Google Scholar
34 Ramzan M., Shahmir N., Alotaibi H., Ghazwani H. A. S., and Muhammad T., Thermal Performance Comparative Analysis of Nanofluid Flows at an Oblique Stagnation Point Considering Xue Model: A Solar Application, Journal of Computational Design and Engineering. (2022) 9, no. 1, 201–215, https://doi.org/10.1093/jcde/qwab076.
10.1093/jcde/qwab076
Web of Science® Google Scholar
35 Tiwari R. K. and Das M. K., Heat Transfer Augmentation in a Two-Sided Lid-Driven Differentially Heated Square Cavity Utilizing Nanofluids, International Journal of Heat and Mass Transfer. (2007) 50, no. 9-10, 2002–2018, https://doi.org/10.1016/j.ijheatmasstransfer.2006.09.034, 2-s2.0-33847201096.
10.1016/j.ijheatmasstransfer.2006.09.034
CAS Web of Science® Google Scholar
36 Sundar L. S., Sharma K. V., Singh M. K., and Sousa A. C. M., Hybrid Nanofluids Preparation, Thermal Properties, Heat Transfer and Friction Factor–A Review, Renewable and Sustainable Energy Reviews. (2017) 68, 185–198, https://doi.org/10.1016/j.rser.2016.09.108, 2-s2.0-84991706046.
10.1016/j.rser.2016.09.108
CAS Web of Science® Google Scholar
37 Ghadikolaei S. S., Yassari M., Sadeghi H., Hosseinzadeh Kh, and Ganji D. D., Investigation on Thermophysical Properties of TiO2-Cu/H2O Hybrid Nanofluid Transport Dependent on Shape Factor in MHD Stagnation Point Flow, Powder Technology. (2017) 322, 428–438, https://doi.org/10.1016/j.powtec.2017.09.006, 2-s2.0-85029799321.
10.1016/j.powtec.2017.09.006
CAS Web of Science® Google Scholar
38 Hayat T. and Nadeem S., Heat Transfer Enhancement With Ag–CuO/Water Hybrid Nanofluid, Results in Physics. (2017) 7, 2317–2324, https://doi.org/10.1016/j.rinp.2017.06.034, 2-s2.0-85024126006.
10.1016/j.rinp.2017.06.034
Web of Science® Google Scholar
39 Labropulu F., Li D., and Pop I., Non-orthogonal Stagnation-Point Flow Towards a Stretching Surface in a Non-Newtonian Fluid with Heat Transfer, International Journal of Thermal Sciences. (2010) 49, no. 6, 1042–1050, https://doi.org/10.1016/j.ijthermalsci.2009.12.005, 2-s2.0-77950300211.
10.1016/j.ijthermalsci.2009.12.005
CAS Web of Science® Google Scholar
40 Nadeem S., Mehmood R., and Akbar N. S., Optimized Analytical Solution for Oblique Flow of a Casson-Nano Fluid with Convective Boundary Conditions, International Journal of Thermal Sciences. (2014) 78, 90–100, https://doi.org/10.1016/j.ijthermalsci.2013.12.001, 2-s2.0-84892704132.
10.1016/j.ijthermalsci.2013.12.001
Web of Science® Google Scholar

All articles

Solar Energy Utilization of Radiative Implication of Trihybrid Xue-Modeled Nanofluid Flow for Oblique Stagnation Point Flows

Abstract

1. Introduction

2. Mathematical Model

3. Problem Statement

3.1. Thermophysical Characteristics of Trihybrid Nanofluids