The system of nonlinear fractional partial differential equations (SNFPDEs) are widely used in modeling various phenomena in applied sciences. Consequently, finding the solutions to SNFPDEs has become paramount. Recently, an analytic method known as the Semiseparation of Variables Method (S-SVM) has been applied to obtain the exact solution of the SNFPDEs by employing the Mittag–Leffler function method. The Salim function is a generalization of the Mittag–Leffler function with two additional parameters. These two additional parameters in the Salim function offer the flexibility and easier use of the Salim function as compared to the Mittag–Leffler function in one parameter. Similarly, the Salim and Faraj function extends the Salim function. In this paper, we introduce two modifications to the S-SVM, namely, the S-SVM via the Salim function (S-SVSFM) and the S-SVM via the Salim and Faraj function (S-SVSFFM). Interestingly, applying the S-SVSFM and the S-SVSFFM independently to solve the SNFPDEs yields an infinite series that converges easily to the exact solution of the SNFPDEs. In addition, the uniqueness of the exact solution of the SNFPDEs is established therein the paper. Choosing the value of α = 1, confirms the integer solution of the SNFPDEs which is depicted in tables. However, we observed that as the values of the α changes continuously from 0.1 to 1.0, the memory and hereditary properties are observed. The findings clearly show that the S-SVSFM and the S-SVSFFM are reliable and powerful analytic methods for finding the exact solution to the SNFPDEs.

1. Introduction

Fractional partial differential equations (FPDEs), as a generalization of integer partial differential equations have attracted significant attention due to their ability to model various physical and biological phenomena more accurately. They are frequently used in various disciplines such as physics, engineering, biology, and economics to describe anomalous diffusion, viscoelastic material behavior, control systems, signal processing, and many more [1–4]. The fractional-order models are more accurate than the integer-order models because fractional-order derivatives are endowed with memory and hereditary properties of different substances [5, 6]. Recently, the system of nonlinear FPDEs (SNFPDEs) has been of much interest because of their applicability in various domains [7, 8].

In recent years, finding the solution to the SNFPDEs has been at the heart of every scientist in the 21st century. Several numerical methods [9–11] have been introduced to solve the SNFPDEs. However, these methods require repeated iterations and are usually accompanied by errors. Conversely, analytic methods which provide a function that describes the underlying mechanism of the problem at hand have been observed by researchers to find the exact solution to the SNFPDEs. In addition, the solutions of the SNFPDEs yielded by analytic methods serve as a benchmark for validating the accuracy of numerical solutions obtained by these numerical methods. Various analytic methods for obtaining an exact solution to SNFPDEs have been introduced, such as the tanh-function method [12], exp-function method [13], Adomian decomposition method (ADM) [14], variational iteration method (VIM) [15], Laplace ADM [16], and Laplace residual power series method [17]. The ADM initially decomposes the nonlinear operators into an infinite sum of Adomian polynomials which is then followed by the inverse partial differential operator of the resulting equation to obtain the series. However, this series may not converge to the exact solution. The authors in [18–20] reported that even when the ADM converges, the solutions are limited to a small region. In addition, the authors in [21, 22] observed that in using the ADM, the obtained series does not converge to the exact solution of the given problem. Furthermore, using software based on the principles of the ADM to compute the exact solution of the SNFPDEs is challenging. For example, the author in [23] has observed this shortcoming of the ADM in searching for solutions to differential equations in functional spaces. In using VIM, the correction functional of the SNFPDEs must be constructed. The correction functional contains the Lagrangian multiplier that has to be determined first before the iteration to generate the series begins. However, determining the Lagrangian multiplier is challenging because several Lagrangian multiplier values are obtained after applying the stationarity condition and only one of them yields the convergent series solution to the SNFPDEs. How would one know the appropriate value of the Lagrangian multiplier to choose that will yield a convergent series solution of the SNFPDEs? This drawback has also been observed by the authors in [24, 25]. Furthermore, solving SNFPDEs using the VIM sometimes yields a divergent series. A similar observation has also been reported by the authors in [26, 27]. The homotopy analysis method (HAM) introduced by the author in [28] contains a convergence control parameter that has to be guessed arbitrarily in order to ensure a convergent solution to the SNFPDEs. One major disadvantage of using this method is that it heavily depends on the choice of the convergence control parameter. However, since there is no rule or procedure for choosing the value of the convergence control parameter, it thereby becomes a great challenge to rely on this method [29]. The homotopy perturbation method (HPM) as observed by the author in [30] is applicable when the convergence control parameter is chosen to be a negative one. Obviously, this HPM is only a special case of HAM [31–35]. The series obtained using HPM is divergent for solving some classes of differential equations [32, 36]. Recently, the S-SVM has been observed for solving FPDEs. This method assumes that a solution to a FPDE is a product of their component functions where one of the component functions is known and the other component is unknown [37]. Thus, the S-SVM due to [37] assumed that one of the component functions of the given FPDE is a Mittag–Leffler function in one parameter and the other component function is unknown. The S-SVM is applied to search for the unknown component function of the FPDE which in turn yields the solution of the FPDE in a functional space. The beauty of research in a class of S-SVM is not fully explored, as there are many functions that not only generalize the Mittag–Leffler function but also possess additional properties. One such function is the Salim function. The Salim function is a generalization of the Mittag–Leffler function in two parameters. Unlike the Mittag–Leffler function in two parameters, the Salim function has two additional parameters which makes its applications flexible. Similarly, the Salim and Faraj function also generalizes the Salim function with two additional parameters. These extra parameters influence the behavior of the function and allow for flexibility in using it to solve SNFPDEs.

In this paper, two modifications to the S-SVM are proposed. Thus, the S-SVM via the Salim function (S-SVSFM) and the S-SVM via the Salim and Faraj function (S-SVSFFM) for obtaining the exact solution of the SNFPDEs. The S-SVSFM and the S-SVSFFM yield the same series which converges rapidly to the exact solution.

The paper is organized as follows. In Section 2, relevant definitions of fractional derivatives and functional spaces are provided therein. The modifies methods of the S-SVM thus, the S-SVSFM and the S-SVSFFM are given in the Section 3 of this paper. In addition, the uniqueness of the exact solution of the SNFPDEs are presented in the same section. The numerical experiment of the exact solution of the SNFPDEs using the modified methods and the conclusion are seen in the Sections 4 and 5, respectively in the paper.

2. Preliminaries

In this section, we present the necessary definitions and preliminaries relevant to our studies.

Definition 1 (Caputo derivative [38]). The Caputo fractional derivative of f(t) is defined as

()

where Γ(·) is the Gamma function and n − 1 < α ≤ n, and n ∈ N.

Lemma 1. If n − 1 < α ≤ n, n ∈ N and , then

Definition 2 (see [39].)One parameter of the Mittag–Leffler function is

()

Definition 3 (Pochhammer symbol [40]). The Pochhammer symbol is defined as

()

Definition 4 (Salim function [41]). The Salim function is defined as

()

where (γ)_k is the Pochhammer symbol.

Definition 5 (Salim and Faraj function [42]). The Salim and Faraj function is defined as

()

where

Definition 6 (Sobolev space [43]). Let Ω be in Rⁿ. Then, the Sobolev space, denoted as W^k,p, is defined as

()

Definition 7 (Contraction mapping [44]). Let (X, | |) be a metric space and G a mapping of X into itself. The operator G is said to be a contraction or a contraction mapping if there exists a real number k, 0 < k < 1, such that

()

3. Methodology

The main concepts underlying the modifications of the S-SVM will be introduced in this section.

We consider the general form of a SNFPDE as

()

with initial condition

()

where

is the Caputo fractional derivative of order 0 < α ≤ 1 for the function u(x, t), L(u(x, t)) and N(u(x, t)) are the linear and nonlinear fractional operators, respectively, and f(x, t) is the forcing term.

3.1. S-SVSFM

In this subsection, the S-SVM is modified by setting one of its component functions with the Salim function. The Salim function generalizes the Mittag–Leffler function and also possesses two additional parameters. The additional parameters allow for a greater flexibility in controlling the function and make it applicable to a wider range of problems.

3.1.1. Steps

Here, we discuss the steps to find the solution of equation (8) together with the initial condition (9) by the S-SVSFM.

1.
A solution to equation (8) is separated into its component functions as
()
where λ^k is the unknown coefficient and (δ)_k and (γ)_k are the Pochhammer symbols. This method is termed as S-SVSFM.
2.
Substituting equation (10) into equation (8) yields
()
3.
We find the partial derivatives in equation (11) with respect to their corresponding independent variables and simplify them to get
()
4.
We now determine the values of lambda recursively from equation (12).
5.
The resulting lambda values obtained from Step 4 are then plugged into equation (10) to obtain the solution in a suitable functional space.

3.2. S-SVSFFM

In this subsection, another modification of the S-SVM is introduced by setting one of its component functions with the Salim and Faraj function. The Salim and Faraj function also generalizes the Salim function. Here, the Salim and Faraj function contains two extra parameters unlike the Salim function. These extra parameters influence the behavior of the function and allow for flexibility in modeling systems with complex memory effects.

3.2.1. Steps

Here, we discuss the steps to find the solution of equation (8) together with the initial condition (9) by the S-SVSFFM.

1.
A solution to equation (8) is separated into its component function as
()
where λ^k is the unknown coefficient and (γ)_kq and (δ)_kp are the Pochhammer symbols. This method is termed as a S-SVSFFM,
2.
Substituting equation (13) into equation (8) yields
()
3.
We find the partial derivatives in equation (14) with respect to their corresponding independent variables and simplify them to get
()
4.
We now determine the values of lambda recursively from equation (15).
5.
The resulting lambda values obtained from Step 4 are then plugged into equation (13) to obtain the solution in a suitable functional space.

3.3. Uniqueness of Solution of the SNFPDEs

In this section, the contraction mapping theorem is applied to determine the uniqueness of the solution. First, the contraction is stated before applying it to obtain the unique solution of the SNFPDEs.

Theorem 1 (see [45].)Let u(x, t) ∈ C¹(Ω) and their partial derivatives exist, then u(x, t) is a solution of (8) if and only if

()

In order to obtain a unique solution to SNFPDEs, the contraction mapping theorem is given as follows.

Theorem 2. Let (X, |·|) be a Banach space, and G : X⟶X be a contraction mapping. Then, equations (8) with (9) has a unique solution u(x, t) whenever 0 < γ < 1.

Proof 1. The mapping G : C(Ω, |·|)⟶C(Ω, |·|) is defined as

()

Let u₁, u₂ ∈ C(Ω, |·|) be two different solutions of equations (8) with (9), then by using the above equations, we get the following:

()

where η = η₁ + η₂ and γ = (ηT/Γ(α)) < 1, and we get

()

therefore, the mapping G is contraction, and there exists a unique solution u ∈ C(Ω) to equation (8).

3.4. Application of the S-SVSFM for Solving SNFPDEs

In this section, we now apply the S-SVSFM to obtain an exact solution to the SNFPDEs.

Example 1. Let us consider the following SNFPDEs:

()

∀0 < α ≤ 1, with the initial conditions

()

and

()

We assume that a solution to equations (20) and (21) is given as follows:

()

where λ and θ are the unknown coefficients that need to be determined. Here, g₁(x) = u(x, 0) and g₂(x) = v(x, 0). We see that

()

Substituting the assumed solution and their respective partial derivatives of equations (24)–(26) into equations (20) and (21) yields

()

and

()

Expanding the Salim function by considering the first four terms of equations (27) and (28) yields

()

and

()

Expressing the inner product of equations (29) and (30) as

()

The above equation is written as

()

The following results are obtained after substituting equation (33) into equations (27) and (28)

()

and

()

where,

()

By substituting the initial conditions of equations (22) and (23) into equation (34) and simplifying the results, we get

()

Following a similar procedure, equation (35) becomes

()

By using equations (37) and (38), we now determine the following coefficients. Starting from k = 0, we obtain the following lambda and theta values, where

()

and

()

Similarly, when k = 1, we obtain the following results:

()

and

()

Similarly, when k = 2, we obtain the following results:

()

and

()

Expanding equation (24) yields

()

Plugging the obtained λ⁰, λ¹, λ², …, λⁿ values into equation (45) results in

()

Similarly,

()

When α = 1, we obtain the following:

()

We show in the following result that u(x, t) and v(x, t) are the unique solutions of equations (20) and (21).

Theorem 3. The solution for equations (20) and (21) exists and will be unique if

()

Proof 2. Let u(x, t) and u_∗(x, t) be two different solutions of equations (20) and (21). Then,

()

where ψ = (e^−xt^kα)/(Γ(kα + 1)). This implies that the function u(x, t) is Lipschitz continuous in the Banach space, which is similar to v(x, t).

3.5. Application of the S-SVSFFM for Solving SNFPDEs

In this section, we apply the S-SVSFFM to obtain an exact solution to the SNFPDEs.

We consider the SNFPDEs in equations (20) and (21) together with (22) and (23).

We assume that a solution to equations (20) and (21) is given as follows:

()

where λ and θ are the unknown coefficients that need to be determined. Hence, g₁(x) = u(x, 0) and g₂(x) = v(x, 0).

()

By substituting the assumed solution and their respective partial derivatives of equations (54)–(56) into equations (20) and (21), we get

()

By plugging the initial conditions of equations (22) and (23) into equation (57) and simplifying, we get

()

where,

()

Following a similar procedure, we observe that

()

By using equations (59) and (61), we now determine the following coefficients. Starting from k = 0, we obtain the following lambda and theta values, where

()

and,

()

Similarly, when k = 1, we obtain

()

and,

()

Expanding equation (54) yields

()

Plugging the obtained λ⁰, λ¹, λ², …, λⁿ values into equation (66) results in

()

Similarly,

()

When α = 1, then we obtain the following:

()

It can be observed that after substituting the λ and θ values obtained into equation (66) we obtain equation (67). Thus, the obtained λ and θ values are inversely proportional to the Pochhammer symbols introduced in the Salim function as well as in the Salim and Faraj function.

That is, λ¹ = (δ)₁/(γ)₁ cancels the Pochhammer symbols (γ)₁/(δ)₁ in the Salim function. Similarly, λ² = (δ)₂/(γ)₂ cancels the Pochhammer symbols (γ)₂/(δ)₂ in the Salim function. Similar observations can be seen in the Salim and Faraj function. Hence, the results obtained using the S-SVSFM and S-SVSFFM are the same for the SNFPDEs.

3.6. Solution in Sobolev Space

In this section, we show that the solution to the SNFPDEs exists in the Sobolev space.

Using Definition (6), we begin by showing that u(x, t) belongs to L¹([a, b] × [0, t]). Then,

()

where ρ = (−e^−b + e^−a) and

Since ρϕ is finite, it shows that the solution u(x, t) exists in an L¹ space. Similarly, v(x, t) exists in an L¹ space.

Again, we show that (∂u(x, t)/∂x) ∈ L¹(Ω).

However,

()

Hence,

()

where ρ = (e^−b − e^−a) and

Since ρϕ is finite, it shows that (∂u(x, t)/∂x) exists in an L¹ space. Similarly, (∂v(x, t)/∂x) exists in an L¹ space.

Finally, we show that (∂^αu(x, t)/∂t^α) ∈ L¹(Ω).

However,

()

Hence,

()

where ρ = (−e^−b + e^−a) and

Since ρϕ is finite, it shows that (∂^αu(x, t)/∂t^α) exists in an L¹ space. Similarly, (∂^αv(x, t)/∂t^α) exists in an L¹ space. Hence, the solution exists in the Sobolev space.

4. Numerical Experiment

In this section, the numerical results of the u(x, t) and v(x, t) for the given example are evaluated for various values of x and t and fractional order α using the S-SVSFM and the S-SVSFFM and are presented through tables and figures. Since the S-SVSFM and the S-SVSFFM give the same solution, their corresponding results are presented in the same tables and figures.

Tables 1 and 2 exhibit the behavior of the S-SVSFM and the S-SVSFFM solutions for different values of x and t and the fractional order α of equations (20) and (21). It can be observed that when α = 1, the S-SVSFM and the S-SVSFFM solutions of the given example are in excellent agreement with the integer solutions in equations (48) and (49). This confirms that both S-SVSFM and S-SVSFFM are more robust methods.

Table 1. Solution u(x, t) using S-SVSFM and S-SVSFFM.

x	t	α = 0.5	α = 0.7	α = 0.9	α = 1.0
−2	0.1	10.99813	9.27682	8.42973	8.16617
	0.2	13.45977	10.78219	9.46156	9.02501
	0.3	16.21330	12.32888	10.56909	9.97418

−1	0.1	4.02936	3.41163	3.10107	3.00417
	0.2	4.86301	3.96152	3.48035	3.32012
	0.3	5.69350	4.52198	3.88710	3.66930

−0.5	0.1	2.43689	2.06855	1.88086	1.82212
	0.2	2.92847	2.39975	2.11071	2.01375
	0.3	3.41164	2.73564	2.35696	2.22554

0	0.1	1.47153	1.25396	1.14076	1.10517
	0.2	1.75807	1.45261	1.27999	1.22140
	0.3	2.03724	1.65245	1.42890	1.34986

0.5	0.1	0.88715	0.75993	0.69187	0.67032
	0.2	1.05403	0.87846	0.77614	0.74082
	0.3	1.22055	0.99652	0.86605	0.81873

1	0.1	0.53504	0.46037	0.41961	0.40657
	0.2	0.64162	0.53084	0.47056	0.44933
	0.3	0.77214	0.60099	0.52476	0.49659

2	0.1	0.22637	0.16895	0.15432	0.14957
	0.2	0.52999	0.19805	0.17291	0.16530
	0.3	1.35634	0.24726	0.19279	0.18268

Table 2. Solution v(x, t) using S-SVSFM and S-SVSFFM.

x	t	α = 0.5	α = 0.7	α = 0.9	α = 1.0
−2	0.1	0.12031	0.10871	0.11877	0.12246
	0.2	0.33045	0.09637	0.10603	0.11080
	0.3	0.98474	0.09772	0.09513	0.10026

−1	0.1	0.25955	0.29644	0.32296	0.33287
	0.2	0.23452	0.25871	0.28864	0.30119
	0.3	0.24944	0.22995	0.25937	0.27253

−0.5	0.1	0.43022	0.48945	0.53251	0.54881
	0.2	0.37709	0.42862	0.47613	0.49659
	0.3	0.35643	0.38228	0.42824	0.44933

0	0.1	0.71431	0.80779	0.87802	0.90484
	0.2	0.62821	0.70948	0.78529	0.81873
	0.3	0.58472	0.63553	0.70679	0.74082

0.5	0.1	1.18442	1.33273	1.44766	1.49182
	0.2	1.05119	1.17308	1.29504	1.34986
	0.3	0.98773	1.05475	1.16615	1.22140

1	0.1	1.96120	2.19826	2.38684	2.45960
	0.2	1.76073	1.93787	2.13548	2.22554
	0.3	1.69326	1.74770	1.92357	2.01375

2	0.1	5.38414	5.97820	6.48824	6.68589
	0.2	5.13871	5.28201	5.80572	6.04965
	0.3	5.77178	4.80093	5.23150	5.47395

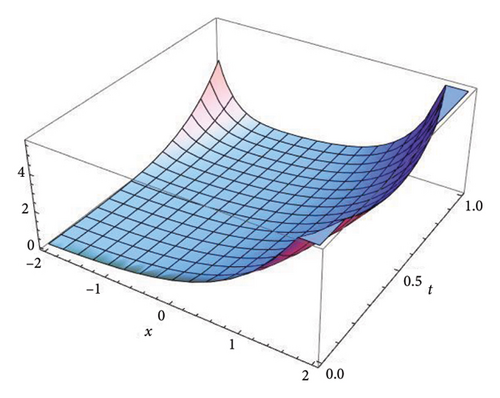
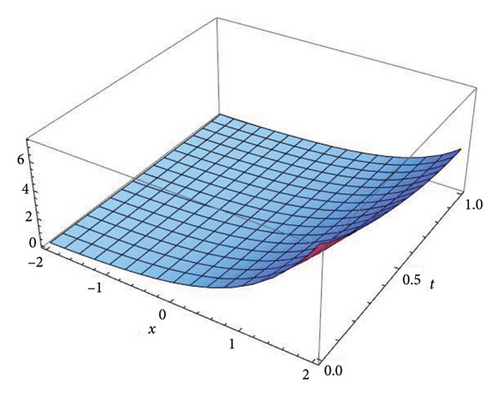
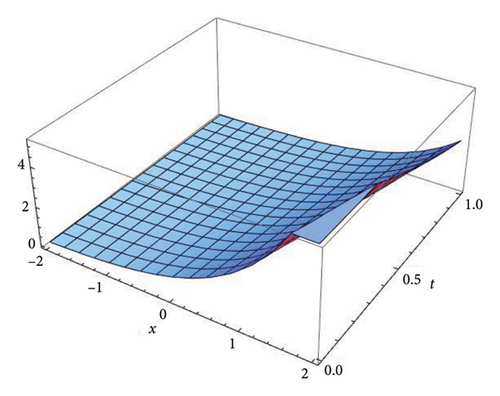
Figure 1 represents the three-dimensional plot for the solution u(x, t) at fractional order α = 0.5, 0.7, 0.9, and 1.0, respectively, using both the S-SVSFM and the S-SVSFFM. The subfigures in Figure 1 show the behavior of the solutions obtained by using the S-SVSFM and the S-SVSFFM. They also show the gradual changes in the behavior of the solution with different values of α, hence depicting the memory property of the SNFPDEs. The convergence of the fractional order solutions toward integer-order solutions has been observed by continuously varying the fractional order. Hence, the graphical representation has confirmed the strong agreement of the exact integer solution with the S-SVSFM and the S-SVSFFM solutions at fractional order α = 1.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

The S-SVSFM and S-SVSFFM solutions u(x, t) for different values of α = 0.5, 0.7, 0.9, 1.0. (a) u(x, t), α = 0.5. (b) u(x, t), α = 0.7. (c) u(x, t), α = 0.9. (d) u(x, t), α = 1.0.

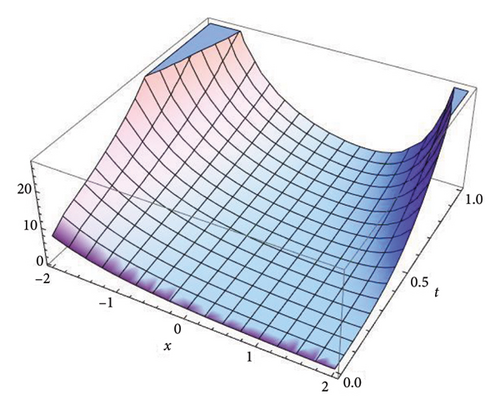
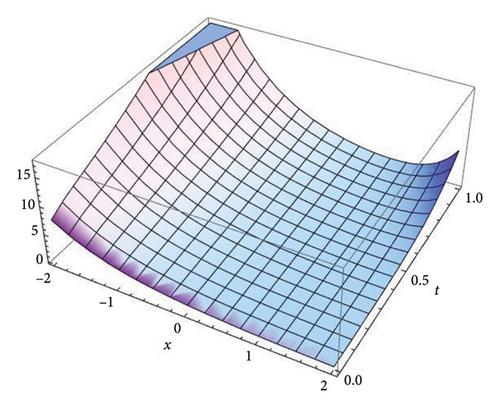
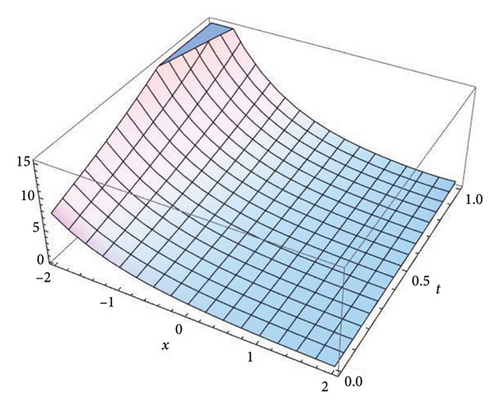
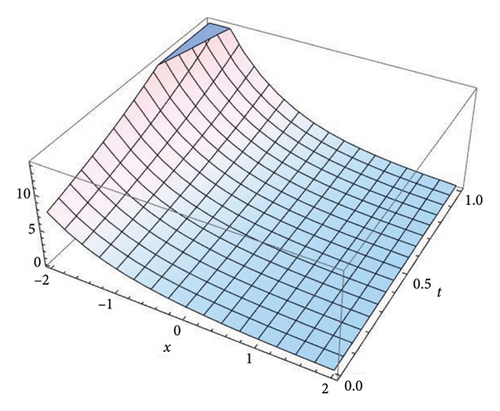
Figure 2 represents the three-dimensional plot for the solution v(x, t) at fractional order α = 0.5, 0.7, 0.9, and 1.0, respectively, using both the S-SVSFM and the S-SVSFFM. These subfigures show the behavior of the solutions obtained by using the S-SVSFM and the S-SVSFFM. They also show the gradual changes in the behavior of the solution with different values of α depicting the memory property of the SNFPDEs.

5. Conclusion

In this paper, we developed two analytic methods called the S-SVSFM and the S-SVSFFM and applied them independently to obtain the exact solution to SNFPDEs. The S-SVSFM and the S-SVSFFM yielded the same result when applied to the SNFPDEs because the lambda and theta values obtained using the S-SVSFM were inversely proportional to the Pochhammer symbols in the Salim function used in the S-SVSFM. Thus, we observed that the (δ)₁/(γ)₁ and (γ)₁/(δ)₁ canceled out when applying the S-SVSFM. A similar observation was seen in the S-SVSFFM. The numerical experiments were presented to observe the role of the fractional order α. Lastly, we determined that the solutions obtained exist in the Sobolev space. The analysis confirmed that the solutions obtained by the S-SVSFM and S-SVSFFM converged rapidly with a few terms. In the future, the proposed methods can be applied to find the analytic solutions of FPDEs and SNFPDEs.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

No funding was received for this research.

Open Research

Data Availability Statement

Data sharing is not applicable to this article as no new data were created or analyzed in this study.

References

1 Hammad H. A. and De la Sen M., Tripled Fixed Point Techniques for Solving System of Tripled-Fractional Differential Equations, Aims Mathematics. (2020) 6, no. 3, 2330–2343, https://doi.org/10.3934/math.2021141.
10.3934/math.2021141
Google Scholar
2 Daraghmeh A., Qatanani N., and Saadeh A., Numerical Solution of Fractional Differential Equations, Applied Mathematics. (2020) 11, no. 11, 1100–1115, https://doi.org/10.4236/am.2020.1111074.
10.4236/am.2020.1111074
Google Scholar
3 Constantinescu C. D., Ramirez J. M., and Zhu W. R., An Application of Fractional Differential Equations to Risk Theory, Finance and Stochastics. (2019) 23, no. 4, 1001–1024, https://doi.org/10.1007/s00780-019-00400-8, 2-s2.0-85069647474.
10.1007/s00780-019-00400-8
Web of Science® Google Scholar
4 Li C., Liu J., and He T., Fractional-Order Rate-Dependent Thermoelastic Diffusion Theory Based on New Definitions of Fractional Derivatives With Non-Singular Kernels and the Associated Structural Transient Dynamic Responses Analysis of Sandwich-Like Composite Laminates, Communications in Nonlinear Science and Numerical Simulation. (2024) 132, no. 1, https://doi.org/10.1016/j.cnsns.2024.107896.
10.1016/j.cnsns.2024.107896
Web of Science® Google Scholar
5 Hai X., Yu Y., Xu C., and Ren G., Stability Analysis of Fractional Differential Equations with the Short-Term Memory Property, Fractional Calculus and Applied Analysis. (2022) 25, no. 3, 962–994, https://doi.org/10.1007/s13540-022-00049-9.
10.1007/s13540-022-00049-9
Web of Science® Google Scholar
6 Yadav S. K. and Methi G., Application of Fractional Differential Transform Method and Bell Polynomial for Solving System of Fractional Delay Differential Equations, Partial Differential Equations in Applied Mathematics. (2024) 12, no. 1, https://doi.org/10.1016/j.padiff.2024.100971.
10.1016/j.padiff.2024.100971
Google Scholar
7 Khan N. A., Razzaq O. A., Ara A., and Riaz F., Numerical Solution of System of Fractional Differential Equations in Imprecise Environment, Numerical Simulation-From Brain Imaging Turbulent Flows. (2016) 2016, no. 1, 167–186.
Google Scholar
8 Li C. F., Luo X. N., and Zhou Y., Existence of Positive Solutions of the Boundary Value Problem for Nonlinear Fractional Differential Equations, Computers & Mathematics with Applications. (2010) 59, no. 3, 1363–1375, https://doi.org/10.1016/j.camwa.2009.06.029, 2-s2.0-74149083504.
10.1016/j.camwa.2009.06.029
Web of Science® Google Scholar
9 Vargas A. M., Finite Difference Method for Solving Fractional Differential Equations at Irregular Meshes, Mathematics and Computers in Simulation. (2022) 193, no. 1, 204–216, https://doi.org/10.1016/j.matcom.2021.10.010.
10.1016/j.matcom.2021.10.010
Web of Science® Google Scholar
10 Liu T. and Hou M., A Fast Implicit Finite Difference Method for Fractional Ad-Vection-Dispersion Equations With Fractional Derivative Boundary Conditions, Advances in Mathematical Physics. (2017) 2017, no. 1, 1–8, https://doi.org/10.1155/2017/8716752, 2-s2.0-85031900036.
10.1155/2017/8716752
Google Scholar
11 Yang Q., Liu F., and Turner I., Numerical Methods for Fractional Partial Differential Equations With Riesz Space Fractional Derivatives, Applied Mathematical Modelling. (2010) 34, no. 1, 200–218, https://doi.org/10.1016/j.apm.2009.04.006, 2-s2.0-69249214155.
10.1016/j.apm.2009.04.006
Web of Science® Google Scholar
12 Evans D. J. and Raslan K. R., The Tanh Function Method for Solving Some Important Non-Linear Partial Differential Equations, International Journal of Computer Mathematics. (2005) 82, no. 7, 897–905, https://doi.org/10.1080/00207160412331336026, 2-s2.0-27944488725.
10.1080/00207160412331336026
Web of Science® Google Scholar
13 Dehghan M., Manafian Heris J., and Saadatmandi A., Application of the Exp-Function Method for Solving a Partial Differential Equation Arising in Biology and Population Genetics, International Journal of Numerical Methods for Heat and Fluid Flow. (2011) 21, no. 6, 736–753, https://doi.org/10.1108/09615531111148482, 2-s2.0-79960784674.
10.1108/09615531111148482
Web of Science® Google Scholar
14 Adomian G., A New Approach to Nonlinear Partial Differential Equations, Journal of Mathematical Analysis and Applications. (1984) 102, no. 2, 420–434, https://doi.org/10.1016/0022-247x(84)90182-3, 2-s2.0-0021495016.
10.1016/0022-247X(84)90182-3
Web of Science® Google Scholar
15 He J. H., Variational Iteration Method-A Kind of Non-Linear Analytical Technique: Some Examples, International Journal of Non-Linear Mechanics. (1999) 34, no. 4, 699–708, https://doi.org/10.1016/s0020-7462(98)00048-1.
10.1016/S0020-7462(98)00048-1
Web of Science® Google Scholar
16 Sohail M., Khan H., Tchier F., Jebran S., and Nadeem M., The Analytical Analysis of Fractional Differential System via Different Operators and Normalization Functions, Partial Differential Equations in Applied Mathematics. (2024) 10, no. 1, https://doi.org/10.1016/j.padiff.2024.100687.
10.1016/j.padiff.2024.100687
Google Scholar
17 Rab A., Khan S., Khan H. et al., The Fractional Analysis of Thermo-Elasticity Coupled Systems with Non-Linear and Singular Nature, Scientific Reports. (2024) 14, no. 1, https://doi.org/10.1038/s41598-024-56891-9.
10.1038/s41598-024-56891-9
Web of Science® Google Scholar
18 Zurigat M., Momani S., Odibat Z., and Alawneh A., The Homotopy Analysis Method for Handling Systems of Fractional Differential Equations, Applied Mathematical Modelling. (2010) 34, no. 1, 24–35, https://doi.org/10.1016/j.apm.2009.03.024, 2-s2.0-69249202653.
10.1016/j.apm.2009.03.024
Web of Science® Google Scholar
19 Hosseini Fadravi H., Saberi Nik H., and Buzhabadi R., Homotopy Analysis Method for Solving Foam Drainage Equation With Space-And Time-Fractional Derivatives, International Journal of Differential Equations. (2011) 2011, no. 1, https://doi.org/10.1155/2011/237045, 2-s2.0-84861575887.
10.1155/2011/237045
Google Scholar
20 Yulita Molliq R., Noorani M. S. M., Ahmad R. R., and Alomari A. K., Modified Step Variational Iteration Method for Solving Fractional Biochemical Reaction Model, International Journal of Differential Equations. (2011) 2011, no. 1, https://doi.org/10.1155/2011/514384, 2-s2.0-84878605940.
10.1155/2011/514384
Google Scholar
21 Hosseini M. M. and Nasabzadeh H., On the Convergence of Adomian Decomposition Method, Applied Mathematics and Computation. (2006) 182, no. 1, 536–543, https://doi.org/10.1016/j.amc.2006.04.015, 2-s2.0-33750813913.
10.1016/j.amc.2006.04.015
Web of Science® Google Scholar
22 Abassy T. A., Improved Adomian Decomposition Method, Computers and Mathematics With Applications. (2010) 59, no. 1, 42–54, https://doi.org/10.1016/j.camwa.2009.06.009, 2-s2.0-73449134442.
10.1016/j.camwa.2009.06.009
Web of Science® Google Scholar
23 Ghorbani A., Beyond Adomian Polynomials: He Polynomials, Chaos, Solitons & Fractals. (2009) 39, no. 3, 1486–1492, https://doi.org/10.1016/j.chaos.2007.06.034, 2-s2.0-62949242120.
10.1016/j.chaos.2007.06.034
Web of Science® Google Scholar
24 Wu G. C., Challenge in the Variational Iteration Method-A New Approach to Identification of the Lagrange Multipliers, Journal of King Saud University Science. (2013) 25, no. 2, 175–178, https://doi.org/10.1016/j.jksus.2012.12.002, 2-s2.0-84875236585.
10.1016/j.jksus.2012.12.002
Google Scholar
25 Shateri M. and Ganji D. D., Solitary Wave Solutions for a Time-Fraction Generalized Hirota-Satsuma Coupled KdV Equation by a New Analytical Technique, International Journal of Differential Equations. (2010) 2010, no. 1, https://doi.org/10.1155/2010/954674, 2-s2.0-84858112048.
10.1155/2010/954674
Google Scholar
26 Ghorbani A. and Saberi-Nadjafi J., An Effective Modification of He’s Variational Iteration Method, Nonlinear Analysis: Real World Applications. (2009) 10, no. 5, 2828–2833, https://doi.org/10.1016/j.nonrwa.2008.08.008, 2-s2.0-64049113173.
10.1016/j.nonrwa.2008.08.008
Web of Science® Google Scholar
27 He J. H. and Wu X. H., Variational Iteration Method: New Development and Applications, Computers & Mathematics with Applications. (2007) 54, no. 7-8, 881–894, https://doi.org/10.1016/j.camwa.2006.12.083, 2-s2.0-34748870677.
10.1016/j.camwa.2006.12.083
Web of Science® Google Scholar
28 Liao S. J., The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems, 1992, Shanghai Jiao Tong University.
Google Scholar
29 Zheng L. and Zhang X., Modeling and Analysis of Modern Fluid Problems, 2017, Academic Press.
Google Scholar
30 He J., An Approximate Solution Technique Depending on an Artificial Parameter: A Special Example, Communications in Nonlinear Science and Numerical Simulation. (1998) 3, no. 2, 92–97, https://doi.org/10.1016/s1007-5704(98)90070-3, 2-s2.0-0013403638.
10.1016/s1007-5704(98)90070-3
Google Scholar
31 Sajid M. and Hayat T., Comparison of HAM and HPM Methods in Nonlinear Heat Conduction and Convection Equations, Nonlinear Analysis: Real World Applications. (2008) 9, no. 5, 2296–2301, https://doi.org/10.1016/j.nonrwa.2007.08.007, 2-s2.0-48249122259.
10.1016/j.nonrwa.2007.08.007
Web of Science® Google Scholar
32 Turkyilmazoglu M., Some Issues on HPM and HAM Methods: A Convergence Scheme, Mathematical and Computer Modelling. (2011) 53, no. 9-10, 1929–1936, https://doi.org/10.1016/j.mcm.2011.01.022, 2-s2.0-79951947089.
10.1016/j.mcm.2011.01.022
Web of Science® Google Scholar
33 Liao S., Comparison Between the Homotopy Analysis Method and Homotopy Perturbation Method, Applied Mathematics and Computation. (2005) 169, no. 2, 1186–1194, https://doi.org/10.1016/j.amc.2004.10.058, 2-s2.0-25844456083.
10.1016/j.amc.2004.10.058
Web of Science® Google Scholar
34 Song L. and Zhang H., Application of Homotopy Analysis Method to Fractional KdV-Burgers-Kuramoto Equation, Physics Letters A. (2007) 367, no. 1-2, 88–94, https://doi.org/10.1016/j.physleta.2007.02.083, 2-s2.0-34347339334.
10.1016/j.physleta.2007.02.083
CAS Web of Science® Google Scholar
35 Abbasbandy S., The Application of Homotopy Analysis Method to Nonlinear Equations Arising in Heat Transfer, Physics Letters A. (2006) 360, no. 1, 109–113, https://doi.org/10.1016/j.physleta.2006.07.065, 2-s2.0-33750339270.
10.1016/j.physleta.2006.07.065
CAS Web of Science® Google Scholar
36 Liang S. and Jeffrey D. J., Comparison of Homotopy Analysis Method and Homotopy Perturbation Method Through an Evolution Equation, Communications in Nonlinear Science and Numerical Simulation. (2009) 14, no. 12, 4057–4064, https://doi.org/10.1016/j.cnsns.2009.02.016, 2-s2.0-67349162538.
10.1016/j.cnsns.2009.02.016
Web of Science® Google Scholar
37 Rui W., Yang X., and Chen F., Method of Variable Separation for Investigating Exact Solutions and Dynamical Properties of the Time-Fractional Fokker-Planck Equation, Physica A: Statistical Mechanics and Its Applications. (2022) 595, no. 1, https://doi.org/10.1016/j.physa.2022.127068.
10.1016/j.physa.2022.127068
Web of Science® Google Scholar
38 Yulita Molliq R. and Noorani M. S. M., Solving the Fractional Rosenau-Hyman Equation via Variational Iteration Method and Homotopy Perturbation Method, International Journal of Differential Equations. (2012) 2012, no. 1, 1–14, https://doi.org/10.1155/2012/472030, 2-s2.0-84887739911.
10.1155/2012/472030
Google Scholar
39 Mittag-Leffler G. M., Sur la nouvelle fonction Ea (x), CR Academic Science Paris. (1903) 137, no. 2, 554–558.
Google Scholar
40 Srivastava H. M. and Choi J., Zeta and Q-Zeta Functions and Associated Series and Integrals, 2011, Elsevier.
Google Scholar
41 Salim T. O., Some Properties Relating to the Generalized Mittag-Leffler Function, Advances in Applied Mathematical Analysis. (2009) 4, no. 1, 21–30.
Google Scholar
42 Salim T. O. and Faraj A. W., A Generalization of Mittag-Leffler Function and Integral Operator Associated with Fractional Calculus, Journal Fractor Calculation Application. (2012) 3, no. 5.
Google Scholar
43 Johnson W. B. and Lindenstrauss J., Handbook of the Geometry of Banach Spaces, 2001, Elsevier.
10.1016/S1874-5849(01)80021-8
Google Scholar
44 Argyros I., Computational Theory of Iterative Methods, 2007, Elsevier.
Google Scholar
45 Boulares H., Ardjouni A., and Laskri Y., Positive Solutions for Nonlinear Fractional Differential Equations, Positivity. (2017) 21, no. 3, 1201–1212, https://doi.org/10.1007/s11117-016-0461-x, 2-s2.0-85002292056.
10.1007/s11117-016-0461-x
Web of Science® Google Scholar

All articles

Modified Semiseparation of Variables Methods for Solving the System of Nonlinear Fractional Partial Differential Equations

Abstract

1. Introduction

2. Preliminaries