1. Introduction

With the accelerating process of high-tech three-dimensional (3D) war and the integration of information conflict, the concept of the smart ammunition formation (SAF) cooperative combat is expanding and extending and will become more and more important. Under this mode of combat, the ammunition surprises defense, electronic countermeasures, coordinated search capability for moving targets, and integrated combat effectiveness will be substantially improved [1]. Other existing countries, using a combined leader–follower ammunition formation attack mode while utilizing multiple sensors for information integration, fully embody the concept of coordinated warfare [2, 3]. Formation flying was initially developed for satellites and has been greatly developed for unmanned aerial vehicles (UAVs) formation applications [4].

Regarding the technology of formation control and design, scholars have conducted some research on the formation control problems of UAVs as well as robots. In terms of UAV formation, Dargan et al. devised a planar UAV formation maintenance controller grounded in traditional control theory, predicated on the isometric flight of the UAV formation. When the speed of the leader is assumed to be constant, the relative motions of the UAVs in the two directions of the horizontal plane are decoupled, and the PID controllers can be individually designed for the two channels based on the desired spacing deviation [5]. McCamish et al. carried out a further study on the previous work and carried out a UAV formation flight holding controller optimization design, using the sequence quadratic programming (SQP) method to optimize the gain coefficients of the PID controller with a fixed control structure, so that the control effect has been improved [6]. Li et al. analyzed the deviation of the actual distance between UAVs and the desired distance under the inertial coordinate system and established a two-dimensional planar relative kinematic model of the UAV. They applied the full-state feedback to the UAVs’ kinematics model, applying full-state feedback to design a PD controller based on the spacing deviation and its derivative, and this formation-keeping controller had global stability [7]. Boskovic et al. carried out a study on the problem of designing a UAV formation-keeping controller by using the modern control theory method. Taking into account the singularity of the feedback matrix dissimilarities, they designed a semiglobally stable 3D UAV formation–keeping controller [8, 9]. Chang et al. proposed that in order to avoid collisions, the follower UAVs are uniformly distributed on a sphere centered on the leader UAV [10]. Liu et al. investigated the presence of a high mobility scenario with communication delays, the deep reinforcement learning (DRL)–based UAV formation tracking design, and proposed a deep deterministic policy gradient (DDPG) algorithm with extended delay notification [11]. Considering uncertain variable-over-time leadership speeds and network-induced latencies, Wang et al. developed an optimal formation in the quasi-equilibrium and overall dynamic control scenarios [12]. Zhao et al. designed a consensus algorithm for leader-follower and introduced an artificial repulsive field method to guarantee that UAV formations steer clear of obstacles effectively [13]. Shao et al. introduced an enhanced 3D route planning method for UAV formations, leveraging the principles of particle swarm optimization (PSO) [14]. Li et al. integrated optimal control theory into formation control strategies, devising a distributed protocol for achieving optimal formations, and confirmed its stability using graph-theoretic methods [15]. For robot formations, Li et al. introduced a novel distributed reinforcement learning approach, leveraging a soft actor-critic algorithm, to address the challenges of multi-robot coordination [16]. Dai et al. took into account collision avoidance among multiple robots during obstacle navigation. Based on the expected distances and azimuth angles relative to the leader and follower robots, they designed a novel robot prioritization model [17]. Zheng et al. introduced a dynamic embedded structure formation strategy utilizing visual servoing, enabling a team of turtle-mimicking amphibious robots to sustain their parameterized long-distance path [18]. Xie et al. investigated the dynamic leadership mechanism of pigeon nesting and provided new insights into the formation problem [19]. Sharma et al. presented a new technique to analytically calculate the minimum distance between the nearest point and the impediment on the line segment of a rectangular protected area, which was validated by simulation to avoid collision and obstacle [20]. Jiang et al. suggested a new method to realize the decentralized collaborative control of multi-robot formations by utilizing deep neural networks, and the method was validated by simulation [21]. Wang et al. presented a multirobot formation control strategy employing higher order Kalman filtering. This strategy utilizes Taylor expansions for both state and observation equations and introduces a residual variable to enhance estimation accuracy [22]. Wan et al. proposed a multirobot formation trajectory using deep neural networks to achieve decentralized cooperative control using deep neural networks [23].

You et al. explored two types of 3D cooperative guidance systems for thrust-controllable missiles targeting maneuvering enemies, focusing on impact angle constraints. Their aim was to enhance the missiles’ coordinated attack and penetration capabilities [24]. Zhan et al. presented a finite-time optimal coguidance technique aimed at minimizing missile engine load in the line-of-sight (LOS) direction. This technique is particularly relevant to missile formations, which differ significantly from swarm technology research but are of interest to smart swarm applications [25]. The problem of formation control technology, as exemplified by the UAV formation, which is based on generating appropriate control commands to drive each vehicle to achieve the specified constraints on its own state, greatly expands the potential areas of application and opens up new areas of application [26]. Other equipment formation control is mostly similar.

The problem of SAF configuration design refers to the arrangement of formations according to a set geometric structure in real-world flight. The current research mostly simply applies the UAV formation to the SAF, while the type of formation still lacks innovation and development. In the current formation structure, different formation designs have different practical combat effects, such as vertical formation is favorable to avoid radar detection wedge formation is more suitable for the leader-follower mode, which is convenient for data communication and formation development. At present, the common formation configuration mainly includes parallel, wedge, diamond, and vertical formation. In this paper, we will focus on the configuration control of SAF and establish kinetic equations and a formation control model, and simulations were analyzed to ascertain the fundamental dynamics of the formation. The first section of this paper establishes the SAF model. In the second section, the SAF cooperative controller based on the model of the leader-follower scheme will be designed. The third section presents a simulation involving a formation consisting of one leader and four followers. The discussion will focus on the dynamic responses observed when the leader performs lateral maneuvering. The conclusion is illustrated in the last section. The main contribution of this study lies in illustrating a standardized leader–follower SAF formation cooperative framework. The study introduces an innovative intelligent control approach for managing SAF cooperatively. The elements of multichannel control encompass velocity, ballistic inclination angle, and ballistic deflection angles. The simulation results analysis revealed satisfactory convergence in the SAF cooperative control system. The manuscript’s work offers additional options for addressing the SAF collaborative control issue.

2. SAF Model

These advantages highlight the effectiveness of the hierarchical leader–follower framework in addressing the complexities and uncertainties associated with SAF control, setting it apart from classical distributed form.

The SAF operates under a leader–follower model, comprising a single leader ammunition and multiple followers that constitute the formation. The controller design for the SAF necessitates maintaining a safe and desired distance between the leader and the followers, regardless of the leader’s maneuvers. Additionally, the output ranges of the followers’ controllers, including ballistic inclination, declination, and velocity, must be limited. Consequently, it is crucial to ensure acceptable general stability of the formation controller [7].

The leader–follower control approach is a crucial technique for investigating the consistency in cooperative system control [8]. In this method, the leader occupies a unique position, remaining unaffected by other members. It directs the formation’s path, whereas the followers do not require awareness of the formation’s target details. They solely rely on the information sent from the leader [9]. Nevertheless, a disadvantage of this kind of control lies in the relative autonomy between the leader and followers, making it challenging to acquire feedback on tracking errors from the followers.

3. SAF Cooperative Controller Design

As aforementioned, SAF employs a hierarchical leader–follower framework. It utilizes a single leader and a corresponding follower as the fundamental unit for devising a 3D formation controller. This controller is aimed at maintaining the relative distance between the leader and follower within a specified limit, irrespective of the leader’s movements. Additionally, the follower’s ballistic inclination angle, declination angle, and velocity are confined to a narrow range to guarantee the near-stability of the SAF [28].

3.1. Relative Model Between Leader and Follower

To depict the relative position between the leader and follower ammunition, a coordinate system is set up, taking the follower as the point of reference, as illustrated in Figure 1 [29].

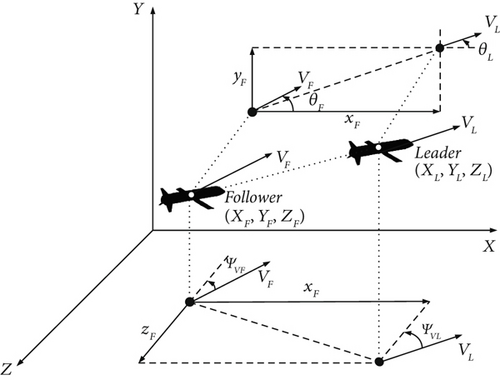
where X_L, Y_L, and Z_L represent the inertial coordinates system of the leader ammunition, respectively. X_F, Y_F, and Z_F are the inertial coordinates system of the follower, respectively. x_F, y_F, and z_F are the relative distances between a leader and the follower in the coordinate system referenced by the follower, respectively. V_L and V_F illustrate the velocity of the leader and follower. θ_L and θ_F are the trajectory inclination angles of the leader and the follower. ψ_VL and ψ_VF represent the ballistic deflection angles of the leader and the follower.

Assuming the follower’s ballistic inclination angle, declination angle, and velocity can be measured, a simplified model is adopted for the SAF control problem. In this model, the motions of both the leader and follower are treated as independent first-order systems [30].

$$ ()

$$ ()

where τ_VL, τ_VF, τ_θL, τ_θF, τ_ψL, and τ_ψF represent the constants associated with the velocity, trajectory inclination angles, and deflection angles of the leader and follower. V_LC and V_FC are the velocity instructions for the leader and follower, respectively. θ_LC and θ_FC describe the leader and follower trajectory tilt instructions. ψ_LC and ψ_FC are the ballistic deflection angle commands for both the leader and the follower.

The equations of motion for the pilot and follower can be displayed as follows:

$$ ()

$$ ()

4. Simulation

As what is mentioned above, the description of the dynamics and cooperative controller of the SAF are illustrated. A four-order Runge–Kutta iteration method is used for the simulation. A SAF contains one leader and four followers for the simulation. Two simulation cases are analyzed in this section to test the applicability of the controller and whether the leader maneuvers during the flight.

4.1. Parameters

• 1.

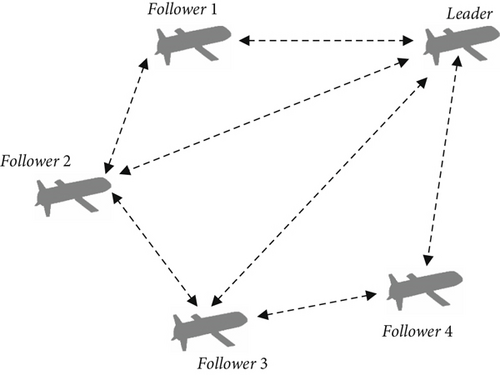
  Communication topology between the leader and followers is shown in Figure 2.

• 2.

  Constants that are related to the leader’s and followers’ velocity, trajectory inclination angles, and deflection angles:

$$

• 3.

  A 3 × 3 diagonal matrix in Equation (17):

$$

• 4.

  Desired distance between the Leader and Followers 1, 2, 3, and 4 in order:

$$

• 5.

  The control commands of the leader’s velocity, trajectory inclination angle, and trajectory deviation angle:

$$

• 6.

  The control commands range of every follower’s velocity, trajectory inclination angle and trajectory deviation angle:

$$

The physical parameters of the leader and followers are shown in Table 1.

Table 1. Parameters of the leader and the followers.

	Leader	Follower 1	Follower 2	Follower 3	Follower 4
Initial position (m)	(5000, 5020, 0.0)	(4980, 5015, 0.0)	(4960, 5010, 0.0)	(4940, 5005, 0.0)	(4920, 5000, 0.0)
V0 (m/s)	240.0
ψ0 (deg)	0.0
ϕ0 (deg)	0.0

4.2. Results

4.2.1. Case 1

In Case 1, there is no lateral maneuvering for the leader. The correctness and stability of the controller are ensured in this case. Figure 3 shows the trajectory of the leader and the followers in 3D space. The relative distance change is illustrated in Figures 4, 5, and 6.

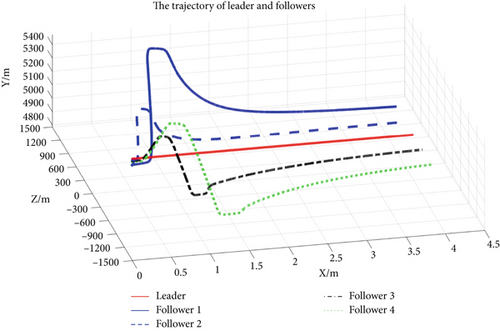
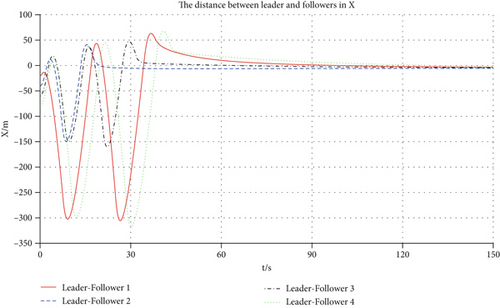
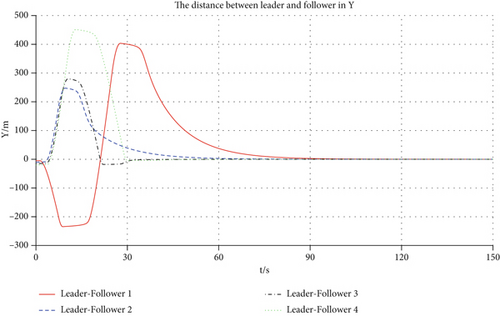
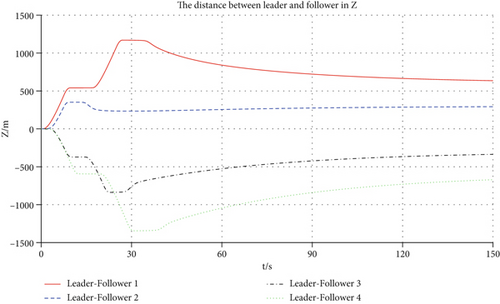
Figure 3 shows the 3D trajectory changes for the leader and the four followers. From the changing drift of the curves, in the X, Y, and Z directions, it can be seen that the followers are steadily approaching the expected relative distance. Figures 4, 5, and 6 denote the relative distance-time profiles of the leader and the follower associated with the X, Y, and Z directions, respectively. From the zero of the trajectory time to 120 s, the relative distance in the X direction gradually satisfies the requirements and is maintained until the calculation ends. At 90 s, the relative distance meets the desired requirements and is maintained in the Y direction. After more than 120 s, the relative distance converges to the expected value in the Z direction.

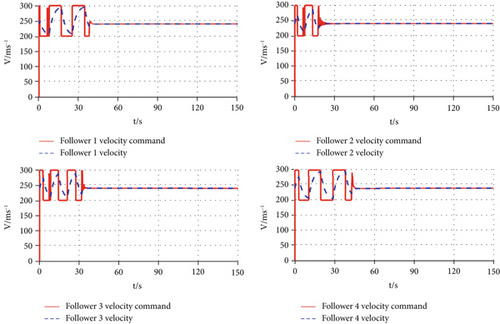
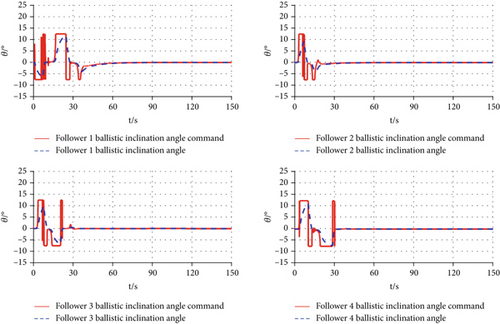
The changes of the followers’ velocity, trajectory inclination angle, and trajectory deviation angle under their control command are illustrated in Figures 7, 8, and 9. The curves show that the changes in followers’ velocity, trajectory inclination angle, and trajectory deviation angle can follow the requirements of the control command and exhibit stable variations.

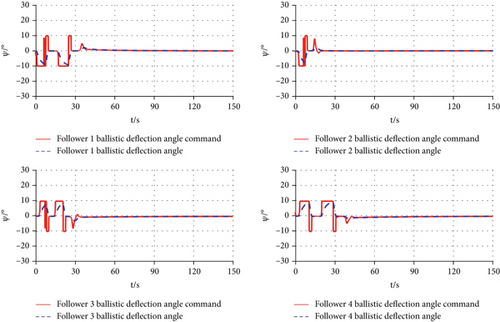
4.2.2. Case 2

The leader acts in almost a 2° lateral sinusoidal maneuver in Case 2. The stability of the controller is evaluated when the leader executes maneuvers within a limited range of amplitudes. Figure 10 depicts the paths taken by both the leader and its followers in 3D space. Changes in the spacing between them are demonstrated through Figures 11, 12, and 13.

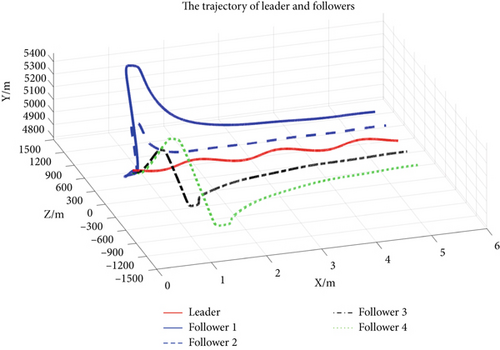
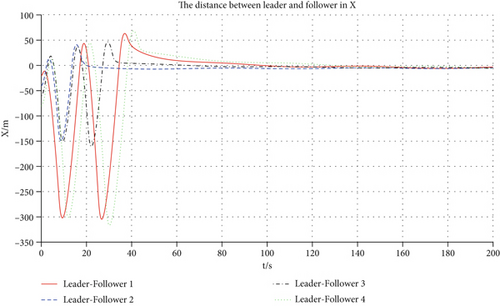
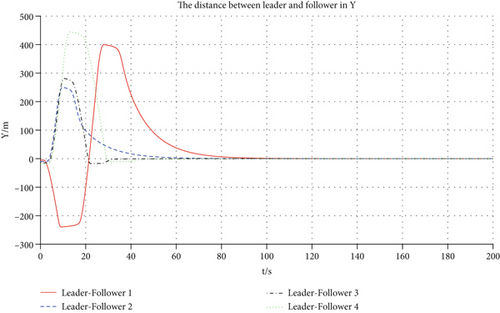
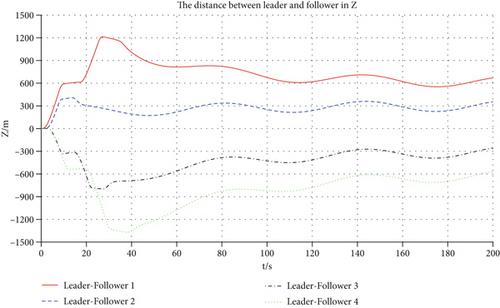
It demonstrates the 3D trajectory variations of the leader and four followers in Figure 10. From the representation of the curves, four followers can steadily approach the desired relative distance in the X, Y, and Z directions. They exhibit the variations over time of the spacing between the leader and followers along the X, Y, and Z axes in Figures 11, 12, and 13, respectively. From the start of the trajectory at time zero until 160 s, the spacing in the X-axis progressively aligns with the specified criteria and remains within a band of ± 10 meters. Subsequent to 100 s, the spacing in the Y axis fulfills the specified criteria and continues to do so until the simulation terminates. After exceeding 120 s, the relative distance oscillates near the target value, maintaining a deviation that stays confined to approximately ± 50 m.

5. Conclusion

This study adopted a leader–follower framework for cooperative control and dynamical analysis within the context of the SAF. The control variables selected encompassed the velocity of the followers, the angle of inclination of their trajectories, and the angle of deviation from the intended path. The design of the 3D controller was predicated on the discrepancy between the actual and desired relative spacing between the leader and its followers. In the simulation segment, a formation comprising one leader and four followers was evaluated, with a primary focus on comparing scenarios with and without lateral maneuvering by the leader. The outcomes of the simulation encompassed spatial trajectories, temporal variations in relative positioning, and the tracking performance of the three control variables and associated commands for both the leader and its followers. The collaborative control framework proposed in this article is based on a hierarchical leader-follower framework, which improves the control efficiency and robustness of the SAF. By adopting a simplified communication topology structure and reducing the information exchange requirements between following nodes, the control framework can adaptively coordinate multi-dimensional parameters such as the ballistic inclination angle, declination angle, and velocity of the formation nodes, accurately maintaining the formation configuration. These results substantiated that collaborative control framework exhibits fast response capability and strong adaptability in both static and dynamic scenarios, providing reliable theoretical support for high-speed ammunition collaborative tasks. Looking ahead, future investigations should take into account both temporal and spatial synchronization between the leader and followers to further explore collaborative dynamic control methodologies.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

Jian Shen conceived and designed the study. Xiaoguang Wang and Shaobo Fan performed most simulations. Pengyun Chen analyzed the data and wrote the first draft of the manuscript. Ziwang Zhang revised the manuscript. Jiacheng Zheng and Xiaofeng Ji supervised the project and reviewed the manuscript.

Funding

This research is supported by the National Natural Science Foundation of China (10.13039/501100001809) (62003314), the Applied Basic Research Project of Shanxi Province, China (10.13039/501100019447) (202403021211090), the Research Project Supported by Shanxi Scholarship Council of China (2023-136), the Heilongjiang Postdoctoral Funding Project (2023-302), and the Shanxi Key Research and Development Program (202202020101001).