Guidance law design is a critical technology that directly influences the interception performance of antitorpedo torpedoes. In response to the performance degradation of classic proportional guidance laws and derivative guidance laws when intercepting high-speed underwater targets and the significant impact of the proportional coefficient on interception miss distance, this paper proposes an intelligent guidance law. Based on the proportional guidance interception law, the law incorporates a variable proportional coefficient based on the deep Q-network (DQN) algorithm from deep reinforcement learning. Integrating engineering design, the intelligent guidance law for antitorpedo torpedoes proposed in this article selects the rate of change in the line-of-sight angle as the state variable, designs a reward function based on interception results, and designs a discretized behavior space based on the commonly used proportional guidance coefficient selection range. The greedy algorithm and temporal difference learning are employed to train the DQN, and the optimal proportional guidance coefficient is selected from the DQN by the real-time state of the torpedo. The feasibility of the proposed guidance law was verified through simulation experiments. The interception effects of the proposed intelligent guidance law and the fixed coefficient proportional guidance law were compared and analyzed in typical situations. The results demonstrated that the reinforcement learning guidance law was significantly superior to the traditional proportional guidance law in terms of miss distance, maneuvering ability consumption, and ballistic straightness and had stronger robustness. Furthermore, the intelligent guidance law for antitorpedo torpedoes proposed in this article enables antitorpedo torpedoes to make autonomous decisions based on the battlefield situation.

1. Introduction

With the continuous improvement of torpedo against resistance and intelligence levels, ship platforms are equipped with various detection and maneuvering capabilities, forcing surface ships to use more ways to defend against it [1]. Currently, surface ships use acoustic decoys, acoustic jammers, and other “soft confrontation” equipment. However, their effectiveness in deception is gradually diminishing, creating an urgent need for reliable active defense solutions. In this context, antitorpedo torpedo (ATT) technology has become one of the key areas of research and development for naval forces worldwide. ATT, as a kind of active “hard kill” defense weapon, has the characteristics of active, flexible, high maneuverability, etc. Due to its high probability of intercepting and destroying torpedoes, ATT plays a crucial role in enhancing the survivability of surface vessels and submarines. Therefore, the study of control and interception methods for ATT is of significant importance. Different from the traditional torpedo, the target of ATT interception is the incoming torpedo, which is characterized by high speed, high mobility, low radiation noise level, small target intensity, etc. This presents a significant challenge in the design of the ATT interception guidance law [2–4].

In light of these challenges, researchers have conducted extensive studies to improve the accuracy and effectiveness of ATT interception. Literature [5] proposes a three-dimensional adaptive PN guidance method for hypersonic vehicles to strike stationary ground targets in a specified direction during the terminal phase. Literature [6, 7] designs and analyzes a biased PN guidance law for passive homing missiles to intercept stationary targets under constrained impact angles. Literature [8] proposed a deep Q-network (DQN)–based deep reinforcement learning (DRL) guidance method, successfully applying DQN to interception tasks and addressing the limitations of traditional methods in intercepting high-speed, highly maneuverable targets. Literature [9] studies the calculation method of the hit probability of ATT in intercepting incoming torpedoes. Literature [10–12] designs two sliding mode guidance laws, one with asymptotic convergence and the other with finite-time convergence. Literature [13] proposes a variable structure control to maintain a constant line-of-sight angle. It establishes simulation models for ATT interception trajectories based on traditional constant lead angle guidance laws and variable structure control-based guidance laws [14]. The results demonstrate that this method exhibits strong robustness, high hit accuracy, and smooth trajectories, outperforming traditional constant lead angle guidance laws. Literature [15] decomposes the spatial motion of ATTs into longitudinal and lateral planes, designing separate guidance rates. This method ensures a higher hit probability for ATT. Literature [16] divides the surface ship defense against incoming torpedoes into four different processes: long-distance segment defense, middle-distance segment defense, close-distance segment defense, and near-boundary segment defense. Based on the ATT interception process under various postures, optimal ATT interception strategies were designed for each distance segment [17, 18]. Most of the above studies on ATT guidance law adopt the traditional guidance method or the proportional guidance law with fixed scale coefficients, although they show certain advantages in some application scenarios, which are unable to adequately adapt to the complex and changing battlefield environment. Especially in high-speed maneuvering target interception missions, the limitations of traditional guidance methods become more and more obvious, as they cannot effectively deal with the high mobility of the target and the complex environmental interference. Therefore, new intelligent methods are urgently needed to compensate for these shortcomings.

With the rapid development of artificial intelligence technology, especially the emergence of DRL algorithms, new opportunities are provided to address the limitations of traditional guidance methods [19–21]. DQN, as a typical reinforcement learning algorithm, has proved its powerful learning ability in several fields. Literature [22] considers the three-body confrontation problem involving an interceptor, target, and defense missile. It uses DRL to estimate the optimal launch time for the defense missile and the optimal guidance law for the target. Gaudet et al. [23] designed the interceptor end guidance law based on metareinforcement learning, which simplified the design of the guidance law and improved the robustness of the guidance law through reinforcement learning algorithms. Literature [24] proposes a DRL-based AUV obstacle avoidance method. Literature [25] proposes a trajectory optimization method for high-speed aircraft based on DRL. These studies fully demonstrate the strong applicability of reinforcement learning algorithms. But there are still fewer DRL-based approaches in the field of ATT guidance.

While existing methods have contributed valuable insights into ATT guidance, traditional guidance methods, such as the tracking method and advance angle method, cannot meet ATT’s requirements for intercepting high-speed incoming torpedoes. Furthermore, due to the limitations of underwater acoustic detection methods, the amount of target information is limited, and the data transmission rate is low. This makes it difficult to directly apply many existing interception guidance methods designed for missiles to ATT. Literature [8] successfully applied DQN to interception tasks and addressing the limitations of traditional methods in intercepting high-speed, highly maneuverable targets. However, its proportional coefficients cannot be adjusted according to changes in the environment. To address these limitations, this paper proposes a DRL-based ATT intercept guidance law with variable proportional coefficients. The approach leverages the DQN DRL algorithm [26, 27] and builds upon the traditional proportional guidance law by incorporating an autonomous decision-making mechanism. The key innovations of this paper are as follows: (1) the integration of DRL to discretize the proportional coefficients in the proportional guidance law to form a behavioral space. This allows the ATT system to automatically select the optimal proportional coefficients based on the target’s dynamic behavior and environmental conditions, thereby improving both interception accuracy and adaptability. (2) Using the relative posture as a judgment condition, the design of a reward function is based on the miss distance to optimize interception accuracy and reduce the miss distance. Through the comparative simulation test with the traditional method, the superiority of the proposed method in terms of guidance accuracy, maneuverability consumption, and trajectory straightness is verified [28].

2. Materials and Methods

2.1. Kinematic Mode

In order to simplify the problem, the kinematic analysis method is usually adopted to study the guidance law design problem, focusing on the relative motion relationship between the ATT and the incoming torpedo (target). To maintain the generality, this paper takes the side plane as the research object to design the guidance law and establishes the relative motion equations between the ATT and the target in the side plane. The relative motion relationship is illustrated in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Side plane ATT-target relative motion.

In Figure 1, V_M and V_T are the velocities of ATT and incoming torpedo (target), respectively; r and q are the relative distances and line-of-sight angles between ATT and target; and θ_M and φ_M, θ_T and φ_T denote the trajectory angle and the leading angle of ATT and target, respectively. Assuming that the two sides have the dynamic characteristics of offline control, the guidance equation can be expressed as follows:

()

where φ_T = −(π + θ_T − q), φ_M = q − θ_M, A_M, and A_T denote the normal acceleration of the ATT and the incoming torpedo, respectively.

According to the guidance equation, the velocity component of the relative velocity of the ATT to the target along the normal direction of the line of sight is as follows:

()

Derivation of the above equation with respect to time yields

()

where d(t) = cosφ_TA_T is the uncertainty term due to target maneuvering, which is typically not directly measurable, but is bounded by d(t) and its derivatives in the case of underwater targets with limited maneuvering capabilities.

Bringing

and

into Equation (3) yields

()

where a_M and a_T are the components of the acceleration of the ATT and the incoming torpedo normal to the line of sight, respectively.

Choosing

, θ_f as the desired angle of fall, U = a_M, F(t) = a_T, and considering U = a_M as the control quantity and F(t) = a_T as the disturbance quantity, the equation of state is established as follows:

()

where

, and

At the initial moment, the initial representation of each state variable is as follows:

()

Then, the proportionality governing law is as follows:

()

where K is the proportionality law coefficient.

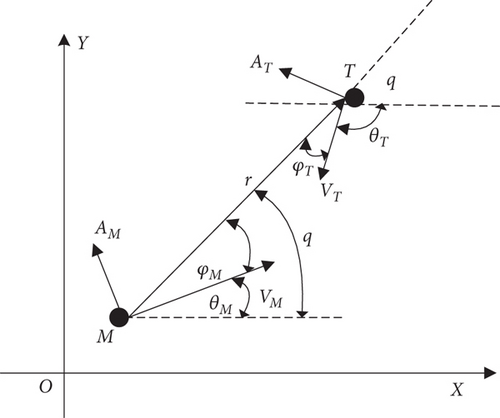
In addition, ballistic straightness is an important factor in describing the performance of the ATT system. Its calculation method is as follows: 10 points are selected along the trajectory, evenly distributed, and the average height of these points is calculated. The ballistic straightness is then obtained by dividing the average height by the distance from the starting point to the endpoint.

2.2. DQN Algorithm

Reinforcement learning algorithms make decisions based on the results of feedback from the environment with the goal of maximizing the reward payoff. Reinforcement learning algorithms are trained to be dynamic, learning autonomously as a result of constant interaction with the environment. The reinforcement learning problem is usually described based on a Markov decision model, which is usually described as a dynamic process F(S, A, P, R, γ) characterized by five parameters, where S is the set of states, A is the set of actions, P is the state transfer function, R is the reward function, and γ is the discount factor.

The Q-learning algorithm is a classical model-free reinforcement learning algorithm. Due to its model-free nature, the subsequent state S_next cannot be obtained directly, generally according to the intelligent body and the environment interaction feedback results, through the form of experiment and sampling to obtain S_next. Based on this, the dynamic process of the Q-learning algorithm is simplified to be described by F_Q(S, A, R, γ). The Q-learning algorithm establishes the mapping between discrete states and discrete actions through the Q-table, and the intelligent body obtains the interaction results with the environment after taking the corresponding actions, continuously updates the Q-table based on the comprehensive evaluation of the results, and then makes the goal and behavioral decisions based on the Q-table and the states.

The training objective of the Q-learning algorithm is to maximize the Q-value function, and the algorithm usually employs temporal difference errors [29] to update the Q-value. In each feedback iteration process, the intelligent agent interacts with the environment by first selecting an action based on the current state, which corresponds to the selection of action a_t in state S_t, and then arrives at the next state S_t+1 after the action a_t has acted. At the same time, according to the reward R_t obtained by the action a_t, the subsequent states of the discounting effect are considered, and the Q-value of the corresponding mapping relationship in the Q-value table is updated by the synthesis of the maximum Q-value [30, 31].

()

The Q-learning algorithms can only handle low-dimensional data as well as the need to discretize the inputs to the state. However, the state space of real-life practical problems is often very large and continuous. Although the DDPG (deep deterministic policy gradient) algorithm can handle more complex continuous action problems, its network structure is relatively complex, its training time is long, and it may face instability issues when applied to high-dimensional state spaces [32]. Therefore, to ensure the performance of the ATT system, we chose to use the DQN algorithm to design the interception guidance law. The core idea of DQN is to approximate the Q-function using deep neural networks, which is particularly suitable for handling continuous state variables such as the line-of-sight rate in the relative motion model of the ATT and target. By leveraging deep neural networks, DQN effectively addresses complex, continuous state spaces, providing powerful learning capabilities for high-dimensional tasks.

To enhance the mapping of the state and action space, a greedy strategy can be used in the behavioral decision-making strategy, that is,

()

where ε is a strategy parameter characterizing that the intelligent body will select random actions in the set of actions with a probability of P(ε) and select actions with a probability of 1 − P(ε) in the Q-table based on the maximum Q-value in the action space using a greedy strategy.

2.3. ATT Autonomous Variable Coefficient Proportional Guidance Law Based on DQN Algorithm

2.3.1. State Space Design

In the guidance process, the line-of-sight angular rate is often chosen as one of the main variables in the guidance law. Therefore, in this paper, the line-of-sight angular rate is chosen as the state space. Considering the variation range of the line-of-sight rate during the ATT interception process and its own overload limitation, the range of the line-of-sight rate is chosen to be [−0.5, 0.5] rad/s. The state inputs of the DQN algorithm can be consecutive, so the line-of-sight rate is inputted directly into the DQN.

2.3.2. Motion Space Design

The proportional guidance law is based on the principle of optimal control, which uses the relative velocity of the ray sight and the rate of change of the line of sight to generate the maneuvering acceleration command required for the interception of the target torpedo, that is,

()

where K is the scale factor,

is the relative velocity, and

is the line-of-sight angular rate.

In the above equation, and are related to the relative state situation, and only the scale factor can be set externally, so the scale factor is used as the action. Since there is a mapping relationship between continuous states and actions in the DQN algorithm, it is necessary to discretize the action space. From the derivation process of the traditional proportional guidance method, it can be seen that usually K takes the value between 2 and 7 and, in this range, is discretized into 51 actions according to the step size of 0.1. Each action represents a proportionality coefficient, and each proportionality coefficient corresponds to each action in the action space. Selecting an action means generating the corresponding proportionality coefficient, and according to the proportionality coefficients, the maneuvering acceleration instruction can be obtained.

2.3.3. Action Selection Strategy Design

In this paper, a greedy strategy is adopted, that is, at the beginning of the algorithm training, a large ε is selected, which makes the intelligent agent search for optimization in a large range. As the learning process continues, the value of ε decreases in order to determine a reasonable action as soon as possible. The pseudocode for the training flow of the ATT variable coefficient proportional guidance law based on the DQN algorithm is shown in Algorithm 1.

Algorithm 1: Guide Law Training Process.

Deep Q-learning with experience replay.
1: Initialize replay memory D to capacity N
2: Initialize action-value function Q with random weights θ
3: Initialize target action-value function with weights θ⁻ = θ
4: For episode = 1, M do
5: Initialize sequence s₁ = {x₁} and preprocessed sequence ϕ₁ = ϕ(s₁)
6: for t = 1, T do
7: With probability ε select a random action a_t
8: otherwise select a_t = argmax_aQ(ϕ(s_t), a; θ)
9: Execute action a_tin emulator and observe reward r_t and image x_t+1
10: Set s_t+1 = s_t, a_t, x_t+1 and preprocess ϕ_t+1 = ϕ(s_t+1)
11: Store transition (ϕ_t, a_t, r_t, ϕ_t+1) in D
12: Sample random minibatch of transitions (ϕ_j, a_j, r_j, ϕ_j+1) from D
13: Set
14: Perform a gradient descent step on with respect to the network parameters θ
15: Every C steps reset
16: end for
17: end for

2.3.4. Reward Function Design

As one of the more critical steps in the DQN algorithm, the advantages and disadvantages after performing different maneuvers are evaluated according to the reward function. In the process of ATT intercepting the target torpedo, if the relative distance change rate between ATT and the target torpedo obtained from two consecutive acoustic cycles is negative and the more the line-of-sight angular rate tends to be close to 0, it means that the ATT keeps approaching the target and aligning itself with the target in the direction of the velocity, which is encouraged by a positive reward. If the ATT off-target amount meets the requirement of hit accuracy, it is recognized by giving a larger reward; otherwise, the reward value is set to 0. The reward function given in this paper consists of process reward R_prac and result reward R_end. The reward for each step is R = R_prac + R_end.

()

where r_damage is the radius of ATT damage and r_min is the off-target amount of ATT when an intercept simulation is finished. When ATT intercepts a target torpedo, an intercept simulation is finished when

changes from negative to positive at a certain moment which means that they are far away from each other.

3. Results and Discussion

Firstly, the training situation is set up as follows: the initial position of the target torpedo (0, 0, and 0 m), the initial trajectory inclination angle (30°), the maximum speed of the target torpedo (25, 30, and 35 m/s, respectively), and the maximum angular velocity (40°/s). The initial sailing depth of the target torpedo is selected to be 50 m, and the initial navigation depth of the target torpedo is selected to be 100 m, respectively. The target torpedo adopts the traditional proportional guidance law to attack surface ships.

Surface ships carry ATT; the position of the ship is 0, 2000, and 0 m; and the ship takes a direct motion with a speed of 10 m/s or a maneuvering motion with a speed of 12 m/s and an angular velocity of 1°/s.

The initial position of the ATT is 0, 2000, and 0 m; the initial ballistic inclination of the ATT is selected as three typical values of 0°, 30°, and −30°, respectively; the speed of the ATT is 35 m/s; and the maximum angular velocity is 70°/s. When the surface ship detects the target torpedo, the ATT is launched to intercept the target torpedo.

The initial typical array posture when the ATT intercepts the target torpedo is shown in Figures 2, 3, and 4.

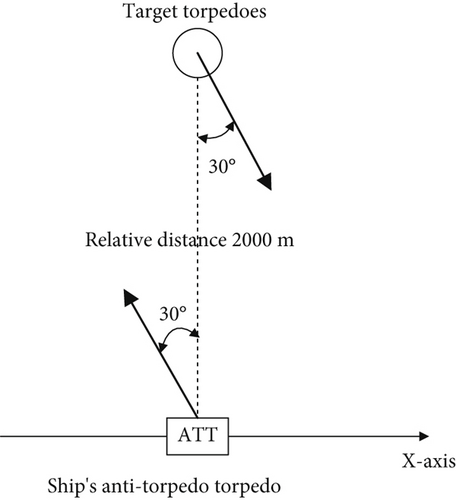
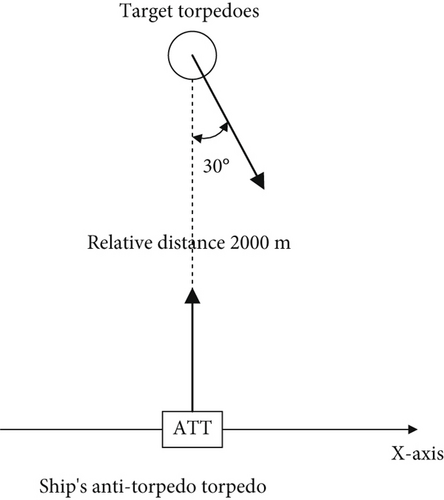
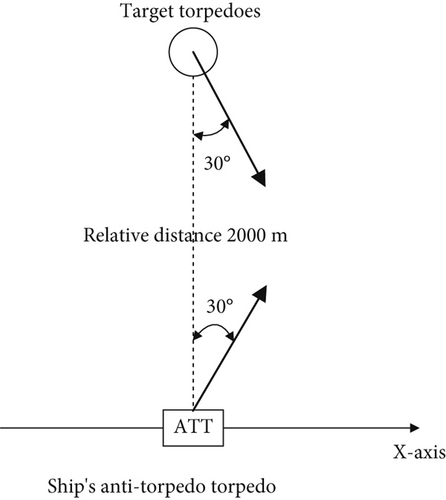
The ATT information is a known quantity, whereas the initial motion information of the incoming target torpedo is an unknown quantity. The depth and speed of the target torpedo are trained randomly; two random values of 50 and 100 m are selected for the depth, and three random values of 25, 30, and 35 m/s are selected for the speed. The surface ship’s maneuvering motion has two types of turning and straight sailing, and there are a total of 36 random initial postures by combining the above random types.

During training, the first randomly extracted posture is used, and after the posture is extracted, 2000 times of learning are performed. In each learning step, ATT receives real-time guidance commands from the DQN algorithm to get the action command. The relative distance of the mine′s eye and the rate of change of the line-of-sight angle are used to generate this command. When the ATT successfully hits the target, or at a certain moment when the value changes from negative to positive, the simulation ends. Then, the system proceeds to the next training simulation.

The DQN algorithm contains many hyperparameters, some of which are highly sensitive to the environment. If the parameters are not set properly, the algorithm may be difficult to converge. Therefore, the hyperparameters need to be constantly adjusted to ensure the convergence of the algorithm during the training of the reinforcement learning task. For the initial environment, we set the following parameters: The learning rate takes the value of 0.001, and the discount rate takes the value of 0.99. The behavioral decision of the ATT is a greedy strategy, which selects the corresponding action in the action space with the parameter ε probability. In the training of the first 400 random postures, ε is assigned to 1, which means that all the actions of ATT come from the action space; in the training of 400~800 random postures, ε is set to 0.1, which means that ATT selects actions randomly with a probability of 0.1 and selects actions according to the current state from the DQN based on the maximum value with a probability of 0.9. This approach takes into account the use of previous experience to obtain a better value with a certain degree of randomness; in 800~1100 random posture trainings, the value of ε is assigned to be 0.05; after 1100 random posture learnings, the value of ε is assigned to be 0, and the ATT selects the action with the maximum Q-value from the DQN according to the current state, until the algorithm converges.

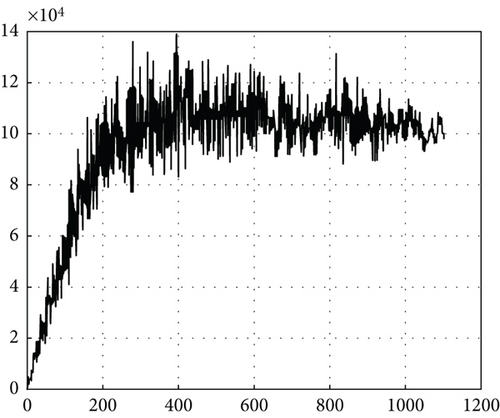
As shown in Figure 5, in the early stages of training, the reward obtained by ATT is small due to less accumulated experience, and the amount of off-target of the guidance law generated in this way is larger. After the training of 200 random postures, richer reward information is accumulated in the DQN; after 400 times of training, the average Q-value becomes larger with the increase of reward obtained by the ATT, which generates the action of each iterative simulation step according to the reward information of the DQN and ultimately makes the algorithm gradually converge, and correspondingly, the ATT can successfully intercept the target and reduce the off-target amount.

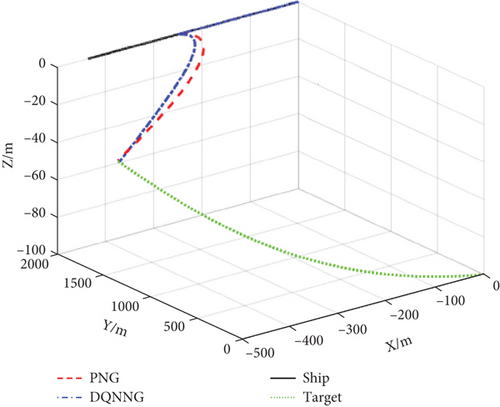
In Figure 6, the blue curve is the ATT intercept trajectory using DQN navigation guidance (DQNNG) after reinforcement learning training, and the red curve is the ATT intercept trajectory using conventional proportional navigation guidance (PNG) under the same simulation conditions.

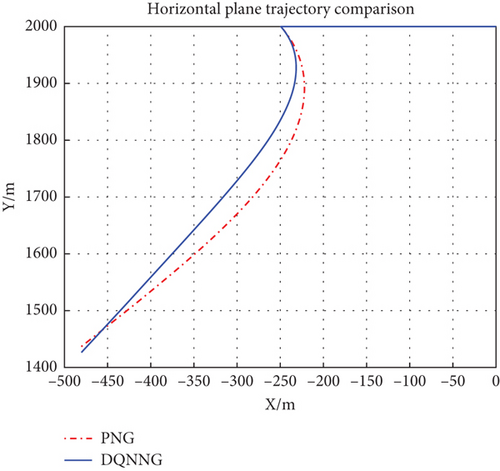
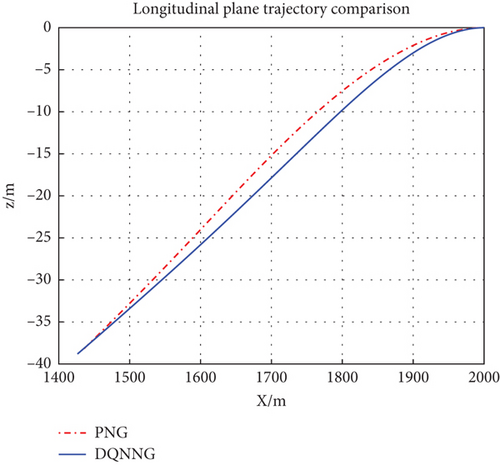
The trajectories of the ATT in the lateral and longitudinal planes, respectively, when the two guidance laws are employed are shown in Figure 7. It can be seen that the DQNNG trajectory is flatter and consumes less maneuvering capability compared to the PNG trajectory. From Figure 8, it can be observed that the line-of-sight angular velocity approaches 0 faster when DQNNG is used and the ATT is aligned to the target with a faster angular velocity. Throughout the interception simulation, the scaling factor K of the PNG is empirically taken to be a fixed value of 4, while the scaling factor K of the DQNNG is a series of varying values, as shown in Figure 9. The variation curve of the guidance command acceleration is shown in Figure 10.

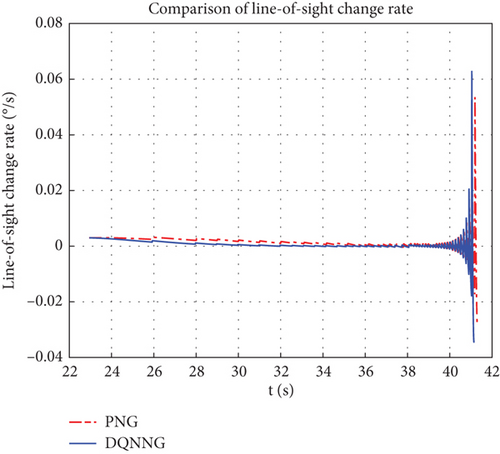
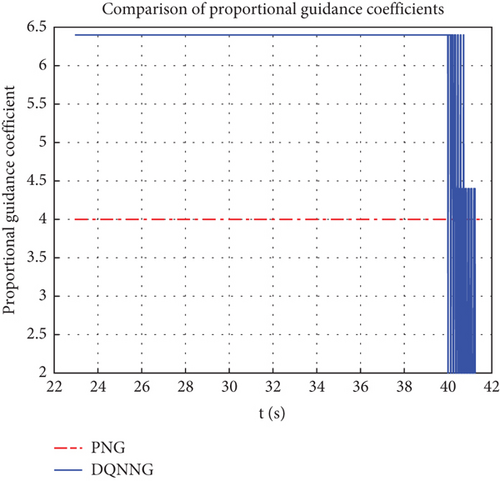
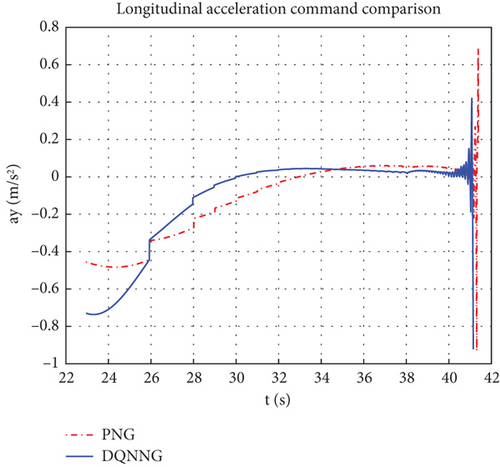
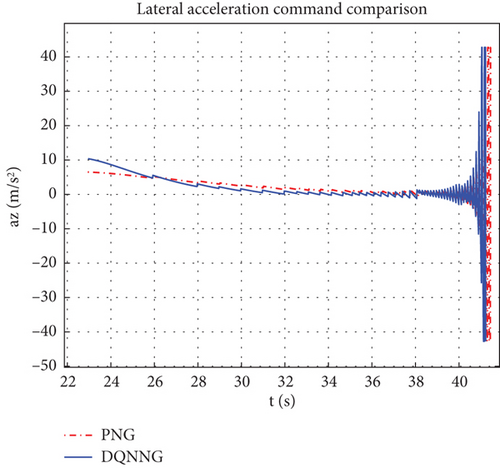
The comparative data of the interception performance between DQNNG and PNG are presented in Table 1. It demonstrates that DQNNG outperforms PNG in several key aspects. DQNNG possesses the capability to make autonomous decisions based on real-time battlefield conditions. By continuously adjusting the scale factor, DQNNG ensures a smaller off-target distance while enabling quicker response to target changes, thereby reducing interception time and improving reaction speed in high-speed and complex environments. Furthermore, the trajectory designed by DQNNG is relatively straight, significantly enhancing the maneuverability of the ATT, reducing overload, and improving guidance accuracy and response speed, while also decreasing maneuvering energy consumption [33]. These advantages are crucial for sustained operational tasks and long-term deployments. As a result, DQNNG demonstrates greater adaptability in complex battlefield scenarios, enhancing overall ATT performance by maintaining high accuracy, minimizing interception time, and reducing resource consumption. This highlights its stronger potential for practical applications.

Table 1. Intercept performance comparison.

Type of guiding law	PNG	DQNNG
Attack time (s)	43.49	43.25
Total motorized energy (m²)	6.02	5.35
Off-target distance (m)	0.84	0.57
Ballistic straightness (/)	0.10	0.07

The traversal simulation of 36 postures using two guidance laws is carried out after the training. The simulation results are shown in Figures 11, 12, and 13. From Figure 11, it can be observed that the amount of off-target is significantly reduced after using the DQNNG guidance law and the off-target distance is reduced by an average of 0.23 m, with an average reduction of 29.08%. The minimum reduction is 0.19 m, while the maximum reduction is 0.27 m.

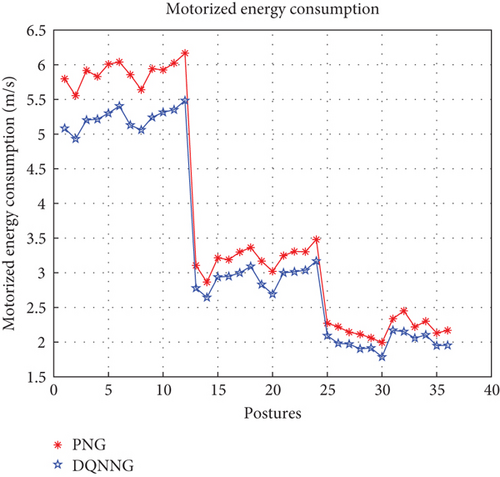
From Figure 12, it can be observed that DQNNG obtains better guidance with less maneuverability consumption than PNG. The average reduction in maneuverability consumption with the DQNNG guidance law is 0.66 m/s, the maximum reduction is 0.73 m/s, and the minimum reduction is 0.58 m/s.

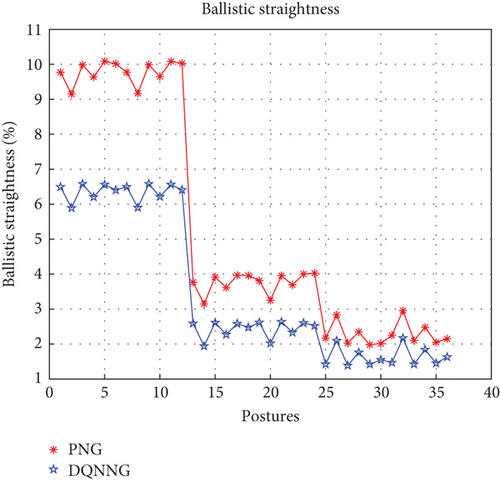
From Figure 13, it can be observed that DQNNG also outperforms PNG in terms of trajectory straightness. This indicates that the earlier attitude adjustment of the ATT makes the rate of change of the line-of-sight angle converge toward zero, which results in a straighter trajectory. The average improvement in straightness after adopting the DQNNG guidance law is 1.8%, the minimum improvement is 0.47%, and the maximum improvement is 3.62%.

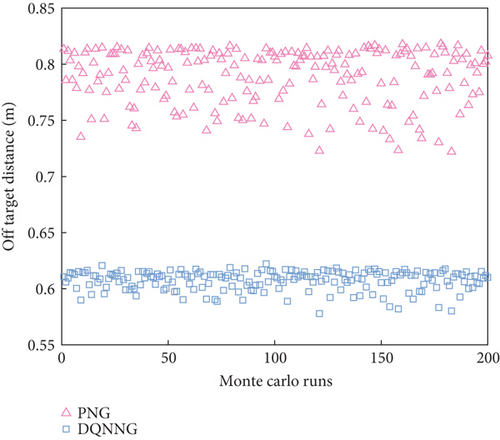
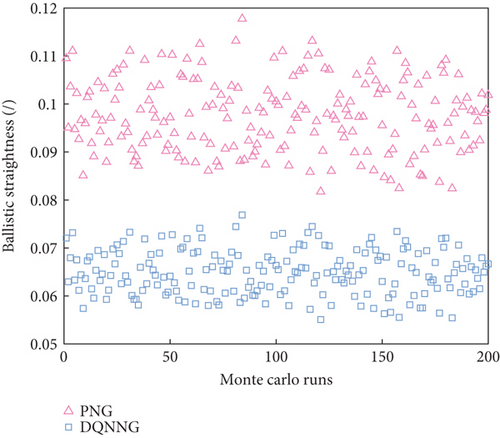
To verify the generalization ability of DQNNG in unknown environments, sensor and noise errors as specified in Reference [34] are applied, and 200 Monte Carlo simulations are conducted for both PNG and DQNNG to evaluate their performance and effectiveness. The initial state of the simulation environment is consistent with the training environment, with the initial states of the target torpedo and ATT randomly generated according to the model described earlier.

Figure 14 illustrates the interception trajectories from 200 Monte Carlo simulations, where the blue curve represents the ATT interception trajectory using DQNNG after reinforcement learning training and the green dashed line represents the target’s motion trajectory.

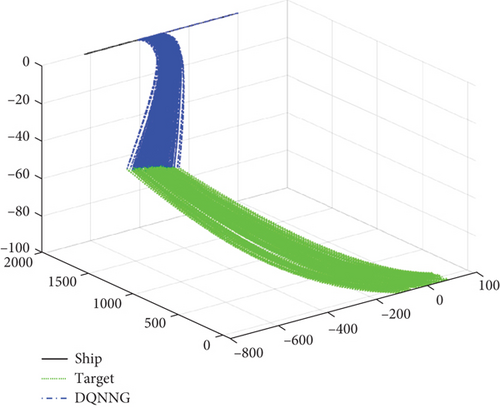
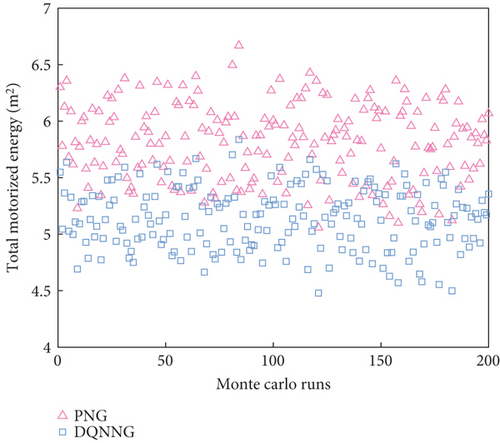
Figure 15 and Table 2 present a comparison of the total motorized energy, off-target distance, and ballistic straightness for PNG and DQNNG over 200 Monte Carlo simulations. The data show that DQNNG performs better in making autonomous decisions by integrating real-time battlefield conditions. By continuously adjusting the scale factor, DQNNG ensures interception accuracy while reducing energy consumption and achieving a flatter ballistic trajectory. Compared to PNG, DQNNG demonstrates superior interception performance. The Monte Carlo test results further confirm that DQNNG has the ability to adapt to unknown disturbance scenarios, highlighting its potential for engineering applications.

Table 2. Average value of Monte Carlo simulation results.

Type of guiding law	PNG	DQNNG
Total motorized energy (m²)	5.82	5.13
Off-target distance (m)	0.79	0.60
Ballistic straightness (/)	0.10	0.06
Attack time (s)	57.91	57.58

4. Conclusions

This paper presents a reinforcement learning-based ATT variable coefficient proportional guidance law, where the proportional coefficients of the PNG guidance law are actions. The range of proportional guidance coefficients is discretized into an action space consisting of 31 actions. A reward function is designed to guide the reinforcement learning algorithm in updating the DQN to increase the final reward on a hit. After several simulation training sessions, the DQN converges. The DQNNG is compared with the PNG through multistance simulation tests. The results clearly demonstrate that the DQNNG has notable improvements over the PNG in terms of trajectory straightness, maneuver energy loss, and guidance accuracy. The DQNNG proposed in this paper is a guidance law based on continuous state space and discrete maneuver space. To further improve guidance performance, the DDPG algorithm can be subsequently used to transform the maneuver space into a continuous state space and maneuver space guidance law.

In future work, sensitivity analysis of the algorithm’s key parameters will be conducted to assess the impact of different parameter combinations on performance, in order to determine the optimal parameter set and provide an effective range for real-world applications. Adaptive parameter adjustment methods will also be explored to further enhance the algorithm’s performance and adaptability. Regarding practical application, the algorithm will be implemented on hardware platforms, and optimization measures will be investigated to ensure it meets the real-time and accuracy requirements for practical combat scenarios.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work was supported by the Northwestern Polytechnical University Education and Teaching Reform Research Project (2025JGG03).

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Bae I. and Hong J., Survey on the Developments of Unmanned Marine Vehicles: Intelligence and Cooperation, Sensors. (2023) 23, no. 10, https://doi.org/10.3390/s23104643, 37430557.
10.3390/s23104643
PubMed Web of Science® Google Scholar
2 Lu J., Song B., and Cui H., Study on the Guided Trajectory of Anti-Torpedo Torpedo, Proceedings of the 2017 Chinese Automation Congress (CAC), 2017, IEEE, 7846–7850.
10.1109/CAC.2017.8244201
Google Scholar
3 Bharati P. V., Rao S. K., and Krishna A. R., Generation and Analysis of Tactics for Anti-Torpedo Defense System, IEEE Conference on Information and Communication Technologies (ICT), 2013, IEEE.
10.1109/CICT.2013.6558125
Google Scholar
4 Liang Y., Tang J., Bai Z., and Li K., Homing Guidance Law Design Against Maneuvering Targets Based on DDPG, International Journal of Aerospace Engineering. (2023) 2023, no. 1, 12, 4188037, https://doi.org/10.1155/2023/4188037.
10.1155/2023/4188037
Web of Science® Google Scholar
5 Lu P., Doman D. B., and Schierman J. D., Adaptive Terminal Guidance for Hypervelocity Impact in Specified Direction, Journal of Guidance, Control, and Dynamics. (2006) 29, no. 2, 269–278, https://doi.org/10.2514/1.14367, 2-s2.0-33645557462.
10.2514/1.14367
Web of Science® Google Scholar
6 Kim T. H., Park B. G., and Tahk M. J., Bias-Shaping Method for Biased Proportional Navigation With Terminal-Angle Constraint, Journal of Guidance, Control, and Dynamics. (2013) 36, no. 6, 1810–1816, https://doi.org/10.2514/1.59252, 2-s2.0-84897584618.
10.2514/1.59252
Web of Science® Google Scholar
7 Liu Q., Shi L., Sun L., Li J., Ding M., and Shu F. S., Path Planning for UAV-Mounted Mobile Edge Computing With Deep Reinforcement Learning, IEEE Transactions on Vehicular Technology. (2020) 69, no. 5, 5723–5728, https://doi.org/10.1109/TVT.2020.2982508.
10.1109/TVT.2020.2982508
Web of Science® Google Scholar
8 Wu M. Y., He X. J., Qiu Z. M., and Chen Z. H., Guidance Law of Interceptors Against a High-Speed Maneuvering Target Based on Deep Q-Network, Transactions of the Institute of Measurement and Control. (2022) 44, no. 7, 1373–1387, https://doi.org/10.1177/01423312211052742.
10.1177/01423312211052742
Web of Science® Google Scholar
9 Zhang S. F., Zhao Q., Guo Y., and Li W. C., Simulation Study on Interception Probability of Anti-Torpedo Torpedo, Applied Mathematics, Modeling and Computer Simulation. (2022) IOS Press, 955–964.
Google Scholar
10 Zhou H. B., Song S. M., and Song J. H., Design of an Observer-Based Sliding Mode Guidance Law With Finite Time Convergence, Journal of Central South University. (2016) 47, 91–97, https://doi.org/10.11817/j.issn.1672-7207.2016.01.014, 2-s2.0-84962575016.
10.11817/j.issn.1672-7207.2016.01.014
Google Scholar
11 Yan C., Xiang X., and Wang C., Towards Real-Time Path Planning Through Deep Reinforcement Learning for a UAV in Dynamic Environments, Journal of Intelligent & Robotic Systems. (2020) 98, no. 2, 297–309, https://doi.org/10.1007/s10846-019-01073-3, 2-s2.0-85073971250.
10.1007/s10846-019-01073-3
Web of Science® Google Scholar
12 He X., Chen Z., Jia F., and Wu M., Guidance Law Based on Zero Effort Miss and Q-Learning Algorithm, Proceedings of the 7th Symposium on Novel Photoelectronic Detection Technology and Applications, 2021, 11763, SPIE, 708–716, https://doi.org/10.1117/12.2586409.
10.1117/12.2586409
Google Scholar
13 Ye H. J. and Zhang X. Y., A New Anti-Torpedo Torpedo′s Guidance Law Based on Variable Structure Control, Proceedings of the 2017 3rd IEEE International Conference on Control Science and Systems Engineering (ICCSSE), 2017, IEEE, 163–166.
Google Scholar
14 Shin H. S. and Li K. B., An Improvement in Three-Dimensional Pure Proportional Navigation Guidance, IEEE Transactions on Aerospace and Electronic Systems. (2021) 57, no. 5, 3004–3014, https://doi.org/10.1109/TAES.2021.3067656.
10.1109/TAES.2021.3067656
Web of Science® Google Scholar
15 Zhang R., Yuan Z., Liu Z., and Zhang C., Simulation of Anti-Torpedo-Torpedo Intercepting Trajectory and Analysis of Hit Probability Under Sliding Mode Guidance, Proceedings of the 2018 10th International Conference on Intelligent Human-Machine Systems and Cybernetics (IHMSC), 2018, IEEE, 133–137.
10.1109/IHMSC.2018.00038
Google Scholar
16 Sun Z. X. and Gu T. J., Research on Anti-Torpedo Torpedo Interception Strategy of Surface Ship, Journal of Unmanned Undersea Systems. (2020) 28, no. 6, 699–705, https://doi.org/10.11993/j.issn.2096-3920.2020.06.016.
10.11993/j.issn.2096-3920.2020.06.016
Google Scholar
17 He S., Shin H. S., and Tsourdos A., Computational Missile Guidance: A Deep Reinforcement Learning Approach, Information Systems. (2021) 18, no. 8, 571–582, https://doi.org/10.2514/1.I010970.
10.2514/1.I010970
Google Scholar
18 Du M. J., Peng C., and Ma J., Deep Reinforcement Learning Based Missile Guidance Law Design for Maneuvering Target Interception, Proceedings of the 2021 40th Chinese Control Conference (CCC), 2021, IEEE, 3733–3738.
10.23919/CCC52363.2021.9549596
Google Scholar
19 Duguleana M. and Mogan G., Neural Networks Based Reinforcement Learning for Mobile Robots Obstacle Avoidance, Expert Systems with Applications. (2016) 62, 104–115, https://doi.org/10.1016/j.eswa.2016.06.021, 2-s2.0-84975032535.
10.1016/j.eswa.2016.06.021
Web of Science® Google Scholar
20 Xin J., Zhao H., Liu D., and Li M., Application of Deep Reinforcement Learning in Mobile Robot Path Planning, Proceedings of the 2017 Chinese Automation Congress (CAC), 2017, IEEE, 7112–7116.
10.1109/CAC.2017.8244061
Google Scholar
21 Nasir Y. S. and Guo D., Deep Reinforcement Learning for Joint Spectrum and Power Allocation in Cellular Networks, Proceedings of the 2021 IEEE Globecom Workshops (GC Wkshps), 2021, 1–6, https://doi.org/10.1109/GCWkshps52748.2021.9681985.
10.1109/GCWkshps52748.2021.9681985
Google Scholar
22 Shalumov V., Cooperative Online Guide-Launch-Guide Policy in a Target-Missile-Defender Engagement Using Deep Reinforcement Learning, Aerospace Science and Technology. (2020) 104, 105996, https://doi.org/10.1016/j.ast.2020.105996.
10.1016/j.ast.2020.105996
Web of Science® Google Scholar
23 Gaudet B., Furfaro R., and Linares R., Reinforcement Learning for Angle-Only Intercept Guidance of Maneuvering Targets, Aerospace Science and Technology. (2020) 99, 105746, https://doi.org/10.1016/j.ast.2020.105746.
10.1016/j.ast.2020.105746
Web of Science® Google Scholar
24 Bhopale P., Kazi F., and Singh N., Reinforcement Learning Based Obstacle Avoidance for Autonomous Underwater Vehicle, Journal of Marine Science and Application. (2019) 18, no. 2, 228–238, https://doi.org/10.1007/s11804-019-00089-3, 2-s2.0-85068549913.
10.1007/s11804-019-00089-3
Web of Science® Google Scholar
25 Shi Y. and Wang Z., A Deep Learning-Based Approach to Real-Time Trajectory Optimization for Hypersonic Vehicles, Proceedings of the AIAA Scitech 2020 Forum, 2020, AIAA, 1–19.
10.2514/6.2020-0023
Google Scholar
26 Mnih V., Kavukcuoglu K., Silver D., Graves A., Antonoglou I., Wierstra D., and Riedmiller M., Playing Atari with Deep Reinforcement Learning, arxiv preprint arxiv:1312.5602, (2013).
Google Scholar
27 Qiu X. Q., Gao C. S., and Jing W. X., Maneuvering Penetration Strategies of Ballistic Missiles Based on Deep Reinforcement Learning, Proceedings of the Institution of Mechanical Engineers, Part G: Journal of Aerospace Engineering. (2022) 236, no. 16, 3494–3504, https://doi.org/10.1177/09544100221088361.
10.1177/09544100221088361
Web of Science® Google Scholar
28 Wang W. W., Wu M. Y., Chen Z. H., and Liu X., Integrated Guidance-and-Control Design for Three-Dimensional Interception Based on Deep-Reinforcement Learning, Aerospace. (2023) 10, no. 2, 167–167, https://doi.org/10.3390/aerospace10020167.
10.3390/aerospace10020167
Web of Science® Google Scholar
29 Mnih V., Kavukcuoglu K., Silver D., Rusu A. A., Veness J., Bellemare M. G., Graves A., Riedmiller M., Fidjeland A. K., Ostrovski G., Petersen S., Beattie C., Sadik A., Antonoglou I., King H., Kumaran D., Wierstra D., Legg S., and Hassabis D., Human-Level Control Through Deep Reinforcement Learning, nature. (2015) 518, no. 7540, 529–533, https://doi.org/10.1038/nature14236, 2-s2.0-84924051598, 25719670.
10.1038/nature14236
CAS PubMed Web of Science® Google Scholar
30 Clifton J. and Laber E., Q-Learning: Theory and Applications, Annual Review of Statistics and its Application. (2020) 7, no. 1, 279–301, https://doi.org/10.1146/annurev-statistics-031219-041220.
10.1146/annurev-statistics-031219-041220
Web of Science® Google Scholar
31 Sola Y., Chaffre T., and Le Chenadec G., Evaluation of a Deep-Reinforcement-Learning-Based Controller for the Control of an Autonomous Underwater Vehicle, Proceedings of the Global Oceans 2020: Singapore–US Gulf Coast, 2020, IEEE, 1–7.
10.1109/IEEECONF38699.2020.9389415
Google Scholar
32 Fu X., Zhu J., Wei Z., Wang H., and Li S., A UAV Pursuit-Evasion Strategy Based on DDPG and Imitation Learning, International Journal of Aerospace Engineering. (2022) 2022, no. 1, 14, 3139610, https://doi.org/10.1155/2022/3139610.
10.1155/2022/3139610
Web of Science® Google Scholar
33 Yagci O. and Nikbay M., Evasive Maneuver Trajectory Optimization of an UCAV Against an Air to Air Missile, Proceedings of the AIAA Aviation 2022 Forum. (2022) .
10.2514/6.2022-3791
Google Scholar
34 Han T., Hu Q. L., Shin H. S., Tsourdos A., and Xin M., Sensor-Based Robust Incremental Three-Dimensional Guidance Law With Terminal Angle Constraint, Journal of Guidance Control and Dynamics. (2021) 44, no. 11, 2016–2030, https://doi.org/10.2514/1.G006038.
10.2514/1.G006038
Web of Science® Google Scholar

All articles

Design of Reinforcement Learning Guidance Law for Antitorpedo Torpedoes

Abstract

1. Introduction