Fuzzy Consensus Cubature Information Filtering for Space Target Tracking
Abstract
A fuzzy distributed nonlinear state estimation issue on the possibilistic framework is investigated in this paper. Firstly, unlike the Gaussian probability distributions on the traditional probability framework, the noises are modeled as fuzzy random variables (FRVs) with trapezoidal possibility distributions (TPDs), and then a fuzzy cubature paradigm is proposed. Secondly, based on the fuzzy cubature paradigm, a novel fuzzy consensus cubature information filtering (FCCIF) algorithm is proposed for sensor networks wherein each agent fuses local fuzzy information with fuzzy information from the neighbors based on the weighted average consensus. Furthermore, under well-known observability and connectivity assumptions, it is proved that the FCCIF possesses guaranteed stability regardless of consensus steps. Finally, a space target tracking simulation is developed to verify the validity of the FCCIF algorithm. The FCCIF algorithm can be used in navigation guidance, radar tracking, sonar ranging, satellite orbit determination, and other practical applications when the noises are suitable for qualitative rather than quantitative description.
1. Introduction
In recent years, space situational awareness (SSA) has attracted extensive attention from various countries [1–3]. Space target tracking is a basic work because other space tasks are based on it [4, 5]. Due to the ability of real-time estimation and nonstationary process tracking [6, 7], the Kalman filter is widely used in space target tracking, which is essentially a nonlinear state estimation issue. The extended Kalman filter (EKF) is a widely used prediction method due to it being simple and easy to understand [8]. However, its Jacobian matrix is difficult to calculate, and it may diverge when ignoring the Taylor expansion terms. The unscented Kalman filter (UKF) algorithm was a sampling filter utilizing the unscented transformation [9]. A key drawback of the UKF is that the calculation of the covariance matrix may be negatively definite. To overcome this limitation, the cubature Kalman filter (CKF) and the square root cubature Kalman filter (SRCKF) were proposed [10, 11].
Due to the limited sensing and computing ability, it is difficult for a single sensor to complete the target track and control task [12]. With the rapid development of sensor networks, distributed filtering and control are widely studied in many existing works. Considering the complex space environment, Jia et al. [13] presents a consensus cubature information filtering (CCIF) algorithm for space target tracking, which can achieve satisfactory results. Hu et al. [14] introduced a Kullback–Leibler divergence-based consensus cubature Kalman filter (CCKF), which can solve the problems of switching topology and different space target sensors with different observation equations. To take advantage of joint tracking, Chen et al. [15] proposed a composite weighted average consensus filter, in which the ground-based radar used a sparse-grid quadrature filter (SGQF) while the space optical sensor (SOS) used an EKF. To use sensors with different sampling times and different sampling rates for collaborative tracking, Hu et al. [16] presented a universal consensus filter (UCF). Jia et al. [17] proposed a diffusion-based enhanced covariance intersection cooperative space target tracking (DECISPOT) filter, which can improve track accuracy when measurements do not exist or are of low accuracy. Zhang et al. [18] studied a distributed strong tracking filter algorithm to resist maneuver uncertainty. Zhou et al. [19] proposed a distributed multiple-model nonlinearity filter for tracking the highly mobile noncooperative targets. Doostmohammadian et al. [20] proposed a distributed estimation approach requiring less networking and communication traffic and was applied to track a mobile target via the formation of unmanned aerial vehicles.
Notably, the event definitions of the abovementioned filtering algorithms are all clear, and the progress and observer noises are assumed to obey a Gaussian distribution. However, in some scenarios, there exists uncertainty [20] and noises that do not obey a Gaussian distribution. For example, because of the space environment, a quantitative description of the relationship between noise and environment is too complicated to be used, so that noise must be quantitatively described with fuzziness [21]. Moreover, due to the drift of the sensor, the measurement results have great uncertainty and a bit of distrust; thus, the measurement noise may not exhibit a Gaussian distribution [21]. Furthermore, for noncooperative targets, the noises have high uncertainty as they often depend on the experience of experts. In these scenarios, the precise, quantitative, and probabilistic Kalman filter is difficult to meet the application requirements [22].
When in face of these scenarios, researchers proposed a multifarious fuzzy Kalman filter (FKF) by combining fuzzy logic [23–25] with the Kalman filter. FKF uses fuzzy logic to express uncertainty so that precise mathematical models are not needed to deal with complex problems. Yan et al. [26] proposed a fuzzy adaptive strong tracking filter, in which the Takagi–Sugeno (T–S) model is used for fuzzy reasoning for GPS navigation. Jwo and Wang [27] proposed a robust adaptive filter using fuzzy logic for a tightly coupled visual-inertial odometry navigation system. Yue et al. [28] proposed an INS/GPS sensor fusion algorithm based on adaptive fuzzy EKF with sensitivity to disturbances. Sabzevari and Chatraei [29] introduced fuzzy random variables (FRVs) with trapezoidal possibility distributions (TPDs) and proposed a novel fuzzy extended Kalman filter (FEKF) for robot localization. Mata et al. [30] proposed a fuzzy square root cubature Kalman filter (FSRCKF) using FRVs to model noises for spatial target localization. Especially for distributed target tracking, Ye et al. [31] proposed a distributed fuzzy information filtering (DFIF) for linear systems, and Lin et al. [32] proposed a distributed FKF under switching topology for linear systems.
However, a fuzzy distributed Kalman filter suitable for space target tracking needs to be studied. A lot of space target tracking researches are based on assumptions that the noises distributed as probability distributions. In practice, there exist a lot of space target with fuzzy uncertainty in which the noises suit to be modeled as FRVs. For example, if noise does not follow a “bell curve” shape, or is unbalanced, or even we feel a bit of distrust on the value obtained subjectively, we can use a possible region to cover the changing characteristics of the noise. Moreover, according to the available information about noises, the noises in some space target measure systems are better suited to being modeled as FRVs rather than random variables (RVs). For example, a radar sensor with an accuracy of ±2 mm, we have some confidence regarding the distribution of the interval values within the system. It is worth noting that the above FKFs are either suitable for the single-sensor case or the linear case, and a fuzzy distributed Kalman filter suit for strong nonlinear state estimation problems has not been fully studied as far as the authors know. Therefore, this study contributes to expanding research results on [29–32] to strong nonlinear state estimation problems. The noises are modeled as FRVs with TPDs so that a fuzzy cubature paradigm can be proposed. Each agent performs a fuzzy cubature paradigm locally and fuses local fuzzy information with fuzzy information from the neighbors based on the weighted average consensus so that a novel fuzzy consensus cubature information filtering (FCCIF) algorithm is proposed. Compared to the FEKF algorithm and the FSRCK algorithm, which only considered the single-sensor case and were not suitable for the distributed network, the FCCIF algorithm in this paper does not rely on a central node to fully obtain global information and can approach the global posterior estimation only by communicating with neighbors. Compared to the algorithm in [31, 32], which considered linear systems, the FCCIF algorithm in this paper suits for strongly nonlinear systems. Furthermore, the mean square estimation errors of position (MSEP) and the mean square estimation errors of velocity (MSEV) of the FCCIF algorithm are 23% and 90% of the fuzzy consensus extended information filtering (FCEIF), which can be obtained by combining the DFIF in [31] and the EKF. The contributions of this research can be summarized as follows: (1) A fuzzy cubature paradigm is proposed by combining the cubature paradigm and the fuzzy filtering to deal with the strong nonlinear state estimation problems with fuzzy noises. (2) A novel FCCIF algorithm is developed by embedding the fuzzy cubature paradigm into the weighted average consensus frame. (3) The stability of the FCCIF algorithm is investigated.
The article is organized as follows. Section 2 presents preliminary information regarding the TPD and graph theory, along with the problem formulation. Section 3 describes the FCCIF for nonlinear systems. Section 4 investigates the stability of the FCCIF algorithm. Section 5 presents the details of the space target tracking simulations. Section 6 presents the concluding remarks.
1.1. Notations
All vectors are denoted by bold lowercase letters. All matrices are denoted by bold uppercase letters. X(∗)T, (∗)TYX, and XY(∗)T represent XXT, XTYX, and XYXT, respectively. ℝn represents the n-dimensional Euclidean space. ℤ+ represents the set of positive integers. Superscript {·}(l) represents the vertexes of a TPD. {·}T and {·}−1 represent the transpose operator and the inverse operator, respectively.
2. Preliminaries and Problem Formulation
We first give the preliminary knowledge of graph theory, FRVs, and TPDs; then extract the fuzzy filtering problem; and finally summarize the main targets of this paper.
2.1. Preliminaries
Consider a network consisting of N nodes. An undirected graph describes the communication between sensors, where respect nodes and edges. The set represents the neighbors of node i. represents the inclusive neighborhood of node i. Let with elements aij respects the adjacent matrix of graph . Let aij > 0 if sensor i and j can exchange information, otherwise aij = 0.
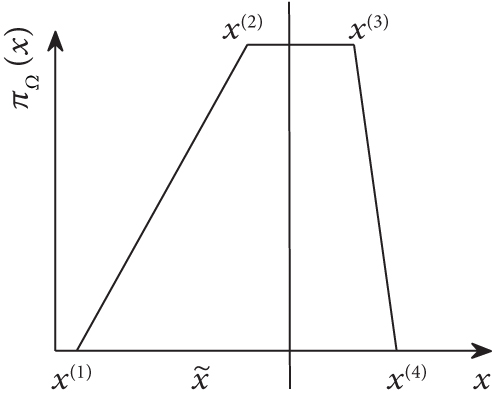
2.2. Problem Formulation
The state xk inherits the uncertainty of the noise, as defined in (10) and (11), and thus, the problem considered in this study is different from the distributed estimate problem based on the probabilistic framework.
Remark 1. In some scenarios, the noises wk and vi,k have fuzzy uncertainty. For example, the noises of the SOS are closely related to the locations of the sun, the target, and the SOS. However, accurate mathematical models are complex enough to be applied. In face of this, the noise covariance is quantitatively described [13]. (The light is defined as “excellent” when the bistatic solar angle is within 0–20, and the measurement noise covariance is 0.8R. The light is defined as “fair” when the bistatic solar angle is within 75–90, and the measurement noise covariance is 1.2R.) This method of quantitative description is a fuzzy one.
Remark 2. Notably, the above method is just the fuzzy logic [34] combining with Gaussian noise. The noises are modeled as several different Gaussian distribution intervals. In this article, however, we considered the situation, where noises obey possibility distribution instead of probability distributions. We modeled the noises as FRVs with the TPDs [29], which is an interval, but completely out of the Gaussian distribution. FRVs can be used to design FKF from the perspective of variable definition. For example, Sabzevari and Chatraei [29] set up FRVs and proposed the FKF for the Doris robot platform location.
Remark 3. FRVs can have many distribution shapes. We restrict the analysis to the trapezoidal distribution because in practical applications, no criterion exist to define the distribution shape between the possible and the impossible regions. The triangular, rectangular, and singleton distributions are particular cases of the trapezoidal distributions. For example, Shao et al. [21] use the maximum possibilistic informational distance principle to build a TPD from a set of data that follows unknown multimodal nonsymmetric probability distributions and to build a triangular possibility distribution from a set of data that follows a skewed normal probability distribution.
In particular, the objective of this paper is to formulate a stable fuzzy distributed filtering for a nonlinear system with fuzzy noise to ensure that each sensor i can increase its posterior estimate by fusing {zj,k|k, Rj,k|k} and from neighbors based on the equation of system (8) and the equation of measure (9).
3. FCCIF
- 1.
Prediction update: Let the prior state estimation of node i at time k − 1 is , and the initialized central gradient, uncertainty matrix, and fuzzy information matrix of are , , and , respectively.
- 2.
Measurement update: The fuzzy volume points are recalculated as
Then, the FCCIF algorithm can be obtained, as summarized in Algorithm 1.
Remark 4. To solve the strong nonlinear state estimation problems under the possibility theory, we put forward a new fuzzy cubature paradigm based on the volume filtering idea under the traditional probability theory. Different from the traditional volume filtering idea, the four vertices and the central gradient of the TPD need to select volume points and reconstruct through nonlinear propagation, so we call it a fuzzy cubature paradigm. Afterward, we propose a FCCIF by combining the average consensus algorithm and the FRV in distributed sensor networks on the possibilistic framework.
-
Algorithm 1: FCCIF algorithm for agent i at time k.
-
Input:The prior information
-
at time instant k − 1.
-
Prediction
-
Compute the fuzzy prediction estimation and
-
Measurement update
-
(1) Compute the the local estimate set , Yi,k|k by
-
(2) Perform consensus on the local estimate set by
-
(3) Update the posterior estimate by equations (27).
-
output: at time instant k.
4. Stability Analysis
Boundedness is an important feature of the algorithm stability. The FCCIF algorithm will be proven mean-square bounded through the Lyapunov analysis in this section [36]. The corresponding prediction estimate error and posterior error are expressed as and , respectively, where , , and xk is the unknown real state. As mentioned in [20], the local observability assumption requires more communication among the sensors. Our algorithm only relies on the assumption of collective observability to guarantee its stability. The relaxation of the observability assumption reduces the quality requirements of the sensors. There are two preliminary assumptions as follows.
Assumption 1. The system is collectively observable, and the undirected graph is connected.
Assumption 2. The consensus matrix Π is primitive and row stochastic.
Now we give the stability result of the algorithm.
Theorem 1. The estimation error of FCCIF algorithm designed for nonlinear systems (8) and (9) is mean-square bounded.
Then, two important lemmas need to be given.
Lemma 1 ([38]). Let Assumptions 1 and 2 hold. Then, there exist positive definite matrices , , , and such that and for k ≥ 1 and any .
Lemma 2 ([39]). Given positive definite vectors v1, ⋯, vN and matrices M1, ⋯, MN for an integer N ≥ 2, the following inequality holds
Now, we can give out the proof.
Proof 1. We define for brevity. Here, stand for vertically concatenating all the vectors into a single column vector.
Now, according to Lemma 1, we get that the noise-related term are bounded in mean square. Hence, Theorem 1 is proved.
5. Numerical Simulations
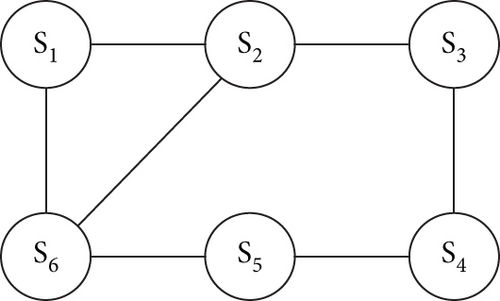
In this section, we will use space target tracking simulation to verify the effectiveness of the FCCIF algorithm. Consider the scenario as shown in Figure 2. There is a network of six space-based tracking satellites to track a noncooperative target through bearing-only measurement.
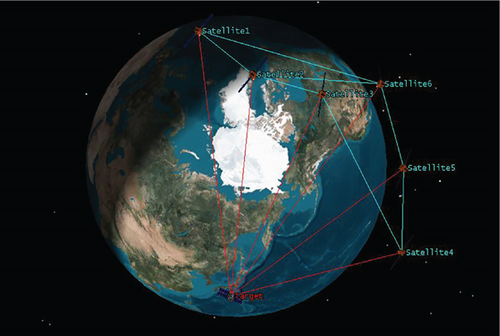
We first give the model of the noncooperative space target and the tracking satellites.
5.1. Dynamics of the Noncooperative Target
5.2. Tracking Satellite Model
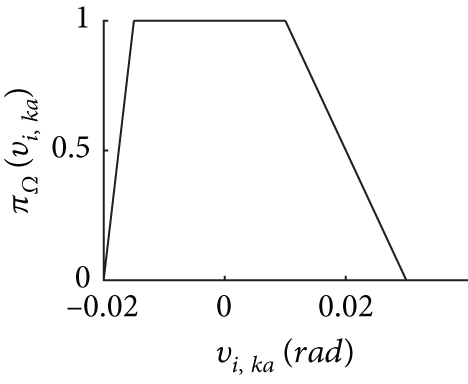
In general, and are modeled as Gaussian distribution. In this study, the noise terms wk and vi,k are modeled as FRVs with TPDs as Figure 3.
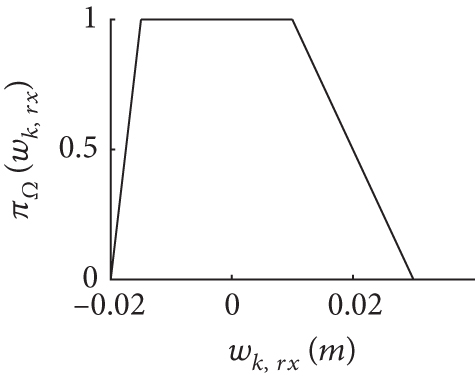
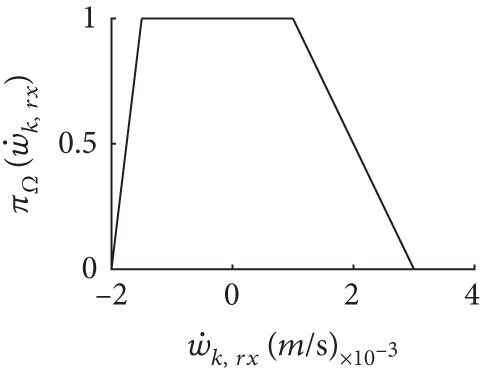
5.3. The Result of Simulation
The orbital elements of the tracking satellites and the space target are given in Table 1. The target’ initial state x0 = [4619km, 3132km, 6630km,−5513m/s,−213.3m/s, 3942.6m/s]T, sample time Ts = 3s, and total simulation time Tt = 900s. Since the initial states of the space target cannot be accurately obtained, they are set as xi,0 = x0 + Δxi,0.
| ah (km) | e | u (rad) | γ (rad) | Γ (rad) | mh (rad) | |
|---|---|---|---|---|---|---|
| Obj | 8667.13 | 0 | 1.29 | 0.25 | 0 | 0.92 |
| Sat1 | 9067.13 | 0 | 1.29 | 2.24 | 0 | 0.92 |
| Sat2 | 8067.10 | 0 | 1.29 | 1.59 | 0 | 0.33 |
| Sat3 | 8667.13 | 0 | 1.29 | 1.81 | 0 | 0.78 |
| Sat4 | 8467.13 | 0 | 1.29 | 2.03 | 0 | 1.23 |
| Sat5 | 8267.13 | 0 | 1.29 | 1.55 | 0 | 1.69 |
| Sat6 | 9067.13 | 0 | 1.29 | 1.54 | 0 | 1.97 |
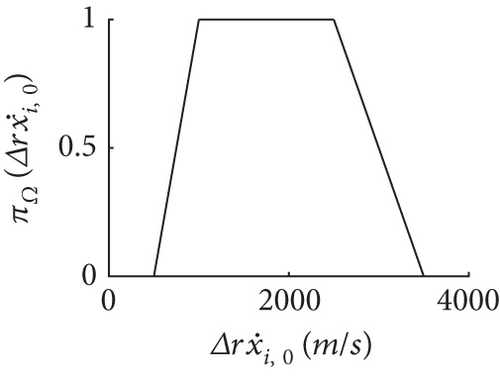
The initial errors are modeled as FRVs with TPDs shown in Figure 4. Then, and are the filter’ initial inputs.
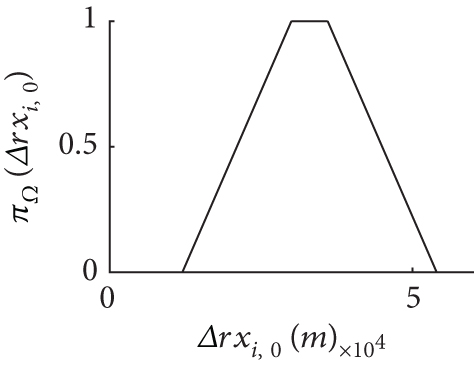
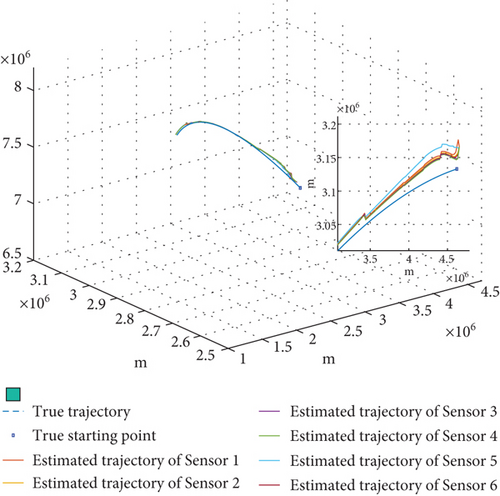
We use the fourth-order Runge–Kutta to make the prediction in FCCIF. The number of consensus iterations is L = 1, and the communication topology of the sensors is shown in Figure 5. By using these simulation settings, a random trajectory of the target was created. Subsequently, the trajectories estimated by each sensor are generated using the FCCIF algorithms as displayed in Figure 6. It is shown that the estimated trajectories generated using the FCCIF algorithms are close to the true trajectory.
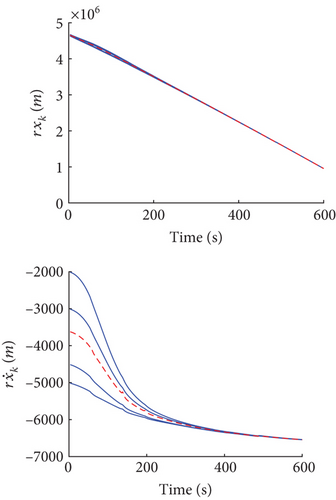
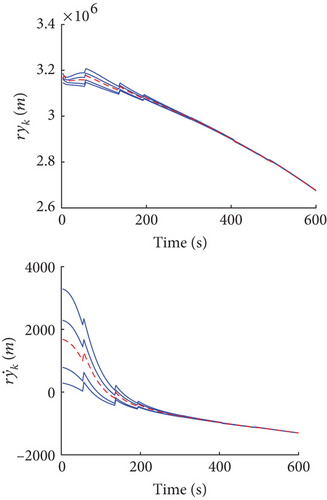
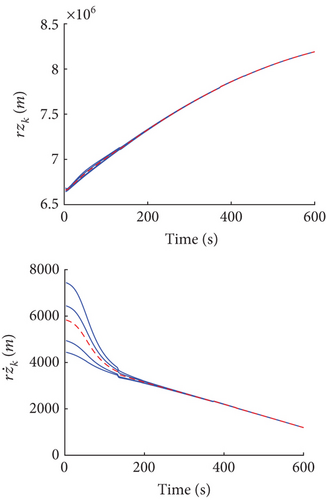
Figures 7, 8, and 9 illustrate the estimates of rxi,k, , ryi,k, , rzi,k, and of the state value by Sensor 1. The solid lines respect the TPD of the fuzzy estimate value, while the dashed line respects the center of gravity of the fuzzy estimate value, that is, the final estimation of the state variable. The dashed line always lies within the solid lines stating that the final estimation is in an area of possibility. Moreover, as time elapses, the area of possibility shrinks, showing that the estimation is convergent. In addition, the area of the TPD is smaller than that of the noise TPD and initial error TPD. This indicates that the degree of fuzzy of the estimation decreases with filtering iterative. Moreover, the iterative distribution of TPD vertices becomes almost four parallel lines, and thus, the size of the possible regions is nearly invariant, which satisfies the requirement of coherence of the size of the regions [20]. Due to the length of the article, the figures for the estimates of the state value by other sensors are omitted.
The MSE of position and velocity of six sensors are given in Figures 10 and 11. The results show that the proposed FCCIF has good filtering accuracy and stability. The results also show that the estimated values of six sensors reach a consensus, which achieves the purpose of distributed filtering. At the same time, for comparison, the MSE of the FCEIF, obtained by combing the DFIF in [32] and the EKF, and the centralized fuzzy cubature information filter (C-FCIF) are also shown in Figures 10 and 11. The prediction update of the FCEIF algorithm adopts the discrete model (47). Because of inadequate research on the C-FCIF, this study caused the FCCIF to degenerate to the C-FCIF by assuming that graph is strongly connected. Notably, the weight ωij,k in C-FCIF is set as ωij,k = 1/N instead of calculating as (26). The corresponding average MSE and percentage of MSE (PMSEP and PMSEV) are given in Table 2. It can be seen that the estimated accuracy of the FCCIF algorithm is close to that of the C-FCIF algorithm and increased more than the FCEIF algorithm, which has relatively large errors when ignoring higher order terms in Taylor expansion. The MSEP and MSEV of FCCIF are 23% and 90% of the FCEIF algorithm, respectively.
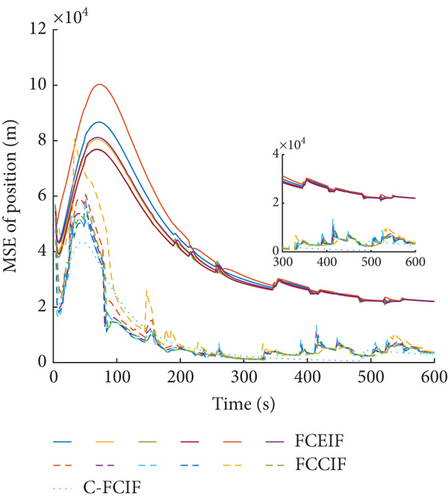
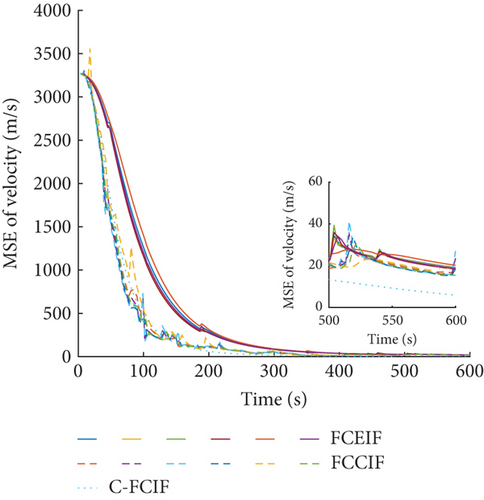
| Algorithm | MSEP (km) | MSEV (km/s) | PMSEP | PMSEV |
|---|---|---|---|---|
| FCEIF | 22.4006 | 0.0183 | 100 | 100 |
| FCCIF | 5.1573 | 0.0165 | 23 | 90 |
| C-FCIF | 3.1955 | 0.0078 | 14 | 43 |
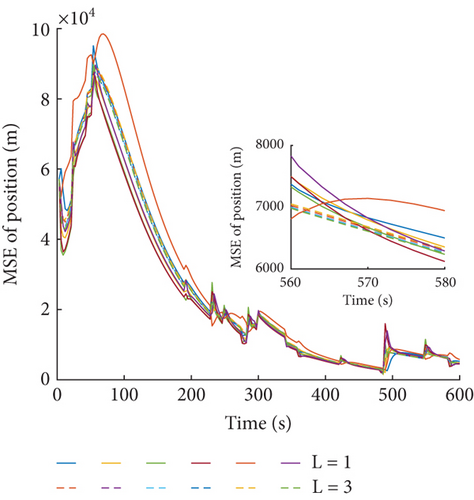
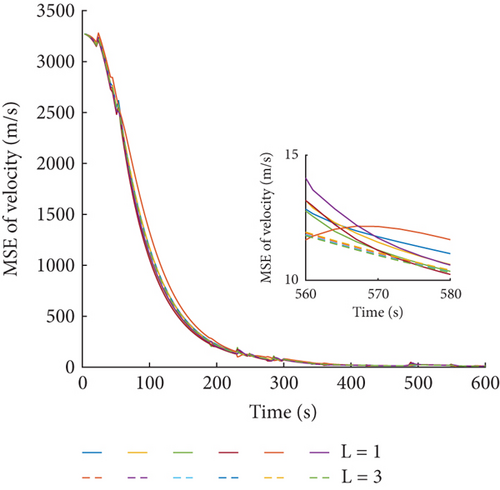
To analyze the influence of the consensus iterations on the estimated result of the FCCIF algorithm, the comparisons of MSE of the FCCIF algorithm with different consensus iterations L = 1 and L = 3 are as shown in Figures 12 and 13, respectively. The results show that as the number of iterations increases, the estimate accuracy improved, and the estimation errors of different sensors become more consistent. However, as the number of iterations increases, more time will be consumed. Therefore, it is necessary to select the appropriate number of iterations by considering the accuracy and consumption comprehensively.
Remark 5. We have not made simulation comparisons between the FCCIF algorithm presented in this paper and the CCIF algorithm in [13], the CCKF algorithm in [14], and so on, which were on the probability framework. It is because the possibility method does not always perform better than the probability method. Instead, we have to choose between these two types of approaches based on the types of knowledge available to describe the system. In applications where uncertainty is managed qualitatively, the possibility version makes more sense, while in applications where uncertainty is managed quantitatively [20], the probability version was more efficient.
Remark 6. As a limitation, the computation burden of FCCIF is significant than the traditional probability version, since all the updating of fuzzy variables must calculate the four feature points of the trapezoidal probability distribution. So the application of FCCIF, as currently formulated, is constrained in cases in which fast computation is required, for instance when dealing with truly big datasets. On the other hand, trapezoidal propagation is easy to cause deformation, which has very strict requirements on the set of initial value and noise parameters, so the convenience of practical operation needs to be further studied.
6. Conclusions
In this paper, the fuzzy noises are modeled as FRVs with TPDs instead of Gaussian distributions, so that the nonlinear estimated problem with fuzzy noises can be solved using a fuzzy cubature paradigm. A novel FCCIF algorithm is proposed by embedding the fuzzy cubature paradigm into the consensus frame. Moreover, under well-known observability and connectivity assumptions, the stability of the FCCIF algorithm is proven. Furthermore, it is verified that the estimated accuracy of the FCCIF algorithm is close to that of the C-FCIF algorithm and increased more than the FCEIF algorithm. The FCCIF algorithm needs to calculate the four feature points of the TPD for filtering iterative, and the calculation amount is larger than that of traditional Kalman filtering. Future work can be focused on examining if the efficiency of the algorithm can be enhanced using different fuzzy information fusion techniques. On the other hand, trapezoidal propagation is easy to cause deformation, which has very strict requirements on the set of initial value and noise parameters, so the convenience of practical operation needs to be further studied.
Conflicts of Interest
The authors declare no conflicts of interest.
Funding
This research received no external funding.
Open Research
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.




