With the large-scale entry of electric vehicles into the grid, the impact on the new power system with new energy as the main status is gradually expanding. Utilizing V2G technology to make vehicle–network interaction, a two-layer hybrid game energy management transaction method for multisource microgrid clusters is proposed. The upper layer constructs a microgrid group transaction model containing an energy management system based on a cooperative game; the lower layer constructs a master–slave game model with each microgrid as the leader and its interest as the objective function, and the follower EV aggregator adjusts the charging and discharging time according to the net power to strive for its maximum interest. The model is optimally solved by the CPLEX solver through simulation cases, and the results verify the effectiveness and superiority of the proposed two-layer hybrid game model.

1. Introduction

Electric vehicles (EVs) are rapidly developing due to their green and artificial intelligence advantages. In a forecast, it was anticipated that by 2020, 2030, and 2050, EVs would comprise 35%, 51%, and 62% of all vehicles in the United States, respectively [1]. EV-to-grid (V2G) and grid-to-EV (G2V) technologies are gradually maturing. However, the large number of EVs entering the grid and the intermittent and fluctuating power output of new energy sources pose serious challenges to the security and economy of the new power system [2]. As one of the best solutions to enhance the reliability of new power systems and promote the consumption of new energy sources, microgrids (MGs) are widely accessible to the power distribution system [3].

With the scientific development of MG clusters in power systems, different MG clusters have different application needs. The authors in [4] introduce a multiparticipant transaction model such as MGs, electricity markets, suppliers, and operators. However, certain contracts must be adhered to for the participating parties to profit from the transaction.The authors in [5] proposed a two-layer optimal scheduling model for multi-MG systems based on hybrid games, constructing a Stackelberg game model for the upper layer MGs and MG aggregators (MAs), and a cooperative game model among the lower layer.

A cooperative game model, among the lower layer MGs, and multiple algorithms are used for their distributed optimal scheduling [6]. Using the island MG as an application, EVs are connected to the island MG cluster, and EV charging and discharging are modeled and optimized with the goal of the lowest system cost. The authors in [7] establish a two-layer robust optimization planning mathematical model based on master–slave game theory for distribution grids and MG clusters, which is solved by using the KKT condition and the columns and constraints generation (C&CG) algorithm, which improves the ability of distribution grids to consume renewable energy sources and also protects the economic interests of MG investors. The authors in [8] propose a MG cluster optimization operation method based on a master–slave game. First, rolling optimization is used to determine the scheduling plan of energy storage batteries, that is, the role of MG operators involved in energy trading; second, a master–slave game model (MSGM) is constructed between MG cluster operators and MG operators. The authors in [9] construct a multiobjective two-stage optimal allocation model for cloud energy storage, solve the model based on nondominated sorting genetic algorithms (GAs)-II, and reasonably allocate the investment, operation cost, and revenue of cloud energy storage system (ESS) based on the Shapley value method. The authors in [10] optimize the economic profit of each entity in a MG using charge–switch–storage–integration (CSSIS) models, a cooperative game based on Nash bargaining between MGs and CSSIS, and propose an alternating direction method of multipliers based on the distributed computation of ADMM to reach a Nash equilibrium.

At present, there has been more research on the large-scale entry of EVs into the grid and the impact of disordered charging on the reliability of power supply, etc. An EV acts as a controllable load or source of output when it is connected to the grid [11], and relying on V2G technology to provide flexible energy storage resources for the grid to cope with power fluctuations and uncertainties further enhances the stability of power systems [12, 13].

Therefore, this paper uses the V2G technology with a scheduling guidance strategy, with orderly charging and charging cost reduction as the main objectives. The authors in [14] focus on customer satisfaction and price incentives to schedule EV resources, which reduces the cost of electricity to the customer and the load peak-to-valley difference. The authors in [15] propose a noncooperative game-based charging scheduling method for distributed energy storage EVs that considers charging time, cost, and renewable energy utilization. The authors in [16] perform classification aggregation to establish a demand response (DR) model based on the differences of EV owners, with the optimization objective of maximizing the smart grid revenue. However, aggregation of EVs was not considered, which resulted in some losses. The authors in [17] focus on plug-in EVs (PEVs) and present the advantages and challenges of V2G technology for smart grid applications. The authors in [18] take the optimal charging and discharging scheduling of EVs as the research object, while considering all the relevant uncertainty factors, and adopt the Stackelberg game theory method to solve the game theory model and propose a new optimization algorithm based on Nash bargaining (NBOA). The authors in [19] utilize V2G to reduce the peak demand and load-shifting capacity of utilities as a backup system for renewable energy sources and use a model-free reinforcement learning (RL) approach to learn optimal sequential charging/discharging decisions. The authors in [20] design an efficient tidal current control method for EVs’ V2G and G2V that can achieve peak load reduction, load balancing, voltage control, and enhanced electrical system stability. The authors in [21] investigate V2G in commercial buildings and propose a two-phase optimization technique, day ahead optimization (DAO) and real-time optimization (RTO), to determine the charging and discharging schedules of EVs participating in the V2G scheme in office buildings.

Based on the above analysis, this paper first starts from the user (U) side and classifies EV Us by integrating the actual energy consumption of EV driving as well as driving habits. Second, the master–slave game theory is used to establish the master–slave game transaction model between MG and EV, and the research process is used to strengthen the autonomous choice behavior of EV Us’ demand with respect to objective conditions. Finally, with the MG cluster cooperative game, this paper proposes a two-layer hybrid game energy management model for multisource MG clusters based on new energy output and EV charging and discharging.

In view of the shortcomings mentioned in the above literature, the main contributions of this paper are as follows:

1.
Constructing a cooperative game transaction model within the upper-level MG cluster to reduce the MG’s dependence on the distribution grid and alleviate the power supply pressure on the grid through cooperative gaming.
2.
Constructing a master–slave game transaction model between the lower MG and EVs to realize mutual benefits through the game of minimum cost of MG and optimal benefit of EVs.
3.
By combining the upper and lower layers with the MG’s maximum gain as the optimization objective and using V2G technology for EV scheduling, the data show the importance of energy management.

In conclusion, this paper proposes a two-layer hybrid game energy management model of a MG cluster with MG as the transaction subject and EV as the follower and investigates the effective enhancement of the overall economic benefits of MG cluster through energy management and revenue allocation.

The structure of the remaining paper is outlined as follows. Section 2 establishes the traditional independent transaction model for MGs. Section 3 establishes the upper-layer MG cluster cooperative game transaction model containing EVs. Section 4 establishes the master–slave game transaction model for the lower-layer MG and EVs. Section 5 presents a case study based on wind power (WP) and load data. Section 6 presents the conclusions of this paper and the highlights of the proposed methodology.

2. Independent Trading Model of Wind and Storage MG Cluster With EVs

2.1. System Structure of Wind–Solar–Storage MG Cluster With EVs

The MG group energy management system (MGGEMS) uses distributed control of multiple MG energy management systems (MGEMSs), utilizing a two-way communication system and smart meters, to obtain the metering values of the MGs in real-time [22], enabling the system to interoperate information between MGs and ensuring smooth transactions within the MG group.

The structure of the WP storage MG cluster studied in this paper consists of several similar MGs in a certain area as shown in Figure 1. The top layer is the distribution grid layer, whose main role is to connect to the grid to supply power purchased by the MG cluster, so as to ensure the normal operation of the MG cluster and to support the function of surplus power online; the upper layer is the MG cluster layer, whose main role is to carry out energy planning and distribution through the energy management system; the lower layer is the MG layer, which mainly includes photovoltaic (PV) operator, PV DC/AC inverter, WP operator, bidirectional AC/DC/AC converter, ESS operator, storage bidirectional AC/DC converter, Us, V2G bidirectional charging units, and WP system operator, system (ESS) operator, bidirectional AC/DC converter for energy storage, EV aggregator (EVA), and control center. Each MG is connected to the distribution grid through the point of common coupling (PCC) [23], that is, the grid connection point. The power generated by new energy sources within the MG should be aimed at meeting its load demand as the highest priority. If there is a power demand, it can be exchanged for a certain amount of energy through the point of grid connection with the distribution grid.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Structure of energy management system for two-layer hybrid gaming wind–solar–storage microgrid cluster with electric vehicles.

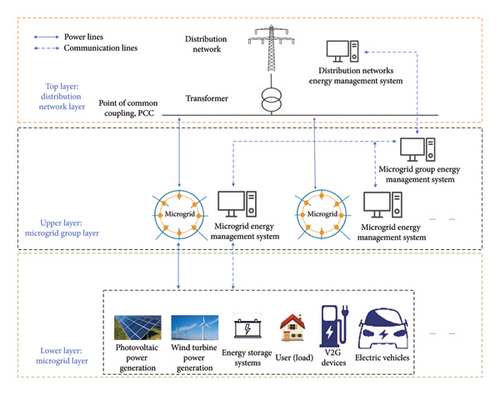
There are differences in the net power characteristics within the same MG cluster due to a variety of reasons such as different EV scheduling strategies, new energy output characteristics, and different load plans within each MG. For the MG cluster and the distribution grid, during the same time, the surplus power MG sells the excess power to the distribution grid at a certain price through the public connection point; the deficit MG needs to purchase power from the distribution grid through the transmission line to meet its load demand. Therefore, if the MG group adopts a cooperative game, the whole MG group is regarded as a coalition, and each MG becomes a participant in the game. Residual power MGs and power-deficit MGs abide by the agreed cooperative transaction agreement and use the residual power within the alliance, that is, the residual power MGs share the excess power through the energy management system, and the energy management system reasonably allocates the power to the power-deficit MGs to achieve the ultimate goal of MG group’s self-sufficiency.

2.2. MG Cluster’s Independent Transaction Modeling

In this paper, the 1-day power generation cycle of the EV–containing wind–solar–storage MG cluster is treated as the computational period T, which is divided into 24 time periods, and the time interval is 1 h. We define the generation power

and the load power

of MG i in time t. We define the net power

as the difference between the two.

()

A surplus power MG with a net power greater than 0 is referred to as a residual power MG, and a lack of power MG with a net power less than 0 is referred to as a deficit MG. The surplus power MG can transmit the excess power to the ESS or to the distribution grid through the PCC public connection point to get a certain amount of revenue from power sales. The power-deficit MG can get a certain amount of discharged power from the ESS, or it can purchase power from the distribution grid through the PCC public connection point and pay a certain amount of power purchase fee.

For the residual power MG, the revenue in time t consists of self-generation and self-consumption revenue and residual power on-grid revenue, and the expenditure mainly consists of new energy operation and maintenance costs, which can be expressed as follows:

()

In the formula, the distribution grid selling price is and the purchasing price is . Generally, the selling price is greater than the purchasing price at the same time, that is, . denotes the revenue of MG i in time t, and denotes the cost of MG i in time t. are the operation and maintenance costs of PV power generation, WP generation, ESSs, and EVs, respectively.

For the power shortage MG, the benefit in time t is the electricity expenditure saved by the MG self-generation and self-consumption, and the expenditure, in addition to the new energy operation and maintenance cost, also needs to be spent on the power purchase cost of purchasing electricity from the distribution grid, which can be expressed as follows:

()

Combining the above equations yields the benefit of MG i over the computational period T as

()

where p_i is denoted as the gain of MG i in the computation period T.

We define

as follows:

()

Then, the expenditure of MG i in the computational period T is

()

In summary, in this trading model, the distribution grid trades independently with each MG according to the above equation.

2.3. Objective Function and Model Constraints

The optimization objective of the wind–solar–storage MG cluster independent trading model is to maximize the revenue, and its objective function is as follows:

()

2.3.1. Restrictive Condition

1.
Power balance constraints:
()
where is the amount of electricity to be purchased by the MG in time t.
2.
ESS constraints:
()
where E_b is the ESS capacity; p_t,ch and p_t,dch are the charging and discharging power of the ESS, respectively; ε_ch and ε_dch indicate charge and discharge state 0–1 integer variable; are the maximum and minimum charging and discharging power per unit time of the ESS; S_soc is the state of charge of the ESS; S_socmin and S_socmax, respectively, are the maximum values of the state of charge; E_rate is the rated capacity of the ESS; and E_BAT is the initial energy storage capacity of the ESS.
3.
Wind and PV power output constraints:
()
where represent the upper and lower bounds of the PV and wind outputs at time t, respectively.
4.
Maximum wind and light abandonment constraints [24]:
()
where ∝, β are the maximum light abandonment rate and wind abandonment rate.

3. MG Group’s Cooperative Trading Model

3.1. Cooperative Game Theory

Game theory is mainly categorized into cooperative and noncooperative games, where cooperative games are the types of games in which multiple participants join together to form a coalition through a binding and enforceable agreement, and the two most important concepts are coalition and distribution [25]. Coalition indicates that the overall coalition payoff should be greater than the sum of the payoffs of the game participants. Allocation means that the participants’ payoffs in the case of alliance allocation should not be less than the payoffs of independent transactions.

For the EV–containing wind and storage MG cluster cooperative trading model, the energy management system carries out energy information sharing within the MG cluster, and the cooperative game can effectively prevent the surplus MGs from selling excess electricity to the distribution grid with lower sales revenue, and at the same time, avoid the power-deficit MGs from paying more power purchase price to the distribution grid (Figure 2).

For the cooperative trading model, the surplus and deficit MGs are the game participants, defined as the total coalition revenue. The total coalition revenue is available after the participants comply with the agreement and form a cooperative coalition and trade power purchase and sale with the overall and distribution grids as follows:

()

We define μ_t as follows:

()

3.2. Shapley-Valued Affiliate Revenue Sharing

After confirming the overall benefits of the cooperative trading model of wind and storage MG cluster, how to distribute the obtained benefits is the next problem to be studied and solved in this paper. Simple distribution by labor does not meet the practical requirements and may lead to the breakup of the alliance relationship, which lacks the significance of the research.

In this paper, we use the Shapley value for the allocation of model benefits, which has the advantage of apportioning the benefits according to the subject’s marginal contribution, and the participant receives a benefit equal to the average of his marginal contribution to the coalition in which he participates [26].

We define a set of coalitions N = {1, 2, …, n}, and for any subset S in the set, we define the function F(s) to be the total revenue of the cooperative coalition in the subset case by applying the Shapley value for the coalitional revenue allocation as

()

where F is the characteristic function and S1 and S2 are the two arbitrary disjoint subsets within the MG cluster, satisfying the premise that all individuals in this set can be assigned using Shapley values.

For this paper, the benefit of the cooperative trading model of the wind and storage MG cluster containing EV is not less than the sum of the benefits of the respective independent trading models. It thus satisfies equation (15). Considering {N, F} as the cooperative response of n MGs, the benefit distribution formula [27] for any MG i is

()

where V_i denotes the allocated revenue of MG i, W(|S|) denotes the weighting factor, and F(s/i) denotes the remaining MG cooperative alliance revenue after removing MG i.

4. MG and EV MSGMs

In this paper, the research object is private EVs, and the charging piles within the MG area are managed by the EVA. According to the information on the EV accessing and leaving the charging piles, the time of the charging piles, and the battery parameters, they are fitted and classified to be reported to the energy management system of the MG and ultimately obtain the intelligent scheduling strategy for the coordinated scheduling of the EVs.

4.1. MG Leaders’ Model

In the MSGM between MG and EV, MG as the leader sets the EV power purchase price h_ch, the discharge subsidy h_dch, and the scheduling based on the net power at time i, and the scheduling quantity is obtained to achieve the optimal power allocation of the internally controllable units with the following cost function:

()

where T is the number of time slots in the scheduling cycle;

are the cost of purchasing and selling electricity from MG to the grid, the cost of WP generation, the cost of PV power generation, and the cost of operation and maintenance of the energy storage in the time slot of t, respectively; and

and

are the charging and discharging power of the EV storage battery. In order to prevent MG from maliciously raising the EV power purchase price and maliciously suppressing the power sales price, this paper constrains, a and b, are the tariff protection coefficients.

4.2. EV Follower Model

According to the tariff strategy set by the leader, each EV owner chooses whether or not to accept EVA’s scheduling strategy to minimize its own cost, with the following cost function:

()

The constraints are similar to those of ESSs.

4.3. MSGM

MG and EV as independent but unequal interests constitute a MSGM. In this paper, it is assumed that EV purchases power at a certain price and discharges a certain subsidy in period t, that is, the set of leader’s strategy is (f_ev, h_ch, h_dch), and the follower EV responds by adjusting the charging and discharging strategy () based on the minimized cost, and MG then optimizes the original strategy according to the response.

According to the definition of Nash equilibrium, there exists a Nash equilibrium solution to be satisfied for the MSGM in this paper.

()

where

are all optimal policies under Nash equilibrium.

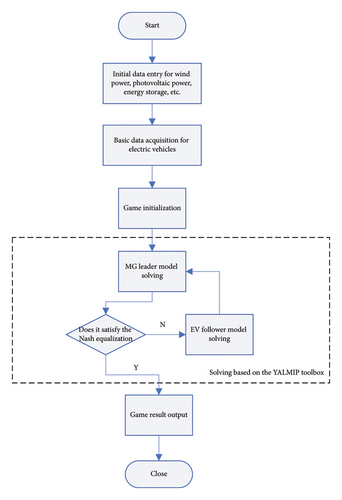
The MSGM solution flow is shown in Figure 3.

5. Algorithm Analysis

In this paper, a MG cluster consisting of three neighboring EV–containing wind and storage MGs under the same region is taken as the research object to simulate and analyze the internal energy management of the MG cluster. It involves energy management, single-objective optimization problems, and hybrid game problems, which are all solved under the MATLAB2021B compilation environment. The prediction curves of intraday wind and PV output and load for each MG in this paper are shown in Figure 4.

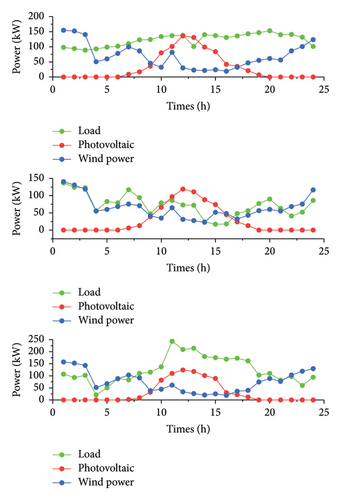
From Figure 4, it can be seen that each MG cannot meet its load requirements in the case of single WP generation or PV power generation and cannot realize self-sufficiency. PV power generation is 9:00–17:00 out of power, and with WP generation, can be self-sufficient most of the time. Therefore, this paper takes the wind and storage MG cluster as the research scenario to build the simulation model.

5.1. Model Parameters

In order to analyze the effectiveness of the cooperative game energy management model of wind and storage MG cluster containing EV proposed in this paper, it is first necessary to obtain the model parameters of each MG and distribution grid under the independent trading mode.

In the model, the MG time-of-day residual power feed-in price and the distribution grid time-of-day electricity selling price are shown in Table 1. The parameters of each MG model, such as the upper and lower limits of PV generating units, wind generating units, ESSs, storage charging and discharging efficiencies, and the operation and maintenance costs per unit time of each generating unit and ESS [28], are shown in Table 2.

Table 1. Time-sharing tariff.

Type of transaction	Electricity price (RMB/kW·h)	Time
Tariffs for electricity sales	Peak value: 1.189	8:00–11:00; 13:00–16:00; 18:00–22:00
	Par value: 0.738	7:00–8:00 11:00–13:00 16:00–18:00
	Valley value: 0.423	0:00–7:00; 22:00–24:00

Feed-in tariffs	0.352	0:00–24:00

Table 2. Parameters of each MG model.

Parameters	MG
Photovoltaic capacity (kW)	200
Wind power capacity (kW)	200
Upper and lower energy storage limits (kW)	100,20
Total EV battery capacity (kW)	200
Charge and discharge efficiency (100%)	90
Initial energy storage (kWh)	80
PV O&M costs (¥/kWh)	0.0096
WT O&M costs (¥/kWh)	0.0296
Energy storage O&M costs (¥/kWh)	0.02
EV O&M costs (¥/kWh)	0.1

5.2. Simulation Results’ Analysis

5.2.1. Global Optimization of GA Transaction Models

For the double-layer MG cluster energy management system proposed in this paper, the traditional approach is to view the multilayer system as a whole and use a global optimization algorithm to solve the problem, so this paper uses the global optimization GA (GO–GA) as a control group for the control experiments. Its first application to power system research can be traced back to the 1990s, and after years of development, it has the ability to global search and avoids falling into the local optimal solution; its ability to adapt to complex systems and adapt to and find the global optimal solution in complex systems is especially suitable for solving large-scale, complex optimization problems in the power system. In this paper, an independent trading model, a GO–GA, and a two-layer hybrid game trading model are built for experimental analysis in two different cases under the same system.

5.2.2. Two-Level Hybrid Game Transaction Models and Controlled Experiments

The total simulation time is set to 24 h. This section simulates the independent trading mode and the two-layer hybrid game trading mode of the wind–solar–storage MG cluster with EVs. To make the graphs more beautiful and easier to observe, this paper introduces the spontaneous gain in equation (2). Finally, the gain comparison of each MG under the two modes is obtained through the optimization algorithm, as shown in Figures 5, 6, and 7.

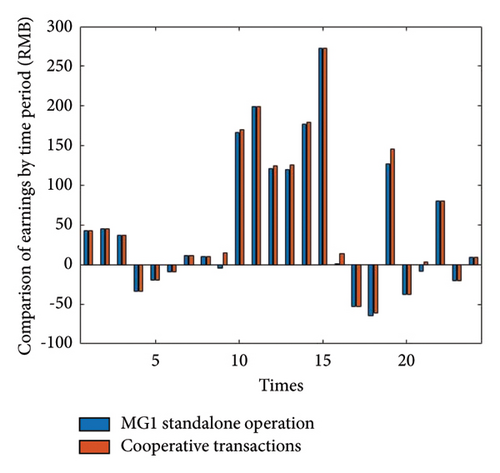
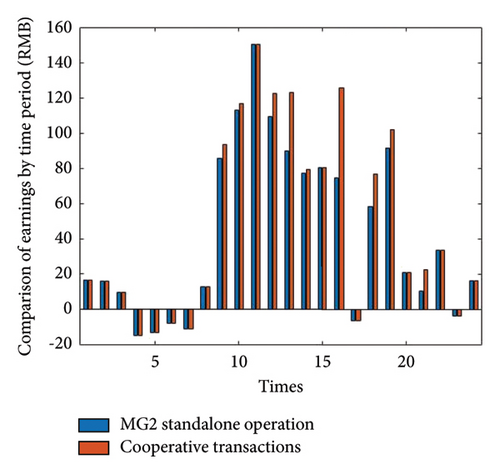
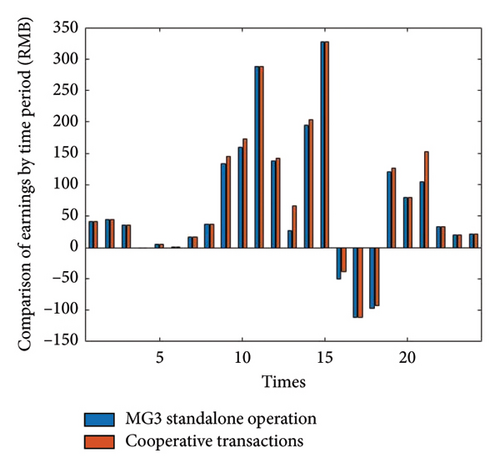
As can be seen from Figures 5, 6, and 7, in the 23:00–8:00 which is the valley tariff region shown in Table 1, both PV and EV V2G are not discharged, and they are discharged by the distribution grid and WP, so the difference between the two-layer hybrid game trading model and the independent trading model gains is small in this time; in the 9:00–22:00 time period, PV starts to discharge, and EVs receive MG energy for the peak tariff region shown in Table 1, management system scheduling, and on-demand scheduling for V2G discharging work; it can be seen that the two-layer hybrid game trading model grows more gains than the standalone trading model in this time. This paper also increases the GO–GA to compare with the method proposed in this paper, and the specific data are shown in Table 3.

Table 3. Comparative results of MG gains.

Microgrid benefits	Microgrid groups	MG1	MG2	MG3
Standalone transaction models (excluding EV)	3086.2	976.0	1120.2	990.0
Global optimization of genetic algorithmic transaction models (excluding EV)	3406.2	1021.1	1278.3	1106.8
Two-level hybrid game transaction models (excluding EV)	3941.6	1076.3	1563.1	1302.2

Standalone transaction models (including EV)	3756.5	1168.1	1011.9	1565.5
Global optimization of genetic algorithmic transaction models (including EV)	3843.6	1204.9	1049.4	1589.3
Two-level hybrid game transaction models (including EV)	4128.6	1249.8	1163.4	1715.4

As seen from Table 3, this paper validates the feasibility and merits of the trading model in multiple scenarios. In the case of excluding EV V2G technology, the GO–GA trading model increases the total return by 10.37% compared to the independent trading model, while the two-layer hybrid game trading model increases by 27.71%; in the case of including EV V2G technology, the GO–GA increases the total return by 2.32% compared to the independent trading model, while the two-layer hybrid game trading model increased by 9.91%.

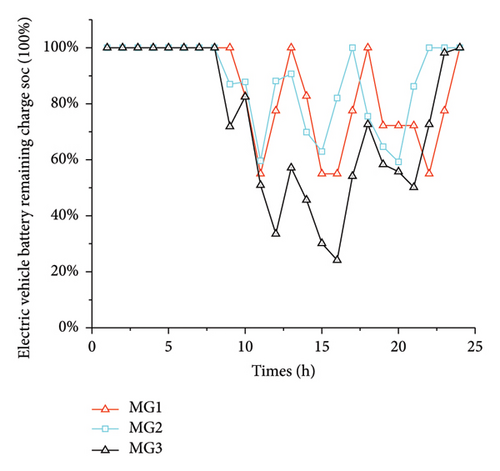
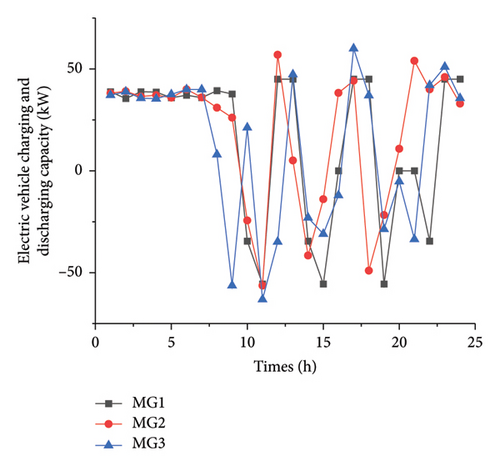
As can be seen from Figures 8 and 9, the EV batteries are still in a charging state although the soc is always 100% in the 0–8 time period; most of the private cars going to work stop charging in the 8–9 time period; they receive EVA scheduling in the 9–22 time period and most of them start charging and end the day’s scheduling in the 22–24 time period.

As seen in Tables 3 and 4, although the introduction of EVs reduced the growth rate of the overall MG cluster revenues, the growth in revenues for EV Us resulted in a mutually beneficial outcome. Under the GO–GA transaction model, the total revenue of EVs grows by 17.83% compared to the standalone transaction model, and under the two-level hybrid game transaction model, the total revenue of EVs grows by 33.58%, and the increased revenue is the Shapley value distribution revenue.

Table 4. Comparative results of EV benefits.

Electric vehicle benefits	Standalone transaction models (including EV)	Global optimization of genetic algorithmic transaction models (including EV)	Two-level hybrid game transaction models (including EV)
Microgrid groups	−1137.9	−935.0	−755.7
MG1	−354.9	−288.9	−219.9
MG2	−447.0	−402.8	−343.6
MG3	−336.0	−243.3	−192.2

5.2.3. Shapley Value Benefit Analysis of the Two-Level Hybrid Game Transaction Models

The benefits of each MG can be calculated using the Shapley value method under the two-layer hybrid game transaction model as shown in Tables 5, 6, and 7.

Table 5. Distribution of MG1’s earnings.

S	MG1	MG1 MG2	MG1 MG3	MG1 MG2 MG3
F (S)	1168.08	2339.96	2890.30	4128.57
F (S − {i})	0	1011.86	1565.53	2873.65
F (S) − F (S − {i})	1168.08	1328.1	1324.77	1254.92
\|S\|	1	2	2	3
W (\|S\|)	1/3	1/6	1/6	1/3
W (\|S\|) [F (S) − F (S-{i})]	389.36	221.35	220.80	418.30

Table 6. Distribution of MG2’s earnings.

S	MG2	MG1 MG2	MG2 MG3	MG1 MG2 MG3
F (S)	1011.86	2339.96	2873.65	4128.57
F (S − {i})	0	1168.08	1565.52	2890.30
F (S) − F (S − {i})	1011.86	1171.88	1308.13	1238.3
\|S\|	1	2	2	3
W (\|S\|)	1/3	1/6	1/6	1/3
W (\|S\|) [F (S) − F (S-{i})]	337.29	195.31	218.02	412.77

Table 7. Distribution of MG3’s earnings.

S	MG3	MG1 MG3	MG2 MG3	MG1 MG2 MG3
F (S)	1565.52	2890.30	2873.65	4128.57
F (S − {i})	0	1167.08	1011.86	2339.96
F (S) − F (S − {i})	1565.52	1723.22	1861.79	1788.61
\|S\|	1	2	2	3
W (\|S\|)	1/3	1/6	1/6	1/3
W (\|S\|) [F (S) − F (S − {i})]	521.84	287.20	310.30	596.20

From Tables 5, 6, and 7, it can be seen that each MG should be allocated to get the benefits of 1249.81, 1163.3, and 1715.38, which are shown in the following formulas:

()

It can be shown that the sum of the respective gains of the three MGs is equal to the total gain from the cooperative trading of the MG cluster, that is, it satisfies

()

In summary, it can be seen that the cooperative trading model of wind and storage MG cluster containing EV in cooperative game mode can effectively improve the economic returns of each MG through the Shapley value assignment.

6. Summary

In this paper, for the new power system energy management under today’s status quo, the cooperative trading model of a multisource MG cluster containing EV with a two-layer hybrid game is proposed with energy sharing as the idea and the following conclusions are drawn:

1.
This paper introduces the cooperative game into a new type of power system, taking the MG group as the main carrier, and through energy management and reasonable use of “cooperative surplus,” it achieves the effect of reducing the rate of abandoned wind and light and improving the overall economic efficiency of the MG group.
2.
In this paper, by constructing a cooperative trading model for the upper MG group and a master–slave game trading model for the lower MGs and EVs, not only can the overall total revenue of the alliance grow by 9.9% but also promotes the EV Us to grow their revenue by 33.6%, compared to the independent trading model.
3.
In this paper, we experimentally conclude that because of the large number of EVs entering the grid, the revenue of the MG group decreases by 17% compared to the growth of the MG group without EVs, but sacrificing part of the growth revenue makes the total revenue of EV Us increase by 33.6%, and the experiments have demonstrated that through energy management, it is possible to achieve joint growth of benefits for multiple participants.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

All authors have contributed equally.

Funding

The research is financially supported by the Key Projects of Natural Science Research in Anhui Universities (Grant no. KJ2021A0471).

Acknowledgments

The research is financially supported by the Key Projects of Natural Science Research in Anhui Universities (Grant no. KJ2021A0471).

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Seyed Beheshti Fini S. A., Shariatmadar S. M., and Amir V., Smart Frequency Control of a Multicarrier Microgrid in the Presence of V2G Electric Vehicles, International Transactions on Electrical Energy Systems. (2023) 2023, 1–14, https://doi.org/10.1155/2023/6205326.
10.1155/2023/6205326
Google Scholar
2 Zhang Z. and Kang C., Challenges and Prospects for Constructing the New-type Power System Towards a Carbon Neutrality Future, Zhongguo Dianji Gongcheng Xuebao/Proceedings of the Chinese Society of Electrical Engineering. (2022) 42, no. 8, 2806–2818.
Google Scholar
3 Chen C. Y., Miao S., and Yao F., Multi-Microgrid-Distribution Network Hierarchical Cooperative Scheduling Strategy Based on Multi-Agent Algorithm, Power system automation. (2023) 47, no. 10, 57–65.
Google Scholar
4 Li X., Yang M., Zhang R., Jiang T., and Fu L., Multi-Agent Stackelberg Game Trading Strategy of Electricity-Gas Multi-Energy Market Considering Participation of Multi-Energy Microgrids, Dianli Zidonghua Shebei/Electric Power Automation Equipment. (2023) 43, no. 5, 145–153.
CAS Google Scholar
5 Chen L., Pan Z., Yu T., and Wang K., Real-Time Optimal Dispatch for Large-Scale Electric Vehicles Based on Dynamic Non-Cooperative Game Theory, Dianli Xitong Zidonghua/Automation of Electric Power Systems. (2019) 43, no. 24, 32–40 and 66.
Google Scholar
6 Huang D., Lü J., Shi S., Li Y., Fu W., and Wang X., Optimal Operation of Island Microgrid Clusters Considering Demand Response, Dianli Xitong Baohu Yu Kongzhi/Power System Protection and Control. (2024) 52, no. 9, 88–98.
Google Scholar
7 Fu Y., Xing X., Li Z., Zhang Z., and Li H., Multi-Stage Robust Optimization Planning of Microgrid Clusters Based on Master-Slave Game, Dianli Zidonghua Shebei/Electric Power Automation Equipment. (2022) 42, no. 4, 1–8.
Google Scholar
8 Rui T., Li G., Hu C., Wang Q., Xu B., and Zhang J., Stackelberg Game Optimization Method for Microgrid Cluster Considering Electricity Price Mechanism, Zhongguo Dianji Gongcheng Xuebao/Proceedings of the Chinese Society of Electrical Engineering. (2020) 40, no. 8, 2535–2545.
Google Scholar
9 Zhang S., Li Y., Liu W., Sun S., Yu P., and Zhang N., Economic, Low-Carbon and Reliable Multi-Objective Optimal Configuration Method of Cloud Energy Storage for Microgrid Clusters, Dianli Xitong Zidonghua/Automation of Electric Power Systems. (2024) 48, no. 1, 21–30.
Google Scholar
10 Cheng S., Zuo X., Wei Z., Ni K., and Wang C., Nash Bargaining-Based Cooperative Game for Distributed Economic Scheduling of Microgrid with Charging-Swapping-Storage Integrated Station, International Journal of Energy Research. (2022) 46, no. 15, 23927–23938, https://doi.org/10.1002/er.8689.
10.1002/er.8689
Web of Science® Google Scholar
11 Femy P. H. and Jayakumar J., A Comprehensive Review on Electric Vehicles: Charging and Control Techniques, Electric Vehicle-Grid Integration, Energy Harvesting and Systems. (2023) 10, no. 1, 1–14, https://doi.org/10.1515/ehs-2021-0083.
10.1515/ehs-2021-0083
Google Scholar
12 Shang Y., Shang Y., Yu H., Shao Z., and Jian L., Achieving Efficient and Adaptable Dispatching for Vehicle-To-Grid Using Distributed Edge Computing and Attention-Based LSTM, IEEE Transactions on Industrial Informatics. (2022) 18, no. 10, 6915–6926, https://doi.org/10.1109/tii.2021.3139361.
10.1109/tii.2021.3139361
Web of Science® Google Scholar
13 Zhang G., Liu H., Xie T., Li H., Zhang K., and Wang R., Research on the Dispatching of Electric Vehicles Participating in Vehicle-To-Grid Interaction: Considering Grid Stability and User Benefits, Energies. (2024) 17, no. 4, https://doi.org/10.3390/en17040812.
10.3390/en17040812
Web of Science® Google Scholar
14 Liu Y., Lin S., Shen Y.i et al., A Multi-Timescale Optimal Scheduling Model for Microgrids Taking into Account Electric Vehicle Participation in Multivariate Demand Response, Electric Power Construction. (2023) 44, no. 10, 51–62.7.
Google Scholar
15 Xu Y., Yang F., Li W., and Huang X., A Game-Theoretic Approach for Optimizing Joint Energy Trading and Electric Vehicle Charging Considering V2G Prices, IEEE Transactions on Power Systems. (2021) 36, no. 2, 1232–1245.
Google Scholar
16 Zhang X., Liao C., Chen X., Deng K., Chen B., and Gong Y., Analysis of Smart Grid Optimal Scheduling Considering the Demand Response of Different EV Owners, International Transactions on Electrical Energy Systems. (2023) 2023, 1–15, https://doi.org/10.1155/2023/6670897.
10.1155/2023/6670897
CAS Web of Science® Google Scholar
17 Viswanath B., Khatod D. K., and Padhy N. P., Optimal Vehicle-To-Grid (V2G) Scheduling of Plug-In Electric Vehicles (PEVs) for Grid Peak Demand Management: A State-Of-The-Art Review, 10th IEEE International Conference on Power Electronics, Drives and Energy Systems, PEDES 2022, 2022.
Google Scholar
18 Saha M., Thakur S. S., and Bhattacharya A., Optimal Scheduling of Electric Vehicles: Leveraging Grid-To-Vehicle (G2V) and Vehicle-To-Grid (V2G) Prices: A Game-Theoretic Approach, 2023 IEEE 3rd International Conference on Sustainable Energy and Future Electric Transportation, SeFet 2023, 2023.
Google Scholar
19 Maeng J., Min D., and Kang Y., Intelligent Charging and Discharging of Electric Vehicles in a Vehicle-To-Grid System Using a Reinforcement Learning-Based Approach, Sustainable Energy, Grids and Networks. (2023) 36, https://doi.org/10.1016/j.segan.2023.101224.
10.1016/j.segan.2023.101224
Web of Science® Google Scholar
20 Ashok Kumar B., Shanmukasri G., Senthilrani S., and Satheesh Kumar S., Bidirectional Power Flow Grid-To-Vehicle & Vehicle-To-Grid (G2V&V2G) in Electric Vehicle, 2023 International Conference on Energy, Materials and Communication Engineering, ICEMCE 2023, 2023.
Google Scholar
21 Chai Y. T., Che H. S., Tan C., Tan W.-N., Yip S.-C., and Gan M.-T., A Two-Stage Optimization Method for Vehicle to Grid Coordination Considering Building and Electric Vehicle User Expectations, International Journal of Electrical Power & Energy Systems. (2023) 148, https://doi.org/10.1016/j.ijepes.2023.108984.
10.1016/j.ijepes.2023.108984
Web of Science® Google Scholar
22 Song K., Dong D., and Li C., Outage Performance Analysis of Multiple Reconfigurable Intelligent Surfaces Assisted Two-Way Communication System, Dianzi Yu Xinxi Xuebao/Journal of Electronics and Information Technology. (2022) 44, no. 7, 2342–2348.
Web of Science® Google Scholar
23 Bullich-Massagué E., Aragüés-Peñalba M., Prieto-Araujo E., Sumper A., and Caire R., Optimal Feeder Flow Control for Grid Connected Microgrids, International Journal of Electrical Power & Energy Systems. (2019) 112, 144–155, https://doi.org/10.1016/j.ijepes.2019.04.047, 2-s2.0-85064890029.
10.1016/j.ijepes.2019.04.047
Web of Science® Google Scholar
24 Yang X., Xu Y., Yang N., Wen B., Zhao K., and Zhang Y., Research on the Reliability and Capacity Allocation of Wind Power-Solar Power-Pumped Storage Hybrid Power System, 2018 China International Conference on Electricity Distribution (CICED). (2018) 2071–2076, https://doi.org/10.1109/ciced.2018.8592027, 2-s2.0-85063141517.
10.1109/CICED.2018.8592027
Google Scholar
25 Fan T., Wang H., Wang W., Li X., and Yan S., Coordinated Optimization Scheduling of Microgrid and Distribution Network Based on Cooperative Game Considering Active/Passive Demand Response, Dianwang Jishu/Power System Technology. (2022) 46, no. 2, 453–462.
Google Scholar
26 Tian X., Chen L., Li X., and Yuan W., Optimal Scheduling for Energy Storage Sharing Among Communities With Photovoltaic Resource Based on Stackelberg Game and Improved Shapley Value, Dianwang Jishu/Power System Technology. (2023) 47, no. 6, 2252–2261.
Google Scholar
27 Wang T., Han J., Shao H. et al., Operation Optimization Method of Rural Microgrid Cluster and Distribution Network Based on Cooperative Game, Journal of Hebei University (Natural Science Edition). (2020) 40, no. 4, 441–448.
Google Scholar
28 Pan X., Yang F., Ma P., Xing Y., Zhang J., and Cao L., A Game-Theoretic Approach of Optimized Operation of AC/DC Hybrid Microgrid Clusters, Energies. (2022) 15, no. 15, https://doi.org/10.3390/en15155537.
10.3390/en15155537
Web of Science® Google Scholar

All articles

Energy Management of V2G-Containing Multiource Microgrid Cluster Based on Two-Layer Hybrid Game

Abstract

1. Introduction

2. Independent Trading Model of Wind and Storage MG Cluster With EVs

2.1. System Structure of Wind–Solar–Storage MG Cluster With EVs

2.2. MG Cluster’s Independent Transaction Modeling